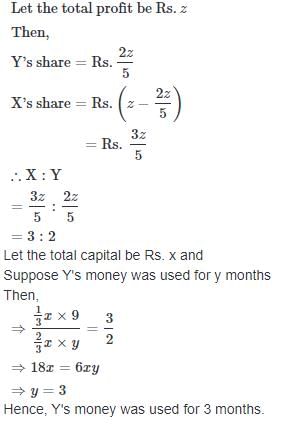All Exams >
CUET Commerce >
General Test Preparation for CUET UG >
All Questions
All questions of Partnership for CUET Commerce Exam
P, Q, R enter into a partnership. P initially invests 25 lakh & adds another 10 lakhs after one year. Q initially invests 35 lakh & withdrawal 10 lakh after 2 years and R invests Rs 30 Lakhs . In what ratio should the profit be divided at the end of 3 years?- a)18 : 19 : 19
- b)18 : 18 : 19
- c)19 : 19 : 18
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
P, Q, R enter into a partnership. P initially invests 25 lakh & adds another 10 lakhs after one year. Q initially invests 35 lakh & withdrawal 10 lakh after 2 years and R invests Rs 30 Lakhs . In what ratio should the profit be divided at the end of 3 years?
a)
18 : 19 : 19
b)
18 : 18 : 19
c)
19 : 19 : 18
d)
None of these

|
Om Banerjee answered |
P : Q : R
= (25 × 1 + 35 × 2) : (35 × 2 : 25 × 1) : (30 × 3)
= 95 : 95 : 90
= 19 : 19: 18
= (25 × 1 + 35 × 2) : (35 × 2 : 25 × 1) : (30 × 3)
= 95 : 95 : 90
= 19 : 19: 18
Two brother invested Rs. 50000 and Rs. 70000 respectively in a business and agreed that 70% of the profits should be divided equally between them and the remaining profit in the ratio of investment. If one brothers gets Rs. 90 more than the other. Find the total profit made in the business ?- a)Rs. 1200
- b)Rs. 1400
- c)Rs. 1600
- d)Rs. 1800
Correct answer is option 'D'. Can you explain this answer?
Two brother invested Rs. 50000 and Rs. 70000 respectively in a business and agreed that 70% of the profits should be divided equally between them and the remaining profit in the ratio of investment. If one brothers gets Rs. 90 more than the other. Find the total profit made in the business ?
a)
Rs. 1200
b)
Rs. 1400
c)
Rs. 1600
d)
Rs. 1800

|
Aashna Roy answered |

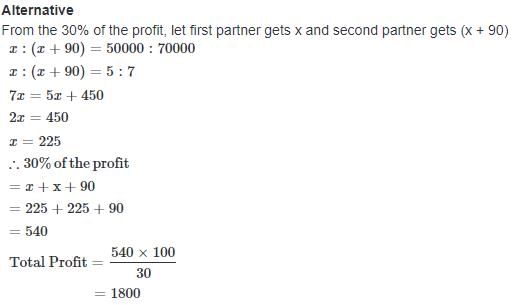
Two partners invest Rs. 125000 and Rs. 85000 respectively in a business and agree that 60% of the profit should be divided equally between them and the remaining profit is to be divided into ratio of their capitals. If one partner gets Rs. 300 more than the other. Find the total profit made in the business ?- a)Rs. 3739.50
- b)Rs. 3937.50
- c)Rs. 3749.50
- d)Rs. 3947.50
Correct answer is option 'B'. Can you explain this answer?
Two partners invest Rs. 125000 and Rs. 85000 respectively in a business and agree that 60% of the profit should be divided equally between them and the remaining profit is to be divided into ratio of their capitals. If one partner gets Rs. 300 more than the other. Find the total profit made in the business ?
a)
Rs. 3739.50
b)
Rs. 3937.50
c)
Rs. 3749.50
d)
Rs. 3947.50

|
Juhi Yadav answered |

A began a business with Rs. 85000, he was joined afterwards by B with Rs. 42500. For how much period does B join, if the profits at the end of the year are divided in the ratio of 3 : 1 ?- a)4 months
- b)5 months
- c)6 months
- d)8 months
Correct answer is option 'D'. Can you explain this answer?
A began a business with Rs. 85000, he was joined afterwards by B with Rs. 42500. For how much period does B join, if the profits at the end of the year are divided in the ratio of 3 : 1 ?
a)
4 months
b)
5 months
c)
6 months
d)
8 months

|
Ritika Choudhary answered |
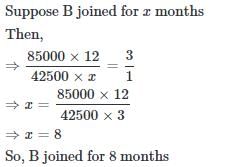
A, B and C enter into a partnership. A initially invests Rs. 25 lakhs and adds another Rs. 10 lakhs after one year. B initially invests Rs. 35 lakhs and withdraws Rs. 10 lakhs after 2 years and C invests Rs. 30 lakhs. In what ratio should the profits be divided at the end of 3 years ?- a)10 : 10 : 9
- b)20 : 20 :19
- c)20 : 19 :18
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
A, B and C enter into a partnership. A initially invests Rs. 25 lakhs and adds another Rs. 10 lakhs after one year. B initially invests Rs. 35 lakhs and withdraws Rs. 10 lakhs after 2 years and C invests Rs. 30 lakhs. In what ratio should the profits be divided at the end of 3 years ?
a)
10 : 10 : 9
b)
20 : 20 :19
c)
20 : 19 :18
d)
None of these
|
|
Aarav Sharma answered |
Given, A initially invests Rs. 25 lakhs and adds another Rs. 10 lakhs after one year, B initially invests Rs. 35 lakhs and withdraws Rs. 10 lakhs after 2 years and C invests Rs. 30 lakhs.
Let's calculate the investment of A over 3 years.
For the first year, A invests Rs. 25 lakhs and for the next two years, he invests Rs. 35 lakhs.
So, the total investment of A = 25 + 35 + 35 = 95 lakhs.
Similarly, let's calculate the investment of B over 3 years.
For the first two years, B invests Rs. 35 lakhs and for the last year, his investment is Rs. 25 lakhs.
So, the total investment of B = 35 + 35 + 25 = 95 lakhs.
The investment of C over 3 years is Rs. 30 lakhs.
Therefore, the ratio of their investments is 95:95:30, which can be simplified to 19:19:6.
Now, let's calculate the profits for 3 years.
Let P be the total profit for 3 years.
For the first year, A gets 1/3 of the profit, B gets 1/3 of the profit and C gets 1/3 of the profit.
For the next two years, A gets 2/5 of the profit, B gets 2/5 of the profit and C gets 1/5 of the profit.
Therefore, the share of profit for A = (1/3)P + (2/5)P = (11/15)P
The share of profit for B = (1/3)P + (2/5)P = (11/15)P
The share of profit for C = (1/3)P + (1/5)P = (8/15)P
Therefore, the ratio of their profits is (11/15):(11/15):(8/15), which can be simplified to 11:11:8.
Hence, option D, None of these, is the correct answer.
Let's calculate the investment of A over 3 years.
For the first year, A invests Rs. 25 lakhs and for the next two years, he invests Rs. 35 lakhs.
So, the total investment of A = 25 + 35 + 35 = 95 lakhs.
Similarly, let's calculate the investment of B over 3 years.
For the first two years, B invests Rs. 35 lakhs and for the last year, his investment is Rs. 25 lakhs.
So, the total investment of B = 35 + 35 + 25 = 95 lakhs.
The investment of C over 3 years is Rs. 30 lakhs.
Therefore, the ratio of their investments is 95:95:30, which can be simplified to 19:19:6.
Now, let's calculate the profits for 3 years.
Let P be the total profit for 3 years.
For the first year, A gets 1/3 of the profit, B gets 1/3 of the profit and C gets 1/3 of the profit.
For the next two years, A gets 2/5 of the profit, B gets 2/5 of the profit and C gets 1/5 of the profit.
Therefore, the share of profit for A = (1/3)P + (2/5)P = (11/15)P
The share of profit for B = (1/3)P + (2/5)P = (11/15)P
The share of profit for C = (1/3)P + (1/5)P = (8/15)P
Therefore, the ratio of their profits is (11/15):(11/15):(8/15), which can be simplified to 11:11:8.
Hence, option D, None of these, is the correct answer.
Aman started a business investing Rs. 70000. Rakhi joined him after six months with an amount of Rs. 105000 and Sagar joined them with Rs. 1.4 lakhs after another six months. The amount of profit earned should be distributed in what ratio among Aman, Rakhi and Sagar respectively, 3 years after Aman started the business ?- a)7 : 6 : 10
- b)12 : 15 : 16
- c)42 : 45 56
- d)Cannot be determined
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Aman started a business investing Rs. 70000. Rakhi joined him after six months with an amount of Rs. 105000 and Sagar joined them with Rs. 1.4 lakhs after another six months. The amount of profit earned should be distributed in what ratio among Aman, Rakhi and Sagar respectively, 3 years after Aman started the business ?
a)
7 : 6 : 10
b)
12 : 15 : 16
c)
42 : 45 56
d)
Cannot be determined
e)
None of these
|
|
Aarav Sharma answered |
Let's calculate the profit distribution step by step:
Step 1: Calculate the total investment
- Aman invested Rs. 70,000 for the entire 3-year period.
- Rakhi invested Rs. 1,05,000 for the last 2.5 years.
- Sagar invested Rs. 1,40,000 for the last 1.5 years.
To calculate the total investment, we need to consider the time period for each investment.
- Aman's investment is for the entire 3 years.
- Rakhi's investment is for the last 2.5 years.
- Sagar's investment is for the last 1.5 years.
So, the total investment will be:
Aman's investment = Rs. 70,000 × 3 = Rs. 210,000
Rakhi's investment = Rs. 1,05,000 × 2.5 = Rs. 262,500
Sagar's investment = Rs. 1,40,000 × 1.5 = Rs. 210,000
Total investment = Aman's investment + Rakhi's investment + Sagar's investment
= Rs. 210,000 + Rs. 262,500 + Rs. 210,000
= Rs. 682,500
Step 2: Calculate the profit distribution ratio
The profit distribution ratio is based on the ratio of investments made by Aman, Rakhi, and Sagar.
Aman's share = Aman's investment / Total investment
= Rs. 210,000 / Rs. 682,500
= 7/ 22
Rakhi's share = Rakhi's investment / Total investment
= Rs. 262,500 / Rs. 682,500
= 15 / 44
Sagar's share = Sagar's investment / Total investment
= Rs. 210,000 / Rs. 682,500
= 16 / 45
Therefore, the profit distribution ratio among Aman, Rakhi, and Sagar is 7:15:16.
So, the correct answer is option B) 12:15:16.
Step 1: Calculate the total investment
- Aman invested Rs. 70,000 for the entire 3-year period.
- Rakhi invested Rs. 1,05,000 for the last 2.5 years.
- Sagar invested Rs. 1,40,000 for the last 1.5 years.
To calculate the total investment, we need to consider the time period for each investment.
- Aman's investment is for the entire 3 years.
- Rakhi's investment is for the last 2.5 years.
- Sagar's investment is for the last 1.5 years.
So, the total investment will be:
Aman's investment = Rs. 70,000 × 3 = Rs. 210,000
Rakhi's investment = Rs. 1,05,000 × 2.5 = Rs. 262,500
Sagar's investment = Rs. 1,40,000 × 1.5 = Rs. 210,000
Total investment = Aman's investment + Rakhi's investment + Sagar's investment
= Rs. 210,000 + Rs. 262,500 + Rs. 210,000
= Rs. 682,500
Step 2: Calculate the profit distribution ratio
The profit distribution ratio is based on the ratio of investments made by Aman, Rakhi, and Sagar.
Aman's share = Aman's investment / Total investment
= Rs. 210,000 / Rs. 682,500
= 7/ 22
Rakhi's share = Rakhi's investment / Total investment
= Rs. 262,500 / Rs. 682,500
= 15 / 44
Sagar's share = Sagar's investment / Total investment
= Rs. 210,000 / Rs. 682,500
= 16 / 45
Therefore, the profit distribution ratio among Aman, Rakhi, and Sagar is 7:15:16.
So, the correct answer is option B) 12:15:16.
A and B started a partnership business investing some amount in the ratio of 3 : 5. C joined then after six months with an amount equal to that of B. In what proportion should the profit at the end of one year be distributed among A, B and C?- a)3 : 5 : 2
- b)3 : 5 : 5
- c)6 : 10 : 5
- d)Data inadequate
Correct answer is option 'C'. Can you explain this answer?
A and B started a partnership business investing some amount in the ratio of 3 : 5. C joined then after six months with an amount equal to that of B. In what proportion should the profit at the end of one year be distributed among A, B and C?
a)
3 : 5 : 2
b)
3 : 5 : 5
c)
6 : 10 : 5
d)
Data inadequate

|
Gayatri Ahuja answered |
Let initial investment of A is 3x and B is 5x, then C investment is also 5x, but most important to note in this question is the time duration of investment
Like, A invested for 12 months, B invested for 12 months and C invested for 6 months.
A : B : C = (3x x 12) : (5x x 12) : (5x x 6)
= 36 : 60 : 30
= 6 : 10 : 5.
Like, A invested for 12 months, B invested for 12 months and C invested for 6 months.
A : B : C = (3x x 12) : (5x x 12) : (5x x 6)
= 36 : 60 : 30
= 6 : 10 : 5.
Aman started a business investing Rs. 70,000. Rakhi joined him after six months with an amount of Rs. 1,05,000 and Sagar joined them with Rs. 1.4 lakhs after another six months. The amount of profit earned should be distributed in what ratio among Aman, Rakhi and Sagar respectively, 3 years after Aman started the business?- a)7 : 6 : 10
- b)12 : 15 : 16
- c)42 : 45 : 56
- d)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
Aman started a business investing Rs. 70,000. Rakhi joined him after six months with an amount of Rs. 1,05,000 and Sagar joined them with Rs. 1.4 lakhs after another six months. The amount of profit earned should be distributed in what ratio among Aman, Rakhi and Sagar respectively, 3 years after Aman started the business?
a)
7 : 6 : 10
b)
12 : 15 : 16
c)
42 : 45 : 56
d)
Cannot be determined

|
Partho Das answered |
Aman : Rakhi : Sagar
= (70,000 x 36) : (1,05,000 x 30) : (1,40,000 x 24)
= 12 : 15 : 16.
= (70,000 x 36) : (1,05,000 x 30) : (1,40,000 x 24)
= 12 : 15 : 16.
Simran started a software business by investing Rs. 50000. After six months, Nanda joined her with a capital of Rs. 80000.After 3 year they earned a profit of Rs 24500 What was Simran's share in the profit?
- a)Rs. 9423
- b)Rs. 10250
- c)Rs. 12500
- d)Rs. 14000
- e)Rs. 10500
Correct answer is option 'E'. Can you explain this answer?
Simran started a software business by investing Rs. 50000. After six months, Nanda joined her with a capital of Rs. 80000.After 3 year they earned a profit of Rs 24500 What was Simran's share in the profit?
a)
Rs. 9423
b)
Rs. 10250
c)
Rs. 12500
d)
Rs. 14000
e)
Rs. 10500
|
|
Aarav Sharma answered |
Given:
Simran invested Rs. 50000
Nanda invested Rs. 80000 after 6 months
To calculate:
Simran's share in the profit
Solution:
Let's calculate the ratio of their profits.
Simran invested for 12 months, whereas Nanda invested for 6 months only.
Simran's investment = Rs. 50000 x 12 = Rs. 600000
Nanda's investment = Rs. 80000 x 6 = Rs. 480000
Ratio of their investments = 600000:480000 = 5:4
Let the total profit be x
Simran's share in the profit = (5/9) x
Now, let's substitute the value of x
Total profit = profit of Simran + profit of Nanda
x = (5/9) x + (4/9) x
Simplifying this equation, we get
(4/9) x = Rs. 10500
Therefore, Simran's share in the profit = (5/9) x (Total profit) = (5/9) x Rs. 10500 = Rs. 5833.33
Hence, the closest option to the calculated answer is option E, Rs. 10500.
Simran invested Rs. 50000
Nanda invested Rs. 80000 after 6 months
To calculate:
Simran's share in the profit
Solution:
Let's calculate the ratio of their profits.
Simran invested for 12 months, whereas Nanda invested for 6 months only.
Simran's investment = Rs. 50000 x 12 = Rs. 600000
Nanda's investment = Rs. 80000 x 6 = Rs. 480000
Ratio of their investments = 600000:480000 = 5:4
Let the total profit be x
Simran's share in the profit = (5/9) x
Now, let's substitute the value of x
Total profit = profit of Simran + profit of Nanda
x = (5/9) x + (4/9) x
Simplifying this equation, we get
(4/9) x = Rs. 10500
Therefore, Simran's share in the profit = (5/9) x (Total profit) = (5/9) x Rs. 10500 = Rs. 5833.33
Hence, the closest option to the calculated answer is option E, Rs. 10500.
Two friends invested Rs.1500 and Rs. 2500 in a business. They earned a profit of Rs. 800. One-half of the profit was divided equally between them and the other half was divided in proportion to their capitals. How much did each of them receive ?- a)Rs. 350 and Rs. 450
- b)Rs. 360 and Rs. 440
- c)Rs. 370 and Rs. 430
- d)Rs. 375 and Rs. 425
Correct answer is option 'A'. Can you explain this answer?
Two friends invested Rs.1500 and Rs. 2500 in a business. They earned a profit of Rs. 800. One-half of the profit was divided equally between them and the other half was divided in proportion to their capitals. How much did each of them receive ?
a)
Rs. 350 and Rs. 450
b)
Rs. 360 and Rs. 440
c)
Rs. 370 and Rs. 430
d)
Rs. 375 and Rs. 425

|
Prashanth Ghoshal answered |
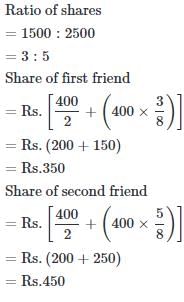
A, B and C jointly thought of engaging themselves in a business venture. It was agreed that A would invest Rs. 6500 for 6 months, B, Rs. 8400 for 5 months and C, Rs. 10,000 for 3 months. A wants to be the working member for which, he was to receive 5% of the profits. The profit earned was Rs. 7400. Calculate the share of B in the profit.- a)Rs. 1900
- b)Rs. 2660
- c)Rs. 2800
- d)Rs. 2840
Correct answer is option 'B'. Can you explain this answer?
A, B and C jointly thought of engaging themselves in a business venture. It was agreed that A would invest Rs. 6500 for 6 months, B, Rs. 8400 for 5 months and C, Rs. 10,000 for 3 months. A wants to be the working member for which, he was to receive 5% of the profits. The profit earned was Rs. 7400. Calculate the share of B in the profit.
a)
Rs. 1900
b)
Rs. 2660
c)
Rs. 2800
d)
Rs. 2840

|
Vandana Sarkar answered |
For managing, A received = 5% of Rs. 7400 = Rs. 370.
Balance = Rs. (7400 - 370) = Rs. 7030.
Ratio of their investments = (6500 x 6) : (8400 x 5) : (10000 x 3)
= 39000 : 42000 : 30000
= 13 : 14 : 10
∴ B's Share
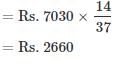
Balance = Rs. (7400 - 370) = Rs. 7030.
Ratio of their investments = (6500 x 6) : (8400 x 5) : (10000 x 3)
= 39000 : 42000 : 30000
= 13 : 14 : 10
∴ B's Share
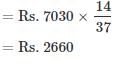
Anand and Deepak started a business investing Rs.22,500 and Rs.35,000 respectively. Out of a total profit of Rs. 13,800. Deepak's share is- a)Rs 9600
- b)Rs 8500
- c)Rs 8450
- d)Rs 8400
Correct answer is option 'D'. Can you explain this answer?
Anand and Deepak started a business investing Rs.22,500 and Rs.35,000 respectively. Out of a total profit of Rs. 13,800. Deepak's share is
a)
Rs 9600
b)
Rs 8500
c)
Rs 8450
d)
Rs 8400

|
Varun Nambiar answered |
Ratio of their shares = 22500 : 35000
=9 : 14
Deepak's share
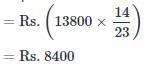
=9 : 14
Deepak's share
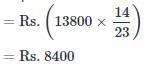
P, Q and R invested Rs. 45000, Rs. 70000 and Rs. 90000 respectively to start a business. At the end of 2 years, they earned a profit of Rs.164000. What will be Q's share in the profit ?- a)Rs. 36000
- b)Rs. 56000
- c)Rs. 64000
- d)Rs. 72000
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
P, Q and R invested Rs. 45000, Rs. 70000 and Rs. 90000 respectively to start a business. At the end of 2 years, they earned a profit of Rs.164000. What will be Q's share in the profit ?
a)
Rs. 36000
b)
Rs. 56000
c)
Rs. 64000
d)
Rs. 72000
e)
None of these

|
Sarthak Chatterjee answered |

Subhash starts a business by investing Rs. 25000. 6 months later Aditya joins him by investing Rs. 15000. After another 6 months Aditya invests an additional amount of Rs. 15000. At the end of 3 years they earn a profit of Rs. 247000. What is Aditya's share in the profit ?- a)Rs. 105000
- b)Rs. 111500
- c)Rs. 123000
- d)Rs. 130000
- e)None of these
Correct answer is option 'E'. Can you explain this answer?
Subhash starts a business by investing Rs. 25000. 6 months later Aditya joins him by investing Rs. 15000. After another 6 months Aditya invests an additional amount of Rs. 15000. At the end of 3 years they earn a profit of Rs. 247000. What is Aditya's share in the profit ?
a)
Rs. 105000
b)
Rs. 111500
c)
Rs. 123000
d)
Rs. 130000
e)
None of these
|
|
Aarav Sharma answered |
Given:
Subhash's investment = Rs. 25000
Aditya's investment after 6 months = Rs. 15000
Aditya's additional investment after another 6 months = Rs. 15000
Total time = 3 years
Total profit = Rs. 247000
Solution:
Let's calculate the total profit share of both Subhash and Aditya.
Subhash's profit share:
Subhash invested for the entire 3 years. Hence, his share in the profit will be calculated based on his investment.
Subhash's profit share = (25000/50000) * 247000
= Rs. 123500
Aditya's profit share:
Aditya invested Rs. 15000 after 6 months and Rs. 15000 after another 6 months. Hence, his investment will be considered for 2.5 years (from 6 months to 3 years).
Aditya's investment for 2.5 years = (15000/2) * 2.5
= Rs. 18750
Aditya's total investment = Rs. 15000 + Rs. 18750
= Rs. 33750
Aditya's profit share = (33750/50000) * 247000
= Rs. 166950
Therefore, Aditya's share in the profit is Rs. 166950. Option E is the correct answer.
Subhash's investment = Rs. 25000
Aditya's investment after 6 months = Rs. 15000
Aditya's additional investment after another 6 months = Rs. 15000
Total time = 3 years
Total profit = Rs. 247000
Solution:
Let's calculate the total profit share of both Subhash and Aditya.
Subhash's profit share:
Subhash invested for the entire 3 years. Hence, his share in the profit will be calculated based on his investment.
Subhash's profit share = (25000/50000) * 247000
= Rs. 123500
Aditya's profit share:
Aditya invested Rs. 15000 after 6 months and Rs. 15000 after another 6 months. Hence, his investment will be considered for 2.5 years (from 6 months to 3 years).
Aditya's investment for 2.5 years = (15000/2) * 2.5
= Rs. 18750
Aditya's total investment = Rs. 15000 + Rs. 18750
= Rs. 33750
Aditya's profit share = (33750/50000) * 247000
= Rs. 166950
Therefore, Aditya's share in the profit is Rs. 166950. Option E is the correct answer.
A and B share profits and losses in a firm in the ratio of 3 : 2. And C entered in the firm as a new partner; his profit sharing ratio is 1/4. If C has taken his share of profit from A and B in equal ratio, then the new profit shearing ratio will be ?- a)19 : 11 : 1
- b)19 : 11 : 10
- c)10 : 11 : 9
- d)10 : 11 : 19
Correct answer is option 'B'. Can you explain this answer?
A and B share profits and losses in a firm in the ratio of 3 : 2. And C entered in the firm as a new partner; his profit sharing ratio is 1/4. If C has taken his share of profit from A and B in equal ratio, then the new profit shearing ratio will be ?
a)
19 : 11 : 1
b)
19 : 11 : 10
c)
10 : 11 : 9
d)
10 : 11 : 19

|
Samarth Sengupta answered |


A, B and C enter into a partnership with capitals in the ratio 5 : 6 : 8. At the end of the business term, they received the profit in the ratio 5 : 3 : 12. Find the ratio of time for which they contributed their capitals ?- a)2 : 1 : 3
- b)1 : 2 : 3
- c)2 : 3 : 1
- d)3 : 2 : 1
Correct answer is option 'A'. Can you explain this answer?
A, B and C enter into a partnership with capitals in the ratio 5 : 6 : 8. At the end of the business term, they received the profit in the ratio 5 : 3 : 12. Find the ratio of time for which they contributed their capitals ?
a)
2 : 1 : 3
b)
1 : 2 : 3
c)
2 : 3 : 1
d)
3 : 2 : 1

|
Debanshi Bajaj answered |

A starts business with Rs. 3500 and after 5 months, B joins with A as his partner. After a year, the profit is divided in the ratio 2 : 3. What is B's contribution in the capital?- a)Rs. 7500
- b)Rs. 8000
- c)Rs. 8500
- d)Rs. 9000
Correct answer is option 'D'. Can you explain this answer?
A starts business with Rs. 3500 and after 5 months, B joins with A as his partner. After a year, the profit is divided in the ratio 2 : 3. What is B's contribution in the capital?
a)
Rs. 7500
b)
Rs. 8000
c)
Rs. 8500
d)
Rs. 9000

|
Om Banerjee answered |
Let B's capital be Rs. x
∴ A's share in 12 months=3500 × 12
And, B's share in 7 months=7x
Let B's capitalbe Rs.x
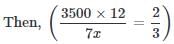
⇒14x=126000
⇒x=9000
∴ A's share in 12 months=3500 × 12
And, B's share in 7 months=7x
Let B's capitalbe Rs.x
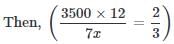
⇒14x=126000
⇒x=9000
Dilip, Ram and Avtar started a shop by investing Rs. 2700, Rs. 8100 and Rs. 7200 respectively. At the end of one year, the profit earned was distributed. If Ram's share was Rs. 3600, what was their total profit ?- a)Rs. 8000
- b)Rs. 10800
- c)Rs. 11600
- d)Data inadequate
Correct answer is option 'A'. Can you explain this answer?
Dilip, Ram and Avtar started a shop by investing Rs. 2700, Rs. 8100 and Rs. 7200 respectively. At the end of one year, the profit earned was distributed. If Ram's share was Rs. 3600, what was their total profit ?
a)
Rs. 8000
b)
Rs. 10800
c)
Rs. 11600
d)
Data inadequate
|
|
Aarav Sharma answered |
Given:
Investment by Dilip = Rs. 2700
Investment by Ram = Rs. 8100
Investment by Avtar = Rs. 7200
Profit earned by Ram = Rs. 3600
To find: Total profit earned by Dilip, Ram, and Avtar
Let's assume the total profit earned by Dilip, Ram, and Avtar is P.
As the profit is distributed in proportion to their investments, we can calculate the ratio of their investments.
Ratio of investments:
Dilip : Ram : Avtar = 2700 : 8100 : 7200
Simplifying the ratio, we get:
Dilip : Ram : Avtar = 1 : 3 : 2
Now, let's calculate the profit received by each person.
Profit received by Dilip = (Dilip's investment / Total investment) * Total profit
Profit received by Dilip = (2700 / (2700 + 8100 + 7200)) * P
Profit received by Dilip = (2700 / 18000) * P
Profit received by Ram = (Ram's investment / Total investment) * Total profit
Profit received by Ram = (8100 / (2700 + 8100 + 7200)) * P
Profit received by Ram = (8100 / 18000) * P
Profit received by Avtar = (Avtar's investment / Total investment) * Total profit
Profit received by Avtar = (7200 / (2700 + 8100 + 7200)) * P
Profit received by Avtar = (7200 / 18000) * P
Given that the profit received by Ram is Rs. 3600, we can equate the profit received by Ram to Rs. 3600 and solve for P.
(8100 / 18000) * P = 3600
8100P = 3600 * 18000
P = (3600 * 18000) / 8100
P = 8000
Therefore, the total profit earned by Dilip, Ram, and Avtar is Rs. 8000.
Hence, the correct answer is option A) Rs. 8000.
Investment by Dilip = Rs. 2700
Investment by Ram = Rs. 8100
Investment by Avtar = Rs. 7200
Profit earned by Ram = Rs. 3600
To find: Total profit earned by Dilip, Ram, and Avtar
Let's assume the total profit earned by Dilip, Ram, and Avtar is P.
As the profit is distributed in proportion to their investments, we can calculate the ratio of their investments.
Ratio of investments:
Dilip : Ram : Avtar = 2700 : 8100 : 7200
Simplifying the ratio, we get:
Dilip : Ram : Avtar = 1 : 3 : 2
Now, let's calculate the profit received by each person.
Profit received by Dilip = (Dilip's investment / Total investment) * Total profit
Profit received by Dilip = (2700 / (2700 + 8100 + 7200)) * P
Profit received by Dilip = (2700 / 18000) * P
Profit received by Ram = (Ram's investment / Total investment) * Total profit
Profit received by Ram = (8100 / (2700 + 8100 + 7200)) * P
Profit received by Ram = (8100 / 18000) * P
Profit received by Avtar = (Avtar's investment / Total investment) * Total profit
Profit received by Avtar = (7200 / (2700 + 8100 + 7200)) * P
Profit received by Avtar = (7200 / 18000) * P
Given that the profit received by Ram is Rs. 3600, we can equate the profit received by Ram to Rs. 3600 and solve for P.
(8100 / 18000) * P = 3600
8100P = 3600 * 18000
P = (3600 * 18000) / 8100
P = 8000
Therefore, the total profit earned by Dilip, Ram, and Avtar is Rs. 8000.
Hence, the correct answer is option A) Rs. 8000.
We have to divided a sum of Rs. 13950 among three persons A, B and C. B must get the double of A's share and C must get 50 less than the double of B's share. The share of A will be ?- a)Rs. 1950
- b)Rs. 1981.25
- c)Rs. 2000
- d)Rs. 2007.75
Correct answer is option 'C'. Can you explain this answer?
We have to divided a sum of Rs. 13950 among three persons A, B and C. B must get the double of A's share and C must get 50 less than the double of B's share. The share of A will be ?
a)
Rs. 1950
b)
Rs. 1981.25
c)
Rs. 2000
d)
Rs. 2007.75

|
Swati Yadav answered |
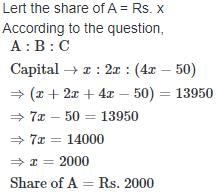
A, B and C started a business investing amounts in the ratio of 5 : 6 : 8 respectively. After one year, C withdrew 50% of the amount and A invested an additional amount of 60% of the original amount invested by him. In what ratio, the profit earned at the end of 2 years should be distributed among A, B and C respectively ?- a)2 : 3 : 3
- b)4 : 3 : 2
- c)13 : 12 : 12
- d)Cannot be determined
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A, B and C started a business investing amounts in the ratio of 5 : 6 : 8 respectively. After one year, C withdrew 50% of the amount and A invested an additional amount of 60% of the original amount invested by him. In what ratio, the profit earned at the end of 2 years should be distributed among A, B and C respectively ?
a)
2 : 3 : 3
b)
4 : 3 : 2
c)
13 : 12 : 12
d)
Cannot be determined
e)
None of these

|
Debanshi Bajaj answered |
Let the initial investments of A, B and C be Rs. 5x, Rs. 6x and Rs. 8x respectively
Then, A : B : C
[5x × 12 + (160% of 5x)] : (6x × 24) : (8x × 12 + 4x × 12)
= 156x : 144x : 144x
= 13 : 12 : 12
Then, A : B : C
[5x × 12 + (160% of 5x)] : (6x × 24) : (8x × 12 + 4x × 12)
= 156x : 144x : 144x
= 13 : 12 : 12
A, B and C enter into a partnership. A invests some money at the beginning, B invests double the amount after six months and C invest thrice the amount after eight months. If the annual profit be Rs. 27000; C's share (in Rs.) is ?- a)Rs. 8625
- b)Rs. 9000
- c)Rs. 10800
- d)Rs. 11250
Correct answer is option 'B'. Can you explain this answer?
A, B and C enter into a partnership. A invests some money at the beginning, B invests double the amount after six months and C invest thrice the amount after eight months. If the annual profit be Rs. 27000; C's share (in Rs.) is ?
a)
Rs. 8625
b)
Rs. 9000
c)
Rs. 10800
d)
Rs. 11250

|
Sanjana Patel answered |

X and Y are partners in a business. They invest in the ratio 5 : 6, at the end of 8 months X withdraws his capital. If they receive profits in the ratio of 5 : 9. Find how long Y's investment was used ?- a)12 months
- b)10 months
- c)15 months
- d)14 months
Correct answer is option 'A'. Can you explain this answer?
X and Y are partners in a business. They invest in the ratio 5 : 6, at the end of 8 months X withdraws his capital. If they receive profits in the ratio of 5 : 9. Find how long Y's investment was used ?
a)
12 months
b)
10 months
c)
15 months
d)
14 months
|
|
Aarav Sharma answered |
Given:
- X and Y are partners in a business.
- They invest in the ratio 5:6.
- X withdraws his capital at the end of 8 months.
- They receive profits in the ratio 5:9.
To find:
- The duration for which Y's investment was used.
Solution:
Let's assume that X invested 5x and Y invested 6x.
Investment Ratio:
X's investment = 5x
Y's investment = 6x
Profit Sharing Ratio:
X's profit share = 5
Y's profit share = 9
Calculation:
Since X withdraws his capital after 8 months, his investment is used for 8 months. Therefore, the ratio of their investments for the remaining duration is:
X's investment = 5x (for 8 months)
Y's investment = 6x (for the remaining months)
The profit sharing ratio is given as 5:9, which means that the ratio of their investments is equal to the ratio of their profit shares. So, we can set up the following equation:
5x/8 = 5/9
Cross-multiplying:
45x = 40
Dividing by 45:
x = 40/45
x = 8/9
Calculating Y's investment:
Y's investment = 6x
Y's investment = 6 * (8/9)
Y's investment = 48/9
Y's investment = 16/3
Calculating the duration for which Y's investment was used:
Since X's investment was used for 8 months, Y's investment was used for the remaining duration:
Total duration - X's duration = Y's duration
12 months - 8 months = 4 months
Therefore, Y's investment was used for 4 months.
Conclusion:
The duration for which Y's investment was used is 4 months, which is equivalent to option A.
- X and Y are partners in a business.
- They invest in the ratio 5:6.
- X withdraws his capital at the end of 8 months.
- They receive profits in the ratio 5:9.
To find:
- The duration for which Y's investment was used.
Solution:
Let's assume that X invested 5x and Y invested 6x.
Investment Ratio:
X's investment = 5x
Y's investment = 6x
Profit Sharing Ratio:
X's profit share = 5
Y's profit share = 9
Calculation:
Since X withdraws his capital after 8 months, his investment is used for 8 months. Therefore, the ratio of their investments for the remaining duration is:
X's investment = 5x (for 8 months)
Y's investment = 6x (for the remaining months)
The profit sharing ratio is given as 5:9, which means that the ratio of their investments is equal to the ratio of their profit shares. So, we can set up the following equation:
5x/8 = 5/9
Cross-multiplying:
45x = 40
Dividing by 45:
x = 40/45
x = 8/9
Calculating Y's investment:
Y's investment = 6x
Y's investment = 6 * (8/9)
Y's investment = 48/9
Y's investment = 16/3
Calculating the duration for which Y's investment was used:
Since X's investment was used for 8 months, Y's investment was used for the remaining duration:
Total duration - X's duration = Y's duration
12 months - 8 months = 4 months
Therefore, Y's investment was used for 4 months.
Conclusion:
The duration for which Y's investment was used is 4 months, which is equivalent to option A.
In a partnership, A invests 1/6 of the capital 1/6 for of the time, B invests 1/3 of the capital for 1/3 of the time and C, the rest of the capital for the whole time. Out of a profit of Rs. 4600, B's share is ?- a)Rs. 650
- b)Rs. 800
- c)Rs. 960
- d)Rs. 1000
Correct answer is option 'B'. Can you explain this answer?
In a partnership, A invests 1/6 of the capital 1/6 for of the time, B invests 1/3 of the capital for 1/3 of the time and C, the rest of the capital for the whole time. Out of a profit of Rs. 4600, B's share is ?
a)
Rs. 650
b)
Rs. 800
c)
Rs. 960
d)
Rs. 1000

|
Samarth Sengupta answered |

A, B, C started a business with their investments in the ratio 1 : 3 : 5. After 4 months, A invested the same amount as before and B as well as C withdrew half of their investments. The ratio of their profits at the end of the year is ?- a)4 : 3 : 5
- b)5 : 6 : 10
- c)6 : 5 : 10
- d)10 : 5 : 6
Correct answer is option 'B'. Can you explain this answer?
A, B, C started a business with their investments in the ratio 1 : 3 : 5. After 4 months, A invested the same amount as before and B as well as C withdrew half of their investments. The ratio of their profits at the end of the year is ?
a)
4 : 3 : 5
b)
5 : 6 : 10
c)
6 : 5 : 10
d)
10 : 5 : 6
|
|
Aarav Sharma answered |
Given:
- Investments ratio of A, B, C = 1:3:5
- After 4 months:
- A invests the same amount as before
- B and C withdraw half of their investments
To find: Ratio of their profits at the end of the year
Solution:
Let's assume the initial investments of A, B, and C as x, 3x, and 5x respectively.
Investments:
- Initial investments:
- A = x
- B = 3x
- C = 5x
- After 4 months:
- A invests the same amount as before = x
- B withdraws half of the investment = 3x/2
- C withdraws half of the investment = 5x/2
Effective Investments:
- After 4 months:
- A = x + x = 2x
- B = 3x - 3x/2 = 3x/2
- C = 5x - 5x/2 = 5x/2
Profit Sharing:
- The profit of a business is usually shared in proportion to the investments made by the partners.
- The ratio of their profits will be equal to the ratio of their effective investments.
Ratio of Profits:
- Ratio of their profits at the end of the year:
- A : B : C = 2x : 3x/2 : 5x/2
Simplifying the Ratio:
- To simplify the ratio, we multiply each part by the least common multiple (LCM) of the denominators, which is 2.
- A : B : C = 2x * 2 : 3x/2 * 2 : 5x/2 * 2
- A : B : C = 4x : 3x : 5x
- A : B : C = 4 : 3 : 5
Answer:
The ratio of their profits at the end of the year is 4 : 3 : 5 (option B).
- Investments ratio of A, B, C = 1:3:5
- After 4 months:
- A invests the same amount as before
- B and C withdraw half of their investments
To find: Ratio of their profits at the end of the year
Solution:
Let's assume the initial investments of A, B, and C as x, 3x, and 5x respectively.
Investments:
- Initial investments:
- A = x
- B = 3x
- C = 5x
- After 4 months:
- A invests the same amount as before = x
- B withdraws half of the investment = 3x/2
- C withdraws half of the investment = 5x/2
Effective Investments:
- After 4 months:
- A = x + x = 2x
- B = 3x - 3x/2 = 3x/2
- C = 5x - 5x/2 = 5x/2
Profit Sharing:
- The profit of a business is usually shared in proportion to the investments made by the partners.
- The ratio of their profits will be equal to the ratio of their effective investments.
Ratio of Profits:
- Ratio of their profits at the end of the year:
- A : B : C = 2x : 3x/2 : 5x/2
Simplifying the Ratio:
- To simplify the ratio, we multiply each part by the least common multiple (LCM) of the denominators, which is 2.
- A : B : C = 2x * 2 : 3x/2 * 2 : 5x/2 * 2
- A : B : C = 4x : 3x : 5x
- A : B : C = 4 : 3 : 5
Answer:
The ratio of their profits at the end of the year is 4 : 3 : 5 (option B).
A starts a business by investing Rs. 28000. After 2 months, B joins with Rs. 20000 and after another 2 months C joins with Rs. 18000. At the end of 10 months from the start of the business, if B withdraws Rs. 2000 and C withdraws Rs. 2000, in what ratio should the profit be distributed among A, B and C at the end of the year ?- a)12 : 7 : 5
- b)12 : 9 : 5
- c)12 : 6 : 3
- d)14 : 7 : 5
Correct answer is option 'A'. Can you explain this answer?
A starts a business by investing Rs. 28000. After 2 months, B joins with Rs. 20000 and after another 2 months C joins with Rs. 18000. At the end of 10 months from the start of the business, if B withdraws Rs. 2000 and C withdraws Rs. 2000, in what ratio should the profit be distributed among A, B and C at the end of the year ?
a)
12 : 7 : 5
b)
12 : 9 : 5
c)
12 : 6 : 3
d)
14 : 7 : 5

|
Samarth Sengupta answered |
A invests money for 12 months
B invests money for 10 months
C invests money for 8 months
Ratio of profit of A to B to C
= 28000 × 12:20000 × 8 + 18000 × 2 : 18000 × 6 + 16000 × 2
= 28 × 12 × 1000 : (160 + 36) × 1000 : (108 + 32) × 1000
= 28 × 12 : 160 + 36 : 108 + 32
= 336 : 196 : 140
= 12 : 7 : 5
B invests money for 10 months
C invests money for 8 months
Ratio of profit of A to B to C
= 28000 × 12:20000 × 8 + 18000 × 2 : 18000 × 6 + 16000 × 2
= 28 × 12 × 1000 : (160 + 36) × 1000 : (108 + 32) × 1000
= 28 × 12 : 160 + 36 : 108 + 32
= 336 : 196 : 140
= 12 : 7 : 5
Sonia started a business investing Rs. 60000. After 6 months Vivek joined him with an amount of Rs. 140000. After 1 year Kirti also joined them with Rs. 120000. After 2 years the business yielded a total profit of Rs. 450000. What is the share of Vivek in the profit ?- a)Rs. 140000
- b)Rs. 198500
- c)Rs. 210000
- d)Rs. 215000
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Sonia started a business investing Rs. 60000. After 6 months Vivek joined him with an amount of Rs. 140000. After 1 year Kirti also joined them with Rs. 120000. After 2 years the business yielded a total profit of Rs. 450000. What is the share of Vivek in the profit ?
a)
Rs. 140000
b)
Rs. 198500
c)
Rs. 210000
d)
Rs. 215000
e)
None of these

|
Krithika Patel answered |

P and Q started a business investing Rs 85000 and Rs 15000 resp. In what ratio the profit earned after 2 years be divided between P and Q respectively.- a)17 : 5
- b)17 : 3
- c)17 : 6
- d)17 : 7
Correct answer is option 'B'. Can you explain this answer?
P and Q started a business investing Rs 85000 and Rs 15000 resp. In what ratio the profit earned after 2 years be divided between P and Q respectively.
a)
17 : 5
b)
17 : 3
c)
17 : 6
d)
17 : 7

|
Ashish Chawla answered |
In this type of question as time frame for both investors is equal then just get the ratio of their investments.
P : Q = 85000 : 15000
= 85 : 15
= 17 : 3
P : Q = 85000 : 15000
= 85 : 15
= 17 : 3
Three partners A , B , C start a business . B's Capital is four times C's capital and twice A's capital is equal to thrice B's capital . If the total profit is Rs 16500 at the end of a year ,Find out B's share in it.- a)Rs. 4000
- b)Rs. 5000
- c)Rs. 6000
- d)Rs. 7000
Correct answer is option 'C'. Can you explain this answer?
Three partners A , B , C start a business . B's Capital is four times C's capital and twice A's capital is equal to thrice B's capital . If the total profit is Rs 16500 at the end of a year ,Find out B's share in it.
a)
Rs. 4000
b)
Rs. 5000
c)
Rs. 6000
d)
Rs. 7000

|
Om Banerjee answered |
Suppose C's capital = x then
B's capital = 4x (Since B's Capital is four times C's capital)
A's capital = 6x ( Since twice A's capital is equal to thrice B's capital)
A : B : C =6x : 4x : x
= 6 : 4 : 1
B's share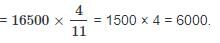
B's capital = 4x (Since B's Capital is four times C's capital)
A's capital = 6x ( Since twice A's capital is equal to thrice B's capital)
A : B : C =6x : 4x : x
= 6 : 4 : 1
B's share
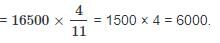
Two friends P and Q started a business investing in the ratio 5 : 6. R joined them after six months investing an amount equal to that of Q's. At the end of the year, 20% profit was earned which was equal to Rs. 98000. What was the amount invested by R?- a)Rs. 105000
- b)Rs. 175000
- c)Rs. 210000
- d)Data inadequate
Correct answer is option 'C'. Can you explain this answer?
Two friends P and Q started a business investing in the ratio 5 : 6. R joined them after six months investing an amount equal to that of Q's. At the end of the year, 20% profit was earned which was equal to Rs. 98000. What was the amount invested by R?
a)
Rs. 105000
b)
Rs. 175000
c)
Rs. 210000
d)
Data inadequate
|
|
Aarav Sharma answered |
Given:
- P and Q started a business investing in the ratio 5:6
- R joined them after six months and invested an amount equal to that of Q's investment
- At the end of the year, a 20% profit was earned, which was equal to Rs. 98000
To find:
- The amount invested by R
Let's assume:
- The initial investments of P and Q are 5x and 6x respectively
- The amount invested by R is also 6x (equal to Q's investment)
Calculating the total investment:
- P's investment for the entire year = 5x * 12 = 60x
- Q's investment for the entire year = 6x * 12 = 72x
- R's investment for the entire year = 6x * 6 = 36x (as R joined after six months)
Total investment for the year = P's investment + Q's investment + R's investment
= 60x + 72x + 36x
= 168x
Calculating the profit earned:
- Profit = 20% of the total investment
= (20/100) * 168x
= 33.6x
Given that the profit earned is equal to Rs. 98000:
33.6x = 98000
Solving for x:
x = 98000 / 33.6
x ≈ 2916.67
Calculating the amount invested by R:
R's investment = 6x
= 6 * 2916.67
≈ Rs. 17500
Therefore, the amount invested by R is approximately Rs. 175000.
- P and Q started a business investing in the ratio 5:6
- R joined them after six months and invested an amount equal to that of Q's investment
- At the end of the year, a 20% profit was earned, which was equal to Rs. 98000
To find:
- The amount invested by R
Let's assume:
- The initial investments of P and Q are 5x and 6x respectively
- The amount invested by R is also 6x (equal to Q's investment)
Calculating the total investment:
- P's investment for the entire year = 5x * 12 = 60x
- Q's investment for the entire year = 6x * 12 = 72x
- R's investment for the entire year = 6x * 6 = 36x (as R joined after six months)
Total investment for the year = P's investment + Q's investment + R's investment
= 60x + 72x + 36x
= 168x
Calculating the profit earned:
- Profit = 20% of the total investment
= (20/100) * 168x
= 33.6x
Given that the profit earned is equal to Rs. 98000:
33.6x = 98000
Solving for x:
x = 98000 / 33.6
x ≈ 2916.67
Calculating the amount invested by R:
R's investment = 6x
= 6 * 2916.67
≈ Rs. 17500
Therefore, the amount invested by R is approximately Rs. 175000.
A, B and C are three partners. They altogether invested Rs. 14000 in business. At the end of the year, A got Rs. 337.50, B Rs. 1125 and C Rs. 637.50 as profit. The difference between the investments of B and A was ?- a)Rs. 2200
- b)Rs. 3200
- c)Rs. 4200
- d)Rs. 5250
Correct answer is option 'D'. Can you explain this answer?
A, B and C are three partners. They altogether invested Rs. 14000 in business. At the end of the year, A got Rs. 337.50, B Rs. 1125 and C Rs. 637.50 as profit. The difference between the investments of B and A was ?
a)
Rs. 2200
b)
Rs. 3200
c)
Rs. 4200
d)
Rs. 5250

|
Anshika Basu answered |

A is a active partner and B is a inactive partner in business. A puts in Rs. 5000 and B puts in Rs. 6000. A received 15% of the profit for managing the business and the rest is divided in proportion to their capitals. The amounts received by A out of the profit of Rs. 880 in all is ?- a)Rs. 132
- b)Rs. 340
- c)Rs. 472
- d)Rs. 492
Correct answer is option 'C'. Can you explain this answer?
A is a active partner and B is a inactive partner in business. A puts in Rs. 5000 and B puts in Rs. 6000. A received 15% of the profit for managing the business and the rest is divided in proportion to their capitals. The amounts received by A out of the profit of Rs. 880 in all is ?
a)
Rs. 132
b)
Rs. 340
c)
Rs. 472
d)
Rs. 492

|
Nandini Yadav answered |
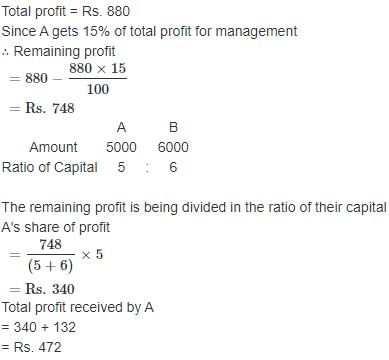
M, P and Q together started a business. M invested Rs. 6500 for 6 months, P invested Rs. 8400 for 5 months and Q invested Rs. 10000 for 3 months. M is working member for which he gets 5% of total profit extra. If the total gain is Rs. 7400, then Q's share is ?- a)Rs. 1900
- b)Rs. 2100
- c)Rs. 3200
- d)Data are incomplete
Correct answer is option 'A'. Can you explain this answer?
M, P and Q together started a business. M invested Rs. 6500 for 6 months, P invested Rs. 8400 for 5 months and Q invested Rs. 10000 for 3 months. M is working member for which he gets 5% of total profit extra. If the total gain is Rs. 7400, then Q's share is ?
a)
Rs. 1900
b)
Rs. 2100
c)
Rs. 3200
d)
Data are incomplete

|
Samarth Sengupta answered |
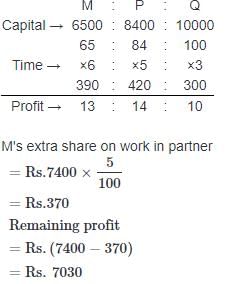

A working partner gets 20% as his commission of the profit after his commission is paid. If the working partner's commission is Rs. 8000, then what is the total profit in the business ?- a)Rs. 47000
- b)Rs. 45000
- c)Rs. 48000
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A working partner gets 20% as his commission of the profit after his commission is paid. If the working partner's commission is Rs. 8000, then what is the total profit in the business ?
a)
Rs. 47000
b)
Rs. 45000
c)
Rs. 48000
d)
None of these

|
Varun Nambiar answered |

A, B, C subscribe Rs. 50,000 for a business. A subscribes Rs. 4000 more than B and B Rs. 5000 more than C. Out of a total profit of Rs. 35,000, A receives- a)Rs. 8400
- b)Rs. 11,900
- c)Rs. 13,600
- d)Rs. 14,700
Correct answer is option 'D'. Can you explain this answer?
A, B, C subscribe Rs. 50,000 for a business. A subscribes Rs. 4000 more than B and B Rs. 5000 more than C. Out of a total profit of Rs. 35,000, A receives
a)
Rs. 8400
b)
Rs. 11,900
c)
Rs. 13,600
d)
Rs. 14,700

|
Debanshi Patel answered |
Let C = x.
Then, B = x + 5000 and A = x + 5000 + 4000 = x + 9000
So, x + x + 5000 + x + 9000 = 50000
⇒ 3x = 36000
⇒ x = 12000
A : B : C = 21000 : 17000 : 12000 = 21 : 17 : 12
So A's Share
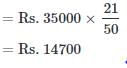
Then, B = x + 5000 and A = x + 5000 + 4000 = x + 9000
So, x + x + 5000 + x + 9000 = 50000
⇒ 3x = 36000
⇒ x = 12000
A : B : C = 21000 : 17000 : 12000 = 21 : 17 : 12
So A's Share
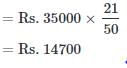
Simran started a software business by investing Rs. 50,000. After six months, Nanda joined her with a capital of Rs. 80,000. After 3 years, they earned a profit of Rs. 24,500. What was Simran's share in the profit?- a)Rs. 9,423
- b)Rs. 10,250
- c)Rs. 12,500
- d)Rs. 10,500
Correct answer is option 'D'. Can you explain this answer?
Simran started a software business by investing Rs. 50,000. After six months, Nanda joined her with a capital of Rs. 80,000. After 3 years, they earned a profit of Rs. 24,500. What was Simran's share in the profit?
a)
Rs. 9,423
b)
Rs. 10,250
c)
Rs. 12,500
d)
Rs. 10,500

|
Saumya Menon answered |

Three partners shared the profit in a business in the ratio 5 : 7 : 8. They had partnered for 14 months, 8 months and 7 months respectively. What was the ratio of their investments?- a)5 : 7 : 8
- b)20 : 49 : 64
- c)38 : 28 : 21
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Three partners shared the profit in a business in the ratio 5 : 7 : 8. They had partnered for 14 months, 8 months and 7 months respectively. What was the ratio of their investments?
a)
5 : 7 : 8
b)
20 : 49 : 64
c)
38 : 28 : 21
d)
None of these

|
Vandana Sarkar answered |
Let their investments be Rs. x for 14 months, Rs. y for 8 months and Rs. z for 7 months respectively.
Then, 14x : 8y : 7z = 5 : 7 : 8.
Now,
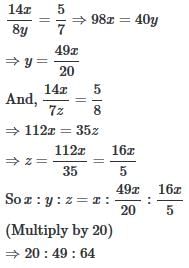
Then, 14x : 8y : 7z = 5 : 7 : 8.
Now,
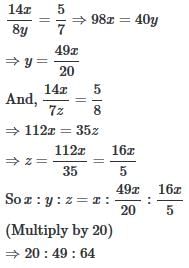
A, B and C enter into a partnership investing Rs 35000, Rs 45000 and Rs 55000 resp. The respective share of A,B and C in an annual profit of Rs 40500 are.- a)Rs. 11500, Rs. 13500, Rs. 16500
- b)Rs. 10500, Rs. 12500, Rs. 16500
- c)Rs. 10500, Rs. 13500, Rs. 15500
- d)Rs. 10500, Rs. 13500, Rs. 16500
Correct answer is option 'D'. Can you explain this answer?
A, B and C enter into a partnership investing Rs 35000, Rs 45000 and Rs 55000 resp. The respective share of A,B and C in an annual profit of Rs 40500 are.
a)
Rs. 11500, Rs. 13500, Rs. 16500
b)
Rs. 10500, Rs. 12500, Rs. 16500
c)
Rs. 10500, Rs. 13500, Rs. 15500
d)
Rs. 10500, Rs. 13500, Rs. 16500

|
Saumya Menon answered |

Prakash, Sachin and Anil started a business jointly investing Rs. 11 lakh, Rs. 16.5 lakh and Rs.8.25 lakh respectively. The profit earned by them in the business at the end of 3 years was Rs. 5 lakh. What will be 50% of Anil's share in the profit ?- a)Rs. 2.25 lakh
- b)Rs. 2.50 lakh
- c)Rs. 3.75 lakh
- d)Rs. 4.50 lakh
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
Prakash, Sachin and Anil started a business jointly investing Rs. 11 lakh, Rs. 16.5 lakh and Rs.8.25 lakh respectively. The profit earned by them in the business at the end of 3 years was Rs. 5 lakh. What will be 50% of Anil's share in the profit ?
a)
Rs. 2.25 lakh
b)
Rs. 2.50 lakh
c)
Rs. 3.75 lakh
d)
Rs. 4.50 lakh
e)
None of these

|
Ashish Chawla answered |
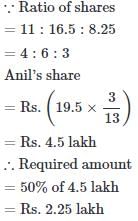
A and B started a business in partnership investing Rs. 20,000 and Rs. 15,000 respectively. After six months, C joined them with Rs. 20,000. What will be B's share in total profit of Rs. 25,000 earned at the end of 2 years from the starting of the business?- a)Rs. 7500
- b)Rs. 9000
- c)Rs. 9500
- d)Rs. 10,000
Correct answer is option 'A'. Can you explain this answer?
A and B started a business in partnership investing Rs. 20,000 and Rs. 15,000 respectively. After six months, C joined them with Rs. 20,000. What will be B's share in total profit of Rs. 25,000 earned at the end of 2 years from the starting of the business?
a)
Rs. 7500
b)
Rs. 9000
c)
Rs. 9500
d)
Rs. 10,000

|
Vandana Sarkar answered |
A : B : C
= (20,000 × 24) : (15,000 × 24) : (20,000 × 18)
= 4 : 3 : 3.
So B's Share
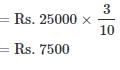
= (20,000 × 24) : (15,000 × 24) : (20,000 × 18)
= 4 : 3 : 3.
So B's Share
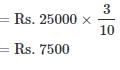
P and Q started a business in the ratio of 2 : 3. After 1 year P left the business but Q continues. After 2 years he had profit of Rs. 26000. What is the profit of Q?- a)Rs. 10400
- b)Rs. 13000
- c)Rs. 15600
- d)Rs. 18500
- e)None of these
Correct answer is option 'E'. Can you explain this answer?
P and Q started a business in the ratio of 2 : 3. After 1 year P left the business but Q continues. After 2 years he had profit of Rs. 26000. What is the profit of Q?
a)
Rs. 10400
b)
Rs. 13000
c)
Rs. 15600
d)
Rs. 18500
e)
None of these

|
Aashna Roy answered |
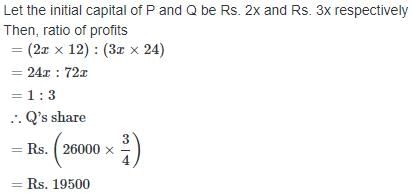
Rahul and Bharti are partners in a business. Rahul contributes 1/4th capital for 15 months and Bharti received 2/3 of profit. For how long Bharti money was used.- a)8 months
- b)10 months
- c)11 months
- d)17 months
Correct answer is option 'B'. Can you explain this answer?
Rahul and Bharti are partners in a business. Rahul contributes 1/4th capital for 15 months and Bharti received 2/3 of profit. For how long Bharti money was used.
a)
8 months
b)
10 months
c)
11 months
d)
17 months
|
|
Sagar Sharma answered |
Problem:
Rahul and Bharti are partners in a business. Rahul contributes 1/4th capital for 15 months and Bharti received 2/3 of profit. For how long Bharti money was used.
Solution:
To solve this problem, we need to calculate the ratio of the capital contributed by Rahul and Bharti, and then use this ratio to find the duration for which Bharti's money was used.
Step 1: Calculate the ratio of capital contributed by Rahul and Bharti
- Let's assume that Rahul contributed R amount of capital.
- According to the problem, Bharti contributed 1/4th of the total capital and the remaining 3/4th capital was contributed by Rahul.
- Therefore, Bharti's capital = (1/4) * Total capital = (1/4) * (3/4) * R = 3/16 * R
Step 2: Calculate the duration for which Bharti's money was used
- Let's assume that Bharti's money was used for 'x' months.
- According to the problem, Bharti received 2/3 of the profit.
- Therefore, Bharti's share of the profit = (2/3) * Total profit
- Since profit is directly proportional to the duration for which the money is used, we can write:
Bharti's share of the profit / Rahul's share of the profit = Duration for which Bharti's money was used / Duration for which Rahul's money was used
(2/3) / (1/3) = x / 15
2/1 = x / 15
x = 30/1 = 30 months
Therefore, Bharti's money was used for 30 months. However, the options provided in the question do not include 30 months. So, we need to find the closest option to 30 months.
Step 3: Find the closest option to 30 months
- The options provided are:
a) 8 months
b) 10 months
c) 11 months
d) 17 months
- The closest option to 30 months is 10 months, which is option b.
Therefore, the correct answer is option b) 10 months.
Rahul and Bharti are partners in a business. Rahul contributes 1/4th capital for 15 months and Bharti received 2/3 of profit. For how long Bharti money was used.
Solution:
To solve this problem, we need to calculate the ratio of the capital contributed by Rahul and Bharti, and then use this ratio to find the duration for which Bharti's money was used.
Step 1: Calculate the ratio of capital contributed by Rahul and Bharti
- Let's assume that Rahul contributed R amount of capital.
- According to the problem, Bharti contributed 1/4th of the total capital and the remaining 3/4th capital was contributed by Rahul.
- Therefore, Bharti's capital = (1/4) * Total capital = (1/4) * (3/4) * R = 3/16 * R
Step 2: Calculate the duration for which Bharti's money was used
- Let's assume that Bharti's money was used for 'x' months.
- According to the problem, Bharti received 2/3 of the profit.
- Therefore, Bharti's share of the profit = (2/3) * Total profit
- Since profit is directly proportional to the duration for which the money is used, we can write:
Bharti's share of the profit / Rahul's share of the profit = Duration for which Bharti's money was used / Duration for which Rahul's money was used
(2/3) / (1/3) = x / 15
2/1 = x / 15
x = 30/1 = 30 months
Therefore, Bharti's money was used for 30 months. However, the options provided in the question do not include 30 months. So, we need to find the closest option to 30 months.
Step 3: Find the closest option to 30 months
- The options provided are:
a) 8 months
b) 10 months
c) 11 months
d) 17 months
- The closest option to 30 months is 10 months, which is option b.
Therefore, the correct answer is option b) 10 months.
Three persons stared a placement business with a capital of Rs. 3000. B invests Rs. 600 less than A and C invests Rs. 300 less than B. What is B's share in a profit of Rs. 886 ?- a)Rs. 443
- b)Rs. 354.40
- c)Rs. 265.80
- d)Rs. 177.20
Correct answer is option 'C'. Can you explain this answer?
Three persons stared a placement business with a capital of Rs. 3000. B invests Rs. 600 less than A and C invests Rs. 300 less than B. What is B's share in a profit of Rs. 886 ?
a)
Rs. 443
b)
Rs. 354.40
c)
Rs. 265.80
d)
Rs. 177.20

|
Aditi Banerjee answered |

A, B and C become partners in a business. A contributes 1/3 rd of the capital for 1/4 th of the time. B contributes 1/5 th of the capital for 1616 th of the time and C the rest of the capital for the whole time. If the profit is Rs. 1820, then the A's share in profit is ?- a)Rs. 130
- b)Rs. 260
- c)Rs. 292
- d)Rs. 304
Correct answer is option 'B'. Can you explain this answer?
A, B and C become partners in a business. A contributes 1/3 rd of the capital for 1/4 th of the time. B contributes 1/5 th of the capital for 1616 th of the time and C the rest of the capital for the whole time. If the profit is Rs. 1820, then the A's share in profit is ?
a)
Rs. 130
b)
Rs. 260
c)
Rs. 292
d)
Rs. 304

|
Nandini Gupta answered |

A, B and C enter into a partnership. They invest Rs. 40000, Rs. 80000 and Rs. 120000 respectively. At the end of the first year, B withdraws Rs. 40000, while at the end of the second year, C withdraws Rs. 80000. In what ratio will the profit be shared at the end of 3 years ?- a)2 : 3 : 5
- b)3 : 4 : 7
- c)4 : 5 :9
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A, B and C enter into a partnership. They invest Rs. 40000, Rs. 80000 and Rs. 120000 respectively. At the end of the first year, B withdraws Rs. 40000, while at the end of the second year, C withdraws Rs. 80000. In what ratio will the profit be shared at the end of 3 years ?
a)
2 : 3 : 5
b)
3 : 4 : 7
c)
4 : 5 :9
d)
None of these

|
Mayank Sharma answered |
A : B : C
(40000 × 36) :(80000 × 12 + 40000 × 24) : (120000 × 24 + 40000 × 12)
= 144 : 192 : 336
= 3 : 4 : 7
(40000 × 36) :(80000 × 12 + 40000 × 24) : (120000 × 24 + 40000 × 12)
= 144 : 192 : 336
= 3 : 4 : 7
A and B entered into partnership with capitals in the ratio 4 : 5. After 3 months, A withdrew 1/4 of his capital and B withdrew 1/5 of his capital. The gain at the end of 10 months was Rs. 760. A's share in this profit is:- a)Rs. 330
- b)Rs. 360
- c)Rs. 380
- d)Rs. 430
Correct answer is option 'A'. Can you explain this answer?
A and B entered into partnership with capitals in the ratio 4 : 5. After 3 months, A withdrew 1/4 of his capital and B withdrew 1/5 of his capital. The gain at the end of 10 months was Rs. 760. A's share in this profit is:
a)
Rs. 330
b)
Rs. 360
c)
Rs. 380
d)
Rs. 430

|
Debanshi Patel answered |
A:B
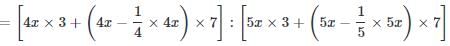
=(12x+21x):(15x+28x)
=33x:43x
=33:43
∴A's share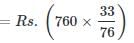
=Rs.330
=(12x+21x):(15x+28x)
=33x:43x
=33:43
∴A's share
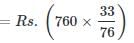
=Rs.330
A and B enter into a partnership with Rs. 50000 and Rs. 60000 respectively. C joins them after x months, contributing Rs. 70000 and B leaves x months before the end of the year. If they share the profit in the ratio of 20 : 18 : 21, then the value of x is = ?- a)3
- b)6
- c)8
- d)9
Correct answer is option 'A'. Can you explain this answer?
A and B enter into a partnership with Rs. 50000 and Rs. 60000 respectively. C joins them after x months, contributing Rs. 70000 and B leaves x months before the end of the year. If they share the profit in the ratio of 20 : 18 : 21, then the value of x is = ?
a)
3
b)
6
c)
8
d)
9

|
Ashwin Malik answered |
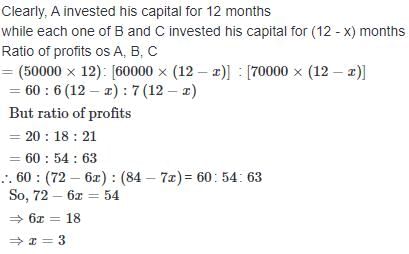
Sumit and Ravi started a business by investing Rs 85000 and 15000 respectively. In what ratio the profit earned after 2 years be divided between Sumit and Ravi respectively.- a)17 : 1
- b)17 : 2
- c)17 : 3
- d)17 : 4
Correct answer is option 'C'. Can you explain this answer?
Sumit and Ravi started a business by investing Rs 85000 and 15000 respectively. In what ratio the profit earned after 2 years be divided between Sumit and Ravi respectively.
a)
17 : 1
b)
17 : 2
c)
17 : 3
d)
17 : 4

|
Abhishek Mehra answered |
Note: If you have clear concept of ratio and proportion chapter then it will really easy for you to solve partnership problems.
P : Q = 85000 : 15000 = 17 : 3
Important to note there that if both have invested for different period of times then we had to multiply with number of months to get the desired ratio.
P : Q = 85000 : 15000 = 17 : 3
Important to note there that if both have invested for different period of times then we had to multiply with number of months to get the desired ratio.
Chapter doubts & questions for Partnership - General Test Preparation for CUET UG 2025 is part of CUET Commerce exam preparation. The chapters have been prepared according to the CUET Commerce exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CUET Commerce 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Partnership - General Test Preparation for CUET UG in English & Hindi are available as part of CUET Commerce exam.
Download more important topics, notes, lectures and mock test series for CUET Commerce Exam by signing up for free.
General Test Preparation for CUET UG
164 videos|628 docs|1136 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup