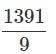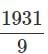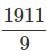All Exams >
Class 5 >
Mathematics for Class 5: NCERT >
All Questions
All questions of Mock Test for Class 5 Exam
A large box contains 18 small boxes and each small box contains 25 chocolate bars. How many chocolate bars are in the large box?- a)400
- b)320
- c)450
- d)156
Correct answer is option 'C'. Can you explain this answer?
A large box contains 18 small boxes and each small box contains 25 chocolate bars. How many chocolate bars are in the large box?
a)
400
b)
320
c)
450
d)
156
|
|
Amit Kumar answered |
No. of Large box = 1
No. of Small box = 18
No. of Chocolate bars in each small box = 25
Total no. of Chocolate bars=25×18=450
No. of Small box = 18
No. of Chocolate bars in each small box = 25
Total no. of Chocolate bars=25×18=450
Simplify the given expression. 3 + 7 × (5 + 1) ÷3 − 2
- a)11
- b)13
- c)15
- d)18
Correct answer is option 'C'. Can you explain this answer?
Simplify the given expression. 3 + 7 × (5 + 1) ÷3 − 2
a)
11
b)
13
c)
15
d)
18
|
|
Edu Impact answered |
3 + 7 × (5 + 1) ÷ 3 − 2
first solve the bracket
3 + 7 x 6 ÷ 3 - 2
now solve divide
3 + 7 x 2 - 2
3 + 14 - 2
15
first solve the bracket
3 + 7 x 6 ÷ 3 - 2
now solve divide
3 + 7 x 2 - 2
3 + 14 - 2
15
A cycle travels at a speed of 45 km/hr. How far will it travel in 36 seconds?
- a)450 m
- b)20 km
- c)36 km
- d)45 km
Correct answer is option 'A'. Can you explain this answer?
A cycle travels at a speed of 45 km/hr. How far will it travel in 36 seconds?
a)
450 m
b)
20 km
c)
36 km
d)
45 km
|
|
Pranav Singh answered |
45 km/h or 45000 meters ÷3600 = 12.5 meters per second x 36 seconds = 450 meters
Answer is the bus travelled a Distance of 450 meters, in Time of 36 seconds, while at Speed of 45 km/h
Answer is the bus travelled a Distance of 450 meters, in Time of 36 seconds, while at Speed of 45 km/h
Mr. & Mrs. Kushal have three daughters. Each of them has two brothers. How many children does the Kushal family have?- a)11
- b)9
- c)7
- d)5
Correct answer is option 'D'. Can you explain this answer?
Mr. & Mrs. Kushal have three daughters. Each of them has two brothers. How many children does the Kushal family have?
a)
11
b)
9
c)
7
d)
5
|
|
Aditi Sharma answered |
The correct answer is 5, all the three girls have two brothers each. So the two boys are the brothers of each of the three sisters.
A box full of buttons has a mass of 2 kg. When it is 1/3 full, its mass is only 800 g. What is the mass of the box?
- a)200 g
- b)150 g
- c)1200 g
- d)600 g
Correct answer is option 'A'. Can you explain this answer?
A box full of buttons has a mass of 2 kg. When it is 1/3 full, its mass is only 800 g. What is the mass of the box?
a)
200 g
b)
150 g
c)
1200 g
d)
600 g
|
|
Stoneridge Institute answered |
let m be mass of box and x be mass of button
m+x=2000 converting 2 kg into g
m+x/3=800
3m+x=2400
2m=400
m=200g
m+x=2000 converting 2 kg into g
m+x/3=800
3m+x=2400
2m=400
m=200g
Anish went to sleep at 9:00 p.m. and woke up at 6:30 a.m. What is the total number of hours Anish slept?- a)3 hours
- b)7 hours
- c)81 hours
- d)91 hours
Correct answer is option 'D'. Can you explain this answer?
Anish went to sleep at 9:00 p.m. and woke up at 6:30 a.m. What is the total number of hours Anish slept?
a)
3 hours
b)
7 hours
c)
81 hours
d)
91 hours
|
|
Aditya Menon answered |
Total number of hours Anish sleep will be 9.5 hours
If 84 is a common multiple of 4 and n, which of the following is not a value of n?- a)6
- b)7
- c)21
- d)24
Correct answer is option 'D'. Can you explain this answer?
If 84 is a common multiple of 4 and n, which of the following is not a value of n?
a)
6
b)
7
c)
21
d)
24
|
|
Saptarshi Kapoor answered |
To find the value of n that is not a common multiple of 4 and 84, we need to determine the factors of 84 and eliminate the values of n that have these factors.
Factors of 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Now, let's check if each option is a factor of 84:
a) Is 6 a factor of 84? Yes, 6 is a factor of 84.
b) Is 7 a factor of 84? Yes, 7 is a factor of 84.
c) Is 21 a factor of 84? Yes, 21 is a factor of 84.
d) Is 24 a factor of 84? No, 24 is not a factor of 84.
Therefore, the value of n that is not a common multiple of 4 and 84 is 24.
Factors of 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Now, let's check if each option is a factor of 84:
a) Is 6 a factor of 84? Yes, 6 is a factor of 84.
b) Is 7 a factor of 84? Yes, 7 is a factor of 84.
c) Is 21 a factor of 84? Yes, 21 is a factor of 84.
d) Is 24 a factor of 84? No, 24 is not a factor of 84.
Therefore, the value of n that is not a common multiple of 4 and 84 is 24.
A circle has diameter 1 m, find radius.- a)2 m
- b)0.5 cm
- c)50 cm
- d)1 m
Correct answer is option 'C'. Can you explain this answer?
A circle has diameter 1 m, find radius.
a)
2 m
b)
0.5 cm
c)
50 cm
d)
1 m
|
|
Ruvaida Reyaz answered |
1 m is equal to 100 cm we have to divide 100 into equal part which is 50 cm so the ans is 50 cm...
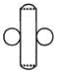
Which part of the circle does segment U represent?
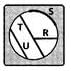
- a)Arc
- b)Diameter
- c)Chord
- d)Radius
Correct answer is option 'C'. Can you explain this answer?
Which part of the circle does segment U represent?


a)
Arc
b)
Diameter
c)
Chord
d)
Radius
|
|
Avinash Patel answered |
A chord of a circle divides the circle into two regions, which are called the segments of the circle. The minor segment is the region bounded by the chord and the minor arc intercepted by the chord. The major segment is the region bounded by the chord and the major arc intercepted by the chord.
If P + Q = 105 and P − Q = 45, what is P:Q ?- a)1 : 5
- b)2 : 5
- c)3 : 5
- d)5 : 2
Correct answer is option 'D'. Can you explain this answer?
If P + Q = 105 and P − Q = 45, what is P:Q ?
a)
1 : 5
b)
2 : 5
c)
3 : 5
d)
5 : 2
|
|
Bibek Shah answered |
I'm sorry, but your question is incomplete. Can you please provide more information or clarify your question?
Eight plants were placed in a row along a street. The distance between the second and the fifth plant was 6 m. What is the distance between the third and the last plant?- a)2 m
- b)12 m
- c)8 m
- d)10 m
Correct answer is option 'D'. Can you explain this answer?
Eight plants were placed in a row along a street. The distance between the second and the fifth plant was 6 m. What is the distance between the third and the last plant?
a)
2 m
b)
12 m
c)
8 m
d)
10 m
|
|
Maulik Singh answered |
Question Analysis:
- There are eight plants in a row along a street.
- The distance between the second and fifth plants is 6 m.
- We need to find the distance between the third and last plant.
Answer Explanation:
To solve this problem, we need to use some basic math concepts. Let us break down the problem into steps:
Step 1: Find the distance between the first and fifth plants.
- We know that the distance between the second and fifth plants is 6 m.
- Therefore, the distance between the first and fifth plants would be 6 m + the distance between the first and second plants.
- As all plants are placed in a row, the distance between each consecutive plant is the same.
- Hence, the distance between the first and second plants is the same as the distance between the fifth and sixth plants.
- Therefore, the distance between the first and fifth plants would be 6 m + the distance between the fifth and sixth plants.
- We know that there are eight plants in total, so the distance between the first and eighth plants would be the sum of the distances between the first and fifth plants and the fifth and eighth plants.
- Therefore, the distance between the first and eighth plants would be:
6 m + distance between fifth and sixth plant + distance between sixth and seventh plant + distance between seventh and eighth plant
Step 2: Find the distance between the third and last plant.
- We know that the distance between the first and eighth plants is the sum of the distances between the first and fifth plants and the fifth and eighth plants.
- We also know that the distance between the first and third plants is the sum of the distances between the first and second plants and the second and third plants.
- Therefore, the distance between the third and eighth plants would be:
(distance between first and eighth plants) - (distance between first and third plants)
- Substituting the values, we get:
(distance between third and eighth plants) = (6 m + distance between fifth and sixth plant + distance between sixth and seventh plant + distance between seventh and eighth plant) - (distance between first and second plant + distance between second and third plant)
Step 3: Calculate the distance between the third and last plant.
- We know that the last plant is the eighth plant.
- Therefore, the distance between the third and last plant would be the sum of the distances between the third and fourth plants, fourth and fifth plants, fifth and sixth plants, sixth and seventh plants, and seventh and eighth plants.
- Substituting the values, we get:
(distance between third and last plant) = distance between third and fourth plant + distance between fourth and fifth plant + distance between fifth and sixth plant + distance between sixth and seventh plant + distance between seventh and eighth plant
- Simplifying the equation, we get:
(distance between third and last plant) = distance between first and eighth plant - (distance between first and second plant + distance between second and third plant)
(distance between third and last plant) = (6 m + distance between fifth and sixth plant + distance between sixth and seventh plant + distance between seventh and eighth plant) - (distance between first and second plant + distance between second and third plant)
(distance between third and last plant) = 6 m + 4x - 2x
(distance between third and last plant) = 6 m + 2x
- Here, x represents the distance between each consecutive plant
- There are eight plants in a row along a street.
- The distance between the second and fifth plants is 6 m.
- We need to find the distance between the third and last plant.
Answer Explanation:
To solve this problem, we need to use some basic math concepts. Let us break down the problem into steps:
Step 1: Find the distance between the first and fifth plants.
- We know that the distance between the second and fifth plants is 6 m.
- Therefore, the distance between the first and fifth plants would be 6 m + the distance between the first and second plants.
- As all plants are placed in a row, the distance between each consecutive plant is the same.
- Hence, the distance between the first and second plants is the same as the distance between the fifth and sixth plants.
- Therefore, the distance between the first and fifth plants would be 6 m + the distance between the fifth and sixth plants.
- We know that there are eight plants in total, so the distance between the first and eighth plants would be the sum of the distances between the first and fifth plants and the fifth and eighth plants.
- Therefore, the distance between the first and eighth plants would be:
6 m + distance between fifth and sixth plant + distance between sixth and seventh plant + distance between seventh and eighth plant
Step 2: Find the distance between the third and last plant.
- We know that the distance between the first and eighth plants is the sum of the distances between the first and fifth plants and the fifth and eighth plants.
- We also know that the distance between the first and third plants is the sum of the distances between the first and second plants and the second and third plants.
- Therefore, the distance between the third and eighth plants would be:
(distance between first and eighth plants) - (distance between first and third plants)
- Substituting the values, we get:
(distance between third and eighth plants) = (6 m + distance between fifth and sixth plant + distance between sixth and seventh plant + distance between seventh and eighth plant) - (distance between first and second plant + distance between second and third plant)
Step 3: Calculate the distance between the third and last plant.
- We know that the last plant is the eighth plant.
- Therefore, the distance between the third and last plant would be the sum of the distances between the third and fourth plants, fourth and fifth plants, fifth and sixth plants, sixth and seventh plants, and seventh and eighth plants.
- Substituting the values, we get:
(distance between third and last plant) = distance between third and fourth plant + distance between fourth and fifth plant + distance between fifth and sixth plant + distance between sixth and seventh plant + distance between seventh and eighth plant
- Simplifying the equation, we get:
(distance between third and last plant) = distance between first and eighth plant - (distance between first and second plant + distance between second and third plant)
(distance between third and last plant) = (6 m + distance between fifth and sixth plant + distance between sixth and seventh plant + distance between seventh and eighth plant) - (distance between first and second plant + distance between second and third plant)
(distance between third and last plant) = 6 m + 4x - 2x
(distance between third and last plant) = 6 m + 2x
- Here, x represents the distance between each consecutive plant
Sam volunteers at an animal shelter 3.5 hrs every week. How many hours would Sam volunteer in 26 weeks?- a)78 hours
- b)90 hours
- c)91 hours
- d)910 hours
Correct answer is option 'C'. Can you explain this answer?
Sam volunteers at an animal shelter 3.5 hrs every week. How many hours would Sam volunteer in 26 weeks?
a)
78 hours
b)
90 hours
c)
91 hours
d)
910 hours

|
Khan Little answered |
91 hours.... because it can be multiplied and saw the correct option. thank you for asking but if I have any mistake.. please correct me
The numbers 2, 3, 4 and 6 are all factors of which number?- a)12
- b)15
- c)16
- d)18
Correct answer is option 'A'. Can you explain this answer?
The numbers 2, 3, 4 and 6 are all factors of which number?
a)
12
b)
15
c)
16
d)
18
|
|
Rohit Chawla answered |
The common factors of all these numbers are 12.
What is the measure of the third angle in a right angled triangle, whose one angle is 52∘?- a)38∘
- b)48∘
- c)52∘
- d)88∘
Correct answer is option 'A'. Can you explain this answer?
What is the measure of the third angle in a right angled triangle, whose one angle is 52∘?
a)
38∘
b)
48∘
c)
52∘
d)
88∘
|
|
Aarushi gupta answered |
The total measure of all 3 angles of any triangle is 180degree. Every right-angled triangle or right triangle has one right angle, and that right angle measures 90 degree; therefore, we can write the following equation for our given right triangle:
The measure of the right angle + the given measure of one of the acute angles + the measure of the third angle = 180degree
90degree + 52degree + the measure of the third angle = 180degree
142degree + the measure of the third angle = 180degree
Now, subtract 142degree from both sides of the equation:
142degree - 142degree + the measure of the third angle = 180degree - 142degree
The measure of the third angle = 38degree
What is the angle between two hands of the clock at 2: 30?- a)100o
- b)105o
- c)120o
- d)110o
Correct answer is option 'B'. Can you explain this answer?
What is the angle between two hands of the clock at 2: 30?
a)
100o
b)
105o
c)
120o
d)
110o
|
|
Jay Rane answered |
To find the angle between the two hands of a clock at a given time, we need to consider the positions of both hands relative to the 12 o'clock position.
At 2:30, the hour hand is pointing directly at the 2, while the minute hand is pointing at the 6.
The hour hand moves 30 degrees in one hour and 0.5 degrees in one minute. Since it is pointing at the 2, it has already moved 60 degrees (2 x 30 degrees) from the 12 o'clock position.
The minute hand moves 360 degrees in one hour and 6 degrees in one minute. Since it is pointing at the 6, it has already moved 180 degrees (6 x 30 degrees) from the 12 o'clock position.
Now, we can find the angle between the two hands by subtracting the smaller angle from the larger angle. In this case, the angle between the hour and minute hand is:
Angle = Larger angle - Smaller angle
= 180 degrees - 60 degrees
= 120 degrees
Therefore, the angle between the two hands of the clock at 2:30 is 120 degrees.
So, the correct answer is option C) 120o.
At 2:30, the hour hand is pointing directly at the 2, while the minute hand is pointing at the 6.
The hour hand moves 30 degrees in one hour and 0.5 degrees in one minute. Since it is pointing at the 2, it has already moved 60 degrees (2 x 30 degrees) from the 12 o'clock position.
The minute hand moves 360 degrees in one hour and 6 degrees in one minute. Since it is pointing at the 6, it has already moved 180 degrees (6 x 30 degrees) from the 12 o'clock position.
Now, we can find the angle between the two hands by subtracting the smaller angle from the larger angle. In this case, the angle between the hour and minute hand is:
Angle = Larger angle - Smaller angle
= 180 degrees - 60 degrees
= 120 degrees
Therefore, the angle between the two hands of the clock at 2:30 is 120 degrees.
So, the correct answer is option C) 120o.
The scale shown is balanced. Each cube on the left side weighs the same amount.

How much does one of the cubes weigh?- a)1 gram
- b)4 grams
- c)5 grams
- d)20 grams
Correct answer is option 'C'. Can you explain this answer?
The scale shown is balanced. Each cube on the left side weighs the same amount.

How much does one of the cubes weigh?

How much does one of the cubes weigh?
a)
1 gram
b)
4 grams
c)
5 grams
d)
20 grams
|
|
Akash Tiwari answered |
The scale is balanced, indicating that the weights on both sides are equal.
To determine the weight of one cube, follow these steps:
- Count the number of cubes on the left side.
- Identify the total weight on the right side.
- Divide the total weight on the right by the number of cubes on the left.
For example:
- If there are 4 cubes on the left and the total weight on the right is 20 grams, then:
- Weight of one cube = Total weight / Number of cubes
- Weight of one cube = 20 grams / 4 = 5 grams.
Thus, one cube weighs 5 grams.
A radio was sold for Rs. 572 at a profit of Rs. 24. Find its cost price.- a)Rs. 596
- b)Rs. 558
- c)Rs. 548
- d)Rs. 580
Correct answer is option 'C'. Can you explain this answer?
A radio was sold for Rs. 572 at a profit of Rs. 24. Find its cost price.
a)
Rs. 596
b)
Rs. 558
c)
Rs. 548
d)
Rs. 580
|
|
Pallavi Gupta answered |
Given, selling price of radio = Rs. 572 and profit = Rs. 24.
Let the cost price of radio be x.
We know that, selling price = cost price + profit
Therefore, x + 24 = 572
Solving for x, we get:
x = 572 - 24
x = 548
Hence, the cost price of radio is Rs. 548.
Therefore, option C is the correct answer.
Let the cost price of radio be x.
We know that, selling price = cost price + profit
Therefore, x + 24 = 572
Solving for x, we get:
x = 572 - 24
x = 548
Hence, the cost price of radio is Rs. 548.
Therefore, option C is the correct answer.
If 2805 ÷ 2.55=1100, find the quotient of 280.5 ÷ 25.5.- a)1.1
- b)1.01
- c)0.11
- d)11
Correct answer is option 'D'. Can you explain this answer?
If 2805 ÷ 2.55=1100, find the quotient of 280.5 ÷ 25.5.
a)
1.1
b)
1.01
c)
0.11
d)
11
|
|
Aryan Khara answered |
OH! Anshuman kumar its your good question.
280.5 ÷ 25.5= 11.
280.5 ÷ 25.5= 11.
What is the H.C.F. of 120, 144 and 216?- a)38
- b)24
- c)120
- d)144
Correct answer is option 'B'. Can you explain this answer?
What is the H.C.F. of 120, 144 and 216?
a)
38
b)
24
c)
120
d)
144
|
|
Ayush Thakur answered |
Correct option will NUMBER(*B*)
If 3 x 2006 = 2005 + 2007 + x, find x.- a)2004
- b)2005
- c)2006
- d)2007
Correct answer is option 'C'. Can you explain this answer?
If 3 x 2006 = 2005 + 2007 + x, find x.
a)
2004
b)
2005
c)
2006
d)
2007
|
|
Gargi Rane answered |
Given that 3 x 2006 = 2005 2007 x
To find the value of x, we can simplify the given expression as:
3 x 2006 = 6018 (multiplying both sides by 3)
2005 2007 x = 6018 (substituting the value of 3 x 2006)
Now, we can isolate the value of x by performing simple algebraic operations:
2005 2007 x = 6018
2007 x = 6018 - 2005 (subtracting 2005 from both sides)
2007 x = 4013
x = 4013/2007 (dividing both sides by 2007)
x = 2
Therefore, the value of x is 2, which corresponds to option C.
To find the value of x, we can simplify the given expression as:
3 x 2006 = 6018 (multiplying both sides by 3)
2005 2007 x = 6018 (substituting the value of 3 x 2006)
Now, we can isolate the value of x by performing simple algebraic operations:
2005 2007 x = 6018
2007 x = 6018 - 2005 (subtracting 2005 from both sides)
2007 x = 4013
x = 4013/2007 (dividing both sides by 2007)
x = 2
Therefore, the value of x is 2, which corresponds to option C.
What is the value of X in 80788, 80888, 80988, X?- a)81,008
- b)81,088
- c)81,889
- d)81,988
Correct answer is option 'B'. Can you explain this answer?
What is the value of X in 80788, 80888, 80988, X?
a)
81,008
b)
81,088
c)
81,889
d)
81,988
|
|
Monika Nehra answered |
B) 81,088 because if we subtract 80,888 from80788 and 80988 from 80788 both gives remainder -100 so means all digit have same difference so if we subtract 81,088 from 80988 it also gives -100 so right answer is 81,088
Aayesha made a profit of Rs. 395 on a pen she sold for Rs. 6235. At what price did she buy it?- a)Rs. 7777
- b)Rs. 5840
- c)Rs. 6630
- d)Rs. 9999
Correct answer is option 'B'. Can you explain this answer?
Aayesha made a profit of Rs. 395 on a pen she sold for Rs. 6235. At what price did she buy it?
a)
Rs. 7777
b)
Rs. 5840
c)
Rs. 6630
d)
Rs. 9999
|
|
Bibek Shah answered |
Given:
- Aayesha made a profit of Rs. 395
- She sold the pen for Rs. 6235
To find: At what price did she buy the pen?
Let's assume the cost price of the pen to be x.
Profit = Selling Price - Cost Price
395 = 6235 - x
Solving for x:
x = 6235 - 395
x = 5840
Therefore, the cost price of the pen is Rs. 5840.
Hence, option 'B' is the correct answer.
- Aayesha made a profit of Rs. 395
- She sold the pen for Rs. 6235
To find: At what price did she buy the pen?
Let's assume the cost price of the pen to be x.
Profit = Selling Price - Cost Price
395 = 6235 - x
Solving for x:
x = 6235 - 395
x = 5840
Therefore, the cost price of the pen is Rs. 5840.
Hence, option 'B' is the correct answer.
Observe the given number line.
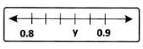
Which decimal number does y represent?- a)0.83
- b)0.85
- c)0.86
- d)0.88
Correct answer is option 'C'. Can you explain this answer?
Observe the given number line.

Which decimal number does y represent?

Which decimal number does y represent?
a)
0.83
b)
0.85
c)
0.86
d)
0.88
|
|
Suresh Kumar answered |
First line after 8 represents 8.2 2nd line 8.4 3rd line 8.6
so it is answer
so it is answer
At what time will the angle between the hours hand and the minutes hand be the greatest?- a)1 : 00
- b)3 : 15
- c)5 : 30
- d)6 : 30
Correct answer is option 'D'. Can you explain this answer?
At what time will the angle between the hours hand and the minutes hand be the greatest?
a)
1 : 00
b)
3 : 15
c)
5 : 30
d)
6 : 30
|
|
Pallavi Gupta answered |
Understanding the Clock Hands
The angle between the hour hand and the minute hand of a clock varies throughout the hour. To determine when this angle is greatest, we need to analyze the positions of the hands at different times.
Key Points about Clock Hands:
- The hour hand moves at a rate of 30 degrees per hour (360 degrees / 12 hours).
- The minute hand moves at a rate of 6 degrees per minute (360 degrees / 60 minutes).
- The angle between the two hands can be calculated using their respective positions.
Analyzing Each Option:
- 1:00:
- Hour hand at 30 degrees (1 * 30)
- Minute hand at 0 degrees
- Angle = 30 degrees
- 3:15:
- Hour hand at 97.5 degrees (3 * 30 + 15 * 0.5)
- Minute hand at 90 degrees (15 * 6)
- Angle = 7.5 degrees
- 5:30:
- Hour hand at 165 degrees (5 * 30 + 30 * 0.5)
- Minute hand at 180 degrees (30 * 6)
- Angle = 15 degrees
- 6:30:
- Hour hand at 195 degrees (6 * 30 + 30 * 0.5)
- Minute hand at 180 degrees (30 * 6)
- Angle = 15 degrees
Determining the Greatest Angle:
Among the options analyzed, the greatest angle occurs at 6:30 when the hour hand is at 195 degrees and the minute hand is at 180 degrees, resulting in an angle of 15 degrees. However, this must be understood in the context of the clock's total movement throughout the hour.
Conclusion:
Thus, the greatest angle between the hour and minute hands occurs at 6:30, making option 'D' the correct answer.
The angle between the hour hand and the minute hand of a clock varies throughout the hour. To determine when this angle is greatest, we need to analyze the positions of the hands at different times.
Key Points about Clock Hands:
- The hour hand moves at a rate of 30 degrees per hour (360 degrees / 12 hours).
- The minute hand moves at a rate of 6 degrees per minute (360 degrees / 60 minutes).
- The angle between the two hands can be calculated using their respective positions.
Analyzing Each Option:
- 1:00:
- Hour hand at 30 degrees (1 * 30)
- Minute hand at 0 degrees
- Angle = 30 degrees
- 3:15:
- Hour hand at 97.5 degrees (3 * 30 + 15 * 0.5)
- Minute hand at 90 degrees (15 * 6)
- Angle = 7.5 degrees
- 5:30:
- Hour hand at 165 degrees (5 * 30 + 30 * 0.5)
- Minute hand at 180 degrees (30 * 6)
- Angle = 15 degrees
- 6:30:
- Hour hand at 195 degrees (6 * 30 + 30 * 0.5)
- Minute hand at 180 degrees (30 * 6)
- Angle = 15 degrees
Determining the Greatest Angle:
Among the options analyzed, the greatest angle occurs at 6:30 when the hour hand is at 195 degrees and the minute hand is at 180 degrees, resulting in an angle of 15 degrees. However, this must be understood in the context of the clock's total movement throughout the hour.
Conclusion:
Thus, the greatest angle between the hour and minute hands occurs at 6:30, making option 'D' the correct answer.
Which of these is formed when two rays emerge from a common end point?- a)A line
- b)A ray
- c)A line segment
- d)An angle
Correct answer is option 'D'. Can you explain this answer?
Which of these is formed when two rays emerge from a common end point?
a)
A line
b)
A ray
c)
A line segment
d)
An angle
|
|
Glitz Classes answered |
When two rays emerge from a common endpoint, they form an angle.
Here’s a brief explanation:
- Rays are straight lines that start at a point and extend infinitely in one direction.
- When two rays share the same starting point, they create an angle between them.
- The measure of this angle is determined by the separation of the two rays.
A cuboids measures 46m × 32m × 16m. How many cubes of edge 8 m can be cut from it?- a)46
- b)72
- c)36
- d)58
Correct answer is option 'A'. Can you explain this answer?
A cuboids measures 46m × 32m × 16m. How many cubes of edge 8 m can be cut from it?
a)
46
b)
72
c)
36
d)
58
|
|
Ruchi Basu answered |
To determine the volume of a cuboid, we need three measurements: length, width, and height. If we are given only one measurement of 46m, we cannot calculate the volume of the cuboid.
There were 15l of oil in a can. A certain amount of oil is used to fill up 4 bottles each of capacity 0.5l . How many similar bottles are needed to fill up the remaining oil?- a)13
- b)26
- c)39
- d)42
Correct answer is option 'B'. Can you explain this answer?
There were 15l of oil in a can. A certain amount of oil is used to fill up 4 bottles each of capacity 0.5l . How many similar bottles are needed to fill up the remaining oil?
a)
13
b)
26
c)
39
d)
42
|
|
Sameer Sengupta answered |
Problem:
There were 15 liters of oil in a can. A certain amount of oil is used to fill up 4 bottles each with a capacity of 0.5 liters. How many similar bottles are needed to fill up the remaining oil?
Solution:
To solve this problem, we need to find the amount of oil remaining after filling up the 4 bottles, and then calculate the number of similar bottles needed to fill up the remaining oil.
Step 1: Calculate the amount of oil used to fill up 4 bottles:
Each bottle has a capacity of 0.5 liters, and we have filled up 4 bottles. Therefore, the amount of oil used is:
0.5 liters/bottle * 4 bottles = 2 liters
Step 2: Calculate the amount of oil remaining in the can:
We started with 15 liters of oil in the can, and we used 2 liters to fill up the 4 bottles. Therefore, the amount of oil remaining in the can is:
15 liters - 2 liters = 13 liters
Step 3: Calculate the number of similar bottles needed to fill up the remaining oil:
Now that we know there are 13 liters of oil remaining, we can calculate the number of similar bottles needed to fill up this amount. Since each bottle has a capacity of 0.5 liters, the number of bottles needed is:
13 liters / 0.5 liters/bottle = 26 bottles
Therefore, the correct answer is option B, 26 bottles.
There were 15 liters of oil in a can. A certain amount of oil is used to fill up 4 bottles each with a capacity of 0.5 liters. How many similar bottles are needed to fill up the remaining oil?
Solution:
To solve this problem, we need to find the amount of oil remaining after filling up the 4 bottles, and then calculate the number of similar bottles needed to fill up the remaining oil.
Step 1: Calculate the amount of oil used to fill up 4 bottles:
Each bottle has a capacity of 0.5 liters, and we have filled up 4 bottles. Therefore, the amount of oil used is:
0.5 liters/bottle * 4 bottles = 2 liters
Step 2: Calculate the amount of oil remaining in the can:
We started with 15 liters of oil in the can, and we used 2 liters to fill up the 4 bottles. Therefore, the amount of oil remaining in the can is:
15 liters - 2 liters = 13 liters
Step 3: Calculate the number of similar bottles needed to fill up the remaining oil:
Now that we know there are 13 liters of oil remaining, we can calculate the number of similar bottles needed to fill up this amount. Since each bottle has a capacity of 0.5 liters, the number of bottles needed is:
13 liters / 0.5 liters/bottle = 26 bottles
Therefore, the correct answer is option B, 26 bottles.
Arrange the following in ascending order of their circumference.(I) 5 rupee coin
(II) Dial of a wall clock which is round
(III) a child's bangle
(IV) a scooter wheel
(V) a ten rupee coin- a)V, IV, III, II, I
- b)I, II, III, IV, V
- c)I, III, V, IV, II
- d)I, V, III, II, IV
Correct answer is option 'D'. Can you explain this answer?
Arrange the following in ascending order of their circumference.
(I) 5 rupee coin
(II) Dial of a wall clock which is round
(III) a child's bangle
(IV) a scooter wheel
(V) a ten rupee coin
(II) Dial of a wall clock which is round
(III) a child's bangle
(IV) a scooter wheel
(V) a ten rupee coin
a)
V, IV, III, II, I
b)
I, II, III, IV, V
c)
I, III, V, IV, II
d)
I, V, III, II, IV

|
Jay Singh answered |
A and b
The average mark of Ravi in 5 tests is 50. What are his total marks?- a)10
- b)100
- c)250
- d)200
Correct answer is option 'C'. Can you explain this answer?
The average mark of Ravi in 5 tests is 50. What are his total marks?
a)
10
b)
100
c)
250
d)
200

|
Indu Gupta answered |
To find Ravi's total marks:
- Calculate the average mark: 50.
- Multiply the average by the number of tests: 5.
- Thus, total marks = 50 x 5 = 250.
Ravi's total marks in the tests are 250.
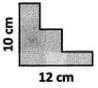
ABCD is a square of side 2016 cm. It is divided as shown in the figure into four equal squares. The top right hand side square is again divided into 4 equal squares. Again the top right hand square is divided into four equal squares.
Find the side of each smallest square.- a)1002 cm
- b)1004 cm
- c)502 cm
- d)252 cm
Correct answer is option 'D'. Can you explain this answer?
ABCD is a square of side 2016 cm. It is divided as shown in the figure into four equal squares. The top right hand side square is again divided into 4 equal squares. Again the top right hand square is divided into four equal squares.

Find the side of each smallest square.
a)
1002 cm
b)
1004 cm
c)
502 cm
d)
252 cm

|
Mira Sharma answered |
252 cm
A cuboid measures 36 m x 24 m x 18 m. How many cubes of edge 6 m can be cut from it.- a)36
- b)72
- c)144
- d)288
Correct answer is option 'B'. Can you explain this answer?
A cuboid measures 36 m x 24 m x 18 m. How many cubes of edge 6 m can be cut from it.
a)
36
b)
72
c)
144
d)
288
|
|
Prabhat mehra answered |
Calculating the Volume of the Cuboid
To determine how many cubes can be cut from the cuboid, we first need to find the volume of the cuboid.
- Volume of the cuboid = Length x Width x Height
- Volume = 36 m x 24 m x 18 m
- Volume = 15552 cubic meters
Calculating the Volume of One Cube
Next, we calculate the volume of one cube with an edge of 6 m.
- Volume of one cube = Side x Side x Side
- Volume = 6 m x 6 m x 6 m
- Volume = 216 cubic meters
Finding the Number of Cubes
Now, we can find out how many cubes can be cut from the cuboid by dividing the volume of the cuboid by the volume of one cube.
- Number of cubes = Volume of the cuboid / Volume of one cube
- Number of cubes = 15552 cubic meters / 216 cubic meters
- Number of cubes = 72
Conclusion
Thus, the total number of 6 m cubes that can be cut from the cuboid measuring 36 m x 24 m x 18 m is:
- Option B: 72 cubes
This calculation shows that the correct answer is indeed option 'B'.
To determine how many cubes can be cut from the cuboid, we first need to find the volume of the cuboid.
- Volume of the cuboid = Length x Width x Height
- Volume = 36 m x 24 m x 18 m
- Volume = 15552 cubic meters
Calculating the Volume of One Cube
Next, we calculate the volume of one cube with an edge of 6 m.
- Volume of one cube = Side x Side x Side
- Volume = 6 m x 6 m x 6 m
- Volume = 216 cubic meters
Finding the Number of Cubes
Now, we can find out how many cubes can be cut from the cuboid by dividing the volume of the cuboid by the volume of one cube.
- Number of cubes = Volume of the cuboid / Volume of one cube
- Number of cubes = 15552 cubic meters / 216 cubic meters
- Number of cubes = 72
Conclusion
Thus, the total number of 6 m cubes that can be cut from the cuboid measuring 36 m x 24 m x 18 m is:
- Option B: 72 cubes
This calculation shows that the correct answer is indeed option 'B'.
A man bought 50 dozen of bananas for Rs. 500.24 bananas got spoiled during transport. He sold remaining bananas at the rate of Rs. 12 per dozen. Find out his profit/loss in the transaction.- a)Rs. 76 loss
- b)Rs. 76 profit
- c)Rs. 98 loss
- d)Rs. 98 profit
Correct answer is option 'B'. Can you explain this answer?
A man bought 50 dozen of bananas for Rs. 500.24 bananas got spoiled during transport. He sold remaining bananas at the rate of Rs. 12 per dozen. Find out his profit/loss in the transaction.
a)
Rs. 76 loss
b)
Rs. 76 profit
c)
Rs. 98 loss
d)
Rs. 98 profit
|
|
Mehul Kapoor answered |
Given:
- Number of bananas bought = 50 dozen
- Cost of bananas = Rs. 500
- Bananas spoiled during transport = 24
- Selling price of remaining bananas = Rs. 12 per dozen
To find:
- Profit or loss in the transaction
Calculation:
Step 1: Calculate the cost price (CP) of the bananas
- Cost of 50 dozen bananas = Rs. 500
- Cost of 1 dozen bananas = Rs. 500/50 = Rs. 10
- Cost price of 24 bananas = Rs. 10 x 24 = Rs. 240
- Cost price of remaining bananas = Rs. 500 - Rs. 240 = Rs. 260
Step 2: Calculate the selling price (SP) of the remaining bananas
- Selling price of 1 dozen bananas = Rs. 12
- Selling price of remaining bananas = Rs. 12 x (50 - 24) = Rs. 12 x 26 = Rs. 312
Step 3: Calculate the profit or loss
- Profit/Loss = SP - CP
- Profit/Loss = Rs. 312 - Rs. 260 = Rs. 52
Step 4: Determine the answer option
- The profit/loss calculated is Rs. 52
- None of the given answer options match the calculated value of Rs. 52
Therefore, the answer provided in the options is incorrect.
- Number of bananas bought = 50 dozen
- Cost of bananas = Rs. 500
- Bananas spoiled during transport = 24
- Selling price of remaining bananas = Rs. 12 per dozen
To find:
- Profit or loss in the transaction
Calculation:
Step 1: Calculate the cost price (CP) of the bananas
- Cost of 50 dozen bananas = Rs. 500
- Cost of 1 dozen bananas = Rs. 500/50 = Rs. 10
- Cost price of 24 bananas = Rs. 10 x 24 = Rs. 240
- Cost price of remaining bananas = Rs. 500 - Rs. 240 = Rs. 260
Step 2: Calculate the selling price (SP) of the remaining bananas
- Selling price of 1 dozen bananas = Rs. 12
- Selling price of remaining bananas = Rs. 12 x (50 - 24) = Rs. 12 x 26 = Rs. 312
Step 3: Calculate the profit or loss
- Profit/Loss = SP - CP
- Profit/Loss = Rs. 312 - Rs. 260 = Rs. 52
Step 4: Determine the answer option
- The profit/loss calculated is Rs. 52
- None of the given answer options match the calculated value of Rs. 52
Therefore, the answer provided in the options is incorrect.
There are 5 Mondays in the month of March in a year. Which day of the week below could not appear in this month also five times?- a)Thursday
- b)Wednesday
- c)Sunday
- d)Saturday
Correct answer is option 'A'. Can you explain this answer?
There are 5 Mondays in the month of March in a year. Which day of the week below could not appear in this month also five times?
a)
Thursday
b)
Wednesday
c)
Sunday
d)
Saturday
|
|
Rhea shah answered |
Explanation:
To determine which day of the week could not appear in the month of March five times, we need to analyze the number of days in March and how they align with the days of the week.
Number of Days in March:
- March has 31 days.
Finding the Pattern:
- To determine the number of times a specific day of the week appears in a given month, we need to divide the total number of days in that month by 7 (the number of days in a week).
- The remainder will indicate the number of additional days that go beyond the complete weeks.
- For example, if the remainder is 0, it means the month starts and ends on the same day of the week, resulting in each day appearing exactly 4 times.
- If the remainder is 1, it means there is one additional day beyond the complete weeks, resulting in one day appearing 5 times, and the rest appearing 4 times.
- By analyzing the patterns for each day of the week, we can determine which day could not appear in the month five times.
Patterns for Each Day of the Week:
- Monday: In a month with 31 days, there will always be 4 Mondays and an additional day that may vary.
- Tuesday: In a month with 31 days, there will always be 4 Tuesdays and an additional day that may vary.
- Wednesday: In a month with 31 days, there will always be 4 Wednesdays and an additional day that may vary.
- Thursday: In a month with 31 days, there will always be 4 Thursdays and an additional day that may vary.
- Friday: In a month with 31 days, there will always be 4 Fridays and an additional day that may vary.
- Saturday: In a month with 31 days, there will always be 4 Saturdays and an additional day that may vary.
- Sunday: In a month with 31 days, there will always be 4 Sundays and an additional day that may vary.
Conclusion:
- Based on the analysis, every day of the week could appear five times in the month of March, as long as there are 31 days.
- Therefore, none of the given options (Thursday, Wednesday, Sunday, Saturday) could not appear in this month five times.
- The correct answer is option 'A' (Thursday).
To determine which day of the week could not appear in the month of March five times, we need to analyze the number of days in March and how they align with the days of the week.
Number of Days in March:
- March has 31 days.
Finding the Pattern:
- To determine the number of times a specific day of the week appears in a given month, we need to divide the total number of days in that month by 7 (the number of days in a week).
- The remainder will indicate the number of additional days that go beyond the complete weeks.
- For example, if the remainder is 0, it means the month starts and ends on the same day of the week, resulting in each day appearing exactly 4 times.
- If the remainder is 1, it means there is one additional day beyond the complete weeks, resulting in one day appearing 5 times, and the rest appearing 4 times.
- By analyzing the patterns for each day of the week, we can determine which day could not appear in the month five times.
Patterns for Each Day of the Week:
- Monday: In a month with 31 days, there will always be 4 Mondays and an additional day that may vary.
- Tuesday: In a month with 31 days, there will always be 4 Tuesdays and an additional day that may vary.
- Wednesday: In a month with 31 days, there will always be 4 Wednesdays and an additional day that may vary.
- Thursday: In a month with 31 days, there will always be 4 Thursdays and an additional day that may vary.
- Friday: In a month with 31 days, there will always be 4 Fridays and an additional day that may vary.
- Saturday: In a month with 31 days, there will always be 4 Saturdays and an additional day that may vary.
- Sunday: In a month with 31 days, there will always be 4 Sundays and an additional day that may vary.
Conclusion:
- Based on the analysis, every day of the week could appear five times in the month of March, as long as there are 31 days.
- Therefore, none of the given options (Thursday, Wednesday, Sunday, Saturday) could not appear in this month five times.
- The correct answer is option 'A' (Thursday).
Chapter doubts & questions for Mock Test - Mathematics for Class 5: NCERT 2025 is part of Class 5 exam preparation. The chapters have been prepared according to the Class 5 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 5 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Mock Test - Mathematics for Class 5: NCERT in English & Hindi are available as part of Class 5 exam.
Download more important topics, notes, lectures and mock test series for Class 5 Exam by signing up for free.
Mathematics for Class 5: NCERT
31 videos|192 docs|41 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup




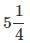
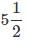
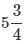







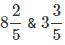 by the difference of
by the difference of
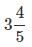

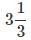

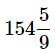 into improper fraction.
into improper fraction.