All Exams >
Commerce >
Online MCQ Tests for Commerce >
All Questions
All questions of Sets for Commerce Exam
The number of proper subsets of the set { 1, 2 , 3 } is :- a)7
- b)5
- c)6
- d)8
Correct answer is 'A'. Can you explain this answer?
The number of proper subsets of the set { 1, 2 , 3 } is :
a)
7
b)
5
c)
6
d)
8

|
Kritika Bajaj answered |
Number of subsets of a given set = 2n
The Shaded region in the following figure illustrates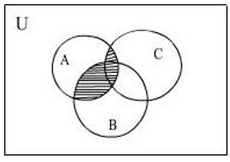
- a)A ∩ ( B ∪ C)
- b)A ∩ B ∩ C
- c)A ∪ B ∪ C
- d)(A ∩ B) ∪ (A ∩ C)
Correct answer is option 'D'. Can you explain this answer?
The Shaded region in the following figure illustrates
a)
A ∩ ( B ∪ C)
b)
A ∩ B ∩ C
c)
A ∪ B ∪ C
d)
(A ∩ B) ∪ (A ∩ C)

|
New Words answered |
First which region is over which region Then We will see that A is on the B so A intersection B and after C is on the A so, A intersection C after that we have to take all intersection part so A intersection B is Union with A intersection C.
The shaded region represents (A ∩ B) ∪ (A ∩ C).
If A = {a, b, c} then the number of proper subsets of A are:
- a)3
- b)10
- c)7
- d)8
Correct answer is option 'C'. Can you explain this answer?
If A = {a, b, c} then the number of proper subsets of A are:
a)
3
b)
10
c)
7
d)
8

|
Pooja Nair answered |
- Number of proper subsets of a given set = 2m - 1, where m is the number of elements.
- Here the number of elements is 3. So the number of proper subsets of A = 23 - 1 = 7.
If Q={x:x=1/y,where y∈N}, then- a)0∈Q
- b)1∈Q
- c)2∈Q
- d)2/3∈Q
Correct answer is option 'B'. Can you explain this answer?
If Q={x:x=1/y,where y∈N}, then
a)
0∈Q
b)
1∈Q
c)
2∈Q
d)
2/3∈Q
|
|
Rohit Jain answered |
As y ∈ N, y can be 1, 2, 3, 4...
∴ x will be 1, 1/2, 1/3, 1/4...
⇒ 1 ∈ Q
∴ x will be 1, 1/2, 1/3, 1/4...
⇒ 1 ∈ Q
Can you explain the answer of this question below:
... moreIf U= set of all whole numbers less than 12, A=set of all whole numbers less than 10, B= Set of all odd natural numbers less than 10, then what is (A∩B)’?
A:{3,5,7,9}
B:{1,3,5,7,9}
C:{0,2,4,6,8,10,11}
D:{1,3,5,7}
The answer is a.
|
|
Hansa Sharma answered |
U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
B = {1, 3, 5, 7, 9}
A ∩ B = {1, 3, 5, 7, 9}
(A ∩ B)’ = U - (A ∩ B)
(A ∩ B)’ = {0, 2, 4, 6, 8, 10, 11}
A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
B = {1, 3, 5, 7, 9}
A ∩ B = {1, 3, 5, 7, 9}
(A ∩ B)’ = U - (A ∩ B)
(A ∩ B)’ = {0, 2, 4, 6, 8, 10, 11}
Can you explain the answer of this question below:If A = {5, 10, 15}, B = ϕ, then B – A is
- A:
5
- B:
{5,10}
- C:
ϕ
- D:
{5,10, 15}
The answer is c.
If A = {5, 10, 15}, B = ϕ, then B – A is
5
{5,10}
ϕ
{5,10, 15}
|
|
Om Desai answered |
If A = {5, 10, 15}, B = ϕ
B - A will have those elements which are in B but not in A.
B - A = ϕ
B - A will have those elements which are in B but not in A.
B - A = ϕ
Which of the following is not an empty set?- a){x : x is a multiple of 7, x < 7, x ∈ N}
- b)Set of common points of two parallel lines in a plane
- c){x : 6 + 2x > 5x + 3, x ∈ N}
- d)Set of smallest whole number
Correct answer is option 'D'. Can you explain this answer?
Which of the following is not an empty set?
a)
{x : x is a multiple of 7, x < 7, x ∈ N}
b)
Set of common points of two parallel lines in a plane
c)
{x : 6 + 2x > 5x + 3, x ∈ N}
d)
Set of smallest whole number

|
Ayush Joshi answered |
As, the set of Whole numbers is {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ...};
So, according to the set of whole numbers above, the smallest whole number should be "0" and therefore the set of smallest whole number is not empty.
The set A = {1,4,9,16,25—} in set builder form is written as- a)A = {x:x is a prime number}
- b)A ={x:x is the cube of a natural number}
- c)A = {x:x is the square of a natural number}
- d)A = {x:x is an even natural number}
Correct answer is 'C'. Can you explain this answer?
The set A = {1,4,9,16,25—} in set builder form is written as
a)
A = {x:x is a prime number}
b)
A ={x:x is the cube of a natural number}
c)
A = {x:x is the square of a natural number}
d)
A = {x:x is an even natural number}
|
|
Krishna Iyer answered |
- We know that, 12 = 1, 22 = 4, 32 = 9, 42 = 16, 52 = 25
- Therefore the set A = {1, 4, 9, 16, 25...} can be written in set builder form as:
A = {x: x is the square of a natural number}
If ordered pair (a + 2b, 9) = (7, 3a + 2b), then the values of a and b are- a)9, 7
- b)1, 3
- c)7, 9
- d)3, 1
Correct answer is option 'B'. Can you explain this answer?
If ordered pair (a + 2b, 9) = (7, 3a + 2b), then the values of a and b are
a)
9, 7
b)
1, 3
c)
7, 9
d)
3, 1

|
Learners Habitat answered |
A+2B=7------(1)
3A+2B=9------(2)
Subtracting (2) from (1)
we get, 2A=2
A=1
Subsitute A=1 in (1)
1+2B=7
2B=6
B=3
therefore A = 1, B = 3
3A+2B=9------(2)
Subtracting (2) from (1)
we get, 2A=2
A=1
Subsitute A=1 in (1)
1+2B=7
2B=6
B=3
therefore A = 1, B = 3
For the set of all natural numbers the universal set can be- a)Set of all odd numbers
- b)Set of all even numbers
- c)Set of all integers
- d)Set of all prime numbers
Correct answer is option 'C'. Can you explain this answer?
For the set of all natural numbers the universal set can be
a)
Set of all odd numbers
b)
Set of all even numbers
c)
Set of all integers
d)
Set of all prime numbers
|
|
Krishna Iyer answered |
Integers contain all the natural numbers. So it can be a universal set for natural numbers. In other options, there are only some of the elements of natural numbers.
Can you explain the answer of this question below: Identify the null set from the following- A:Odd natural numbers divisible by 2
- B:The set which contains only zero as its element
- C:The set of even prime numbers
- D:The set of points common to two intersecting lines
The answer is a.
Identify the null set from the following
A:
Odd natural numbers divisible by 2
B:
The set which contains only zero as its element
C:
The set of even prime numbers
D:
The set of points common to two intersecting lines
|
|
Geetika Shah answered |
Since none of the odd number is divisible by 2, so it would be a null set.
If A = {1, 3, 6}, B = {4, 8} then A x A is- a){(1, 3), (1, 6), (3, 1) {(3, 6), (6, 1), (6, 3)}
- b){(1, 1), (1, 3), (1, 6), {(3, 1), (3, 3), (3, 6), {(6, 1), (6, 3), (6, 6)}
- c){(1, 4), (1, 8), (3, 4), {(3, 8), (6, 4), (6, 8)}
- d){(1, 1), (3, 3), (6, 6)}
Correct answer is option 'B'. Can you explain this answer?
If A = {1, 3, 6}, B = {4, 8} then A x A is
a)
{(1, 3), (1, 6), (3, 1) {(3, 6), (6, 1), (6, 3)}
b)
{(1, 1), (1, 3), (1, 6), {(3, 1), (3, 3), (3, 6), {(6, 1), (6, 3), (6, 6)}
c)
{(1, 4), (1, 8), (3, 4), {(3, 8), (6, 4), (6, 8)}
d)
{(1, 1), (3, 3), (6, 6)}
|
|
Raghav Bansal answered |
It is distributive law.
If in class XI of a certain school, 24 students got distinction in mathematics, 19 students got distinction in physics and 15 students got distinction in both the subjects,then the number of students in class XI is :- a)43
- b)58
- c)28
- d)39
Correct answer is option 'C'. Can you explain this answer?
If in class XI of a certain school, 24 students got distinction in mathematics, 19 students got distinction in physics and 15 students got distinction in both the subjects,then the number of students in class XI is :
a)
43
b)
58
c)
28
d)
39

|
Lohit Matani answered |
r :- c
Explanation:- Students got distinction in mathematics = 24
Student got distinction in physics = 19
Students got distinction in both= 15
Total number of students = (24+19)-15
= 28
Explanation:- Students got distinction in mathematics = 24
Student got distinction in physics = 19
Students got distinction in both= 15
Total number of students = (24+19)-15
= 28
U= set of all teachers in a schoolB= Set of all Mathematics teachers in a schoolSo B’=?- a)set of all non mathematics teachers
- b)set of all language teachers
- c)set of all non science teachers
- d)Set of all science teachers
Correct answer is option 'A'. Can you explain this answer?
U= set of all teachers in a schoolB= Set of all Mathematics teachers in a schoolSo B’=?
a)
set of all non mathematics teachers
b)
set of all language teachers
c)
set of all non science teachers
d)
Set of all science teachers
|
|
Nandini Iyer answered |
U = Set of all teachers in a school
B = Set of all Mathematics teachers in a school
B’ = U – B = Set of all Non-Mathematics teachers in a school
B = Set of all Mathematics teachers in a school
B’ = U – B = Set of all Non-Mathematics teachers in a school
Can you explain the answer of this question below: If P = {1, 2, 3, 4}, then the number of subsets in its power set will be- A:8
- B:16
- C:4
- D:6
The answer is b.
If P = {1, 2, 3, 4}, then the number of subsets in its power set will be
A:
8
B:
16
C:
4
D:
6
|
|
Om Desai answered |
Number of elements in a power set = 2n, where n = number of elements in the set P.
Hence, 24 = 16.
Hence, 24 = 16.
Given the sets A = {1, 2, 3}, B = {3, 4}, C = {4, 5, 6}, then A ∪ (B ∩ C) is
- a){1, 2, 3, 4}
- b){1, 2, 3, 4, 5, 6}
- c){1, 2, 4, 5}
- d){3}
Correct answer is option 'A'. Can you explain this answer?
Given the sets A = {1, 2, 3}, B = {3, 4}, C = {4, 5, 6}, then A ∪ (B ∩ C) is
a)
{1, 2, 3, 4}
b)
{1, 2, 3, 4, 5, 6}
c)
{1, 2, 4, 5}
d)
{3}
|
|
Pooja Shah answered |
B ∩ C = {4}, as only 4 is common between B and C
∴ A ∪ (B ∩ C) = {1, 2, 3, 4}.
∴ A ∪ (B ∩ C) = {1, 2, 3, 4}.
Which of the following is a finite set?- a)Set of roots of the equation x2 – 25 = 0
- b)Set of natural numbers
- c)The set of lines parallel to y – axis
- d)The set of numbers which are multiples of 5
Correct answer is 'A'. Can you explain this answer?
Which of the following is a finite set?
a)
Set of roots of the equation x2 – 25 = 0
b)
Set of natural numbers
c)
The set of lines parallel to y – axis
d)
The set of numbers which are multiples of 5
|
|
Hansa Sharma answered |
- A finite set is a set that has a finite number of elements.
- Since x2 – 25 = 0 has finite number of elements. So it is a finite set.
Choose the incorrect statement- a)If a set has only one element, we call it a singleton set.
- b)Set of all even prime numbers is a subset of set of all natural numbers.
- c)Φ is not a subset of any set.
- d)Every set is a subset of itself.
Correct answer is option 'C'. Can you explain this answer?
Choose the incorrect statement
a)
If a set has only one element, we call it a singleton set.
b)
Set of all even prime numbers is a subset of set of all natural numbers.
c)
Φ is not a subset of any set.
d)
Every set is a subset of itself.

|
Rohit Joshi answered |
A set A is a proper subset of a set B if A is a subset of B and there is at least one element of B that's not an element of A. Thus, the void set is a subset of all sets, and it's a proper subset of every set except itself
If A, B and C are any three sets , then A – (B∩C) is equal to- a)(A – B) ∩ C
- b)(A – B) ∪ C
- c)(A – B) ∩ (A – C)
- d)(A – C) ∩ (B – C)
Correct answer is option 'B'. Can you explain this answer?
If A, B and C are any three sets , then A – (B∩C) is equal to
a)
(A – B) ∩ C
b)
(A – B) ∪ C
c)
(A – B) ∩ (A – C)
d)
(A – C) ∩ (B – C)
|
|
Hansa Sharma answered |
Set S of odd positive an odd integer less than 10 is {1, 3, 5, 7, 9}. Then, Cardinality of set S = |S| which is 5.
A is a set with 6 elements. So, the number of subsets is:- a)12
- b)32
- c)24
- d)64
Correct answer is option 'D'. Can you explain this answer?
A is a set with 6 elements. So, the number of subsets is:
a)
12
b)
32
c)
24
d)
64
|
|
Neha Joshi answered |
{1, 2, 3, 4, 5, 6} is a set of 6 elements, so it has 26 = 64 subsets
Choose the correct statementa){2} ⊆ {1,4,6}... moreb){2,4,6} ⊂ {2}c){2} ⊂ {2,4,6}d){2} ⊇ {2,4,6}Correct answer is option 'C'. Can you explain this answer?
|
|
Leelu Bhai answered |
Yes option C is correct as {2} is a subset of {2, 4, 6}.
If 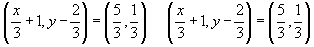 = 22 then x and y =
= 22 then x and y =- a)x=3,y=1
- b)x = 3, y=6
- c)x=1 ,y=2
- d)
x = 2, y = 1
Correct answer is option 'D'. Can you explain this answer?
If 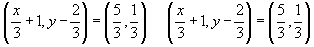
= 22 then x and y =
a)
x=3,y=1
b)
x = 3, y=6
c)
x=1 ,y=2
d)
x = 2, y = 1
|
|
Lavanya Menon answered |
R × ( P' ∪ Q' )'=R × [( P' )' ∩ ( Q' )' ] =R × (P ∩ Q) = (R × P) ∩ (R × Q)
If U= set of all whole numbers less than 12, A=set of all whole numbers less than 10, B= Set of all odd natural numbers less than 10, then what is (A∩B)’?- a){3,5,7,9}
- b){0,1,3,5,7,9}
- c){0,2,4,6,8,10,11}
- d){1,3,5,7}
Correct answer is option 'A'. Can you explain this answer?
If U= set of all whole numbers less than 12, A=set of all whole numbers less than 10, B= Set of all odd natural numbers less than 10, then what is (A∩B)’?
a)
{3,5,7,9}
b)
{0,1,3,5,7,9}
c)
{0,2,4,6,8,10,11}
d)
{1,3,5,7}
|
|
Hansa Sharma answered |
U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
B = {1, 3, 5, 7, 9}
A ∩ B = {1, 3, 5, 7, 9}
(A ∩ B)’ = U - (A ∩ B)
(A ∩ B)’ = {0, 2, 4, 6, 8, 10, 11}
A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
B = {1, 3, 5, 7, 9}
A ∩ B = {1, 3, 5, 7, 9}
(A ∩ B)’ = U - (A ∩ B)
(A ∩ B)’ = {0, 2, 4, 6, 8, 10, 11}
If Q = {x : x = 1/y , where y ∈ N} , then- a)1 ∈ Q
- b)0 ∈ Q
- c)1/2 ∈ Q
- d)2 ∈ Q
Correct answer is option 'B'. Can you explain this answer?
If Q = {x : x = 1/y , where y ∈ N} , then
a)
1 ∈ Q
b)
0 ∈ Q
c)
1/2 ∈ Q
d)
2 ∈ Q
|
|
Pooja Shah answered |
We know that
n(A∪B)=n(A)+n(B)−n(A∩B)......(i)
n(A∪B)=n(A)+n(B)-n(A∩B)......(i)
Case 1 From (i) , it is clear that n(A∪B)
n(A∪B) will be maximum when n(A∩B)=0
In that case,
n(A∪B)=n(A)+n(B)=(3+6)=9
∴ Maximum number of elements in
(A∪B)=9
Case 2 From (i) , it is clear that n(A∪B)
n(A∪B) will be minimum when n(A∩B)=0 maximum ,i.e, when
n(A∩B)=3
In this case,
n(A∪B)=n(A)+n(B)−n(A∩B)=(3+6−3)=6
∴ minimum number of elements in
A∪B=6
A = set of all trianglesB = set of all right triangles
A – B=?- a)set of all equilateral triangles
- b)set of all triangles which have all three angles different
- c)set of all isosceles triangles
- d)set of all triangles which do not have one right angle
Correct answer is option 'D'. Can you explain this answer?
A = set of all triangles
B = set of all right triangles
A – B=?
A – B=?
a)
set of all equilateral triangles
b)
set of all triangles which have all three angles different
c)
set of all isosceles triangles
d)
set of all triangles which do not have one right angle
|
|
Geetika Shah answered |
A = Set of all triangles
B = Set of all right triangles
A – B = Set of triangles after removing all right triangles from A
= Set of all triangles which do not have right angle
B = Set of all right triangles
A – B = Set of triangles after removing all right triangles from A
= Set of all triangles which do not have right angle
If A = {2, 4, 6, 8} and U = {1, 2, 3, 4, 5, 6, 7, 8, 9,}, then A’=- a){1,3,5,7,9}
- b){1,3,5,7}
- c){1,3,5,6,9}
- d){1,3,5,8,9}
Correct answer is 'A'. Can you explain this answer?
If A = {2, 4, 6, 8} and U = {1, 2, 3, 4, 5, 6, 7, 8, 9,}, then A’=
a)
{1,3,5,7,9}
b)
{1,3,5,7}
c)
{1,3,5,6,9}
d)
{1,3,5,8,9}
|
|
Pooja Shah answered |
U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {2, 4, 6, 8}
A’ = U – A
A’ = {1, 3, 5, 7, 9}
A = {2, 4, 6, 8}
A’ = U – A
A’ = {1, 3, 5, 7, 9}
A—B is read as ?- a) Difference of B and A
- b) Difference of A and B of B and A
- c) None of the above
- d) Both a and b
Correct answer is option 'B'. Can you explain this answer?
A—B is read as ?
a)
Difference of B and A
b)
Difference of A and B of B and A
c)
None of the above
d)
Both a and b
|
|
Gaurav Kumar answered |
x2 = 16 ⇒ x = ±4 and 2x = 6 ⇒x = 3
There is no value of x which satisfies both the above equations. Thus, A = φ
Given 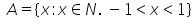 1 and B = {0, 1, 2, 3, 4, 5, 6} then A x B is
1 and B = {0, 1, 2, 3, 4, 5, 6} then A x B is- a){ (1, 6), (1, 7), (2, 5), (2, 6), (2, 7)}
- b)Φ
- c){(3, 5), (3, 6), (4, 5), (4, 6)}
- d)Infinite
Correct answer is option 'B'. Can you explain this answer?
Given 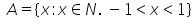 1 and B = {0, 1, 2, 3, 4, 5, 6} then A x B is
1 and B = {0, 1, 2, 3, 4, 5, 6} then A x B is
a)
{ (1, 6), (1, 7), (2, 5), (2, 6), (2, 7)}
b)
Φ
c)
{(3, 5), (3, 6), (4, 5), (4, 6)}
d)
Infinite
|
|
Krishna Iyer answered |
A = Φ
B = {0, 1, 2, 3, 4, 5, 6}
A × B = Φ (Cartesian product with an empty set is an empty set)
B = {0, 1, 2, 3, 4, 5, 6}
A × B = Φ (Cartesian product with an empty set is an empty set)
From the sets given below, select equal sets :A = { 2, 4, 8, 12}, B = { 1, 2, 3, 4},
C = { 4, 8, 12, 14}, D = { 3, 1, 4, 2}- a)A and C
- b)A and B
- c)B and D
- d)B and C
Correct answer is option 'C'. Can you explain this answer?
From the sets given below, select equal sets :
A = { 2, 4, 8, 12}, B = { 1, 2, 3, 4},
C = { 4, 8, 12, 14}, D = { 3, 1, 4, 2}
C = { 4, 8, 12, 14}, D = { 3, 1, 4, 2}
a)
A and C
b)
A and B
c)
B and D
d)
B and C

|
Mansi Chopra answered |
The sets are equal, if they have the exact same elements in them. Since option B & D have exactly same number of elements in them So, B & D are equal sets.
Two finite sets have m and n elements. The total number of subsets of the first set is 48 more than the total number of subsets of the second set. The values of m and n are- a)6 , 3
- b)6 , 4
- c)7 , 4
- d)3 , 3
Correct answer is option 'B'. Can you explain this answer?
Two finite sets have m and n elements. The total number of subsets of the first set is 48 more than the total number of subsets of the second set. The values of m and n are
a)
6 , 3
b)
6 , 4
c)
7 , 4
d)
3 , 3
|
|
Preeti Iyer answered |
Total number of subsets of the first set = 2m
Total number of subsets of the second set = 2n
2m = 2n + 48
By hit and trial,
m = 6, n = 4
Total number of subsets of the second set = 2n
2m = 2n + 48
By hit and trial,
m = 6, n = 4
If the number of outcomes in collection are 2 and the distinct outcomes are 4 then the count value according to permutations is- a)2
- b)12
- c)24
- d)4
Correct answer is option 'C'. Can you explain this answer?
If the number of outcomes in collection are 2 and the distinct outcomes are 4 then the count value according to permutations is
a)
2
b)
12
c)
24
d)
4
|
|
Naina Sharma answered |
The number of non- empty subsets =
2n − 1 = 24 − 1 = 16 − 1 = 15
2n − 1 = 24 − 1 = 16 − 1 = 15
Can you explain the answer of this question below: If A = {-1, 1, 2}, then n(A x A x A) =
- A:
9
- B:
16
- C:
27
- D:
3
The answer is c.
If A = {-1, 1, 2}, then n(A x A x A) =
9
16
27
3
|
|
Om Desai answered |
n(A) = 3
n(A × A × A) = n(A) * n(A) * n(A)
n(A × A × A) = 3 * 3 * 3 = 27
n(A × A × A) = n(A) * n(A) * n(A)
n(A × A × A) = 3 * 3 * 3 = 27
Consider the set A of all divisors of 30. How many subsets of A contains even divisors only?- a)2
- b)16
- c)28
- d)4
Correct answer is 'B'. Can you explain this answer?
Consider the set A of all divisors of 30. How many subsets of A contains even divisors only?
a)
2
b)
16
c)
28
d)
4
|
|
Himaja Ammu answered |
Set of divisors of 30={1,2,3,6,10,15,30} in these the even divisors r={2,6,10,30} we know no.of subsets to any set=2^n so answer is 2^4=16
The number of elements in the Power set P(S) of the set S = [ [ Φ] , 1, [ 2, 3 ]] is- a)2
- b)4
- c)8
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The number of elements in the Power set P(S) of the set S = [ [ Φ] , 1, [ 2, 3 ]] is
a)
2
b)
4
c)
8
d)
None of these
|
|
Preeti Iyer answered |
There’s a result in mathematics used for this. It says that a power set B of any set A is a set of all the subsets of A and the number of elements of B will be 2^n where n is the number of elements of A.
So taking your question as an example;
A = {1,2,3}
B : set of all subsets of A
List out all the subsets of A - {1},{2},{3},{1,2},{2,3},{1,3},{1,2,3},{empty set}
Number of elements in A (n) = 3
so 23 = 8
So, B = {{1},{2},{3},{1,2},{2,3},{1,3},{1,2,3},{empty set}}
and the number of elements are 8.
So taking your question as an example;
A = {1,2,3}
B : set of all subsets of A
List out all the subsets of A - {1},{2},{3},{1,2},{2,3},{1,3},{1,2,3},{empty set}
Number of elements in A (n) = 3
so 23 = 8
So, B = {{1},{2},{3},{1,2},{2,3},{1,3},{1,2,3},{empty set}}
and the number of elements are 8.
If set A has 4 elements and B = {5, 6}, then the number of elements in A x B are- a)9
- b)8
- c)7
- d)10
Correct answer is 'B'. Can you explain this answer?
If set A has 4 elements and B = {5, 6}, then the number of elements in A x B are
a)
9
b)
8
c)
7
d)
10
|
|
Pooja Shah answered |
n(A) = 4
B = {5, 6}
n(B) = 2
n(A x B) = n(A)*n(B) = 4*2 = 8
B = {5, 6}
n(B) = 2
n(A x B) = n(A)*n(B) = 4*2 = 8
In a class of 40 students 14 take physics and 29 take chemistry. If 5 students take both, how many students take neither of the subjects?
- a)5
- b)14
- c)38
- d)2
Correct answer is option 'D'. Can you explain this answer?
In a class of 40 students 14 take physics and 29 take chemistry. If 5 students take both, how many students take neither of the subjects?
a)
5
b)
14
c)
38
d)
2
|
|
Krishna Iyer answered |
Total students who took any of the subjects = 40 - x
Let x be the no. of students who took neither of the subjects
Then, 40 - x = 14 + 29 - 5
⇒ x = 2
Let x be the no. of students who took neither of the subjects
Then, 40 - x = 14 + 29 - 5
⇒ x = 2
If U = {1,2, 3, ….,10}, A = {2, 4, 6}, B = {3, 4, 6, 8, 10,}, then (A ∩ B)’ is- a){1,2, 3, 5, 7, 8, 9, 10}
- b){1, 3, 5, 7, 8, 9, 10}
- c){1, 5, 7, 9}
- d){1,2, 3, …,10}
Correct answer is option 'A'. Can you explain this answer?
If U = {1,2, 3, ….,10}, A = {2, 4, 6}, B = {3, 4, 6, 8, 10,}, then (A ∩ B)’ is
a)
{1,2, 3, 5, 7, 8, 9, 10}
b)
{1, 3, 5, 7, 8, 9, 10}
c)
{1, 5, 7, 9}
d)
{1,2, 3, …,10}
|
|
Geetika Shah answered |
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {2, 4, 6}
B = {3, 4, 6, 8, 10}
A ∩ B = {4, 6}
(A ∩ B)’ = U – (A ∩ B)
= {1, 2, 3, 5, 7, 8, 9, 10}
A = {2, 4, 6}
B = {3, 4, 6, 8, 10}
A ∩ B = {4, 6}
(A ∩ B)’ = U – (A ∩ B)
= {1, 2, 3, 5, 7, 8, 9, 10}
Let U = {1,2,3,4,5,6,7,8,9,10} , A = {1,2,5} , B = {6,7}. Then A∩B’ is :- a)A
- b)B
- c)B’
- d)none
Correct answer is option 'A'. Can you explain this answer?
Let U = {1,2,3,4,5,6,7,8,9,10} , A = {1,2,5} , B = {6,7}. Then A∩B’ is :
a)
A
b)
B
c)
B’
d)
none
|
|
Pooja Shah answered |
- B' gives us all the elements in U other than 6 and 7 i.e., B' = {1, 2, 3, 4, 5, 8, 9, 10}
- The intersection of this set with A will be the common elements in both of these (A and B') i.e., = {1, 2, 5} which is set A itself.
Which of the following has only one subset?- a){ }
- b){5}
- c){4,5}
- d){0}
Correct answer is option 'A'. Can you explain this answer?
Which of the following has only one subset?
a)
{ }
b)
{5}
c)
{4,5}
d)
{0}
|
|
Vijay Kumar answered |
- Every set has the empty set as a subset. So if a set has 1 element, like {0}, then it will have 2 subsets: itself and the empty set, which is denoted by { }.
- So, if a set has only one subset, then this set must be the empty set.
If n (P) = 5, n(Q) = 12 and n(P U Q) = 14 then n(P ∩ Q) =
- a)3
- b)4
- c)5
- d)7
Correct answer is option 'A'. Can you explain this answer?
If n (P) = 5, n(Q) = 12 and n(P U Q) = 14 then n(P ∩ Q) =
a)
3
b)
4
c)
5
d)
7
|
|
Hansa Sharma answered |
n (P) = 5, n(Q) = 12 and n(PUQ) = 14
n(PUQ) = n(P) + n(Q) - n(P∩Q)
14 = 5 + 12 - n(P∩Q)
n(P∩Q) = 3
n(PUQ) = n(P) + n(Q) - n(P∩Q)
14 = 5 + 12 - n(P∩Q)
n(P∩Q) = 3
If A = { x : x = 2n , n ≤ 6, n ∈ N} and B = { x : x = 4n , n ≤ 2, n ∈ N}, then A – B is- a){3, 4, 5, 6}
- b){4, 16}
- c){ 2, 4, 8,16, 32, 64 }
- d){2, 8, 32, 64}
Correct answer is option 'D'. Can you explain this answer?
If A = { x : x = 2n , n ≤ 6, n ∈ N} and B = { x : x = 4n , n ≤ 2, n ∈ N}, then A – B is
a)
{3, 4, 5, 6}
b)
{4, 16}
c)
{ 2, 4, 8,16, 32, 64 }
d)
{2, 8, 32, 64}
|
|
Geetika Shah answered |
A = {x : x = 2n, n ≤ 6}
For (n = 1,2,3,4,5,6) {2,4,8,16,32,64}
B = {x : x = 4n, n ≤ 2}
For (n = 1,2) {4,8}
A - B = {2, 8, 32, 64}
For (n = 1,2,3,4,5,6) {2,4,8,16,32,64}
B = {x : x = 4n, n ≤ 2}
For (n = 1,2) {4,8}
A - B = {2, 8, 32, 64}
If A × B = {(x, a), (x, b), (y,a), (y, b)} then A =- a){x,y}
- b){a,b}
- c){x,x,y,y}
- d){x,a}
Correct answer is option 'A'. Can you explain this answer?
If A × B = {(x, a), (x, b), (y,a), (y, b)} then A =
a)
{x,y}
b)
{a,b}
c)
{x,x,y,y}
d)
{x,a}
|
|
Krishna Iyer answered |
A × B = {(x, a), (x, b), (y, a), (y, b)}
A = {x, y}
A = {x, y}
Let a, b ∈ R and a < b , then [a, b] implies- a){x : a ≤ x ≤ b}
- b){x : a < x ≤ b}
- c){x : a < x < b}
- d){x : a ≤ x < b}
Correct answer is option 'A'. Can you explain this answer?
Let a, b ∈ R and a < b , then [a, b] implies
a)
{x : a ≤ x ≤ b}
b)
{x : a < x ≤ b}
c)
{x : a < x < b}
d)
{x : a ≤ x < b}
|
|
Krishna Iyer answered |
Square brackets [a, b] implies that values of a and b should be included in the range of x i.e., a ≤ x ≤ b.
In which of the following statements, set P is not a subset of Q:- a)P = {a,e} and Q = Set of vowels in English alphabets
- b)P = {0, 1, 2, 3, 4} and Q = { x:x < 4, x ∈ N}
- c)P = Set of equilateral triangles in a plane and Q = Set of triangles in the plane
- d)P = Set of even natural numbers and Q = Set of integers
Correct answer is option 'B'. Can you explain this answer?
In which of the following statements, set P is not a subset of Q:
a)
P = {a,e} and Q = Set of vowels in English alphabets
b)
P = {0, 1, 2, 3, 4} and Q = { x:x < 4, x ∈ N}
c)
P = Set of equilateral triangles in a plane and Q = Set of triangles in the plane
d)
P = Set of even natural numbers and Q = Set of integers
|
|
Gaurav Kumar answered |
- P contains {0, 1, 2, 3, 4} and Q contain natural numbers which start with 1 and P = {0, 1, 2, 3, 4} Q = {1, 2, 3}
- Here P isn't a subset of Q because all the elements of P are not in Q.
A set has 7 elements. The number of elements in its power set is:- a)32
- b)24
- c)128
- d)64
Correct answer is option 'C'. Can you explain this answer?
A set has 7 elements. The number of elements in its power set is:
a)
32
b)
24
c)
128
d)
64
|
|
Geetika Shah answered |
Number of elements in power set = 27 = 128
If A = {1, 2, 3, 4}, B = {3, 4} and C = {2, 3} then n ((A ∩ B x C)- a)2
- b)8
- c)4
- d)16
Correct answer is option 'C'. Can you explain this answer?
If A = {1, 2, 3, 4}, B = {3, 4} and C = {2, 3} then n ((A ∩ B x C)
a)
2
b)
8
c)
4
d)
16
|
|
Gaurav Kumar answered |
A = {1, 2, 3, 4}, B = {3, 4} and C = {2, 3}
(A ∩ B) = {3, 4} C = {2, 3}
(A ∩ B x C) = {3,4} x {2,3}
⇒ {(3,2) (3,3) (4,2) (4,3)}
(A ∩ B) = {3, 4} C = {2, 3}
(A ∩ B x C) = {3,4} x {2,3}
⇒ {(3,2) (3,3) (4,2) (4,3)}
Chapter doubts & questions for Sets - Online MCQ Tests for Commerce 2025 is part of Commerce exam preparation. The chapters have been prepared according to the Commerce exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Commerce 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Sets - Online MCQ Tests for Commerce in English & Hindi are available as part of Commerce exam.
Download more important topics, notes, lectures and mock test series for Commerce Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup












