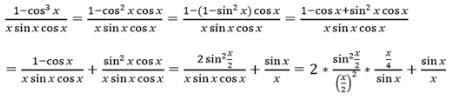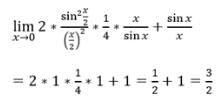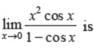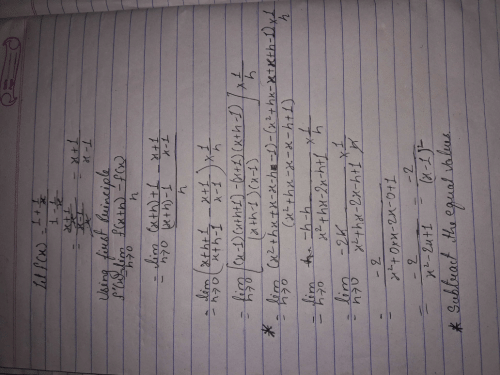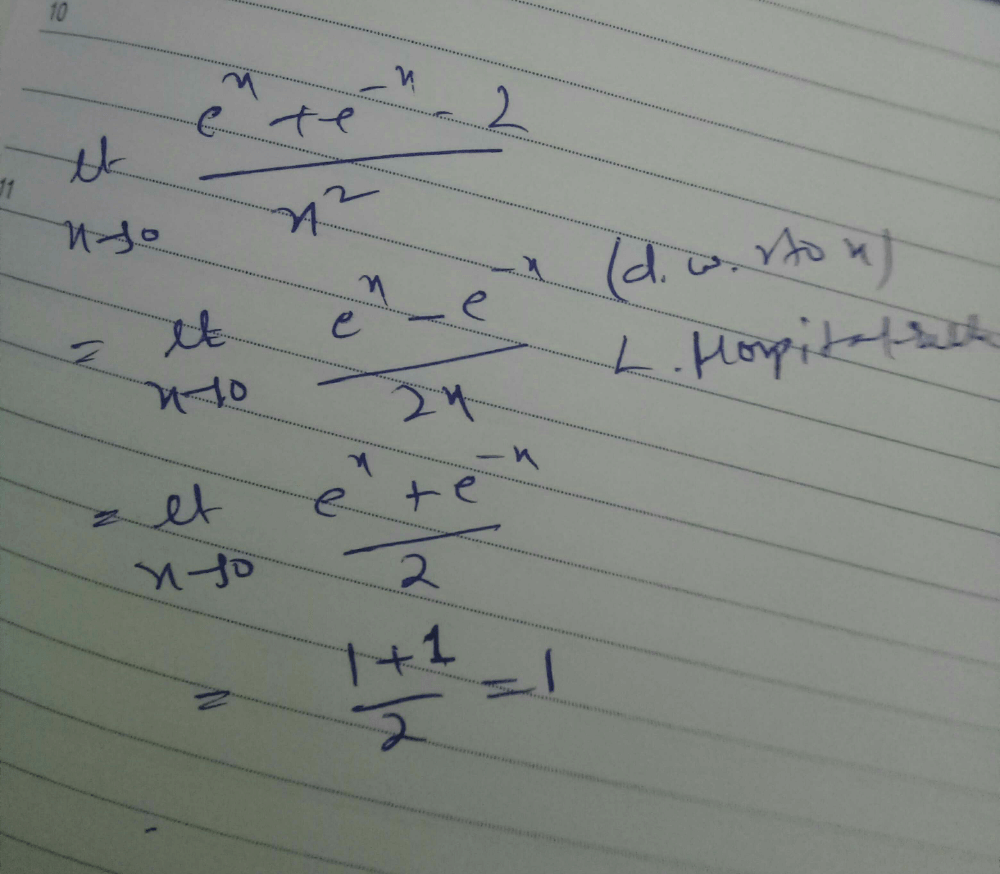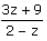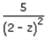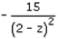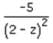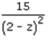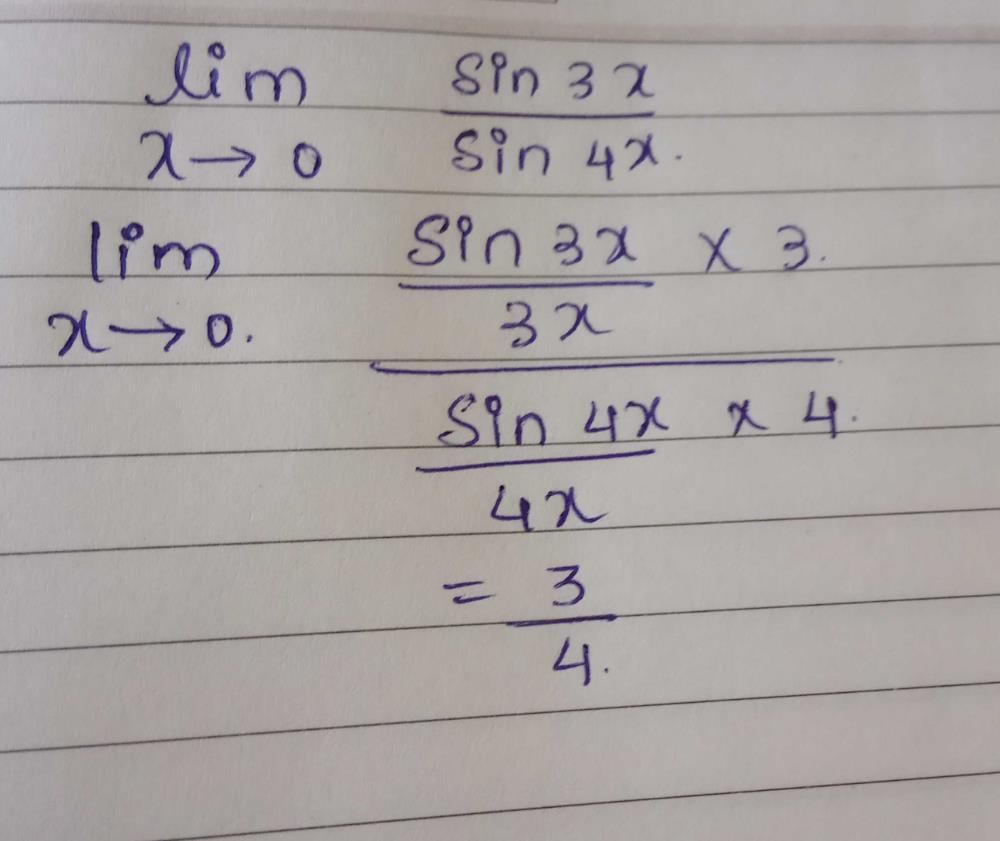All Exams >
Commerce >
Online MCQ Tests for Commerce >
All Questions
All questions of Limits and Derivatives for Commerce Exam
- a)1
- b)1/3
- c)1/2
- d)0
Correct answer is option 'B'. Can you explain this answer?
a)
1
b)
1/3
c)
1/2
d)
0
|
|
Krishna Iyer answered |
lim(x → 0) (tanx-x)/x2 tanx
As we know that tan x = sinx/cosx
lim(x → 0) (sinx/cosx - x)/x2(sinx/cosx)
lim(x → 0) (sinx - xcosx)/(x2 sinx)
lim(x → 0) cosx - (-xsinx + cosx)/(x2cosx + sinx (2x))
lim(x → 0) (cosx + xsinx - cosx)/x2cosx + 2xsinx)
lim(x → 0) sinx/(xcosx + 2sinx)
Hence it is 0/0 form, apply L hospital rule
lim(x → 0) cosx/(-xsinx + cosx + 2cosx)
⇒ 1/(0+1+2)
= 1/3
As we know that tan x = sinx/cosx
lim(x → 0) (sinx/cosx - x)/x2(sinx/cosx)
lim(x → 0) (sinx - xcosx)/(x2 sinx)
lim(x → 0) cosx - (-xsinx + cosx)/(x2cosx + sinx (2x))
lim(x → 0) (cosx + xsinx - cosx)/x2cosx + 2xsinx)
lim(x → 0) sinx/(xcosx + 2sinx)
Hence it is 0/0 form, apply L hospital rule
lim(x → 0) cosx/(-xsinx + cosx + 2cosx)
⇒ 1/(0+1+2)
= 1/3
The derivative of f(x) = 99x at x = 100 is:- a)9900
- b)0
- c)99
- d)100
Correct answer is option 'C'. Can you explain this answer?
The derivative of f(x) = 99x at x = 100 is:
a)
9900
b)
0
c)
99
d)
100
|
|
Raghav Bansal answered |
f'(100) = lim(h→0) [f(100+h) - f(100)]/h
= lim(h→0) [99(100+h) - 99(100)]/h
= lim(h→0) [9900 + 99h - 9900]/h
= lim(h→0) 99h/h
= lim(h→0) 99
= 99
= lim(h→0) [99(100+h) - 99(100)]/h
= lim(h→0) [9900 + 99h - 9900]/h
= lim(h→0) 99h/h
= lim(h→0) 99
= 99
If is a real valued function and c is a point in its domain, then 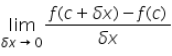 is ;
is ;- a)f (x)
- b)f’ (x)
- c)f (c)
- d)f’ (c)
Correct answer is option 'D'. Can you explain this answer?
If is a real valued function and c is a point in its domain, then 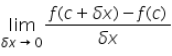 is ;
is ;
a)
f (x)
b)
f’ (x)
c)
f (c)
d)
f’ (c)
|
|
Gaurav Kumar answered |
This is a formula for finding derivative or differentiation which is represented by
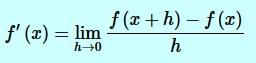 but here at the place of x , c is written So this is equal to f'(c)
but here at the place of x , c is written So this is equal to f'(c)
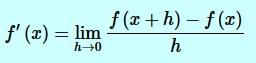 but here at the place of x , c is written So this is equal to f'(c)
but here at the place of x , c is written So this is equal to f'(c)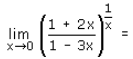
- a)e5
- b)e4
- c)e2
- d)e3
Correct answer is option 'A'. Can you explain this answer?
a)
e5
b)
e4
c)
e2
d)
e3

|
Manish Aggarwal answered |
lim (x → 0) [((1-3x)+5x)/(1-3x)]1/x
lim (x → 0) [1 + 5x/(1-3x)]1/x
= elim(x → 0) (1 + 5x/(1-3x) - 1) * (1/x)
= elim(x → 0) (5x/(1-3x)) * (1/x)
= elim(x → 0) (5x/(1-3x))
= e5
lim (x → 0) [1 + 5x/(1-3x)]1/x
= elim(x → 0) (1 + 5x/(1-3x) - 1) * (1/x)
= elim(x → 0) (5x/(1-3x)) * (1/x)
= elim(x → 0) (5x/(1-3x))
= e5
Let (tan α) x + (sin α) y = α and (α cosec α) x + (cos α) y = 1 be two variable straight lines, α being the parameter. Let P be the point of intersection of the lines. In the limiting position when α→ 0, the coordinates of P are- a)(2 , 1)
- b) (–2 ,–1)
- c)(–2 , 1)
- d)(2 , –1)
Correct answer is option 'D'. Can you explain this answer?
Let (tan α) x + (sin α) y = α and (α cosec α) x + (cos α) y = 1 be two variable straight lines, α being the parameter. Let P be the point of intersection of the lines. In the limiting position when α→ 0, the coordinates of P are
a)
(2 , 1)
b)
(–2 ,–1)
c)
(–2 , 1)
d)
(2 , –1)

|
Maths Learner answered |
Can anyone explain the question and concept
Derivative of sum of two functions is sum of the derivatives of the functions. If , f and g be two functions such that their derivatives are defined in ______.- a)Common domain
- b)Their individual domains
- c)Universally
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
Derivative of sum of two functions is sum of the derivatives of the functions. If , f and g be two functions such that their derivatives are defined in ______.
a)
Common domain
b)
Their individual domains
c)
Universally
d)
None of the above
|
|
Gaurav Kumar answered |
- The process of determining the derivative of a function is known as differentiation. It is clearly visible that the basic concept of derivative of a function is closely intertwined with limits. Therefore, it can be expected that the rules of derivatives are similar to that of limits.
- The following rules are a part of algebra of derivatives:
Consider f and g to be two real-valued functions such that the differentiation of these functions is defined in a common domain.
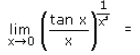
- a)∞
- b)e
- c)e1/3
- d)1
Correct answer is option 'C'. Can you explain this answer?
a)
∞
b)
e
c)
e1/3
d)
1

|
Ciel Knowledge answered |
lim(x → 0) (tanx/x)(1/x^2)
= (1)∞
elim(x → 0) (1/x2)(tanx/x - 1)
= elim(x → 0) ((tanx - x)/x3) .....(1)
lim(x → 0) ((tanx - x)/x3)
(0/0) form, Apply L hospital rule
lim(x → 0) [sec2x -1]/3x2
lim(x → 0) [tan2x/3x2]
= 1/3 lim(x → 0) [tan2x/x2]
= 1/3 * 1
= e1/3
= (1)∞
elim(x → 0) (1/x2)(tanx/x - 1)
= elim(x → 0) ((tanx - x)/x3) .....(1)
lim(x → 0) ((tanx - x)/x3)
(0/0) form, Apply L hospital rule
lim(x → 0) [sec2x -1]/3x2
lim(x → 0) [tan2x/3x2]
= 1/3 lim(x → 0) [tan2x/x2]
= 1/3 * 1
= e1/3
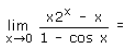
- a)e
- b)1
- c)log 2
- d)2 log 2
Correct answer is option 'D'. Can you explain this answer?
a)
e
b)
1
c)
log 2
d)
2 log 2
|
|
Krishna Iyer answered |
lim(x → 0) (x2x - x)/(1-cosx)
lim(x → 0) x2(2x - 1)/x(1-cosx)
By formula : lim(x → 0) (ax - 1)/x = log a
lim(x → 0) x2 log2/(1-cosx)
Differentiate it
lim(x → 0) 2x log2/(sinx)
= 2 log2
lim(x → 0) x2(2x - 1)/x(1-cosx)
By formula : lim(x → 0) (ax - 1)/x = log a
lim(x → 0) x2 log2/(1-cosx)
Differentiate it
lim(x → 0) 2x log2/(sinx)
= 2 log2
The derivate of x3 - 20x at x = 10 is :- a)280
- b)320
- c)250
- d)180
Correct answer is option 'A'. Can you explain this answer?
The derivate of x3 - 20x at x = 10 is :
a)
280
b)
320
c)
250
d)
180
|
|
Yash Patel answered |
Y=x3-20x
dy/dx=3x2-20
(dy/dx) at x=10 is
=3×100-20
=280
dy/dx=3x2-20
(dy/dx) at x=10 is
=3×100-20
=280
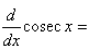
- a)sec2 x
- b)sec x. tan x
- c)- cosec x. cot x
- d)- cot2 x
Correct answer is option 'C'. Can you explain this answer?
a)
sec2 x
b)
sec x. tan x
c)
- cosec x. cot x
d)
- cot2 x
|
|
Krishna Iyer answered |
y = cosecx
= 1/sinx= (sinx)−1
⇒ dy/dx=−(sinx)−2 × d/dx(sinx)
= −cosx/sin2x
= −cosx/sinx ×(1/sinx)
= −cot x cosec x
= 1/sinx= (sinx)−1
⇒ dy/dx=−(sinx)−2 × d/dx(sinx)
= −cosx/sin2x
= −cosx/sinx ×(1/sinx)
= −cot x cosec x

- a)y + 1
- b)1/y
- c)y
- d)y – 1
Correct answer is option 'C'. Can you explain this answer?
a)
y + 1
b)
1/y
c)
y
d)
y – 1
|
|
Om Desai answered |
Since the number of terms is finite, just differentiate term by term using the power rule.
dy/dx = 0 + 1 + 2x/2! + 3x2/3! + ... + nxn-1/n!
dy/dx = 1 + x + x2/2! + ... + xn-1/(n -1)!
Compare dy/dx to y and note that the last term of y, which is xn/n!, is not in dy/dx, while all the other terms of y are in dy/dx.
Then dy/dx = y - xn/n!
⇒ dy/dx + xn/n! = y
dy/dx = 0 + 1 + 2x/2! + 3x2/3! + ... + nxn-1/n!
dy/dx = 1 + x + x2/2! + ... + xn-1/(n -1)!
Compare dy/dx to y and note that the last term of y, which is xn/n!, is not in dy/dx, while all the other terms of y are in dy/dx.
Then dy/dx = y - xn/n!
⇒ dy/dx + xn/n! = y
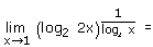
- a)e
- b)1/e
- c)2e
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
a)
e
b)
1/e
c)
2e
d)
None of these

|
Praveen Kumar answered |
lim(x → 1) (log2 2x)1/log2x
= lim(x →1) (log22 + log2x)1/log2x
As we know that {log ab = log a + log b}
lim(x → 1) {1 + log2x}1/log2x
log2x → 0
Put t = log2x
lim(t → 0) {1 + t}1/t
= e
= lim(x →1) (log22 + log2x)1/log2x
As we know that {log ab = log a + log b}
lim(x → 1) {1 + log2x}1/log2x
log2x → 0
Put t = log2x
lim(t → 0) {1 + t}1/t
= e
The value of the limit 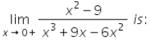
- a)Not defined
- b)0
- c)6
- d)3
Correct answer is option 'A'. Can you explain this answer?
The value of the limit 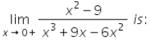
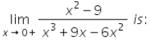
a)
Not defined
b)
0
c)
6
d)
3
|
|
Krishna Iyer answered |
lim (x2-9)/x3+9x-6x2
Lim x=0
lim[(0)2 - 9]/ (0)3 + 9(0) - 6(0)2
-9/0 (which is not defined)
Lim x=0
lim[(0)2 - 9]/ (0)3 + 9(0) - 6(0)2
-9/0 (which is not defined)

- a)3
- b)1/2
- c)2
- d)1/3
Correct answer is option 'C'. Can you explain this answer?

a)
3
b)
1/2
c)
2
d)
1/3

|
Sushil Kumar answered |
limx→1x9−1/x5−1 has indeterminate initial form (it has form 0/0). Therefore 1is a zero and x−1 a factor of both the numerator and the denominator.
limx→1 x10−1/x5−1
= limx→1[(x−1)(x8+x7+x4….⋅+x+1)]/(x−1)(x5+x6+x4+⋅⋅⋅+x+1)
= (1+1+1+1+.....upto 10 terms)/(1+1+1+⋅⋅⋅upto 5 terms)
= 10/5 = 2
limx→1 x10−1/x5−1
= limx→1[(x−1)(x8+x7+x4….⋅+x+1)]/(x−1)(x5+x6+x4+⋅⋅⋅+x+1)
= (1+1+1+1+.....upto 10 terms)/(1+1+1+⋅⋅⋅upto 5 terms)
= 10/5 = 2
Let f be any function, such that 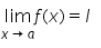 exists, then
exists, then 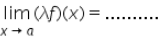
- a)λℓ
- b)ℓ
- c)1
- d)λ
Correct answer is option 'A'. Can you explain this answer?
Let f be any function, such that 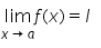 exists, then
exists, then 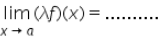
a)
λℓ
b)
ℓ
c)
1
d)
λ
|
|
Om Desai answered |
lim(x → a) f(x) = l
λf(x) = λl
λf(x) = λl

- a)
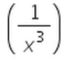
- b)
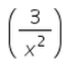
- c)
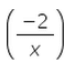
- d)
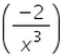
Correct answer is option 'D'. Can you explain this answer?
a)
b)
c)
d)
|
|
Lavanya Menon answered |
d/dx(1/x2 ) = -2 (x -2-1) = -2* (x-3) = -2/x3
As x → a, f(x) → l, then l is called the……..of the function f(X) which is symbolically written as…….- a)
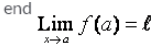
- b)
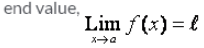
- c)
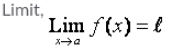
- d)
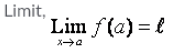
Correct answer is option 'C'. Can you explain this answer?
As x → a, f(x) → l, then l is called the……..of the function f(X) which is symbolically written as…….
a)
b)
c)
d)

|
Ambition Institute answered |
The number L is called the limit of function f(x) as x → a if and only if, for every ε>0 there exists δ>0
which is written as
lim (x → a) |f(x) − l|
lim (x → a) f(x) = l
which is written as
lim (x → a) |f(x) − l|
lim (x → a) f(x) = l
Evaluate 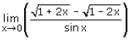
- a)1/2
- b)1/4
- c)4
- d)2
Correct answer is option 'D'. Can you explain this answer?
Evaluate 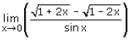
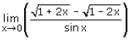
a)
1/2
b)
1/4
c)
4
d)
2

|
Praveen Kumar answered |
If we substitute the value of x=0 in numerator and denominator, we get the indeterminate form 0/0 . We should use L'hopital's rule.
lim x→ 0 (√1+2x-√1-2x)/sinx
Differentiate it we get
lim x→ 0 (1/√1+2x) + (1/√1-2x)/cosx
= (1/√1+2(0)) + (1/√1-2(0))/cos 0
=2
lim x→ 0 (√1+2x-√1-2x)/sinx
Differentiate it we get
lim x→ 0 (1/√1+2x) + (1/√1-2x)/cosx
= (1/√1+2(0)) + (1/√1-2(0))/cos 0
=2
The value of 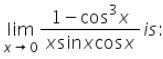
- a)3/5
- b)3/2
- c)3/4
- d)2/5
Correct answer is option 'B'. Can you explain this answer?
The value of 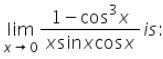
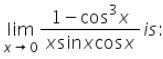
a)
3/5
b)
3/2
c)
3/4
d)
2/5
|
|
Neha Joshi answered |
After applying L'Hôpital's Rule and taking the limit as �x approaches 0, the limit of the derivatives is 3223, which confirms our initial computation of the limit
Derivative of sum of two functions is …… of the derivatives of the functions.- a)Product
- b)Sum
- c)Division
- d)Difference
Correct answer is option 'B'. Can you explain this answer?
Derivative of sum of two functions is …… of the derivatives of the functions.
a)
Product
b)
Sum
c)
Division
d)
Difference
|
|
Naina Bansal answered |
In calculus, the sum rule in differentiation is a method of finding the derivative of a function that is the sum of two other functions for which derivatives exist. This is a part of the linearity of differentiation.
 is equal to
is equal to - a)1/6
- b)
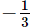
- c)
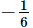
- d)0
Correct answer is option 'C'. Can you explain this answer?
 is equal to
is equal to a)
1/6
b)
c)
d)
0
|
|
Stan answered |
Sinx -x/x^3 it is in 0/0 form
so use L hospital rule,
using it we get : cosX-1/3x^2
again using : -sinX/3*2X=-1/6 lim sinx/x=-1/6
If f(x) = 2, then 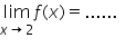
- a)2
- b)1
- c)4
- d)0
Correct answer is option 'A'. Can you explain this answer?
If f(x) = 2, then 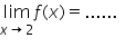
a)
2
b)
1
c)
4
d)
0
|
|
Pooja Shah answered |
f(x) = 2
Hence it doesnt contain any variable
so, lim(x → 2) f(x) = 2
Hence it doesnt contain any variable
so, lim(x → 2) f(x) = 2
If the right and left hand limits coincide, we call that common value as the limit of f(x) at x = a and denote it by- a)
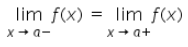
- b)
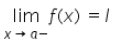
- c)
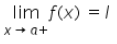
- d)
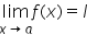
Correct answer is option 'D'. Can you explain this answer?
If the right and left hand limits coincide, we call that common value as the limit of f(x) at x = a and denote it by
a)
b)
c)
d)
|
|
Gaurav Kumar answered |
If the right-hand and left-hand limits coincide, we say the common value as the limit of f(x) at x = a and denote it by limx→a f(x) = l
- If limx→a- f(x) is the expected value of f at x = a given the values of ‘f’ near x to the left of a. This value is known as the left-hand limit of ‘f’ at a.
- If limx→a+ f(x) is the expected value of f at x = a given the values of ‘f’ near x to the right of a. This value is known as the right-hand limit of f(x) at a.
The derivative of the function f(x) = 2x2+3x-3 at x = – 2 is:- a)– 10
- b)– 5
- c)10
- d) 5
Correct answer is option 'B'. Can you explain this answer?
The derivative of the function f(x) = 2x2+3x-3 at x = – 2 is:
a)
– 10
b)
– 5
c)
10
d)
5
|
|
Neha Joshi answered |
2x2 + 3x - 3 =0
dy/dx = 4x + 3
At x = -2
4(-2) + 3 = -5
dy/dx = 4x + 3
At x = -2
4(-2) + 3 = -5
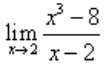
- a)12
- b)18
- c)16
- d)14
Correct answer is option 'A'. Can you explain this answer?
a)
12
b)
18
c)
16
d)
14

|
Rakhi Kumari answered |
It's very easy man... Go for l'hospital method.. This method is only applied when u ve 0/0 form after applying the limit 2 so when u get this form differentiate it... I hope u know differentiation ... On differentiating u get 3x^2 and now simply putting the limit u get the value 12... I hope it works for u
The dervative of the function 3x2 - x is :- a)4x
- b)2x – 1
- c)3x
- d)6x – 1
Correct answer is option 'D'. Can you explain this answer?
The dervative of the function 3x2 - x is :
a)
4x
b)
2x – 1
c)
3x
d)
6x – 1
|
|
Neha Joshi answered |
dy/dx = 3x2-x
dy/dx = 3(2)x(2-1) - 1x(1-1)
= 6x-1
dy/dx = 3(2)x(2-1) - 1x(1-1)
= 6x-1
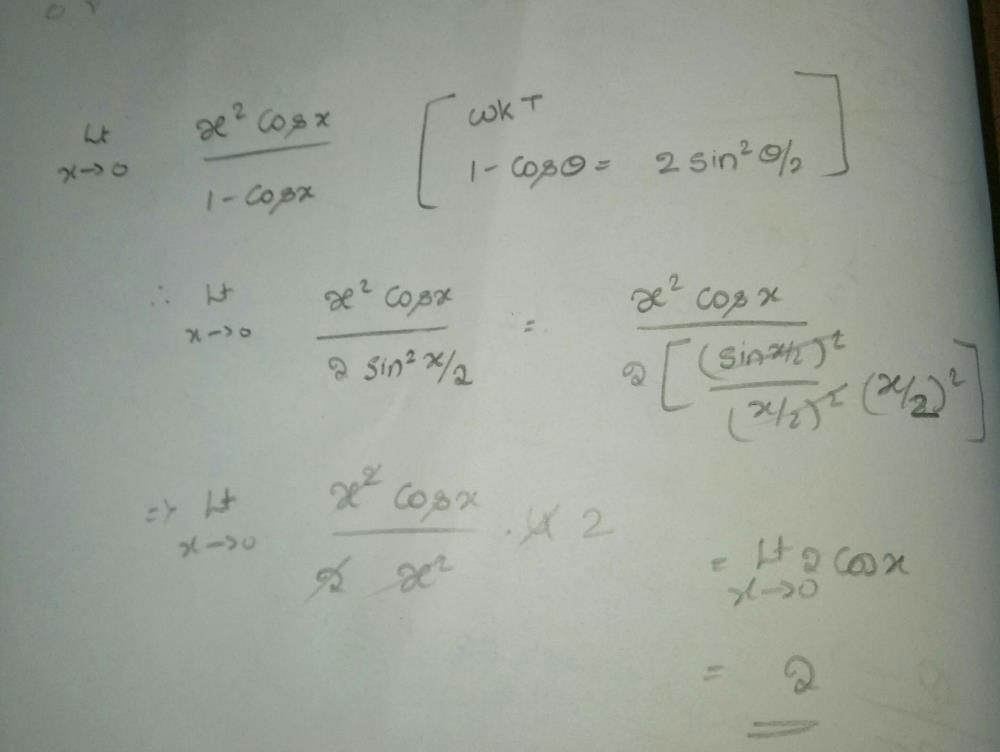
The value of the limit 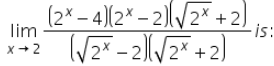
- a)4
- b)16
- c)8
- d)2
Correct answer is option 'C'. Can you explain this answer?
The value of the limit 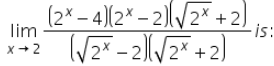
a)
4
b)
16
c)
8
d)
2

|
Shiksha Academy answered |
lim x → 2 [(2x - 4) (2x - 2) ((√2x) + 2)]/[(√2x - 2) (√2x - 2)]
= lim x → 2 [(2x - 4) (2 *4)]/(√2x - 2)
= 2 lim(x → 2) [(√2x)2 - (2)2]/(√2x - 2)
= 2 lim(x → 2) [(√2x)2 + 2) (√2x)2 - 2)]/(√2x - 2)
= 8
= lim x → 2 [(2x - 4) (2 *4)]/(√2x - 2)
= 2 lim(x → 2) [(√2x)2 - (2)2]/(√2x - 2)
= 2 lim(x → 2) [(√2x)2 + 2) (√2x)2 - 2)]/(√2x - 2)
= 8
The derivative of the constant function f(x)=a for a fixed real number ‘a’ is:- a)a
- b)1
- c)2
- d)0
Correct answer is option 'D'. Can you explain this answer?
The derivative of the constant function f(x)=a for a fixed real number ‘a’ is:
a)
a
b)
1
c)
2
d)
0
|
|
Pooja Shah answered |
Let f(x) = a, where a is a fixed real number.
So, f(x+h) = a
So, d/dx(f(x)) = lim(h→0)f[(x+h)−f(x)]/h
= lim(h→0) (a−a)/h
= 0
Hence, d/dx(a) = 0 , where a is a fixed real number.
So, f(x+h) = a
So, d/dx(f(x)) = lim(h→0)f[(x+h)−f(x)]/h
= lim(h→0) (a−a)/h
= 0
Hence, d/dx(a) = 0 , where a is a fixed real number.
The derivate of the function 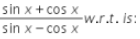
- a)
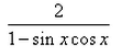
- b)
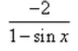
- c)

- d)
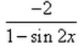
Correct answer is option 'D'. Can you explain this answer?
The derivate of the function 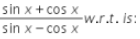
a)
b)
c)
d)
|
|
Gaurav Kumar answered |
Given, y = (sinx+cosx)/(sinx−cosx)
∴ dydx = [(sinx−cosx)(cosx−sinx)−(sinx+cosx)(cosx+sinx)]/(sinx−cosx)2
[by quotient rule]
= [(−sinx−cosx)2 − (sinx+cosx)2]/(sinx−cosx)2
− [(sinx−cosx)2 − (sinx+cosx)2]/(sinx−cosx)2
= − [(sin2x + cos2x − 2sinxcosx + sin2x + cos2x + 2sinxcosx)]/(sinx−cosx)2
= −2/(sinx−cosx)2
= -2/(sin2x + cos2x - 2sinxcosx)
= - 2/(1 - sin2x)
∴ dydx = [(sinx−cosx)(cosx−sinx)−(sinx+cosx)(cosx+sinx)]/(sinx−cosx)2
[by quotient rule]
= [(−sinx−cosx)2 − (sinx+cosx)2]/(sinx−cosx)2
− [(sinx−cosx)2 − (sinx+cosx)2]/(sinx−cosx)2
= − [(sin2x + cos2x − 2sinxcosx + sin2x + cos2x + 2sinxcosx)]/(sinx−cosx)2
= −2/(sinx−cosx)2
= -2/(sin2x + cos2x - 2sinxcosx)
= - 2/(1 - sin2x)
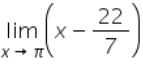
- a)π – 22/7
- b)π
- c)0
- d)(7x-22)/7
Correct answer is option 'A'. Can you explain this answer?
a)
π – 22/7
b)
π
c)
0
d)
(7x-22)/7
|
|
Lavanya Menon answered |
lim(x → π ) (x - 22/7)
Taking limit, we get
⇒ π - 22/7
Taking limit, we get
⇒ π - 22/7
Chapter doubts & questions for Limits and Derivatives - Online MCQ Tests for Commerce 2025 is part of Commerce exam preparation. The chapters have been prepared according to the Commerce exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Commerce 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Limits and Derivatives - Online MCQ Tests for Commerce in English & Hindi are available as part of Commerce exam.
Download more important topics, notes, lectures and mock test series for Commerce Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily
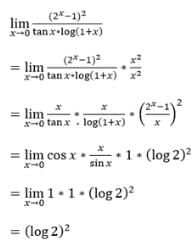


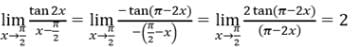
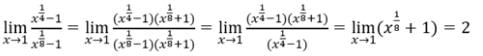

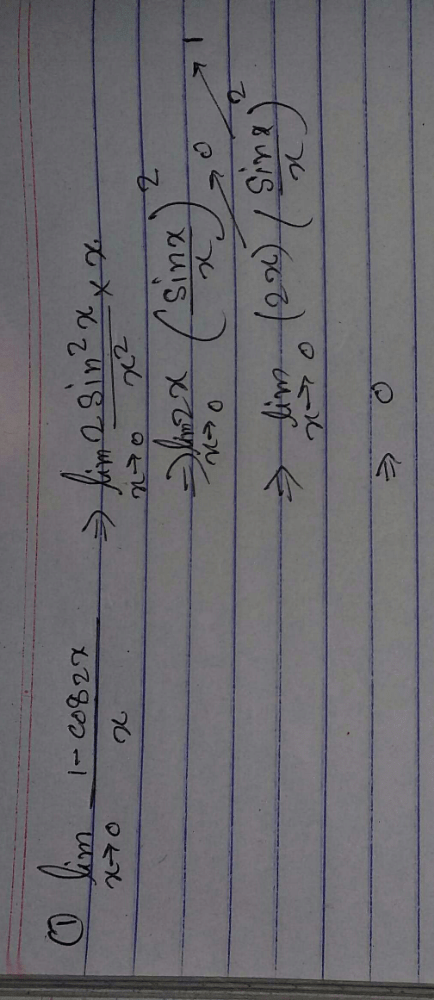
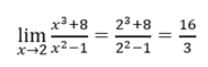
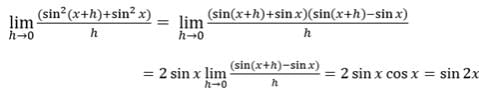
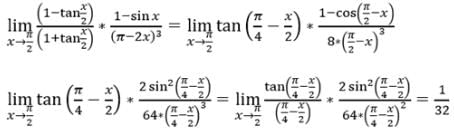
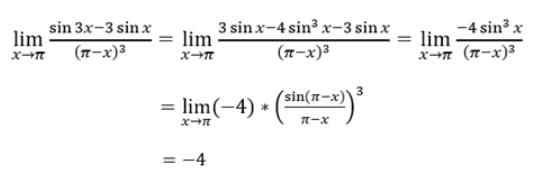
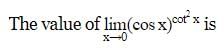

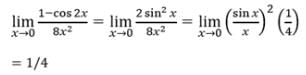
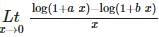 is equal to
is equal to