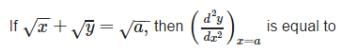All Exams >
Commerce >
Online MCQ Tests for Commerce >
All Questions
All questions of Continuity and Differentiability for Commerce Exam
If the function f (x) = x2– 8x + 12 satisfies the condition of Rolle’s Theorem on (2, 6), find the value of c such that f ‘(c) = 0- a)6
- b)4
- c)8
- d)2
Correct answer is option 'B'. Can you explain this answer?
If the function f (x) = x2– 8x + 12 satisfies the condition of Rolle’s Theorem on (2, 6), find the value of c such that f ‘(c) = 0
a)
6
b)
4
c)
8
d)
2

|
Dr Manju Sen answered |
f (x) = x2 - 8x + 12
Function satisfies the condition of Rolle's theorem for (2,6).
We need to find c for which f’(c) = 0
f’(x) = 2x – 8
f’(c) = 2c – 8 = 0
c = 4
Function satisfies the condition of Rolle's theorem for (2,6).
We need to find c for which f’(c) = 0
f’(x) = 2x – 8
f’(c) = 2c – 8 = 0
c = 4
If xy = 2, then dy/dx is- a)-x2/2
- b)y2
- c)-2/x2
- d)-y/x
Correct answer is option 'D'. Can you explain this answer?
If xy = 2, then dy/dx is
a)
-x2/2
b)
y2
c)
-2/x2
d)
-y/x
|
|
Hansa Sharma answered |
xy = 2
x dy/dx + y = 0
x dy/dx = -y
dy/dx = -y/x
x dy/dx + y = 0
x dy/dx = -y
dy/dx = -y/x
When Rolle’s Theorem is verified for f(x) on [a, b] then there exists c such that- a)c ε [a, b] such that f'(c) = 0
- b)c ε (a, b) such that f'(c) = 0
- c)c ε (a, b] such that f'(c) = 0
- d)c ε [a, b) such that f'(c) = 0
Correct answer is option 'B'. Can you explain this answer?
When Rolle’s Theorem is verified for f(x) on [a, b] then there exists c such that
a)
c ε [a, b] such that f'(c) = 0
b)
c ε (a, b) such that f'(c) = 0
c)
c ε (a, b] such that f'(c) = 0
d)
c ε [a, b) such that f'(c) = 0
|
|
Abhinay Tripathi answered |
Answer is
B) c ∈ (a, b) such that f'(c) = 0.
Statement for Rolle’s Theorem :
Suppose that a function f(x) is continuous on the closed interval [a,b] and differentiable on the open interval (a,b). Then if f(a)=f(b), then there exists at least one point c in the open interval (a,b) for which f′(c)=0.
B) c ∈ (a, b) such that f'(c) = 0.
Statement for Rolle’s Theorem :
Suppose that a function f(x) is continuous on the closed interval [a,b] and differentiable on the open interval (a,b). Then if f(a)=f(b), then there exists at least one point c in the open interval (a,b) for which f′(c)=0.
Whta is the derivatve of y = log5 (x)- a)
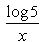
- b)
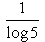
- c)

- d)
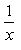
Correct answer is option 'C'. Can you explain this answer?
Whta is the derivatve of y = log5 (x)
a)
b)
c)
d)
|
|
Tanuja Kapoor answered |
y = log5 x = ln x/ln 5 → change of base
= ln x/ln 5
dy/dx = 1/ln5⋅1/x → 1/ln5 is a constant, so we don't change it
= 1/(x ln 5)
= ln x/ln 5
dy/dx = 1/ln5⋅1/x → 1/ln5 is a constant, so we don't change it
= 1/(x ln 5)

- a)– 1
- b)0
- c)1
- d)1/2
Correct answer is option 'D'. Can you explain this answer?
a)
– 1
b)
0
c)
1
d)
1/2

|
Angad Gupta answered |
We have to use L'Hopital Rule It is in the form 0/0 So first we have to differentiate it After differentiating we get sinx/2x Then again differentiate it We get cosx/2 and now we get the answer as 1/2
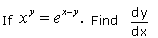
- a)
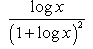
- b)
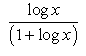
- c)
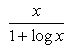
- d)
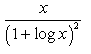
Correct answer is option 'A'. Can you explain this answer?
a)
b)
c)
d)
|
|
Lavanya Menon answered |
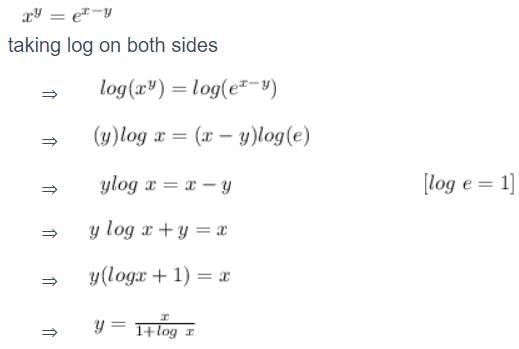
On differentiating both sides with respect to x
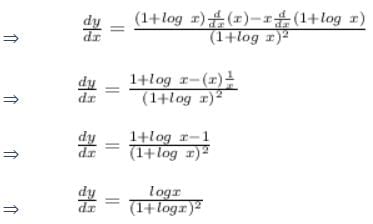
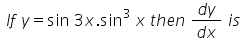
- a)3 cos2 x. cos 4x
- b)cos 3x. cos3x
- c)-9 cos 3x. cos2x sinx
- d)3 sin2x.sin 4x
Correct answer is option 'D'. Can you explain this answer?
a)
3 cos2 x. cos 4x
b)
cos 3x. cos3x
c)
-9 cos 3x. cos2x sinx
d)
3 sin2x.sin 4x
|
|
Deepak Kapoor answered |
Given: y = sin 3x . sin3

= 3 sin2x.sin 4x

= 3 sin2x.sin 4x
Differentiate sin2(θ2 + 1) with respect to θ2- a)sin(2θ2 + 1)
- b)cos(2θ2 + 2)
- c)sin(2θ2 + 2)
- d)cos(2θ2 + 1)
Correct answer is option 'C'. Can you explain this answer?
Differentiate sin2(θ2 + 1) with respect to θ2
a)
sin(2θ2 + 1)
b)
cos(2θ2 + 2)
c)
sin(2θ2 + 2)
d)
cos(2θ2 + 1)

|
Gunjan Lakhani answered |
y = sin2(θ2+1)
v = θ2
dy/d(v) = dydθ/dvdθ
dy/dthη = sin2(V+1)
= 2sin(V+1)⋅cos(V+1)dv/dθ
= 2sin(θ2+1)cos(θ2+1)
= sin2(θ2+1).
v = θ2
dy/d(v) = dydθ/dvdθ
dy/dthη = sin2(V+1)
= 2sin(V+1)⋅cos(V+1)dv/dθ
= 2sin(θ2+1)cos(θ2+1)
= sin2(θ2+1).
A real function f is said to be continuous if it is continuous at every point in …… .- a)[-∞,∞]
- b)The range of f
- c)The domain of f
- d)Any interval of real numbers
Correct answer is option 'A'. Can you explain this answer?
A real function f is said to be continuous if it is continuous at every point in …… .
a)
[-∞,∞]
b)
The range of f
c)
The domain of f
d)
Any interval of real numbers
|
|
Saranya Choudhury answered |
Its domain. This means that for any point x in the domain of f, as x approaches a certain value a, the value of f(x) approaches f(a). In other words, there are no sudden jumps or gaps in the graph of f.
More formally, a function f is continuous at a point a if:
1. f(a) is defined (i.e. a is in the domain of f).
2. The limit of f(x) as x approaches a exists (i.e. the left and right-hand limits are equal).
3. The limit of f(x) as x approaches a is equal to f(a).
If a function is continuous at every point in its domain, it is called a continuous function. Continuous functions have many useful properties and are often used in mathematical models and real-world applications.
More formally, a function f is continuous at a point a if:
1. f(a) is defined (i.e. a is in the domain of f).
2. The limit of f(x) as x approaches a exists (i.e. the left and right-hand limits are equal).
3. The limit of f(x) as x approaches a is equal to f(a).
If a function is continuous at every point in its domain, it is called a continuous function. Continuous functions have many useful properties and are often used in mathematical models and real-world applications.
Geometrically the Mean Value theorem ensures that there is at least one point on the curve f(x) , whose abscissa lies in (a, b) at which the tangent is- a)Parallel to the x axis
- b)Parallel to the y axis
- c)Parallel to the line joining the end points of the curve
- d)Parallel to the line y = x
Correct answer is option 'C'. Can you explain this answer?
Geometrically the Mean Value theorem ensures that there is at least one point on the curve f(x) , whose abscissa lies in (a, b) at which the tangent is
a)
Parallel to the x axis
b)
Parallel to the y axis
c)
Parallel to the line joining the end points of the curve
d)
Parallel to the line y = x

|
Ujjwal Gupta answered |
No, option C is correct answer.
If 3 sin(xy) + 4 cos (xy) = 5, then 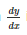 = .....
= .....- a)

- b)
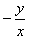
- c)
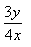
- d)

Correct answer is option 'B'. Can you explain this answer?
If 3 sin(xy) + 4 cos (xy) = 5, then 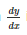 = .....
= .....
a)
b)
c)
d)

|
Dr Manju Sen answered |
3sinxy + 4cosxy = 5
⇒ 5(3/5 sinxy + 4/5 cosxy) = 5
⇒ (3/5 sinxy + 4/5 cosxy) = 1
now (3/5)²+(4/5)² = 1
so let, 3/5 = cosA
⇒ 4/5 = sinA
So , (3/5 sinxy + 4/5 cosxy) = 1
⇒ (cosAsinxy + sinAcosxy) = 1
⇒ sin(A+xy) = 1
⇒ A + xy = 2πk + π/2 (k is any integer)
⇒ sin⁻¹(4/5) + xy = 2πk + π/2
differenciating both sides with respect to x
0 + xdy/dx + y = 0
dy/dx = -y/x
⇒ 5(3/5 sinxy + 4/5 cosxy) = 5
⇒ (3/5 sinxy + 4/5 cosxy) = 1
now (3/5)²+(4/5)² = 1
so let, 3/5 = cosA
⇒ 4/5 = sinA
So , (3/5 sinxy + 4/5 cosxy) = 1
⇒ (cosAsinxy + sinAcosxy) = 1
⇒ sin(A+xy) = 1
⇒ A + xy = 2πk + π/2 (k is any integer)
⇒ sin⁻¹(4/5) + xy = 2πk + π/2
differenciating both sides with respect to x
0 + xdy/dx + y = 0
dy/dx = -y/x
Can you explain the answer of this question below:The derivatve of f(x) = 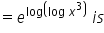
- A:
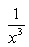
- B:
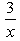
- C:
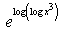
- D:
3x2
The answer is b.
The derivatve of f(x) =
3x2

|
.mie. answered |
Here in this function ....firstly... exponential and logarithmic fn are anti to each other...
and therefore cncl out ech other....
here..
in this e and log cncl out ech other... and we are left with ....
log x^3.....
acc to formula..
log m^n = n log m
therefore...
3 log x
so we reduced our eq to this
then taking derivative....
its 3/x
Which of the following functions are not continuous.- a)
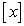
- b)
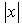
- c)ex
- d)
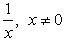
Correct answer is option 'A'. Can you explain this answer?
Which of the following functions are not continuous.
a)
b)
c)
ex
d)

|
Anu answered |
b,c,and d are continuous and [x] is discontinuous at integer points.
y = log(sec + tan x)
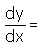
- a)sec x tan x – 1
- b)sec x
- c)sec x tan x + 1
- d)tan x
Correct answer is option 'B'. Can you explain this answer?
y = log(sec + tan x)
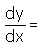
a)
sec x tan x – 1
b)
sec x
c)
sec x tan x + 1
d)
tan x
|
|
Lavanya Menon answered |
y = log(secx + tanx)
dy/dx = 1/(secx + tanx){(secxtanx) + sec2x}
= secx(secx + tanx)/(secx + tanx)
= secx
dy/dx = 1/(secx + tanx){(secxtanx) + sec2x}
= secx(secx + tanx)/(secx + tanx)
= secx
Derivatve of f(x) 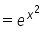 is given by
is given by
- a)
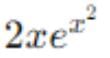
- b)
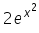
- c)
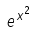
- d)

Correct answer is option 'A'. Can you explain this answer?
Derivatve of f(x) 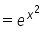 is given by
is given by
a)
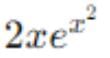
b)
c)
d)
|
|
Neha Sharma answered |
y 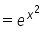
The derivative of y = ef(x)is dy/dx = f'(x)ef(x)
In this case, f(x) = x2 , and the derivative of x2 = 2x
Therefore, f'(x)= 2x,
dy/dx = 2x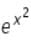
The derivative of y = ef(x)is dy/dx = f'(x)ef(x)
In this case, f(x) = x2 , and the derivative of x2 = 2x
Therefore, f'(x)= 2x,
dy/dx = 2x
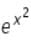
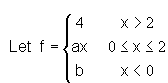 For what values of a and b, f is a continuous function.
For what values of a and b, f is a continuous function.- a)a=2,b=0
- b)a=1,b=0
- c)a=0,b=2
- d)a=0,b=0
Correct answer is 'A'. Can you explain this answer?
a)
a=2,b=0
b)
a=1,b=0
c)
a=0,b=2
d)
a=0,b=0
|
|
Tejas Verma answered |
For continuity: LHL=RHL
at x=2,
LHL: x < 2 ⇒ f(x) = 2*a
RHL: x ≥ 2 ⇒ f(x) = 4
For continuity: LHL = RHL
⇒ 2a = 4 ⇒ a = 2
LHL: x < 2 ⇒ f(x) = 2*a
RHL: x ≥ 2 ⇒ f(x) = 4
For continuity: LHL = RHL
⇒ 2a = 4 ⇒ a = 2
at x = 0,
LHL: x < 0 ⇒ f(x) = b
RHL: x ≥ 0 ⇒ f(x) = 0 * a
For continuity: LHL = RHL
⇒ b = 0
LHL: x < 0 ⇒ f(x) = b
RHL: x ≥ 0 ⇒ f(x) = 0 * a
For continuity: LHL = RHL
⇒ b = 0
Find the derivate of y = sin4x + cos4x- a)– sin 2x
- b)4 sin3 x + 4 cos3 x
- c)– sin 4x
- d)4 sin x cos x cos 2x
Correct answer is option 'C'. Can you explain this answer?
Find the derivate of y = sin4x + cos4x
a)
– sin 2x
b)
4 sin3 x + 4 cos3 x
c)
– sin 4x
d)
4 sin x cos x cos 2x

|
Mohit Rajpoot answered |
y=sin4x, and z=cos4x
So by using chain rule
df(x)/dx = dsin4x/dx + dcos4x/dx
=dy4/dy * dy/dx + dz4/dz * dzdx
=dy4/dy * dsinxdx + dz4/dz * dcosx/dx
=4y(4−1)⋅cosx+4z(4−1)⋅(−sinx)
=4sin3xcosx − 4cos3xsinx
=4sinxcosx(sin2x − cos2x)
=2sin2x(−cos2x)
=−2sin2xcos2x
=−sin4x
So by using chain rule
df(x)/dx = dsin4x/dx + dcos4x/dx
=dy4/dy * dy/dx + dz4/dz * dzdx
=dy4/dy * dsinxdx + dz4/dz * dcosx/dx
=4y(4−1)⋅cosx+4z(4−1)⋅(−sinx)
=4sin3xcosx − 4cos3xsinx
=4sinxcosx(sin2x − cos2x)
=2sin2x(−cos2x)
=−2sin2xcos2x
=−sin4x

- a)
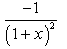
- b)

- c)
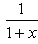
- d)
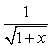
Correct answer is option 'A'. Can you explain this answer?
a)
b)
c)
d)

|
Sushil Kumar answered |
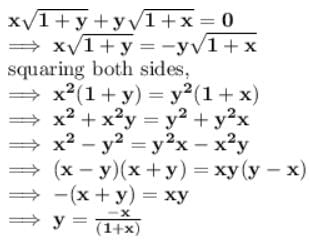
now differentiate y with respect to x,
dy/dx = -{[x d/dx(1+x) - (1+x)dx/dx]}/(1+x2)
= -1/(1+x)2
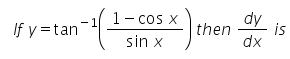
Correct answer is option 'A'. Can you exp... morelain this answer?
|
|
Aryan Khanna answered |
y = tan-1(1-cosx)/sinx
y = tan-1{2sin2(x/2)/(2sin(x/2)cos(x/2)}
y = tan-1{tan x/2}
y = x/2 => dy/dx = 1/2
y = tan-1{2sin2(x/2)/(2sin(x/2)cos(x/2)}
y = tan-1{tan x/2}
y = x/2 => dy/dx = 1/2
Function f(x) = log x + 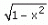 is continuous at
is continuous at- a)(0,1)
- b)[-1,1]
- c)(0,∞)
- d)(0,1]
Correct answer is option 'D'. Can you explain this answer?
Function f(x) = log x + 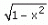 is continuous at
is continuous at
a)
(0,1)
b)
[-1,1]
c)
(0,∞)
d)
(0,1]
|
|
Om Desai answered |
- [-1,1] cannot be continuous interval because log is not defined at 0.
- The value of x cannot be greater than 1 because then the function will become complex.
- (0,1) will not be considered because its continuous at 1 as well. Hence D is the correct option.
F(x) = tan (log x)
F'(x) =- a)sec2 (logx)
- b)
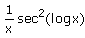
- c)
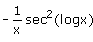
- d)-x sec2 (logx)
Correct answer is option 'B'. Can you explain this answer?
F(x) = tan (log x)
F'(x) =
F'(x) =
a)
sec2 (logx)
b)
c)
d)
-x sec2 (logx)

|
Virendra Singh answered |
I have chosen (b) but it is showing (d) is correct
Let f and g be differentiable functions such that fog = I, the identity function. If g’ (a) = 2 and g (a) = b, then f ‘ (b) =- a)1/2
- b)2
- c)-2
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Let f and g be differentiable functions such that fog = I, the identity function. If g’ (a) = 2 and g (a) = b, then f ‘ (b) =
a)
1/2
b)
2
c)
-2
d)
none of these

|
Divey Sethi answered |
f(g(x)) = x
f'(g(x)) g'(x) = 1
put x = a
f'(b) g'(a) = 1
2 f'(b) = 1
f'(b) = 1/2
f'(g(x)) g'(x) = 1
put x = a
f'(b) g'(a) = 1
2 f'(b) = 1
f'(b) = 1/2
The derivative of 2x tan x is- a)2x log 2 [ sec2 x + tan x]
- b)2x tan x [sec x + log 2]
- c)2x [sec2 x + log 2 tan x]
- d)2x [sec2 x + tan x]
Correct answer is option 'C'. Can you explain this answer?
The derivative of 2x tan x is
a)
2x log 2 [ sec2 x + tan x]
b)
2x tan x [sec x + log 2]
c)
2x [sec2 x + log 2 tan x]
d)
2x [sec2 x + tan x]

|
Sushil Kumar answered |
dy/dx = 2x(tanx)' + tanx (2x)'
dy/dx = 2x (secx)2 + 2x tanx log2 , {since , (ax)' = ax loga (x)'}
dy/dx = 2x[(Secx)2 + log2 tanx]
dy/dx = 2x (secx)2 + 2x tanx log2 , {since , (ax)' = ax loga (x)'}
dy/dx = 2x[(Secx)2 + log2 tanx]

- a)

- b)

- c)
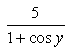
- d)
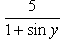
Correct answer is option 'C'. Can you explain this answer?
a)
b)
c)
d)
|
|
Poonam Reddy answered |
y + sin y = 5x
dy/dx + cos ydy/dx = 5
dy/dx = 5/(1+cos y)
dy/dx + cos ydy/dx = 5
dy/dx = 5/(1+cos y)
If f(x) = ex, then the value of f'(-3) is- a)log (3)
- b)e2
- c)log (-3)
- d)e-3
Correct answer is option 'D'. Can you explain this answer?
If f(x) = ex, then the value of f'(-3) is
a)
log (3)
b)
e
2
c)
log (-3)
d)
e-3

|
Infinity Academy answered |
As, f (x) = ex
Similarly, f (-3) = e-3
Similarly, f (-3) = e-3
If f(x) = | x | ∀ x ∈ R, then- a)f is discontinuous at x = 0
- b)f is derivable at x = 0 and f ‘ (0) = 1
- c)f is derivable at x = 0 but f’ (0) ≠
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
If f(x) = | x | ∀ x ∈ R, then
a)
f is discontinuous at x = 0
b)
f is derivable at x = 0 and f ‘ (0) = 1
c)
f is derivable at x = 0 but f’ (0) ≠
d)
none of these

|
Sakshi Jain answered |
|X| is a continuous function ,which is clear from its graph but at x=0,|X| is not differentiable since it has a sharp edge at x=0 . hence 'd' is correct option.
Can you explain the answer of this question below:
- A:
1/2
- B:
0
- C:
1
- D:
none of these
The answer is b.
1/2
0
1
none of these

|
Shivani answered |
Apply L-hospital rule.....u will get the ans....
The value of c for which Lagrange’s theorem f(x) = |x| in the interval [-1, 1] is- a)1/2
- b)1
- c)-1/2
- d)non-existent in the interval
Correct answer is option 'D'. Can you explain this answer?
The value of c for which Lagrange’s theorem f(x) = |x| in the interval [-1, 1] is
a)
1/2
b)
1
c)
-1/2
d)
non-existent in the interval

|
Rakhi Kumari answered |
Since Fx =|x| therefore it's graph will be considerd only in the x axis but not in y axis and also its been in the closed interval [-1, 1] so other options will be neglected

- a)

- b)

- c)

- d)

Correct answer is option 'B'. Can you explain this answer?
a)
b)
c)
d)

|
Suhani Dangarh answered |
Put x=tan thita. then you will get. 2 tan inverse x then differentiate
The differential coffcient 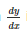 of the equation yx = e(x - y) is :
of the equation yx = e(x - y) is :- a)
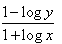
- b)
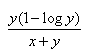
- c)
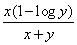
- d)
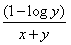
Correct answer is option 'B'. Can you explain this answer?
The differential coffcient 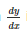 of the equation yx = e(x - y) is :
of the equation yx = e(x - y) is :
a)
b)
c)
d)

|
Ambition Institute answered |
Taking log both the sides
xlogy = (x-y)loge
Differentiate it with respect to x, we get
x/y dy/dx = logy = loge - xloge dy/dx
dy/dx = (loge - logy)/(x/y + loge)
= y(1 - loge)/(x + y)
xlogy = (x-y)loge
Differentiate it with respect to x, we get
x/y dy/dx = logy = loge - xloge dy/dx
dy/dx = (loge - logy)/(x/y + loge)
= y(1 - loge)/(x + y)

- a)

- b)
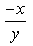
- c)
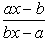
- d)
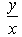
Correct answer is option 'D'. Can you explain this answer?
a)
b)
c)
d)
|
|
Rocky Gupta answered |
X^a y^b = (x + y)^(a + b)
taking ln on both sides :-
alnx + b lny = (a + b) ln(x + y)
diff both sides w.r.t x :-
a/x + by'/y = ( (a + b)/(x + y) ) + (((a + b) y'))/(x + y)
or,
a/x - (a +b)/(x + y) = y'[((a + b) / (x + y)) - b/y]
or,
(ax + ay - ax - bx)/x = y' [ (ay + by - bx - by)/y] (cancel (x + y))
or,
y' = dy/dx = ( y (ay - bx) )/(x( ay - bx)) = y/x
therefore we can easily say that the option (D) is the correct answer
taking ln on both sides :-
alnx + b lny = (a + b) ln(x + y)
diff both sides w.r.t x :-
a/x + by'/y = ( (a + b)/(x + y) ) + (((a + b) y'))/(x + y)
or,
a/x - (a +b)/(x + y) = y'[((a + b) / (x + y)) - b/y]
or,
(ax + ay - ax - bx)/x = y' [ (ay + by - bx - by)/y] (cancel (x + y))
or,
y' = dy/dx = ( y (ay - bx) )/(x( ay - bx)) = y/x
therefore we can easily say that the option (D) is the correct answer

- a)
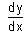
- b)

- c)
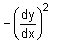
- d)
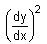
Correct answer is option 'D'. Can you explain this answer?
a)
b)
c)
d)

|
Knowledge Hub answered |
ey =1/ (x+5)
Taking log both side we get
log ey = log {1/(5+x)}
then, y = log {1/(5+x)}
Differentiating both side ,
dy/dx =( x+5) . {-1/(5+x)²}
dy/dx = -1/(5+x) ……..( 1)
Again Differentiating, d²y/dx²= 1/(5+x)²
d²y/dx²= {-1/(5+x)}²
From equation (1)
d²y/dx² = {dy/dx}²
Taking log both side we get
log ey = log {1/(5+x)}
then, y = log {1/(5+x)}
Differentiating both side ,
dy/dx =( x+5) . {-1/(5+x)²}
dy/dx = -1/(5+x) ……..( 1)
Again Differentiating, d²y/dx²= 1/(5+x)²
d²y/dx²= {-1/(5+x)}²
From equation (1)
d²y/dx² = {dy/dx}²
Direction: Read the following text and answer the following questions on the basis of the same:Ms. Remka of city school is teaching chain rule to her students with the help of a flow-chartThe chain rule says that if h and g are functions and f(x) = g(h(x)), then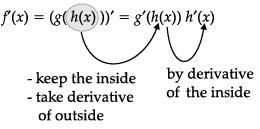 Let f(x) = sin x and g(x) = x3d/dx sin x3 _______.
Let f(x) = sin x and g(x) = x3d/dx sin x3 _______.- a)cos (x3)
- b)–cos (x3)
- c)3x2 sin (x3)
- d)3x2 cos (x3)
Correct answer is option 'D'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
Ms. Remka of city school is teaching chain rule to her students with the help of a flow-chart
The chain rule says that if h and g are functions and f(x) = g(h(x)), then

Let f(x) = sin x and g(x) = x3
d/dx sin x3 _______.
a)
cos (x3)
b)
–cos (x3)
c)
3x2 sin (x3)
d)
3x2 cos (x3)
|
|
Varun Kapoor answered |
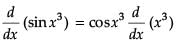
= 3x2 cosx3
If f (x) = [x sin p x] { where [x] denotes greatest integer function}, then f (x) is
- a) Continuous at x = 0
- b) Continuous in (-1, 0)
- c) Differentiable at x = 1
- d) Differentiable in (-1, 1)
Correct answer is option 'A'. Can you explain this answer?
If f (x) = [x sin p x] { where [x] denotes greatest integer function}, then f (x) is
a)
Continuous at x = 0b)
Continuous in (-1, 0)c)
Differentiable at x = 1d)
Differentiable in (-1, 1)|
|
Asha Choudhury answered |
Solution:
To determine the continuity and differentiability of f(x), we need to evaluate left-hand limit, right-hand limit and the derivative of f(x) at every point in the domain of f(x).
Left-hand limit of f(x):
As x approaches 0 from the left, [x] approaches -1 and sin(px) oscillates between -1 and 1. Therefore, f(x) oscillates between -x and x. Thus, the left-hand limit of f(x) as x approaches 0 is:
lim x→0- f(x) = lim x→0- [x sin(px)] = lim x→0- (-x) = 0.
Right-hand limit of f(x):
As x approaches 0 from the right, [x] approaches 0 and sin(px) oscillates between -1 and 1. Therefore, f(x) oscillates between 0 and x. Thus, the right-hand limit of f(x) as x approaches 0 is:
lim x→0+ f(x) = lim x→0+ [x sin(px)] = lim x→0+ (0) = 0.
Since the left-hand limit and right-hand limit are equal, f(x) is continuous at x=0.
Derivative of f(x):
For x≠0, f(x) is piecewise linear with slope sin(px) and jump discontinuity at every integer multiple of 1/p. Therefore, f(x) is not differentiable at these points.
Since f(x) is continuous at x=0 and not differentiable at any other point, the correct answer is option 'A'.
To determine the continuity and differentiability of f(x), we need to evaluate left-hand limit, right-hand limit and the derivative of f(x) at every point in the domain of f(x).
Left-hand limit of f(x):
As x approaches 0 from the left, [x] approaches -1 and sin(px) oscillates between -1 and 1. Therefore, f(x) oscillates between -x and x. Thus, the left-hand limit of f(x) as x approaches 0 is:
lim x→0- f(x) = lim x→0- [x sin(px)] = lim x→0- (-x) = 0.
Right-hand limit of f(x):
As x approaches 0 from the right, [x] approaches 0 and sin(px) oscillates between -1 and 1. Therefore, f(x) oscillates between 0 and x. Thus, the right-hand limit of f(x) as x approaches 0 is:
lim x→0+ f(x) = lim x→0+ [x sin(px)] = lim x→0+ (0) = 0.
Since the left-hand limit and right-hand limit are equal, f(x) is continuous at x=0.
Derivative of f(x):
For x≠0, f(x) is piecewise linear with slope sin(px) and jump discontinuity at every integer multiple of 1/p. Therefore, f(x) is not differentiable at these points.
Since f(x) is continuous at x=0 and not differentiable at any other point, the correct answer is option 'A'.

- a)2t
- b)1/2a
- c)-t/2a
- d)t/4a
Correct answer is option 'B'. Can you explain this answer?
a)
2t
b)
1/2a
c)
-t/2a
d)
t/4a

|
Knowledge Hub answered |
y = at4, x = 2at2
dy/dt = 4at3 dx/dt = 4at => dt/dx = 1/4at
Divide dy/dt by dx/dt, we get
dy/dx = t2
d2 y/dx2 = 2t dt/dx……………….(1)
Put the value of dt/dx in eq(1)
d2 y /dx2 = 2t(1/4at)
= 1/2a
dy/dt = 4at3 dx/dt = 4at => dt/dx = 1/4at
Divide dy/dt by dx/dt, we get
dy/dx = t2
d2 y/dx2 = 2t dt/dx……………….(1)
Put the value of dt/dx in eq(1)
d2 y /dx2 = 2t(1/4at)
= 1/2a
Differentiate 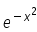 with respect to x.
with respect to x.- a)
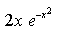
- b)
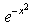
- c)
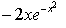
- d)
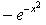
Correct answer is option 'C'. Can you explain this answer?
Differentiate 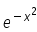 with respect to x.
with respect to x.
a)
b)
c)
d)
|
|
Tejas Verma answered |
y = e^(-x)2.................(1)
Put u = (-x)2
du/dx = -2x dx
Differentiating eq(1) y = eu
dy/du = e^u
⇒ dy/dx = (dy/du) * (du/dx)
= (eu) * (-2x)
⇒ - 2xe(-x2)
Put u = (-x)2
du/dx = -2x dx
Differentiating eq(1) y = eu
dy/du = e^u
⇒ dy/dx = (dy/du) * (du/dx)
= (eu) * (-2x)
⇒ - 2xe(-x2)
Examine the continuity of function 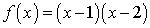
- a)Discontinuous at x=1,2
- b)Discontinuous at x=1
- c)Continuous everywhere.
- d)Discontinuous at x=2
Correct answer is option 'C'. Can you explain this answer?
Examine the continuity of function 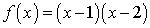
a)
Discontinuous at x=1,2
b)
Discontinuous at x=1
c)
Continuous everywhere.
d)
Discontinuous at x=2
|
|
Om Desai answered |
Lim f (x) = lim (x-1)(x-2) at x tend to k
► So it get k2-3k+2
► Now f (k) = k2 -3k+2
► So f (x) =f (k) so continous at everywhere
Chapter doubts & questions for Continuity and Differentiability - Online MCQ Tests for Commerce 2025 is part of Commerce exam preparation. The chapters have been prepared according to the Commerce exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Commerce 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Continuity and Differentiability - Online MCQ Tests for Commerce in English & Hindi are available as part of Commerce exam.
Download more important topics, notes, lectures and mock test series for Commerce Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup

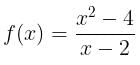
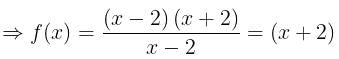 Therefore, f(x) continuous everywhere.
Therefore, f(x) continuous everywhere.