All Exams >
CDS >
Elementary Mathematics for CDS >
All Questions
All questions of Mensuration: Volume, Surface Area & Solid Figures for CDS Exam
Find the perimeter of the a square with side 4cm.- a)16 cm
- b)12 cm
- c)10 cm
- d)8 cm
Correct answer is option 'A'. Can you explain this answer?
Find the perimeter of the a square with side 4cm.
a)
16 cm
b)
12 cm
c)
10 cm
d)
8 cm

|
Sreesha Phalod answered |
Sol. perimeter of square=4* sides
=4*4 (sides is 4)
=16.
=4*4 (sides is 4)
=16.
ABCD is a square of side 10 cm. What is the area of the least-sized square that may be inscribed in ABCD with its vertices on the sides of ABCD?- a)0 cm2
- b)25 cm2
- c)50 cm2
- d)66.66 cm2
Correct answer is option 'A'. Can you explain this answer?
ABCD is a square of side 10 cm. What is the area of the least-sized square that may be inscribed in ABCD with its vertices on the sides of ABCD?
a)
0 cm2
b)
25 cm2
c)
50 cm2
d)
66.66 cm2

|
Athira Sen answered |
The vertices of the smaller square will be on the midpoints of the sides of the larger square.
Find the volume of a cuboid whose length is 8 cm, width is 3 cm and height is 5 cm. - a)135 cm3
- b)125 cm3
- c)120 cm3
- d)130 cm3
Correct answer is option 'C'. Can you explain this answer?
Find the volume of a cuboid whose length is 8 cm, width is 3 cm and height is 5 cm.
a)
135 cm3
b)
125 cm3
c)
120 cm3
d)
130 cm3
|
|
Tanishq Joshi answered |
Finding Volume of a Cuboid
Given: length = 8 cm, width = 3 cm, height = 5 cm
To find: Volume of the cuboid
Formula: Volume of a cuboid = length x width x height
Substituting the given values in the formula, we get:
Volume = 8 cm x 3 cm x 5 cm
Volume = 120 cm3
Therefore, the correct answer is option C, 120 cm3.
Given: length = 8 cm, width = 3 cm, height = 5 cm
To find: Volume of the cuboid
Formula: Volume of a cuboid = length x width x height
Substituting the given values in the formula, we get:
Volume = 8 cm x 3 cm x 5 cm
Volume = 120 cm3
Therefore, the correct answer is option C, 120 cm3.
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Mensuration, Class 8, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic. Q.Find the volume of a cuboid whose length is 8 cm, breadth 6 cm and height 3.5 cm. - a)215 cm3
- b)172 cm3
- c)150 cm3
- d)168 cm3
Correct answer is option 'D'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Mensuration, Class 8, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic.
Q.
Find the volume of a cuboid whose length is 8 cm, breadth 6 cm and height 3.5 cm.
a)
215 cm3
b)
172 cm3
c)
150 cm3
d)
168 cm3
|
|
Ankita Shah answered |
Given,
Length (l) = 8 cm
Breadth (b) = 6 cm
Height (h) = 3.5 cm
We know that the volume of a cuboid is given by the formula:
Volume = length × breadth × height
Substituting the given values, we get:
Volume = 8 cm × 6 cm × 3.5 cm
Volume = 168 cm³
Therefore, the volume of the given cuboid is 168 cm³.
Hence, the correct option is (d) 168 cm³.
Length (l) = 8 cm
Breadth (b) = 6 cm
Height (h) = 3.5 cm
We know that the volume of a cuboid is given by the formula:
Volume = length × breadth × height
Substituting the given values, we get:
Volume = 8 cm × 6 cm × 3.5 cm
Volume = 168 cm³
Therefore, the volume of the given cuboid is 168 cm³.
Hence, the correct option is (d) 168 cm³.
Find the area of a triangle whose base is 4 cm and altitude is 6 cm.- a)10 cm2
- b)14 cm2
- c)16 cm2
- d)12 cm2
Correct answer is option 'D'. Can you explain this answer?
Find the area of a triangle whose base is 4 cm and altitude is 6 cm.
a)
10 cm2
b)
14 cm2
c)
16 cm2
d)
12 cm2
|
|
Kavya Saxena answered |
We know that area of triangle is equals to 1/2 base × altitude.
Here, base = 4 cm and altitude = 6 cm.
So, area = 1/2 × 4 × 6= 24 /2= 12 cm2.
Here, base = 4 cm and altitude = 6 cm.
So, area = 1/2 × 4 × 6= 24 /2= 12 cm2.
What is the area of an equilateral triangle of side 16 cm?- a)48√3 cm2
- b)128√3 cm2
- c)9.6√3 cm2
- d)64√3 cm2
Correct answer is option 'D'. Can you explain this answer?
What is the area of an equilateral triangle of side 16 cm?
a)
48√3 cm2
b)
128√3 cm2
c)
9.6√3 cm2
d)
64√3 cm2
|
|
Preeti Khanna answered |
Area of an equilateral triangle = √3/4 S2
If S = 16, Area of triangle = √3/4 * 16 * 16 = 64√3 cm2
PQRST is a pentagon in which all the interior angles are unequal. A circle of radius ‘r’ is inscribed in each of the vertices. Find the area of portion of circles falling inside the pentagon. - a)πr2
- b)1.5πr2
- c)2πr2
- d)1.25πr2
Correct answer is option 'B'. Can you explain this answer?
PQRST is a pentagon in which all the interior angles are unequal. A circle of radius ‘r’ is inscribed in each of the vertices. Find the area of portion of circles falling inside the pentagon.
a)
πr2
b)
1.5πr2
c)
2πr2
d)
1.25πr2
|
|
Preeti Khanna answered |
Since neither angles nor sides are given in the question, immediately the sum of angles of pentagon should come in mind. To use it,
We know the area of the sectors of a circle is given as,
We know the area of the sectors of a circle is given as,
Note => The above concept is applicable for a polygon of n sides.
Choice (B) is therefore, the correct answer.
Correct Answer: 1.5πr2
Choice (B) is therefore, the correct answer.
Correct Answer: 1.5πr2
Find the number of bricks, each measuring 25 cm × 12.5 cm × 7.5 cm, required to construct a wall 12 m long, 5 m high and 0.25 m thick, while the sand and cement mixture occupies 5% of the totalvolume of wall.- a)6080
- b)3040
- c)1520
- d)12160
Correct answer is option 'A'. Can you explain this answer?
Find the number of bricks, each measuring 25 cm × 12.5 cm × 7.5 cm, required to construct a wall 12 m long, 5 m high and 0.25 m thick, while the sand and cement mixture occupies 5% of the totalvolume of wall.
a)
6080
b)
3040
c)
1520
d)
12160

|
Talent Skill Learning answered |
Volume of wall = 1200 × 500 × 25 = 15000000 cm3
Volume of cement = 5% of 15000000 = 750000 cm3
Remaining volume = 15000000 – 750000 = 14250000 cm3
Volume of a brick = 25 × 12.5 × 7.5 = 2343.75 cm3
Volume of cement = 5% of 15000000 = 750000 cm3
Remaining volume = 15000000 – 750000 = 14250000 cm3
Volume of a brick = 25 × 12.5 × 7.5 = 2343.75 cm3
There is a right circular cone with base radius 3 units and height 4 units. The surface of this right circular cone is painted. It is then cut into two parts by a plane parallel to the base so that the volume of the top part (the small cone) divided by the volume of the frustum equals the painted area of the top part divided by the painted area of the bottom part. The height of the small cone is- a)7/3
- b)5/4
- c)5/2
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
There is a right circular cone with base radius 3 units and height 4 units. The surface of this right circular cone is painted. It is then cut into two parts by a plane parallel to the base so that the volume of the top part (the small cone) divided by the volume of the frustum equals the painted area of the top part divided by the painted area of the bottom part. The height of the small cone is
a)
7/3
b)
5/4
c)
5/2
d)
None of these
|
|
Kajal Kumar answered |
Take the total surface area of the initial cone into consideration and then proceed.
PQRS is a circle and circles are drawn with PO, QO, RO and SO as diameters. Areas A and B are marked. A/B is equal to: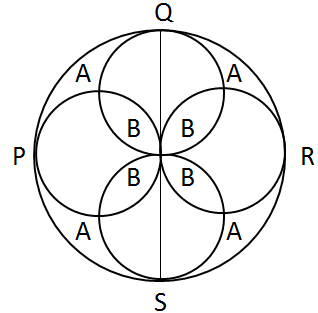
- a)π
- b)1
- c)π/4
- d)2
Correct answer is option 'B'. Can you explain this answer?
PQRS is a circle and circles are drawn with PO, QO, RO and SO as diameters. Areas A and B are marked. A/B is equal to:
a)
π
b)
1
c)
π/4
d)
2

|
Divey Sethi answered |
Such questions are all about visualization and ability to write one area in terms of others.
Here, Let the radius of PQRS be 2r
∴ Radius of each of the smaller circles = 2r/2 = r
∴ Area A can be written as:
A = π (2r)2 – 4 x π(r)2 (Area of the four smaller circles) + B (since, B has been counted twice in the previous subtraction)
Here, Let the radius of PQRS be 2r
∴ Radius of each of the smaller circles = 2r/2 = r
∴ Area A can be written as:
A = π (2r)2 – 4 x π(r)2 (Area of the four smaller circles) + B (since, B has been counted twice in the previous subtraction)
A = 4πr2 - 4πr2 + B
A = B
A/B = 1
A = B
A/B = 1
Choice (B) is therefore, the correct answer.
Correct Answer: 1
Correct Answer: 1
Two cones have their heights in the ratio 1 : 2 and the diameters of their bases are in the ratio 2 :1. What will be the ratio of their volumes?- a)4 : 1
- b)2 : 1
- c)3 : 2
- d)1 : 1
Correct answer is option 'B'. Can you explain this answer?
Two cones have their heights in the ratio 1 : 2 and the diameters of their bases are in the ratio 2 :1. What will be the ratio of their volumes?
a)
4 : 1
b)
2 : 1
c)
3 : 2
d)
1 : 1
|
|
Aarav Sharma answered |
Given information:
- Heights of two cones are in the ratio of 1:2
- Diameters of their bases are in the ratio of 2:1
To find:
Ratio of their volumes
Solution:
Let the height of the first cone be h1 and the height of the second cone be h2.
Let the diameter of the base of the first cone be d1 and the diameter of the base of the second cone be d2.
Let the radius of the base of the first cone be r1 and the radius of the base of the second cone be r2.
From the given information, we know that:
h1 : h2 = 1 : 2
d1 : d2 = 2 : 1
We also know that the volume of a cone is given by:
V = (1/3)πr^2h
where r is the radius of the base and h is the height of the cone.
We can use the information about the diameters of the bases to find the ratio of the radii:
r1 = (d1/2) and r2 = (d2/2)
r1 : r2 = (d1/2) : (d2/2) = d1 : d2 = 2 : 1
Now, we can use the information about the heights to find the ratio of the volumes:
V1/V2 = (1/3)πr1^2h1 / (1/3)πr2^2h2
V1/V2 = r1^2h1 / r2^2h2
V1/V2 = [(d1/2)^2h1] / [(d2/2)^2h2]
V1/V2 = (d1^2/4)(h1/h2)(1/d2^2)
Substituting the given ratios:
V1/V2 = (2^2/4)(1/2)(1/1^2)
V1/V2 = 1/2
Therefore, the ratio of the volumes of the two cones is 2:1. Hence, option B is the correct answer.
- Heights of two cones are in the ratio of 1:2
- Diameters of their bases are in the ratio of 2:1
To find:
Ratio of their volumes
Solution:
Let the height of the first cone be h1 and the height of the second cone be h2.
Let the diameter of the base of the first cone be d1 and the diameter of the base of the second cone be d2.
Let the radius of the base of the first cone be r1 and the radius of the base of the second cone be r2.
From the given information, we know that:
h1 : h2 = 1 : 2
d1 : d2 = 2 : 1
We also know that the volume of a cone is given by:
V = (1/3)πr^2h
where r is the radius of the base and h is the height of the cone.
We can use the information about the diameters of the bases to find the ratio of the radii:
r1 = (d1/2) and r2 = (d2/2)
r1 : r2 = (d1/2) : (d2/2) = d1 : d2 = 2 : 1
Now, we can use the information about the heights to find the ratio of the volumes:
V1/V2 = (1/3)πr1^2h1 / (1/3)πr2^2h2
V1/V2 = r1^2h1 / r2^2h2
V1/V2 = [(d1/2)^2h1] / [(d2/2)^2h2]
V1/V2 = (d1^2/4)(h1/h2)(1/d2^2)
Substituting the given ratios:
V1/V2 = (2^2/4)(1/2)(1/1^2)
V1/V2 = 1/2
Therefore, the ratio of the volumes of the two cones is 2:1. Hence, option B is the correct answer.
Four spheres each of radius 10 cm lie on a horizontal table so that the centres of the spheres form a square of side 20 cm. A fifth sphere also of radius 10 cm is placed on them so that it touches each of these spheres without disturbing them. How many cm above the table is the centre of the fifth sphere?- a)10√6
- b)10(1 + √2)
- c)10(1 + √3)
- d)10(4 - √2)
Correct answer is option 'B'. Can you explain this answer?
Four spheres each of radius 10 cm lie on a horizontal table so that the centres of the spheres form a square of side 20 cm. A fifth sphere also of radius 10 cm is placed on them so that it touches each of these spheres without disturbing them. How many cm above the table is the centre of the fifth sphere?
a)
10√6
b)
10(1 + √2)
c)
10(1 + √3)
d)
10(4 - √2)

|
Hridoy Mehra answered |
OA= 10
OA= 10
To find the value of PA, go through the options now.
To find the value of PA, go through the options now.
Find the volume of a cuboid whose length is 8 cm, breadth 6 cm and height 3.5 cm. - a)150 cm3
- b)168 cm2
- c)215 cm3
- d)168 cm3
Correct answer is option 'D'. Can you explain this answer?
Find the volume of a cuboid whose length is 8 cm, breadth 6 cm and height 3.5 cm.
a)
150 cm3
b)
168 cm2
c)
215 cm3
d)
168 cm3

|
Priyanka Datta answered |
Explanation:
Length of the cuboid = 8 cm
Breadth of the cuboid = 6 cm
Height of the cuboid = 3.5 cm
Volume of the cuboid = length × breadth × height
= 8 x 6 x 3.5 = 168cm3
Therefore,volume of the cuboid = 168cm3
If the edge of a cube is 1 cm then which of the following is its total surface area?- a)1 cm2
- b)4 cm2
- c)6 cm2
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If the edge of a cube is 1 cm then which of the following is its total surface area?
a)
1 cm2
b)
4 cm2
c)
6 cm2
d)
none of these
|
|
Stuti Basak answered |
Explanation:
To find the total surface area of a cube, we need to find the area of all its six faces and add them up. Since all the faces of a cube are identical squares, we can find the area of one face and multiply it by 6 to get the total surface area.
Given, the edge of the cube is 1 cm. Therefore, the area of one face of the cube is:
Area of square = side × side
Area of square = 1 cm × 1 cm
Area of square = 1 cm²
To find the total surface area of the cube, we need to multiply the area of one face by 6:
Total surface area of cube = 6 × area of one face
Total surface area of cube = 6 × 1 cm²
Total surface area of cube = 6 cm²
Therefore, the total surface area of the cube is 6 cm², which is option C.
To find the total surface area of a cube, we need to find the area of all its six faces and add them up. Since all the faces of a cube are identical squares, we can find the area of one face and multiply it by 6 to get the total surface area.
Given, the edge of the cube is 1 cm. Therefore, the area of one face of the cube is:
Area of square = side × side
Area of square = 1 cm × 1 cm
Area of square = 1 cm²
To find the total surface area of the cube, we need to multiply the area of one face by 6:
Total surface area of cube = 6 × area of one face
Total surface area of cube = 6 × 1 cm²
Total surface area of cube = 6 cm²
Therefore, the total surface area of the cube is 6 cm², which is option C.
_________ of a solid is the sum of the areas of its faces.- a)Volume
- b)Surface area
- c)Perimeter
- d)Area
Correct answer is option 'B'. Can you explain this answer?
_________ of a solid is the sum of the areas of its faces.
a)
Volume
b)
Surface area
c)
Perimeter
d)
Area
|
|
Sagar Sharma answered |
Surface area of a solid is the sum of the areas of its faces.
The surface area of a solid is a measure of the total area of all the surfaces or faces of the solid. It can be thought of as the amount of material needed to cover the entire surface of the solid.
Explanation:
A solid object is three-dimensional and has length, width, and height. It is made up of multiple faces, which are two-dimensional shapes that form the boundaries of the solid. The surface area of a solid is the sum of the areas of all these faces.
For example, consider a cube. A cube has six faces, each of which is a square. To find the surface area of the cube, we need to calculate the area of each face and then sum them up.
The formula for finding the area of a square is side length squared. So, if the side length of the cube is 's', then the area of each face is s^2. Since there are six faces, the total surface area of the cube is 6s^2.
Similarly, for other solid objects such as rectangular prisms, cylinders, spheres, etc., the surface area is calculated by finding the area of each face and adding them together.
The surface area is an important concept in geometry and has practical applications in fields such as architecture, engineering, and manufacturing. It helps in determining the amount of material required to construct a solid object or the amount of paint needed to cover its surface.
In summary, the surface area of a solid is the sum of the areas of all its faces. It is a measure of the total area of the surface of the solid and is calculated by finding the area of each face and adding them together.
The surface area of a solid is a measure of the total area of all the surfaces or faces of the solid. It can be thought of as the amount of material needed to cover the entire surface of the solid.
Explanation:
A solid object is three-dimensional and has length, width, and height. It is made up of multiple faces, which are two-dimensional shapes that form the boundaries of the solid. The surface area of a solid is the sum of the areas of all these faces.
For example, consider a cube. A cube has six faces, each of which is a square. To find the surface area of the cube, we need to calculate the area of each face and then sum them up.
The formula for finding the area of a square is side length squared. So, if the side length of the cube is 's', then the area of each face is s^2. Since there are six faces, the total surface area of the cube is 6s^2.
Similarly, for other solid objects such as rectangular prisms, cylinders, spheres, etc., the surface area is calculated by finding the area of each face and adding them together.
The surface area is an important concept in geometry and has practical applications in fields such as architecture, engineering, and manufacturing. It helps in determining the amount of material required to construct a solid object or the amount of paint needed to cover its surface.
In summary, the surface area of a solid is the sum of the areas of all its faces. It is a measure of the total area of the surface of the solid and is calculated by finding the area of each face and adding them together.
In the setup of the previous two questions, how is h related to n?- a)h = √2n
- b)h=√17n
- c)h = n
- d)h = √l3n
Correct answer is option 'C'. Can you explain this answer?
In the setup of the previous two questions, how is h related to n?
a)
h = √2n
b)
h=√17n
c)
h = n
d)
h = √l3n

|
Prateek Menon answered |
Equate the lengths of strings obtained from the above two questions.
An order was placed for the supply of a carpet whose breadth was 6 m and length was 1.44 times the breadth. What be the cost of a carpet whose length and breadth are 40% more and 25% more respectively than the first carpet. Given that the ratio of carpet is Rs. 45 per sq m?- a)Rs. 4082.40
- b)Rs. 3868.80
- c)Rs. 4216.20
- d)Rs. 3642.40
Correct answer is option 'A'. Can you explain this answer?
An order was placed for the supply of a carpet whose breadth was 6 m and length was 1.44 times the breadth. What be the cost of a carpet whose length and breadth are 40% more and 25% more respectively than the first carpet. Given that the ratio of carpet is Rs. 45 per sq m?
a)
Rs. 4082.40
b)
Rs. 3868.80
c)
Rs. 4216.20
d)
Rs. 3642.40
|
|
Aarav Sharma answered |
Given:
- Breadth of the first carpet = 6 m
- Length of the first carpet = 1.44 times the breadth
To find:
- Cost of a carpet whose length and breadth are 40% more and 25% more respectively than the first carpet
Formula:
- Area of a rectangle = Length × Breadth
Calculation:
1. Length of the first carpet:
- Length = 1.44 × Breadth
- Length = 1.44 × 6
- Length = 8.64 m
2. Area of the first carpet:
- Area = Length × Breadth
- Area = 8.64 × 6
- Area = 51.84 sq m
3. Increased length and breadth of the second carpet:
- Length = 1.4 × Length of the first carpet
- Length = 1.4 × 8.64
- Length = 12.096 m
- Breadth = 1.25 × Breadth of the first carpet
- Breadth = 1.25 × 6
- Breadth = 7.5 m
4. Area of the second carpet:
- Area = Length × Breadth
- Area = 12.096 × 7.5
- Area = 90.72 sq m
5. Cost of the carpet:
- Cost per sq m = Rs. 45
- Cost of the first carpet = Area of the first carpet × Cost per sq m
- Cost of the first carpet = 51.84 × 45
- Cost of the first carpet = Rs. 2332.80
- Cost of the second carpet = Area of the second carpet × Cost per sq m
- Cost of the second carpet = 90.72 × 45
- Cost of the second carpet = Rs. 4082.40
Therefore, the cost of the carpet whose length and breadth are 40% more and 25% more respectively than the first carpet is Rs. 4082.40, which is option A.
- Breadth of the first carpet = 6 m
- Length of the first carpet = 1.44 times the breadth
To find:
- Cost of a carpet whose length and breadth are 40% more and 25% more respectively than the first carpet
Formula:
- Area of a rectangle = Length × Breadth
Calculation:
1. Length of the first carpet:
- Length = 1.44 × Breadth
- Length = 1.44 × 6
- Length = 8.64 m
2. Area of the first carpet:
- Area = Length × Breadth
- Area = 8.64 × 6
- Area = 51.84 sq m
3. Increased length and breadth of the second carpet:
- Length = 1.4 × Length of the first carpet
- Length = 1.4 × 8.64
- Length = 12.096 m
- Breadth = 1.25 × Breadth of the first carpet
- Breadth = 1.25 × 6
- Breadth = 7.5 m
4. Area of the second carpet:
- Area = Length × Breadth
- Area = 12.096 × 7.5
- Area = 90.72 sq m
5. Cost of the carpet:
- Cost per sq m = Rs. 45
- Cost of the first carpet = Area of the first carpet × Cost per sq m
- Cost of the first carpet = 51.84 × 45
- Cost of the first carpet = Rs. 2332.80
- Cost of the second carpet = Area of the second carpet × Cost per sq m
- Cost of the second carpet = 90.72 × 45
- Cost of the second carpet = Rs. 4082.40
Therefore, the cost of the carpet whose length and breadth are 40% more and 25% more respectively than the first carpet is Rs. 4082.40, which is option A.
A cube whose edge is 20 cm long has circle on each of its faces painted black. What is the totalarea of the unpainted surface of the cube if the circles are of the largest area possible?- a)85.71 cm2
- b)257.14 cm2
- c)514.28 cm2
- d)331.33 cm2
Correct answer is option 'C'. Can you explain this answer?
A cube whose edge is 20 cm long has circle on each of its faces painted black. What is the totalarea of the unpainted surface of the cube if the circles are of the largest area possible?
a)
85.71 cm2
b)
257.14 cm2
c)
514.28 cm2
d)
331.33 cm2

|
Manisha Roy answered |
Surface area of the cube = 6a2 = 6 × (20)2
= 2400
Area of 6 circles of radius 10 cm = 6pr2
= 6 × p × 100
= 1885.71
Remaining area = 2400 – 1884 = 514.28
= 2400
Area of 6 circles of radius 10 cm = 6pr2
= 6 × p × 100
= 1885.71
Remaining area = 2400 – 1884 = 514.28
The area of a rhombus is 200 cm², and one of its diagonals is 20 cm. The length of the other diagonal is _____- a)20 cm
- b)20 m
- c)22 cm
- d)22 m
Correct answer is option 'A'. Can you explain this answer?
The area of a rhombus is 200 cm², and one of its diagonals is 20 cm. The length of the other diagonal is _____
a)
20 cm
b)
20 m
c)
22 cm
d)
22 m
|
|
Roshni Chauhan answered |
Understanding the Area of a Rhombus
The area of a rhombus can be calculated using the formula:
- Area = (d1 * d2) / 2
where d1 and d2 are the lengths of the diagonals.
Given Information
- Area = 200 cm²
- One diagonal (d1) = 20 cm
Finding the Other Diagonal
To find the length of the second diagonal (d2), we can rearrange the area formula:
- 200 = (20 * d2) / 2
Now, let's solve for d2:
- First, multiply both sides by 2:
- 400 = 20 * d2
- Next, divide both sides by 20:
- d2 = 400 / 20
- d2 = 20 cm
Conclusion
The length of the other diagonal (d2) is 20 cm.
Final Answer
The correct answer is option 'A' (20 cm).
This shows that both diagonals of the rhombus can be equal, which is a special case where the rhombus is also a square.
The area of a rhombus can be calculated using the formula:
- Area = (d1 * d2) / 2
where d1 and d2 are the lengths of the diagonals.
Given Information
- Area = 200 cm²
- One diagonal (d1) = 20 cm
Finding the Other Diagonal
To find the length of the second diagonal (d2), we can rearrange the area formula:
- 200 = (20 * d2) / 2
Now, let's solve for d2:
- First, multiply both sides by 2:
- 400 = 20 * d2
- Next, divide both sides by 20:
- d2 = 400 / 20
- d2 = 20 cm
Conclusion
The length of the other diagonal (d2) is 20 cm.
Final Answer
The correct answer is option 'A' (20 cm).
This shows that both diagonals of the rhombus can be equal, which is a special case where the rhombus is also a square.
A pit 7.5 metre long, 6 metre wide and 1.5 metre deep is dug in a field. Find the volume of soilremoved in cubic metres.- a)135 m3
- b)101.25 m3
- c)50.625 m3
- d)67.5 m3
Correct answer is option 'D'. Can you explain this answer?
A pit 7.5 metre long, 6 metre wide and 1.5 metre deep is dug in a field. Find the volume of soilremoved in cubic metres.
a)
135 m3
b)
101.25 m3
c)
50.625 m3
d)
67.5 m3

|
Saanvi Sarkar answered |
Volume of soil removed = l × b × h
= 7.5 × 6 × 1.5 = 67.5 m3
= 7.5 × 6 × 1.5 = 67.5 m3
Find the radius of the circle inscribed in a triangle whose sides are 8 cm, 15 cm and 17 cm.- a)4 cm
- b)5 cm
- c)3 cm
- d)2√2 cm
Correct answer is option 'C'. Can you explain this answer?
Find the radius of the circle inscribed in a triangle whose sides are 8 cm, 15 cm and 17 cm.
a)
4 cm
b)
5 cm
c)
3 cm
d)
2√2 cm
|
|
Sagar Sharma answered |
Step 1: Find the semi-perimeter of the triangle
- The semi-perimeter of a triangle is calculated by adding all three sides of the triangle and dividing by 2.
- In this case, the sides of the triangle are 8 cm, 15 cm, and 17 cm.
- The semi-perimeter, s, is given by s = (8 + 15 + 17) / 2 = 20 cm.
Step 2: Use Heron's Formula to find the area of the triangle
- Heron's formula states that the area of a triangle with sides a, b, and c and semi-perimeter s is given by the formula:
Area = √(s(s - a)(s - b)(s - c))
- Substituting the values, we get Area = √(20(20 - 8)(20 - 15)(20 - 17)) = √(20*12*5*3) = √(3600) = 60 cm².
Step 3: Use the formula for the radius of the inscribed circle
- The radius of the inscribed circle in a triangle with sides a, b, and c and area A is given by the formula:
Radius = A/s
- Substituting the values, we get Radius = 60/20 = 3 cm.
Therefore, the radius of the circle inscribed in the triangle with sides 8 cm, 15 cm, and 17 cm is 3 cm. Hence, the correct answer is option 'C'.
- The semi-perimeter of a triangle is calculated by adding all three sides of the triangle and dividing by 2.
- In this case, the sides of the triangle are 8 cm, 15 cm, and 17 cm.
- The semi-perimeter, s, is given by s = (8 + 15 + 17) / 2 = 20 cm.
Step 2: Use Heron's Formula to find the area of the triangle
- Heron's formula states that the area of a triangle with sides a, b, and c and semi-perimeter s is given by the formula:
Area = √(s(s - a)(s - b)(s - c))
- Substituting the values, we get Area = √(20(20 - 8)(20 - 15)(20 - 17)) = √(20*12*5*3) = √(3600) = 60 cm².
Step 3: Use the formula for the radius of the inscribed circle
- The radius of the inscribed circle in a triangle with sides a, b, and c and area A is given by the formula:
Radius = A/s
- Substituting the values, we get Radius = 60/20 = 3 cm.
Therefore, the radius of the circle inscribed in the triangle with sides 8 cm, 15 cm, and 17 cm is 3 cm. Hence, the correct answer is option 'C'.
John Nash, an avid mathematician, had his room constructed such that the floor of the room was an equilateral triangle in shape instead of the usual rectangular shape. One day he brought home a bird and tied it to one end of a string and then tied the other end of the string to one of the corners of his room. The next day, he untied the other end of the string from the corner of the room and tied it to a point exactly at the center of the floor of the room. Assuming that the dimensions of the room are relatively large compared to the length of the string, find the number of times, by which the maximum possible space in which the bird can fly, increase.- a)4
- b)5
- c)6
- d)7
Correct answer is option 'B'. Can you explain this answer?
John Nash, an avid mathematician, had his room constructed such that the floor of the room was an equilateral triangle in shape instead of the usual rectangular shape. One day he brought home a bird and tied it to one end of a string and then tied the other end of the string to one of the corners of his room. The next day, he untied the other end of the string from the corner of the room and tied it to a point exactly at the center of the floor of the room. Assuming that the dimensions of the room are relatively large compared to the length of the string, find the number of times, by which the maximum possible space in which the bird can fly, increase.
a)
4
b)
5
c)
6
d)
7

|
Ashwin Chawla answered |
Consider the length of the string less than or equal to the inradius of the floor. At the comer of the floor you will find a sixth part of a hemisphere and at the centre it will be a hemisphere.
The square of side 1 cm are cut from four comers of a sheet of tin (having length = 1 and breadth = b) in order to form an open box. If the whole sheet of tin was rolled along its length to form a cylinder, then the volume of the cylinder is equal to (343/4) cm3. Find the volume of the box. (1 and b are integers)- a)154 cm3
- b)100 cm3
- c)126 cm3
- d)Insufficient data
Correct answer is option 'B'. Can you explain this answer?
The square of side 1 cm are cut from four comers of a sheet of tin (having length = 1 and breadth = b) in order to form an open box. If the whole sheet of tin was rolled along its length to form a cylinder, then the volume of the cylinder is equal to (343/4) cm3. Find the volume of the box. (1 and b are integers)
a)
154 cm3
b)
100 cm3
c)
126 cm3
d)
Insufficient data

|
Mrinalini Basu answered |
The length of the rectangle will be equal to the circumference of the base of the cylinder.
The maximum distance between two points of the unit cube is- a)√2 + 1
- b)√2
- c)√3
- d)√2 + √3
Correct answer is option 'C'. Can you explain this answer?
The maximum distance between two points of the unit cube is
a)
√2 + 1
b)
√2
c)
√3
d)
√2 + √3
|
|
Aarav Sharma answered |
The maximum distance between two points of the unit cube can be found by considering the two opposite corners of the cube. The coordinates of these corners are (0,0,0) and (1,1,1).
Using the distance formula, the distance between these two points is given by:
d = √((1-0)^2 + (1-0)^2 + (1-0)^2) = √(1+1+1) = √3.
So, the maximum distance between two points of the unit cube is √3.
Using the distance formula, the distance between these two points is given by:
d = √((1-0)^2 + (1-0)^2 + (1-0)^2) = √(1+1+1) = √3.
So, the maximum distance between two points of the unit cube is √3.
The perimeter of a sector of a circle of radius 5.7 m is 27.2 m. Find the area of the sector.- a)90.06 cm2
- b)135.09 cm2
- c)45 cm2
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
The perimeter of a sector of a circle of radius 5.7 m is 27.2 m. Find the area of the sector.
a)
90.06 cm2
b)
135.09 cm2
c)
45 cm2
d)
None of these
|
|
Sagar Sharma answered |
Understanding the Problem
The problem gives us the perimeter of a sector of a circle with a radius of 5.7 m, which is 27.2 m. We need to find the area of the sector.
Components of a Sector's Perimeter
The perimeter of a sector comprises two radii and the arc length. The formula for the perimeter (P) is:
P = 2r + l
Where:
- r = radius
- l = arc length
Given:
- r = 5.7 m
- P = 27.2 m
Finding the Arc Length
We can rearrange the perimeter formula to find the arc length (l):
l = P - 2r
Substituting the values:
l = 27.2 - 2(5.7)
Calculating:
l = 27.2 - 11.4 = 15.8 m
Finding the Angle in Radians
The arc length is related to the radius and the angle (θ) in radians by the formula:
l = r * θ
Rearranging gives us:
θ = l / r
Substituting the values:
θ = 15.8 / 5.7
Calculating the angle:
θ ≈ 2.77 radians
Calculating the Area of the Sector
The area (A) of a sector is given by:
A = (1/2) * r^2 * θ
Substituting the values:
A = (1/2) * (5.7^2) * 2.77
Calculating:
A ≈ 39.2 m²
Since the options given are in cm², we convert:
39.2 m² = 3920 cm²
Conclusion
Since the calculated area (3920 cm²) does not match any given options, the correct answer is indeed option 'D' - None of these.
The problem gives us the perimeter of a sector of a circle with a radius of 5.7 m, which is 27.2 m. We need to find the area of the sector.
Components of a Sector's Perimeter
The perimeter of a sector comprises two radii and the arc length. The formula for the perimeter (P) is:
P = 2r + l
Where:
- r = radius
- l = arc length
Given:
- r = 5.7 m
- P = 27.2 m
Finding the Arc Length
We can rearrange the perimeter formula to find the arc length (l):
l = P - 2r
Substituting the values:
l = 27.2 - 2(5.7)
Calculating:
l = 27.2 - 11.4 = 15.8 m
Finding the Angle in Radians
The arc length is related to the radius and the angle (θ) in radians by the formula:
l = r * θ
Rearranging gives us:
θ = l / r
Substituting the values:
θ = 15.8 / 5.7
Calculating the angle:
θ ≈ 2.77 radians
Calculating the Area of the Sector
The area (A) of a sector is given by:
A = (1/2) * r^2 * θ
Substituting the values:
A = (1/2) * (5.7^2) * 2.77
Calculating:
A ≈ 39.2 m²
Since the options given are in cm², we convert:
39.2 m² = 3920 cm²
Conclusion
Since the calculated area (3920 cm²) does not match any given options, the correct answer is indeed option 'D' - None of these.
The perimeter of a triangle is 28 cm and the inradius of the triangle is 2.5 cm. What is the area of the triangle?- a)25 cm2
- b)42 cm2
- c)35 cm2
- d)70 cm2
Correct answer is option 'C'. Can you explain this answer?
The perimeter of a triangle is 28 cm and the inradius of the triangle is 2.5 cm. What is the area of the triangle?
a)
25 cm2
b)
42 cm2
c)
35 cm2
d)
70 cm2
|
|
Yash Patel answered |
Area of a triangle = r * s
Where r is the inradius and s is the semi perimeter of the triangle.
Area of triangle = 2.5 * 28/2 = 35 cm2
The whole surface of a rectangular block is 8788 square cm. If length, breadth and height are inthe ratio of 4 : 3 : 2, find length.- a)26 cm
- b)52 cm
- c)104 cm
- d)13 cm
Correct answer is option 'B'. Can you explain this answer?
The whole surface of a rectangular block is 8788 square cm. If length, breadth and height are inthe ratio of 4 : 3 : 2, find length.
a)
26 cm
b)
52 cm
c)
104 cm
d)
13 cm

|
Nandini Singh answered |
Let the common ratio be = x
Then, length = 4x, breadth = 3x and height = 2x
As per question;
2(4x x 3x + 3x x 2x + 2x x 4x) = 8788
2(12x2 + 6x2 + 8x2) = 8788 fi 52x2 = 8788
fi x = 13
Length = 4x = 52 cm
Then, length = 4x, breadth = 3x and height = 2x
As per question;
2(4x x 3x + 3x x 2x + 2x x 4x) = 8788
2(12x2 + 6x2 + 8x2) = 8788 fi 52x2 = 8788
fi x = 13
Length = 4x = 52 cm
The area of a rectangular field is 52000 m². This rectangular area has been drawn on a map to the scale 1 cm to 100 m. The length is shown as 3.25 cm on the map. The breadth of the rectangular field is : - a)210 m
- b)150 m
- c)160 m
- d)123 m
Correct answer is option 'C'. Can you explain this answer?
The area of a rectangular field is 52000 m². This rectangular area has been drawn on a map to the scale 1 cm to 100 m. The length is shown as 3.25 cm on the map. The breadth of the rectangular field is :
a)
210 m
b)
150 m
c)
160 m
d)
123 m
|
|
Kavya Saxena answered |
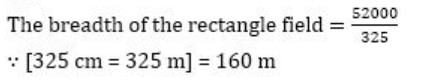
The inner circumference of a circular track is 440 cm. The track is 14 cm wide. Find the diameterof the outer circle of the track.- a)84 cm
- b)168 cm
- c)336 cm
- d)77 cm
Correct answer is option 'B'. Can you explain this answer?
The inner circumference of a circular track is 440 cm. The track is 14 cm wide. Find the diameterof the outer circle of the track.
a)
84 cm
b)
168 cm
c)
336 cm
d)
77 cm

|
Prasad Banerjee answered |
Let inner radius = A; then 2pr = 440 \ p = 70
Radius of outer circle = 70 + 14 = 84 cm
Outer diameter = 2 × Radius = 2 × 84 = 168
Radius of outer circle = 70 + 14 = 84 cm
Outer diameter = 2 × Radius = 2 × 84 = 168
The area of the circle is 2464 cm2 and the ratio of the breadth of the rectangle to radius of the circle is 6:7. If the circumference of the circle is equal to the perimeter of the rectangle, then what is the area of the rectangle.- a)1456 cm2
- b)1536 cm2
- c)1254 cm2
- d)5678 cm2
Correct answer is option 'B'. Can you explain this answer?
The area of the circle is 2464 cm2 and the ratio of the breadth of the rectangle to radius of the circle is 6:7. If the circumference of the circle is equal to the perimeter of the rectangle, then what is the area of the rectangle.
a)
1456 cm2
b)
1536 cm2
c)
1254 cm2
d)
5678 cm2
|
|
Luminary Institute answered |
Area of the circle=πr2
2464 = 22/7 * r2
Radius of the circle=28 cm
Circumference of the circle=2 * π* r =2 * 22/7 * 28
= 176 cm
Breadth of the rectangle=6/7 * 28=24 cm
Perimeter of the rectangle=2 * (l + b)
176 = 2 * (l + 24)
Length of the rectangle = 64 cm
Area of the rectangle = l * b = 24 * 64 = 1536 cm2
Three circles with radius 2 cm touch each other as shown :- 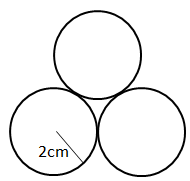
- a)3π(4+√3)2
- b)π/2(4+2√3)2
- c)π/4(4+2√3)2
- d)12π−π/2(4+2√3)2
Correct answer is option 'B'. Can you explain this answer?
Three circles with radius 2 cm touch each other as shown :-
a)
3π(4+√3)2
b)
π/2(4+2√3)2
c)
π/4(4+2√3)2
d)
12π−π/2(4+2√3)2

|
Mainak Majumdar answered |
(This can easily be derived using trigonometry. However, please remember this formula. It is useful at places)
Anil grows tomatoes in his backyard which is in the shape of a square. Each tomato takes 1 cm2 in his backyard. This year, he has been able to grow 131 more tomatoes than last year. The shape of the backyard remained a square. How many tomatoes did Anil produce this year?- a)4225
- b)4096
- c)4356
- d)Insufficient Data
Correct answer is option 'C'. Can you explain this answer?
Anil grows tomatoes in his backyard which is in the shape of a square. Each tomato takes 1 cm2 in his backyard. This year, he has been able to grow 131 more tomatoes than last year. The shape of the backyard remained a square. How many tomatoes did Anil produce this year?
a)
4225
b)
4096
c)
4356
d)
Insufficient Data

|
Naveen Jain answered |
Let the area of backyard be x2 this year and y2 last year
∴ X2- Y2 = 131
=) (X+Y) (X-Y) = 131
Now, 131 is a prime number (a unique one too. Check out its properties on Google). Also, always identify the prime number given in a question. Might be helpful in cracking the solution.
=) (X+Y) (X-Y) = 131 x 1
=) X+Y = 131
X-Y = 1
=) 2X = 132 =) X = 66
and Y = 65
∴ Number of tomatoes produced this year = 662 = 4356
Choice (C) is therefore, the correct answer.
Correct Answer: 4356
∴ X2- Y2 = 131
=) (X+Y) (X-Y) = 131
Now, 131 is a prime number (a unique one too. Check out its properties on Google). Also, always identify the prime number given in a question. Might be helpful in cracking the solution.
=) (X+Y) (X-Y) = 131 x 1
=) X+Y = 131
X-Y = 1
=) 2X = 132 =) X = 66
and Y = 65
∴ Number of tomatoes produced this year = 662 = 4356
Choice (C) is therefore, the correct answer.
Correct Answer: 4356
Two circles touch internally. The sum of their areas is 116p cm2 and distance between theircentres is 6 cm. Find the radii of the circles.- a)10 cm, 4 cm
- b)11 cm, 4 cm
- c)9 cm, 5 cm
- d)10 cm, 5 cm
Correct answer is option 'A'. Can you explain this answer?
Two circles touch internally. The sum of their areas is 116p cm2 and distance between theircentres is 6 cm. Find the radii of the circles.
a)
10 cm, 4 cm
b)
11 cm, 4 cm
c)
9 cm, 5 cm
d)
10 cm, 5 cm
|
|
Aarav Sharma answered |
Given:
- Two circles touch internally.
- Sum of their areas is 116p cm2
- Distance between their centres is 6 cm.
To find:
- Radii of the circles.
Solution:
Let the radii of the two circles be r1 and r2 respectively.
Step 1: Write the formula for the area of a circle.
Area of a circle = πr^2
Step 2: Write the formula for the distance between the centres of two circles.
Distance between the centres of two circles = √((x2 - x1)^2 + (y2 - y1)^2)
Step 3: Write the equation for the sum of the areas of the two circles.
πr1^2 + πr2^2 = 116p
Step 4: Write the equation for the distance between the centres of the two circles.
Distance between the centres of two circles = r1 + r2 + 6
Step 5: Simplify the equation for the distance between the centres of the two circles.
r1 + r2 + 6 = √((x2 - x1)^2 + (y2 - y1)^2)
r1 + r2 + 6 = √(0^2 + 6^2)
r1 + r2 + 6 = 6√2
Step 6: Solve the system of equations to find the values of r1 and r2.
πr1^2 + πr2^2 = 116p
r1 + r2 + 6 = 6√2
We can solve this system of equations by substitution.
r2 = 6√2 - r1 - 6
Substituting for r2 in the first equation, we get:
πr1^2 + π(6√2 - r1 - 6)^2 = 116p
Simplifying and solving for r1, we get:
r1 = 4 cm or 10 cm
Using the equation for r2, we can find the value of r2 for each value of r1:
If r1 = 4 cm, then r2 = 10 cm
If r1 = 10 cm, then r2 = 4 cm
Therefore, the radii of the two circles are 10 cm and 4 cm.
Answer: Option (a) 10 cm, 4 cm.
- Two circles touch internally.
- Sum of their areas is 116p cm2
- Distance between their centres is 6 cm.
To find:
- Radii of the circles.
Solution:
Let the radii of the two circles be r1 and r2 respectively.
Step 1: Write the formula for the area of a circle.
Area of a circle = πr^2
Step 2: Write the formula for the distance between the centres of two circles.
Distance between the centres of two circles = √((x2 - x1)^2 + (y2 - y1)^2)
Step 3: Write the equation for the sum of the areas of the two circles.
πr1^2 + πr2^2 = 116p
Step 4: Write the equation for the distance between the centres of the two circles.
Distance between the centres of two circles = r1 + r2 + 6
Step 5: Simplify the equation for the distance between the centres of the two circles.
r1 + r2 + 6 = √((x2 - x1)^2 + (y2 - y1)^2)
r1 + r2 + 6 = √(0^2 + 6^2)
r1 + r2 + 6 = 6√2
Step 6: Solve the system of equations to find the values of r1 and r2.
πr1^2 + πr2^2 = 116p
r1 + r2 + 6 = 6√2
We can solve this system of equations by substitution.
r2 = 6√2 - r1 - 6
Substituting for r2 in the first equation, we get:
πr1^2 + π(6√2 - r1 - 6)^2 = 116p
Simplifying and solving for r1, we get:
r1 = 4 cm or 10 cm
Using the equation for r2, we can find the value of r2 for each value of r1:
If r1 = 4 cm, then r2 = 10 cm
If r1 = 10 cm, then r2 = 4 cm
Therefore, the radii of the two circles are 10 cm and 4 cm.
Answer: Option (a) 10 cm, 4 cm.
ABCD is a square drawn inside a square PTRS of sides 4 cm by joining midpoints of the sides PR, PT, TS, SR. Another square is drawn inside ABCD similarly. This process is repeated infinite number of times. Find the sum of all the squares.
- a)16 cm2
- b)28 cm2
- c)32 cm2
- d)Infinite
Correct answer is option 'C'. Can you explain this answer?
ABCD is a square drawn inside a square PTRS of sides 4 cm by joining midpoints of the sides PR, PT, TS, SR. Another square is drawn inside ABCD similarly. This process is repeated infinite number of times. Find the sum of all the squares.
a)
16 cm2
b)
28 cm2
c)
32 cm2
d)
Infinite

|
Rajdeep Verma answered |
If we write the infinite series of area of squares:
= 42 + (2√2)2 + 22 + ……. infinite
Since it is a decreasing series sum of infinite terms can be approximated.
= 16 + 8 + 4 +………infinite
The cost of white washing one m2 is Rs 50. What will be the maximum amount saved in painting the room in the most economical way, if the sum of the length, breadth and height is 21 m and all the sides are integers (floor is not to be white washed)?- a)Rs 1,08,050
- b)Rs 8,400
- c)Rs 9,300
- d)Rs 8,540
Correct answer is option 'C'. Can you explain this answer?
The cost of white washing one m2 is Rs 50. What will be the maximum amount saved in painting the room in the most economical way, if the sum of the length, breadth and height is 21 m and all the sides are integers (floor is not to be white washed)?
a)
Rs 1,08,050
b)
Rs 8,400
c)
Rs 9,300
d)
Rs 8,540

|
Hridoy Mehra answered |
The amount saved would be maximum only when the difference of maximum area and minimum area to be painted is maximum.
Find the number of spheres of the maximum volume that can be accommodated in the above region.- a)324
- b)323
- c)162
- d)161
Correct answer is option 'D'. Can you explain this answer?
Find the number of spheres of the maximum volume that can be accommodated in the above region.
a)
324
b)
323
c)
162
d)
161
|
|
Aarav Sharma answered |
To find the maximum number of spheres that can be accommodated in a given region, we need to consider the volume of the region and the volume of each sphere.
Given information:
- The region is not specified, but we know it can accommodate spheres.
- The volume of each sphere is also not specified.
To solve this problem, we can follow these steps:
1. Determine the volume of the region:
- The volume of the region is not given in the question.
- Without the volume of the region, it is not possible to find the maximum number of spheres that can be accommodated.
- We need more information about the region to proceed.
2. Determine the volume of each sphere:
- The volume of each sphere is not given in the question.
- Without the volume of each sphere, it is not possible to find the maximum number of spheres that can be accommodated.
- We need more information about the spheres to proceed.
Since we do not have sufficient information about the region or the spheres, we cannot determine the maximum number of spheres that can be accommodated. Therefore, none of the provided options (a, b, c, d) can be considered as the correct answer.
To solve this problem, we would need additional information such as the volume of the region and/or the volume of each sphere. Without these details, it is not possible to find the maximum number of spheres that can be accommodated.
Given information:
- The region is not specified, but we know it can accommodate spheres.
- The volume of each sphere is also not specified.
To solve this problem, we can follow these steps:
1. Determine the volume of the region:
- The volume of the region is not given in the question.
- Without the volume of the region, it is not possible to find the maximum number of spheres that can be accommodated.
- We need more information about the region to proceed.
2. Determine the volume of each sphere:
- The volume of each sphere is not given in the question.
- Without the volume of each sphere, it is not possible to find the maximum number of spheres that can be accommodated.
- We need more information about the spheres to proceed.
Since we do not have sufficient information about the region or the spheres, we cannot determine the maximum number of spheres that can be accommodated. Therefore, none of the provided options (a, b, c, d) can be considered as the correct answer.
To solve this problem, we would need additional information such as the volume of the region and/or the volume of each sphere. Without these details, it is not possible to find the maximum number of spheres that can be accommodated.
A closed wooden box measures externally 10 cm long, 8 cm broad and 6 cm high. Thickness ofwood is 0.5 cm. Find the volume of wood used.- a)230 cubic cm
- b)165 cubic cm
- c)330 cubic cm
- d)300 cubic cm.
Correct answer is option 'B'. Can you explain this answer?
A closed wooden box measures externally 10 cm long, 8 cm broad and 6 cm high. Thickness ofwood is 0.5 cm. Find the volume of wood used.
a)
230 cubic cm
b)
165 cubic cm
c)
330 cubic cm
d)
300 cubic cm.

|
Manisha Roy answered |
Volume of wood used = External volume – Outer Volume
fi (10 × 8 × 6) – (10 – 1) × (8 – 1) × (6 – 1)
fi 480 – (9 × 7 × 5) = 165 cm2
fi (10 × 8 × 6) – (10 – 1) × (8 – 1) × (6 – 1)
fi 480 – (9 × 7 × 5) = 165 cm2
All five faces of a regular pyramid with a square base are found to be of the same area. The height of the pyramid is 3 cm. The total area of all its surfaces (in cm2) is- a)8
- b)10
- c)12
- d)16
Correct answer is option 'C'. Can you explain this answer?
All five faces of a regular pyramid with a square base are found to be of the same area. The height of the pyramid is 3 cm. The total area of all its surfaces (in cm2) is
a)
8
b)
10
c)
12
d)
16

|
Prateek Menon answered |
Equate the area of the square ABCD and triangle PDC and find a relation between the slant height and the length of the base of the pyramid
If the parallel sides of a parallelogram are 2 cm apart and their sum is 10 cm then its area is:- a)20 cm2
- b)5 cm2
- c)10 cm2
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If the parallel sides of a parallelogram are 2 cm apart and their sum is 10 cm then its area is:
a)
20 cm2
b)
5 cm2
c)
10 cm2
d)
none of these
|
|
Srestha Menon answered |
Understanding the Parallelogram Area
To find the area of a parallelogram, we can use the formula:
Area = base × height
Where:
- The base is the length of one of the parallel sides.
- The height is the perpendicular distance between the parallel sides.
Given Information
- The distance between the parallel sides (height) = 2 cm
- The sum of the lengths of the parallel sides = 10 cm
Finding the Base
Since we have the sum of the two parallel sides, we can define their lengths as follows:
Let one side be "a" and the other side be "b". According to the problem:
a + b = 10 cm
To find the area, we need the length of one of the sides. For simplicity, let's assume both sides are equal. Thus:
a = b = 10 cm / 2 = 5 cm
Calculating the Area
Now, substituting the values into the area formula:
Area = base × height
Area = 5 cm × 2 cm
Area = 10 cm²
Conclusion
The area of the parallelogram is 10 cm². Hence, the correct answer is option 'C'. This demonstrates how understanding the properties of parallelograms can help solve geometry problems effectively.
To find the area of a parallelogram, we can use the formula:
Area = base × height
Where:
- The base is the length of one of the parallel sides.
- The height is the perpendicular distance between the parallel sides.
Given Information
- The distance between the parallel sides (height) = 2 cm
- The sum of the lengths of the parallel sides = 10 cm
Finding the Base
Since we have the sum of the two parallel sides, we can define their lengths as follows:
Let one side be "a" and the other side be "b". According to the problem:
a + b = 10 cm
To find the area, we need the length of one of the sides. For simplicity, let's assume both sides are equal. Thus:
a = b = 10 cm / 2 = 5 cm
Calculating the Area
Now, substituting the values into the area formula:
Area = base × height
Area = 5 cm × 2 cm
Area = 10 cm²
Conclusion
The area of the parallelogram is 10 cm². Hence, the correct answer is option 'C'. This demonstrates how understanding the properties of parallelograms can help solve geometry problems effectively.
A cuboid of length 20 m, breadth 15 m and height 12 m is lying on a table. The cuboid is cut into two equal halves by a plane which is perpendicular to the base and passes through a pair of diagonally opposite points of that surface. Then, a second cut is made by a plane which is parallel to the surface of the table again dividing the cuboid into two equal halves. Now this cuboid is divided into four pieces. Out of these four pieces, one piece is now removed from its place. What is the total surface area of the remaining portion of the cuboid?- a)1290 m2
- b)1380 m2
- c)1440 m2
- d)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
A cuboid of length 20 m, breadth 15 m and height 12 m is lying on a table. The cuboid is cut into two equal halves by a plane which is perpendicular to the base and passes through a pair of diagonally opposite points of that surface. Then, a second cut is made by a plane which is parallel to the surface of the table again dividing the cuboid into two equal halves. Now this cuboid is divided into four pieces. Out of these four pieces, one piece is now removed from its place. What is the total surface area of the remaining portion of the cuboid?
a)
1290 m2
b)
1380 m2
c)
1440 m2
d)
Cannot be determined

|
Srishti Joshi answered |
Since we don’t know that the cut is made parallel to which face, we cannot determine the surface area.
The length of each side of a cube is 24 cm. The volume of the cube is equal to the volume of a cuboid. If the breadth and the height of the cuboid are 32 cm and 12 cm, respectively, then what will be the length of the cuboid?- a)36
- b)27
- c)16
- d)20
Correct answer is option 'A'. Can you explain this answer?
The length of each side of a cube is 24 cm. The volume of the cube is equal to the volume of a cuboid. If the breadth and the height of the cuboid are 32 cm and 12 cm, respectively, then what will be the length of the cuboid?
a)
36
b)
27
c)
16
d)
20
|
|
Nitin Majumdar answered |
Volume of the Cube
To find the volume of the cube, we use the formula:
- Volume = side × side × side
For a cube with each side measuring 24 cm:
- Volume = 24 cm × 24 cm × 24 cm = 13,824 cm³
Volume of the Cuboid
The volume of the cuboid is also given to be equal to the volume of the cube, which is 13,824 cm³.
Dimensions of the Cuboid
We know the following dimensions of the cuboid:
- Breadth = 32 cm
- Height = 12 cm
Let the length of the cuboid be denoted as 'l'. The formula for the volume of the cuboid is:
- Volume = length × breadth × height
Substituting the known values:
- 13,824 cm³ = l × 32 cm × 12 cm
Calculating the Length
Now, we need to solve for 'l':
1. First, calculate the product of the breadth and height:
- 32 cm × 12 cm = 384 cm²
2. Now, substitute this into the volume equation:
- 13,824 cm³ = l × 384 cm²
3. To find 'l', divide both sides by 384 cm²:
- l = 13,824 cm³ / 384 cm²
- l = 36 cm
Conclusion
Thus, the length of the cuboid is 36 cm.
The correct answer is option 'A'.
To find the volume of the cube, we use the formula:
- Volume = side × side × side
For a cube with each side measuring 24 cm:
- Volume = 24 cm × 24 cm × 24 cm = 13,824 cm³
Volume of the Cuboid
The volume of the cuboid is also given to be equal to the volume of the cube, which is 13,824 cm³.
Dimensions of the Cuboid
We know the following dimensions of the cuboid:
- Breadth = 32 cm
- Height = 12 cm
Let the length of the cuboid be denoted as 'l'. The formula for the volume of the cuboid is:
- Volume = length × breadth × height
Substituting the known values:
- 13,824 cm³ = l × 32 cm × 12 cm
Calculating the Length
Now, we need to solve for 'l':
1. First, calculate the product of the breadth and height:
- 32 cm × 12 cm = 384 cm²
2. Now, substitute this into the volume equation:
- 13,824 cm³ = l × 384 cm²
3. To find 'l', divide both sides by 384 cm²:
- l = 13,824 cm³ / 384 cm²
- l = 36 cm
Conclusion
Thus, the length of the cuboid is 36 cm.
The correct answer is option 'A'.
In a swimming pool measuring 90 m by 40 m, 150 men take a dip. If the average displacement ofwater by a man is 8 cubic metres, what will be rise in water level?- a)30 cm
- b)50 cm
- c)20 cm
- d)33.33 cm
Correct answer is option 'D'. Can you explain this answer?
In a swimming pool measuring 90 m by 40 m, 150 men take a dip. If the average displacement ofwater by a man is 8 cubic metres, what will be rise in water level?
a)
30 cm
b)
50 cm
c)
20 cm
d)
33.33 cm
|
|
Aarav Sharma answered |
To find the rise in water level, we need to calculate the total volume of water displaced by the men and then divide it by the area of the pool.
Given information:
- Length of the pool = 90 m
- Width of the pool = 40 m
- Number of men = 150
- Average displacement of water by a man = 8 cubic meters
Let's calculate the total volume of water displaced by the men:
Total volume = Average displacement per man * Number of men
= 8 cubic meters/man * 150 men
= 1200 cubic meters
Now, let's calculate the rise in water level:
Rise in water level = Total volume / Area of the pool
Area of the pool = Length of the pool * Width of the pool
= 90 m * 40 m
= 3600 square meters
Rise in water level = 1200 cubic meters / 3600 square meters
= 1/3 meters
= 0.3333 meters
= 33.33 cm
Therefore, the rise in water level is 33.33 cm.
Hence, the correct answer is option D) 33.33 cm.
Given information:
- Length of the pool = 90 m
- Width of the pool = 40 m
- Number of men = 150
- Average displacement of water by a man = 8 cubic meters
Let's calculate the total volume of water displaced by the men:
Total volume = Average displacement per man * Number of men
= 8 cubic meters/man * 150 men
= 1200 cubic meters
Now, let's calculate the rise in water level:
Rise in water level = Total volume / Area of the pool
Area of the pool = Length of the pool * Width of the pool
= 90 m * 40 m
= 3600 square meters
Rise in water level = 1200 cubic meters / 3600 square meters
= 1/3 meters
= 0.3333 meters
= 33.33 cm
Therefore, the rise in water level is 33.33 cm.
Hence, the correct answer is option D) 33.33 cm.
The short and the long hands of a clock are 4 cm and 6 cm long respectively. What will be sum ofdistances travelled by their tips in 4 days? (Take p = 3.14)- a)954.56 cm
- b)3818.24 cm
- c)2909.12 cm
- d)2703.56 cm
Correct answer is option 'B'. Can you explain this answer?
The short and the long hands of a clock are 4 cm and 6 cm long respectively. What will be sum ofdistances travelled by their tips in 4 days? (Take p = 3.14)
a)
954.56 cm
b)
3818.24 cm
c)
2909.12 cm
d)
2703.56 cm

|
Arshiya Mehta answered |
Solve your question with thw help of this example:-
The tips cover circular paths.
The hour hand covers 4 complete circles in 2 days (48 hours)
Distance = 2 x 22/7 x 4 x 4 = 100.57 cm
The minute hand covers = 48 Circles in 2 days (Each hour = 1 circle)
Distance = 2 x 22/7 x 6 x 48 = 1810.23 cm
Total distance = 100.57 + 1810.23 = 1910.8 cm
In a right angled triangle, find the hypotenuse if base and perpendicular are respectively 36015 cmand 48020 cm.- a)69125 cm
- b)60025 cm
- c)391025 cm
- d)60125 cm
Correct answer is option 'B'. Can you explain this answer?
In a right angled triangle, find the hypotenuse if base and perpendicular are respectively 36015 cmand 48020 cm.
a)
69125 cm
b)
60025 cm
c)
391025 cm
d)
60125 cm

|
Nandini Singh answered |
Let hypotenuse = x cm
Then, by Pythagoras theorem:
x2 = (48020)2 + (36015)2
x fi 60025 cm
Then, by Pythagoras theorem:
x2 = (48020)2 + (36015)2
x fi 60025 cm
Under the Indian Posts and Telegraph Act 1885, any package in the form of a right circular cylinder will not be accepted if the sum of its height and the diameter of its base exceeds 10 inches. The height (in inches) of a package of maximum volume that would be accepted is- a)10/3
- b)20/3
- c)10
- d)20
Correct answer is option 'A'. Can you explain this answer?
Under the Indian Posts and Telegraph Act 1885, any package in the form of a right circular cylinder will not be accepted if the sum of its height and the diameter of its base exceeds 10 inches. The height (in inches) of a package of maximum volume that would be accepted is
a)
10/3
b)
20/3
c)
10
d)
20

|
Hridoy Mehra answered |
Volume is maximum when radius is equal to height.
A bicycle wheel makes 5000 revolutions in moving 11 km. What is the radius of the wheel?- a)70 cm
- b)135 cm
- c)17.5 cm
- d)35 cm
Correct answer is option 'D'. Can you explain this answer?
A bicycle wheel makes 5000 revolutions in moving 11 km. What is the radius of the wheel?
a)
70 cm
b)
135 cm
c)
17.5 cm
d)
35 cm

|
Debolina Roy answered |
Let the radius of the wheel be = p
Then 5000 × 2pr = 1100000 cm fi r = 35 cm
Then 5000 × 2pr = 1100000 cm fi r = 35 cm
Chapter doubts & questions for Mensuration: Volume, Surface Area & Solid Figures - Elementary Mathematics for CDS 2025 is part of CDS exam preparation. The chapters have been prepared according to the CDS exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CDS 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Mensuration: Volume, Surface Area & Solid Figures - Elementary Mathematics for CDS in English & Hindi are available as part of CDS exam.
Download more important topics, notes, lectures and mock test series for CDS Exam by signing up for free.
Elementary Mathematics for CDS
174 videos|104 docs|134 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily











