All Exams >
Airforce X Y / Indian Navy SSR >
Mathematics for Airmen Group X >
All Questions
All questions of Complex numbers for Airforce X Y / Indian Navy SSR Exam
Principal argument of z = -√3+i is :- a)5π/6
- b)π/6
- c)-5π/6
- d)none
Correct answer is option 'A'. Can you explain this answer?
Principal argument of z = -√3+i is :
a)
5π/6
b)
π/6
c)
-5π/6
d)
none
|
Tarun answered |
Ar(z)= tan(1/√3)=π/6
since it lies in second quadrant
so it will be = π -π/6 = 5π/6
since it lies in second quadrant
so it will be = π -π/6 = 5π/6
The small positive integer ‘n’ for which (1+i)2n = (1-i)2n is :- a)2
- b)4
- c)8
- d)12
Correct answer is option 'A'. Can you explain this answer?
The small positive integer ‘n’ for which (1+i)2n = (1-i)2n is :
a)
2
b)
4
c)
8
d)
12
|
Vivek Patel answered |
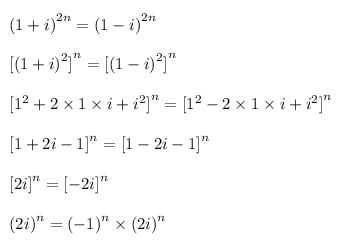
The numbers are same on both sides but with a negative sign. So they will be same if (-1)^n is positive.
So values of n are even numbers.
smallest positive even number is 2.
Thus, value of n is 2.
So values of n are even numbers.
smallest positive even number is 2.
Thus, value of n is 2.
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for "Complex Number" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations. 1. Number of solutions to the equation (1 –i)x = 2x is :- a)1
- b)2
- c)3
- d)no solution
Correct answer is option 'A'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for "Complex Number" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
1. Number of solutions to the equation (1 –i)x = 2x is :
a)
1
b)
2
c)
3
d)
no solution
|
Sid Gupta answered |
X is 0
If z3 – 2z2 + 4z – 8 = 0 then :- a)|z| = 1
- b)|z| = 2
- c)|z| = 3
- d)none
Correct answer is option 'B'. Can you explain this answer?
If z3 – 2z2 + 4z – 8 = 0 then :
a)
|z| = 1
b)
|z| = 2
c)
|z| = 3
d)
none
|
Faizan Khan answered |
z3 – 2z2 + 4z – 8 = 0
⇒ (z − 2)(z2 + 4)=0
⇒ z − 2 = 0 : z = 2
⇒ z2 + 4 = 0 : z = 2i, z = −2i
∴ z = 2, z = 2i, z = −2i
∴ ∣z∣ = 2
⇒ (z − 2)(z2 + 4)=0
⇒ z − 2 = 0 : z = 2
⇒ z2 + 4 = 0 : z = 2i, z = −2i
∴ z = 2, z = 2i, z = −2i
∴ ∣z∣ = 2
i1 + i2 + i3 + i4 + ……… + i1000 =- a)0
- b)1
- c)-1
- d)none
Correct answer is option 'A'. Can you explain this answer?
i1 + i2 + i3 + i4 + ……… + i1000 =
a)
0
b)
1
c)
-1
d)
none
|
Ishita Reddy answered |
i = √-1
i = i
i² = (√-1)² = - 1
i³ = i² * i = - 1 * i = - i
i⁴ = (i²)² = (-1)² = 1
i + i² + i³ + i⁴
= i - 1 - i + 1
= i - i + 1 - 1
= 0 + 0
= 0
i + i² + i³ + i⁴ = 0
⇒ i1 + i2 + i3 + i4 + ……… + i1000
⇒ 0 + 0 +........0(250 times)
⇒ 0
i = i
i² = (√-1)² = - 1
i³ = i² * i = - 1 * i = - i
i⁴ = (i²)² = (-1)² = 1
i + i² + i³ + i⁴
= i - 1 - i + 1
= i - i + 1 - 1
= 0 + 0
= 0
i + i² + i³ + i⁴ = 0
⇒ i1 + i2 + i3 + i4 + ……… + i1000
⇒ 0 + 0 +........0(250 times)
⇒ 0
a2 + b2- a)(a + b )(a-b)
- b)(a + ib)(a -ib)
- c)(a + b )(a- ib)
- d)(a + ib )(a - b)
Correct answer is option 'B'. Can you explain this answer?
a2 + b2
a)
(a + b )(a-b)
b)
(a + ib)(a -ib)
c)
(a + b )(a- ib)
d)
(a + ib )(a - b)
|
|
Faizan Khan answered |
(a + ib) x (a - ib)
= a2 - i2b2
we know i2=-1
so, equation becomes a2 -(-1)b2 =
a2 + b2
If the cube roots of unity are 1,ω,ω2 then 1 + ω + ω2 =- a)0
- b)1
- c)-1
- d) ω
Correct answer is option 'A'. Can you explain this answer?
If the cube roots of unity are 1,ω,ω2 then 1 + ω + ω2 =
a)
0
b)
1
c)
-1
d)
ω
|
|
Ishita Reddy answered |
The sum of the three cube roots of unity is zero i.e.,
1+ω+ω2=0.
We know that, the sum of the three cube roots of unity
|z1 + z2 | =- a)> |Z1| + |Z2|
- b)≤|Z1| + |Z2|
- c)≤ Z1 + Z2
- d)> Z1 + Z2
Correct answer is option 'B'. Can you explain this answer?
|z1 + z2 | =
a)
> |Z1| + |Z2|
b)
≤|Z1| + |Z2|
c)
≤ Z1 + Z2
d)
> Z1 + Z2
|
Ashwani Mishra answered |
|z1 + z2|=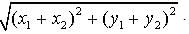 
.
|z1| + |z2|=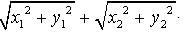
.
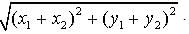.|z1| + |z2|=
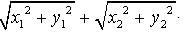.We have to prove that
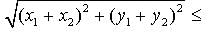
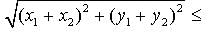
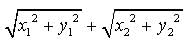is true.Square both sides.
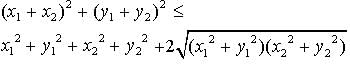
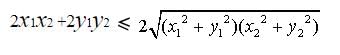Square both sides again.2x1x2y1y2 ≦ x12y22 + y12x22 and we get
0 ≦ (y1x2 - x1y2)2.
It is true because x1, x2, y1, y2 are all real.
Which one is not a root of the fourth root of unity.- a)i
- b)1
- c)i/√2
- d)-i
Correct answer is option 'C'. Can you explain this answer?
Which one is not a root of the fourth root of unity.
a)
i
b)
1
c)
i/√2
d)
-i
|
Nithin Bharadwaj answered |
For any integer n, the nth root of a number k is a number that, when multiplied by itself n times, yields k.
Check the options.
Option a, b, d when multipled by itself for 4 times yields 1.
So the answer is c
Check the options.
Option a, b, d when multipled by itself for 4 times yields 1.
So the answer is c
Value of ω1999 + ω299 + 1 is :- a)0
- b)1
- c)-1
- d)2
Correct answer is option 'A'. Can you explain this answer?
Value of ω1999 + ω299 + 1 is :
a)
0
b)
1
c)
-1
d)
2
|
Beats Unfolded answered |
Divide the numbers in the power by 3. Then look for the remainder. 1999/3 = 1(remainder), 299 = 2(remainder). Now replace 1999 by its respective remainder i.e* 1* & 299 by *2* in the original question which leaves you with ( w^2 + w + 1) which equals "0" according to property. Thanks :)
If a,b (a≠b), are the real roots of the equation (k + 1)(x2 + x + 1)2 + (k - 1)(x4 + x2 + 1) = 0, k ≠ 1, 0. Then the product of the roots is- a)(k + 1)/(k - 1)
- b)1
- c)(k2 + 1)/(k2 - 1)
- d)3
Correct answer is option 'B'. Can you explain this answer?
If a,b (a≠b), are the real roots of the equation (k + 1)(x2 + x + 1)2 + (k - 1)(x4 + x2 + 1) = 0, k ≠ 1, 0.
Then the product of the roots is
a)
(k + 1)/(k - 1)
b)
1
c)
(k2 + 1)/(k2 - 1)
d)
3
|
Nikita Singh answered |
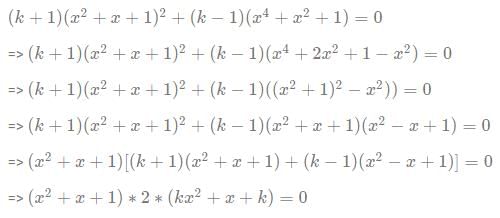
Since the equation (x2 + x + 1) = 0 . oes not have any real roots, the roots of the original equation will be the root of the equation (kx2 + x + k) = 0
Hence product of the roots = k/k = 1
If , arg(z) < 0, then arg(-z) – arg(z) =- a) π
- b)–π/4
- c)π/4
- d)π/2
Correct answer is option 'A'. Can you explain this answer?
If , arg(z) < 0, then arg(-z) – arg(z) =
a)
π
b)
–π/4
c)
π/4
d)
π/2
|
Raghavendra Sharma answered |
arg(Z)<0
==> arg(Z) = - theta
==> arg(-z) = pi - theta
==> difference = pi
If ω is an imaginary cube root of unity, then (1 + ω – ω2)7 equals :- a) 128 ω
- b)128 ω2
- c)-128 ω
- d) -128 ω2
Correct answer is option 'D'. Can you explain this answer?
If ω is an imaginary cube root of unity, then (1 + ω – ω2)7 equals :
a)
128 ω
b)
128 ω2
c)
-128 ω
d)
-128 ω2
|
Ishani Rane answered |
As w is a cube root of unity,
We have
1+w+w^2 = 0.
So 1+w = -w^2
Now 1+w-w^2 = -w^2-w2 = -2w^2.
So (1+w-w^2)^7 = (-2w^2)^7 = (-2)^7 x w^14.
We also know that w^3 = 1.
So (w^3)^2 also = 1
Similarly w^12=1
So, finally we have w^14 = w^2.
And hence answer is -2^7w^2 = -128w^2
|z1 - z2 | =- a)> |Z1| + |Z2|
- b)≤|Z1| + |Z2|
- c)≤ Z1 + Z2
- d)> Z1 + Z2
Correct answer is option 'B'. Can you explain this answer?
|z1 - z2 | =
a)
> |Z1| + |Z2|
b)
≤|Z1| + |Z2|
c)
≤ Z1 + Z2
d)
> Z1 + Z2
|
Aarav Sharma answered |
|z1- z2| = |(x1 + iy1) - (x2 + iy2)| = |(x1 - x2) + i(y1 - y2)| = sqrt((x1 - x2)^2 + (y1 - y2)^2)
Chapter doubts & questions for Complex numbers - Mathematics for Airmen Group X 2025 is part of Airforce X Y / Indian Navy SSR exam preparation. The chapters have been prepared according to the Airforce X Y / Indian Navy SSR exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Airforce X Y / Indian Navy SSR 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Complex numbers - Mathematics for Airmen Group X in English & Hindi are available as part of Airforce X Y / Indian Navy SSR exam.
Download more important topics, notes, lectures and mock test series for Airforce X Y / Indian Navy SSR Exam by signing up for free.
Mathematics for Airmen Group X
152 videos|196 docs|201 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup