All Exams >
RRB NTPC/ASM/CA/TA >
Mathematics for RRB NTPC / ASM >
All Questions
All questions of Harmonic Progressions for RRB NTPC/ASM/CA/TA Exam
Three numbers 5, p and 10 are in Harmonic progression if p = ?- a)10/3
- b)20/3
- c)3/10
- d)3/20
Correct answer is option 'B'. Can you explain this answer?
Three numbers 5, p and 10 are in Harmonic progression if p = ?
a)
10/3
b)
20/3
c)
3/10
d)
3/20

|
G.K Academy answered |
Concept:
Three numbers x, y, and z are in H.P if and only if y 
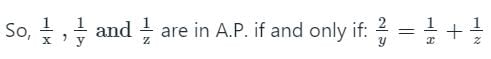
Calculation:

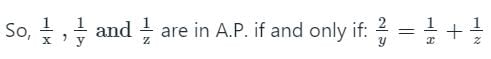
Calculation:
Given: Three numbers 5, p and 10 are in Harmonic progression

Now, According to the concept used


Now, According to the concept used

If 1/4, 1/x, 1/10 are in HP, then what is the value of x?- a)5
- b)6
- c)7
- d)8
Correct answer is option 'C'. Can you explain this answer?
If 1/4, 1/x, 1/10 are in HP, then what is the value of x?
a)
5
b)
6
c)
7
d)
8
|
|
Pranab Goyal answered |
Given:
1/4, 1/x, 1/10 are in Harmonic Progression (HP)
To find:
The value of x
Solution:
Harmonic Progression (HP):
In a Harmonic Progression (HP), the reciprocals of the terms are in Arithmetic Progression (AP).
Given terms:
1/4, 1/x, 1/10
Reciprocals of the given terms:
4/1, x/1, 10/1
As per the concept of HP:
2 * (1/x) = (1/4) + (1/10)
Solving the equation:
2/x = (10 + 4) / 40
2/x = 14 / 40
x = 40 / 14
x = 20 / 7
x = 7
Therefore, the value of x is 7.
Hence, the correct answer is option C) 7.
1/4, 1/x, 1/10 are in Harmonic Progression (HP)
To find:
The value of x
Solution:
Harmonic Progression (HP):
In a Harmonic Progression (HP), the reciprocals of the terms are in Arithmetic Progression (AP).
Given terms:
1/4, 1/x, 1/10
Reciprocals of the given terms:
4/1, x/1, 10/1
As per the concept of HP:
2 * (1/x) = (1/4) + (1/10)
Solving the equation:
2/x = (10 + 4) / 40
2/x = 14 / 40
x = 40 / 14
x = 20 / 7
x = 7
Therefore, the value of x is 7.
Hence, the correct answer is option C) 7.
If a, b, c are in geometric progression, then logax x, logbx x and logcx x are in- a)Arithmetic progression
- b)Geometric progression
- c)Harmonic progression
- d)Arithmetico-geometric progression
Correct answer is option 'C'. Can you explain this answer?
If a, b, c are in geometric progression, then logax x, logbx x and logcx x are in
a)
Arithmetic progression
b)
Geometric progression
c)
Harmonic progression
d)
Arithmetico-geometric progression

|
Iq Funda answered |
Concept:
If a, b, c are in geometric progression then b2 = ac
If b - a = c - b, than a, b, c are in AP.
If 1/a, 1/b, 1/c are in AP than a, b, c are in HP.
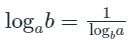
Calculation:
If a, b, c are in geometric progression then b2 = ac
So, by multiplying both side by x2 and taking log on both side to the base x

How many two digit numbers are divisible by 7?- a)13
- b)15
- c)11
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
How many two digit numbers are divisible by 7?
a)
13
b)
15
c)
11
d)
None of these

|
G.K Academy answered |
CONCEPT:
Let us suppose a be the first term and d be the common difference of an AP. Then the nth term of an AP is given by:an = a + (n - 1) × d.
Note: If l is the last term of a sequence, then l = an = a + (n - 1) × d.
CALCULATION:
Here we have to find two digit numbers which are divisible by 7.
i.e 14, 21,............,98 is an AP sequence with first term a = 14, common difference d = 7 and the last term l = 98.
As we know that, if l is the last term of a sequence, then l = an = a + (n - 1) × d
⇒ 98 = 14 + (n - 1) × 7
⇒ 84 = 7(n - 1)
⇒ 12 = n - 1
⇒ n = 13
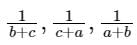 are in HP, then which of the following is/are correct?1. a, b, c are in AP2. (b + c)2, (c + a)2, (a + b)2 are in GP. Select the correct answer using the code given below.
are in HP, then which of the following is/are correct?1. a, b, c are in AP2. (b + c)2, (c + a)2, (a + b)2 are in GP. Select the correct answer using the code given below.- a)1 only
- b)2 only
- c)Both 1 and 2
- d)Neither 1 nor 2
Correct answer is option 'A'. Can you explain this answer?
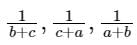 are in HP, then which of the following is/are correct?
are in HP, then which of the following is/are correct?1. a, b, c are in AP
2. (b + c)2, (c + a)2, (a + b)2 are in GP. Select the correct answer using the code given below.
a)
1 only
b)
2 only
c)
Both 1 and 2
d)
Neither 1 nor 2

|
EduRev SSC CGL answered |
Concept:
- If a, b and c are three terms in GP then b2 = ab and vice-versa
- If three terms a, b, c are in HP, then
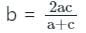 and vice-versa
and vice-versa - When three quantities are in AP, the middle one is called as the arithmetic mean of the other two.
- If a, b and c are three terms in AP then
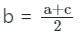
- and vice-versa
- If a, b and c are in A.P then 1/a, 1/b, 1/c are in H.P and vice-versa
Calculation:
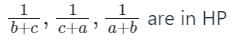
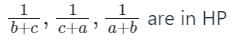
(b + c), (c + a) and (a + b) are in A.P
⇒ 2(c + a) = b + c + a + b
⇒ 2c + 2a = 2b + a + c -----(i)
⇒ 2c + 2a - 2b - a - c = 0
⇒ 2b = c + a
So, a, b, c are in AP
Now, Let (b + c)2, (c + a)2, (a + b)2 are in GP
(c + a)2 = √[(b + c).(a + b)]2
⇒ c2 + a2 + 2ac = (b + c).(a + b)
⇒ c2 + a2 + 2ac = ab + b2 + ac + bc
⇒ c2 + a2 - b2 + ac - ab - bc = 0
From here we are unable to check the relation between a, b and c
So, Our assumption was wrong
So, (b + c)2, (c + a)2, (a + b)2 are not in GP.
Chapter doubts & questions for Harmonic Progressions - Mathematics for RRB NTPC / ASM 2025 is part of RRB NTPC/ASM/CA/TA exam preparation. The chapters have been prepared according to the RRB NTPC/ASM/CA/TA exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for RRB NTPC/ASM/CA/TA 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Harmonic Progressions - Mathematics for RRB NTPC / ASM in English & Hindi are available as part of RRB NTPC/ASM/CA/TA exam.
Download more important topics, notes, lectures and mock test series for RRB NTPC/ASM/CA/TA Exam by signing up for free.
Mathematics for RRB NTPC / ASM
146 videos|113 docs|98 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









