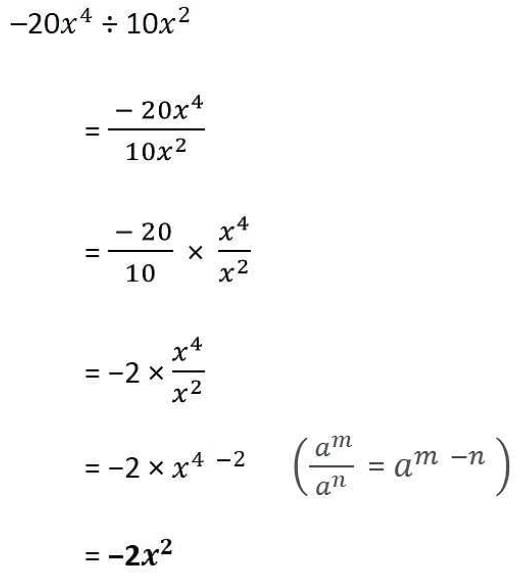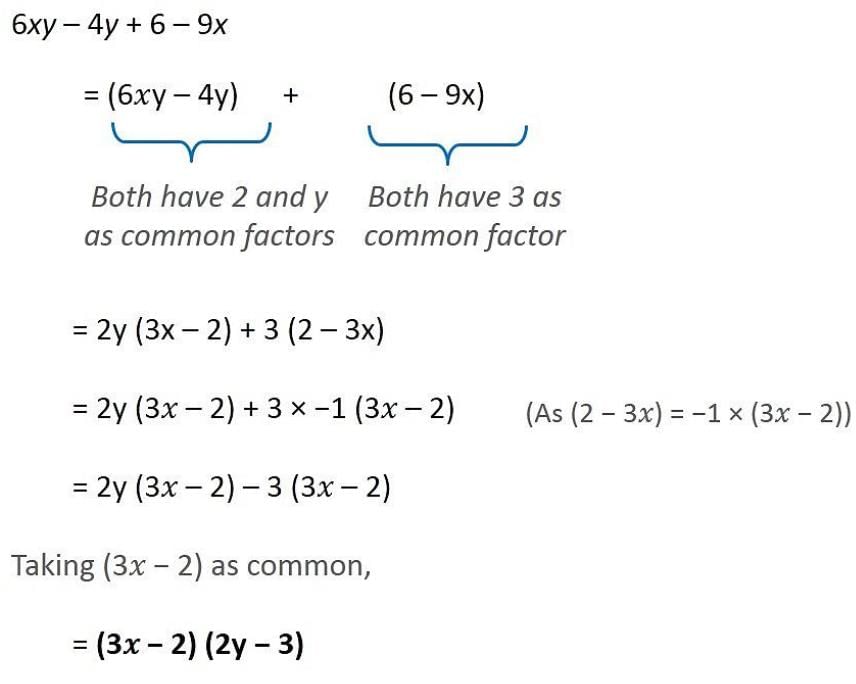All Exams >
Super TET >
Mathematics for Super TET >
All Questions
All questions of Factoring for Super TET Exam
Factorise: x2+ 8x + 16
- a)(x+ 3)2
- b)(x+ 2)2
- c)(x+ 4)2
- d)(x+ 5)2
Correct answer is option 'C'. Can you explain this answer?
Factorise: x2+ 8x + 16
a)
(x+ 3)2
b)
(x+ 2)2
c)
(x+ 4)2
d)
(x+ 5)2
|
Geetika Shah answered |
C ) (x2 +8x +16)
= (x2 + 4x + 4x + 16)
= ( x2 + 4x ) + (4x + 16 )
= x(x + 4 ) +4(x + 4 )
=(x + 4)(x + 4)
=(x + 4)2
= (x2 + 4x + 4x + 16)
= ( x2 + 4x ) + (4x + 16 )
= x(x + 4 ) +4(x + 4 )
=(x + 4)(x + 4)
=(x + 4)2
Solve: 7x2y2z2÷14xyza)(1/2)xyzb)(3/2)xyzc)(3/4)xyzd)(2/1)xyzCorrect answer is option 'A'. Can you explain this answer?
|
Target Study Academy answered |
7x²y²z²÷14xyz
=(7/14)(x²/x)(y²/y)(z²/z)
=1/2(x)(y)(z)
=1/2xyz.
=(7/14)(x²/x)(y²/y)(z²/z)
=1/2(x)(y)(z)
=1/2xyz.
Factorise: x2+x y+ 8x+ 8y- a)(x + 8) (x + y)
- b)(x + y)
- c)(x + 8)
- d)(x + 9) (x – y)
Correct answer is option 'A'. Can you explain this answer?
Factorise: x2+x y+ 8x+ 8y
a)
(x + 8) (x + y)
b)
(x + y)
c)
(x + 8)
d)
(x + 9) (x – y)
|
Aditi Saxena answered |
x^2 + xy + 8x + 8y = x[x + y] + 8[x + y]
= (x + y)(x + 8)
What are the factors of ax+by+bx+az+ay+bz?
- a)(bx+ay),(ax+by)
- b)(a+b),(2x+2y+2z)
- c)(x+y+z),(a+b)
- d)(x+y−z),(a−b)
Correct answer is option 'C'. Can you explain this answer?
What are the factors of ax+by+bx+az+ay+bz?
a)
(bx+ay),(ax+by)
b)
(a+b),(2x+2y+2z)
c)
(x+y+z),(a+b)
d)
(x+y−z),(a−b)
|
|
Geetika Shah answered |
ax+by+bx+az+ay+bz, rearranging we get ax+ay+az+bx+by+bz
a(x+y+z)+b(x+y+z)=(a+b)(x+y+z). Hence the factors are (a+b), (x+y+z)
a(x+y+z)+b(x+y+z)=(a+b)(x+y+z). Hence the factors are (a+b), (x+y+z)
Find the common factors of 2y, 22xy.- a)2y
- b)2
- c)22
- d)y
Correct answer is option 'A'. Can you explain this answer?
Find the common factors of 2y, 22xy.
a)
2y
b)
2
c)
22
d)
y
|
|
Amit Sharma answered |
Only 2y is common in both the terms
Divide the given polynomial by the given monomial: (x3+ 2x2+ 3x) ÷ 2x- a)1/2 (x2+2x+3)
- b)1/2
- c)(x2+2x+3)
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Divide the given polynomial by the given monomial: (x3+ 2x2+ 3x) ÷ 2x
a)
1/2 (x2+2x+3)
b)
1/2
c)
(x2+2x+3)
d)
none of these
|
|
Ananya Das answered |
(x3+2x2+3x)/2x
=x(x2+2x+3)/2x
=(x2+2x+3)/2
=x(x2+2x+3)/2x
=(x2+2x+3)/2
Factorize x² + 8x + 12
- a)(x + 2)(x + 6)
- b)(x + 3)(x + 4)
- c)3x + 12
- d)3x - 12
Correct answer is option 'A'. Can you explain this answer?
Factorize x² + 8x + 12
a)
(x + 2)(x + 6)
b)
(x + 3)(x + 4)
c)
3x + 12
d)
3x - 12
|
Kaavya Saha answered |
x² + 8x + 12
two no whose product is 12 and sum is 8
ie. 2 and 6 so;
x2+2x+6x+12
x(x+2)+6(x+2)
(x+2)(x+6)
two no whose product is 12 and sum is 8
ie. 2 and 6 so;
x2+2x+6x+12
x(x+2)+6(x+2)
(x+2)(x+6)
What are the factors of x4+2x2+9?
- a)(x2+2x+3), (x2−2x+3)
- b)(x2+3), (x2−3)
- c)(x2+2x+3), (x2+2x+3)
- d)(x2+3), (x2+3)
Correct answer is option 'A'. Can you explain this answer?
What are the factors of x4+2x2+9?
a)
(x2+2x+3), (x2−2x+3)
b)
(x2+3), (x2−3)
c)
(x2+2x+3), (x2+2x+3)
d)
(x2+3), (x2+3)
|
Trisha Vashisht answered |
Given equation is x4 + 2x2 + 9
We can rewrite this as,
(x2)2 + 6x2 + 9 − 4x2
⇒ (x2 + 3)2 − (2x)2
....Since a2 + 2ab + b2 = (a+b)2
⇒ x4 + 2x2 + 9 = (x2 − 2x + 3)(x2 + 2x + 3)
....Since a2 − b2 = (a+b)(a−b)
We can rewrite this as,
(x2)2 + 6x2 + 9 − 4x2
⇒ (x2 + 3)2 − (2x)2
....Since a2 + 2ab + b2 = (a+b)2
⇒ x4 + 2x2 + 9 = (x2 − 2x + 3)(x2 + 2x + 3)
....Since a2 − b2 = (a+b)(a−b)
Can you explain the answer of this question below:Divide as directed: 26xy (x + 5) (y – 4) ÷ 13x (y – 4)
- A:
2y (x + 5)
- B:
(x + 5)
- C:
2y
- D:
None of these
The answer is A.
Divide as directed: 26xy (x + 5) (y – 4) ÷ 13x (y – 4)
2y (x + 5)
(x + 5)
2y
None of these
|
Kavya Saxena answered |
26xy(x + 5) (y - 4) / 13x(y - 4)
Cancelling 13x(y-4)
=2y(x+5)
Cancelling 13x(y-4)
=2y(x+5)
Which of the following is quotient obtained on dividing –18 xyz2 by –3 xz?
- a)6 Yz
- b)–6 yz
- c)6 xy2
- d)6 xy
Correct answer is option 'A'. Can you explain this answer?
Which of the following is quotient obtained on dividing –18 xyz2 by –3 xz?
a)
6 Yz
b)
–6 yz
c)
6 xy2
d)
6 xy
|
|
Geetika Shah answered |
–18 xyz2/–3 xz x and x gets cancelled,-18 gets divided by -3 .and z2 gets divided by z so only one z remain in numerator So the quotient obtained is 6yz
How many factors does (x9−x) have?
- a)9
- b)4
- c)2
- d)5
Correct answer is option 'D'. Can you explain this answer?
How many factors does (x9−x) have?
a)
9
b)
4
c)
2
d)
5
|
Vivek Rana answered |
f(x) = x9- x
The degree of f(x) = 9
So , this polynomial will have 9 zeros
therefore it will have 9 factors
The degree of f(x) = 9
So , this polynomial will have 9 zeros
therefore it will have 9 factors
Factorise: p4– 81
- a)(p – 3) (p + 3) (p2+ 9)
- b)(p + 3) (p2+ 9)
- c)(p – 3) (p + 3)
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Factorise: p4– 81
a)
(p – 3) (p + 3) (p2+ 9)
b)
(p + 3) (p2+ 9)
c)
(p – 3) (p + 3)
d)
none of these
|
Malavika Basu answered |
We have p4 - 81 = (p2)2 - (9)2
Now using a2 - b2 = (a + b)(a - b), we have
(p2)2 - (9)2 = (p2 + 9)(p2 -9)
We can factorise p2 - 9 further as
p2 - 9 = (p)2 - (3)2
= (p + 3)(p - 3)
∴ p4 - 81 = (p + 3)(p - 3)(p2 + 9)
Can you explain the answer of this question below:Factorise: 4y2−12y+ 9
- A:
(7y− 5)2
- B:
(5y− 3)2
- C:
(2y− 5)2
- D:
(2y− 3)2
The answer is D.
Factorise: 4y2−12y+ 9
(7y− 5)2
(5y− 3)2
(2y− 5)2
(2y− 3)2
|
|
Kavya Saxena answered |
We have 4y2 - 12y+9. comparing the equation with (a-b)2=a2-2ab+b2,gives us a2=(2y)2,2ab=2*3*2y and b2=(3)2.Hence the answer is (2y-3)2.
Factorise: 10x2 − 18x3 + 14x4- a)2x2
- b)2x2(9x2−5x+7)
- c)(7x2−9x+5)
- d) 2x2(7x2−9x+5)
Correct answer is option 'D'. Can you explain this answer?
Factorise: 10x2 − 18x3 + 14x4
a)
2x2
b)
2x2(9x2−5x+7)
c)
(7x2−9x+5)
d)
2x2(7x2−9x+5)
|
Baishali Mehta answered |
10x2 − 18x3 + 14x4 = 2x(5x− 9x2 + 7x3) = 2x2(5− 9x + 7x2)
When we factorise an expression, we write it as a ________ of factors.- a)product
- b)difference
- c)sum
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
When we factorise an expression, we write it as a ________ of factors.
a)
product
b)
difference
c)
sum
d)
none of these
|
|
Aditya Shah answered |
When we factorise an algebraic expression, we write it as a product of factors. These factors may be numbers, algebraic variables or algebraic expressions.
From the following, which are the factors of a2 - b + ab - a?
- a)(a−1)and (a−b)
- b)(a+b)and (a−1)
- c)(a+1)and (a−b)
- d)(a+b) and (a+1)
Correct answer is option 'B'. Can you explain this answer?
From the following, which are the factors of a2 - b + ab - a?
a)
(a−1)and (a−b)
b)
(a+b)and (a−1)
c)
(a+1)and (a−b)
d)
(a+b) and (a+1)
|
Rohit Sharma answered |
a² - b + ab - a = a² + ab - b - a
= ( a² + ab ) - ( b + a )
= a ( a + b) - (a + b )
= ( a + b) ( a - 1 )
= ( a² + ab ) - ( b + a )
= a ( a + b) - (a + b )
= ( a + b) ( a - 1 )
What are the factors of x2+xy−2xz−2yz?- a)(x−y) and (x+2z)
- b)(x+y) and (x−2z)
- c)(x−y)and (x−2z)
- d)(x+y) and (x+2z)
Correct answer is option 'B'. Can you explain this answer?
What are the factors of x2+xy−2xz−2yz?
a)
(x−y) and (x+2z)
b)
(x+y) and (x−2z)
c)
(x−y)and (x−2z)
d)
(x+y) and (x+2z)
|
|
Aditya Shah answered |
x² + xy - 2xz - 2yz
x(x + y).-2z(x + y)
(x - 2z)(x + y)
What is the coefficient of 'a' when 9a2+18a is divided by (a+2)?- a)18
- b)9
- c)1/2
- d)2
Correct answer is option 'B'. Can you explain this answer?
What is the coefficient of 'a' when 9a2+18a is divided by (a+2)?
a)
18
b)
9
c)
1/2
d)
2
|
|
Gaurav Mukherjee answered |
Coefficient of a when 9a^2 - 18a is divided by (a - 2)
To find the coefficient of a, we need to perform long division as shown below:
9a - 18
(a - 2) | 9a^2 + 0a - 18
9a^2 - 18a
------------
18a - 18
18a - 36
--------
18
Therefore, the remainder is 18 and the quotient is 9a + 18. The coefficient of a in the quotient is 9, so the answer is option B) 9.
To find the coefficient of a, we need to perform long division as shown below:
9a - 18
(a - 2) | 9a^2 + 0a - 18
9a^2 - 18a
------------
18a - 18
18a - 36
--------
18
Therefore, the remainder is 18 and the quotient is 9a + 18. The coefficient of a in the quotient is 9, so the answer is option B) 9.
Amrit and Pankaj expanded (x−5)2. Amrit's answer is x2−25 and Pankaj's answer is x2−10x+25. Which of the following statements is correct?
- a)Amrit's answer is correct.
- b)Pankaj's answer is wrong.
- c)Both got correct answer.
- d)Pankaj's answer is correct.
Correct answer is option 'D'. Can you explain this answer?
Amrit and Pankaj expanded (x−5)2. Amrit's answer is x2−25 and Pankaj's answer is x2−10x+25. Which of the following statements is correct?
a)
Amrit's answer is correct.
b)
Pankaj's answer is wrong.
c)
Both got correct answer.
d)
Pankaj's answer is correct.
|
Priya Chakraborty answered |
(x−5)2 = x2−10x+25 using
(a−b)2 = a2−2ab+b2. So, Pankaj's answer is correct.
The expression (p2+7p+10) is factorized and then divided by (p+5). What is the quotient?- a)p−5
- b)p−2
- c)p+2
- d)p+5
Correct answer is option 'C'. Can you explain this answer?
The expression (p2+7p+10) is factorized and then divided by (p+5). What is the quotient?
a)
p−5
b)
p−2
c)
p+2
d)
p+5
|
|
Aditya Shah answered |
p^2 + 7p + 10 / p + 5
p^2 + 5p + 2p + 10 / p+5
p ( p + 5 ) + 2(p + 5 ) / p+5
( p+5) ( p+ 2 ) / p + 5
( p+2)
For x2+2x+5 to be a factor of x4+ px2+q, what must the respective values of p and q be?
- a)−2 and 5
- b)5 and 25
- c)10 and 20
- d)6 and 25
Correct answer is option 'D'. Can you explain this answer?
For x2+2x+5 to be a factor of x4+ px2+q, what must the respective values of p and q be?
a)
−2 and 5
b)
5 and 25
c)
10 and 20
d)
6 and 25
|
Neha Banerjee answered |
x^4+px^2+q.
=x^2(x^2+2x+5)-2x^3–5x^2+px^2+q.
=x^2(x^2+2x+5)-2x(x^2+2x+5)+4x^2+10x-5x^2+px^2+q.
=x^2(x^2+2x+5)-2x(x^2+2x+5)+(p-1). x^2+10x+q.
=x^2(x^2+2x+5)-2x(x^2+2x+5)+(p-1)(x^2+2x+5)-2(p-1).x-5(p-1)+10x+q.
=(x^2+2x+5) (x^2–2x+p) +2(6-p).x+5(1-p)+q.
=Divisor � Q +R.
Remainder = 0
2(6-p).x+(5–5p+q)= 0.
2(6-p)x+(5–5p+q)= 0.x + 0.
Equating the coeff. of x and constant term.
2(6-p) = 0 => p = 6 and
5–5p+q = 0.
5–5�6+q = 0.
q = 30–5 = 25
p = 6 and q = 25 , Answer.
Choose the factors of 15x2−26x+8 from the following.
- a)(3x−4),(5x+2)
- b)(3x−4),(5x−2)
- c)(3x+4),(5x−2)
- d)(3x+4),(5x+2)
Correct answer is option 'B'. Can you explain this answer?
Choose the factors of 15x2−26x+8 from the following.
a)
(3x−4),(5x+2)
b)
(3x−4),(5x−2)
c)
(3x+4),(5x−2)
d)
(3x+4),(5x+2)
|
|
Priya Chakraborty answered |
15x2−26x+8 =15x2−20x−6x+8 =5x(3x−4)−2(3x−4) =(3x−4)(5x−2)
If (x2+3x+5)(x2−3x+5) = m2−n2, what is the value of m?
- a)x2−3x
- b)3x
- c)x2+5
- d)x2+3x
Correct answer is option 'C'. Can you explain this answer?
If (x2+3x+5)(x2−3x+5) = m2−n2, what is the value of m?
a)
x2−3x
b)
3x
c)
x2+5
d)
x2+3x
|
Gitanjali Kaur answered |
(x2+3x+5)(x2−3x+5) = (x2+5+3x)(x2+5−3x) = (x2+5)2−(3x)2 = m2−n2
∴ m = x2+5
∴ m = x2+5
Divide the given polynomial by the given monominal: 8 (x3y2z2 + x2y3z2 + x2y2z3) ÷ 4x2y2z2- a)(x + y + z)
- b)2(x + y + z)
- c)2
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
Divide the given polynomial by the given monominal: 8 (x3y2z2 + x2y3z2 + x2y2z3) ÷ 4x2y2z2
a)
(x + y + z)
b)
2(x + y + z)
c)
2
d)
none of these
|
|
Nitin Sen answered |
To divide a polynomial by a monomial, we need to divide each term in the polynomial by the monomial.
Given polynomial: 8x^3y^2z^2 - x^2y^3z^2 - x^2y^2z^3
Given monomial: 8
Dividing each term by the monomial 8:
(8x^3y^2z^2)/8 = x^3y^2z^2
(-x^2y^3z^2)/8 = -1/8 * x^2y^3z^2
(-x^2y^2z^3)/8 = -1/8 * x^2y^2z^3
Therefore, the result of dividing the given polynomial by the monomial 8 is:
x^3y^2z^2 - (1/8)x^2y^3z^2 - (1/8)x^2y^2z^3
Given polynomial: 8x^3y^2z^2 - x^2y^3z^2 - x^2y^2z^3
Given monomial: 8
Dividing each term by the monomial 8:
(8x^3y^2z^2)/8 = x^3y^2z^2
(-x^2y^3z^2)/8 = -1/8 * x^2y^3z^2
(-x^2y^2z^3)/8 = -1/8 * x^2y^2z^3
Therefore, the result of dividing the given polynomial by the monomial 8 is:
x^3y^2z^2 - (1/8)x^2y^3z^2 - (1/8)x^2y^2z^3
Which of the following statements is correct?
- a)(a−4)(a−2) = a2+8−6a
- b)(2p+3q)(p−q) = 2p2−3q2
- c)3p2/4p2 = 0
- d)4(m−5) = 4m−5
Correct answer is option 'A'. Can you explain this answer?
Which of the following statements is correct?
a)
(a−4)(a−2) = a2+8−6a
b)
(2p+3q)(p−q) = 2p2−3q2
c)
3p2/4p2 = 0
d)
4(m−5) = 4m−5
|
Harsh Datta answered |
(a−4)(a−2) = a2−4a−2a+8 = a2−6a+8 So, the statement in option (A) is correct.
Which of the following is one of the factors of x4+4?
- a)x2+2
- b)(x² + 2 + 2x)(x² + 2 - 2x)
- c)x2−2
- d)x2+2x−2
Correct answer is option 'B'. Can you explain this answer?
Which of the following is one of the factors of x4+4?
a)
x2+2
b)
(x² + 2 + 2x)(x² + 2 - 2x)
c)
x2−2
d)
x2+2x−2
|
Amrutha Saini answered |
x4+4
adding and subtracting 4x2
x4+4+4x2−4x2
(x2)2+22+2∗2∗x2−(2x)2
(x2+2)2−(2x)2(a+b)2=a2+b2+2ab
(x2+2−2x)(x2+2+2x)(a2−b2)=(a+b)(a−b)
Find the factors of6 mn−4n+6−9m.- a)(2m−1) and (2n−4)
- b)(4m−1) and (n−3)
- c)(3m−2) and (2n−3)
- d)(4m−4) and (n−1)
Correct answer is option 'C'. Can you explain this answer?
Find the factors of6 mn−4n+6−9m.
a)
(2m−1) and (2n−4)
b)
(4m−1) and (n−3)
c)
(3m−2) and (2n−3)
d)
(4m−4) and (n−1)
|
|
Aditya Shah answered |
6mn-9m-4n+6
take 3m common
3m(2n-3)-2(2n-3)
(3m-2)(2n-3)
Which of the following are the factors of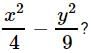 
- a)
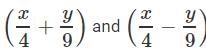
- b)
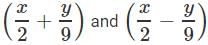
- c)
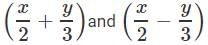
- d)
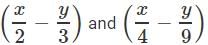
Correct answer is option 'C'. Can you explain this answer?
Which of the following are the factors of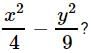
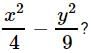
a)
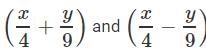
b)
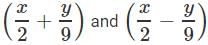
c)
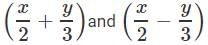
d)
|
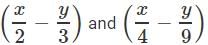
Riddhi Chhabra answered |
X²/4 - y²/9
Taking both in brackets of square as 2² is 4 and 3² is 9
(x/2)²-(y/3)²
now using the property (a-b)²=(a+b)(a-b)
(x/2+y/3) (x/2-y-3)
Hence the answer is option C .
Taking both in brackets of square as 2² is 4 and 3² is 9
(x/2)²-(y/3)²
now using the property (a-b)²=(a+b)(a-b)
(x/2+y/3) (x/2-y-3)
Hence the answer is option C .
Find the factors of b2−7b+12.
- a)(b−4),(b−8)
- b)(b−3),(b−4)
- c)(b−10),(b−1)
- d)(b−7),(b−9)
Correct answer is option 'B'. Can you explain this answer?
Find the factors of b2−7b+12.
a)
(b−4),(b−8)
b)
(b−3),(b−4)
c)
(b−10),(b−1)
d)
(b−7),(b−9)
|
Saanvi Joshi answered |
b2 - 7b+12=b2-3b-4b+12=b(b-3)-4(b-3)=(b-3)(b-4)
What are the factors of x4+y4+x2y2?
- a)(x2+y2) and (x2+y2−xy)
- b)(x2+y2)and (x2−y2)
- c)(x2+y2+xy) and (x2+y2−xy)
- d)Factorization is not possibl
Correct answer is option 'C'. Can you explain this answer?
What are the factors of x4+y4+x2y2?
a)
(x2+y2) and (x2+y2−xy)
b)
(x2+y2)and (x2−y2)
c)
(x2+y2+xy) and (x2+y2−xy)
d)
Factorization is not possibl
|
Gargi Shah answered |
x4+y4+x2y2 =(x4+y4+2x2y2)−x2y2 =(x2+y2)2−(xy)2
=(x2+y2+xy)(x2+y2−xy)
=(x2+y2+xy)(x2+y2−xy)
Chapter doubts & questions for Factoring - Mathematics for Super TET 2025 is part of Super TET exam preparation. The chapters have been prepared according to the Super TET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Super TET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Factoring - Mathematics for Super TET in English & Hindi are available as part of Super TET exam.
Download more important topics, notes, lectures and mock test series for Super TET Exam by signing up for free.
Mathematics for Super TET
80 videos|69 docs|51 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup