All Exams >
GRE >
Quantitative Reasoning for GRE >
All Questions
All questions of Inequalities for GRE Exam
(√(8) / -x ) < 2. Which of the following values could be x?- a)-2
- b)-1
- c)-3
- d)-4
- e)All of the answers choices are valid.
Correct answer is option 'B'. Can you explain this answer?
(√(8) / -x ) < 2. Which of the following values could be x?
a)
-2
b)
-1
c)
-3
d)
-4
e)
All of the answers choices are valid.

|
Talent Skill Learning answered |
The equation simplifies to x > -1.41. -1 is the answer.
If –1 < w < 1, all of the following must also be greater than –1 and less than 1 EXCEPT for which choice?- a)|w|0.5
- b)w/2
- c)3w/2
- d)w2
- e)|w|
Correct answer is option 'C'. Can you explain this answer?
If –1 < w < 1, all of the following must also be greater than –1 and less than 1 EXCEPT for which choice?
a)
|w|0.5
b)
w/2
c)
3w/2
d)
w2
e)
|w|

|
Talent Skill Learning answered |
3w/2 will become greater than 1 as soon as w is greater than two thirds. It will likewise become less than –1 as soon as w is less than negative two thirds. All the other options always return values between –1 and 1.
Each of the following is equivalent to xy/z * (5(x + y)) EXCEPT:- a)xy(5y + 5x)/z
- b)xy(5x + 5y)/z
- c)5x²y + 5xy²/z
- d)5x² + y²/z
- e)None
Correct answer is option 'D'. Can you explain this answer?
Each of the following is equivalent to xy/z * (5(x + y)) EXCEPT:
a)
xy(5y + 5x)/z
b)
xy(5x + 5y)/z
c)
5x²y + 5xy²/z
d)
5x² + y²/z
e)
None

|
Talent Skill Learning answered |
Choice a is equivalent because we can say that technically we are multiplying two fractions together: (xy)/z and (5(x + y))/1. We multiply the numerators together and the denominators together and end up with xy (5x + 5y)/z. xy (5y + 5x)/z is also equivalent because it is only simplifying what is inside the parentheses and switching the order- the commutative property tells us this is still the same expression. 5x²y + 5xy²/z is equivalent as it is just a simplified version when the numerators are multiplied out. Choice 5x² + y²/z is not equivalent because it does not account for all the variables that were in the given expression and it does not use FOIL correctly.
Solve for the y-intercept:
3y + 11 ≥ 5y + 6x − 1
Possible Answers:- a)−12
- b)3
- c)-6
- d)6
- e)-3
Correct answer is option 'D'. Can you explain this answer?
Solve for the y-intercept:
3y + 11 ≥ 5y + 6x − 1
Possible Answers:
3y + 11 ≥ 5y + 6x − 1
Possible Answers:
a)
−12
b)
3
c)
-6
d)
6
e)
-3

|
Talent Skill Learning answered |
Don't forget to switch the inequality direction if you multiply or divide by a negative.
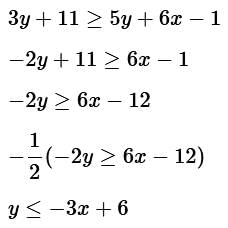
Now that we have the equation in slope-intercept form, we can see that the y-intercept is 6.
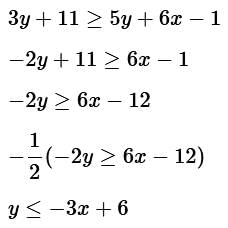
Now that we have the equation in slope-intercept form, we can see that the y-intercept is 6.
What values of x make the following statement true?
|x – 3| < 9- a)–6 < x < 12
- b)–3 < x < 9
- c)x < 12
- d)–12 < x < 6
- e)6 < x < 12
Correct answer is option 'E'. Can you explain this answer?
What values of x make the following statement true?
|x – 3| < 9
|x – 3| < 9
a)
–6 < x < 12
b)
–3 < x < 9
c)
x < 12
d)
–12 < x < 6
e)
6 < x < 12

|
Talent Skill Learning answered |
Solve the inequality by adding 3 to both sides to get x < 12. Since it is absolute value, x – 3 > –9 must also be solved by adding 3 to both sides so: x > –6 so combined.
Find the slope of the inequality equation y − 7 < x + 2y − 14- a)1
- b)0
- c)7
- d)-7
- e)-1
Correct answer is option 'E'. Can you explain this answer?
Find the slope of the inequality equation y − 7 < x + 2y − 14
a)
1
b)
0
c)
7
d)
-7
e)
-1

|
Talent Skill Learning answered |
The answer is:
y − 7 < x + 2y − 14
−y − 7 < x − 14
−1(−y < x − 7)
y> − x + 7
From the equation we can see that the slope is –1.
y − 7 < x + 2y − 14
−y − 7 < x − 14
−1(−y < x − 7)
y> − x + 7
From the equation we can see that the slope is –1.
Quantitative Comparison
Quantity A: 3x + 4y
Quantity B: 4x + 3y- a)Quantity A is greater.
- b)The relationship cannot be determined from the information given.
- c)The two quantities are equal.
- d)Quantity B is greater.
- e)None
Correct answer is option 'B'. Can you explain this answer?
Quantitative Comparison
Quantity A: 3x + 4y
Quantity B: 4x + 3y
Quantity A: 3x + 4y
Quantity B: 4x + 3y
a)
Quantity A is greater.
b)
The relationship cannot be determined from the information given.
c)
The two quantities are equal.
d)
Quantity B is greater.
e)
None

|
Talent Skill Learning answered |
The question does not give us any specifics about the variables x and y.
If we substitute the same numbers for x and y (say, x = 1 and y = 1), the two expressions are equal.
If we substitute different number in for x and y (say, x = 2 and y = 1), the two expressions are not equal.
If there are two possible outcomes, then we need more information to determine which quantity is greater. Don't be afraid to pick "The relationship cannot be determined from the information given" as an answer choice on the GRE!
For how many positive integers, x, is it true that x4 < 27x?- a)1
- b)2
- c)3
- d)More than 3
- e)None
Correct answer is option 'B'. Can you explain this answer?
For how many positive integers, x, is it true that x4 < 27x?
a)
1
b)
2
c)
3
d)
More than 3
e)
None

|
Talent Skill Learning answered |
Since x is positive, we can divide both sides of the inequality by x:
x4 < 27x ⇒ x3 < 27 ⇒ x < 3 ⇒ x = 1 or 2.
x4 < 27x ⇒ x3 < 27 ⇒ x < 3 ⇒ x = 1 or 2.
The cost, in cents, of manufacturing x pencils is 1200 + 12x, where 1200 is the number of cents required to run the factory regardless of the number of pencils made, and 20 represents the per-unit cost, in cents, of making each pencil. The pencils sell for 50 cents each. What number of pencils would need to be sold so that the revenue received is at least equal to the manufacturing cost? - a)40
- b)36
- c)33
- d)27
- e)30
Correct answer is option 'A'. Can you explain this answer?
The cost, in cents, of manufacturing x pencils is 1200 + 12x, where 1200 is the number of cents required to run the factory regardless of the number of pencils made, and 20 represents the per-unit cost, in cents, of making each pencil. The pencils sell for 50 cents each. What number of pencils would need to be sold so that the revenue received is at least equal to the manufacturing cost?
a)
40
b)
36
c)
33
d)
27
e)
30

|
Talent Skill Learning answered |
If each pencil sells at 50 cents, x pencils will sell at 50x. The smallest value of x such that
50x ≥ 1200 + 20x
x ≥ 40
50x ≥ 1200 + 20x
x ≥ 40
Let S be the set of numbers that contains all of values of x such that 2x + 4 < 8. Let T contain all of the values of x such that -2x +3 < 8. What is the sum of all of the integer values that belong to the intersection of S and T?- a)-3
- b)2
- c)-2
- d)0
- e)-7
Correct answer is option 'C'. Can you explain this answer?
Let S be the set of numbers that contains all of values of x such that 2x + 4 < 8. Let T contain all of the values of x such that -2x +3 < 8. What is the sum of all of the integer values that belong to the intersection of S and T?
a)
-3
b)
2
c)
-2
d)
0
e)
-7

|
Talent Skill Learning answered |
First, we need to find all of the values that are in the set S, and then we need to find the values in T. Once we do this, we must find the numbers in the intersection of S and T, which means we must find the values contained in BOTH sets S and T.
S contains all of the values of x such that 2x + 4 < 8. We need to solve this inequality.
2x + 4 < 8
Subtract 4 from both sides.
2x < 4
Divide by 2.
x < 2
Thus, S contains all of the values of x that are less than (but not equal to) 2.
Now, we need to do the same thing to find the values contained in T.
-2x + 3 < 8
Subtract 3 from both sides.
-2x < 5
Divide both sides by -2. Remember, when multiplying or dividing an inequality by a negative number, we must switch the sign.
x > -5/2
Therefore, T contains all of the values of x that are greater than -5/2, or -2.5.
Next, we must find the values that are contained in both S and T. In order to be in both sets, these numbers must be less than 2, but also greater than -2.5. Thus, the intersection of S and T consists of all numbers between -2.5 and 2.
The question asks us to find the sum of the integers in the intersection of S and T. This means we must find all of the integers between -2.5 and 2.
The integers between -2.5 and 2 are the following: -2, -1, 0, and 1. We cannot include 2, because the values in S are LESS than but not equal to 2.
Lastly, we add up the values -2, -1, 0, and 1. The sum of these is -2.
The answer is -2.
S contains all of the values of x such that 2x + 4 < 8. We need to solve this inequality.
2x + 4 < 8
Subtract 4 from both sides.
2x < 4
Divide by 2.
x < 2
Thus, S contains all of the values of x that are less than (but not equal to) 2.
Now, we need to do the same thing to find the values contained in T.
-2x + 3 < 8
Subtract 3 from both sides.
-2x < 5
Divide both sides by -2. Remember, when multiplying or dividing an inequality by a negative number, we must switch the sign.
x > -5/2
Therefore, T contains all of the values of x that are greater than -5/2, or -2.5.
Next, we must find the values that are contained in both S and T. In order to be in both sets, these numbers must be less than 2, but also greater than -2.5. Thus, the intersection of S and T consists of all numbers between -2.5 and 2.
The question asks us to find the sum of the integers in the intersection of S and T. This means we must find all of the integers between -2.5 and 2.
The integers between -2.5 and 2 are the following: -2, -1, 0, and 1. We cannot include 2, because the values in S are LESS than but not equal to 2.
Lastly, we add up the values -2, -1, 0, and 1. The sum of these is -2.
The answer is -2.
Chapter doubts & questions for Inequalities - Quantitative Reasoning for GRE 2025 is part of GRE exam preparation. The chapters have been prepared according to the GRE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GRE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Inequalities - Quantitative Reasoning for GRE in English & Hindi are available as part of GRE exam.
Download more important topics, notes, lectures and mock test series for GRE Exam by signing up for free.
Quantitative Reasoning for GRE
124 videos|102 docs|108 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









