All Exams >
Grade 8 >
Science for Grade 8 >
All Questions
All questions of Communicating with Signals for Grade 8 Exam
What is the period of the following signal, x(t) = sin(18*pi*t + 78 deg)?- a) 1⁄9
- b) 2⁄9
- c) 1⁄3
- d) 4⁄9
Correct answer is option 'B'. Can you explain this answer?
What is the period of the following signal, x(t) = sin(18*pi*t + 78 deg)?
a)
1⁄9
b)
2⁄9
c)
1⁄3
d)
4⁄9
|
|
Kajal Yadav answered |
The period of a sinusoidal signal of the form x(t) = A*sin(ωt + φ) is given by T = 2π/ω, where ω is the angular frequency. In this case, ω = 18π, so the period is T = 2π/(18π) = 1/9 seconds. The phase angle (in degrees) does not affect the period. Therefore, the period of the given signal is 1/9 seconds.
A sinusoidal signal x(t) = 2sin(100t + π/3) is passed through a square law device defined by input-output relation y(t) = x2(t), then the DC component in the signal is:- a)4
- b)2
- c)1
- d)2√3 / √2
Correct answer is option 'B'. Can you explain this answer?
A sinusoidal signal x(t) = 2sin(100t + π/3) is passed through a square law device defined by input-output relation y(t) = x2(t), then the DC component in the signal is:
a)
4
b)
2
c)
1
d)
2√3 / √2
|
|
Dipanjan Nambiar answered |
Understanding the Sinusoidal Signal
The given sinusoidal signal is:
- x(t) = 2sin(100t + π/3)
This signal oscillates between -2 and +2, with a frequency determined by the coefficient of t.
Passing through the Square Law Device
The square law device has the relationship:
- y(t) = x^2(t)
To find the output signal, we need to compute x^2(t):
- y(t) = (2sin(100t + π/3))^2
- y(t) = 4sin^2(100t + π/3)
Using Trigonometric Identity
We can simplify sin^2 using the identity:
- sin^2(θ) = (1 - cos(2θ))/2
Applying this to our equation:
- y(t) = 4 * (1 - cos(200t + 2π/3))/2
- y(t) = 2(1 - cos(200t + 2π/3))
- y(t) = 2 - 2cos(200t + 2π/3)
Identifying the DC Component
The DC component of a signal is defined as the constant term (the part that does not oscillate). From the expression of y(t):
- The term "2" is the DC component.
- The term "-2cos(200t + 2π/3)" oscillates and does not contribute to the DC component.
Conclusion
Thus, the DC component in the signal y(t) is:
- 2
The correct answer is option 'B'.
The given sinusoidal signal is:
- x(t) = 2sin(100t + π/3)
This signal oscillates between -2 and +2, with a frequency determined by the coefficient of t.
Passing through the Square Law Device
The square law device has the relationship:
- y(t) = x^2(t)
To find the output signal, we need to compute x^2(t):
- y(t) = (2sin(100t + π/3))^2
- y(t) = 4sin^2(100t + π/3)
Using Trigonometric Identity
We can simplify sin^2 using the identity:
- sin^2(θ) = (1 - cos(2θ))/2
Applying this to our equation:
- y(t) = 4 * (1 - cos(200t + 2π/3))/2
- y(t) = 2(1 - cos(200t + 2π/3))
- y(t) = 2 - 2cos(200t + 2π/3)
Identifying the DC Component
The DC component of a signal is defined as the constant term (the part that does not oscillate). From the expression of y(t):
- The term "2" is the DC component.
- The term "-2cos(200t + 2π/3)" oscillates and does not contribute to the DC component.
Conclusion
Thus, the DC component in the signal y(t) is:
- 2
The correct answer is option 'B'.
For a periodic signal v(t) = 30 sin100t + 10 cos300t + 6 sin(500t + π/4), the fundamental frequency in rad/s is _____.- a)100
- b)300
- c)500
- d)1500
Correct answer is option 'A'. Can you explain this answer?
For a periodic signal v(t) = 30 sin100t + 10 cos300t + 6 sin(500t + π/4), the fundamental frequency in rad/s is _____.
a)
100
b)
300
c)
500
d)
1500
|
|
Luminary Institute answered |
Given, the signal
V (t) = 30 sin 100t + 10 cos 300 t + 6 sin (500t+π/4)
So, we have
ω1 = 100 rads
ω2 = 300 rads
ω3 = 500 rads
∴ The respective time periods are
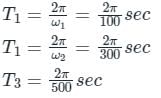
So, the fundamental time period of the signal is
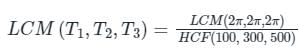
as, 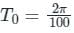
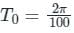
∴ The fundamental frequency,
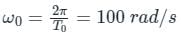
What are the steady state values of the signals, 1-exp(-t), and 1-k*exp(-k*t)?- a)1, k
- b)1, 1/k
- c)k, k
- d)1, 1
Correct answer is option 'D'. Can you explain this answer?
What are the steady state values of the signals, 1-exp(-t), and 1-k*exp(-k*t)?
a)
1, k
b)
1, 1/k
c)
k, k
d)
1, 1
|
|
Kalyan Patel answered |
Consider limit at t tending to infinity, we obtain 1 for both cases.
Y (t) = x (t/5) is _______- a)Compressed signal
- b)Expanded signal
- c)Time shifted signal
- d)Amplitude scaled signal by factor 1/5
Correct answer is option 'B'. Can you explain this answer?
Y (t) = x (t/5) is _______
a)
Compressed signal
b)
Expanded signal
c)
Time shifted signal
d)
Amplitude scaled signal by factor 1/5

|
Charvi Kaur answered |
Explanation:
The given equation is Y(t) = x(t/5), which implies that the output signal Y(t) is obtained by compressing the input signal x(t) by a factor of 5. This means that the signal is scaled down in time, and the time axis is compressed.
Therefore, the correct option is (B) Expanded signal.
Here are some key points to understand:
- The input signal x(t) is compressed by a factor of 5. This means that the time axis is scaled down by a factor of 5.
- The output signal Y(t) is obtained by applying this compression to the input signal.
- Since the time axis is compressed, the signal appears to expand in amplitude. This is because the same amount of signal is now squeezed into a smaller time interval.
- Therefore, the output signal Y(t) is an expanded signal, as compared to the input signal x(t).
In summary, the given equation Y(t) = x(t/5) represents an expanded signal, as the input signal is compressed in time to obtain the output signal.
The given equation is Y(t) = x(t/5), which implies that the output signal Y(t) is obtained by compressing the input signal x(t) by a factor of 5. This means that the signal is scaled down in time, and the time axis is compressed.
Therefore, the correct option is (B) Expanded signal.
Here are some key points to understand:
- The input signal x(t) is compressed by a factor of 5. This means that the time axis is scaled down by a factor of 5.
- The output signal Y(t) is obtained by applying this compression to the input signal.
- Since the time axis is compressed, the signal appears to expand in amplitude. This is because the same amount of signal is now squeezed into a smaller time interval.
- Therefore, the output signal Y(t) is an expanded signal, as compared to the input signal x(t).
In summary, the given equation Y(t) = x(t/5) represents an expanded signal, as the input signal is compressed in time to obtain the output signal.
Which of the following signals is monotonic?- a)x(t) = t3 – 2t
- b)x(t) = sin(t)
- c)x(t) = sin22(t) + cos22(t) – 2t
- d)x(t) = log(cos(t))
Correct answer is option 'C'. Can you explain this answer?
Which of the following signals is monotonic?
a)
x(t) = t3 – 2t
b)
x(t) = sin(t)
c)
x(t) = sin22(t) + cos22(t) – 2t
d)
x(t) = log(cos(t))
|
|
Aditya Deshmukh answered |
Reduces to 1 – 2t, which is a strictly decreasing function.
Is the function y[n] = y[n-1] + x[n] stable in nature?- a)It is stable
- b)It is unstable
- c)Both stable and unstable
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
Is the function y[n] = y[n-1] + x[n] stable in nature?
a)
It is stable
b)
It is unstable
c)
Both stable and unstable
d)
None of the mentioned
|
|
Anoushka Kumar answered |
It is BIBO stable in nature, i.e. bounded input-bounded output stable.
Unit Impulse function is obtained by using the limiting process on which among the following functions?- a)Triangular Function
- b)Rectangular Function
- c)Signum Function
- d)Sinc Function
Correct answer is option 'B'. Can you explain this answer?
Unit Impulse function is obtained by using the limiting process on which among the following functions?
a)
Triangular Function
b)
Rectangular Function
c)
Signum Function
d)
Sinc Function
|
|
Gauri Yadav answered |
Unit Impulse Function
The unit impulse function, also known as the Dirac delta function, is a mathematical function that is used to model an idealized impulse or an infinitesimally short pulse. It is often denoted as δ(t) or δ[n], where t is a continuous variable and n is a discrete variable.
Limiting Process
The unit impulse function can be obtained by using a limiting process on the rectangular function. The rectangular function, also known as the boxcar function, is a function that is equal to 1 within a certain interval and 0 outside that interval.
Explanation
To understand how the unit impulse function is obtained from the rectangular function, let's consider a rectangular function with width 2a centered at the origin:
f(t) = 1 for -a ≤ t ≤ a
f(t) = 0 otherwise
Now, let's define a sequence of rectangular functions with decreasing widths:
f1(t) = 1 for -a/2 ≤ t ≤ a/2
f1(t) = 0 otherwise
f2(t) = 1 for -a/4 ≤ t ≤ a/4
f2(t) = 0 otherwise
f3(t) = 1 for -a/8 ≤ t ≤ a/8
f3(t) = 0 otherwise
...
We can observe that as the width of the rectangular function approaches zero, its height approaches infinity in such a way that the area under the curve remains constant. This is the key idea behind the limiting process.
Now, let's define the unit impulse function as the limit of this sequence of rectangular functions as the width approaches zero:
δ(t) = lim [f1(t), f2(t), f3(t), ...]
The unit impulse function is defined such that it is zero for all values of t except at t = 0, where it is infinitely high. However, the area under the curve of the unit impulse function is equal to 1.
Conclusion
In conclusion, the unit impulse function is obtained by using the limiting process on the rectangular function. As the width of the rectangular function approaches zero, its height approaches infinity in such a way that the area under the curve remains constant. This mathematical concept allows us to model an idealized impulse or an infinitesimally short pulse, which is useful in various fields of science and engineering, including signal processing and control systems.
The unit impulse function, also known as the Dirac delta function, is a mathematical function that is used to model an idealized impulse or an infinitesimally short pulse. It is often denoted as δ(t) or δ[n], where t is a continuous variable and n is a discrete variable.
Limiting Process
The unit impulse function can be obtained by using a limiting process on the rectangular function. The rectangular function, also known as the boxcar function, is a function that is equal to 1 within a certain interval and 0 outside that interval.
Explanation
To understand how the unit impulse function is obtained from the rectangular function, let's consider a rectangular function with width 2a centered at the origin:
f(t) = 1 for -a ≤ t ≤ a
f(t) = 0 otherwise
Now, let's define a sequence of rectangular functions with decreasing widths:
f1(t) = 1 for -a/2 ≤ t ≤ a/2
f1(t) = 0 otherwise
f2(t) = 1 for -a/4 ≤ t ≤ a/4
f2(t) = 0 otherwise
f3(t) = 1 for -a/8 ≤ t ≤ a/8
f3(t) = 0 otherwise
...
We can observe that as the width of the rectangular function approaches zero, its height approaches infinity in such a way that the area under the curve remains constant. This is the key idea behind the limiting process.
Now, let's define the unit impulse function as the limit of this sequence of rectangular functions as the width approaches zero:
δ(t) = lim [f1(t), f2(t), f3(t), ...]
The unit impulse function is defined such that it is zero for all values of t except at t = 0, where it is infinitely high. However, the area under the curve of the unit impulse function is equal to 1.
Conclusion
In conclusion, the unit impulse function is obtained by using the limiting process on the rectangular function. As the width of the rectangular function approaches zero, its height approaches infinity in such a way that the area under the curve remains constant. This mathematical concept allows us to model an idealized impulse or an infinitesimally short pulse, which is useful in various fields of science and engineering, including signal processing and control systems.
The signal denoted by x(t) is known as - a)discrete time signal
- b)continuous time signal
- c)both (1) and (2)
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
The signal denoted by x(t) is known as
a)
discrete time signal
b)
continuous time signal
c)
both (1) and (2)
d)
None of the above
|
|
Tanya Chauhan answered |
Continuous Time Signal vs Discrete Time Signal
Continuous time signals and discrete time signals are two types of signals that are commonly used in the field of signal processing. The main difference between these two types of signals lies in the way they are defined and represented.
Continuous Time Signal:
A continuous time signal x(t) is defined for all values of time t in a continuous manner. This means that the signal is defined at every instant of time in a continuous fashion. The signal can take on any value at any point in time and can be represented by a continuous function.
Examples of continuous time signals include audio signals, video signals, and most real-world signals that are measured or observed in a continuous manner.
Discrete Time Signal:
A discrete time signal x(n) is defined only at specific points in time. The signal is represented by a sequence of values that are sampled at discrete points in time. These discrete points are usually equally spaced and are represented by an index n.
Examples of discrete time signals include digital audio signals, sampled data from sensors, and most signals that are processed by digital systems.
Explanation of the Correct Answer:
The signal denoted by x(t) is known as a continuous time signal. This is because the signal is denoted by a continuous variable "t" and is defined for all values of time in a continuous manner. The signal can take on any value at any point in time, and its representation would require a continuous function.
The other options provided in the question are not correct because:
- Option (a) states that the signal is a discrete time signal, which is not true.
- Option (c) states that the signal is both a discrete time signal and a continuous time signal, which is not correct. The signal cannot be both at the same time.
- Option (d) states that none of the above options are correct, which is also not true.
Therefore, the correct answer is option (b), which states that the signal denoted by x(t) is a continuous time signal.
Continuous time signals and discrete time signals are two types of signals that are commonly used in the field of signal processing. The main difference between these two types of signals lies in the way they are defined and represented.
Continuous Time Signal:
A continuous time signal x(t) is defined for all values of time t in a continuous manner. This means that the signal is defined at every instant of time in a continuous fashion. The signal can take on any value at any point in time and can be represented by a continuous function.
Examples of continuous time signals include audio signals, video signals, and most real-world signals that are measured or observed in a continuous manner.
Discrete Time Signal:
A discrete time signal x(n) is defined only at specific points in time. The signal is represented by a sequence of values that are sampled at discrete points in time. These discrete points are usually equally spaced and are represented by an index n.
Examples of discrete time signals include digital audio signals, sampled data from sensors, and most signals that are processed by digital systems.
Explanation of the Correct Answer:
The signal denoted by x(t) is known as a continuous time signal. This is because the signal is denoted by a continuous variable "t" and is defined for all values of time in a continuous manner. The signal can take on any value at any point in time, and its representation would require a continuous function.
The other options provided in the question are not correct because:
- Option (a) states that the signal is a discrete time signal, which is not true.
- Option (c) states that the signal is both a discrete time signal and a continuous time signal, which is not correct. The signal cannot be both at the same time.
- Option (d) states that none of the above options are correct, which is also not true.
Therefore, the correct answer is option (b), which states that the signal denoted by x(t) is a continuous time signal.
Y(t) = x(0.5t)- a)Is time shifted signal
- b)Is compressed time signal
- c)Is amplitude scaled signal
- d)Is expanded time scale signal
Correct answer is option 'D'. Can you explain this answer?
Y(t) = x(0.5t)
a)
Is time shifted signal
b)
Is compressed time signal
c)
Is amplitude scaled signal
d)
Is expanded time scale signal
|
|
Sanvi Kapoor answered |
When the α value is less than one in time scaling then the signal is said to be expanded or dilated
Which of the following is an example of amplitude scaling?- a)Electronic amplifier
- b)Electronic attenuator
- c)Both amplifier and attenuator
- d)Adder
Correct answer is option 'C'. Can you explain this answer?
Which of the following is an example of amplitude scaling?
a)
Electronic amplifier
b)
Electronic attenuator
c)
Both amplifier and attenuator
d)
Adder
|
|
Kabir Singhania answered |
Amplitude Scaling
Amplitude scaling refers to the process of adjusting the amplitude or strength of a signal. It is commonly used in electronic circuits to control the magnitude of a signal. There are several devices and techniques that can be employed for amplitude scaling, including electronic amplifiers, electronic attenuators, and adders.
Electronic Amplifier
An electronic amplifier is a device that increases the amplitude of a signal. It takes a weak input signal and produces a larger output signal, thereby amplifying the original signal. Amplifiers are widely used in various applications, such as audio systems, telecommunication systems, and instrumentation.
Amplifiers can be categorized into different types based on their operating characteristics, such as voltage amplifiers, current amplifiers, power amplifiers, and operational amplifiers. Each type of amplifier has its own specific purpose and application.
Electronic Attenuator
An electronic attenuator is a device that reduces the amplitude of a signal. It is used to decrease the strength of a signal without introducing significant distortion or noise. Attenuators are commonly used in communication systems, audio equipment, and test and measurement setups.
Attenuators are available in various configurations, including fixed attenuators and variable attenuators. Fixed attenuators provide a fixed level of attenuation, while variable attenuators allow for adjustable attenuation levels. Attenuators are often expressed in terms of decibels (dB), which indicate the amount of attenuation provided.
Amplitude Scaling using Amplifier and Attenuator
The correct answer to the question is option 'C', which states that both an amplifier and an attenuator are examples of amplitude scaling devices. This means that both devices can be used to adjust the amplitude of a signal, albeit in opposite directions.
An amplifier increases the amplitude of a signal, while an attenuator decreases it. Depending on the requirements of a particular application, either an amplifier or an attenuator can be used to achieve the desired amplitude scaling.
Adder
The option 'D', which suggests an adder as an example of amplitude scaling, is incorrect. An adder is a device used in digital circuits to perform addition operations, such as adding two binary numbers. It is not used for amplitude scaling purposes.
In conclusion, amplitude scaling can be achieved using both amplifiers and attenuators. Amplifiers increase the amplitude of a signal, while attenuators decrease it. These devices are widely used in electronic circuits to control and adjust the strength of a signal, depending on the specific requirements of a given application.
Amplitude scaling refers to the process of adjusting the amplitude or strength of a signal. It is commonly used in electronic circuits to control the magnitude of a signal. There are several devices and techniques that can be employed for amplitude scaling, including electronic amplifiers, electronic attenuators, and adders.
Electronic Amplifier
An electronic amplifier is a device that increases the amplitude of a signal. It takes a weak input signal and produces a larger output signal, thereby amplifying the original signal. Amplifiers are widely used in various applications, such as audio systems, telecommunication systems, and instrumentation.
Amplifiers can be categorized into different types based on their operating characteristics, such as voltage amplifiers, current amplifiers, power amplifiers, and operational amplifiers. Each type of amplifier has its own specific purpose and application.
Electronic Attenuator
An electronic attenuator is a device that reduces the amplitude of a signal. It is used to decrease the strength of a signal without introducing significant distortion or noise. Attenuators are commonly used in communication systems, audio equipment, and test and measurement setups.
Attenuators are available in various configurations, including fixed attenuators and variable attenuators. Fixed attenuators provide a fixed level of attenuation, while variable attenuators allow for adjustable attenuation levels. Attenuators are often expressed in terms of decibels (dB), which indicate the amount of attenuation provided.
Amplitude Scaling using Amplifier and Attenuator
The correct answer to the question is option 'C', which states that both an amplifier and an attenuator are examples of amplitude scaling devices. This means that both devices can be used to adjust the amplitude of a signal, albeit in opposite directions.
An amplifier increases the amplitude of a signal, while an attenuator decreases it. Depending on the requirements of a particular application, either an amplifier or an attenuator can be used to achieve the desired amplitude scaling.
Adder
The option 'D', which suggests an adder as an example of amplitude scaling, is incorrect. An adder is a device used in digital circuits to perform addition operations, such as adding two binary numbers. It is not used for amplitude scaling purposes.
In conclusion, amplitude scaling can be achieved using both amplifiers and attenuators. Amplifiers increase the amplitude of a signal, while attenuators decrease it. These devices are widely used in electronic circuits to control and adjust the strength of a signal, depending on the specific requirements of a given application.
Consider a signal x(t) = 4 cos (2t/3) + 8 sin (0.5t) + 7 sin (t/3 – π/6)Calculate the fundamental period.- a)6π seconds
- b)2π seconds
- c)12π seconds
- d)π seconds
Correct answer is option 'C'. Can you explain this answer?
Consider a signal x(t) = 4 cos (2t/3) + 8 sin (0.5t) + 7 sin (t/3 – π/6)
Calculate the fundamental period.
a)
6π seconds
b)
2π seconds
c)
12π seconds
d)
π seconds
|
|
Siya Goyal answered |
To find the amplitude and frequency components of the given signal x(t), we can break it down into its cosine and sine components separately:
x(t) = 4 cos (2t/3) + 8 sin (0.5t) + 7 sin (t/3)
The amplitude of a cosine or sine function can be found by taking the coefficient in front of it.
For the cosine component:
Amplitude = 4
For the sine components:
Amplitude = 8 for sin (0.5t)
Amplitude = 7 for sin (t/3)
The frequency of a cosine or sine function can be found by taking the coefficient of t inside the function and dividing it by 2π.
For the cosine component:
Frequency = 2/3π
For the sine components:
Frequency = 0.5/2π = 1/4π for sin (0.5t)
Frequency = 1/3π for sin (t/3)
Therefore, the amplitude and frequency components of the given signal x(t) are as follows:
Amplitude:
Cosine component = 4
Sine component 1 = 8
Sine component 2 = 7
Frequency:
Cosine component = 2/3π
Sine component 1 = 1/4π
Sine component 2 = 1/3π
x(t) = 4 cos (2t/3) + 8 sin (0.5t) + 7 sin (t/3)
The amplitude of a cosine or sine function can be found by taking the coefficient in front of it.
For the cosine component:
Amplitude = 4
For the sine components:
Amplitude = 8 for sin (0.5t)
Amplitude = 7 for sin (t/3)
The frequency of a cosine or sine function can be found by taking the coefficient of t inside the function and dividing it by 2π.
For the cosine component:
Frequency = 2/3π
For the sine components:
Frequency = 0.5/2π = 1/4π for sin (0.5t)
Frequency = 1/3π for sin (t/3)
Therefore, the amplitude and frequency components of the given signal x(t) are as follows:
Amplitude:
Cosine component = 4
Sine component 1 = 8
Sine component 2 = 7
Frequency:
Cosine component = 2/3π
Sine component 1 = 1/4π
Sine component 2 = 1/3π
Find the magnitude of exp(jwt). Find the boundness of sin(t) and cos(t).- a)1, [-1,2], [-1,2].
- b)0.5, [-1,1], [-1,1].
- c)1, [-1,1], [-1,2].
- d)1, [-1,1], [-1,1].
Correct answer is option 'D'. Can you explain this answer?
Find the magnitude of exp(jwt). Find the boundness of sin(t) and cos(t).
a)
1, [-1,2], [-1,2].
b)
0.5, [-1,1], [-1,1].
c)
1, [-1,1], [-1,2].
d)
1, [-1,1], [-1,1].
|
|
Aaditya Choudhary answered |
The sin(t)and cos(t) can be found using Euler’s rule.
We define y[n] = nx[n] – (n-1)x[n]. Now, z[n] = z[n-1] + y[n]. Is z[n] a causal system?- a)No
- b)Yes
Correct answer is option 'B'. Can you explain this answer?
We define y[n] = nx[n] – (n-1)x[n]. Now, z[n] = z[n-1] + y[n]. Is z[n] a causal system?
a)
No
b)
Yes
|
|
Hiral Kulkarni answered |
As the value of the function depends solely on the value of the input at a time presently and/or in the past, it is a causal system.
AM radio signal is an example for __________- a)y (t) = a x (t)
- b)y (t) = x1 (t) + x2 (t)
- c)y (t) = x1 (t) * x2 (t)
- d)y (t) = -x(t)
Correct answer is option 'C'. Can you explain this answer?
AM radio signal is an example for __________
a)
y (t) = a x (t)
b)
y (t) = x1 (t) + x2 (t)
c)
y (t) = x1 (t) * x2 (t)
d)
y (t) = -x(t)
|
|
Sarita Yadav answered |
AM radio signal is an example for y (t) = x1 (t) * x2 (t) where, x1 (t) consists of an audio signal plus a dc component and x2 (t) is a sinusoidal signal called carrier wave.
Consider below figure , is the given y (t) an integration of x (t)?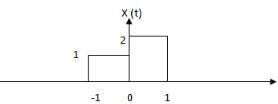
- a)Y (t) = ∫x (t).dt
- b)Y (t) = ∫x2 (t).dt
- c)Y (t) = 3* ∫x (t).dt
- d)Y (t) = 3* ∫x2 (t).dt
Correct answer is option 'A'. Can you explain this answer?
Consider below figure , is the given y (t) an integration of x (t)?

a)
Y (t) = ∫x (t).dt
b)
Y (t) = ∫x2 (t).dt
c)
Y (t) = 3* ∫x (t).dt
d)
Y (t) = 3* ∫x2 (t).dt
|
|
Luminary Institute answered |
The given y (t) is integral of x (t) and amplitude 3 remains constant for t > 1.
It is because of the properties of integration.
It is because of the properties of integration.
We define y[n] = nx[n] – (n-1)x[n]. Now, z[n] = z[n-1] + y[n], is z[n] stable?- a)Yes
- b) No
Correct answer is option 'A'. Can you explain this answer?
We define y[n] = nx[n] – (n-1)x[n]. Now, z[n] = z[n-1] + y[n], is z[n] stable?
a)
Yes
b)
No
|
|
Aaditya Choudhary answered |
As we take the sum of y[n], terms cancel out and deem z[n] to be BIBO stable.
Express the following finite discrete-time signal as the difference of two unit step sequences: x[n] = 1, for 0 ≤ n ≤ 5; and 0 otherwise.- a)u[n] – u[n - 6]
- b)u[n - 5] – u[n - 6]
- c)u[n - 6] – u[n - 5]
- d)u[n] – u[n - 5]
Correct answer is option 'A'. Can you explain this answer?
Express the following finite discrete-time signal as the difference of two unit step sequences: x[n] = 1, for 0 ≤ n ≤ 5; and 0 otherwise.
a)
u[n] – u[n - 6]
b)
u[n - 5] – u[n - 6]
c)
u[n - 6] – u[n - 5]
d)
u[n] – u[n - 5]
|
|
Harshit Thakkar answered |
To express the given finite discrete-time signal as the difference of two unit step sequences, we need to find two unit step sequences that sum up to the given signal.
The unit step sequence u[n] is defined as follows:
u[n] = 1, for n >= 0
u[n] = 0, for n < />
Let's denote the two unit step sequences as u1[n] and u2[n].
u1[n] will represent the step at n = 0, and u2[n] will represent the step at n = N (where N is the last sample of the given signal).
So, u1[n] = u[n] and u2[n] = u[n - N].
Now, let's express the given signal x[n] in terms of the unit step sequences:
x[n] = 1, for 0 <= n=""><=>
0, otherwise
To express x[n] as the difference of two unit step sequences, we can use the following equation:
x[n] = u1[n] - u2[n]
Substituting the expressions for u1[n] and u2[n], we have:
x[n] = u[n] - u[n - N]
Therefore, the given finite discrete-time signal x[n] can be expressed as the difference of two unit step sequences: x[n] = u[n] - u[n - N].
The unit step sequence u[n] is defined as follows:
u[n] = 1, for n >= 0
u[n] = 0, for n < />
Let's denote the two unit step sequences as u1[n] and u2[n].
u1[n] will represent the step at n = 0, and u2[n] will represent the step at n = N (where N is the last sample of the given signal).
So, u1[n] = u[n] and u2[n] = u[n - N].
Now, let's express the given signal x[n] in terms of the unit step sequences:
x[n] = 1, for 0 <= n=""><=>
0, otherwise
To express x[n] as the difference of two unit step sequences, we can use the following equation:
x[n] = u1[n] - u2[n]
Substituting the expressions for u1[n] and u2[n], we have:
x[n] = u[n] - u[n - N]
Therefore, the given finite discrete-time signal x[n] can be expressed as the difference of two unit step sequences: x[n] = u[n] - u[n - N].
Consider the following system ‘S’ where x(n) is the input and y(n) is the output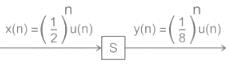
- a)The system s is linear, time invariant, stable.
- b)The system s is non-linear, time variant, unstable.
- c)The system s is non-linear, time invariant, stable.
- d)The system s is non-linear, time variant, stable.
Correct answer is option 'C'. Can you explain this answer?
Consider the following system ‘S’ where x(n) is the input and y(n) is the output

a)
The system s is linear, time invariant, stable.
b)
The system s is non-linear, time variant, unstable.
c)
The system s is non-linear, time invariant, stable.
d)
The system s is non-linear, time variant, stable.
|
|
Yash Patel answered |
Here the input is bounded and the output is also bounded.
Hence the system is stable.
The system is non-linear as it follows y(n) = x3(n).
The system is time-invariant as no operations are made on n.
For a double sided function, which is odd, what will be the integral of the function from -infinity to +infinity equal to?- a)Non-zero Finite
- b)Zero
- c)Infinite
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
For a double sided function, which is odd, what will be the integral of the function from -infinity to +infinity equal to?
a)
Non-zero Finite
b)
Zero
c)
Infinite
d)
None of the mentioned
|
|
Raghav Nambiar answered |
For an odd function, f(-x) = -f(x), thus the integrals will cancel each other, giving zero.
Which of the component performs integration operation?- a)Resistor
- b)Diode
- c)Capacitor
- d)Inductor
Correct answer is option 'C'. Can you explain this answer?
Which of the component performs integration operation?
a)
Resistor
b)
Diode
c)
Capacitor
d)
Inductor
|
|
Ravi Singh answered |
Capacitor performs integration. V (t) developed across capacitor is given by
v (t) = (1/C)* ∫t-∞ i (∂).d∂, I (t) is the current flowing through a capacitor of capacitance C.
v (t) = (1/C)* ∫t-∞ i (∂).d∂, I (t) is the current flowing through a capacitor of capacitance C.
Find where the signal x(t) = 1/(t2 – 3t + 2) finds its maximum value between (1.25, 1.75):- a)1.40
- b)1.45
- c)1.55
- d)1.50
Correct answer is option 'D'. Can you explain this answer?
Find where the signal x(t) = 1/(t2 – 3t + 2) finds its maximum value between (1.25, 1.75):
a)
1.40
b)
1.45
c)
1.55
d)
1.50
|
|
Siddharth Khanna answered |
Differentiate the function for an optima, put it to zero, we will obtain t = 1.5 as the required instant.
Evaluate the following function in terms of t: {integral from 0 to t}{Integral from -inf to inf}d(t)- a) 1⁄t
- b)1⁄t2
- c)t
- d)t2
Correct answer is option 'C'. Can you explain this answer?
Evaluate the following function in terms of t: {integral from 0 to t}{Integral from -inf to inf}d(t)
a)
1⁄t
b)
1⁄t2
c)
t
d)
t2
|
|
Aashna Dey answered |
The first integral is 1, and the overall integral evaluates to t.
Which of the following signals are monotonic in nature?- a)1-exp(-t)
- b)1-exp(sin(t))
- c)log(tan(t))
- d)cos(t)
Correct answer is option 'A'. Can you explain this answer?
Which of the following signals are monotonic in nature?
a)
1-exp(-t)
b)
1-exp(sin(t))
c)
log(tan(t))
d)
cos(t)
|
|
Rajeev Menon answered |
All of the other functions have a periodic element in them, which means the function attains the same value after a period of time, which should not occur for a monotonic function.
Let f(t) be a continuous-time signal and let F(ω) be its Fourier Transform defined by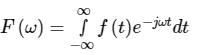 Define g(t) by
Define g(t) by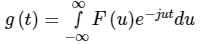 What is the relationship between f(t) and g(t)?
What is the relationship between f(t) and g(t)?- a)g(t) would always be proportional to f(t)
- b)g(t) would be proportional to f(t) if f(t) is an even function
- c)g(t) would be proportional to f(t) only if f(t) is a sinusoidal function
- d)g(t) would never be proportional to f(t)
Correct answer is option 'B'. Can you explain this answer?
Let f(t) be a continuous-time signal and let F(ω) be its Fourier Transform defined by
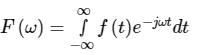
Define g(t) by
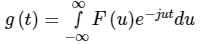
What is the relationship between f(t) and g(t)?
a)
g(t) would always be proportional to f(t)
b)
g(t) would be proportional to f(t) if f(t) is an even function
c)
g(t) would be proportional to f(t) only if f(t) is a sinusoidal function
d)
g(t) would never be proportional to f(t)
|
|
Ravi Singh answered |
Given the Fourier transform pair,
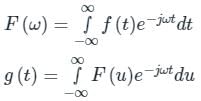
The Inverse Fourier transform of F (ω) is given as
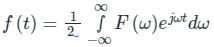
Replacing t by ‘ –t ‘ and ω by u in the above expression, we have,
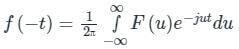
If f (t) is even, then f (-t) = f (t)
∴ g (t) = 2π f (t)
⇒ g (t) will be proportional to f (t), if f (t) is an even function.
Discrete-time signals are ________- a)Continuous in amplitude and continuous in time
- b)Continuous in amplitude and discrete in time
- c)Discrete in amplitude and discrete in time
- d)Discrete in amplitude and continuous in time
Correct answer is option 'B'. Can you explain this answer?
Discrete-time signals are ________
a)
Continuous in amplitude and continuous in time
b)
Continuous in amplitude and discrete in time
c)
Discrete in amplitude and discrete in time
d)
Discrete in amplitude and continuous in time
|
|
Ananya Kapoor answered |
Discrete-time signals are Continuous in amplitude and discrete in time
Definition of Discrete-time Signals:
A discrete-time signal is a sequence of values that is defined only at specific points in time. The values of a discrete-time signal are usually represented as amplitudes at equally spaced time intervals. These time intervals are discrete and separated by a fixed duration.
Explanation:
To understand why discrete-time signals are continuous in amplitude and discrete in time, let's break down the characteristics of these signals.
Continuous in amplitude:
- Amplitude refers to the magnitude or intensity of the signal.
- In discrete-time signals, the amplitude is continuous, meaning it can take on any value within a certain range.
- For example, if we have a discrete-time signal representing the temperature of a room, the amplitude can be any real number within the range of possible temperatures.
Discrete in time:
- Time refers to the instances or points at which the signal is defined.
- In discrete-time signals, the time is discrete, meaning it is defined only at specific points or intervals.
- These intervals are equally spaced and separated by a fixed duration.
- For example, if we have a discrete-time signal representing the voltage of an electrical circuit, the time instances could be measured every second, and the signal would be defined only at those specific time points.
Illustration:
Let's consider an example to further illustrate this concept. Suppose we have a discrete-time signal representing the daily temperature readings at noon for a week. The signal values would be the temperatures recorded at noon each day, and the time instances would be the days of the week.
- The amplitude of the signal would represent the temperature values, which can take on any real number within the range of possible temperatures.
- The time instances would be discrete and separated by a fixed duration of one day.
Conclusion:
In summary, discrete-time signals are continuous in amplitude because they can take on any value within a certain range. However, they are discrete in time because they are defined only at specific points or intervals, which are equally spaced and separated by a fixed duration.
Definition of Discrete-time Signals:
A discrete-time signal is a sequence of values that is defined only at specific points in time. The values of a discrete-time signal are usually represented as amplitudes at equally spaced time intervals. These time intervals are discrete and separated by a fixed duration.
Explanation:
To understand why discrete-time signals are continuous in amplitude and discrete in time, let's break down the characteristics of these signals.
Continuous in amplitude:
- Amplitude refers to the magnitude or intensity of the signal.
- In discrete-time signals, the amplitude is continuous, meaning it can take on any value within a certain range.
- For example, if we have a discrete-time signal representing the temperature of a room, the amplitude can be any real number within the range of possible temperatures.
Discrete in time:
- Time refers to the instances or points at which the signal is defined.
- In discrete-time signals, the time is discrete, meaning it is defined only at specific points or intervals.
- These intervals are equally spaced and separated by a fixed duration.
- For example, if we have a discrete-time signal representing the voltage of an electrical circuit, the time instances could be measured every second, and the signal would be defined only at those specific time points.
Illustration:
Let's consider an example to further illustrate this concept. Suppose we have a discrete-time signal representing the daily temperature readings at noon for a week. The signal values would be the temperatures recorded at noon each day, and the time instances would be the days of the week.
- The amplitude of the signal would represent the temperature values, which can take on any real number within the range of possible temperatures.
- The time instances would be discrete and separated by a fixed duration of one day.
Conclusion:
In summary, discrete-time signals are continuous in amplitude because they can take on any value within a certain range. However, they are discrete in time because they are defined only at specific points or intervals, which are equally spaced and separated by a fixed duration.
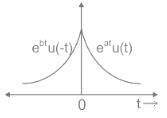
The impulse response h(t) of a continuous time, linear time invariant system is described by h(t) = eat u(t) + ebt u(-t) where, u(t) denots the unit step function and a and b are real constants. This system is stable if - a)both a and b are positive
- b)a is positive and b is negative
- c)a is negative and b is positive
- d)both a and b are negative
Correct answer is option 'C'. Can you explain this answer?
The impulse response h(t) of a continuous time, linear time invariant system is described by h(t) = eat u(t) + ebt u(-t) where, u(t) denots the unit step function and a and b are real constants. This system is stable if
a)
both a and b are positive
b)
a is positive and b is negative
c)
a is negative and b is positive
d)
both a and b are negative
|
|
Sanvi Kapoor answered |
Concept:
An LTI system is stable if and only if its impulse response is absolutely integrable.
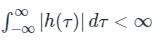
Calculation:
Given,
h(t) = eat u(t) + ebt u(-t)
h(t) = h1(t) + h2(t)
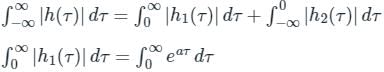
∵ τ > 0 therefore, for absolute integrability a < 0
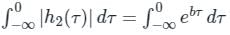
∵ τ < 0 therefore, for absolute integrability b > 0
∴ h(t) should be in the form shown in the figure below:
Which of the following is NOT one of the representations of discrete-time signals?- a)Sequence representation
- b)Graphical representation
- c)Analytical representation
- d)Tabular representation
Correct answer is option 'C'. Can you explain this answer?
Which of the following is NOT one of the representations of discrete-time signals?
a)
Sequence representation
b)
Graphical representation
c)
Analytical representation
d)
Tabular representation
|
|
Aadhya Sharma answered |
Introduction:
Discrete-time signals are signals that are defined at distinct points in time. They are commonly used in digital signal processing and are represented in various ways to facilitate analysis and processing. This question asks us to identify the representation of discrete-time signals that is NOT one of the standard representations.
Explanation:
The various representations of discrete-time signals are as follows:
a) Sequence representation:
A sequence is a discrete-time signal that is represented by a set of numbers arranged in a specific order. It is the most fundamental representation of a discrete-time signal and provides the actual values of the signal at each point in time.
b) Graphical representation:
Graphical representation involves plotting the values of a discrete-time signal on a graph, with time on the x-axis and signal amplitude on the y-axis. This representation helps visualize the signal and can provide insights into its characteristics and behavior.
c) Analytical representation:
Analytical representation refers to expressing a discrete-time signal in terms of a mathematical function or equation. This representation is often used when the signal can be described by a known mathematical model or when analyzing the signal using mathematical techniques.
d) Tabular representation:
Tabular representation involves presenting the values of a discrete-time signal in a table format, with time and corresponding signal values listed in rows or columns. This representation is useful for organizing and comparing the values of the signal at different points in time.
Conclusion:
Among the given options, the representation of discrete-time signals that is NOT standard is the 'Analytical representation'. While sequences, graphical representation, and tabular representation are commonly used to describe and analyze discrete-time signals, analytical representation is not a commonly employed method.
Discrete-time signals are signals that are defined at distinct points in time. They are commonly used in digital signal processing and are represented in various ways to facilitate analysis and processing. This question asks us to identify the representation of discrete-time signals that is NOT one of the standard representations.
Explanation:
The various representations of discrete-time signals are as follows:
a) Sequence representation:
A sequence is a discrete-time signal that is represented by a set of numbers arranged in a specific order. It is the most fundamental representation of a discrete-time signal and provides the actual values of the signal at each point in time.
b) Graphical representation:
Graphical representation involves plotting the values of a discrete-time signal on a graph, with time on the x-axis and signal amplitude on the y-axis. This representation helps visualize the signal and can provide insights into its characteristics and behavior.
c) Analytical representation:
Analytical representation refers to expressing a discrete-time signal in terms of a mathematical function or equation. This representation is often used when the signal can be described by a known mathematical model or when analyzing the signal using mathematical techniques.
d) Tabular representation:
Tabular representation involves presenting the values of a discrete-time signal in a table format, with time and corresponding signal values listed in rows or columns. This representation is useful for organizing and comparing the values of the signal at different points in time.
Conclusion:
Among the given options, the representation of discrete-time signals that is NOT standard is the 'Analytical representation'. While sequences, graphical representation, and tabular representation are commonly used to describe and analyze discrete-time signals, analytical representation is not a commonly employed method.
What is the value of d[0], such that d[n] is the unit impulse function?- a)0
- b)0.5
- c)1.5
- d)1
Correct answer is option 'D'. Can you explain this answer?
What is the value of d[0], such that d[n] is the unit impulse function?
a)
0
b)
0.5
c)
1.5
d)
1
|
|
Prisha Kulkarni answered |
The unit impulse function has value 1 at n = 0 and zero everywhere else.
Determine the value of the summation: ∑∞n= -∞ δ(n + 3)(n2 + n).- a)3
- b)6
- c)9
- d)12
Correct answer is option 'B'. Can you explain this answer?
Determine the value of the summation: ∑∞n= -∞ δ(n + 3)(n2 + n).
a)
3
b)
6
c)
9
d)
12
|
|
Lekha Malhotra answered |
To determine the value of the summation, you need to provide the specific equation or numbers that are being summed. Please provide more information.
The special case of a finite-duration sequence is given as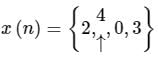 The sequence x(n) into a sum of weighted impulse sequences will be
The sequence x(n) into a sum of weighted impulse sequences will be- a)2δ(n + 1) + 4δ(n) + 3δ(n – 2)
- b)2δ(n) + 4δ(n –1) + 3δ(n – 3)
- c)2δ(n) + 4δ(n –1) + 3δ(n – 2)
- d)2δ(n + 1) + 4δ(n) + 3δ(n – 1)
Correct answer is option 'A'. Can you explain this answer?
The special case of a finite-duration sequence is given as
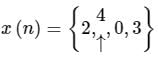
The sequence x(n) into a sum of weighted impulse sequences will be
a)
2δ(n + 1) + 4δ(n) + 3δ(n – 2)
b)
2δ(n) + 4δ(n –1) + 3δ(n – 3)
c)
2δ(n) + 4δ(n –1) + 3δ(n – 2)
d)
2δ(n + 1) + 4δ(n) + 3δ(n – 1)
|
|
Sarita Yadav answered |
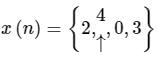
The arrow indicates the origin. This can be represented as:
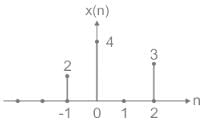
In terms of unit impulse sequences, this can be represented as:
x(n) = 2δ(n + 1) + 4δ(n) + 3δ(n – 2)
The function y[n] = sin(x[n]) is periodic - a)True
- b) False
Correct answer is option 'B'. Can you explain this answer?
The function y[n] = sin(x[n]) is periodic
a)
True
b)
False
|
|
Kalyan Patel answered |
‘y’ will be periodic only if x attains the same value after some time, T. However, if x is a one-one discrete function, it may not be possible for some x[n].
Y (t) = x (2t) is ________- a)Compressed signal
- b)Expanded signal
- c)Shifted signal
- d)Amplitude scaled signal by a factor of 2
Correct answer is option 'A'. Can you explain this answer?
Y (t) = x (2t) is ________
a)
Compressed signal
b)
Expanded signal
c)
Shifted signal
d)
Amplitude scaled signal by a factor of 2

|
Shivani Yadav answered |
Compressed signal
Explanation:
- The given signal is Y(t) = x(2t), which means the input signal x(t) is being multiplied by a factor of 2 in the argument of t.
- This leads to a compression of the signal in the time domain. This is because the same input signal is being represented in a shorter time duration.
- To understand this, let us consider an example. Suppose x(t) is a signal that represents a sine wave with a period of T seconds. If we apply the transformation Y(t) = x(2t), then the resulting signal will have a period of T/2 seconds. This is because the time axis has been compressed by a factor of 2.
- Therefore, we can conclude that the given signal Y(t) = x(2t) is a compressed signal.
Explanation:
- The given signal is Y(t) = x(2t), which means the input signal x(t) is being multiplied by a factor of 2 in the argument of t.
- This leads to a compression of the signal in the time domain. This is because the same input signal is being represented in a shorter time duration.
- To understand this, let us consider an example. Suppose x(t) is a signal that represents a sine wave with a period of T seconds. If we apply the transformation Y(t) = x(2t), then the resulting signal will have a period of T/2 seconds. This is because the time axis has been compressed by a factor of 2.
- Therefore, we can conclude that the given signal Y(t) = x(2t) is a compressed signal.
Which of these operations doesn’t affect the amplitude of the signal:- a)Time reversal
- b)Amplitude scaling
- c)Signal addition
- d)Signal multiplication
Correct answer is option 'A'. Can you explain this answer?
Which of these operations doesn’t affect the amplitude of the signal:
a)
Time reversal
b)
Amplitude scaling
c)
Signal addition
d)
Signal multiplication
|
|
Ravi Singh answered |
In time reversal only the time variable is affected and not the amplitude.
Determine the discrete-time signal: x(n) = 1 for n ≥ 0 and x(n) = 0 for n < 0- a)Unit ramp sequence
- b)Unit impulse sequence
- c)Exponential sequence
- d)Unit step sequence
Correct answer is option 'D'. Can you explain this answer?
Determine the discrete-time signal: x(n) = 1 for n ≥ 0 and x(n) = 0 for n < 0
a)
Unit ramp sequence
b)
Unit impulse sequence
c)
Exponential sequence
d)
Unit step sequence
|
|
Urvashi Verma answered |
Since the condition for the signal is given as "x(n) = 1 for n < 0",="" this="" means="" that="" the="" signal="" is="" equal="" to="" 1="" for="" all="" negative="" values="" of="" n.="" in="" other="" words,="" the="" signal="" is="" non-zero="" only="" for="" negative="" values="" of="" n.="" 0",="" this="" means="" that="" the="" signal="" is="" equal="" to="" 1="" for="" all="" negative="" values="" of="" n.="" in="" other="" words,="" the="" signal="" is="" non-zero="" only="" for="" negative="" values="" of="" />
Determine the product of two signals: x1 (n) = {2, 1, 1.5, 3}; x2 (n) = { 1, 1.5, 0, 2}.- a){2, 1.5, 0, 6}
- b){2, 1.5, 6, 0}
- c){2, 0, 1.5, 6}
- d){2, 1.5, 0, 3}
Correct answer is option 'A'. Can you explain this answer?
Determine the product of two signals: x1 (n) = {2, 1, 1.5, 3}; x2 (n) = { 1, 1.5, 0, 2}.
a)
{2, 1.5, 0, 6}
b)
{2, 1.5, 6, 0}
c)
{2, 0, 1.5, 6}
d)
{2, 1.5, 0, 3}
|
|
Rahul Ahuja answered |
Given:
Two signals: x1(n) = {2, 1, 1.5, 3} and x2(n) = {1, 1.5, 0, 2}.
To Find:
The product of the two signals.
Solution:
To find the product of two signals, we need to multiply the corresponding elements of the two signals.
Given x1(n) = {2, 1, 1.5, 3} and x2(n) = {1, 1.5, 0, 2}, the product of the two signals can be calculated as follows:
x1(n) * x2(n) = {2 * 1, 1 * 1.5, 1.5 * 0, 3 * 2}
= {2, 1.5, 0, 6}
Therefore, the product of the two signals x1(n) and x2(n) is {2, 1.5, 0, 6}.
Answer:
The correct answer is option A) {2, 1.5, 0, 6}.
Two signals: x1(n) = {2, 1, 1.5, 3} and x2(n) = {1, 1.5, 0, 2}.
To Find:
The product of the two signals.
Solution:
To find the product of two signals, we need to multiply the corresponding elements of the two signals.
Given x1(n) = {2, 1, 1.5, 3} and x2(n) = {1, 1.5, 0, 2}, the product of the two signals can be calculated as follows:
x1(n) * x2(n) = {2 * 1, 1 * 1.5, 1.5 * 0, 3 * 2}
= {2, 1.5, 0, 6}
Therefore, the product of the two signals x1(n) and x2(n) is {2, 1.5, 0, 6}.
Answer:
The correct answer is option A) {2, 1.5, 0, 6}.
The condition for periodicity of continuous time signal is:- a)x(t) = x(t + T0)
- b)x(t) = 1/(x(t - T0))
- c)x(t) = x(t - T0)
- d)x(t) = 1/(x(t + T0))
Correct answer is option 'A'. Can you explain this answer?
The condition for periodicity of continuous time signal is:
a)
x(t) = x(t + T0)
b)
x(t) = 1/(x(t - T0))
c)
x(t) = x(t - T0)
d)
x(t) = 1/(x(t + T0))
|
|
Advika Yadav answered |
Periodicity of Continuous Time Signal
The condition for periodicity of a continuous time signal x(t) is given by the equation x(t) = x(t + T0), where T0 is the period of the signal.
Explanation
- Periodicity in a continuous time signal means that the signal repeats itself after a certain interval.
- The condition x(t) = x(t + T0) means that the signal value at any time t is equal to the signal value at time t + T0.
- This condition ensures that the signal repeats itself every T0 seconds.
- If this condition is satisfied, then the signal is said to be periodic with a period of T0.
Therefore, the correct condition for periodicity of a continuous time signal is x(t) = x(t + T0) (option 'A').
The condition for periodicity of a continuous time signal x(t) is given by the equation x(t) = x(t + T0), where T0 is the period of the signal.
Explanation
- Periodicity in a continuous time signal means that the signal repeats itself after a certain interval.
- The condition x(t) = x(t + T0) means that the signal value at any time t is equal to the signal value at time t + T0.
- This condition ensures that the signal repeats itself every T0 seconds.
- If this condition is satisfied, then the signal is said to be periodic with a period of T0.
Therefore, the correct condition for periodicity of a continuous time signal is x(t) = x(t + T0) (option 'A').
How is a linear function described as?- a)Zero in Finite out
- b)Zero in infinite out
- c)Zero in zero out
- d)Zero in Negative out
Correct answer is option 'C'. Can you explain this answer?
How is a linear function described as?
a)
Zero in Finite out
b)
Zero in infinite out
c)
Zero in zero out
d)
Zero in Negative out
|
|
Ravi Singh answered |
The system needs to give a zero output for a zero input so as to conserve the law of additivity, to ensure linearity.
Compute d[n]d[n-1] + d[n-1]d[n-2] for n = 0, 1, 2.- a)0, 1, 2
- b)0, 0, 1
- c)1, 0, 0
- d)0, 0, 0
Correct answer is option 'D'. Can you explain this answer?
Compute d[n]d[n-1] + d[n-1]d[n-2] for n = 0, 1, 2.
a)
0, 1, 2
b)
0, 0, 1
c)
1, 0, 0
d)
0, 0, 0
|
|
Saumya Basak answered |
Only one of the values can be one at a time, others will be forced to zero, due to the delta function.
Which of the following is an example of physical device which adds the signals?- a)Radio
- b)Audio mixer
- c)Frequency divider
- d)Subtractor
Correct answer is option 'B'. Can you explain this answer?
Which of the following is an example of physical device which adds the signals?
a)
Radio
b)
Audio mixer
c)
Frequency divider
d)
Subtractor
|
|
Eesha Kapoor answered |
Introduction:
An audio mixer is a physical device that combines and processes audio signals from multiple sources. It allows for control over the volume, tone, and other audio parameters of each input signal. The mixer then adds these signals together to create a final output signal.
Explanation:
An audio mixer is an example of a physical device that adds signals. Let's understand why it is the correct answer.
1. Radio:
A radio is a device that receives radio signals and converts them into audio signals. However, it does not add signals together. It simply receives and plays the signals.
2. Audio Mixer:
An audio mixer, also known as a mixing console or soundboard, is designed to combine and manipulate multiple audio signals. It typically has several input channels, each capable of accepting an audio signal from a different source. These sources can include microphones, musical instruments, and playback devices.
3. Frequency Divider:
A frequency divider is a circuit or device that takes an input signal and divides its frequency by a certain factor. It is commonly used in digital systems and communication applications. However, it does not add signals together.
4. Subtractor:
A subtractor is a circuit or device that performs the mathematical operation of subtraction. It takes two input signals and produces an output signal that is the difference between the two inputs. It does not add signals together.
Conclusion:
Among the given options, the audio mixer is the only device that adds signals together. It is commonly used in audio production, live sound reinforcement, and recording studios to mix multiple audio sources into a final output signal.
An audio mixer is a physical device that combines and processes audio signals from multiple sources. It allows for control over the volume, tone, and other audio parameters of each input signal. The mixer then adds these signals together to create a final output signal.
Explanation:
An audio mixer is an example of a physical device that adds signals. Let's understand why it is the correct answer.
1. Radio:
A radio is a device that receives radio signals and converts them into audio signals. However, it does not add signals together. It simply receives and plays the signals.
2. Audio Mixer:
An audio mixer, also known as a mixing console or soundboard, is designed to combine and manipulate multiple audio signals. It typically has several input channels, each capable of accepting an audio signal from a different source. These sources can include microphones, musical instruments, and playback devices.
3. Frequency Divider:
A frequency divider is a circuit or device that takes an input signal and divides its frequency by a certain factor. It is commonly used in digital systems and communication applications. However, it does not add signals together.
4. Subtractor:
A subtractor is a circuit or device that performs the mathematical operation of subtraction. It takes two input signals and produces an output signal that is the difference between the two inputs. It does not add signals together.
Conclusion:
Among the given options, the audio mixer is the only device that adds signals together. It is commonly used in audio production, live sound reinforcement, and recording studios to mix multiple audio sources into a final output signal.
What is the time period of the function x[n] = exp(jwn)?- a)pi/2w
- b)pi/w
- c)2pi/w
- d)4pi/w
Correct answer is option 'C'. Can you explain this answer?
What is the time period of the function x[n] = exp(jwn)?
a)
pi/2w
b)
pi/w
c)
2pi/w
d)
4pi/w
|
|
Sharmila Kulkarni answered |
The given function x[n] = exp(jwn) represents a discrete-time complex exponential signal. Let's break down the components of this function and understand its properties.
Components of the function:
- n: The variable n represents the discrete time index. It takes on integer values and represents different time instances in the sequence.
- w: The variable w represents the angular frequency of the signal. It determines the rate at which the complex exponential oscillates.
- j: The symbol j represents the imaginary unit (√(-1)).
Understanding the time period:
The time period of a function represents the smallest interval after which the function repeats itself. In this case, we need to find the time period of the given function x[n] = exp(jwn).
To find the time period, we need to determine the values of n for which the function repeats itself. In other words, we need to find the smallest positive integer value of n such that x[n] is equal to x[n + T], where T represents the time period.
Let's evaluate x[n + T]:
x[n + T] = exp(jw(n + T))
= exp(jwn + jwt)
For the function to repeat itself, x[n] should be equal to x[n + T]. Therefore, we have the equation:
exp(jwn) = exp(jwn + jwt)
To solve this equation, we can equate the arguments (exponentials) to each other:
jwn = jwn + jwt
Now, we can cancel out the jwn terms:
0 = jwt
Since j is not equal to 0, we can divide both sides of the equation by jw:
0 = t
This indicates that the time period T is 0. However, the time period cannot be zero because it would mean that the function does not repeat itself. Therefore, we need to consider the next possible value for T.
The next possible value for T is when jwt is equal to a multiple of 2π. This ensures that the exponential term repeats itself. Therefore, we have the equation:
jwt = 2πk, where k is an integer
Now, we can solve for T:
T = 2πk / w
Since we are looking for the smallest positive value of T, the smallest positive value for k should be 1. Therefore, the time period T is given by:
T = 2π / w
Comparing the options:
a) pi/2w
b) pi/w
c) 2pi/w
d) 4pi/w
The correct answer is option 'C', 2π/w, which matches the derived expression for the time period T.
Components of the function:
- n: The variable n represents the discrete time index. It takes on integer values and represents different time instances in the sequence.
- w: The variable w represents the angular frequency of the signal. It determines the rate at which the complex exponential oscillates.
- j: The symbol j represents the imaginary unit (√(-1)).
Understanding the time period:
The time period of a function represents the smallest interval after which the function repeats itself. In this case, we need to find the time period of the given function x[n] = exp(jwn).
To find the time period, we need to determine the values of n for which the function repeats itself. In other words, we need to find the smallest positive integer value of n such that x[n] is equal to x[n + T], where T represents the time period.
Let's evaluate x[n + T]:
x[n + T] = exp(jw(n + T))
= exp(jwn + jwt)
For the function to repeat itself, x[n] should be equal to x[n + T]. Therefore, we have the equation:
exp(jwn) = exp(jwn + jwt)
To solve this equation, we can equate the arguments (exponentials) to each other:
jwn = jwn + jwt
Now, we can cancel out the jwn terms:
0 = jwt
Since j is not equal to 0, we can divide both sides of the equation by jw:
0 = t
This indicates that the time period T is 0. However, the time period cannot be zero because it would mean that the function does not repeat itself. Therefore, we need to consider the next possible value for T.
The next possible value for T is when jwt is equal to a multiple of 2π. This ensures that the exponential term repeats itself. Therefore, we have the equation:
jwt = 2πk, where k is an integer
Now, we can solve for T:
T = 2πk / w
Since we are looking for the smallest positive value of T, the smallest positive value for k should be 1. Therefore, the time period T is given by:
T = 2π / w
Comparing the options:
a) pi/2w
b) pi/w
c) 2pi/w
d) 4pi/w
The correct answer is option 'C', 2π/w, which matches the derived expression for the time period T.
In discrete signal, if y [n] = x [k x n] and k > 1 then ______- a)Some samples are lost from x [n]
- b)Some samples are added to x [n]
- c)It has no effect on samples
- d)Samples will be increased with factor k
Correct answer is option 'A'. Can you explain this answer?
In discrete signal, if y [n] = x [k x n] and k > 1 then ______
a)
Some samples are lost from x [n]
b)
Some samples are added to x [n]
c)
It has no effect on samples
d)
Samples will be increased with factor k
|
|
Gia Bhatia answered |
Is an integer greater than 1, this means that the output signal y[n] is obtained by stretching or compressing the input signal x[n] along the time axis by a factor of k.
For example, if k = 2, then the output signal y[n] will be obtained by stretching the input signal x[n] by a factor of 2. This means that the samples of y[n] will occur at every other sample position of x[n].
Similarly, if k = 0.5, then the output signal y[n] will be obtained by compressing the input signal x[n] by a factor of 0.5. This means that the samples of y[n] will occur at twice the rate as the samples of x[n].
In general, the value of k determines the rate at which the input signal x[n] is stretched or compressed to obtain the output signal y[n] in discrete time.
For example, if k = 2, then the output signal y[n] will be obtained by stretching the input signal x[n] by a factor of 2. This means that the samples of y[n] will occur at every other sample position of x[n].
Similarly, if k = 0.5, then the output signal y[n] will be obtained by compressing the input signal x[n] by a factor of 0.5. This means that the samples of y[n] will occur at twice the rate as the samples of x[n].
In general, the value of k determines the rate at which the input signal x[n] is stretched or compressed to obtain the output signal y[n] in discrete time.
The operation performed in which a new signals is defined by adding/subtracting a finite time value from it is- a)Time Shifting
- b)Amplitude scaling
- c)Time scaling
- d)Signal multiplication
Correct answer is option 'A'. Can you explain this answer?
The operation performed in which a new signals is defined by adding/subtracting a finite time value from it is
a)
Time Shifting
b)
Amplitude scaling
c)
Time scaling
d)
Signal multiplication
|
|
Sarita Yadav answered |
In time signal finite time value is added or subtracted from it.
For the signal x(t) = a – b*exp(-ct), what is the steady state value, and the initial value?- a)c, b
- b)c, c-a
- c)a, a-b
- d)b, a-b
Correct answer is option 'C'. Can you explain this answer?
For the signal x(t) = a – b*exp(-ct), what is the steady state value, and the initial value?
a)
c, b
b)
c, c-a
c)
a, a-b
d)
b, a-b
|
|
Anshika Nambiar answered |
Put the limits as t tends to infinity and as t tends to zero.
For a bounded function, is the integral of the function from -infinity to +infinity defined and finite?- a)Yes
- b)Never
- c)Not always
- d)None of the mentioned
Correct answer is option 'C'. Can you explain this answer?
For a bounded function, is the integral of the function from -infinity to +infinity defined and finite?
a)
Yes
b)
Never
c)
Not always
d)
None of the mentioned
|
|
Abhay Khanna answered |
The correct answer is option 'C' - Not always.
Explanation:
A bounded function is a function that has a finite range. In other words, the function does not take on values that go to infinity or negative infinity.
When we talk about the integral of a bounded function from -infinity to infinity, we are referring to the improper integral. The improper integral is defined as the limit of the definite integral as the limits of integration approach infinity and negative infinity.
In some cases, the integral of a bounded function from -infinity to infinity may be defined and finite. This occurs when the function has a well-behaved behavior as the limits of integration go to infinity and negative infinity.
However, there are cases when the integral of a bounded function from -infinity to infinity is not defined or is infinite. This happens when the function has oscillations, or when it approaches infinity or negative infinity as the limits of integration are reached.
For example, consider the function f(x) = sin(x) / x. This function is bounded because the range of sin(x) is between -1 and 1, and dividing by x does not change the boundedness. However, the integral of this function from -infinity to infinity is not defined because it oscillates and does not converge to a finite value.
Therefore, the integral of a bounded function from -infinity to infinity is not always defined and finite. It depends on the behavior of the function as the limits of integration approach infinity and negative infinity.
Explanation:
A bounded function is a function that has a finite range. In other words, the function does not take on values that go to infinity or negative infinity.
When we talk about the integral of a bounded function from -infinity to infinity, we are referring to the improper integral. The improper integral is defined as the limit of the definite integral as the limits of integration approach infinity and negative infinity.
In some cases, the integral of a bounded function from -infinity to infinity may be defined and finite. This occurs when the function has a well-behaved behavior as the limits of integration go to infinity and negative infinity.
However, there are cases when the integral of a bounded function from -infinity to infinity is not defined or is infinite. This happens when the function has oscillations, or when it approaches infinity or negative infinity as the limits of integration are reached.
For example, consider the function f(x) = sin(x) / x. This function is bounded because the range of sin(x) is between -1 and 1, and dividing by x does not change the boundedness. However, the integral of this function from -infinity to infinity is not defined because it oscillates and does not converge to a finite value.
Therefore, the integral of a bounded function from -infinity to infinity is not always defined and finite. It depends on the behavior of the function as the limits of integration approach infinity and negative infinity.
Is the signal x(t) = exp(-t)*sin(t) periodic in nature?- a)Yes
- b)No
Correct answer is option 'B'. Can you explain this answer?
Is the signal x(t) = exp(-t)*sin(t) periodic in nature?
a)
Yes
b)
No

|
Himanshu Prasad answered |
Though sin(t) is a periodic function, exp(-t) is not a periodic function, thus leading to non-periodicity.
Time scaling is an operation performed on- a)Independent variable
- b)Dependent variable
- c)Neither
- d)Both
Correct answer is option 'A'. Can you explain this answer?
Time scaling is an operation performed on
a)
Independent variable
b)
Dependent variable
c)
Neither
d)
Both
|
|
Diya Choudhary answered |
Understanding Time Scaling
Time scaling is a fundamental operation in signal processing and systems analysis, particularly relevant in the field of Electronics and Communication Engineering (ECE).
What is Time Scaling?
Time scaling involves modifying the time variable in a function, which is typically represented as the independent variable in mathematical equations. This operation adjusts the speed at which a signal is processed or observed.
Why is it Applied to the Independent Variable?
- Independent Variable Role: In the context of functions, the independent variable (usually time) dictates the input to the system or signal.
- Impact on Signal Characteristics: By scaling time, the characteristics of the signal, such as frequency and duration, are altered. For instance, if a signal is compressed in time, its frequency increases, leading to a higher pitch in audio signals.
Examples of Time Scaling
- Compression: If a signal x(t) is compressed in time to x(at), where 'a' is a positive constant greater than 1, the signal occurrence happens faster, effectively increasing its frequency.
- Expansion: Conversely, expanding the signal, x(t/a) for 'a' greater than 1, stretches the signal in time, decreasing the frequency.
Conclusion
Since time scaling modifies the time axis while keeping the dependent variable (output) intact, it is specifically an operation performed on the independent variable. This understanding is crucial for analyzing and designing systems in signal processing and communication engineering.
Time scaling is a fundamental operation in signal processing and systems analysis, particularly relevant in the field of Electronics and Communication Engineering (ECE).
What is Time Scaling?
Time scaling involves modifying the time variable in a function, which is typically represented as the independent variable in mathematical equations. This operation adjusts the speed at which a signal is processed or observed.
Why is it Applied to the Independent Variable?
- Independent Variable Role: In the context of functions, the independent variable (usually time) dictates the input to the system or signal.
- Impact on Signal Characteristics: By scaling time, the characteristics of the signal, such as frequency and duration, are altered. For instance, if a signal is compressed in time, its frequency increases, leading to a higher pitch in audio signals.
Examples of Time Scaling
- Compression: If a signal x(t) is compressed in time to x(at), where 'a' is a positive constant greater than 1, the signal occurrence happens faster, effectively increasing its frequency.
- Expansion: Conversely, expanding the signal, x(t/a) for 'a' greater than 1, stretches the signal in time, decreasing the frequency.
Conclusion
Since time scaling modifies the time axis while keeping the dependent variable (output) intact, it is specifically an operation performed on the independent variable. This understanding is crucial for analyzing and designing systems in signal processing and communication engineering.
What is the value of u[1], where u[n] is the unit step function?- a)1
- b)0.5
- c)0
- d)-1
Correct answer is option 'A'. Can you explain this answer?
What is the value of u[1], where u[n] is the unit step function?
a)
1
b)
0.5
c)
0
d)
-1
|
|
Aaditya Choudhary answered |
The unit step function u[n] = 1 for all n>=0, hence u[1] = 1.
Chapter doubts & questions for Communicating with Signals - Science for Grade 8 2025 is part of Grade 8 exam preparation. The chapters have been prepared according to the Grade 8 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 8 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Communicating with Signals - Science for Grade 8 in English & Hindi are available as part of Grade 8 exam.
Download more important topics, notes, lectures and mock test series for Grade 8 Exam by signing up for free.
Science for Grade 8
76 videos|170 docs|65 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily

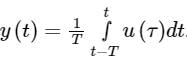 . If the input u is a sinusoidal signal of frequency
. If the input u is a sinusoidal signal of frequency  , then in steady state, the output will lag u (in degree) by
, then in steady state, the output will lag u (in degree) by