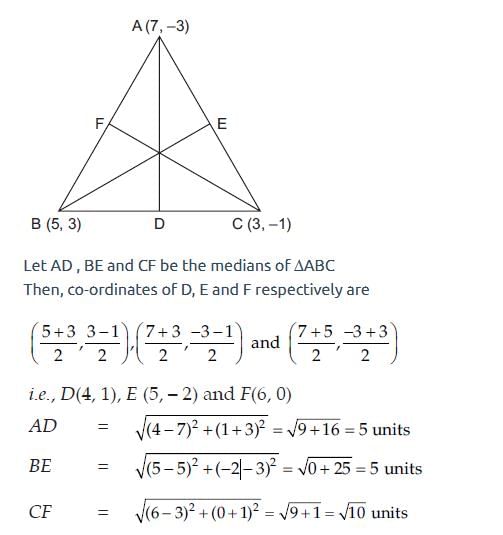
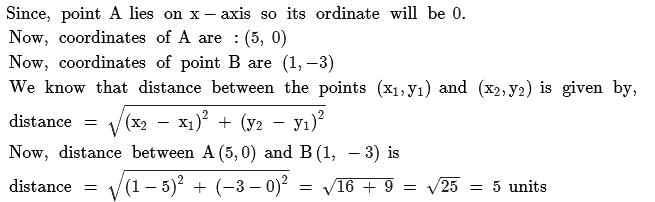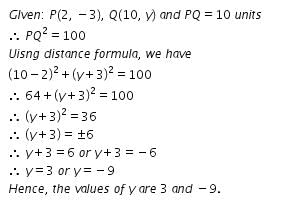All Exams >
ACT >
Mathematics for ACT >
All Questions
All questions of Coordinate Geometry for ACT Exam
The line  intersects the y-axis at the point P and the line
intersects the y-axis at the point P and the line 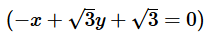 intersects the y-axis at the
intersects the y-axis at the
point R. If these two lines intersect at point Q, what is the measure of ∠PQR?- a)15o
- b)30o
- c)60o
- d)75o
- e)90o
Correct answer is option 'D'. Can you explain this answer?
The line  intersects the y-axis at the point P and the line
intersects the y-axis at the point P and the line 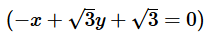 intersects the y-axis at the
intersects the y-axis at the
point R. If these two lines intersect at point Q, what is the measure of ∠PQR?
point R. If these two lines intersect at point Q, what is the measure of ∠PQR?
a)
15o
b)
30o
c)
60o
d)
75o
e)
90o
|
|
Anaya Patel answered |
Given
- The line
intersects the y-axis at the point P
- The line
intersects the y-axis at the point R
- The lines
and
0
- intersect at point Q,
To Find: ∠PQR = ?
Approach
- In order to answer this question, we first need to be able to draw ΔPQR in the coordinate plane.
- Once we’ve drawn ΔPQR, we’ll be able to use trigonometric ratios to find the required angle
- In order to draw ΔPQR in the coordinate plane, we need to know the coordinates of points P, Q and R.
Working out
- Finding the coordinates of R
- R is the point of intersection of line
with x = 0 (this is the equation of
the y-axis)
- Therefore, the coordinates of point R are (0, -1)
- R is the point of intersection of line
- Finding the coordinates of Q
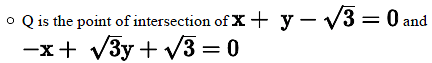
- Thus, the coordinates of point Q are (
Drawing ΔPQR in the coordinate plane
- Now that we know the coordinates of P, Q and R, we can draw ΔPQR in the coordinate plane as under:
Finding ∠PQR
∠PQR = ∠PQO + ∠OQR
∠PQR = ∠PQO + ∠OQR
If the co – ordinates of a point are (3, – 7), then its ordinate is- a)– 7
- b)3
- c)– 3
- d)7
Correct answer is option 'A'. Can you explain this answer?
If the co – ordinates of a point are (3, – 7), then its ordinate is
a)
– 7
b)
3
c)
– 3
d)
7
|
|
Rajeev Kumar answered |
Abscissa is denoted for the coordinates of X axis, therefore the coordinates of point on X axis is 3.
Coordinate line is denoted for Y axis, therefore the coordinates of point on Y axis is -7.
Coordinate line is denoted for Y axis, therefore the coordinates of point on Y axis is -7.
If (a, 0) , (0, b) and (x, y) are collinear, then- a)ay – bx = 1
- b)ay + bx = ab
- c)ax – by = ab
- d)ax + by = 1
Correct answer is option 'B'. Can you explain this answer?
If (a, 0) , (0, b) and (x, y) are collinear, then
a)
ay – bx = 1
b)
ay + bx = ab
c)
ax – by = ab
d)
ax + by = 1

|
Naroj Boda answered |
Explanation:
If given points are collinear, the area of triangle formed by these three points is 0.
The point where the perpendicular bisector of the line segment joining the points A(2, 5) and B(4, 7) cuts is:- a)(0, 0)
- b)(3, 6)
- c)(6, 3)
- d)(2, 5)
Correct answer is option 'B'. Can you explain this answer?
The point where the perpendicular bisector of the line segment joining the points A(2, 5) and B(4, 7) cuts is:
a)
(0, 0)
b)
(3, 6)
c)
(6, 3)
d)
(2, 5)
|
|
Kavya Saxena answered |
Method to Solve :
Perpendicular bisector = Cuts at mid point, and is perpendicular
First find the mid point
x coordinate = 1+4 / 2 = 2.5
y coordinate = 5+6 / 2 = 5.5
Mid point = (2.5, 5.5)
Then find the slope of the bisector :
Slope of the given line = (5-6) / (1-4) = 1/3
Slope of given line multiplied by slope of bisector = -1
Slope of bisector = -1 / (1/3)
= -3
Use the point slope form to find the bisector's formula :
-3 = (5.5 - y) / (2.5 - x)
-7.5 + 3x = 5.5 - y
3x + y - 13 = 0
Transform the formula into slope-intercept form
3x + y - 13 = 0
y = -3x + 13
Because slope-intercept form is y = mx + c, where m is the slope and c is the y-intercept
Therefore the perpendicular bisector cuts the y-axis at (0,13)
Which of the following line is parallel to the given line 3x + 4y = 12 and has a negative y-intercept.- a)6x + 9y + 12 = 0
- b)9x + 12y + 36 = 0
- c)9x+ 12y- 36 = 0
- d)6x + 9y + 28 = 0
- e)6x + 9y - 28 = 0
Correct answer is option 'B'. Can you explain this answer?
Which of the following line is parallel to the given line 3x + 4y = 12 and has a negative y-intercept.
a)
6x + 9y + 12 = 0
b)
9x + 12y + 36 = 0
c)
9x+ 12y- 36 = 0
d)
6x + 9y + 28 = 0
e)
6x + 9y - 28 = 0

|
Parth Singh answered |
**Given Line:** 3x + 4y = 12
**Parallel Line:** A line is parallel to the given line if and only if it has the same slope.
To determine the slope of the given line, we need to rearrange the equation in slope-intercept form (y = mx + b), where m is the slope and b is the y-intercept.
**Rearranging the given line:**
3x + 4y = 12
4y = -3x + 12
y = (-3/4)x + 3
**Slope:** The slope of the given line is -3/4.
Now, let's analyze the answer choices to find the line that has a negative y-intercept and the same slope as the given line.
**Answer Choices:**
a) 6x + 9y + 12 = 0
b) 9x + 12y + 36 = 0
c) 9x + 12y - 36 = 0
d) 6x + 9y + 28 = 0
e) 6x + 9y - 28 = 0
**Analyzing Each Answer Choice:**
a) 6x + 9y + 12 = 0
This equation does not have the same slope as the given line (-3/4). It is not parallel.
b) 9x + 12y + 36 = 0
This equation can be rewritten as 3x + 4y + 12 = 0. The slope is -3/4, which is the same as the given line. It also has a negative y-intercept. Therefore, this line is parallel to the given line.
c) 9x + 12y - 36 = 0
This equation can be rewritten as 3x + 4y - 12 = 0. The slope is -3/4, which is the same as the given line. However, it does not have a negative y-intercept. Therefore, this line is not parallel.
d) 6x + 9y + 28 = 0
This equation does not have the same slope as the given line (-3/4). It is not parallel.
e) 6x + 9y - 28 = 0
This equation can be rewritten as 2x + 3y - 9 = 0. The slope is -2/3, which is not the same as the given line. It is not parallel.
**Conclusion:**
The line that is parallel to the given line 3x + 4y = 12 and has a negative y-intercept is option b) 9x + 12y + 36 = 0.
**Parallel Line:** A line is parallel to the given line if and only if it has the same slope.
To determine the slope of the given line, we need to rearrange the equation in slope-intercept form (y = mx + b), where m is the slope and b is the y-intercept.
**Rearranging the given line:**
3x + 4y = 12
4y = -3x + 12
y = (-3/4)x + 3
**Slope:** The slope of the given line is -3/4.
Now, let's analyze the answer choices to find the line that has a negative y-intercept and the same slope as the given line.
**Answer Choices:**
a) 6x + 9y + 12 = 0
b) 9x + 12y + 36 = 0
c) 9x + 12y - 36 = 0
d) 6x + 9y + 28 = 0
e) 6x + 9y - 28 = 0
**Analyzing Each Answer Choice:**
a) 6x + 9y + 12 = 0
This equation does not have the same slope as the given line (-3/4). It is not parallel.
b) 9x + 12y + 36 = 0
This equation can be rewritten as 3x + 4y + 12 = 0. The slope is -3/4, which is the same as the given line. It also has a negative y-intercept. Therefore, this line is parallel to the given line.
c) 9x + 12y - 36 = 0
This equation can be rewritten as 3x + 4y - 12 = 0. The slope is -3/4, which is the same as the given line. However, it does not have a negative y-intercept. Therefore, this line is not parallel.
d) 6x + 9y + 28 = 0
This equation does not have the same slope as the given line (-3/4). It is not parallel.
e) 6x + 9y - 28 = 0
This equation can be rewritten as 2x + 3y - 9 = 0. The slope is -2/3, which is not the same as the given line. It is not parallel.
**Conclusion:**
The line that is parallel to the given line 3x + 4y = 12 and has a negative y-intercept is option b) 9x + 12y + 36 = 0.
If the distance between the points (p, – 5) and (2, 7) is 13 units, then the value of ‘p’ is- a)– 3, 7
- b)3, – 7
- c)– 3, – 7
- d)3, 7
Correct answer is option 'A'. Can you explain this answer?
If the distance between the points (p, – 5) and (2, 7) is 13 units, then the value of ‘p’ is
a)
– 3, 7
b)
3, – 7
c)
– 3, – 7
d)
3, 7
|
|
Ravi Singh answered |
Explanation:
Let point A be (p,−5) and point B (2, 7) and distance between A and B = 13 units
The base of an equilateral triangle ABC lies on the y – axis. The co – ordinates of the point C is (0, – 3). If origin is the midpoint of BC, then the co – ordinates of B are- a)(0, 3)
- b)(3, 0)
- c)( – 3, 0)
- d)(0, – 3)
Correct answer is option 'A'. Can you explain this answer?
The base of an equilateral triangle ABC lies on the y – axis. The co – ordinates of the point C is (0, – 3). If origin is the midpoint of BC, then the co – ordinates of B are
a)
(0, 3)
b)
(3, 0)
c)
( – 3, 0)
d)
(0, – 3)

|
Bank Exams India answered |
Explanation:
Let the coordinate of B be (0,a).
It is given that (0, 0) is the mid-point of BC.
It is given that (0, 0) is the mid-point of BC.
Therefore 0 = (0 + 0) /2 , 0 =(a - 3) /2 a - 3 = 0 , a = 3
Therefore, the coordinates of B are (0, 3).
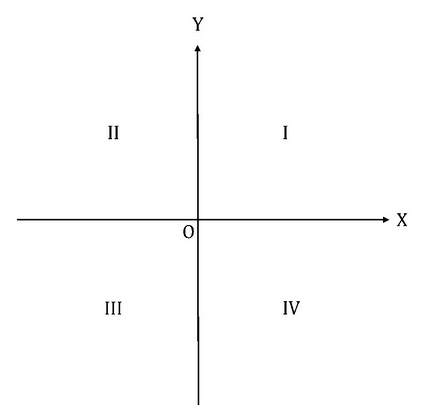 The graph of the equation x2y = k, where k < 0, lies in which two quadrants shown above?
The graph of the equation x2y = k, where k < 0, lies in which two quadrants shown above?- a) I and II
- b)II and III
- c)III and IV
- d)I and IV
- e)I and III
Correct answer is option 'C'. Can you explain this answer?
The graph of the equation x2y = k, where k < 0, lies in which two quadrants shown above?
a)
I and II
b)
II and III
c)
III and IV
d)
I and IV
e)
I and III

|
Mukesh Jindal answered |
X square is equal to k/y
as we know x square will always be positive so k/y has to be positive and k is negative so to make k/y positive y has to be negative so ans. is c
as we know x square will always be positive so k/y has to be positive and k is negative so to make k/y positive y has to be negative so ans. is c
The point ( – 3, 5) lies in the ___________ quadrant- a)III
- b)II
- c)I
- d)IV
Correct answer is option 'B'. Can you explain this answer?
The point ( – 3, 5) lies in the ___________ quadrant
a)
III
b)
II
c)
I
d)
IV

|
Target Study Academy answered |
Explanation:
Since x−coordinate is negative and y−coordinate is positive.Therefore, the point (−3,5) lies in II quadrant.
In the xy–coordinate plane, a line segment is drawn to join the points A (2, 1) and C(4, 3). If point B lies on line segment AC, is AB = BC?(1) The x-coordinate of point B is 3(2) The y-coordinate of point B is 2- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
In the xy–coordinate plane, a line segment is drawn to join the points A (2, 1) and C(4, 3). If point B lies on line segment AC, is AB = BC?
(1) The x-coordinate of point B is 3
(2) The y-coordinate of point B is 2
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Arjun Iyer answered |
Steps 1 & 2: Understand Question and Draw Inferences
The given information can be represented visually as under:
We need to find if AB = BC, that is, if B is the mid-point of AC?
- From the figure, it is clear that the answer is YES only if:
- The x-coordinate of B = (mid-point between the x-coordinates of points A and C) = mid-point between (2 and
- AND, the y-coordinate of B = (mid-point between the y-coordinates of points A and C) = mid-point between
- So, we see that the answer is YES if the coordinates of point B are (3, 2)
- Now, we are given that point B lies on the line segment AC.
- Since we know the coordinates of both points A and C, we can find the equation of line segment AC:
- Starting with the general equation: y = mx + c, where m is the slope of the line and c is the y-intercept
- Since this line passes through point A (2, 1), we can write: 1 = 2m + c . . . (1)
- And, since this line passes through point C(4, 3), we can write: 3 = 4m + c . . .(2)
- (2) – (1): 2 = 2m
- So, m = 1
- From (1): 1 = 2 + c
- So, c = -1
- Therefore, the equation of line AC = y = x – 1
- Since point B lies on line AC, it will satisfy this equation.
- Since we know the coordinates of both points A and C, we can find the equation of line segment AC:
- So, if we know either the x-coordinate or the y-coordinate of point B, we will be able to find the other coordinate of point B using the equation of the line.
- Once we know both the x- and the y- coordinates of point B, the answer will be YES if these coordinates are (3, 2); else the answer will be NO
- Thus, in order to answer the question, we only need to know either the x- or the y-coordinate of point B
- The x-coordinate of B = (mid-point between the x-coordinates of points A and C) = mid-point between (2 and
Step 3: Analyze Statement 1 independently
Statement 1 says that ‘The x-coordinate of point B is 3’
- Since we know the x-coordinate of point B, using the equation of line AC (y = x – 1), we can find the y-coordinate of point B
- Therefore, we can answer if the coordinates of point B are (3,2) or not
- So, Statement 1 alone is sufficient to answer the question
Step 4: Analyze Statement 2 independently
Statement 2 says that ‘The y-coordinate of point B is 2’
- Since we know the y-coordinate of point B, using the equation of line AC (y = x – 1), we can find the x-coordinate of point B
- Therefore, we can answer if the coordinates of point B are (3,2) or not
- So, Statement 2 alone is sufficient to answer the question
Step 5: Analyze Both Statements Together (if needed)
Since we’ve already arrived at a unique answer in Steps 3 and 4, this step is not required
Hence, the correct answer is Option D.
In the xy-plane, a circle C is drawn with center at (1, 2) and radius equal to 5. Is line l a tangent to the circle C?(1) Point A with coordinates (a, b) lies on line l such that a(a-2) +b(b-4) ≤ 20.(2) The x-intercept of line l is 10.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
In the xy-plane, a circle C is drawn with center at (1, 2) and radius equal to 5. Is line l a tangent to the circle C?
(1) Point A with coordinates (a, b) lies on line l such that a(a-2) +b(b-4) ≤ 20.
(2) The x-intercept of line l is 10.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Nitya Kumar answered |
Given information:
- Circle C has center at (1, 2) and radius 5.
- Line l is a line in the xy-plane.
To determine:
- Whether line l is a tangent to circle C.
Approach:
- To determine if line l is tangent to circle C, we need to find the point of intersection between the line and the circle.
- If there is only one point of intersection, then the line is a tangent. If there are two points of intersection, then the line is not a tangent.
Statement 1:
- Point A with coordinates (a, b) lies on line l such that a(a-2) + b(b-4) = 20.
Statement 2:
- The x-intercept of line l is 10.
Analysis of statement 1:
- The equation a(a-2) + b(b-4) = 20 represents a curve in the xy-plane.
- This curve could be a circle, an ellipse, or some other shape.
- Without any information about the line l, we cannot determine if it intersects the circle C at a single point or two points.
- Therefore, statement 1 alone is not sufficient to answer the question.
Analysis of statement 2:
- The x-intercept of a line is the x-coordinate of the point where the line intersects the x-axis.
- If the x-intercept of line l is 10, it means that the line passes through the point (10, 0).
- However, this information alone does not provide any insight into whether the line is tangent to the circle or intersects it at multiple points.
- Therefore, statement 2 alone is not sufficient to answer the question.
Conclusion:
- From the analysis of both statements, neither statement alone is sufficient to answer the question.
- Therefore, the correct answer is option E: Statements (1) and (2) together are not sufficient to answer the question asked, and additional data specific to the problem are needed.
- Circle C has center at (1, 2) and radius 5.
- Line l is a line in the xy-plane.
To determine:
- Whether line l is a tangent to circle C.
Approach:
- To determine if line l is tangent to circle C, we need to find the point of intersection between the line and the circle.
- If there is only one point of intersection, then the line is a tangent. If there are two points of intersection, then the line is not a tangent.
Statement 1:
- Point A with coordinates (a, b) lies on line l such that a(a-2) + b(b-4) = 20.
Statement 2:
- The x-intercept of line l is 10.
Analysis of statement 1:
- The equation a(a-2) + b(b-4) = 20 represents a curve in the xy-plane.
- This curve could be a circle, an ellipse, or some other shape.
- Without any information about the line l, we cannot determine if it intersects the circle C at a single point or two points.
- Therefore, statement 1 alone is not sufficient to answer the question.
Analysis of statement 2:
- The x-intercept of a line is the x-coordinate of the point where the line intersects the x-axis.
- If the x-intercept of line l is 10, it means that the line passes through the point (10, 0).
- However, this information alone does not provide any insight into whether the line is tangent to the circle or intersects it at multiple points.
- Therefore, statement 2 alone is not sufficient to answer the question.
Conclusion:
- From the analysis of both statements, neither statement alone is sufficient to answer the question.
- Therefore, the correct answer is option E: Statements (1) and (2) together are not sufficient to answer the question asked, and additional data specific to the problem are needed.
The vertices of a quadrilateral are (1, 7), (4, 2), ( – 1, – 1) and ( – 4, 4). The quadrilateral is a- a)square
- b)parallelogram
- c)rhombus
- d)rectangle
Correct answer is option 'A'. Can you explain this answer?
The vertices of a quadrilateral are (1, 7), (4, 2), ( – 1, – 1) and ( – 4, 4). The quadrilateral is a
a)
square
b)
parallelogram
c)
rhombus
d)
rectangle
|
|
Sagar Sharma answered |
Given Information:
The vertices of the quadrilateral are (1, 7), (4, 2), (1, 1), and (4, 4).
Explanation:
To determine the type of quadrilateral formed by these vertices, we need to consider the properties of different quadrilaterals.
Square:
A square is a quadrilateral with all sides of equal length and all angles equal to 90 degrees.
Parallelogram:
A parallelogram is a quadrilateral in which opposite sides are parallel.
Rhombus:
A rhombus is a quadrilateral with all sides of equal length.
Rectangle:
A rectangle is a quadrilateral with all angles equal to 90 degrees.
Using Properties:
To determine the type of quadrilateral, we can analyze the given vertices and their properties.
Side Lengths:
Using the distance formula, we can calculate the lengths of the sides of the quadrilateral:
AB = √[(4-1)^2 + (2-7)^2] = √[9 + 25] = √34
BC = √[(4-1)^2 + (4-2)^2] = √[9 + 4] = √13
CD = √[(1-4)^2 + (1-4)^2] = √[9 + 9] = √18
DA = √[(1-4)^2 + (1-7)^2] = √[9 + 36] = √45
Angle Measures:
Using the slope formula, we can calculate the slopes of the sides of the quadrilateral:
mAB = (2-7)/(4-1) = -5/3
mBC = (4-2)/(4-1) = 2/3
mCD = (1-4)/(1-4) = 3/0 (undefined)
mDA = (1-7)/(1-4) = 6/-3 = -2
Analysis:
- The quadrilateral does not have all sides of equal length, so it is not a square or a rhombus.
- The quadrilateral does not have all angles equal to 90 degrees, so it is not a rectangle.
- The quadrilateral does not have opposite sides that are parallel, so it is not a parallelogram.
Conclusion:
Based on the analysis above, the quadrilateral formed by the given vertices is not a square, parallelogram, rhombus, or rectangle. Therefore, the correct answer is option 'A' (None of the above).
The vertices of the quadrilateral are (1, 7), (4, 2), (1, 1), and (4, 4).
Explanation:
To determine the type of quadrilateral formed by these vertices, we need to consider the properties of different quadrilaterals.
Square:
A square is a quadrilateral with all sides of equal length and all angles equal to 90 degrees.
Parallelogram:
A parallelogram is a quadrilateral in which opposite sides are parallel.
Rhombus:
A rhombus is a quadrilateral with all sides of equal length.
Rectangle:
A rectangle is a quadrilateral with all angles equal to 90 degrees.
Using Properties:
To determine the type of quadrilateral, we can analyze the given vertices and their properties.
Side Lengths:
Using the distance formula, we can calculate the lengths of the sides of the quadrilateral:
AB = √[(4-1)^2 + (2-7)^2] = √[9 + 25] = √34
BC = √[(4-1)^2 + (4-2)^2] = √[9 + 4] = √13
CD = √[(1-4)^2 + (1-4)^2] = √[9 + 9] = √18
DA = √[(1-4)^2 + (1-7)^2] = √[9 + 36] = √45
Angle Measures:
Using the slope formula, we can calculate the slopes of the sides of the quadrilateral:
mAB = (2-7)/(4-1) = -5/3
mBC = (4-2)/(4-1) = 2/3
mCD = (1-4)/(1-4) = 3/0 (undefined)
mDA = (1-7)/(1-4) = 6/-3 = -2
Analysis:
- The quadrilateral does not have all sides of equal length, so it is not a square or a rhombus.
- The quadrilateral does not have all angles equal to 90 degrees, so it is not a rectangle.
- The quadrilateral does not have opposite sides that are parallel, so it is not a parallelogram.
Conclusion:
Based on the analysis above, the quadrilateral formed by the given vertices is not a square, parallelogram, rhombus, or rectangle. Therefore, the correct answer is option 'A' (None of the above).
A circle is tangent to the x-axis at 2 and the y-axis at 2. What is the area of the region between the circle and the origin?- a)Less than 1
- b)Between 1 and 3
- c)Between 3 and 5
- d)Between 5 and 7
- e)Greater than 7
Correct answer is option 'A'. Can you explain this answer?
A circle is tangent to the x-axis at 2 and the y-axis at 2. What is the area of the region between the circle and the origin?
a)
Less than 1
b)
Between 1 and 3
c)
Between 3 and 5
d)
Between 5 and 7
e)
Greater than 7

|
Sinjini Mukherjee answered |
Step 1: Question statement and Inferences
A circle tangent to the x-axis at 2 and the y-axis at 2 looks like this:
You know that the radius of the circle is 2, making the area of the circle 4π.
Step 2: Finding required values
To find the region between the circle and the origin, measure the 2 × 2 square, and subtract the quarter circle from it. If the area of the circle is 4π, then the quarter circle is π.
Step 3: Calculating the final answer
4 – π is the area between the circle and the origin.
π = 3.14 and 4 – 3.14 is less than 1.
Answer: Option (A)
In which quadrant does the point (x,y) lie?(1) (x, y+1) lies in the IInd Quadrant.(2) (x + 3, y) lies in the IIIrd Quadrant.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'B'. Can you explain this answer?
In which quadrant does the point (x,y) lie?
(1) (x, y+1) lies in the IInd Quadrant.
(2) (x + 3, y) lies in the IIIrd Quadrant.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Palak Yadav answered |
Statement (1): (x, y) lies in the IInd Quadrant.
This statement tells us that the point (x, y) lies in the second quadrant. The second quadrant is the top-left quadrant on the coordinate plane. It is characterized by having negative x-coordinates and positive y-coordinates. Therefore, based on this statement alone, we can conclude that the x-coordinate of the point (x, y) is negative and the y-coordinate is positive.
Statement (2): (x - 3, y) lies in the IIIrd Quadrant.
This statement tells us that the point (x - 3, y) lies in the third quadrant. The third quadrant is the bottom-left quadrant on the coordinate plane. It is characterized by having negative x-coordinates and negative y-coordinates. Therefore, based on this statement alone, we can conclude that the x-coordinate of the point (x - 3, y) is negative and the y-coordinate is negative.
Both statements together:
Combining the information from both statements, we know that the x-coordinate of the point (x - 3, y) is negative and the y-coordinate is negative. Additionally, we know that the x-coordinate of the point (x, y) is negative and the y-coordinate is positive.
Analysis:
From statement (1) alone, we know that the point (x, y) lies in the second quadrant, which means the x-coordinate is negative and the y-coordinate is positive. However, we don't have any information about the signs of the coordinates individually.
From statement (2) alone, we know that the point (x - 3, y) lies in the third quadrant, which means the x-coordinate is negative and the y-coordinate is negative. Again, we don't have any information about the signs of the coordinates individually.
However, when we combine both statements, we can deduce that the x-coordinate of the point (x, y) is negative and the y-coordinate is positive. This information is sufficient to determine that the point (x, y) lies in the second quadrant.
Therefore, statement (2) alone is sufficient to answer the question, while statement (1) alone is not sufficient. The correct answer is option B.
This statement tells us that the point (x, y) lies in the second quadrant. The second quadrant is the top-left quadrant on the coordinate plane. It is characterized by having negative x-coordinates and positive y-coordinates. Therefore, based on this statement alone, we can conclude that the x-coordinate of the point (x, y) is negative and the y-coordinate is positive.
Statement (2): (x - 3, y) lies in the IIIrd Quadrant.
This statement tells us that the point (x - 3, y) lies in the third quadrant. The third quadrant is the bottom-left quadrant on the coordinate plane. It is characterized by having negative x-coordinates and negative y-coordinates. Therefore, based on this statement alone, we can conclude that the x-coordinate of the point (x - 3, y) is negative and the y-coordinate is negative.
Both statements together:
Combining the information from both statements, we know that the x-coordinate of the point (x - 3, y) is negative and the y-coordinate is negative. Additionally, we know that the x-coordinate of the point (x, y) is negative and the y-coordinate is positive.
Analysis:
From statement (1) alone, we know that the point (x, y) lies in the second quadrant, which means the x-coordinate is negative and the y-coordinate is positive. However, we don't have any information about the signs of the coordinates individually.
From statement (2) alone, we know that the point (x - 3, y) lies in the third quadrant, which means the x-coordinate is negative and the y-coordinate is negative. Again, we don't have any information about the signs of the coordinates individually.
However, when we combine both statements, we can deduce that the x-coordinate of the point (x, y) is negative and the y-coordinate is positive. This information is sufficient to determine that the point (x, y) lies in the second quadrant.
Therefore, statement (2) alone is sufficient to answer the question, while statement (1) alone is not sufficient. The correct answer is option B.
In the xy- plane, lines l and k intersect at point A whose x and y coordinates are positive. If the lines l and k are not parallel to either of the axes, is the product of the slopes of line l and k greater than zero?
(1) The product of the x-intercepts of the lines l and k is negative.
(2) The product of the y-intercepts of the lines l and k is positive.- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'C'. Can you explain this answer?
In the xy- plane, lines l and k intersect at point A whose x and y coordinates are positive. If the lines l and k are not parallel to either of the axes, is the product of the slopes of line l and k greater than zero?
(1) The product of the x-intercepts of the lines l and k is negative.
(2) The product of the y-intercepts of the lines l and k is positive.
(1) The product of the x-intercepts of the lines l and k is negative.
(2) The product of the y-intercepts of the lines l and k is positive.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Moumita Sen answered |
Understanding the Problem
To determine if the product of the slopes of lines l and k is greater than zero, we analyze the slopes based on their intercepts.
Key Concepts
- Lines in the Plane: The slopes of two lines can indicate whether they are increasing or decreasing. If both slopes are positive or both are negative, their product is positive. If one is positive and the other is negative, the product is negative.
- Intercepts: The x-intercepts and y-intercepts provide insight into the slopes of the lines.
Statement Analysis
Statement (1): The product of the x-intercepts of lines l and k is negative.
- If the product of the x-intercepts is negative, one line must cross the x-axis to the left of the origin (negative x-intercept) and the other must cross to the right (positive x-intercept).
- This indicates that one line has a positive slope and the other has a negative slope, leading to a product of slopes that is negative.
- Thus, this statement alone is sufficient.
Statement (2): The product of the y-intercepts of lines l and k is positive.
- If the product of the y-intercepts is positive, both y-intercepts could either be positive or both could be negative.
- However, this does not provide clear information about the slopes of the lines; they could be either both positive or both negative.
- Therefore, this statement alone is insufficient.
Combining Statements
By combining both statements:
- Statement (1) indicates that one slope is positive and the other is negative.
- Statement (2, while not sufficient alone) confirms that both y-intercepts maintain a consistent slope behavior.
Since we know from Statement (1) that the slopes are of opposite signs, we conclude the product of the slopes is negative.
Conclusion
- Statement (1) alone is sufficient, while Statement (2) alone is not sufficient.
- Together, they reinforce the conclusions about slope behavior, confirming that both statements together are necessary to fully understand the relationships.
Thus, the correct answer is option 'C': both statements together are sufficient, but neither is sufficient alone.
To determine if the product of the slopes of lines l and k is greater than zero, we analyze the slopes based on their intercepts.
Key Concepts
- Lines in the Plane: The slopes of two lines can indicate whether they are increasing or decreasing. If both slopes are positive or both are negative, their product is positive. If one is positive and the other is negative, the product is negative.
- Intercepts: The x-intercepts and y-intercepts provide insight into the slopes of the lines.
Statement Analysis
Statement (1): The product of the x-intercepts of lines l and k is negative.
- If the product of the x-intercepts is negative, one line must cross the x-axis to the left of the origin (negative x-intercept) and the other must cross to the right (positive x-intercept).
- This indicates that one line has a positive slope and the other has a negative slope, leading to a product of slopes that is negative.
- Thus, this statement alone is sufficient.
Statement (2): The product of the y-intercepts of lines l and k is positive.
- If the product of the y-intercepts is positive, both y-intercepts could either be positive or both could be negative.
- However, this does not provide clear information about the slopes of the lines; they could be either both positive or both negative.
- Therefore, this statement alone is insufficient.
Combining Statements
By combining both statements:
- Statement (1) indicates that one slope is positive and the other is negative.
- Statement (2, while not sufficient alone) confirms that both y-intercepts maintain a consistent slope behavior.
Since we know from Statement (1) that the slopes are of opposite signs, we conclude the product of the slopes is negative.
Conclusion
- Statement (1) alone is sufficient, while Statement (2) alone is not sufficient.
- Together, they reinforce the conclusions about slope behavior, confirming that both statements together are necessary to fully understand the relationships.
Thus, the correct answer is option 'C': both statements together are sufficient, but neither is sufficient alone.
In the xy-plane, what is the area of the region bounded by y +2x ≥ 3, y –x ≥ -6 and the line, that is perpendicular to x = 0 and passes
through the origin?- a)9/4
- b)27/4
- c)9
- d)27/2
- e)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
In the xy-plane, what is the area of the region bounded by y +2x ≥ 3, y –x ≥ -6 and the line, that is perpendicular to x = 0 and passes
through the origin?
through the origin?
a)
9/4
b)
27/4
c)
9
d)
27/2
e)
Cannot be determined

|
Manasa Gupta answered |
Given
- y +2x ≥ 3
- y –x ≥ -6
- Line perpendicular to x=0 and passing through origin
- The equation x = 0 represents the y-axis
- So, the given line is perpendicular to the y-axis and passes through the origin
- Therefore, the given line is the x-axis
To Find: Area bounded by the region y +2x ≥ 3, y –x ≥ -6 and x-axis
Approach:
1. For finding the area bounded by the region, we need to first draw the line segments y +2x = 3 and y – x = 6
2. Once we draw these line segment, we need to find the side of each line segment where the region specified in the question statement lies
2. Once we draw these line segment, we need to find the side of each line segment where the region specified in the question statement lies
- For finding the region, we will put the coordinates of the origin (0,0) in the inequality. If the inequality is satisfied, the region lies towards the side of the line containing the origin, else it lies on the opposite side of the line containing the origin.
3. Once we have the region, we will find the area of the region using the standard geometry formulas
Working out:
1. The line segment y +2x = 3 will intersect the y-axis at (3,0) and x-axis at 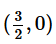
- The region y +2x – 3 ≥ 0 will be satisfied by the region, which does not contain the origin, as putting (0,0) in the inequality does not satisfy the inequality.
2. Similarly, the line segment y-x ≥ 6 will intersect the y-axis at (-6,0) and x-axis at (6,0).
- The region y-x ≥ -6 will consist of the region, which contains the origin.
3. So, the vertex points of the region are 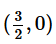 ,(6,0) and (3, -3)
,(6,0) and (3, -3)
4. We know that area of a triangle = ½ * base * height
- Let’s consider the base as the x-axis, thus length of the base
- Height of the triangle would be the magnitude of y-coordinate of point (3, -3) = 3
5. Thus area of the triangle = 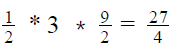
Hence the correct answer is Option B.
Three consecutive vertices of a parallelogram ABCD are A(1, 2), B(1, 0) and C(4, 0). The co – ordinates of the fourth vertex D are- a)( – 4, – 2)
- b)(4, 2)
- c)(4, – 2)
- d)( – 4, 2)
Correct answer is option 'B'. Can you explain this answer?
Three consecutive vertices of a parallelogram ABCD are A(1, 2), B(1, 0) and C(4, 0). The co – ordinates of the fourth vertex D are
a)
( – 4, – 2)
b)
(4, 2)
c)
(4, – 2)
d)
( – 4, 2)
|
|
Yash Patel answered |
Method to Solve :
Let the co-ordinates of the fourth vertex D be (x, y).
We know that diagonals of a parallelogram bisect each other.
Mid-point of BD = Mid-point of AC
Coordinates of the mid-point of BD are [1 + x/2 , 0+y/2]
Coordinates of the mid-point of AC are [1+4/2 , 2+0/2]=[5/2,1]
1+x/2=5/2
x+1=5
x=4
0+y/2=1
y=2
Thus, the co-ordinates of the vertex D are (4, 2).
If L1 passes through points in each quadrant except the IIIrd quadrant, then is the slope of the line L2 positive?(1) L2 is perpendicular to L1.(2) L1 and L2 intersect in the Ist quadrant.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'A'. Can you explain this answer?
If L1 passes through points in each quadrant except the IIIrd quadrant, then is the slope of the line L2 positive?
(1) L2 is perpendicular to L1.
(2) L1 and L2 intersect in the Ist quadrant.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Palak Yadav answered |
Statement 1: L2 is perpendicular to L1.
Statement 2: L1 and L2 intersect in the 1st quadrant.
We need to determine if the slope of line L2 is positive.
To solve this problem, let's analyze each statement separately and then evaluate their combined impact.
Statement 1: L2 is perpendicular to L1.
- If L1 passes through points in each quadrant except the 3rd quadrant, it means that L1 is angled upwards and does not have a negative slope.
- If L2 is perpendicular to L1, it means that L2 is angled downwards and has a negative slope.
- Therefore, the slope of L2 is negative, not positive.
Statement 1 alone is sufficient.
Statement 2: L1 and L2 intersect in the 1st quadrant.
- If L1 and L2 intersect in the 1st quadrant, it means that both lines have positive slopes.
- However, this information does not provide any direct information about the slope of L2.
- Therefore, statement 2 alone is not sufficient to determine the slope of L2.
Combining both statements:
- From statement 1, we know that the slope of L2 is negative.
- From statement 2, we know that L1 and L2 have positive slopes.
- Combining these two pieces of information, we can conclude that the slope of L2 is negative and not positive.
Therefore, both statements together are not sufficient to determine the slope of L2.
The correct answer is (A).
Statement 2: L1 and L2 intersect in the 1st quadrant.
We need to determine if the slope of line L2 is positive.
To solve this problem, let's analyze each statement separately and then evaluate their combined impact.
Statement 1: L2 is perpendicular to L1.
- If L1 passes through points in each quadrant except the 3rd quadrant, it means that L1 is angled upwards and does not have a negative slope.
- If L2 is perpendicular to L1, it means that L2 is angled downwards and has a negative slope.
- Therefore, the slope of L2 is negative, not positive.
Statement 1 alone is sufficient.
Statement 2: L1 and L2 intersect in the 1st quadrant.
- If L1 and L2 intersect in the 1st quadrant, it means that both lines have positive slopes.
- However, this information does not provide any direct information about the slope of L2.
- Therefore, statement 2 alone is not sufficient to determine the slope of L2.
Combining both statements:
- From statement 1, we know that the slope of L2 is negative.
- From statement 2, we know that L1 and L2 have positive slopes.
- Combining these two pieces of information, we can conclude that the slope of L2 is negative and not positive.
Therefore, both statements together are not sufficient to determine the slope of L2.
The correct answer is (A).
If the x-intercept of line L is -5 and the slope is equal to 5/2, Find the y-intercept of the line L.- a)-2
- b)-5/2
- c)2
- d)5/2
- e)25/2
Correct answer is option 'E'. Can you explain this answer?
If the x-intercept of line L is -5 and the slope is equal to 5/2, Find the y-intercept of the line L.
a)
-2
b)
-5/2
c)
2
d)
5/2
e)
25/2

|
Abhishek Choudhury answered |
Given information:
- X-intercept of line L is -5
- Slope of line L is 5/2
To find:
- Y-intercept of line L
Solution:
The x-intercept is the point at which the line intersects the x-axis, which means that the y-coordinate of this point is zero. Therefore, we can use this information to find the y-intercept.
Let's first write the equation of the line using the slope-intercept form, which is y = mx + b, where m is the slope and b is the y-intercept.
We know that the slope of the line is 5/2, so we can substitute that into the equation:
y = (5/2)x + b
We also know that the x-intercept of the line is -5. We can use this information to find the value of the y-intercept by plugging in -5 for x and 0 for y:
0 = (5/2)(-5) + b
Simplifying this equation, we get:
0 = -25/2 + b
Adding 25/2 to both sides, we get:
25/2 = b
Therefore, the y-intercept of the line is 25/2, which is option E.
Answer: E) 25/2
- X-intercept of line L is -5
- Slope of line L is 5/2
To find:
- Y-intercept of line L
Solution:
The x-intercept is the point at which the line intersects the x-axis, which means that the y-coordinate of this point is zero. Therefore, we can use this information to find the y-intercept.
Let's first write the equation of the line using the slope-intercept form, which is y = mx + b, where m is the slope and b is the y-intercept.
We know that the slope of the line is 5/2, so we can substitute that into the equation:
y = (5/2)x + b
We also know that the x-intercept of the line is -5. We can use this information to find the value of the y-intercept by plugging in -5 for x and 0 for y:
0 = (5/2)(-5) + b
Simplifying this equation, we get:
0 = -25/2 + b
Adding 25/2 to both sides, we get:
25/2 = b
Therefore, the y-intercept of the line is 25/2, which is option E.
Answer: E) 25/2
In a rectangular coordinate plane, points A(3,4), B(6,-5), C(-4,-3) and D(-2,2) are joined to form a quadrilateral. What is the area, in square units, of quadrilateral ABCD?- a)35
- b)37.5
- c)45
- d)52.5
- e)60
Correct answer is option 'D'. Can you explain this answer?
In a rectangular coordinate plane, points A(3,4), B(6,-5), C(-4,-3) and D(-2,2) are joined to form a quadrilateral. What is the area, in square units, of quadrilateral ABCD?
a)
35
b)
37.5
c)
45
d)
52.5
e)
60

|
Nilotpal Sen answered |
Given
- The given information corresponds to the following diagram:
To Find: Area of quadrilateral ABCD
Approach
- To find the area of quadrilateral ABCD, we’ll use the method of addition and subtraction of areas.
- We will extend the quadrilateral such that it forms rectangular figures – rectangles or right-angled triangles. This can be done as under:
2. So, Area of Quadrilateral ABCD = (Area of Rectangle QBPS) – (ar ΔAPB + ar ΔBQC + ar ΔCRD + ar of square DRST + ar ΔATD)
Looking at the answer choices, we see that the correct answer is Option D
On the x-y coordinate grid, are points A and B equidistant from the origin? (1) |x| = |y| for point A and |x| = |y| for point B(2) |x|, |y| of point A = |x|, |y| of point B- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'B'. Can you explain this answer?
On the x-y coordinate grid, are points A and B equidistant from the origin?
(1) |x| = |y| for point A and |x| = |y| for point B
(2) |x|, |y| of point A = |x|, |y| of point B
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Palak Yadav answered |
Given information:
- Points A and B are represented on the x-y coordinate grid.
- We need to determine if points A and B are equidistant from the origin.
Statement 1: |x| = |y| for point A and |x| = |y| for point B
- This means that the absolute values of the x-coordinates and y-coordinates of both points are equal.
- We can visualize this as the points lying on the lines y = x and y = -x.
- However, this information alone does not provide the exact coordinates of points A and B, so we cannot determine their distance from the origin.
Statement 2: |x|, |y| of point A = |x|, |y| of point B
- This statement tells us that the absolute values of the x-coordinates and y-coordinates of both points are equal.
- Similar to statement 1, this information alone does not provide the exact coordinates of points A and B, so we cannot determine their distance from the origin.
Combining both statements:
- Both statements provide the same information, that the absolute values of the x-coordinates and y-coordinates of both points are equal.
- However, since we still do not know the exact coordinates of points A and B, we cannot determine their distance from the origin.
Conclusion:
- Neither statement alone is sufficient to determine if points A and B are equidistant from the origin.
- Therefore, the correct answer is option B: Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- Points A and B are represented on the x-y coordinate grid.
- We need to determine if points A and B are equidistant from the origin.
Statement 1: |x| = |y| for point A and |x| = |y| for point B
- This means that the absolute values of the x-coordinates and y-coordinates of both points are equal.
- We can visualize this as the points lying on the lines y = x and y = -x.
- However, this information alone does not provide the exact coordinates of points A and B, so we cannot determine their distance from the origin.
Statement 2: |x|, |y| of point A = |x|, |y| of point B
- This statement tells us that the absolute values of the x-coordinates and y-coordinates of both points are equal.
- Similar to statement 1, this information alone does not provide the exact coordinates of points A and B, so we cannot determine their distance from the origin.
Combining both statements:
- Both statements provide the same information, that the absolute values of the x-coordinates and y-coordinates of both points are equal.
- However, since we still do not know the exact coordinates of points A and B, we cannot determine their distance from the origin.
Conclusion:
- Neither statement alone is sufficient to determine if points A and B are equidistant from the origin.
- Therefore, the correct answer is option B: Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
In the xy-plane, the line y = k is the perpendicular bisector of the line segment PQ and the line x = h is the perpendicular bisector of the line segment RQ. If the coordinates of the point R are (-h, -k), then what are the coordinates of the point P?- a)(-5h, -5k)
- b)(-3h, -3k)
- c)(2h, 2k)
- d)(3h, 3k)
- e)(5h, 5k)
Correct answer is option 'D'. Can you explain this answer?
In the xy-plane, the line y = k is the perpendicular bisector of the line segment PQ and the line x = h is the perpendicular bisector of the line segment RQ. If the coordinates of the point R are (-h, -k), then what are the coordinates of the point P?
a)
(-5h, -5k)
b)
(-3h, -3k)
c)
(2h, 2k)
d)
(3h, 3k)
e)
(5h, 5k)

|
Mihir Nambiar answered |
Step 1: Question statement and Inferences
Drawing the axes and the lines y = k and x = h given in the question on xy-plane:
Based on the figure drawn by us, plotting the point R whose coordinates are (-h, -k): 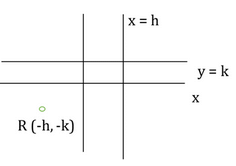
Step 2:Finding required values
Since the line x = h is the perpendicular to QR, the y-coordinate of point R must also be equal to –k. RA and QA are perpendicular to the line x = h, the y-coordinate of R, A and Q are equal. Therefore, the coordinates of point A are (h, -k).
RA = AQ = h – (-h) = 2h
The coordinates of point Q are (h + 2h, -k) or (3h, -k).
Step 3: Calculating the final answer
Since the line y = k is perpendicular to PQ, the x-coordinate of P, B and Q are equal, i.e. 3h.
Since QB = BP, and QB = k – (-k) = 2k, the y-coordinate of point P is k + 2k = 3k.
The coordinates of the point P are (3h, 3k).
(D) is the correct answer.
 On the x-y coordinate grid, if points P, Q, and R make a triangle (not shown), what is the area of the triangle? (1) Point Q lies on the x-axis 6 units from point P.(2) Point R is 5 units away from the x-axis
On the x-y coordinate grid, if points P, Q, and R make a triangle (not shown), what is the area of the triangle? (1) Point Q lies on the x-axis 6 units from point P.(2) Point R is 5 units away from the x-axis- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?
On the x-y coordinate grid, if points P, Q, and R make a triangle (not shown), what is the area of the triangle?
(1) Point Q lies on the x-axis 6 units from point P.
(2) Point R is 5 units away from the x-axis
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Rhea Gupta answered |
Steps 1 & 2: Understand Question and Draw Inferences
To find the area of the triangle, you need the base and the height.
With point P on the x-axis, knowing points Q and R will help you find the base and height.
Step 3: Analyze Statement 1
(1) Point Q lies on the x-axis 6 units from point P.
This gives you the base of the triangle. Whether point Q is left or right of point P, the triangle base is 6. However, you still need the height.
Statement 1 is not sufficient.
Step 4: Analyze Statement 2
(2) Point R is 5 units away from the x-axis
If the base of the triangle is on the x-axis, then knowing point R is 5 away gives you a height of 5. However, with this statement alone, you don’t have the base, and you don’t know whether the base is on the x-axis..
Statement 2 is not sufficient.
Step 5: Analyze Both Statements Together (if needed)
From statement 1, you know that the base is on the x-axis and that it has a length of 6.
From statement 2, because the base is on the x axis, you know the height is 5.
These are all you need to calculate the area of the triangle. The left-right placement of points Q and R don’t affect the area calculation:
Area = ½ * 6 * 5 = 15
Answer: Option (C)
 On the x-y coordinate grid, does the line passing through point P (not shown) have a slope greater than 2?(1) Point P has an x-value of 1 and is 2 units away from the origin(2) The line does not pass through Quadrant IV
On the x-y coordinate grid, does the line passing through point P (not shown) have a slope greater than 2?(1) Point P has an x-value of 1 and is 2 units away from the origin(2) The line does not pass through Quadrant IV- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?
On the x-y coordinate grid, does the line passing through point P (not shown) have a slope greater than 2?
(1) Point P has an x-value of 1 and is 2 units away from the origin
(2) The line does not pass through Quadrant IV
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Shivam Ghoshal answered |
Steps 1 & 2: Understand Question and Draw Inferences
To find whether the slope is greater than 2, you need information on the orientation of the line. This can come from two points of the line or at least one point that the line passes above or below.
Step 3: Analyze Statement 1
(1) Point P has an x-value of 1 and is 2 units away from the origin
Statement 1 tells you that from the origin, point P creates a right triangle. Use the Pythagorean Theorem to find the y-value: (The triangle base is the x-value of 1, the hypotenuse is the distance of 2, and the height is the y-value)
The height of the triangle, which is the y-value of point p, has an absolute value of √3, making it either √3 or –√3. However, you need two points to draw the line, and you don’t know whether point P is in quadrant I or IV.
Statement 1 is not sufficient.
Step 4: Analyze Statement 2
(2) The line does not pass through Quadrant IV
Statement 2 tells you that the slope is positive (to avoid Quadrant IV), but you don’t know whether it’s greater than 2.
Statement 2 is not sufficient.
Step 5: Analyze Both Statements Together (if needed)
From statement 1, you know the (x, y) values of point P are either (1, √3) or (1, –√3), placing point P in either Quadrant I or IV.
From statement 2, you know that point P is in Quadrant I. You also know the line cannot cross into Quadrant IV.
As shown above, the slope is√3. The line can rotate clockwise, making the slope less, but it cannot rotate counterclockwise, as that would bring it into Quadrant IV. Taken together, you know that the slope is not greater than 2.
Statements 1 and 2 together are sufficient.
Answer: Option (C)
In the xy-plane, the circle C centered at the origin O is intersected by a line l at two points A and B. A line from O is drawn to AB intersecting AB at point D, such that the product of the slopes of OD and AB is -1. If the line l does not pass through origin and the coordinates of point D are (1, -1), what is the radius of the circle?(1) The x intercept of line l is 2.
(2) The product of the x coordinates of points A and B as well as the product of the y coordinates of points A and B is zero.- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'B'. Can you explain this answer?
In the xy-plane, the circle C centered at the origin O is intersected by a line l at two points A and B. A line from O is drawn to AB intersecting AB at point D, such that the product of the slopes of OD and AB is -1. If the line l does not pass through origin and the coordinates of point D are (1, -1), what is the radius of the circle?
(1) The x intercept of line l is 2.
(2) The product of the x coordinates of points A and B as well as the product of the y coordinates of points A and B is zero.
(2) The product of the x coordinates of points A and B as well as the product of the y coordinates of points A and B is zero.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Pranab Dasgupta answered |
Step 1 & 2: Understand Question and Draw Inference
- Circle C with center at (0, 0)
- Line l intersects the circle at A and B
- OD is perpendicular to AB, where D is a point on line segment AB with coordinates (1, -1)
- As OD is a perpendicular from the center of circle C to chord AB, D must be the midpoint of AB
- Since the coordinates of point O are (0,0) and of point D are (1, -1), Slope of line OD =
- Slope of line AB * Slope of line OD = -1
- (Slope of line AB)*(-1)= -1
- Slope of line AB = 1
- Since we’ve inferred that the slope of line AB is 1, we can write the Equation of line AB as: y = 1*x + c, that is, y = x + c
- As AB passes through (1, -1), we have -1 = 1 + c, i.e. c = -2
- Equation of line AB : y = x – 2
- To find: Radius of the circle, say r, That is, the length of OA (or OB)
- To answer this question, we need the coordinates of points A or B so that we can then find the distance between points O(0,0) and points A or B.
Step 3 : Analyze Statement 1 independent
(1) The x intercept of line l is 2.
We know from the equation of the line, that x- intercept of the line is 2. Hence, there is no added information provided.
We know from the equation of the line, that x- intercept of the line is 2. Hence, there is no added information provided.
Insufficient to answer
Step 4 : Analyze Statement 2 independent
(2) The product of the x coordinates of points A and B as well as the product of the y coordinates of points A and B is zero.
- Let the coordinates of point A be (x1, y1) and coordinates of point B be(x2 , y2).
- x * x = 0
- Either of x or x or both are zero
- y * y = 0
- Either of y or y or both are zero
- x and y both cannot be zero, as that would mean that point A is the origin. Similarly x and y cannot be zero at the same time.
- So, coordinates of point A and B can be (0, y ) and (x , 0) or vice versa, i.e. they lie on the y-axis and the x-axis respectively.
- Now, we know that equation of line AB : y = x – 2.
- Putting coordinates of point A(0, y ) in the equation, we have y = 0 – 2, i.e. y = -2
- So, Coordinates of point A(0, -2)
As we know the coordinate of point A, we can calculate the radius of the circle C.
Sufficient to answer.
Sufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
As we have a unique answer from step-4, this step is not required.
Answer: B
Answer: B
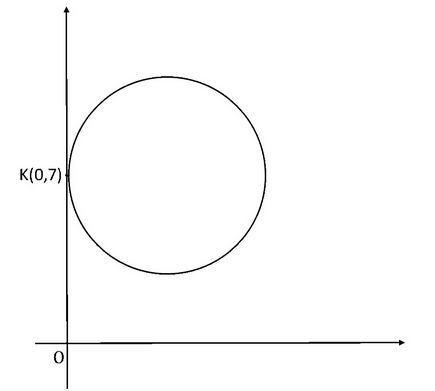 In the given diagram, the circle touches the y-axis at the point K whose coordinate is (0,7). If the area of triangle CKO is 21 units2, where C is the centre of the circle, find the area of the circle.
In the given diagram, the circle touches the y-axis at the point K whose coordinate is (0,7). If the area of triangle CKO is 21 units2, where C is the centre of the circle, find the area of the circle.- a)16π
- b)21π
- c)24π
- d)36π
- e)49π
Correct answer is option 'D'. Can you explain this answer?
In the given diagram, the circle touches the y-axis at the point K whose coordinate is (0,7). If the area of triangle CKO is 21 units2, where C is the centre of the circle, find the area of the circle.
a)
16π
b)
21π
c)
24π
d)
36π
e)
49π

|
Preitee Ranjan Pradhan answered |
 Lines a and b, not shown, lie in the rectangular coordinate system shown above. Is the slope of line a greater than the slope of line b?(1) Line a does not intersect quadrant III.(2) Line b intersects quadrant IV.
Lines a and b, not shown, lie in the rectangular coordinate system shown above. Is the slope of line a greater than the slope of line b?(1) Line a does not intersect quadrant III.(2) Line b intersects quadrant IV.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'E'. Can you explain this answer?
Lines a and b, not shown, lie in the rectangular coordinate system shown above. Is the slope of line a greater than the slope of line b?
(1) Line a does not intersect quadrant III.
(2) Line b intersects quadrant IV.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Kirti Roy answered |
Step 1 & 2 – Understand the question and draw inferences from the question statement.
Given: lines a and b are in the graph
To find: Comparison of the slopes of the lines
Step 3 – Analyze Statement 1 Independently
Per statement 1, line a does not intersect quadrant III
Inference 1: Line a can have a zero slope, a negative slope or an undefined slope. However, it cannot have a positive slope.
Since Statement 1 does not tell you anything about line b , the information provided in Statement 1 is not sufficient to arrive at a unique answer.
Step 4 – Analyze Statement 2 Independently
Per Statement 2, line b intersects quadrant IV
Inference 2: line b has any kind of slope
Inference 3: if the slope is positive, the y-intercept is negative
Since Statement 2 does not tell you anything about line a , the information provided in Statement 2 is not sufficient to arrive at a unique answer.
Step 5 – Analyze Both Statements Together
To analyze both statements together, we will put the inferences from both statements. Here is the data that we have:
Inference 1: Line a can't have a positive slope.
Inference 2: line b has any kind of slope
Inference 3: if the slope is positive, the y-intercept is negative
Though we know the slope of line a is negative, we know nothing of the slope of line b . Inference 3 does not help. The question cannot be answered.
Answer: Option (E)
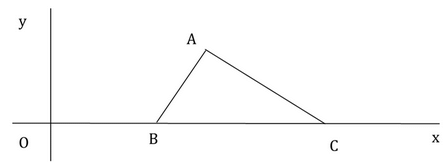 In the rectangular coordinate system above, if OB < BC then is the area of the triangle ABC lesser than 12 square units?(1) Point A lies above the line y = 5(2) The mid-point of B and C is (6, 0)
In the rectangular coordinate system above, if OB < BC then is the area of the triangle ABC lesser than 12 square units?(1) Point A lies above the line y = 5(2) The mid-point of B and C is (6, 0)- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'E'. Can you explain this answer?
In the rectangular coordinate system above, if OB < BC then is the area of the triangle ABC lesser than 12 square units?
(1) Point A lies above the line y = 5
(2) The mid-point of B and C is (6, 0)
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Sounak Iyer answered |
Steps 1 & 2: Understand Question and Draw Inferences
In order to determine any information about the area of a triangle, we must try to obtain information about its base and height since
the area of a triangle = (1/2)*base*height
If the base is taken as the length of line segment BC, then the height is the y-coordinate of point A.
Step 3: Analyze Statement 1
If the point A lies above the line y = 5 and the side BC lies on the x-axis, then the height of the triangle is more than 5 units. We have no information about the length of the base BC.
INSUFFICIENT.
Step 4: Analyze Statement 2
Let’s assume the coordinates of point B to be (b, 0) and the coordinates of point C to be (c, 0).
If the mid-point of B and C is (6, 0) then
(b+c)/2 = 6
c = 12 – b
Length of BC = 12 – b – b = 12 – 2b
Since OB < BC, we have
b < 12 – 2b
b < 4
We cannot infer anything about the base BC from this, apart from the fact that the length of BC will always be greater than 4 units.
There is also no information about the height of the triangle ABC.
INSUFFICIENT.
Step 5: Analyze Both Statements Together (if needed)
Combining statements (1) and (2),
We have Height > 5 and b < 4
We have information about the height but still we are unsure about the base BC and so we cannot conclude if the area of the triangle ABC is greater than 12 or less than 12.
INSUFFICIENT.
(E) is the correct answer.
In the xy-plane, Region R is bounded by the line segments with equations, 2x + |4y| = 20 and x=0, whereas Region P is bounded by the line segments with equations |4x| + 2y = 20 and y = 0. If the function A(B) is defined as the area of Region B, what is the value of |A(P) – 2A(R)|?- a)0
- b)25
- c)50
- d)75
- e)100
Correct answer is option 'C'. Can you explain this answer?
In the xy-plane, Region R is bounded by the line segments with equations, 2x + |4y| = 20 and x=0, whereas Region P is bounded by the line segments with equations |4x| + 2y = 20 and y = 0. If the function A(B) is defined as the area of Region B, what is the value of |A(P) – 2A(R)|?
a)
0
b)
25
c)
50
d)
75
e)
100

|
Manasa Gupta answered |
Given
- Region R is bounded by
- 2x + |4y| = 20 and
- x=0, whereas
- Region P is bounded by
- |4x| + 2y = 20 and
- y = 0
- A(B) = area of Region B
To Find: |A(P) – 2A(R)|?
- We need to find the area of regions P and R to answer the question
Approach
- Region R
- For finding the area of region R, we need to draw the following line segments:
- x = 0
- 2x +4|y| = 20. As we are given |y|, the value of |y| will depend on the value of y
- If y ≥0, then |y| = y.
- So, we have equation of the line segment as 2x + 4y = 20, i.e. x + 2y = 10 and
- If y < 0, then |y| = -y.
- So, we have equation of the line segment as 2x – 4y = 20, i.e. x – 2y = 10
- If y ≥0, then |y| = y.
- Once we draw these line segments, we will find the area of the region bounded by the line segments using standard formulas.
- For finding the area of region R, we need to draw the following line segments:
- Region P
- For finding the area of region R, we need to draw the following line segments:
- y = 0
- |4x| + 2y = 20. As we are given |x|, the value of |x| will depend on the value of x.
- If x ≥0, then |x| = x.
- So, we have the equation as 4x + 2y = 20, i.e. 2x + y = 10 and
- If x < 0, then |x| = -x.
- So, we have the equation of the line segment as 4x – 2y = -20, i.e. 2x – y = -10
- If x ≥0, then |x| = x.
- For finding the area of region R, we need to draw the following line segments:
- Once we draw these line segments, we will find the area of the region bounded by the line segments using standard formulas
Working out
1. Finding A(R)
a. Assuming y-axis to be the base, we have EF = 5 – (-5) = 10
b. Height = x-coordinate of point D = 10
c. Area of region R = ½ * 10 * 10 = 50
d. A(R) = 50……. (1)
a. Assuming y-axis to be the base, we have EF = 5 – (-5) = 10
b. Height = x-coordinate of point D = 10
c. Area of region R = ½ * 10 * 10 = 50
d. A(R) = 50……. (1)
2. Finding A(P)
a. Assuming x-axis to be the base, we have BD = 5 – (-5) = 10
b. Height = y-coordinate of point A = 10
a. Assuming x-axis to be the base, we have BD = 5 – (-5) = 10
b. Height = y-coordinate of point A = 10
c. Area of region P = ½ * 10 * 10 = 50
d. A(P) = 50…….(2)
d. A(P) = 50…….(2)
3. Using (1) and (2), we have
a. |A(P) – 2A(R)| = | 50 – 2*50| = |-50| = 50
Answer: C
a. |A(P) – 2A(R)| = | 50 – 2*50| = |-50| = 50
Answer: C
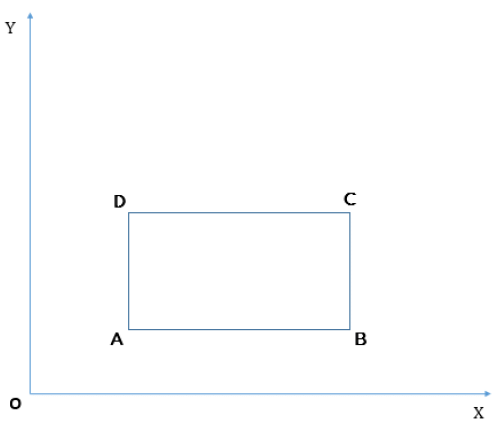 In the xy-plane given above, if the parallelogram ABCD has all its sides equal, is ABCD a square?
In the xy-plane given above, if the parallelogram ABCD has all its sides equal, is ABCD a square?
(1) The lines connecting AC and BD have the product of their slopes equal to -1
(2) Points A and D have the same x-coordinates- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'E'. Can you explain this answer?
In the xy-plane given above, if the parallelogram ABCD has all its sides equal, is ABCD a square?
(1) The lines connecting AC and BD have the product of their slopes equal to -1
(2) Points A and D have the same x-coordinates
(1) The lines connecting AC and BD have the product of their slopes equal to -1
(2) Points A and D have the same x-coordinates
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Prashanth Chawla answered |
Step 1 & 2: Understand Question and Draw Inference
Given: Parallelogram ABCD has all its sides equal
To find: If ABCD is a square?
So, we need to find if one of the angles of ABCD is a right angle.
To find: If ABCD is a square?
So, we need to find if one of the angles of ABCD is a right angle.
Step 3 : Analyze Statement 1 independent
(1) Statement 1 states that "The lines connecting AC and BD have the product of their slopes equal to -1"
- The diagonals are perpendicular to each other. Hence ABCD may be a rhombus or a square.
- Thus, Statement 1 is Insufficient to answer the question.
Step 4 : Analyze Statement 2 independent
- (2) Statement 2 states that "Points A and D have the same x-coordinates"
- ∠DAB would be equal to 90 if points D and A have the same x-coordinates and A and B have the same y-coordinates.
- The statement does not tell us about the y-coordinates of A and B.
- Thus, Statement 2 is also Insufficient to answer the question.
Step 5: Analyze Both Statements Together (if needed)
- Combining the statements does not give us any extra information about the parallelogram ABCD.
- Hence both statements together are also insufficient to answer the question.
Thus, the correct answer is Option E .
 In the xy-plane shown, is the slope of line l non-negative?
In the xy-plane shown, is the slope of line l non-negative?
1. The line passes through quadrants II and III.
2. For each pair of coordinates (x,y) lying on line l, the product of x and y is not always non-negative.- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'E'. Can you explain this answer?
In the xy-plane shown, is the slope of line l non-negative?
1. The line passes through quadrants II and III.
2. For each pair of coordinates (x,y) lying on line l, the product of x and y is not always non-negative.
1. The line passes through quadrants II and III.
2. For each pair of coordinates (x,y) lying on line l, the product of x and y is not always non-negative.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Ameya Yadav answered |
Step 1 & 2: Understand Question and Draw Inference
To Find:
- Is the slope of line l negative?
Step 3 : Analyze Statement 1 independent
(1) Statement 1 states that "The line passes through quadrants II and III".
- Following cases are possible:
- If the line also passes through quadrant-I, the slope of the line will be positive
- If the line also passes through quadrant- IV, the slope of the line will be negative.
- If the line passes through quadrants II and III only and is parallel to y-axis, the slope of the line will be infinity.
Hence, Statement 1 is insufficient to answer
Step 4 : Analyze Statement 2 independent
(2) Statement 2 states that "For each pair of coordinates (x, y) lying on the line l, the product of x and y is not always non-negative."
- x * y < 0 for some points on line l. This is possible when the line passes through either quadrant-II, IV or both:
- If Line l passes through quadrant- II but not quadrant-IV, then Slope of the line is positive
- If Line l passes through quadrant- IV but not quadrant-II, then Slope of the line is positive
- If Line l passes through both quadrant –II and IV, then Slope of the line is negative
Hence, Statement 2 is insufficient to answer
Step 5: Analyze Both Statements Together (if needed)
1. Line l passes through quadrants-II and III
2. Line l passes through quadrant II, or IV or both
2. Line l passes through quadrant II, or IV or both
Following cases are possible:
- Line l passes through quadrants II, III and IV : Slope of the line is negative
- Line l passes through I, II and III : Slope of the line is positive
As we do not have a unique answer, hence by combining both the statements also it is insufficient to answer the question.
Thus, the correct answer is Option E .
Thus, the correct answer is Option E .
In the xy-plane, two circles C and R are drawn such that Circle C has its center at the origin and radius equal to 5 and Circle R has its center at (2, 3) and radius equal to 5. Which of the following is the equation of the line that passes through the intersection points of circles C and R?- a)
- b)
- c)
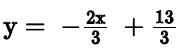
- d)
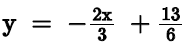
- e)

Correct answer is option 'D'. Can you explain this answer?
In the xy-plane, two circles C and R are drawn such that Circle C has its center at the origin and radius equal to 5 and Circle R has its center at (2, 3) and radius equal to 5. Which of the following is the equation of the line that passes through the intersection points of circles C and R?
a)
b)
c)
d)
e)

|
Manasa Gupta answered |
- Circle R
- Origin = (2, 3)
- Radius = 5
- Now, all the points that lie on the Circle R will be at a distance of 5
units (i.e. the radius) from the centre of the circle(2, 3)
To Find: The equation of the line that passes through the intersection point of Circle C and R?
Approach:
- To find the equation of a line that passes through the intersection points of Circles C and R, we need to find two points that lie on the line.
- As the line passes through the two intersection points of the circles C and R, the equation of the line will satisfy these two intersection points.
- Also the two intersection points of the circles should satisfy the equation of all the points lying on both the circles.
- So, we can equate the equations of the points lying on circle C and R to find the equation of the line passing through the intersection points.
Working out:
- Equation of all the points lying on Circle C:
- Equation of all the points lying on Circle R:
- Equating both the equations, will give us the equation of the line that passes these intersection points:
Thus, the line segment that passes through the intersection points of Circle C
and R should have itsequation as
and R should have itsequation as
Answer: D
In the rectangular coordinate system are the points A and B equidistant from point C (1, 0)?
(1) Points A and B lie on circle R, which passes through origin and has a radius equal to 1.
(2) The bisector of the line segment AB passes through point C- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'E'. Can you explain this answer?
In the rectangular coordinate system are the points A and B equidistant from point C (1, 0)?
(1) Points A and B lie on circle R, which passes through origin and has a radius equal to 1.
(2) The bisector of the line segment AB passes through point C
(1) Points A and B lie on circle R, which passes through origin and has a radius equal to 1.
(2) The bisector of the line segment AB passes through point C
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Nilotpal Sen answered |
step 1 & 2: Understand Question and Draw Inference
To Find: If points A and B are equidistant from C (1, 0)?
Step 3 : Analyze Statement 1 independent
(1) Points A and B lie on circle R, which passes through origin and has a radius equal to 1.
- There can be various circles possible with radius = 1 and passing through origin. Refer the diagram:
- If points A and B lie on the circle with center at C(1, 0), points A and B will be equidistant from C
- For all the other cases, points A and B may not be equidistant from
Insufficient to answer
Step 4 : Analyze Statement 2 independent
(2) The bisector of the line segment AB passes through point C
- Following cases are possible:
- If the bisector of the line segment AB is the perpendicular bisector, then all the points on the perpendicular bisector will be equidistant from A and B.
- If the bisector is not a perpendicular bisector then point C may or may not be equidistant from points A and B.
- If point C lies on line AB as well as on the bisector of AB then, points A and B will be equidistant from C.
- If point C lies on the bisector of AB then but not on AB, points A and B will not be equidistant from point C.
- Insufficient to answer
Step 5: Analyze Both Statements Together (if needed)
Both the statements combined does not give us any extra information to answer
the question.
the question.
Insufficient to answer
Answer: E
Answer: E
 In the xy-plane, a trapezium ABCD has one of its parallel sides AB on the x-axis with vertex A at the origin. The x-coordinate of point B is 6 and the length of the smaller parallel side CD is 2 less than the length of the longer parallel side. If the side AD lies on the line with the equation y = x and the area of the trapezium is 5 square units, what is the coordinate of point C?
In the xy-plane, a trapezium ABCD has one of its parallel sides AB on the x-axis with vertex A at the origin. The x-coordinate of point B is 6 and the length of the smaller parallel side CD is 2 less than the length of the longer parallel side. If the side AD lies on the line with the equation y = x and the area of the trapezium is 5 square units, what is the coordinate of point C?- a)(1,1)
- b)(1,5)
- c)(5,1)
- d)(5,5)
- e)(6,1)
Correct answer is option 'C'. Can you explain this answer?
In the xy-plane, a trapezium ABCD has one of its parallel sides AB on the x-axis with vertex A at the origin. The x-coordinate of point B is 6 and the length of the smaller parallel side CD is 2 less than the length of the longer parallel side. If the side AD lies on the line with the equation y = x and the area of the trapezium is 5 square units, what is the coordinate of point C?
a)
(1,1)
b)
(1,5)
c)
(5,1)
d)
(5,5)
e)
(6,1)

|
Ameya Yadav answered |
Given
Trapezium ABCD with AB on x-axis
- Coordinates of A = (0,0)
- x-coordinate of B =6
- Coordinate of B (6,0)
- CD = AB – 2
- AD lies on the line y =x
- Let’s assume the coordinate of point D (a, a)
- Ar(ABCD) = 5
To Find: Coordinates of point C?
Approach:
- As AB lies on x-axis and CD is parallel to AB, the y-coordinate of point C will be equal to y-coordinate of point D, i.e. a
- The x-coordinate of point C will be x-coordinate of point D + length of CD, i.e. (a + CD)
- Now, we have expressed the coordinates of point C in terms of a and length of CD
- Now, we are given that the length of CD is 2 less than the length of AB. As we know the coordinates of points A and B, we can find the length of AB and hence the length of CD.
- So, we now need to find the value of a to find the coordinates of point C We know that area of trapezium ABCD = ½ * (AB + CD) * distance between AB and CD
- As we are given the value of the area of the trapezium, AB and CD, we will get the distance between the parallel lines from the above equation.
- Now, the distance between the parallel lines will be equal to the y-coordinate of point C. Thus, we will get the value of a from here.
Working out
- Length of AB = x-coordinate of point B – x coordinate of point A = 6 – 0 = 6 units
- Hence, length of CD = 6 – 2 = 4 units
- So, coordinate of point C = (a + CD, a) = (a+4, a)
- Area of trapezium ABCD = ½ *(AB+CD) * distance between AB and CD
- As distance between AB and CD is equal to the y-coordinate of point C, we can write
- Area if trapezium = 5 = ½ *(6+4) * (a)
- Thus a = 1 and a+4 = 5
- Hence, coordinate of point C (5, 1)
- Thus, the correct answer is Option C
Of all the points that satisfy the equation x2+ y2 =25 approximately what percentage of the points also satisfy the
inequality xy ≥ 0?- a)25%
- b)33%
- c)50%
- d)75%
- e)80%
Correct answer is option 'C'. Can you explain this answer?
Of all the points that satisfy the equation x2+ y2 =25 approximately what percentage of the points also satisfy the
inequality xy ≥ 0?
inequality xy ≥ 0?
a)
25%
b)
33%
c)
50%
d)
75%
e)
80%

|
Pallavi Choudhury answered |
Given
x2+ y2 =25
To Find: Percentage of points lying on the circle that satisfies xy ≥ 0?
Approach and Working
- x2 + y2 = 25
- If we compare it with the distance formula:
- ■ D2 = [(xi - x2)2 + (yi - y2)2]
- ■ If (x2, y2) is considered as the origin, (x, y) as the other point
- ■ We can write: (x-0)2 + (y-0)2 = 52
- ■ Thus, we are looking for all the points which are at a distance of 5 units from the origin.
- o If we try to plot it on a graph, we will notice that
- This equation represents all the points lying on a Circle C with center(0,0) and radius of 5 units.
- If we compare it with the distance formula:
- xy > 0, when the x and the y coordinates have the same signs, except for the case when either of x or y = 0
- x and y coordinates have the same signs in the 1st and the 3rd quadrant. So, we need to find the percentage of points of circle C that lie in the 1st and the 3rd quadrant.
- A circle with center at origin will pass through all the 4 quadrants.
- So, if we find the arc length of the circle in the 1st quadrant and the 3rd quadrant, we can divide it by the total arc length of the circle (i.e. the circumference) to find the percentage of points satisfying the inequality xy > 0
- We can see from the figure above that by symmetry, arc length of the circle in each quadrant = 1/4th of its total circumference = ¼ * 2πr
- So, the total arc length present in the 1st and the 3rd quadrant = (¼ + ¼) *2πr = ½ *2πr
- Hence, 50% of the points that lie on the circle, satisfy the inequality xy ≥0
- And the correct answer is OPTION C
In the rectangular coordinate system, lines L1 and L2 intersect at point C. Are the lines L1 and L2 perpendicular to each other?(1) The product of the slopes of lines L1 and L2 is at a distance of 1 unit from 0 on the number line.(2) Lines x = 0 and y = 0 are the perpendicular bisectors of lines L1 and L2 respectively.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
In the rectangular coordinate system, lines L1 and L2 intersect at point C. Are the lines L1 and L2 perpendicular to each other?
(1) The product of the slopes of lines L1 and L2 is at a distance of 1 unit from 0 on the number line.
(2) Lines x = 0 and y = 0 are the perpendicular bisectors of lines L1 and L2 respectively.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Manasa Gupta answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Lines L1 and L2 intersect at point C
To Find:
- If lines L1 and L2 are perpendicular?
- Let’s assume the slopes of lines L1 and L2 be m1 and m2
- So, we need to find if m1 * m2 = -1?
Step 3: Analyze Statement 1 independently
(1) Statement 1 states that: "The product of the slopes of lines L1 and L2 is at a distance of 1 unit from 0 on the number line."
- Numbers that are at a distance of 1 unit from 0 on the number line:
- 0 + 1 = 1 and
- 0 – 1 = -1
- So, as per Statement 1, Product of slopes, that is,= m1 * m2 = 1 or -1
- If m1 * m2 = 1, lines L1 and L2 are not perpendicular to each other
- If m1 * m2 = -1, lines L1 and L2 are perpendicular to each other
- Thus, statement 1 is not sufficient to answer.
Step 4: Analyze Statement 2 independently
(2) Statement 2 states that: "Lines x = 0 and y = 0 are the perpendicular bisectors of lines L1 and L2 respectively."
- As x= 0 is the perpendicular bisector of line L1, L1 is perpendicular to line x= 0 i.e. L1 is the y –axis
- As y = 0 is the perpendicular bisector of line L2, L2 is perpendicular to line y = 0 i.e. L2 is the x –axis
- Since x axis and y-axis are perpendicular to each other, lines L1 and L2 will also be perpendicular to each other.
- Hence, Statement 2 is sufficient to answer the question
Step 5: Analyze Both Statements Together (if needed)
As we have got a unique answer from step-4, this step is not required.
- Thus the correct answer is Option B.
What is the area of the triangle formed between the lines y – x =2, 3x + 4y = 29 and y = 2?- a)4.5
- b)6
- c)9
- d)10.5
- e)12
Correct answer is option 'D'. Can you explain this answer?
What is the area of the triangle formed between the lines y – x =2, 3x + 4y = 29 and y = 2?
a)
4.5
b)
6
c)
9
d)
10.5
e)
12

|
Nilotpal Sen answered |
Given
3 lines:
- y – x = 2
- 3x + 4y = 29
- y = 2
To Find : The area of the triangle formed between these 3 lines
Approach:
- In order to find the area, we first need to know the coordinates of the 3 vertices of the triangle formed.
- Each vertex of the triangle is the point of intersection of 2 of these 3 given lines. So, we’ll solve each pair of 2 lines to determine their point of intersection (that is, the vertices of the triangle)
- Then, we’ll plot these plots in the x-y plane and find the area of the triangle.
Working out:
Finding the vertices of the triangle
- Let’s find these vertices one by one:
- Intersection of y-x =2 and 3x +4y =29
- From y – x = 2, we get y = x + 2
- Substituting this in the equation 3x + 4y = 29, we get:
- 3x + 4(x+2) = 29
- 7x + 8 = 29
- 7x = 21
- So, x = 3
- And, y = 3+2 = 5
- So, one vertex of the triangle is (3,5)
- Intersection of y-x =2 and y=2
- Putting y = 2 in y – x = 2, we get 2 – x = 2. So, x = 0
- So, the 2 vertex of the triangle is (0,2)
- Intersection of 3x +4y =29 and y=2
- Putting y = 2 in 3x + 4y = 29, we get 3x + 4(2) = 29
- 3x = 21
- So, x = 7
- The y-coordinate of this vertex will of course be 2 only
- So, the 3 vertex of the triangle is (7,2)
- So, we can represent the triangle as under:
Finding the area of the triangle
Looking at the answer choices, we see that the correct answer is Option D
 The figure above shows a circle whose diameter AB lies on the x-axis as shown. Triangle ACB is a right-angled triangle whose side AC makes an angle of 30? with side AB. If the coordinates of points A and B are (0,0) and (4,0) respectively, what is the y-coordinate of point C?
The figure above shows a circle whose diameter AB lies on the x-axis as shown. Triangle ACB is a right-angled triangle whose side AC makes an angle of 30? with side AB. If the coordinates of points A and B are (0,0) and (4,0) respectively, what is the y-coordinate of point C?- a)

- b)
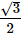
- c)
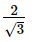
- d)
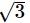
- e)
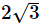
Correct answer is option 'D'. Can you explain this answer?
The figure above shows a circle whose diameter AB lies on the x-axis as shown. Triangle ACB is a right-angled triangle whose side AC makes an angle of 30? with side AB. If the coordinates of points A and B are (0,0) and (4,0) respectively, what is the y-coordinate of point C?
a)
b)
c)
d)
e)

|
Pranab Dasgupta answered |
Given
- Circle with diameter AB
- Length of the diameter = AB = 4 units
- Right triangle ACB
- ∠CAB = 30
- Hypotenuse AB = 4 units
To Find : y – coordinate of point C
Approach:
- Since AB coincides with the x-axis, the y-coordinate of point C will be equal to the perpendicular distance of point C from AB
So, referring to the above figure, we can write: y – coordinate of point C = CP
So, in order to answer the question, we need to know the value of CP
So, in order to answer the question, we need to know the value of CP
- Now, area of right triangle ACB = ½ * AB * CP
- We already know the measure of AB. So, if we find the area of the triangle, we’ll be able to find CP
- We can write another expression for the area of right triangle ACB:
- Area of right triangle ACB = ½ * AC * BC
- In right triangle ACB, we know the measure of side AB and angle CAB = 30 and angle ACB = 90o
- Thus, angle ABC = 180o – 30o – 90o = 60o
- WE can conclude that triangle ABC is a 30-60-90 Triangle.
- So, using the side ratio property of 30-60-90 Triangle, we can easily find AC and BC, and hence the area of the triangle.
Working out:
Finding BC and AC
In right triangle ACB,
In right triangle ACB,
- BC : AC : AB = 1 : √3 : 2
- BC : AB = 1 : 2
- Since AB = 4
- So, BC = 2 units
- AC : AB = √3 : 2
- Since AB = 4
- So, AC = 2√3units
1. Finding the area of triangle ACB
Area of right triangle ACB = ½ AC * BC = ½ * 2√3 * 2 =
2√3 square units
2. Finding CP
½ * CP * AB = 2√3 square units
½ *CP * 4 = 2√3
CP = √3 units
3. Getting to the answer
Therefore, the y-coordinate of point C =CP = √3 units
Looking at the answer choices, we see that the correct answer is OPTION D
Area of right triangle ACB = ½ AC * BC = ½ * 2√3 * 2 =
2√3 square units
2. Finding CP
½ * CP * AB = 2√3 square units
½ *CP * 4 = 2√3
CP = √3 units
3. Getting to the answer
Therefore, the y-coordinate of point C =CP = √3 units
Looking at the answer choices, we see that the correct answer is OPTION D
Rectangle ABCD is drawn in the xy-plane such that side AB is parallel to the x-axis and the side AD is parallel to the y-axis. What are the coordinates of point D?(1) The coordinates of point A are (2, 3)(2) The coordinates of point C are (4, 8)- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
Rectangle ABCD is drawn in the xy-plane such that side AB is parallel to the x-axis and the side AD is parallel to the y-axis. What are the coordinates of point D?
(1) The coordinates of point A are (2, 3)
(2) The coordinates of point C are (4, 8)
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Pranab Dasgupta answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given: Rectangle ABCD in the xy-plane
- Since AB is parallel to the x-axis,
- Points A and B will have the same y-coordinates
- Since side CD of the rectangle will be parallel to side AB, points C and D too will have the same y-coordinates
- Since AD is parallel to the y-axis,
- Points A and D will have the same x-coordinates
- Since side BC of the rectangle will be parallel to side AD, points B and C too will have the same x-coordinates
To find: Coordinates of point D
Step 3: Analyze Statement 1 independently
Statement 1 says that ‘The coordinates of point A are (2, 3)’
- This means, the x-coordinate of point D is 2
- However, since we do not know the y-coordinate of point D, Statement 1 alone is not sufficient
Step 4: Analyze Statement 2 independently
Statement 2 says that ‘The coordinates of point C are (4, 8)’
- This means, the y-coordinate of point D is 8
- However, since we do not know the x-coordinate of point D, Statement 2 alone is not sufficient
Step 5: Analyze Both Statements Together (if needed)
- From Statement 1, the x- coordinate of point D is 2
- From Statement 2, the y-coordinate of point D is 8
- So, the coordinates of point D are (2,8)
Thus, by combining the 2 statements, we do get a unique answer
Answer: Option C
In the xy-plane, is the x-intercept of the line y = mx + b positive? (m and b are non-zero numbers)(1) The y-intercept of the line m2y = bx + m is positive.(2) The x-intercept of the line 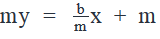 is positive
is positive - a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?
In the xy-plane, is the x-intercept of the line y = mx + b positive? (m and b are non-zero numbers)
(1) The y-intercept of the line m2y = bx + m is positive.
(2) The x-intercept of the line 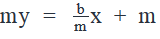 is positive
is positive
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Advait Malik answered |
Steps 1 & 2: Understand Question and Draw Inferences
Let’s find the x-intercept of the given line.
When the line intercepts the x-axis, the y-coordinate becomes 0.
Substituting y = 0 in the given equation of the line,
The question thus becomes
Multiplying by -1 on both sides of the inequality, the question modifies to
Step 3: Analyze Statement 1
To compare the given line with the general form of the equation (y= mx + c), we divide both sides of the equation with m2.
The equation becomes y
we see that the y-intercept of the given line m2y = bx + m is 1/m
The statement tells us that 1/m>0
Using this information, we can only say that m > 0.
However, b/m can be negative or not depending on whether b is negative or not.
INSUFFICIENT.
Step 4: Analyze Statement 2
In order to find the x-intercept of the given equation of line my = x + m, we substitute y = 0 in the given equation to get
Since 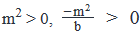 only when b < 0.
only when b < 0.
Is b/m < 0 ? We cannot be sure because we only know that b < 0. b/m
can be less than 0 or not depending on whether m is positive or not.
Step 5: Analyze Both Statements Together (if needed)
Combining statements (1) and (2),
we have m > 0 and b < 0.
This means that b/m < 0 for all such values of m and b.
SUFFICIENT.
(C) is the answer.
In a rectangular coordinate plane, AB is the diameter of a circle and point C lies on the circle. If the coordinates of points A and B are (-1,0) and (5,0), and the area of triangle ABC is 6√2 square units, which of the following can be the coordinates of point C?- a)
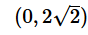
- b)
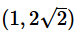
- c)
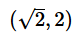
- d)
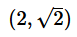
- e)

Correct answer is option 'B'. Can you explain this answer?
In a rectangular coordinate plane, AB is the diameter of a circle and point C lies on the circle. If the coordinates of points A and B are (-1,0) and (5,0), and the area of triangle ABC is 6√2 square units, which of the following can be the coordinates of point C?
a)
b)
c)
d)
e)

|
Rajdeep Nair answered |
Given:
- The given information corresponds to the following diagram:
In ΔABC
- Length of side AB = 5 – (-1) = 6 units
- Side AB is the diameter of the circle
- So, ∠ACB is the angle in a semicircle
- Therefore, ∠ABC = 900
- Also, Radius of circle = 6/2 = 3 units
- So, OB = 3 units, where O is the center of the circle
- The coordinate of point O will be (2,0)
- Area of ΔABC = 6√2 square units
To find: Possible coordinates of point C
Approach and Working:
- We know the area of ΔABC.
- As per the formula, the area of this triangle = ½ * base * height = ½ * AB * the perpendicular dropped from C on AB.
- Now AB lies on the x-axis. So, what will be the length of the perpendicular dropped from C on AB ?
- It will be equal to the y-coordinate of C.
- So, we can write:
- ½ (AB)(y-coordinate of point C) = 6√2
- ½* 6* (y-coordinate of point C) = 6√2
- (y-coordinate of point C) = 2√2
- To find the x-coordinate of C, we can use the distance formula.
- The distance between the center and C is 3 units. Thus, we can write:
- D = √[(x-2)2 + (2√2 -0)2]
- 3 = √[(x2-4x +4 + 8]
- x2 -4x +12 = 9
- x2 -4x + 3 = 0
- (x-1)* (x-3) = 0
- Therefore, x can be either 1 or 3.
- Looking at the answer choices, we see that only option B (1,2√2) satisfy.
- Thus, the correct answer is Option B.
 In the given diagram, ABCD is a square and the coordinate of B is (5,5). If the length of each side is 2 units and AB is parallel to the y-axis, find the coordinate of D.
In the given diagram, ABCD is a square and the coordinate of B is (5,5). If the length of each side is 2 units and AB is parallel to the y-axis, find the coordinate of D.- a)(3,5)
- b)(5,3)
- c)(7,3)
- d)(7,5)
- e)(7,7)
Correct answer is option 'C'. Can you explain this answer?
In the given diagram, ABCD is a square and the coordinate of B is (5,5). If the length of each side is 2 units and AB is parallel to the y-axis, find the coordinate of D.
a)
(3,5)
b)
(5,3)
c)
(7,3)
d)
(7,5)
e)
(7,7)

|
Srikar Mukkavilli answered |
Coordinates of B are (5,5) and length of each side is 2.
Coming 2 units down along side AB we get A as (5,5-2)=>(5,3).
Coming 2 units right along side AD we get B as (5+2,3)=>(7,3).
Hence,
c) (7,3) is the right option.
Coming 2 units down along side AB we get A as (5,5-2)=>(5,3).
Coming 2 units right along side AD we get B as (5+2,3)=>(7,3).
Hence,
c) (7,3) is the right option.
 Regular hexagon ABCDEF is symmetrical about the x-axis and the y-axis in a rectangular coordinate plane, as shown above. If the coordinates of point D are (2,0), what is the area, in square units, of rectangle BCEF?
Regular hexagon ABCDEF is symmetrical about the x-axis and the y-axis in a rectangular coordinate plane, as shown above. If the coordinates of point D are (2,0), what is the area, in square units, of rectangle BCEF?- a)√3
- b)3
- c)2√3
- d)4√3
- e)8√3
Correct answer is option 'D'. Can you explain this answer?
Regular hexagon ABCDEF is symmetrical about the x-axis and the y-axis in a rectangular coordinate plane, as shown above. If the coordinates of point D are (2,0), what is the area, in square units, of rectangle BCEF?
a)
√3
b)
3
c)
2√3
d)
4√3
e)
8√3

|
Nilotpal Sen answered |
Given:
- Regular hexagon ABCDEF
- This means, each interior angle of this hexagon will measure 120o
- (Here’s how you can calculate this: Measure of each angle of a regular n-sided polygon =
- So, for a regular hexagon (n =6), each interior angle =
- Let each side of this hexagon measure a units
- Hexagon ABCDEF is symmetrical about the x-axis and the y-axis.
- This means, the center of the coordinate plane O(0,0) lies at the exact center of the hexagon
- Point D(2,0)
- To find: ar(Rectangle BCEFApproach:
- We need to find the value of Ar(Rectangle BCEF)
- Note that since the origin lies at the exact center of the hexagon, and hence also at the center of rectangle BCEF, it will divide rectangle BCEF into 4 smaller and identical rectangles.
- Let’s label one of these rectangles as OGCH
- So, Ar(Rectangle BCEF) = 4*ar(Rectangle OGCH)
- (Here’s how you can calculate this: Measure of each angle of a regular n-sided polygon =
- This means, each interior angle of this hexagon will measure 120o
2. ar(Rectangle OGCH)= CG*CH
- Since the hexagon is symmetrical about the x-axis,
- And, since the hexagon is symmetrical about the y-axis,
- So, if we can find CG and a, we can answer the question.
. Now, OG + GD = OD
- We know the value of OD.
- Using trigonometric ratios in right triangle CGD, we can express DG in terms of hypotenuse a (Note that the hypotenuse of this triangle is the side of regular hexagon ABCDEF, and so, is equal to a units)
- We already know the value of OG in terms of a
- So, from this equation, we can find the value of a
4. Also, in right triangle CGD, using trigonometric ratios, we can express CG in terms of hypotenuse a.
- So, once we know the value of a, we can find the value of CG as well
Working Out:
- Finding the value of a
- Finding the value of CG
Working towards the final answer
- Therefore, ar(Rectangle BCEF)
- Looking at the answer choices, we see that the correct answer is Option D
Chapter doubts & questions for Coordinate Geometry - Mathematics for ACT 2025 is part of ACT exam preparation. The chapters have been prepared according to the ACT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for ACT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Coordinate Geometry - Mathematics for ACT in English & Hindi are available as part of ACT exam.
Download more important topics, notes, lectures and mock test series for ACT Exam by signing up for free.
Mathematics for ACT
144 videos|100 docs|61 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup