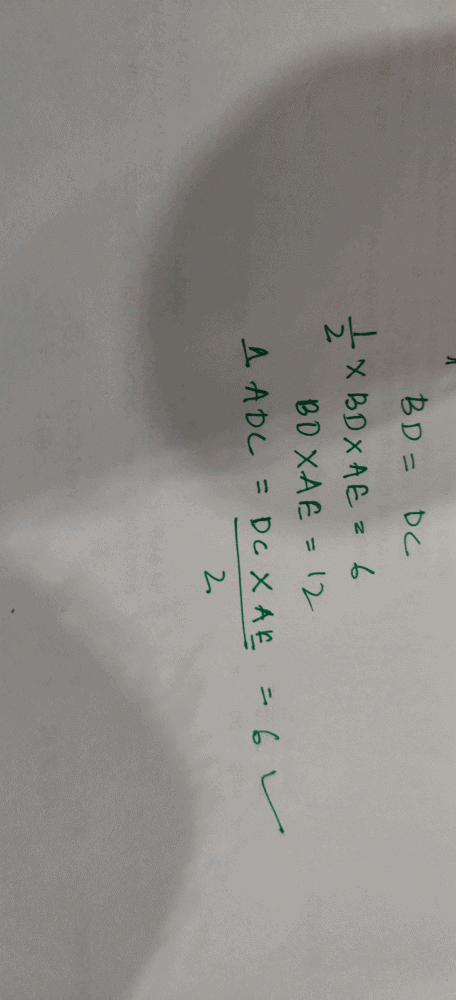All Exams >
SAT >
Mathematics for Digital SAT >
All Questions
All questions of Lines, Angles and Triangles for SAT Exam
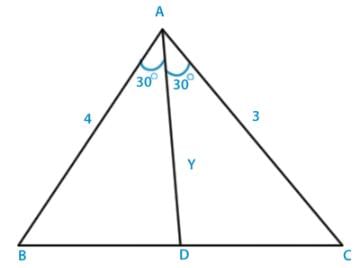
In a triangle ABC, the internal bisector of the angle A meets BC at D. If AB = 4, AC = 3 and ∠ A = 600, then length of AD is :- a)2√3
- b)(12√3) / 7
- c)(15√3) / 8
- d)(6√3) / 7
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
In a triangle ABC, the internal bisector of the angle A meets BC at D. If AB = 4, AC = 3 and ∠ A = 600, then length of AD is :
a)
2√3
b)
(12√3) / 7
c)
(15√3) / 8
d)
(6√3) / 7
e)
None of these
|
|
Lavanya Menon answered |
Let BC = x and Ad = y, then as per bisector theorem,
BD /DC = AB /AC = 4 /3
Hence, BD = 4x/7 and DC = 3x/7
Now, in Δ ABD using cosine rule,
cos 300 = [{42 +y2 - (16x2/49)} /2*3*y]
Or, 4√3y =[{16 +y2 - (16x2/49)}] --------- (i)
Similarly in Δ ADC,
cos 300 = [{32 +y2 - (9x2/49)} /2*3*y]
Or, 3√3y =[{9 +y2 - (9x2/49)}] --------- (ii)
From equation (i) and (ii), we get
y = 12√3 /7.
ABC is a triangle in which AB = 4 cm and BC = 7cm. What is the possible range of values of CA?- a)-3< CA < 3
- b)-3< CA <11
- c)3< CA<11
- d)5<CA<12
- e)5<CA<17
Correct answer is option 'C'. Can you explain this answer?
ABC is a triangle in which AB = 4 cm and BC = 7cm. What is the possible range of values of CA?
a)
-3< CA < 3
b)
-3< CA <11
c)
3< CA<11
d)
5<CA<12
e)
5<CA<17
|
|
Lavanya Menon answered |
Possible range of values of CA will be |AB - BC| < CA < |AB + BC|
So possible range of values of CA will be 3 < CA <11
In triangle PQR length of the side QR is less than twice the length of the side PQ by 2 cm. Length of the side PR exceeds the length of the side PQ by 10 cm. The perimeter is 40 cm. The length of the smallest side of the triangle PQR is :- a)6 cm
- b)8 cm
- c)7 cm
- d)10 cm
- e)9 cm
Correct answer is option 'B'. Can you explain this answer?
In triangle PQR length of the side QR is less than twice the length of the side PQ by 2 cm. Length of the side PR exceeds the length of the side PQ by 10 cm. The perimeter is 40 cm. The length of the smallest side of the triangle PQR is :
a)
6 cm
b)
8 cm
c)
7 cm
d)
10 cm
e)
9 cm

|
Nandita Yadav answered |
In Δ PQR,
QR +2 = 2PQ
QR = 2PQ - 2 ------- (2)
PR = PQ + 10 ----- (2)
Perimeter = 40 m
PQ + QR + Rp = 40
Putting the value of PQ and QR from equation (1) and (2),
Pq + 2PQ - 2 + PQ +10 = 40
4PQ = 32
PQ = 8 cm which is the smallest side of the triangle.
QR +2 = 2PQ
QR = 2PQ - 2 ------- (2)
PR = PQ + 10 ----- (2)
Perimeter = 40 m
PQ + QR + Rp = 40
Putting the value of PQ and QR from equation (1) and (2),
Pq + 2PQ - 2 + PQ +10 = 40
4PQ = 32
PQ = 8 cm which is the smallest side of the triangle.
The complement angle of 80° is- a)18 / π radian
- b)5π / 9 radian
- c)π / 18 radian
- d)9 / 5π radian
Correct answer is option 'C'. Can you explain this answer?
The complement angle of 80° is
a)
18 / π radian
b)
5π / 9 radian
c)
π / 18 radian
d)
9 / 5π radian

|
Rutuja Banerjee answered |
Complement Angle Calculation:
The complement angle of a given angle is the angle that, when added to the given angle, equals 90 degrees. In this case, we are given the angle of 80 degrees and we need to find its complement angle.
Calculation:
- The complement angle of 80 degrees can be calculated as follows:
- Complement angle = 90 degrees - 80 degrees
- Complement angle = 10 degrees
Conversion to Radians:
To convert the complement angle from degrees to radians, we use the conversion factor: 1 degree = π / 180 radians.
- Complement angle in radians = 10 degrees x (π / 180)
- Complement angle in radians = π / 18 radians
Therefore, the complement angle of 80 degrees is π / 18 radians, which corresponds to option 'c'.
The complement angle of a given angle is the angle that, when added to the given angle, equals 90 degrees. In this case, we are given the angle of 80 degrees and we need to find its complement angle.
Calculation:
- The complement angle of 80 degrees can be calculated as follows:
- Complement angle = 90 degrees - 80 degrees
- Complement angle = 10 degrees
Conversion to Radians:
To convert the complement angle from degrees to radians, we use the conversion factor: 1 degree = π / 180 radians.
- Complement angle in radians = 10 degrees x (π / 180)
- Complement angle in radians = π / 18 radians
Therefore, the complement angle of 80 degrees is π / 18 radians, which corresponds to option 'c'.
In the given figure AB || CD, ∠A = 128°, ∠E = 144°. Then, ∠FCD is equal to :

- a)72°
- b)64°
- c)136°
- d)92°
Correct answer is option 'D'. Can you explain this answer?
In the given figure AB || CD, ∠A = 128°, ∠E = 144°. Then, ∠FCD is equal to :


a)
72°
b)
64°
c)
136°
d)
92°

|
Pioneer Academy answered |
As per the given figure,
Through E draw EE’ || AB || CD.
Then, ∠AEE’ = 180° ‒ ∠BAE = (180° ‒ 128°) = 52°.
(Interior angles on the same side of the transversal are supplementary.)
Now, ∠E’EC = (144° ‒ 52°) = 92°.
∠FCD = ∠E’EC = 92° (Corr. ∠s).
Hence, option D is correct.
Through E draw EE’ || AB || CD.
Then, ∠AEE’ = 180° ‒ ∠BAE = (180° ‒ 128°) = 52°.
(Interior angles on the same side of the transversal are supplementary.)
Now, ∠E’EC = (144° ‒ 52°) = 92°.
∠FCD = ∠E’EC = 92° (Corr. ∠s).
Hence, option D is correct.
If one arm of an angle is respectively parallel to the arm of another angle formed with a common line between them, then the two angles are- a)Neither equal nor supplementary
- b)not equal but supplementary
- c)equal but not supplementary
- d)Either equal or supplementary
Correct answer is option 'B'. Can you explain this answer?
If one arm of an angle is respectively parallel to the arm of another angle formed with a common line between them, then the two angles are
a)
Neither equal nor supplementary
b)
not equal but supplementary
c)
equal but not supplementary
d)
Either equal or supplementary
|
|
Rahul Kapoor answered |
If one arm of an angle is respectively parallel to the arm of another angle formed with a common line between them, then the two angles are not equal but supplementary.
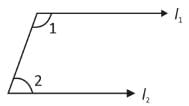
If l1 || l2 ⇒ ∠1 + ∠2 = 180°
(Supplementary)

If l1 || l2 ⇒ ∠1 + ∠2 = 180°
(Supplementary)
Hence, option B is correct.
ABC and BDC are two triangles as shown in the given figure. If BDC is an isosceles triangle in which BD = DC. Find the value of ∠BDC.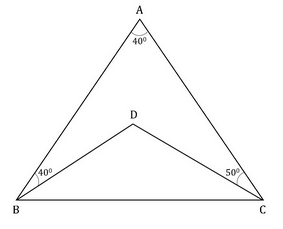
- a)25o
- b)50o
- c)65o
- d)130o
- e)140o
Correct answer is option 'D'. Can you explain this answer?
ABC and BDC are two triangles as shown in the given figure. If BDC is an isosceles triangle in which BD = DC. Find the value of ∠BDC.
a)
25o
b)
50o
c)
65o
d)
130o
e)
140o

|
Aditya Joshi answered |
Since BD = CD,AngleDBC = AngleDCB (Let them be x)
Now three sides of triangles sums up to 180.AngleABC + AngleCBA + AngleCAB = 18040 +40+50+x+x = 180solving this, x = 25.
in triangle DBC,25+25+AngleDBC = 180angleDBC = 130
Now three sides of triangles sums up to 180.AngleABC + AngleCBA + AngleCAB = 18040 +40+50+x+x = 180solving this, x = 25.
in triangle DBC,25+25+AngleDBC = 180angleDBC = 130
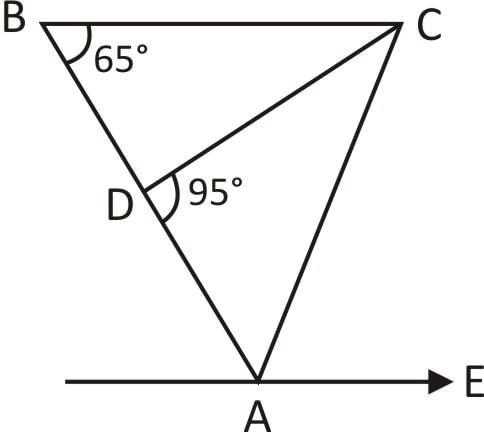
In the figure given below, ABC is a triangle. BC is parallel to AE. If BC = AC, then what is the value of ∠CAE?
- a)20°
- b)30°
- c)40°
- d)50°
Correct answer is option 'D'. Can you explain this answer?
In the figure given below, ABC is a triangle. BC is parallel to AE. If BC = AC, then what is the value of ∠CAE?


a)
20°
b)
30°
c)
40°
d)
50°

|
Pioneer Academy answered |
Given that, BC || AE
∠CBA + ∠EAB = 180°
⇒ ∠EAB = 180° – 65° = 115°
∵ BC = AC
Hence, ΔABC is an isosceles triangle.
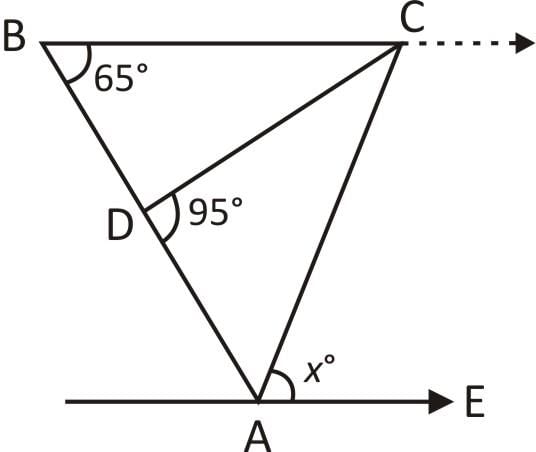
⇒ ∠CBA = ∠CAB = 65°
Now, ∠EAB = ∠EAC + ∠CAB
⇒ 115° = x + 65° ⇒ x = 50°.
Hence, option D is correct.
∠CBA + ∠EAB = 180°
⇒ ∠EAB = 180° – 65° = 115°
∵ BC = AC
Hence, ΔABC is an isosceles triangle.

⇒ ∠CBA = ∠CAB = 65°
Now, ∠EAB = ∠EAC + ∠CAB
⇒ 115° = x + 65° ⇒ x = 50°.
Hence, option D is correct.
The point of intersection of the altitudes of a triangle is called its:- a)Incentre
- b)Excentre
- c)Orthocentre
- d)Centroid
- e)none of these
Correct answer is option 'C'. Can you explain this answer?
The point of intersection of the altitudes of a triangle is called its:
a)
Incentre
b)
Excentre
c)
Orthocentre
d)
Centroid
e)
none of these
|
|
Alok Verma answered |
The three (possibly extended) altitudes intersect in a single point, called the orthocenter of the triangle, usually denoted by H. The orthocenter lies inside the triangle if and only if the triangle is acute (i.e. does not have an angle greater than or equal to a right angle).
The supplement of 154° 30’ is :- a)25° 30’
- b)44° 45’
- c)158° 45’
- d)168° 30’
Correct answer is option 'A'. Can you explain this answer?
The supplement of 154° 30’ is :
a)
25° 30’
b)
44° 45’
c)
158° 45’
d)
168° 30’

|
Pioneer Academy answered |
Supplement of 154° 30’ is 180° ‒ (154° 30’)
= (179° 30’) ‒ (154° 30’) {since 1° = 60’}
= 25° 30’.
= (179° 30’) ‒ (154° 30’) {since 1° = 60’}
= 25° 30’.
The straight lines AD and BC intersect one another at the point O. If ∠AOB + ∠BOD + ∠DOC = 274°, then ∠AOC is :- a)86°
- b)90°
- c)94°
- d)137°
Correct answer is option 'A'. Can you explain this answer?
The straight lines AD and BC intersect one another at the point O. If ∠AOB + ∠BOD + ∠DOC = 274°, then ∠AOC is :
a)
86°
b)
90°
c)
94°
d)
137°
|
|
Rahul Kapoor answered |
As we know that the sum of all the angles around a point is 360°.
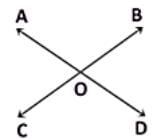
(∠AOB + ∠BOD + ∠DOC) + ∠AOC = 360°
∴ 274° + ∠AOC = 360° or ∠AOC = 86°.
Hence, option A is correct.

(∠AOB + ∠BOD + ∠DOC) + ∠AOC = 360°
∴ 274° + ∠AOC = 360° or ∠AOC = 86°.
Hence, option A is correct.
In the trapezium PQRS, QR || PS, ∠Q = 90°, PQ = QR and ∠PRS = 20°. If ∠TSR = θ, then the value of θ is:

- a)75°
- b)55°
- c)65°
- d)45°
Correct answer is option 'C'. Can you explain this answer?
In the trapezium PQRS, QR || PS, ∠Q = 90°, PQ = QR and ∠PRS = 20°. If ∠TSR = θ, then the value of θ is:


a)
75°
b)
55°
c)
65°
d)
45°

|
BT Educators answered |
In the given figure,
PQ = QR and ∠PQR = 90° ⇒ ∠QPR = ∠QRP = 45°.
∴ ∠QRS = (45° + 20°) = 65°.
∴ θ = ∠QRS = 65° (alt. ∠s)
PQ = QR and ∠PQR = 90° ⇒ ∠QPR = ∠QRP = 45°.
∴ ∠QRS = (45° + 20°) = 65°.
∴ θ = ∠QRS = 65° (alt. ∠s)
Hence, option C is correct.
Two right angled triangles are congruent if :
I.The hypotenuse of one triangle is equal to the hypotenuse of the other.
II.a side for one triangle is equal to the corresponding side of the other.
III.Sides of the triangles are equal.
IV. An angle of the triangle are equal.
Of these statements, the correct ones are combination of:- a)I and II
- b)II and III
- c)I and III
- d)IV only
- e)I and IV
Correct answer is option 'A'. Can you explain this answer?
Two right angled triangles are congruent if :
I.The hypotenuse of one triangle is equal to the hypotenuse of the other.
II.a side for one triangle is equal to the corresponding side of the other.
III.Sides of the triangles are equal.
IV. An angle of the triangle are equal.
Of these statements, the correct ones are combination of:
I.The hypotenuse of one triangle is equal to the hypotenuse of the other.
II.a side for one triangle is equal to the corresponding side of the other.
III.Sides of the triangles are equal.
IV. An angle of the triangle are equal.
Of these statements, the correct ones are combination of:
a)
I and II
b)
II and III
c)
I and III
d)
IV only
e)
I and IV

|
Hridoy Desai answered |
Explanation:
To determine which statements are correct for two right-angled triangles to be congruent, let's analyze each statement one by one:
I. The hypotenuse of one triangle is equal to the hypotenuse of the other.
This statement is correct. The hypotenuse is the side opposite the right angle in a right-angled triangle. If the hypotenuse of one triangle is equal to the hypotenuse of another triangle, then the triangles are congruent by the Hypotenuse-Leg Congruence Theorem.
II. A side for one triangle is equal to the corresponding side of the other.
This statement is correct. If a side of one triangle is equal to the corresponding side of another triangle, then the triangles are congruent by the Side-Side-Side (SSS) Congruence Theorem.
III. Sides of the triangles are equal.
This statement is incorrect. While it is true that if all three sides of one triangle are equal to the corresponding sides of another triangle, then the triangles are congruent, this statement does not specify which sides are equal. It is possible for two triangles to have equal sides but still not be congruent because the angles may be different.
IV. An angle of the triangle is equal.
This statement is incorrect. While it is true that if all three angles of one triangle are equal to the corresponding angles of another triangle, then the triangles are congruent, this statement only mentions that "an angle" is equal. It does not specify which angle is equal, and therefore, it cannot be used to determine congruence.
Conclusion:
The correct statements for two right-angled triangles to be congruent are I. The hypotenuse of one triangle is equal to the hypotenuse of the other and II. A side for one triangle is equal to the corresponding side of the other. Therefore, the correct answer is option 'A': I and II.
To determine which statements are correct for two right-angled triangles to be congruent, let's analyze each statement one by one:
I. The hypotenuse of one triangle is equal to the hypotenuse of the other.
This statement is correct. The hypotenuse is the side opposite the right angle in a right-angled triangle. If the hypotenuse of one triangle is equal to the hypotenuse of another triangle, then the triangles are congruent by the Hypotenuse-Leg Congruence Theorem.
II. A side for one triangle is equal to the corresponding side of the other.
This statement is correct. If a side of one triangle is equal to the corresponding side of another triangle, then the triangles are congruent by the Side-Side-Side (SSS) Congruence Theorem.
III. Sides of the triangles are equal.
This statement is incorrect. While it is true that if all three sides of one triangle are equal to the corresponding sides of another triangle, then the triangles are congruent, this statement does not specify which sides are equal. It is possible for two triangles to have equal sides but still not be congruent because the angles may be different.
IV. An angle of the triangle is equal.
This statement is incorrect. While it is true that if all three angles of one triangle are equal to the corresponding angles of another triangle, then the triangles are congruent, this statement only mentions that "an angle" is equal. It does not specify which angle is equal, and therefore, it cannot be used to determine congruence.
Conclusion:
The correct statements for two right-angled triangles to be congruent are I. The hypotenuse of one triangle is equal to the hypotenuse of the other and II. A side for one triangle is equal to the corresponding side of the other. Therefore, the correct answer is option 'A': I and II.
In ΔLMN, LM = |x-7|, MN = |x-4| and NL = x + 1, where x is a number whose value is not known. Is ΔLMN an acute triangle (a triangle each of whose angles measures less than 90∘)?(1) NM = 10(2) LM = 7- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
In ΔLMN, LM = |x-7|, MN = |x-4| and NL = x + 1, where x is a number whose value is not known. Is ΔLMN an acute triangle (a triangle each of whose angles measures less than 90∘)?
(1) NM = 10
(2) LM = 7
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Shivam Ghoshal answered |
Statement 1: NM = 10
Statement 2: LM = 7
To determine if LMN is an acute triangle, we need to compare the lengths of its sides.
Analysis of Statement 1:
NM = 10
Since we know the length of NM, we can find the difference between LM and NL by subtracting NM from MN.
MN - NM = |x-4| - 10 = |x-4|-10
Since we don't have any information about LM or NL, we cannot determine if LMN is an acute triangle based on this statement alone.
Analysis of Statement 2:
LM = 7
Since we know the length of LM, we can find the difference between LM and MN by subtracting LM from MN.
MN - LM = |x-4| - 7 = |x-4|-7
Again, since we don't have any information about NL or the value of x, we cannot determine if LMN is an acute triangle based on this statement alone.
Analysis of Statements 1 and 2 together:
Combining the information from both statements, we have:
NM = 10
LM = 7
Using these values, we can find the difference between LM and NL as well as the difference between LM and MN.
MN - NM = |x-4| - 10 = |x-4|-10
MN - LM = |x-4| - 7 = |x-4|-7
However, even with this additional information, we still cannot determine if LMN is an acute triangle because we do not know the value of x or have any constraints on its range.
Therefore, neither statement alone nor both statements together are sufficient to answer the question.
Hence, the correct answer is option D.
Statement 2: LM = 7
To determine if LMN is an acute triangle, we need to compare the lengths of its sides.
Analysis of Statement 1:
NM = 10
Since we know the length of NM, we can find the difference between LM and NL by subtracting NM from MN.
MN - NM = |x-4| - 10 = |x-4|-10
Since we don't have any information about LM or NL, we cannot determine if LMN is an acute triangle based on this statement alone.
Analysis of Statement 2:
LM = 7
Since we know the length of LM, we can find the difference between LM and MN by subtracting LM from MN.
MN - LM = |x-4| - 7 = |x-4|-7
Again, since we don't have any information about NL or the value of x, we cannot determine if LMN is an acute triangle based on this statement alone.
Analysis of Statements 1 and 2 together:
Combining the information from both statements, we have:
NM = 10
LM = 7
Using these values, we can find the difference between LM and NL as well as the difference between LM and MN.
MN - NM = |x-4| - 10 = |x-4|-10
MN - LM = |x-4| - 7 = |x-4|-7
However, even with this additional information, we still cannot determine if LMN is an acute triangle because we do not know the value of x or have any constraints on its range.
Therefore, neither statement alone nor both statements together are sufficient to answer the question.
Hence, the correct answer is option D.
Triangle ABC is an isosceles triangle with AB = AC and AD is the perpendicular dropped from vertex A on the side BC. What is the perimeter of triangle ABC?(1) ∠BAD = 2∠ACD(2) The perimeter of triangle ADB is 15 + 5√3- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
Triangle ABC is an isosceles triangle with AB = AC and AD is the perpendicular dropped from vertex A on the side BC. What is the perimeter of triangle ABC?
(1) ∠BAD = 2∠ACD
(2) The perimeter of triangle ADB is 15 + 5√3
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Arka Basu answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given:
- Isosceles ΔABC
- AB = AC
- So, perpendicular AD will bisect side BC.
- If we assume ∠ ABC to be xo, the different ∠s in the figure can be represented as below:
To find: Perimeter of ΔABC
- =AB + BC + CA
- = 2AB + BC
So, in order to find the perimeter, we need to know AC and BC
Knowing the ∠s may help us (because we may then employ trigonometric ratios)
Step 3: Analyze Statement 1 independently
(1) ∠BAD = 2∠ACD
90°- x° = 2x°
⇒ 3x° = 90°
⇒ x° = 30°
But we don’t know the magnitude of any side of the triangle. So, we cannot yet use trigonometric ratios to find the sides of the triangle.
Not sufficient.
Step 4: Analyze Statement 2 independently
(2) The perimeter of triangle ADB is 15 + 5√3
The value of 2AB + BC depends on the value of AD.
Since we do not know the value of AD, we cannot find the required value
Not sufficient.
- From Statement 2
- Using Equation II, a unique value of AD will be obtained
- Using Equation I, the value of 2AB + BC will be obtained
Sufficient.
Answer: Option C
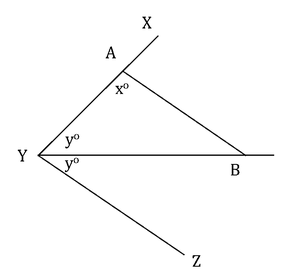 If yo = 45o, is xo = 90o?I. AB is parallel to YZII. AB = AY
If yo = 45o, is xo = 90o?I. AB is parallel to YZII. AB = AY- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficien
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'D'. Can you explain this answer?
If yo = 45o, is xo = 90o?
I. AB is parallel to YZ
II. AB = AY
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficien
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Rhea Gupta answered |
Steps 1 & 2: Understand Question and Draw Inferences
In ΔABY,
xo + yo + Angle ABY = 180o
- xo + 45o + Angle ABY = 180o
- xo + Angle ABY = 135o
We need to find if x is a right angle or not, i.e. if x = 90o.
For this we need the value of Angle ABY.
Step 3: Analyze Statement 1
Given that AB is parallel to YZ.
- xo + 2yo = 180 (Since both of them are consecutive interior angles).
Given that y = 45o
- x = 90o
Therefore, statement 1 is sufficient to arrive at a unique answer.
Step 4: Analyze Statement 2
Given AB = AY.
Therefore, Angle ABY = yo = 45o (given)
Therefore, xo + 45o = 135o
- x = 90o
Therefore, statement 2 is sufficient to arrive at a unique answer.
Step 5: Analyze Both Statements Together (if needed)
Since we arrived at a unique answer in at least one of step 3 and step 4, this step is not necessary.
Correct Answer: D
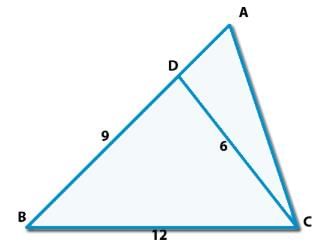
Consider the triangle shown in the figure where BC = 12 cm, Db = 9 cm, CD = 6 cm and What is the ratio of the perimeter of the triangle ADC to that of the triangle BDC ?
- a)7:9
- b)8:9
- c)6:9
- d)5:9
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
Consider the triangle shown in the figure where BC = 12 cm, Db = 9 cm, CD = 6 cm and What is the ratio of the perimeter of the triangle ADC to that of the triangle BDC ?


a)
7:9
b)
8:9
c)
6:9
d)
5:9
e)
None of these

|
Nayanika Bajaj answered |
Here, ∠ACB = c+180-(2c-b) = 180-(b+c)
So, We can say that Δ BCD and &delta ABC will be similar.
According to property of similarity,
AB/12 = 12/9
Hence,
AB = 16
AC/6 = 12/9
AC = 8
Hence, AD = 7 and AC = 8
Now,
Perimeter of Delta; ADC / Perimeter of &delta BDC,
= (6+7+8)/(9+6+12)
= 21/27 = 7/9.
So, We can say that Δ BCD and &delta ABC will be similar.
According to property of similarity,
AB/12 = 12/9
Hence,
AB = 16
AC/6 = 12/9
AC = 8
Hence, AD = 7 and AC = 8
Now,
Perimeter of Delta; ADC / Perimeter of &delta BDC,
= (6+7+8)/(9+6+12)
= 21/27 = 7/9.
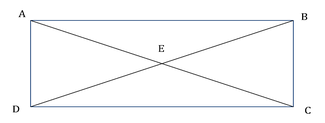 In the figure shown above, point E is the intersection point of the diagnoals AC and BD of rectangle ABCD. Is AB greater than BC?
In the figure shown above, point E is the intersection point of the diagnoals AC and BD of rectangle ABCD. Is AB greater than BC? - AE = 5 cms and AB = 7.25 cm
- The perimeter of AEB is greater than the perimeter of BEC
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is 'D'. Can you explain this answer?
In the figure shown above, point E is the intersection point of the diagnoals AC and BD of rectangle ABCD. Is AB greater than BC?
- AE = 5 cms and AB = 7.25 cm
- The perimeter of AEB is greater than the perimeter of BEC
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.
|
|
Aisha Gupta answered |
Steps 1 & 2: Understand Question and Draw Inferences
In the given rectangle ABCD, we need to find if AB > BC, i.e., if the length is greater than the breadth.
Note that AC and BD are the diagonals of the rectangle and E is their point of intersection.
In right triangle ADC, by Pythagoras Theorem,
AD2 + DC2 = AC2 . . . (1)
Similarly, in right triangle DCB,
DC2 + BC2 = DB2 . . . (2)
Equation (1) – Equation (2):
AD2 – BC2 = AC2 – DB2
Being opposite sides of a rectangle, AD = BC
Therefore, the above equation becomes:
0 = AC2 – DB2Therefore, AC = DB.
Thus, we observe that the two diagonals of the rectangle are equal.
As we know that diagonals of a rectangle bisect each other, we can write
AE = BE = CE = DE = AC/2 = BD/2
(Now, it is also easy to notice that the rectangle is symmetrical about point E.
Therefore, point E will divide each diagonal in half. )
Step 3: Analyze Statement 1
Given AE = 5
- AC = 10
Also, given that AB = 7.25
Notice that ABC is a right angled triangle. Applying Pythagoras theorem
AC2 = AB2 + BC2
- BC2 = 102 – 7.252
Therefore, we can calculate the value of BC and so we can arrive at a unique answer on whether AB is greater than BC or not.
Statement 1 is sufficient to arrive at a unique answer.
Step 4: Analyze Statement 2
Perimeter of AEB > Perimeter of BEC
- AE + BE + AB > BE + CE + BC
- AB > BC (Since we already noted that AE = BE = CE = DE)
Statement 2 is sufficient to arrive at a unique answer.
Step 5: Analyze Both Statements Together (if needed)
We arrived at a unique answer in step 3 and step 4 above. Therefore, this step is not needed.
Correct Answer: D
In the given figure, if AOB is a straight line, then the value of x is:

- a)90°
- b)45°
- c)22.5°
- d)150°
Correct answer is option 'B'. Can you explain this answer?
In the given figure, if AOB is a straight line, then the value of x is:


a)
90°
b)
45°
c)
22.5°
d)
150°

|
Wizius Careers answered |
As, (x + 30°) + 45° + (x + 15°) = 180°
⇒ x = 45°.
⇒ x = 45°.
What is the value of a?
(1) The area of an equilateral triangle of side length 3a units is 9√3 square units
(2) The area of an isosceles triangle whose sides are of length 4a, 4a and a units is 3√7 square units- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'D'. Can you explain this answer?
What is the value of a?
(1) The area of an equilateral triangle of side length 3a units is 9√3 square units
(2) The area of an isosceles triangle whose sides are of length 4a, 4a and a units is 3√7 square units
(1) The area of an equilateral triangle of side length 3a units is 9√3 square units
(2) The area of an isosceles triangle whose sides are of length 4a, 4a and a units is 3√7 square units
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Pallabi Sengupta answered |
Steps 1 & 2: Understand Question and Draw Inferences
To find: the value of a
Step 3: Analyze Statement 1 independently
- Area of an equilateral Δ of side length 3a is 9√3
So, a = 2 (rejecting a = -2 because the side of a triangle, 3a, cannot be negative)
Thus, Statement 1 alone is sufficient to answer the question
Thus, Statement 1 alone is sufficient to answer the question
Step 4: Analyze Statement 2 independently
- The area of an isosceles triangle whose sides are of length 4a, 4a and a units is 3√7 square units
- Let’s draw the given triangle:
- A perpendicular on the side that measures a units from the opposite vertex will bisect this side (Property of Isosceles triangles)
- Let the height of the perpendicular be h
- So, by applying Pythagoras Theorem,
=> 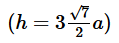 (Rejecting the negative value of h since the length of a perpendicular cannot be negative)
(Rejecting the negative value of h since the length of a perpendicular cannot be negative)
so a2 =4
That is, a = 2 (rejecting a = -2 because the side of a triangle, 3a, cannot be
negative)
negative)
Thus, Statement 2 alone is sufficient to answer the question
Step 5: Analyze both Statements together (if needed)
Since we’ve already arrived at a unique answer in each of Steps 3 and 4, this
step is not required
Since we’ve already arrived at a unique answer in each of Steps 3 and 4, this
step is not required
Answer: Option D
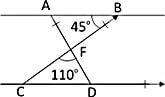
In the given figure, AB || CD, m∠ABF = 45° and m∠CFC = 110°. Then, m∠FDC is:
- a)25°
- b)45°
- c)35°
- d)30°
Correct answer is option 'A'. Can you explain this answer?
In the given figure, AB || CD, m∠ABF = 45° and m∠CFC = 110°. Then, m∠FDC is:


a)
25°
b)
45°
c)
35°
d)
30°

|
Pioneer Academy answered |
As in the given figure,
∠FCD = ∠FBA = 45° (alt. ∠s)
∴ ∠FDC = 180° ‒ (110° + 45°) = 25°.
Hence, option A is correct.
∠FCD = ∠FBA = 45° (alt. ∠s)
∴ ∠FDC = 180° ‒ (110° + 45°) = 25°.
Hence, option A is correct.
Consider the following statementsI. The locus of points which are equidistant from two parallel lines is a line parallel to both of them and drawn mid way between them.
II. The perpendicular distance of any point on this locus line from two original parallel lines are equal. Further, no point outside this locus line has this property.Which of the above statements is/are correct?- a)Only I
- b)Only II
- c)Both I and II
- d)Neither I nor II
Correct answer is option 'C'. Can you explain this answer?
Consider the following statements
I. The locus of points which are equidistant from two parallel lines is a line parallel to both of them and drawn mid way between them.
II. The perpendicular distance of any point on this locus line from two original parallel lines are equal. Further, no point outside this locus line has this property.
II. The perpendicular distance of any point on this locus line from two original parallel lines are equal. Further, no point outside this locus line has this property.
Which of the above statements is/are correct?
a)
Only I
b)
Only II
c)
Both I and II
d)
Neither I nor II
|
|
Rahul Kapoor answered |
Statements I and II are both true, because the locus of points which are equidistant from two parallel lines is a line parallel to both of them and draw mid way between them.
Also, it is true that the perpendicular distances of any point on this locus line from two original parallel lines are equal. Further, no point outside this locus line has this property.
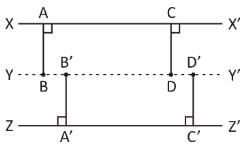
Hence, option C is correct.
Also, it is true that the perpendicular distances of any point on this locus line from two original parallel lines are equal. Further, no point outside this locus line has this property.

Hence, option C is correct.

In the figure given above LOM is a straight line. What is the value of x°?- a)45°
- b)60°
- c)70°
- d)80°
Correct answer is option 'B'. Can you explain this answer?

In the figure given above LOM is a straight line. What is the value of x°?
a)
45°
b)
60°
c)
70°
d)
80°

|
Pioneer Academy answered |
From the given figure,
∠LOQ + ∠QOP + ∠POM = 180°
(straight line)
∴ (x° + 20°) + 50° + (x° – 10°) = 180°
⇒ 2x° + 60° = 180° ⇒ 2x° = 120°
∴ x° = 60°
Hence, optuion B is correct.
∠LOQ + ∠QOP + ∠POM = 180°
(straight line)
∴ (x° + 20°) + 50° + (x° – 10°) = 180°
⇒ 2x° + 60° = 180° ⇒ 2x° = 120°
∴ x° = 60°
Hence, optuion B is correct.
In the given figure, line CE is drawn parallel to DB. If ∠BAD = 110°, ∠ABD = 30°, ∠ADC = 75° and ∠BCD = 60°, then the value of x° is:
- a)45°
- b)75°
- c)85°
- d)120°
Correct answer is option 'C'. Can you explain this answer?
In the given figure, line CE is drawn parallel to DB. If ∠BAD = 110°, ∠ABD = 30°, ∠ADC = 75° and ∠BCD = 60°, then the value of x° is:


a)
45°
b)
75°
c)
85°
d)
120°

|
EduRev GMAT answered |
As in the given figure,
∠ADB = 180° ‒ (110° + 30°) = 40°.
So, ∠BDC = (75° ‒ 40°) = 35°.
∠ADB = 180° ‒ (110° + 30°) = 40°.
So, ∠BDC = (75° ‒ 40°) = 35°.
∴ ∠DBC = 180° ‒ (60° + 35°) = 85°.
∴ ∠BCE = ∠DBC = 85° (alt. ∠s).
So, x = 85°.
Hence, option C is correct.
Hence, option C is correct.
Is the perimeter of triangle ABC greater than 6 cm? (1) One side of triangle ABC measures 3 cm (2) The lengths of the three sides of triangle ABC are consecutive integers - a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'D'. Can you explain this answer?
Is the perimeter of triangle ABC greater than 6 cm?
(1) One side of triangle ABC measures 3 cm
(2) The lengths of the three sides of triangle ABC are consecutive integers
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Ananya Iyer answered |
Steps 1 & 2: Understand Question and Draw Inferences
Let’s say the sides of the triangle are a, b, and c.
Let the perimeter of the triangle be X.
Thus, X = a + b + c
We need to find whether X > 6
Since we don’t have any other information, let’s move on to the analysis of the statement 1.
Step 3: Analyse Statement 1
Statement 1 says: One side of triangle ABC measures 3 cm.
Let’s assume a = 3 cm
Now, we know that the sum of two sides of a triangle is always greater than the third side.
So, we can write:
b + c > a
Adding a to both sides of this inequality, we get:
a + b + c > 2a
That is, X > 2a
Substituting a = 3 cm in this inequality, we get:
X > 6 cm
Thus, Statement 1 alone is sufficient to answer the question.
Step 4: Analyse Statement 2
Statement 2 says: The lengths of the three sides of triangle ABC are consecutive integers.
So, the lengths of the sides are n, (n+1), (n+2) cm, where n is a positive integer.
Perimeter X = n + (n+1) + (n+2)
X = 3n + 3
X = 3(n+1)
Now, we know that the sum of two sides of a triangle is always greater than the third side.
This means, we can write:
n + (n+1) > n + 2
2n + 1 > n + 2
n > 1
Adding 1 to both sides of this inequality:
n + 1 > 2
We know that multiplying both sides of an inequality with a positive number doesn’t change the inequality. Therefore, multiplying both sides of the above inequality with 3:
3(n+1) > 6
This means, X > 6
Thus, Statement 2 alone is sufficient to determine if X > 6
Step 5: Analyse Both Statements Together (if needed)
Since we got the answer to the question in Steps 3 and 4, we don’t need to perform this step.
Answer: Option (D)
In the given figure AB || CD, ∠ALC = 60° and EC is the bisector of ∠LCD. If EF || AB then the value of ∠CEF is
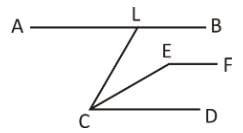
- a)120°
- b)140°
- c)150°
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
In the given figure AB || CD, ∠ALC = 60° and EC is the bisector of ∠LCD. If EF || AB then the value of ∠CEF is


a)
120°
b)
140°
c)
150°
d)
None of these

|
Notes Wala answered |
∠ALC = ∠LCD = 60°
[∵ Alternate angles]
EC is the bisector of ∠LCD
∴ ∠ ECD = (1 / 2) × ∠ LCD
= (1 / 2) × 60º = 30º
∠CEF + ∠ECD = 180°
[∵ Pair of interior angles]
∠CEF + 30° = 180°
∠CEF = 180° – 30° = 150°
Hence, option C is correct.
In the adjoining figure, ∠ABC = 100°, ∠EDC = 120° and AB || DE. Then, ∠BCD is equal to:

- a)80°
- b)60°
- c)40°
- d)20°
Correct answer is option 'C'. Can you explain this answer?
In the adjoining figure, ∠ABC = 100°, ∠EDC = 120° and AB || DE. Then, ∠BCD is equal to:


a)
80°
b)
60°
c)
40°
d)
20°

|
Pioneer Academy answered |
In the given figure,
Produce AB to meet CD at F.
∠BFD = ∠EDF = 120° (alt. ∠s)
∠BFC = (180° ‒ 120°) = 60°.
∠CBF = (180° ‒ 100°) = 80°.
∴ ∠BCF = 180° ‒ (60° + 80°) = 40°.
Hence, option C is correct.
Produce AB to meet CD at F.
∠BFD = ∠EDF = 120° (alt. ∠s)
∠BFC = (180° ‒ 120°) = 60°.
∠CBF = (180° ‒ 100°) = 80°.
∴ ∠BCF = 180° ‒ (60° + 80°) = 40°.
Hence, option C is correct.
If two supplementary angles differ by 44°, then one of the angle is:- a)72°
- b)102°
- c)65°
- d)68°
Correct answer is option 'D'. Can you explain this answer?
If two supplementary angles differ by 44°, then one of the angle is:
a)
72°
b)
102°
c)
65°
d)
68°

|
Hridoy Desai answered |
If two supplementary angles differ by 44 degrees, we can set up the equation:
x + (x + 44) = 180
Simplifying this equation, we have:
2x + 44 = 180
Subtracting 44 from both sides, we get:
2x = 136
Dividing both sides by 2, we find:
x = 68
So, one angle is 68 degrees, and the other angle (which differs by 44 degrees) is 112 degrees.
x + (x + 44) = 180
Simplifying this equation, we have:
2x + 44 = 180
Subtracting 44 from both sides, we get:
2x = 136
Dividing both sides by 2, we find:
x = 68
So, one angle is 68 degrees, and the other angle (which differs by 44 degrees) is 112 degrees.
In a Δ ABC, (1 / 2) ∠A + (1 / 3) ∠C + (1 / 2) ∠B = 80°, then what is the value of ∠C?
- a)35°
- b)40°
- c)60°
- d)70°
Correct answer is option 'C'. Can you explain this answer?
In a Δ ABC, (1 / 2) ∠A + (1 / 3) ∠C + (1 / 2) ∠B = 80°, then what is the value of ∠C?
a)
35°
b)
40°
c)
60°
d)
70°

|
Advait Roy answered |
In a sentence, it seems that the sentence is incomplete. Could you please provide more information or complete the sentence?
In Δ PQR, PS is the bisector of ∠ P and PT ⊥ OR, then ∠ TPS is equal to:- a)∠Q + ∠ R
- b)900 + 1/2 ∠Q
- c)900 - 1/2 ∠R
- d)1/2 (∠ Q - ∠ R)
- e)None of These
Correct answer is option 'D'. Can you explain this answer?
In Δ PQR, PS is the bisector of ∠ P and PT ⊥ OR, then ∠ TPS is equal to:
a)
∠Q + ∠ R
b)
900 + 1/2 ∠Q
c)
900 - 1/2 ∠R
d)
1/2 (∠ Q - ∠ R)
e)
None of These

|
Abhishek Kapoor answered |
∠1 + ∠2 = ∠3 [PS is bisector.] ------ (1)
∠Q = 900 - ∠1
∠R = 900 -∠2 - ∠3
So,
∠Q - ∠R = (900 - ∠1) - (900 - ∠2 - ∠3)
∠Q - ∠R = ∠2 + ∠3 - ∠1
∠Q - ∠ R = ∠2 + (∠1 + ∠2) -∠1[using equation 1]
∠Q - ∠R = 2 ∠2
1/2 * (∠Q - ∠R) = ∠TPS.
∠Q = 900 - ∠1
∠R = 900 -∠2 - ∠3
So,
∠Q - ∠R = (900 - ∠1) - (900 - ∠2 - ∠3)
∠Q - ∠R = ∠2 + ∠3 - ∠1
∠Q - ∠ R = ∠2 + (∠1 + ∠2) -∠1[using equation 1]
∠Q - ∠R = 2 ∠2
1/2 * (∠Q - ∠R) = ∠TPS.
In ΔABC, point D lies on the side AB between vertices A and B.
If CD = CB, is AD > BC?
(1) ∠ADC = 110
(2) ∠ACD = 30
- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'C'. Can you explain this answer?
In ΔABC, point D lies on the side AB between vertices A and B.
If CD = CB, is AD > BC?
(1) ∠ADC = 110
(2) ∠ACD = 30
If CD = CB, is AD > BC?
(1) ∠ADC = 110
(2) ∠ACD = 30
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Mrinalini Dasgupta answered |
step 1 & 2: Understand Question and Draw Inference
Given:
Given:
Representing the given information visually as below:
- In triangle BCD, CD = CB
- So, angles opposite to these sides will be equal. Let these angles measure Xo
- Let ∠ACD = y∘
- So, the different angles in this figure will be as under:
To find: If AD > BC
- That is, if AD > CD (since BC = CD)
- That is, if in triangle ADC,
- ∠ACD > ∠DAC (since sides opposite to greater angles are greater)
- That is, y∘ > x∘ − y∘
- That is, 2y∘ > x∘
- So, the answer to the question will be YES if
- 2y∘ > x∘
Step 3 : Analyze Statement 1 independent
Step 4 : Analyze Statement 2 independent
Step 5: Analyze Both Statements Together (if needed)
From Statement 1:x = 70∘
From Statement 2: y = 30∘
From Statement 2: y = 30∘
Since we now know the values of xo and yo we can determine if 2yo > Xo
Thus, the 2 statements together are sufficient to answer the question.
Answer: Option C
The complement of 72° 40’ is :- a)107° 20’
- b)27° 20’
- c)17° 20’
- d)12° 40’
Correct answer is option 'C'. Can you explain this answer?
The complement of 72° 40’ is :
a)
107° 20’
b)
27° 20’
c)
17° 20’
d)
12° 40’
|
|
Rahul Kapoor answered |
Complement of 72° 40’ is 90° ‒ (72° 40’)
= (89° 60’) ‒ (72° 40’) {since 1° = 60’}
= 17° 20’
= (89° 60’) ‒ (72° 40’) {since 1° = 60’}
= 17° 20’
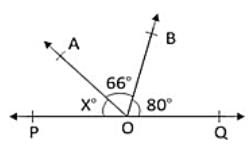
In the given figure, the value of x, that would make POQ a straight line, is :
- a)50°
- b)44°
- c)34°
- d)33°
Correct answer is option 'C'. Can you explain this answer?
In the given figure, the value of x, that would make POQ a straight line, is :


a)
50°
b)
44°
c)
34°
d)
33°
|
|
Rahul Kapoor answered |
POQ will be a straight line,
If 80° + 66° + x = 180°, i.e. x = 34°.
If 80° + 66° + x = 180°, i.e. x = 34°.
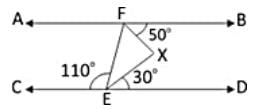
In the given figure, if AB || CD, then ∠FXE is equal to:
- a)30°
- b)50°
- c)70°
- d)80°
Correct answer is option 'D'. Can you explain this answer?
In the given figure, if AB || CD, then ∠FXE is equal to:


a)
30°
b)
50°
c)
70°
d)
80°
|
|
Rahul Kapoor answered |
As per the given figure,
∠BFE = ∠CEF = 110° (alt. ∠s).
So, ∠XFE = ∠BFE ‒ ∠BFX = (110° ‒ 50°) = 60°.
And on straight line CD,
110° + ∠FEX + 30° = 180° ⇒ ∠FEX = 40°.
Now, ∠XFE + ∠FEX + ∠FXE = 180° ⇒ 60° + 40° + ∠FXE = 180°.
∴ ∠FXE = 80°.
Hence, option D is correct.
∠BFE = ∠CEF = 110° (alt. ∠s).
So, ∠XFE = ∠BFE ‒ ∠BFX = (110° ‒ 50°) = 60°.
And on straight line CD,
110° + ∠FEX + 30° = 180° ⇒ ∠FEX = 40°.
Now, ∠XFE + ∠FEX + ∠FXE = 180° ⇒ 60° + 40° + ∠FXE = 180°.
∴ ∠FXE = 80°.
Hence, option D is correct.
In the figure given below, AB is parallel to CD. ∠ABC = 65°, ∠CDE = 15° and AB = AE. What is the value of ∠AEF?

- a)30°
- b)35°
- c)40°
- d)45°
Correct answer is option 'B'. Can you explain this answer?
In the figure given below, AB is parallel to CD. ∠ABC = 65°, ∠CDE = 15° and AB = AE. What is the value of ∠AEF?


a)
30°
b)
35°
c)
40°
d)
45°
|
|
Rahul Kapoor answered |
Given that,
∠ABC = 65° and ∠CDE = 15°
Here, ∠ABC + ∠TCB = 180°
(∵ AB || CD)
∠TCB = 180° – ∠ABC
∴ ∠TCB = 180° – 65° = 115°
∵ ∠TCB + ∠DCB = 180°
(Linear pair)
∴ ∠DCB = 65°
Now, in ΔCDE
∠CED = 180° – (∠ECD + ∠EDC)
(∵ ∠ECD = ∠BCD)
= 180° – (– 65° + 15° ) = 100°
∵ ∠DEC + ∠FEC = 180°

∵ ∠DEC + ∠FEC = 180°
⇒ ∠FEC = 180° – 100° = 80°
Given that, AB = AE.
i.e. ΔABE an isosceles triangle.
∴ ∠ABE = ∠AEB = 65°
∵ ∠AEB + ∠AEF + ∠FEC = 180°
(straight line)
⇒ 65° + x° + 80° = 180°
∴ x° = 180° – 145° = 35°.
Hence, option B is correct.
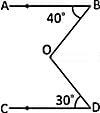
In the given figure, AB || CD, ∠ABO = 40° and ∠CDO = 30°. If ∠DOB = x°, then the value of x is:
- a)35°
- b)110°
- c)70°
- d)140°
Correct answer is option 'C'. Can you explain this answer?
In the given figure, AB || CD, ∠ABO = 40° and ∠CDO = 30°. If ∠DOB = x°, then the value of x is:


a)
35°
b)
110°
c)
70°
d)
140°

|
Notes Wala answered |
In the given figure,

Through O draw EOF parallel to AB & so to CD.
∴ ∠BOF = ∠ABO = 40° (alt. ∠s)
Similarly, ∠FOD = ∠CDO = 30° (alt. ∠s)
∴ ∠BOD = (40° + 30°) = 70°.
So, x = 70°.

Through O draw EOF parallel to AB & so to CD.
∴ ∠BOF = ∠ABO = 40° (alt. ∠s)
Similarly, ∠FOD = ∠CDO = 30° (alt. ∠s)
∴ ∠BOD = (40° + 30°) = 70°.
So, x = 70°.
Hence, option C is correct.
Two straight lines AB and CD cut each other at O. If ∠BOD = 63°, then ∠BOC is:- a)63°
- b)117°
- c)17°
- d)153°
Correct answer is option 'B'. Can you explain this answer?
Two straight lines AB and CD cut each other at O. If ∠BOD = 63°, then ∠BOC is:
a)
63°
b)
117°
c)
17°
d)
153°
|
|
Rahul Kapoor answered |
As given ∠BOD = 63°
Since COD is a straight line, we have:
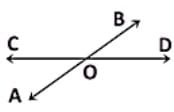
∠BOC + ∠BOD = 180°. So, ∠BOC = (180° ‒ 63°) = 117°.
Since COD is a straight line, we have:

∠BOC + ∠BOD = 180°. So, ∠BOC = (180° ‒ 63°) = 117°.
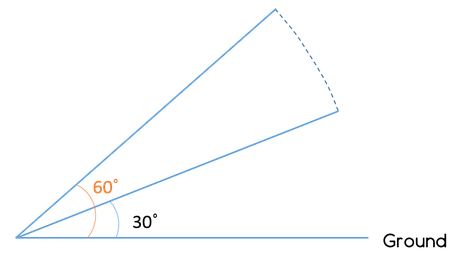 The figure above shows the position, at two instants of time, of a 10-meter-long rod as it was falling down to the ground. If one end of the rod was pinned to the ground, by what vertical distance did the rod fall between the two instants of time?
The figure above shows the position, at two instants of time, of a 10-meter-long rod as it was falling down to the ground. If one end of the rod was pinned to the ground, by what vertical distance did the rod fall between the two instants of time?- a)
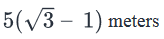
- b)

- c)

- d)
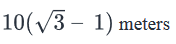
- e)

Correct answer is option 'A'. Can you explain this answer?
The figure above shows the position, at two instants of time, of a 10-meter-long rod as it was falling down to the ground. If one end of the rod was pinned to the ground, by what vertical distance did the rod fall between the two instants of time?
a)
b)
c)
d)
e)
|
|
Aarav Sharma answered |
Given:
- Length of rod = 10 meters
- Angle with the ground at 1st instant = 60o
- Angle with the ground at 2nd instant = 30o
To find:
- Vertical distance covered between the 2 instants
Approach:
- We will first try to understand the question
- To do so, let us:
- Drop perpendiculars from the free end of the rod at both instants of time
- Label the triangles thus formed
- From the diagram, it is clear that we need to find AB – PQ
- (Note: if you are not sure how AB – PQ is equal to the vertical distance covered by the ladder, drop a perpendicular PX on AB. You’ll see that BQPX is a rectangle and so, PQ = BX. So, AB – PQ = AB – BX = AX. The ladder was earlier at a height of A and it is now at a height of X. So, the distance AX clearly denotes the vertical distance covered by the ladder.)
- Thus, we need to find AB – PQ
- AB is a side of right ΔOBA, which is 30-60- 90 Triangle and angle AOB = 60o
- PQ is a side of right ΔOQP, which is also a 30-60-90 Triangle with angle POQ = 30o
- In each of the 2 right triangles, we know a side and two angles.
- So, by using side ratio property of 30-60-90 triangle, we can find the required values
Working Out:
- Finding AB
- In right ΔOBA
- OB: AB: OA = 1: √3: 2
- We know OA = 10
- AB: OA = √3: 2
- Thus AB = 5√3
- In right ΔOBA
- Finding PQ
- In right ΔOQP
- PQ: OQ: PO = 1: √3: 2
- We know PO = 10
- PQ: PO = 1: 2
- Thus PQ = 5
- In right ΔOQP
- Thus, AB – PQ = 5√3 – 5 = 5 (√3 -1) meters
- Therefore, the correct answer is Option A.
In the figure given above, EC is parallel to AB, ∠ECD = 70° and ∠BDO = 20°. What is the value of ∠OBD?
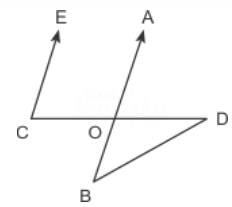
- a)20°
- b)30°
- c)40°
- d)50°
Correct answer is option 'D'. Can you explain this answer?
In the figure given above, EC is parallel to AB, ∠ECD = 70° and ∠BDO = 20°. What is the value of ∠OBD?


a)
20°
b)
30°
c)
40°
d)
50°

|
Notes Wala answered |
Given that, EC || AB
∴ ∠ECO + ∠AOC = 180°
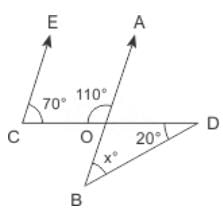
⇒ ∠AOC = 180° – 70° = 110°
∴ ∠ECO + ∠AOC = 180°

⇒ ∠AOC = 180° – 70° = 110°
∴ ∠BOD = ∠AOC = 110°
(alternate angle)
Now, in ΔOBD
∠BOD + ∠ODB + ∠DBO = 180°
∴ 110° + 20° + x° = 180° ⇒ x° = 50°.
Hence, option D is correct.
The angles x°, a°, c° and (π – b)° are indicated in the figure given below. Which one of the following is correct?
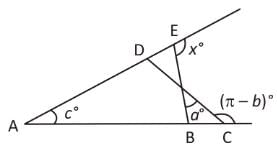
- a)x° = a° + c° – b°
- b)x° = b° – a° – c°
- c)x° = a° + b° + c°
- d)x° = a° – b° + c°
Correct answer is option 'C'. Can you explain this answer?
The angles x°, a°, c° and (π – b)° are indicated in the figure given below. Which one of the following is correct?


a)
x° = a° + c° – b°
b)
x° = b° – a° – c°
c)
x° = a° + b° + c°
d)
x° = a° – b° + c°
|
|
Rahul Kapoor answered |
∠PCT + ∠PCB = π
(Linear pair)
(Linear pair)
∠PCB = π – (π – b°) = b° ..... (i)

In ΔBPC,

In ΔBPC,
∠PCB + ∠BPC + ∠PBC = π
∠PBC = π – ∠PCB – ∠BPC = π – b° – a° ..... (ii)
∵ ∠ABE + ∠EBC = π
(∵ ∠PBC = ∠EBC) (linear pair)
∠ABE = π – ∠PBC = π – (π – b° – a°) = a° + b° ...(iii)
(∵ ∠PBC = ∠EBC) (linear pair)
∠ABE = π – ∠PBC = π – (π – b° – a°) = a° + b° ...(iii)
Now, in ΔABE
Sum of two interior angles = Exterior angle
∠EAB + ∠ABE = ∠BES ⇒ c° + b° + a° = x°
∴ x° = a° + b° + c°.
Hence, option C is correct.
A wheel makes 12 revolutions per min. The angle in radian described by a spoke of the wheel in 1 s is:- a)5π/2
- b)2π/5
- c)3π/5
- d)4π/5
Correct answer is option 'B'. Can you explain this answer?
A wheel makes 12 revolutions per min. The angle in radian described by a spoke of the wheel in 1 s is:
a)
5π/2
b)
2π/5
c)
3π/5
d)
4π/5

|
Advait Roy answered |
To find the angle described by a spoke of the wheel in 1 second, we need to find the angle described by the wheel in 1 second and then divide it by the number of spokes on the wheel.
The wheel makes 12 revolutions per minute, so it makes 12 * 2π radians per minute.
To find the angle described by the wheel in 1 second, we divide by 60 (since there are 60 seconds in a minute): (12 * 2π) / 60 = 2π/5 radians per second.
Since there are typically 4 spokes on a wheel, we divide the angle described by the wheel in 1 second by 4 to find the angle described by a spoke in 1 second: (2π/5) / 4 = π/10 radians per second.
Therefore, the angle described by a spoke of the wheel in 1 second is π/10 radians.
The wheel makes 12 revolutions per minute, so it makes 12 * 2π radians per minute.
To find the angle described by the wheel in 1 second, we divide by 60 (since there are 60 seconds in a minute): (12 * 2π) / 60 = 2π/5 radians per second.
Since there are typically 4 spokes on a wheel, we divide the angle described by the wheel in 1 second by 4 to find the angle described by a spoke in 1 second: (2π/5) / 4 = π/10 radians per second.
Therefore, the angle described by a spoke of the wheel in 1 second is π/10 radians.
Consider the following statementsIf two straight lines intersect, then
I. vertically opposite angles are equal.
II. vertically opposite angles are supplementary.
III. adjacent angles are complementary.Which of the statements given above is/are correct?- a)Only III
- b)Only I
- c)II and III
- d)II and II
Correct answer is option 'B'. Can you explain this answer?
Consider the following statements
If two straight lines intersect, then
I. vertically opposite angles are equal.
II. vertically opposite angles are supplementary.
III. adjacent angles are complementary.
I. vertically opposite angles are equal.
II. vertically opposite angles are supplementary.
III. adjacent angles are complementary.
Which of the statements given above is/are correct?
a)
Only III
b)
Only I
c)
II and III
d)
II and II
|
|
Rahul Kapoor answered |
Here, AB and CD are two lines.

If two straight lines intersect, then opposite vertically angles are equal.
Hence, option B is correct.

If two straight lines intersect, then opposite vertically angles are equal.
Hence, option B is correct.
In the given figure, AOB is a straight line. If ∠AOC + ∠BOD = 85°, then ∠COD is:
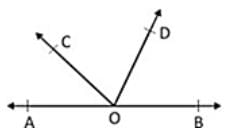
- a)85°
- b)90°
- c)95°
- d)100°
Correct answer is option 'C'. Can you explain this answer?
In the given figure, AOB is a straight line. If ∠AOC + ∠BOD = 85°, then ∠COD is:


a)
85°
b)
90°
c)
95°
d)
100°

|
Pioneer Academy answered |
Clearly,
∠AOC + ∠COD + ∠BOD = 180°
∴ 85° + ∠COD = 180°. So, ∠COD = (180° ‒ 85°) = 95°.
Hence, option C is correct.
∠AOC + ∠COD + ∠BOD = 180°
∴ 85° + ∠COD = 180°. So, ∠COD = (180° ‒ 85°) = 95°.
Hence, option C is correct.
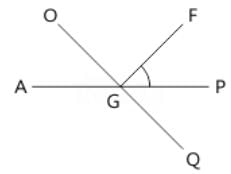
In the given figure lines AP and OQ intersect at G. If ∠AGO + ∠PGF = 70° and ∠PGQ = 40°. Find the angle value of ∠PGF.
- a)31°
- b)35°
- c)30°
- d)20°
Correct answer is option 'C'. Can you explain this answer?
In the given figure lines AP and OQ intersect at G. If ∠AGO + ∠PGF = 70° and ∠PGQ = 40°. Find the angle value of ∠PGF.


a)
31°
b)
35°
c)
30°
d)
20°

|
Notes Wala answered |
As AP is a straight line and rays GO and GF stands on it.
∴ ∠AGO + ∠OGF + ∠PGF = 180°
∴ ∠AGO + ∠OGF + ∠PGF = 180°
⇒ (∠AGO + ∠PGF) + ∠OGF = 180°
⇒ 70° + ∠OGF = 180°
⇒ ∠OGF = 180° – 70°
⇒ ∠OGF = 110°
As, OQ is a straight line, rays GF and GP stands on it.
∠OGF + ∠PGF + ∠PGQ = 180°
Putting the value of ∠OGF & ∠PGQ
110° + ∠PGF + 40° = 180°
∠PGF = 180° – 150° = 30°
Hence, option C is correct.
Hence, option C is correct.
A right angled triangle, right angled at point B has angles such that a<c<b where a, b, c correspond to the angles at points A, B, C. If the area of the triangle is 2 which of the following inequality indicates the range of values of side BC.- a)0 < BC < 2
- b)0 < BC < √2
- c)0 < BC < 4
- d)0<BC < 2√2
- e)0 < BC < 8
Correct answer is option 'A'. Can you explain this answer?
A right angled triangle, right angled at point B has angles such that a<c<b where a, b, c correspond to the angles at points A, B, C. If the area of the triangle is 2 which of the following inequality indicates the range of values of side BC.
a)
0 < BC < 2
b)
0 < BC < √2
c)
0 < BC < 4
d)
0<BC < 2√2
e)
0 < BC < 8

|
Moumita Sen answered |
Since it is given that ΔABC is right angled at B, Angle ABC = 90∘
Also, area of ΔABC = ½ * AB * BC = 2
AB*BC = 4
But it is given that a < c
Therefore, BC < AB
In the extreme case of BC = AB (which is not possible according to the given condition),
BC = AB = 2
However, since BC < AB
BC should be less than 2 and AB should be greater than 2.
Therefore, BC < 2
Also, since BC is a side of a triangle, it is positive and greater than zero
Therefore, BC > 0
Combining the above two inequalities, we get:
0 < BC < 2
Correct Answer: A
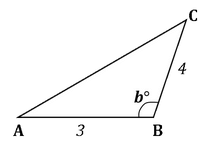 The figure above shows a triangle ABC in which the measure of ∠ABC, b∘is greater than 90∘ If AB = 3 units and BC = 4 units, which of the following can be the measure of side AC?
The figure above shows a triangle ABC in which the measure of ∠ABC, b∘is greater than 90∘ If AB = 3 units and BC = 4 units, which of the following can be the measure of side AC? - 6
- 7
- 8
- a)I only
- b)II only
- c)III only
- d)I, II and III
- e)None of the above
Correct answer is option 'A'. Can you explain this answer?
The figure above shows a triangle ABC in which the measure of ∠ABC, b∘is greater than 90∘
If AB = 3 units and BC = 4 units, which of the following can be the measure of side AC?
- 6
- 7
- 8
a)
I only
b)
II only
c)
III only
d)
I, II and III
e)
None of the above

|
Mrinalini Dasgupta answered |
Given:
- An obtuse triangle, 2 of whose sides are AB = 3 and BC = 4 units
To find:
- The possible measure of the side AC that is opposite to the obtuse angle
Approach & Working:
- To answer the question, we need to think of the constraints on AC. From the theory of triangles, we can figure that there are 2 constraints on AC:
- Constraint 1: Since triangle ABC is obtuse-angled at B, AC2 > AB2 + BC2
- Constraint 2: The sum of any 2 sides of a triangle must be greater than the 3rd side. So, AB + BC > AC
- So, we will work out the range of possible values of AC by applying these 2 constraints, and then see, which of the 3 given values fit this range.
- Applying Constraint 1
- AC2 > 32 + 42
- AC2 > 9 + 16
- AC2 > 25
- So, AC > 5
- Applying Constraint 2
- AB + BC > AC
- So, 3 + 4 > AC
- 7 > AC
- Rewritten as: AC < 7
- Getting to the answer
- Thus, we see that 5 < AC < 7
- The only value, out of the 3 options, that satisfies this range is Option I
Thus, the correct answer is Option A
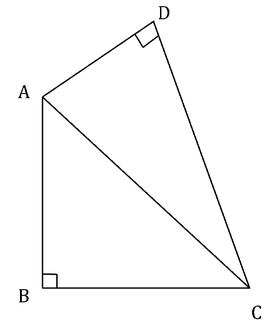 Is AD > BC?I. Angle CAB = Angle BCAII. CD > AB
Is AD > BC?I. Angle CAB = Angle BCAII. CD > AB- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'B'. Can you explain this answer?
Is AD > BC?
I. Angle CAB = Angle BCA
II. CD > AB
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Athira Choudhury answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given a quadrilateral ABCD with right angles at B and D.
We need to find if AD > BC is true.
Step 3: Analyze Statement 1
Given that Angle CAB = Angle BCA
Therefore, in ΔABC,
Angle CAB = Angle BCA = 45o
Therefore, BC = AB
This doesn’t give us any relation between AD and BC.
So statement 1 is not sufficient to arrive at a unique answer.
Step 4: Analyze Statement 2
Given that CD > AB.
In the right angled triangle ABC, we have
AC2 = AB2 + BC2
Similarly, in the right angled triangle ADC, we have
AC2 = AD2 + CD2
Therefore,
AD2 + CD2 = AB2 + BC2……………. (I)
Given that CD > AB
- CD2 > AB2
In other words, a term in the LHS of (I) is greater than another term in the RHS of (I)
So for (I) to be true (the equality to hold true), the remaining terms on either sides of LHS and RHS should compensate for the imbalance created by CD2 and AB2.
From (I),
CD2 -AB2 = BC2 -AD2
Let’s say CD2 – AB2 = k (a positive number since CD2 > AB2)
Then
BC2 – AD2 = k (the same positive number).
Therefore, BC2 > AD2
- BC > AD
Therefore, statement 2 is sufficient to arrive at a unique answer.
Step 5: Analyze Both Statements Together (if needed)
We arrived at a unique answer in step 4 above. Therefore, this step is not needed.
Correct Answer: B
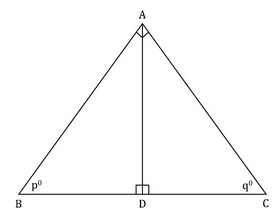 From the given diagram, find the area of triangle ABC.
From the given diagram, find the area of triangle ABC. - po = qo
- The product of AB and AC is 9.
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
From the given diagram, find the area of triangle ABC.
- po = qo
- The product of AB and AC is 9.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Preitee Ranjan Pradhan answered |

In a triangle ABC,∠ A = 900, AL is drawn perpendicular to BC, Then ∠ BAL is equal to:
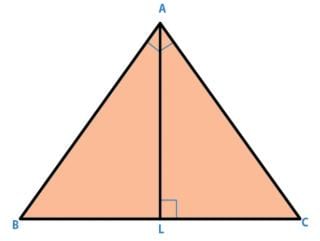
- a)∠ALC
- b)∠ACB
- c)∠BAC
- d)∠B - ∠BAL
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
In a triangle ABC,∠ A = 900, AL is drawn perpendicular to BC, Then ∠ BAL is equal to:


a)
∠ALC
b)
∠ACB
c)
∠BAC
d)
∠B - ∠BAL
e)
None of these

|
Nayanika Bajaj answered |
∠ BAL + ∠ B + 900 = 1800
or, ∠ BAL + ∠ B = 900
or, ∠ BAL = 900 - ∠ B ----------- (1)
Now, in Δ ABC,
∠ ACB + ∠ B + ∠ A = 1800
∠ ACB = 900
-∠ B ----- (2)
From, (1) and (2),
∠ BAL = ∠ ACB.
or, ∠ BAL + ∠ B = 900
or, ∠ BAL = 900 - ∠ B ----------- (1)
Now, in Δ ABC,
∠ ACB + ∠ B + ∠ A = 1800
∠ ACB = 900
-∠ B ----- (2)
From, (1) and (2),
∠ BAL = ∠ ACB.
Chapter doubts & questions for Lines, Angles and Triangles - Mathematics for Digital SAT 2025 is part of SAT exam preparation. The chapters have been prepared according to the SAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for SAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Lines, Angles and Triangles - Mathematics for Digital SAT in English & Hindi are available as part of SAT exam.
Download more important topics, notes, lectures and mock test series for SAT Exam by signing up for free.
Mathematics for Digital SAT
184 videos|124 docs|75 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily