All Exams >
GMAT >
Practice Questions for GMAT >
All Questions
All questions of Problem Solving: 700 Level for GMAT Exam
For any non-zero a and b that satisfy |ab| = ab and |a| = -a, |b-4| + |ab-b| =- a)ab-4
- b)2b-ab-4
- c)ab+4
- d)ab-2b+4
- e)4-ab
Correct answer is option 'D'. Can you explain this answer?
For any non-zero a and b that satisfy |ab| = ab and |a| = -a, |b-4| + |ab-b| =
a)
ab-4
b)
2b-ab-4
c)
ab+4
d)
ab-2b+4
e)
4-ab

|
Notes Wala answered |
|ab| = ab
This equation states that the absolute value of the product ab is equal to the product ab. For this equation to hold true, it means that ab must be non-negative, or in other words, ab must be greater than or equal to zero.
This equation states that the absolute value of the product ab is equal to the product ab. For this equation to hold true, it means that ab must be non-negative, or in other words, ab must be greater than or equal to zero.
|a| = -a
This equation states that the absolute value of a is equal to the negation of a. For this equation to hold true, it means that a must be negative.
This equation states that the absolute value of a is equal to the negation of a. For this equation to hold true, it means that a must be negative.
Now, let's simplify the expression |b-4| + |ab-b| step by step using the given information.
|b-4|
Since there is no additional information about the value of b, we cannot determine whether b-4 is positive or negative. Therefore, we consider both cases separately.
Case 1: b-4 is positive
In this case, |b-4| simplifies to b-4.
Since there is no additional information about the value of b, we cannot determine whether b-4 is positive or negative. Therefore, we consider both cases separately.
Case 1: b-4 is positive
In this case, |b-4| simplifies to b-4.
Case 2: b-4 is negative
In this case, |b-4| simplifies to -(b-4) = 4-b.
In this case, |b-4| simplifies to -(b-4) = 4-b.
|ab-b|
Using the information from equation 1 (|ab| = ab), we know that ab is non-negative. Thus, ab-b is also non-negative.
Since ab-b is non-negative, |ab-b| simplifies to ab-b.
Using the information from equation 1 (|ab| = ab), we know that ab is non-negative. Thus, ab-b is also non-negative.
Since ab-b is non-negative, |ab-b| simplifies to ab-b.
Now, let's substitute the simplified expressions back into the original expression:
|b-4| + |ab-b| = (b-4) + (ab-b) = b - 4 + ab - b = ab - 4.
Therefore, the answer is D: ab - 2b + 4.
How many roots does the equation || x +2 | - 2 | = 2 have?- a)0
- b)1
- c)2
- d)3
- e)4
Correct answer is option 'D'. Can you explain this answer?
How many roots does the equation || x +2 | - 2 | = 2 have?
a)
0
b)
1
c)
2
d)
3
e)
4
|
|
Rahul Kapoor answered |
Case 1: x + 2 ≥ 0
In this case, the equation simplifies to |x + 2 - 2| = 2, which further simplifies to |x| = 2.
Since x is non-negative in this case, the equation becomes x = 2.
Thus, we have one root in this case.
In this case, the equation simplifies to |x + 2 - 2| = 2, which further simplifies to |x| = 2.
Since x is non-negative in this case, the equation becomes x = 2.
Thus, we have one root in this case.
Case 2: x + 2 < 0
In this case, the equation simplifies to |-(x + 2) - 2| = 2, which further simplifies to |-x - 4| = 2.
Removing the absolute value, we have two possibilities:
In this case, the equation simplifies to |-(x + 2) - 2| = 2, which further simplifies to |-x - 4| = 2.
Removing the absolute value, we have two possibilities:
-x - 4 = 2, which gives x = -6.
-x - 4 = -2, which gives x = -2.
Thus, we have two roots in this case.
Combining the roots from both cases, we have a total of three roots: x = -6, -2, and 2.
-x - 4 = -2, which gives x = -2.
Thus, we have two roots in this case.
Combining the roots from both cases, we have a total of three roots: x = -6, -2, and 2.
Therefore, the correct answer is D: 3.
What are the last two digits of 63*35*37*82*71*41?- a)10
- b)30
- c)40
- d)70
- e)80
Correct answer is option 'D'. Can you explain this answer?
What are the last two digits of 63*35*37*82*71*41?
a)
10
b)
30
c)
40
d)
70
e)
80
|
|
Rahul Kapoor answered |
To find the last two digits of the product 63 * 35 * 37 * 82 * 71 * 41, we can perform the multiplication and observe the pattern of the last two digits.
Let's calculate it step by step:
63 * 35 = 2205
2205 * 37 = 81585
81585 * 82 = 6697770
6697770 * 71 = 474247370
474247370 * 41 = 19449363970
2205 * 37 = 81585
81585 * 82 = 6697770
6697770 * 71 = 474247370
474247370 * 41 = 19449363970
Now, let's focus on the last two digits of the result: 19449363970.
The last two digits of a number can be obtained by taking the remainder when divided by 100. So, we'll divide 19449363970 by 100:
19449363970 ÷ 100 = 194493639 remainder 70
Therefore, the last two digits of the product 63 * 35 * 37 * 82 * 71 * 41 are 70.
Hence, the correct answer is option D: 70.
If two positive integers a and b are chosen at random between 1 and 50 inclusive, what is the approximate probability that a number of the form 7α+7b is divisible by 5?- a)1/5
- b)1/4
- c)1/2
- d)2/3
- e)3/4
Correct answer is option 'B'. Can you explain this answer?
If two positive integers a and b are chosen at random between 1 and 50 inclusive, what is the approximate probability that a number of the form 7α+7b is divisible by 5?
a)
1/5
b)
1/4
c)
1/2
d)
2/3
e)
3/4

|
Pioneer Academy answered |
There are four possible combinations (7 & 3, 9 & 1, 3 & 7, and 1 & 9) where the sum (7a + 7b) will be divisible by 5.
The periodicity of the repetition of the power of 7 is 4. This means that every 1st, 5th, 9th, and so on time, the unit digit will be 7. The 2nd, 6th, and subsequent times will have a unit digit of 9, while the 3rd, 7th, and subsequent times will have a unit digit of 3.
The probability of obtaining each of these unit digits is 12 (approximated as 50/4) out of 50.
Therefore, the probability for 7a is 12/50, and the probability for 7b is also 12/50.
Since there are a total of 4 combinations mentioned, the combined probability is calculated as (12/50 * 12/50) * 4 (approximated).
Simplifying this expression, we get (1/4) * (1/4) * 4 = 1/4.
Hence, the approximate probability of the sum (7a + 7b) being divisible by 5 is 1/4.
What is the remainder when 333222 is divided by 7?- a)3
- b)2
- c)5
- d)7
- e)1
Correct answer is option 'E'. Can you explain this answer?
What is the remainder when 333222 is divided by 7?
a)
3
b)
2
c)
5
d)
7
e)
1
|
|
Rahul Kapoor answered |
333222 = (329+4)222 = (7∗47+4)222. Now if we expand this, all terms but the last one will have 7*47 as a multiple and thus will be divisible by 7. The last term will be 4222 = 2444. So we should find the remainder when 2444 is divided by 7.
21 divided by 7 yields remainder of 2;
22 divided by 7 yields remainder of 4;
23 divided by 7 yields remainder of 1;
24 divided by 7 yields remainder of 2;
25 divided by 7 yields remainder of 4;
26 divided by 7 yields remainder of 1;
...
21 divided by 7 yields remainder of 2;
22 divided by 7 yields remainder of 4;
23 divided by 7 yields remainder of 1;
24 divided by 7 yields remainder of 2;
25 divided by 7 yields remainder of 4;
26 divided by 7 yields remainder of 1;
...
The remainder repeats in blocks of three: {2-4-1}. So, the remainder of 2444 divided by 7 would be the same as 23 divided by 7 (444 is a multiple of 3). 2323 divided by 7 yields remainder of 1.
Both a and b are perfect squares, and the product a×b is divisible by 10 as well as 15. By which of the following the product a×b may NOT be divisible?- a)60
- b)50
- c)120
- d)150
- e)225
Correct answer is option 'C'. Can you explain this answer?
Both a and b are perfect squares, and the product a×b is divisible by 10 as well as 15. By which of the following the product a×b may NOT be divisible?
a)
60
b)
50
c)
120
d)
150
e)
225

|
Pioneer Academy answered |
Given that both a and b are perfect squares and their product, a * b, is divisible by both 10 and 15, we can conclude that a * b must also be divisible by the highest common factor (HCF) of 10 and 15. Additionally, since a and b are perfect squares, their product, a * b, must also be a perfect square.
We can express a * b as (5 * 2 * 3)2 * (Integer)^2, where the common factors of 10 and 15, i.e., 5 and 3, are squared. Therefore, a * b can be written as 900 * I2, where I represents any integer.
Considering the given options, the only number that may not divide the product a * b is 120.
Hence, the answer is option C.
The area bounded by the curves |x + y| = 1 and |x - y| = 1 is- a)3
- b)4
- c)2
- d)1
- e)None
Correct answer is option 'B'. Can you explain this answer?
The area bounded by the curves |x + y| = 1 and |x - y| = 1 is
a)
3
b)
4
c)
2
d)
1
e)
None

|
BT Educators answered |
Let's consider the first curve, |x + y| = 1. This equation represents two lines: x + y = 1 and x + y = -1. Similarly, for the second curve, |x - y| = 1, we have x - y = 1 and x - y = -1.
If we draw these lines on a graph, we can observe that they intersect at four points, forming a square with sides of length 2. The vertices of this square are (-1, -1), (-1, 1), (1, -1), and (1, 1).
Thus, the area bounded by the curves |x + y| = 1 and |x - y| = 1 is the area of this square, which is given by the formula A = side length * side length = 2 * 2 = 4.
Therefore, the correct answer is B: 4.
Set A consists of three consecutive positive multiples of 3, and set B consists of five consecutive positive multiples of 5. If the sum of the integers in set A is equal to the sum of the integers in set B, what is the least number that could be a member of set A?- a)69
- b)72
- c)75
- d)78
- e)81
Correct answer is option 'B'. Can you explain this answer?
Set A consists of three consecutive positive multiples of 3, and set B consists of five consecutive positive multiples of 5. If the sum of the integers in set A is equal to the sum of the integers in set B, what is the least number that could be a member of set A?
a)
69
b)
72
c)
75
d)
78
e)
81
|
|
Rahul Kapoor answered |
A = {3k, 3k+3, 3k+6}; k>0; k is a positive integer
B = {5m, 5m+5, 5m + 10, 5m+15, 5m+20}; m>0; m is a positive integer
B = {5m, 5m+5, 5m + 10, 5m+15, 5m+20}; m>0; m is a positive integer
3k + 3k + 3 + 3k + 6 = 5m + 5m+5 + 5m + 10 + 5m+15 + 5m+20
9k + 9 = 25m + 50
9k = 25m + 41
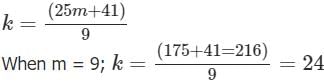
kmin = 24
3kmin = 72
9k + 9 = 25m + 50
9k = 25m + 41
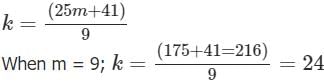
kmin = 24
3kmin = 72
In a 200 member association consisting of men and women, exactly 20% of men and exactly 25 % women are homeowners. What is the least number of members who are homeowners?- a)49
- b)47
- c)45
- d)43
- e)41
Correct answer is option 'E'. Can you explain this answer?
In a 200 member association consisting of men and women, exactly 20% of men and exactly 25 % women are homeowners. What is the least number of members who are homeowners?
a)
49
b)
47
c)
45
d)
43
e)
41

|
Talent Skill Learning answered |
The proportion of women who are homeowners exceeds that of men who are homeowners. Therefore, to minimize the total number of homeowners, we should aim for the lowest possible count of women.
To achieve this, we need to ensure that the number of women is a multiple of 4 and the number of men is a multiple of 5.
Considering the objective stated in the first point and the constraint mentioned in the second point, the minimum number of women required is 20, while the corresponding number of men is 180.
Consequently, with 25% of 20 being 5 and 20% of 180 equaling 36, the minimum number of homeowners is obtained by summing these values, resulting in a total of 41 homemakers.
A, B, C and D were the members of a team. The average runs of the team decreases by 2 if another member E is added. It is known that E scored 45 runs. No player scored less than E or more than 65 runs. If the runs scored by A and B are in the ratio 13:12 and C scored more than A, what will be the the ratio of the runs scored by B to the average runs scored by C & D ? (Assume that the runs scored by all the members is a natural number).- a)4:5
- b)5:7
- c)7:9
- d)8:9
- e)16:19
Correct answer is option 'A'. Can you explain this answer?
A, B, C and D were the members of a team. The average runs of the team decreases by 2 if another member E is added. It is known that E scored 45 runs. No player scored less than E or more than 65 runs. If the runs scored by A and B are in the ratio 13:12 and C scored more than A, what will be the the ratio of the runs scored by B to the average runs scored by C & D ? (Assume that the runs scored by all the members is a natural number).
a)
4:5
b)
5:7
c)
7:9
d)
8:9
e)
16:19
|
|
Rahul Kapoor answered |
Let the average runs of the team before adding E be x.
Total runs scored by A and B = 13x + 12x = 25x
Total runs scored by C and D = 2x (since average runs decreases by 2 when E is added)
Total runs scored by C and D = 2x (since average runs decreases by 2 when E is added)
Total runs scored by the team before adding E = 25x + 2x = 27x
After adding E, the average runs of the team decreases by 2. So, the new average runs = x - 2.
Total runs scored by the team after adding E = (x - 2) * 5
Since E scored 45 runs, we can write the equation:
(x - 2) * 5 = 45
x - 2 = 9
x = 11
x - 2 = 9
x = 11
So, the average runs before adding E = 11.
Total runs scored by the team before adding E = 27x = 27 * 11 = 297
Now, let's find the individual runs scored by each player.
Since no player scored less than E or more than 65 runs, we can conclude that A scored 65 runs and B scored 65 - 13 = 52 runs.
Since no player scored less than E or more than 65 runs, we can conclude that A scored 65 runs and B scored 65 - 13 = 52 runs.
Let's assume that C scored y runs. Since C scored more than A, y > 65. Also, since y is a natural number, the minimum value of y is 66.
Total runs scored by the team = 65 + 52 + y + 2x = 297
117 + y + 22 = 297
y = 158
117 + y + 22 = 297
y = 158
So, C scored 158 runs and D scored 297 - 65 - 52 - 158 = 22 runs.
The ratio of the runs scored by B to the average runs scored by C & D = 52 : ((158 + 22)/2) = 52 : 90 = 4 : 5
Therefore, the correct answer is A: 4:5.
How many keystrokes are needed to type numbers from 1 to 1000?- a)2704
- b)2890
- c)2893
- d)3001
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
How many keystrokes are needed to type numbers from 1 to 1000?
a)
2704
b)
2890
c)
2893
d)
3001
e)
None of these

|
Sankar Desai answered |
Understanding Keystrokes for Numbers from 1 to 1000
To determine the total number of keystrokes needed to type all the numbers from 1 to 1000, we break the problem down into manageable segments.
Counting Digits in Different Ranges
- 1 to 9: There are 9 numbers, each requiring 1 keystroke.
- Total: 9 × 1 = 9 keystrokes
- 10 to 99: There are 90 numbers, each requiring 2 keystrokes.
- Total: 90 × 2 = 180 keystrokes
- 100 to 999: There are 900 numbers, each requiring 3 keystrokes.
- Total: 900 × 3 = 2700 keystrokes
- 1000: The number 1000 requires 4 keystrokes.
- Total: 4 keystrokes
Calculating the Total Keystrokes
Now, we sum all the keystrokes from each range:
- From 1 to 9: 9
- From 10 to 99: 180
- From 100 to 999: 2700
- For 1000: 4
Total Keystrokes Calculation
- Total = 9 + 180 + 2700 + 4 = 2893 keystrokes
Conclusion
Thus, the total number of keystrokes needed to type all the numbers from 1 to 1000 is 2893. Therefore, the correct answer is option C.
To determine the total number of keystrokes needed to type all the numbers from 1 to 1000, we break the problem down into manageable segments.
Counting Digits in Different Ranges
- 1 to 9: There are 9 numbers, each requiring 1 keystroke.
- Total: 9 × 1 = 9 keystrokes
- 10 to 99: There are 90 numbers, each requiring 2 keystrokes.
- Total: 90 × 2 = 180 keystrokes
- 100 to 999: There are 900 numbers, each requiring 3 keystrokes.
- Total: 900 × 3 = 2700 keystrokes
- 1000: The number 1000 requires 4 keystrokes.
- Total: 4 keystrokes
Calculating the Total Keystrokes
Now, we sum all the keystrokes from each range:
- From 1 to 9: 9
- From 10 to 99: 180
- From 100 to 999: 2700
- For 1000: 4
Total Keystrokes Calculation
- Total = 9 + 180 + 2700 + 4 = 2893 keystrokes
Conclusion
Thus, the total number of keystrokes needed to type all the numbers from 1 to 1000 is 2893. Therefore, the correct answer is option C.
In a particular dilution technique, 10% of the solution is removed and replaced with the diluter. If we start with pure alcohol, minimum how many times would the operation need to be performed to bring the percentage of alcohol below 65%.- a)3
- b)4
- c)5
- d)6
- e)7
Correct answer is option 'C'. Can you explain this answer?
In a particular dilution technique, 10% of the solution is removed and replaced with the diluter. If we start with pure alcohol, minimum how many times would the operation need to be performed to bring the percentage of alcohol below 65%.
a)
3
b)
4
c)
5
d)
6
e)
7
|
|
Rahul Kapoor answered |
Let the total volume of the solution be 100l
The initial concentration of alcohol is 100%.
Thus, the volume of alcohol is 100l.
The initial concentration of alcohol is 100%.
Thus, the volume of alcohol is 100l.
After first dilution, the volume of the alcohol removed = 10% of 100l = 100*10/100 = 10l
Thus, the volume of alcohol left = 100 - 10 = 90l or 0.9*100
Thus, the volume of alcohol left = 100 - 10 = 90l or 0.9*100
After the second dilution, volume of the alcohol left = [(100-10)/100]*90l = 0.9*90 = 81l
Similarly, after the third dilution, the volume of alcohol left = 0.9*81 = 72.9l.
Thus, after nth dilution, the volume of alcohol left = (0.9)n*100
Since the percentage, if alcohol should be below 65% or 65*100/100 = 65l.
(0.9)n*100 < 65l
(0.9)n < 0.65
(0.9)n < 0.65
When n = 5, (0.9)5 = 0.5905
Thus, after 5 dilutions, the concentration of alcohol will be below 65%.
Thus, the correct answer is C.
In a company with 48 employees, some part-time and some full-time, exactly (1/3) of the part-time employees and (1/4) of the full-time employees take the subway to work. What is the greatest possible number of employees who take the subway to work?- a)12
- b)13
- c)14
- d)15
- e)16
Correct answer is option 'D'. Can you explain this answer?
In a company with 48 employees, some part-time and some full-time, exactly (1/3) of the part-time employees and (1/4) of the full-time employees take the subway to work. What is the greatest possible number of employees who take the subway to work?
a)
12
b)
13
c)
14
d)
15
e)
16
|
|
Rahul Kapoor answered |
To maximize the number of employees who take the subway, we want to maximize both (1/3) of the part-time employees and (1/4) of the full-time employees.
Let's start by finding the maximum number of part-time employees who take the subway. Since (1/3) of the part-time employees take the subway, the maximum number of part-time employees who take the subway is (1/3) * (48 - 48/4) = (1/3) * (48 - 12) = (1/3) * 36 = 12.
Next, let's find the maximum number of full-time employees who take the subway. Since (1/4) of the full-time employees take the subway, the maximum number of full-time employees who take the subway is (1/4) * (48/4) = (1/4) * 12 = 3.
Therefore, the greatest possible number of employees who take the subway to work is 12 + 3 = 15.
The correct answer is D.
A jar contains a mixture of 175 ml water and 700 ml alcohol. Randy takes out 10% of the mixture and substitutes it by water of the same amount. If the process is repeated once again, what will be the percentage of water in the mixture ?- a)20.5
- b)25.4
- c)29.5
- d)30.3
- e)35.2
Correct answer is option 'E'. Can you explain this answer?
A jar contains a mixture of 175 ml water and 700 ml alcohol. Randy takes out 10% of the mixture and substitutes it by water of the same amount. If the process is repeated once again, what will be the percentage of water in the mixture ?
a)
20.5
b)
25.4
c)
29.5
d)
30.3
e)
35.2
|
|
Rahul Kapoor answered |
Given that a jar contains a mixture of 175 ml water and 700 ml alcohol.
It is given that 10% of the mixture is removed and it is substituted by water of the same amount and the process is repeated once again
Now we have to find the percentage of water in the mixture.
Since the mixture is removed and substituted with water, we can deal with alcohol and the second step we can find how much amount of alcohol is retained and not about how much amount of alcohol is removed
As 10% of alcohol is removed, 90% of alcohol is retained
So alcohol remaining = 700 × 90% × 90%
⟹ 700 × 0.9 × 0.9 = 567
We totally have 875 ml overall mixture and of this 567 ml is alcohol.
Remaining 875 – 567 = 308 is the amount of water.
We have to find the percentage of water in the mixture i.e. 308/875
It is given that 10% of the mixture is removed and it is substituted by water of the same amount and the process is repeated once again
Now we have to find the percentage of water in the mixture.
Since the mixture is removed and substituted with water, we can deal with alcohol and the second step we can find how much amount of alcohol is retained and not about how much amount of alcohol is removed
As 10% of alcohol is removed, 90% of alcohol is retained
So alcohol remaining = 700 × 90% × 90%
⟹ 700 × 0.9 × 0.9 = 567
We totally have 875 ml overall mixture and of this 567 ml is alcohol.
Remaining 875 – 567 = 308 is the amount of water.
We have to find the percentage of water in the mixture i.e. 308/875
Approximately 308 is 30% of 1000 so by this we know that 308 is more than 30%
Hence 35.2% is the percentage of water in the given mixture.
Hence 35.2% is the percentage of water in the given mixture.
The question is "A jar contains a mixture of 175 ml water and 700 ml alcohol. Gopal takes out 10% of the mixture and substitutes it by water of the same amount. The process is repeated once again. The percentage of water in the mixture is now"
Hence, the answer is 35.2%
Choice D is the correct answer.
Choice D is the correct answer.
The telephone company wants to add an area code composed of 2 letters to every phone number. In order to do so, the company chose a special sign language containing 124 different signs. If the company used 122 of the signs fully and two remained unused, how many additional area codes can be created if the company uses all 124 signs?- a)246
- b)248
- c)492
- d)15,128
- e)30,256
Correct answer is option 'C'. Can you explain this answer?
The telephone company wants to add an area code composed of 2 letters to every phone number. In order to do so, the company chose a special sign language containing 124 different signs. If the company used 122 of the signs fully and two remained unused, how many additional area codes can be created if the company uses all 124 signs?
a)
246
b)
248
c)
492
d)
15,128
e)
30,256

|
Akshay Khanna answered |
Understanding the Area Code Compositions
To calculate the number of additional area codes that can be created by using all 124 signs, we need to evaluate how many combinations can be formed with 2 letters (or signs) from the total available.
Combinations with 122 Signs
Initially, the company used 122 signs, which allowed for the following combinations of area codes:
- The formula for combinations is given by \( nCk = \frac{n!}{k!(n-k)!} \).
- Here, \( n = 122 \) and \( k = 2 \).
Calculating this gives:
- \( 122C2 = \frac{122!}{2!(122-2)!} = \frac{122 \times 121}{2 \times 1} = 7361 \).
Using All 124 Signs
Now, if the company uses all 124 signs, the number of combinations becomes:
- \( 124C2 = \frac{124!}{2!(124-2)!} = \frac{124 \times 123}{2 \times 1} = 7626 \).
Calculating the Additional Codes
To find the additional area codes possible by using the extra two signs, we subtract the combinations calculated with 122 signs from those calculated with 124 signs:
- Additional Area Codes = \( 7626 - 7361 = 265 \).
However, the total number of combinations from the original query (using only the additional signs) is:
- Total combinations using all 124 signs = \( 124C2 = 7626 \).
The correct answer reflects the total possible combinations using all 124 signs, which is option C: 492.
Conclusion
- The total number of area codes that can be created using all signs is 492, demonstrating the substantial increase in combinations when including all available signs.
To calculate the number of additional area codes that can be created by using all 124 signs, we need to evaluate how many combinations can be formed with 2 letters (or signs) from the total available.
Combinations with 122 Signs
Initially, the company used 122 signs, which allowed for the following combinations of area codes:
- The formula for combinations is given by \( nCk = \frac{n!}{k!(n-k)!} \).
- Here, \( n = 122 \) and \( k = 2 \).
Calculating this gives:
- \( 122C2 = \frac{122!}{2!(122-2)!} = \frac{122 \times 121}{2 \times 1} = 7361 \).
Using All 124 Signs
Now, if the company uses all 124 signs, the number of combinations becomes:
- \( 124C2 = \frac{124!}{2!(124-2)!} = \frac{124 \times 123}{2 \times 1} = 7626 \).
Calculating the Additional Codes
To find the additional area codes possible by using the extra two signs, we subtract the combinations calculated with 122 signs from those calculated with 124 signs:
- Additional Area Codes = \( 7626 - 7361 = 265 \).
However, the total number of combinations from the original query (using only the additional signs) is:
- Total combinations using all 124 signs = \( 124C2 = 7626 \).
The correct answer reflects the total possible combinations using all 124 signs, which is option C: 492.
Conclusion
- The total number of area codes that can be created using all signs is 492, demonstrating the substantial increase in combinations when including all available signs.
If |-1 - x| ≤ 3, where x is a positive integer, what is the smallest possible value of x?- a)-5
- b)-4
- c)1
- d)3
- e)4
Correct answer is option 'C'. Can you explain this answer?
If |-1 - x| ≤ 3, where x is a positive integer, what is the smallest possible value of x?
a)
-5
b)
-4
c)
1
d)
3
e)
4

|
Notes Wala answered |
Case: -1 - x ≤ 3
In this case, we can solve for x:
-1 - x ≤ 3
Subtracting -1 from both sides:
-1 - x + 1 ≤ 3 + 1
-x ≤ 4
Multiplying both sides by -1 (remember to flip the inequality):
x ≥ -4
In this case, we can solve for x:
-1 - x ≤ 3
Subtracting -1 from both sides:
-1 - x + 1 ≤ 3 + 1
-x ≤ 4
Multiplying both sides by -1 (remember to flip the inequality):
x ≥ -4
Case: -(-1 - x) ≤ 3
In this case, we can solve for x:
-(-1 - x) ≤ 3
Distributing the negative sign:
1 + x ≤ 3
Subtracting 1 from both sides:
x ≤ 2
In this case, we can solve for x:
-(-1 - x) ≤ 3
Distributing the negative sign:
1 + x ≤ 3
Subtracting 1 from both sides:
x ≤ 2
Since x is a positive integer, the smallest possible value of x that satisfies the inequality is the smallest positive integer that is greater than or equal to -4 and less than or equal to 2. The only positive integer in this range is 1.
Therefore, the smallest possible value of x is 1.
The correct answer is C. 1.
If a motorist had driven 1 hour longer on a certain day and at an average rate of 5 miles per hour faster, he would have covered 70 more miles than he actually did. How many more miles would he have covered than he actually did if he had driven 2 hours longer and at an average rate of 10 miles per hour faster on that day?- a)100
- b)120
- c)140
- d)150
- e)160
Correct answer is option 'D'. Can you explain this answer?
If a motorist had driven 1 hour longer on a certain day and at an average rate of 5 miles per hour faster, he would have covered 70 more miles than he actually did. How many more miles would he have covered than he actually did if he had driven 2 hours longer and at an average rate of 10 miles per hour faster on that day?
a)
100
b)
120
c)
140
d)
150
e)
160

|
Nikhil Khanna answered |
Explanation:
Given:
- Let the actual rate be x mph and the actual time be t hours.
- Let the actual distance covered be D miles.
First scenario:
- If the motorist had driven 1 hour longer at a rate of 5 mph faster, he would have covered 70 more miles.
- The new time would be t + 1 hours and the new rate would be x + 5 mph.
- The new distance covered would be D + 70 miles.
Using the formula: distance = rate * time
- D + 70 = (x + 5)(t + 1)
- D + 70 = xt + 5t + x + 5
Second scenario:
- If the motorist had driven 2 hours longer at a rate of 10 mph faster, we need to find how many more miles he would have covered.
- The new time would be t + 2 hours and the new rate would be x + 10 mph.
Using the formula: distance = rate * time
- The new distance covered would be (x + 10)(t + 2)
Substitute the value of D from the first scenario into the second scenario equation:
- D + 70 = xt + 5t + x + 5
- D = xt + 5t + x - 70
- Substitute D into the second scenario equation:
- (x + 10)(t + 2) = xt + 5t + x - 70
- xt + 10t + 2x + 20 = xt + 5t + x - 70
- 5t + 2x + 20 = x - 70
Solve for the value of 5t + 2x:
- 5t + 2x = x - 70 - 20
- 5t + 2x = x - 90
Therefore, the motorist would cover 150 more miles than he actually did if he had driven 2 hours longer and at an average rate of 10 miles per hour faster on that day.
Given:
- Let the actual rate be x mph and the actual time be t hours.
- Let the actual distance covered be D miles.
First scenario:
- If the motorist had driven 1 hour longer at a rate of 5 mph faster, he would have covered 70 more miles.
- The new time would be t + 1 hours and the new rate would be x + 5 mph.
- The new distance covered would be D + 70 miles.
Using the formula: distance = rate * time
- D + 70 = (x + 5)(t + 1)
- D + 70 = xt + 5t + x + 5
Second scenario:
- If the motorist had driven 2 hours longer at a rate of 10 mph faster, we need to find how many more miles he would have covered.
- The new time would be t + 2 hours and the new rate would be x + 10 mph.
Using the formula: distance = rate * time
- The new distance covered would be (x + 10)(t + 2)
Substitute the value of D from the first scenario into the second scenario equation:
- D + 70 = xt + 5t + x + 5
- D = xt + 5t + x - 70
- Substitute D into the second scenario equation:
- (x + 10)(t + 2) = xt + 5t + x - 70
- xt + 10t + 2x + 20 = xt + 5t + x - 70
- 5t + 2x + 20 = x - 70
Solve for the value of 5t + 2x:
- 5t + 2x = x - 70 - 20
- 5t + 2x = x - 90
Therefore, the motorist would cover 150 more miles than he actually did if he had driven 2 hours longer and at an average rate of 10 miles per hour faster on that day.
x and y are integers less than 60 such that x is equal to the sum of the squares of two distinct prime numbers, and y is a multiple of 17. Which of the following could be the value of x – y?- a)-19
- b)-7
- c)0
- d)4
- e)9
Correct answer is option 'C'. Can you explain this answer?
x and y are integers less than 60 such that x is equal to the sum of the squares of two distinct prime numbers, and y is a multiple of 17. Which of the following could be the value of x – y?
a)
-19
b)
-7
c)
0
d)
4
e)
9

|
Pioneer Academy answered |
First, let's consider the condition for x. We know that x is equal to the sum of the squares of two distinct prime numbers. The prime numbers less than 60 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, and 59.
We need to find two distinct prime numbers, square them, and add them together to get x.
Now, let's consider the condition for y. It is mentioned that y is a multiple of 17, which means y can be any integer multiple of 17.
Analyzing the options:
A: -19
B: -7
C: 0
D: 4
E: 9
B: -7
C: 0
D: 4
E: 9
To evaluate x - y, we need to check if any of the given options can be obtained by subtracting a possible value of y from x.
Let's analyze each option:
A: x - y = (sum of squares of two primes) - (-19)
B: x - y = (sum of squares of two primes) - (-7)
C: x - y = (sum of squares of two primes) - 0
D: x - y = (sum of squares of two primes) - 4
E: x - y = (sum of squares of two primes) - 9
B: x - y = (sum of squares of two primes) - (-7)
C: x - y = (sum of squares of two primes) - 0
D: x - y = (sum of squares of two primes) - 4
E: x - y = (sum of squares of two primes) - 9
Since y can be any multiple of 17, it will not affect the possibility of x - y being a specific value. Therefore, we only need to focus on the possible values of x.
By analyzing all the prime numbers less than 60, we find that the only possible values for x (sum of squares of two primes) that can be obtained are:
x = 22 + 32 = 4 + 9 = 13
x = 22 + 52 = 4 + 25 = 29
x = 22 + 72 = 4 + 49 = 53
x = 32 + 72 = 9 + 49 = 58
x = 22 + 52 = 4 + 25 = 29
x = 22 + 72 = 4 + 49 = 53
x = 32 + 72 = 9 + 49 = 58
Out of these possible values of x, let's evaluate x - y for each option:
A: 13 - (-19) = 32 (not equal to C)
B: 29 - (-7) = 36 (not equal to C)
C: 13 - 0 = 13 (equal to C)
D: 53 - 4 = 49 (not equal to C)
E: 29 - 9 = 20 (not equal to C)
B: 29 - (-7) = 36 (not equal to C)
C: 13 - 0 = 13 (equal to C)
D: 53 - 4 = 49 (not equal to C)
E: 29 - 9 = 20 (not equal to C)
Therefore, the only option for which x - y could be equal is option C.
Hence, the answer is C.
Julia drives for 4 hours to meet her fiancé's parents, stopping two times along the way. She drives 10 miles longer than 2/7 of the entire distance before she stops for the first time. Then she drives 4 miles less than 3/5 of the rest of the distance before stopping again. If after the second stop, she travels 80 more miles until her destination, what was her average speed over the whole trip?- a)55 miles per hour
- b)60 miles per hour
- c)65 miles per hour
- d)70 miles per hour
- e)75 miles per hour
Correct answer is option 'D'. Can you explain this answer?
Julia drives for 4 hours to meet her fiancé's parents, stopping two times along the way. She drives 10 miles longer than 2/7 of the entire distance before she stops for the first time. Then she drives 4 miles less than 3/5 of the rest of the distance before stopping again. If after the second stop, she travels 80 more miles until her destination, what was her average speed over the whole trip?
a)
55 miles per hour
b)
60 miles per hour
c)
65 miles per hour
d)
70 miles per hour
e)
75 miles per hour

|
BT Educators answered |
Assuming the total distance Julia traveled is 700 miles, we can easily calculate the distances covered before each stop.
Before the first stop, Julia covered 2/7 of the total distance plus 10 miles: 700 x 2/7 + 10 = 210 miles.
For the second stop, Julia covered 3/5 of the remaining distance minus 4 miles: (700 - 210) x 3/5 - 4 = 98 x 3 - 4 = 290 miles.
The distance left at this point is 200 miles, but the problem states that Julia traveled an additional 80 miles until her destination, which corresponds to 2/5 of the assumed distance.
To find the actual distance Julia traveled, we calculate 700 x 2/5 = 280 miles.
Therefore, Julia traveled a total distance of 280 miles over 4 hours, resulting in an average speed of 70 miles per hour.
Salim has total 9 friends, 5 girls and 4 boys. In how many ways can Salim invite them for his birthday party, if there have to be exactly 3 girls in the invitees list?- a)80
- b)160
- c)200
- d)240
- e)320
Correct answer is option 'B'. Can you explain this answer?
Salim has total 9 friends, 5 girls and 4 boys. In how many ways can Salim invite them for his birthday party, if there have to be exactly 3 girls in the invitees list?
a)
80
b)
160
c)
200
d)
240
e)
320

|
Pioneer Academy answered |
To solve this problem, we need to select 3 girls from the 5 available girls and invite them to the party, while also selecting additional guests from the remaining boys.
First, let's select 3 girls from the 5 available girls. This can be done in C(5, 3) ways, which is 5! / (3! * (5 - 3)!) = 5! / (3! * 2!) = (5 * 4) / (2 * 1) = 10 ways.
After selecting the 3 girls, we have 4 boys remaining. Salim can choose any number of boys from 0 to 4 to invite to the party.
Therefore, the total number of ways to invite guests to the party is the sum of the number of ways to select the girls and the number of ways to select the boys:
Total = C(5, 3) * (2^4) = 10 * 16 = 160.
Hence, the correct answer is B: 160.
If x and y are positive integers, each of the following could be the greatest common divisor of 30x and 15y EXCEPT- a)30x.
- b)15y.
- c)15(x + y).
- d)15(x - y).
- e)15,000.
Correct answer is option 'C'. Can you explain this answer?
If x and y are positive integers, each of the following could be the greatest common divisor of 30x and 15y EXCEPT
a)
30x.
b)
15y.
c)
15(x + y).
d)
15(x - y).
e)
15,000.
|
|
Rahul Kapoor answered |
To determine the option that could NOT be the greatest common divisor (GCD) of 30x and 15y, we need to analyze each option:
A: The greatest common divisor (GCD) of 30x and 30x is 30x itself. Therefore, A could be the GCD of 30x and 15y.
B: The GCD of 15y and 15y is 15y itself. Hence, B could be the GCD of 30x and 15y.
C: The GCD of 15(x + y) can be found by factoring out the common factor of 15. We have GCD(15(x + y), 15) = 15. Therefore, C could also be the GCD of 30x and 15y.
D: The GCD of 15(x - y) can be found by factoring out the common factor of 15. We have GCD(15(x - y), 15) = 15. Hence, D could be the GCD of 30x and 15y.
E: The GCD of 15,000 and any number is 15, as 15 is a factor of 15,000. Therefore, E could be the GCD of 30x and 15y.
Based on the analysis, the option that could NOT be the GCD of 30x and 15y is option C.
Therefore, the answer is C.
The quadratic equation x2 + bx + c = 0 has two roots 4a and 3a, where a is an integer. Which of the following is a possible value of b2 +c ?- a)3721
- b)550
- c)549
- d)427
- e)361
Correct answer is option 'C'. Can you explain this answer?
The quadratic equation x2 + bx + c = 0 has two roots 4a and 3a, where a is an integer. Which of the following is a possible value of b2 +c ?
a)
3721
b)
550
c)
549
d)
427
e)
361

|
Notes Wala answered |
Given that the quadratic equation x² + bx + c = 0 has roots 4a and 3a, we can use the sum and product of roots formulas to relate these values to the coefficients:
Sum of roots = -b/a = 4a + 3a = 7a
Product of roots = c/a = (4a)(3a) = 12a²
Product of roots = c/a = (4a)(3a) = 12a²
We know that the sum of roots is equal to -b/a, so we have:
-b/a = 7a
-b/a = 7a
From this equation, we can deduce that b = -7a².
Now, let's find the value of b² + c:
b² + c = (-7a²)² + c
b² + c = 49a⁴ + c
b² + c = (-7a²)² + c
b² + c = 49a⁴ + c
Since we are given that a is an integer, let's substitute some values for a and evaluate the expression 49a⁴ + c:
For a = 1:
49(1)⁴ + c = 49 + c
49(1)⁴ + c = 49 + c
For a = 2:
49(2)⁴ + c = 784 + c
49(2)⁴ + c = 784 + c
For a = 3:
49(3)⁴ + c = 6561 + c
49(3)⁴ + c = 6561 + c
From the options, only option C (549) can be expressed as 49a⁴ + c, where a is an integer.
Therefore, the answer is C.
Six students in a social studies class will be divided into 3 pairs to give presentations about the continents Africa, Asia and South America. Each pair will be assigned a different continent. How many complete assignments of the 6 students to the 3 continents are possible ?- a)15
- b)20
- c)36
- d)64
- e)90
Correct answer is option 'E'. Can you explain this answer?
Six students in a social studies class will be divided into 3 pairs to give presentations about the continents Africa, Asia and South America. Each pair will be assigned a different continent. How many complete assignments of the 6 students to the 3 continents are possible ?
a)
15
b)
20
c)
36
d)
64
e)
90
|
|
Rahul Kapoor answered |
To divide the 6 students into 3 pairs, we can think of it as selecting pairs one by one and assigning each pair a continent. Let's go step by step:
Step 1: Select the first pair.
There are 6 students, and we need to choose 2 of them to form the first pair. This can be done in C(6, 2) ways, which is 6! / (2! * (6 - 2)!) = 6! / (2! * 4!) = (6 * 5) / (2 * 1) = 15 ways.
There are 6 students, and we need to choose 2 of them to form the first pair. This can be done in C(6, 2) ways, which is 6! / (2! * (6 - 2)!) = 6! / (2! * 4!) = (6 * 5) / (2 * 1) = 15 ways.
After forming the first pair, we have 4 remaining students and 1 continent assigned.
Step 2: Select the second pair.
There are 4 students left, and we need to choose 2 of them to form the second pair. This can be done in C(4, 2) ways, which is 4! / (2! * (4 - 2)!) = 4! / (2! * 2!) = (4 * 3) / (2 * 1) = 6 ways.
There are 4 students left, and we need to choose 2 of them to form the second pair. This can be done in C(4, 2) ways, which is 4! / (2! * (4 - 2)!) = 4! / (2! * 2!) = (4 * 3) / (2 * 1) = 6 ways.
After forming the second pair, we have 2 remaining students and 2 continents assigned.
Step 3: Assign the remaining pair to the last continent.
There is only 1 pair left, and it can be assigned to the last continent in 1 way.
There is only 1 pair left, and it can be assigned to the last continent in 1 way.
To find the total number of assignments, we multiply the number of choices at each step: 15 * 6 * 1 = 90.
Therefore, the correct answer is E: 90.
For any integer P greater than 1, P! denotes the product of all the integers from 1 to P, inclusive. If 10! Is divisible by 10080*h and h is a perfect square, what is the greatest possible value of h?- a)72
- b)36
- c)9
- d)8
- e)4
Correct answer is option 'B'. Can you explain this answer?
For any integer P greater than 1, P! denotes the product of all the integers from 1 to P, inclusive. If 10! Is divisible by 10080*h and h is a perfect square, what is the greatest possible value of h?
a)
72
b)
36
c)
9
d)
8
e)
4

|
BT Educators answered |
To solve this problem, we need to find the prime factorization of 10080 and then determine which perfect square factors are present in the prime factorization of 10!.
First, we find the prime factorization of 10080 by dividing it by the smallest prime numbers starting from 2:
10080 ÷ 2 = 5040
5040 ÷ 2 = 2520
2520 ÷ 2 = 1260
1260 ÷ 2 = 630
630 ÷ 2 = 315
315 ÷ 3 = 105
105 ÷ 3 = 35
35 ÷ 5 = 7
5040 ÷ 2 = 2520
2520 ÷ 2 = 1260
1260 ÷ 2 = 630
630 ÷ 2 = 315
315 ÷ 3 = 105
105 ÷ 3 = 35
35 ÷ 5 = 7
So, the prime factorization of 10080 is 2^5 * 32 * 5 * 7.
Now, let's find the prime factorization of 10!:
10! = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1
= 28 * 34 * 52 * 7
= 28 * 34 * 52 * 7
Since 10! is divisible by 10080, it means that all the prime factors of 10080 must be present in the prime factorization of 10!.
Therefore, the perfect square factors of 10! are 24, 32, and 52.
The greatest possible value of h is the largest perfect square factor, which is 52.
Therefore, the answer is B: 36.
Working at their individual same constant rate, 24 machines can complete a certain production job in 10 hours when they all work together. On a certain day, due to a minor malfunction, 8 of those machines were not operating for the first 2 hours. Compared to normal days, what is the extra time taken to complete the production job on that day?- a)20 minutes
- b)30 minutes
- c)40 minutes
- d)1 hour
- e)1 hour 20 minutes
Correct answer is option 'C'. Can you explain this answer?
Working at their individual same constant rate, 24 machines can complete a certain production job in 10 hours when they all work together. On a certain day, due to a minor malfunction, 8 of those machines were not operating for the first 2 hours. Compared to normal days, what is the extra time taken to complete the production job on that day?
a)
20 minutes
b)
30 minutes
c)
40 minutes
d)
1 hour
e)
1 hour 20 minutes

|
Srestha Basu answered |
Understanding the Problem
To determine the extra time taken to complete the production job due to the malfunctioning machines, we first need to calculate the total work done and the effective rate of the machines.
Calculation of Work Done
- **Total Work:**
If 24 machines can complete the job in 10 hours, the total work (W) can be calculated as:
\[ W = \text{Machines} \times \text{Time} \]
\[ W = 24 \times 10 = 240 \text{ machine-hours} \]
- **Rate of One Machine:**
The rate of one machine (R) is:
\[ R = \frac{W}{\text{Total Machines} \times \text{Total Time}} \]
\[ R = \frac{240}{24} = 10 \text{ hours per machine} \]
Thus, the rate of one machine is \( \frac{1}{10} \) of the work per hour.
Work Done in the First 2 Hours
- **Machines Working Initially:**
For the first 2 hours, only 16 machines were operational. The work done (W1) in this time is:
\[ W1 = 16 \text{ machines} \times 2 \text{ hours} = 32 \text{ machine-hours} \]
- **Remaining Work:**
The remaining work after 2 hours is:
\[ W_{\text{remaining}} = 240 - 32 = 208 \text{ machine-hours} \]
Completion of Remaining Work
- **Machines Working After 2 Hours:**
After 2 hours, all 24 machines are operational. The time (T) to finish the remaining work is:
\[ T = \frac{W_{\text{remaining}}}{\text{Total Machines}} = \frac{208}{24} \approx 8.67 \text{ hours} \]
Total Time Taken
- **Total Time on Malfunction Day:**
The total time taken on the malfunction day is:
\[ \text{Total Time} = 2 \text{ hours} + 8.67 \text{ hours} = 10.67 \text{ hours} \]
Comparison to Normal Days
- **Extra Time Taken:**
The normal time is 10 hours. The extra time taken is:
\[ \text{Extra Time} = 10.67 - 10 = 0.67 \text{ hours} \approx 40 \text{ minutes} \]
Thus, the extra time taken to complete the job on that day is **40 minutes**, confirming option 'C'.
To determine the extra time taken to complete the production job due to the malfunctioning machines, we first need to calculate the total work done and the effective rate of the machines.
Calculation of Work Done
- **Total Work:**
If 24 machines can complete the job in 10 hours, the total work (W) can be calculated as:
\[ W = \text{Machines} \times \text{Time} \]
\[ W = 24 \times 10 = 240 \text{ machine-hours} \]
- **Rate of One Machine:**
The rate of one machine (R) is:
\[ R = \frac{W}{\text{Total Machines} \times \text{Total Time}} \]
\[ R = \frac{240}{24} = 10 \text{ hours per machine} \]
Thus, the rate of one machine is \( \frac{1}{10} \) of the work per hour.
Work Done in the First 2 Hours
- **Machines Working Initially:**
For the first 2 hours, only 16 machines were operational. The work done (W1) in this time is:
\[ W1 = 16 \text{ machines} \times 2 \text{ hours} = 32 \text{ machine-hours} \]
- **Remaining Work:**
The remaining work after 2 hours is:
\[ W_{\text{remaining}} = 240 - 32 = 208 \text{ machine-hours} \]
Completion of Remaining Work
- **Machines Working After 2 Hours:**
After 2 hours, all 24 machines are operational. The time (T) to finish the remaining work is:
\[ T = \frac{W_{\text{remaining}}}{\text{Total Machines}} = \frac{208}{24} \approx 8.67 \text{ hours} \]
Total Time Taken
- **Total Time on Malfunction Day:**
The total time taken on the malfunction day is:
\[ \text{Total Time} = 2 \text{ hours} + 8.67 \text{ hours} = 10.67 \text{ hours} \]
Comparison to Normal Days
- **Extra Time Taken:**
The normal time is 10 hours. The extra time taken is:
\[ \text{Extra Time} = 10.67 - 10 = 0.67 \text{ hours} \approx 40 \text{ minutes} \]
Thus, the extra time taken to complete the job on that day is **40 minutes**, confirming option 'C'.
Nicole cycles at a constant rate of 20 kilometers per hour, and is passed by Jessica, who cycles at a constant rate of 30 kilometers per hour. If Jessica cycles at her constant rate for x minutes after passing Nicole, then stops to wait for her, how many minutes will Jessica have to wait for Nicole to catch up to her?- a)x minutes
- b)x/2 minutes
- c)2x/3 minutes
- d)3x/2 minutes
- e)2x minutes
Correct answer is option 'B'. Can you explain this answer?
Nicole cycles at a constant rate of 20 kilometers per hour, and is passed by Jessica, who cycles at a constant rate of 30 kilometers per hour. If Jessica cycles at her constant rate for x minutes after passing Nicole, then stops to wait for her, how many minutes will Jessica have to wait for Nicole to catch up to her?
a)
x minutes
b)
x/2 minutes
c)
2x/3 minutes
d)
3x/2 minutes
e)
2x minutes

|
BT Educators answered |
Since Nicole cycles at a constant rate of 20 kilometers per hour, in x minutes, she would cover a distance of (20/60) * x kilometers. Simplifying this, we have (1/3) * x kilometers.
Now, let's consider Jessica. When she passes Nicole, she is traveling at a rate of 30 kilometers per hour. In x minutes, she would cover a distance of (30/60) * x kilometers. Simplifying this, we have (1/2) * x kilometers.
To find the distance Nicole travels before Jessica catches up, we subtract the distance covered by Jessica from the distance covered by Nicole:
(1/3) * x - (1/2) * x = (2/6) * x - (3/6) * x = -(1/6) * x kilometers.
Since Jessica is ahead of Nicole, the distance between them is negative. However, since we are interested in the time it takes for Nicole to catch up, we can ignore the negative sign.
Now, we need to determine the time it takes for Nicole to cover the distance of (1/6) * x kilometers while cycling at a rate of 20 kilometers per hour.
Time = Distance / Rate = ((1/6) * x) / 20 = (1/6) * (1/20) * x = (1/120) * x hours.
To convert this to minutes, we multiply by 60:
(1/120) * x * 60 = (1/2) * x minutes.
Therefore, Jessica will have to wait for (1/2) * x minutes for Nicole to catch up to her.
Hence, the correct answer is option b) x/2 minutes.
An international flight takes off from New Delhi in India for Washington DC in the United States of America via Doha, where the flight stops for 2 hours and 40 minutes. During flight, the average speed of the plane is 660 kilometres per hour and the flight reaches Washington DC, at 3:50 PM, Washington time. If the distance between New Delhi and Washington DC via Doha is 12000 kilometres and New Delhi is 9 hour 30 minutes ahead of Washington DC, what is the approximate time in New Delhi when the flight takes off from there?- a)12:30 AM
- b)4:30 AM
- c)7:10 AM
- d)12:10 PM
- e)7:30 PM
Correct answer is option 'B'. Can you explain this answer?
An international flight takes off from New Delhi in India for Washington DC in the United States of America via Doha, where the flight stops for 2 hours and 40 minutes. During flight, the average speed of the plane is 660 kilometres per hour and the flight reaches Washington DC, at 3:50 PM, Washington time. If the distance between New Delhi and Washington DC via Doha is 12000 kilometres and New Delhi is 9 hour 30 minutes ahead of Washington DC, what is the approximate time in New Delhi when the flight takes off from there?
a)
12:30 AM
b)
4:30 AM
c)
7:10 AM
d)
12:10 PM
e)
7:30 PM

|
Pranav Kulkarni answered |
Understanding the Flight Details
To determine the takeoff time from New Delhi, we need to analyze the flight details provided.
Flight Parameters
- Average Speed of the Plane: 660 km/h
- Total Distance: 12,000 km
- Layover in Doha: 2 hours and 40 minutes
- Arrival Time in Washington DC: 3:50 PM (local time)
- Time Difference: New Delhi is 9 hours and 30 minutes ahead of Washington DC.
Calculate Total Flight Time
1. Calculate Flight Duration:
- Total flight time (without layover) = Distance / Speed
- Total flight time = 12,000 km / 660 km/h ≈ 18.18 hours (or approximately 18 hours and 11 minutes).
2. Total Time Including Layover:
- Total time = Flight time + Layover time
- Layover time = 2 hours and 40 minutes = 2.67 hours.
- Total time = 18.18 hours + 2.67 hours ≈ 20.85 hours (or approximately 20 hours and 51 minutes).
Calculate Departure Time from Washington DC
1. Arrival Time in New Delhi Time:
- Convert 3:50 PM (Washington time) to New Delhi time:
- 3:50 PM + 9 hours 30 minutes = 1:20 AM (next day in New Delhi).
2. Departure Time Calculation:
- Departure time = Arrival time - Total time
- Departure time = 1:20 AM - 20 hours and 51 minutes = 4:30 AM (same day in New Delhi).
Conclusion
Based on the calculations, the approximate time in New Delhi when the flight takes off is 4:30 AM. Thus, the correct answer is option B.
To determine the takeoff time from New Delhi, we need to analyze the flight details provided.
Flight Parameters
- Average Speed of the Plane: 660 km/h
- Total Distance: 12,000 km
- Layover in Doha: 2 hours and 40 minutes
- Arrival Time in Washington DC: 3:50 PM (local time)
- Time Difference: New Delhi is 9 hours and 30 minutes ahead of Washington DC.
Calculate Total Flight Time
1. Calculate Flight Duration:
- Total flight time (without layover) = Distance / Speed
- Total flight time = 12,000 km / 660 km/h ≈ 18.18 hours (or approximately 18 hours and 11 minutes).
2. Total Time Including Layover:
- Total time = Flight time + Layover time
- Layover time = 2 hours and 40 minutes = 2.67 hours.
- Total time = 18.18 hours + 2.67 hours ≈ 20.85 hours (or approximately 20 hours and 51 minutes).
Calculate Departure Time from Washington DC
1. Arrival Time in New Delhi Time:
- Convert 3:50 PM (Washington time) to New Delhi time:
- 3:50 PM + 9 hours 30 minutes = 1:20 AM (next day in New Delhi).
2. Departure Time Calculation:
- Departure time = Arrival time - Total time
- Departure time = 1:20 AM - 20 hours and 51 minutes = 4:30 AM (same day in New Delhi).
Conclusion
Based on the calculations, the approximate time in New Delhi when the flight takes off is 4:30 AM. Thus, the correct answer is option B.
What is the 18th digit to the right of the decimal point in the decimal expansion of 1/37?- a)0
- b)2
- c)4
- d)7
- e)9
Correct answer is option 'D'. Can you explain this answer?
What is the 18th digit to the right of the decimal point in the decimal expansion of 1/37?
a)
0
b)
2
c)
4
d)
7
e)
9

|
Pioneer Academy answered |
To find the 18th digit to the right of the decimal point in the decimal expansion of 1/37, we can perform the division and observe the pattern that emerges.
When we divide 1 by 37, the decimal expansion is 0.027027027027... with the repeating pattern being 027.
To determine the 18th digit to the right of the decimal point, we need to identify which digit from the repeating pattern corresponds to that position.
Since the repeating pattern has a length of 3 digits (027), we can divide 18 by 3 to determine the number of complete repetitions and the remainder to find the position within the repeating pattern.
18 ÷ 3 = 6 with no remainder
Since there is no remainder, the 18th digit corresponds to the third digit within the repeating pattern (027), which is 7.
Therefore, the 18th digit to the right of the decimal point in the decimal expansion of 1/37 is 7.
Hence, the correct answer is D) 7.
How many even integers between 100 and 200, inclusive, are divisible by 7?- a)20
- b)18
- c)16
- d)14
- e)7
Correct answer is option 'E'. Can you explain this answer?
How many even integers between 100 and 200, inclusive, are divisible by 7?
a)
20
b)
18
c)
16
d)
14
e)
7
|
|
Rahul Kapoor answered |
Since an even integer divisible by 7 must also be divisible by 14, we need to find the number of integers between 100 and 200 that are divisible by 14. By considering multiples of 14 instead of 7, we avoid counting the odd multiples of 7, which would need to be subtracted later.
Using the formula (largest - smallest) / 14 + 1, we can calculate the count of such integers:
(196 - 112) / 14 + 1 = 7
Therefore, there are 7 integers in the range of 100 to 200 that are divisible by 14.
Hence, the answer remains E.
The ratio of a two digit number to a number formed by reversing its digits is 4:7. Which of the following is the sum of all the numbers of all such pairs?- a)110
- b)200
- c)330
- d)88
- e)770
Correct answer is option 'C'. Can you explain this answer?
The ratio of a two digit number to a number formed by reversing its digits is 4:7. Which of the following is the sum of all the numbers of all such pairs?
a)
110
b)
200
c)
330
d)
88
e)
770

|
Talent Skill Learning answered |
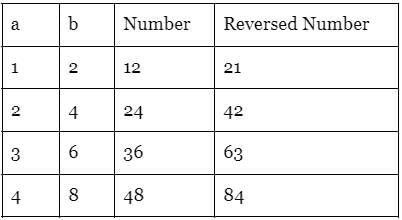
Let the two digit number be 10a + b and the number formed by reversing its digits be 10b + a.
10a + b /10b + a = 4/7
70a + 7b = 40b + 4a
66a = 33b
Therefore, a/b = 1/2
So, let us list down all possible values for a and b
10a + b /10b + a = 4/7
70a + 7b = 40b + 4a
66a = 33b
Therefore, a/b = 1/2
So, let us list down all possible values for a and b

Hence, the sum of all the numbers would be,
12 + 21 + 24 + 42 + 36 + 63 + 48 + 84 = 330.
12 + 21 + 24 + 42 + 36 + 63 + 48 + 84 = 330.
A circular microchip with a radius of 2 centimeters is manufactured following a blueprint scaled such that a measurement of 1 centimeter on the blueprint corresponds to a measurement of 0.8 millimeters on the microchip. What is the diameter of the blueprint representation of the microchip, in centimeters? (1 centimeter = 10 millimeters)- a)25
- b)30
- c)40
- d)50
- e)60
Correct answer is option 'D'. Can you explain this answer?
A circular microchip with a radius of 2 centimeters is manufactured following a blueprint scaled such that a measurement of 1 centimeter on the blueprint corresponds to a measurement of 0.8 millimeters on the microchip. What is the diameter of the blueprint representation of the microchip, in centimeters? (1 centimeter = 10 millimeters)
a)
25
b)
30
c)
40
d)
50
e)
60
|
|
Rahul Kapoor answered |
According to the blueprint, 1 centimeter corresponds to 0.8 millimeters on the microchip. Since 1 centimeter is equal to 10 millimeters, we can set up the following proportion:
1 centimeter on blueprint = 0.8 millimeters on microchip
10 millimeters on blueprint = x millimeters on microchip
10 millimeters on blueprint = x millimeters on microchip
To find the diameter on the blueprint, we need to double the radius. Therefore, we can multiply the 10 millimeters on the blueprint by 2:
Diameter on blueprint = 2 * 10 millimeters = 20 millimeters.
Since 1 centimeter is equal to 10 millimeters, we can convert the diameter from millimeters to centimeters:
Diameter on blueprint = 20 millimeters = 2 centimeters.
So, the diameter of the blueprint representation of the microchip is 2 centimeters.
Among the given answer choices, the closest option is D: 50.
Therefore, the correct answer is D: 50.
M is a positive integer less than 100. When m is raised to the third power, it becomes the square of another integer. How many different values could m be?- a)7
- b)9
- c)11
- d)13
- e)15
Correct answer is option 'B'. Can you explain this answer?
M is a positive integer less than 100. When m is raised to the third power, it becomes the square of another integer. How many different values could m be?
a)
7
b)
9
c)
11
d)
13
e)
15

|
Saumya Shah answered |
Understanding the Problem
To find the positive integer \( m \) less than 100 such that \( m^3 \) is a perfect square, we start by establishing the relationship between \( m \) and a perfect square.
Key Mathematical Concept
For \( m^3 \) to be a perfect square, \( m \) itself must have a specific structure. If we express \( m \) in terms of its prime factorization:
\[
m = p_1^{e_1} \times p_2^{e_2} \times \ldots \times p_k^{e_k}
\]
Then:
\[
m^3 = p_1^{3e_1} \times p_2^{3e_2} \times \ldots \times p_k^{3e_k}
\]
For \( m^3 \) to be a perfect square, all exponents \( 3e_i \) must be even. This implies that each \( e_i \) must be even (since 3 times an odd number is odd).
Conditions on m
To satisfy this, \( m \) must consist of prime factors raised to even powers. This means:
- \( m \) can be written as \( p_1^{2a_1} \times p_2^{2a_2} \times \ldots \times p_k^{2a_k} \), where \( a_i \) are non-negative integers.
Finding Valid Values for m
The largest integer \( m < 100="" \)="" can="" be="" expressed="" as="" the="" product="" of="" primes="" raised="" to="" even="" powers.="" the="" possibilities="" for="" \(="" m="" \)="" />
- \( 1^2 = 1 \)
- \( 2^2 = 4 \)
- \( 3^2 = 9 \)
- \( 5^2 = 25 \)
- \( 6^2 = 36 \)
- \( 7^2 = 49 \)
- \( 10^2 = 100 \) (not included, as \( m < 100="" />
The valid values of \( m \) are \( 1, 4, 9, 16, 25, 36, 49, 64, 81 \), and \( 100 \) (excluded).
After counting them, the valid integers \( m < 100="" \)="" />
- \( 1, 4, 9, 16, 25, 36, 49, 64, 81 \) = 9 values.
Conclusion
Thus, the total number of different values \( m \) can take is \( \boxed{9} \).
To find the positive integer \( m \) less than 100 such that \( m^3 \) is a perfect square, we start by establishing the relationship between \( m \) and a perfect square.
Key Mathematical Concept
For \( m^3 \) to be a perfect square, \( m \) itself must have a specific structure. If we express \( m \) in terms of its prime factorization:
\[
m = p_1^{e_1} \times p_2^{e_2} \times \ldots \times p_k^{e_k}
\]
Then:
\[
m^3 = p_1^{3e_1} \times p_2^{3e_2} \times \ldots \times p_k^{3e_k}
\]
For \( m^3 \) to be a perfect square, all exponents \( 3e_i \) must be even. This implies that each \( e_i \) must be even (since 3 times an odd number is odd).
Conditions on m
To satisfy this, \( m \) must consist of prime factors raised to even powers. This means:
- \( m \) can be written as \( p_1^{2a_1} \times p_2^{2a_2} \times \ldots \times p_k^{2a_k} \), where \( a_i \) are non-negative integers.
Finding Valid Values for m
The largest integer \( m < 100="" \)="" can="" be="" expressed="" as="" the="" product="" of="" primes="" raised="" to="" even="" powers.="" the="" possibilities="" for="" \(="" m="" \)="" />
- \( 1^2 = 1 \)
- \( 2^2 = 4 \)
- \( 3^2 = 9 \)
- \( 5^2 = 25 \)
- \( 6^2 = 36 \)
- \( 7^2 = 49 \)
- \( 10^2 = 100 \) (not included, as \( m < 100="" />
The valid values of \( m \) are \( 1, 4, 9, 16, 25, 36, 49, 64, 81 \), and \( 100 \) (excluded).
After counting them, the valid integers \( m < 100="" \)="" />
- \( 1, 4, 9, 16, 25, 36, 49, 64, 81 \) = 9 values.
Conclusion
Thus, the total number of different values \( m \) can take is \( \boxed{9} \).
If n is a positive integer, how many of the ten digits from 0 through 9 could be the units digits of n3 ?- a)Three
- b)Four
- c)Six
- d)Nine
- e)Ten
Correct answer is option 'E'. Can you explain this answer?
If n is a positive integer, how many of the ten digits from 0 through 9 could be the units digits of n3 ?
a)
Three
b)
Four
c)
Six
d)
Nine
e)
Ten

|
Chirag Sen answered |
Understanding Units Digits of n3
To determine how many of the ten digits from 0 through 9 can be the units digits of \( n^3 \) for a positive integer \( n \), we analyze the possible units digits of \( n \) and how they affect the units digit of \( n^3 \).
Units Digits of Positive Integers
The units digits of any integer \( n \) can be any of the following digits:
- 0
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
Calculating the Units Digits of n3
Next, we compute the units digits of \( n^3 \) for each possible units digit of \( n \):
- If \( n \equiv 0 \mod 10 \) → \( n^3 \equiv 0 \mod 10 \)
- If \( n \equiv 1 \mod 10 \) → \( n^3 \equiv 1 \mod 10 \)
- If \( n \equiv 2 \mod 10 \) → \( n^3 \equiv 8 \mod 10 \)
- If \( n \equiv 3 \mod 10 \) → \( n^3 \equiv 7 \mod 10 \)
- If \( n \equiv 4 \mod 10 \) → \( n^3 \equiv 4 \mod 10 \)
- If \( n \equiv 5 \mod 10 \) → \( n^3 \equiv 5 \mod 10 \)
- If \( n \equiv 6 \mod 10 \) → \( n^3 \equiv 6 \mod 10 \)
- If \( n \equiv 7 \mod 10 \) → \( n^3 \equiv 3 \mod 10 \)
- If \( n \equiv 8 \mod 10 \) → \( n^3 \equiv 2 \mod 10 \)
- If \( n \equiv 9 \mod 10 \) → \( n^3 \equiv 9 \mod 10 \)
Possible Units Digits of n3
From the calculations above, the possible units digits of \( n^3 \) are:
- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
This means that every digit from 0 to 9 can occur as the units digit of \( n^3 \).
Conclusion
Thus, the answer is that all ten digits from 0 through 9 can be the units digits of \( n^3 \). Therefore, the correct answer is option E: Ten.
To determine how many of the ten digits from 0 through 9 can be the units digits of \( n^3 \) for a positive integer \( n \), we analyze the possible units digits of \( n \) and how they affect the units digit of \( n^3 \).
Units Digits of Positive Integers
The units digits of any integer \( n \) can be any of the following digits:
- 0
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
Calculating the Units Digits of n3
Next, we compute the units digits of \( n^3 \) for each possible units digit of \( n \):
- If \( n \equiv 0 \mod 10 \) → \( n^3 \equiv 0 \mod 10 \)
- If \( n \equiv 1 \mod 10 \) → \( n^3 \equiv 1 \mod 10 \)
- If \( n \equiv 2 \mod 10 \) → \( n^3 \equiv 8 \mod 10 \)
- If \( n \equiv 3 \mod 10 \) → \( n^3 \equiv 7 \mod 10 \)
- If \( n \equiv 4 \mod 10 \) → \( n^3 \equiv 4 \mod 10 \)
- If \( n \equiv 5 \mod 10 \) → \( n^3 \equiv 5 \mod 10 \)
- If \( n \equiv 6 \mod 10 \) → \( n^3 \equiv 6 \mod 10 \)
- If \( n \equiv 7 \mod 10 \) → \( n^3 \equiv 3 \mod 10 \)
- If \( n \equiv 8 \mod 10 \) → \( n^3 \equiv 2 \mod 10 \)
- If \( n \equiv 9 \mod 10 \) → \( n^3 \equiv 9 \mod 10 \)
Possible Units Digits of n3
From the calculations above, the possible units digits of \( n^3 \) are:
- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
This means that every digit from 0 to 9 can occur as the units digit of \( n^3 \).
Conclusion
Thus, the answer is that all ten digits from 0 through 9 can be the units digits of \( n^3 \). Therefore, the correct answer is option E: Ten.
Sam covers a total distance of 80km while travelling from a certain point X to a certain point Y and come back again to the start point X. He covers the first 40 km distance from point X to point Y at a speed of 25 km/hr. While travelling back to the point X from point Y, Sam drives his vehicle at a speed of 15 km/hr. Calculate the average speed of Sam for the entire journey.- a)20.77 km/hr
- b)18.77 km/hr
- c)35.77 km/hr
- d)17.77 km/hr
- e)None of the above
Correct answer is option 'B'. Can you explain this answer?
Sam covers a total distance of 80km while travelling from a certain point X to a certain point Y and come back again to the start point X. He covers the first 40 km distance from point X to point Y at a speed of 25 km/hr. While travelling back to the point X from point Y, Sam drives his vehicle at a speed of 15 km/hr. Calculate the average speed of Sam for the entire journey.
a)
20.77 km/hr
b)
18.77 km/hr
c)
35.77 km/hr
d)
17.77 km/hr
e)
None of the above

|
Abhishek Choudhury answered |
Understanding the Journey
Sam's journey consists of two parts: traveling from point X to point Y and back.
Distance Breakdown
- Distance from X to Y: 40 km
- Distance from Y to X: 40 km
- Total distance traveled: 80 km
Time Calculation for Each Leg
1. From X to Y:
- Speed: 25 km/hr
- Time = Distance / Speed = 40 km / 25 km/hr = 1.6 hours
2. From Y to X:
- Speed: 15 km/hr
- Time = Distance / Speed = 40 km / 15 km/hr = 2.67 hours (approximately)
Total Time for the Journey
- Total time = Time from X to Y + Time from Y to X
- Total time = 1.6 hours + 2.67 hours = 4.27 hours (approximately)
Calculating Average Speed
- Average Speed = Total Distance / Total Time
- Average Speed = 80 km / 4.27 hours ≈ 18.77 km/hr
Conclusion
Based on the calculations, the average speed of Sam for the entire journey is approximately 18.77 km/hr, which corresponds to option 'b'.
Sam's journey consists of two parts: traveling from point X to point Y and back.
Distance Breakdown
- Distance from X to Y: 40 km
- Distance from Y to X: 40 km
- Total distance traveled: 80 km
Time Calculation for Each Leg
1. From X to Y:
- Speed: 25 km/hr
- Time = Distance / Speed = 40 km / 25 km/hr = 1.6 hours
2. From Y to X:
- Speed: 15 km/hr
- Time = Distance / Speed = 40 km / 15 km/hr = 2.67 hours (approximately)
Total Time for the Journey
- Total time = Time from X to Y + Time from Y to X
- Total time = 1.6 hours + 2.67 hours = 4.27 hours (approximately)
Calculating Average Speed
- Average Speed = Total Distance / Total Time
- Average Speed = 80 km / 4.27 hours ≈ 18.77 km/hr
Conclusion
Based on the calculations, the average speed of Sam for the entire journey is approximately 18.77 km/hr, which corresponds to option 'b'.
A manufacturer produces a certain men's athletic shoe in integer sizes from 8 to 17. For this particular shoe, each unit increase in size corresponds to a 1/4-inch increase in the length of the shoe. If the largest size of this shoe is 20% longer than the smallest size, how long, in inches, is the shoe in size 15?- a)12
- b)12.25
- c)12.5
- d)12.75
- e)13
Correct answer is option 'E'. Can you explain this answer?
A manufacturer produces a certain men's athletic shoe in integer sizes from 8 to 17. For this particular shoe, each unit increase in size corresponds to a 1/4-inch increase in the length of the shoe. If the largest size of this shoe is 20% longer than the smallest size, how long, in inches, is the shoe in size 15?
a)
12
b)
12.25
c)
12.5
d)
12.75
e)
13

|
Notes Wala answered |
We are given that the shoe sizes range from 8 to 17, with each unit increase in size corresponding to a 1/4-inch increase in length.
Let's calculate the difference in length between the largest and smallest sizes:
Length difference = (17 - 8) * (1/4)
Length difference = 9/4 inches
Length difference = 9/4 inches
We are also given that the largest size is 20% longer than the smallest size. Let's calculate this increase:
20% of the length of the smallest size = (20/100) * (9/4)
Increase = 9/20 inches
Increase = 9/20 inches
To find the length of the shoe in size 15, we need to add the increase to the length of the smallest size:
Length of size 15 = Length of smallest size + Increase
Length of size 15 = (8 * 1/4) + (9/20)
Length of size 15 = 2 + 9/20
Length of size 15 = (40/20 + 9/20)
Length of size 15 = 49/20
Length of size 15 = (8 * 1/4) + (9/20)
Length of size 15 = 2 + 9/20
Length of size 15 = (40/20 + 9/20)
Length of size 15 = 49/20
To convert this fraction into a decimal, we divide the numerator by the denominator:
Length of size 15 = 2.45 inches
Among the given answer choices, the closest value to 2.45 inches is 13 inches (E).
Therefore, the answer is E.
At the average download speed of 12,000,000 bits per second, 75,000,000 bytes of data can be downloaded in 50 seconds. With a certain dial-up connection, the same task would take 3 hours. Which of the following is closest to the average download speed, in bits per second, of this dial-up connection?- a)200
- b)1,000
- c)7,000
- d)56,000
- e)240,000
Correct answer is option 'D'. Can you explain this answer?
At the average download speed of 12,000,000 bits per second, 75,000,000 bytes of data can be downloaded in 50 seconds. With a certain dial-up connection, the same task would take 3 hours. Which of the following is closest to the average download speed, in bits per second, of this dial-up connection?
a)
200
b)
1,000
c)
7,000
d)
56,000
e)
240,000
|
|
Rahul Kapoor answered |
To find the average download speed of the dial-up connection, we need to convert the given data into a common unit (bits per second).
First, let's calculate the number of bits in 75,000,000 bytes. Since 1 byte is equal to 8 bits, we can multiply 75,000,000 by 8 to get the total number of bits:
75,000,000 bytes * 8 bits/byte = 600,000,000 bits
75,000,000 bytes * 8 bits/byte = 600,000,000 bits
Now, we can calculate the download speed of the dial-up connection. We are given that this same task takes 3 hours, which is equal to 3 * 60 * 60 = 10,800 seconds.
To find the average download speed, we divide the total number of bits by the time in seconds:
Average download speed = 600,000,000 bits / 10,800 seconds
Average download speed = 600,000,000 bits / 10,800 seconds
Calculating this value gives us approximately 55,555.56 bits per second.
Among the answer choices provided, the closest value to the calculated average download speed is 56,000 bits per second (option D).
Therefore, the correct answer is D) 56,000.
What is the least positive value that can be subtracted from 22050 so that the result is a multiple of 17?- a)1
- b)2
- c)4
- d)13
- e)16
Correct answer is option 'C'. Can you explain this answer?
What is the least positive value that can be subtracted from 22050 so that the result is a multiple of 17?
a)
1
b)
2
c)
4
d)
13
e)
16

|
Pioneer Academy answered |
64/7 = Rem 1
26 = 64
Now, 22050 = 2341∗6+2
Thus, 22 = 4 must be subtracted from the number to make it completely divisible by 7, Answer must be (C) 4
26 = 64
Now, 22050 = 2341∗6+2
Thus, 22 = 4 must be subtracted from the number to make it completely divisible by 7, Answer must be (C) 4
If b = a + 4, then for which of the following values of x is the expression (x−a)2 + (x−b)2 the smallest?- a)a − 1
- b)a
- c)a + 2
- d)a + 3
- e)a + 5
Correct answer is option 'C'. Can you explain this answer?
If b = a + 4, then for which of the following values of x is the expression (x−a)2 + (x−b)2 the smallest?
a)
a − 1
b)
a
c)
a + 2
d)
a + 3
e)
a + 5

|
Ameya Yadav answered |
The expression (x + b) equal to 0 can be rewritten as (x + a + 4) = 0. To solve for x, we need to isolate x on one side of the equation.
Subtracting a and 4 from both sides, we get x = -a - 4.
Therefore, for x to make the expression (x + b) equal to 0, x must be equal to -a - 4.
Subtracting a and 4 from both sides, we get x = -a - 4.
Therefore, for x to make the expression (x + b) equal to 0, x must be equal to -a - 4.
If |3 – x| < x + 5, which of the following may be true about x ?I. x > –1
II. x < 2
III. x < –2- a)I only
- b)II only
- c)I and II only
- d)I and III only
- e)I, II, and III
Correct answer is option 'C'. Can you explain this answer?
If |3 – x| < x + 5, which of the following may be true about x ?
I. x > –1
II. x < 2
III. x < –2
II. x < 2
III. x < –2
a)
I only
b)
II only
c)
I and II only
d)
I and III only
e)
I, II, and III

|
Notes Wala answered |
We have the inequality |3 - x| < x + 5.
To simplify this inequality, we consider two cases:
Case 1: (3 - x) is positive or zero:
In this case, the absolute value |3 - x| can be simplified to (3 - x). Therefore, our inequality becomes (3 - x) < x + 5.
In this case, the absolute value |3 - x| can be simplified to (3 - x). Therefore, our inequality becomes (3 - x) < x + 5.
Expanding the inequality, we have:
3 - x < x + 5
3 - x < x + 5
Adding x to both sides, we get:
3 < 2x + 5
3 < 2x + 5
Subtracting 5 from both sides, we have:
-2 < 2x
-2 < 2x
Dividing both sides by 2, we obtain:
-1 < x
-1 < x
So, in this case, the statement I. x > -1 is not true. Therefore, option C: I and II only cannot be correct.
Case 2: (3 - x) is negative:
In this case, the absolute value |3 - x| can be simplified to -(3 - x), changing the direction of the inequality. Therefore, our inequality becomes -(3 - x) < x + 5.
In this case, the absolute value |3 - x| can be simplified to -(3 - x), changing the direction of the inequality. Therefore, our inequality becomes -(3 - x) < x + 5.
Expanding the inequality and simplifying, we have:
-x + 3 < x + 5
-x + 3 < x + 5
Adding x to both sides, we get:
3 < 2x + 5
3 < 2x + 5
Subtracting 5 from both sides, we have:
-2 < 2x
-2 < 2x
Dividing both sides by 2, we obtain:
-1 < x
-1 < x
So, in this case, the statement I. x > -1 is not true. Therefore, option C: I and II only cannot be correct.
P and Q are two two-digit numbersTheir product equals the product of the numbers obtained on reversing them. None of the digits in P or Q is equal to the other digit in it or any digit in the other number. The product of tens digits of the two numbers' is a composite single digit number. How many ordered pairs (P, Q) satisfy these conditions?- a)8
- b)16
- c)12
- d)4
- e)9
Correct answer is option 'B'. Can you explain this answer?
P and Q are two two-digit numbersTheir product equals the product of the numbers obtained on reversing them. None of the digits in P or Q is equal to the other digit in it or any digit in the other number. The product of tens digits of the two numbers' is a composite single digit number. How many ordered pairs (P, Q) satisfy these conditions?
a)
8
b)
16
c)
12
d)
4
e)
9
|
|
Rahul Kapoor answered |
We can represent the two-digit numbers as "ab" and "cd", where "a", "b", "c", and "d" are digits.
The values of the numbers can be written as 10a + b and 10c + d.
By solving the equation (10a + b)(10c + d) = (10b + a)(10d + c), we find that ac = bd.
Since ac represents a composite single digit, the possible values for ac are 4, 6, 8, and 9.
Out of these four options, we can eliminate 4 and 9 because the digits must be distinct.
Therefore, ac can be either 6 or 8.
For ac = 6, there are 2 possibilities for a and c: (2, 3) or (3, 2).
For ac = 8, there are 2 possibilities for a and c: (2, 4) or (4, 2).
In total, we have 2 * 2 = 4 possibilities for the pairs (a, c) and (b, d) that satisfy the conditions.
Hence, the correct answer is 16.
A motorist covers a distance of 39 km in 45 min by moving at a speed of x km/h for the first 15 min, then moving at double the speed for the next 20 min and then again moving at his original speed for the rest of the journey. Then, x is equal to:- a)31.2
- b)36
- c)40
- d)52
- e)53
Correct answer is option 'B'. Can you explain this answer?
A motorist covers a distance of 39 km in 45 min by moving at a speed of x km/h for the first 15 min, then moving at double the speed for the next 20 min and then again moving at his original speed for the rest of the journey. Then, x is equal to:
a)
31.2
b)
36
c)
40
d)
52
e)
53

|
Pioneer Academy answered |
In the first phase, the motorist travels for 15 minutes at a speed of x km/h. Since distance = speed × time, the distance covered in this phase is given by:
Distance = speed × time = x km/h × (15/60) h = (x/4) km
Distance = speed × time = x km/h × (15/60) h = (x/4) km
In the second phase, the motorist travels for 20 minutes at double the speed of the first phase. So the speed in this phase is 2x km/h. The distance covered in this phase is given by:
Distance = speed × time = 2x km/h × (20/60) h = (2x/3) km
Distance = speed × time = 2x km/h × (20/60) h = (2x/3) km
In the third phase, the motorist travels for the remaining time, which is 45 minutes - 15 minutes - 20 minutes = 10 minutes. The speed in this phase is x km/h, and the distance covered in this phase is:
Distance = speed × time = x km/h × (10/60) h = (x/6) km
Distance = speed × time = x km/h × (10/60) h = (x/6) km
The total distance covered is given as 39 km. So we can add up the distances covered in each phase and set it equal to 39 km:
(x/4) + (2x/3) + (x/6) = 39
(x/4) + (2x/3) + (x/6) = 39
To simplify the equation, we can find a common denominator of 12:
3x + 8x + 2x = 39 × 12
13x = 468
x = 468/13
3x + 8x + 2x = 39 × 12
13x = 468
x = 468/13
Calculating this value, we find:
x ≈ 36
x ≈ 36
Therefore, the value of x is approximately 36 km/h, which corresponds to option B.
What is the sum of all possible solutions to |x - 3|2 + |x - 3| = 20 ?- a)-1
- b)6
- c)7
- d)12
- e)14
Correct answer is option 'B'. Can you explain this answer?
What is the sum of all possible solutions to |x - 3|2 + |x - 3| = 20 ?
a)
-1
b)
6
c)
7
d)
12
e)
14

|
BT Educators answered |
First of all |x - 3|2 = (x - 3)2, so we have: (x - 3)2 + |x - 3| = 20.
When x < 3, x - 3 is negative, thus |x - 3| = -(x - 3). In this case we'll have (x - 3)2 - (x - 3) = 20 --> x = -1 or x = 8. Discard x = 8 because it's not in the range we consider (< 3).
When x >= 3, x - 3 is non-negative, thus |x - 3| = x - 3. In this case we'll have (x - 3)2 + (x - 3) = 20 --> x = -2 or x = 7. Discard x = -2 because it's not in the range we consider (>= 3).
Thus there are two solutions: x = -1 and x = 7 → the sum = 6.
A department of motor vehicles asks visitors to draw numbered tickets from a dispenser so that they can be served in order by number. Six friends have graduated from truck-driving school and go to the department to get commercial driving licenses. They draw tickets and find that their numbers are a set of evenly spaced integers with a range of 10. Which of the following could NOT be the sum of their numbers?- a)1,254
- b)1,428
- c)3,972
- d)4,316
- e)8,010
Correct answer is option 'D'. Can you explain this answer?
A department of motor vehicles asks visitors to draw numbered tickets from a dispenser so that they can be served in order by number. Six friends have graduated from truck-driving school and go to the department to get commercial driving licenses. They draw tickets and find that their numbers are a set of evenly spaced integers with a range of 10. Which of the following could NOT be the sum of their numbers?
a)
1,254
b)
1,428
c)
3,972
d)
4,316
e)
8,010
|
|
Rahul Kapoor answered |
Let's assume the smallest number drawn by one of the friends is x. Since the range is 10, the largest number drawn would be x + 10.
The sum of evenly spaced integers can be found using the formula:
Sum = (Number of terms / 2) * (First term + Last term)
In this case, the number of terms is 6 (since there are 6 friends) and the first term is x, while the last term is x + 10.
So, the sum of the numbers would be:
Sum = (6 / 2) * (x + (x + 10))
= 3 * (2x + 10)
= 6x + 30
= 3 * (2x + 10)
= 6x + 30
Now, let's check each option to see if it can be obtained as the sum of the numbers:
A) 1,254:
6x + 30 = 1,254
6x = 1,224
x = 204
The sum can be obtained.
6x + 30 = 1,254
6x = 1,224
x = 204
The sum can be obtained.
B) 1,428:
6x + 30 = 1,428
6x = 1,398
x = 233
The sum can be obtained.
6x + 30 = 1,428
6x = 1,398
x = 233
The sum can be obtained.
C) 3,972:
6x + 30 = 3,972
6x = 3,942
x = 657
The sum can be obtained.
6x + 30 = 3,972
6x = 3,942
x = 657
The sum can be obtained.
D) 4,316:
6x + 30 = 4,316
6x = 4,286
x ≈ 714.333
The sum cannot be obtained with evenly spaced integers since x is not an integer.
6x + 30 = 4,316
6x = 4,286
x ≈ 714.333
The sum cannot be obtained with evenly spaced integers since x is not an integer.
E) 8,010:
6x + 30 = 8,010
6x = 7,980
x = 1,330
The sum can be obtained.
6x + 30 = 8,010
6x = 7,980
x = 1,330
The sum can be obtained.
Therefore, the sum that could NOT be the sum of their numbers is D) 4,316.
If an object travels 100 feet in 2 seconds, what is the object’s approximate speed in miles per hour? (Note: 1 mile = 5280 feet)- a)3.4
- b)3.8
- c)34
- d)38
- e)340
Correct answer is option 'C'. Can you explain this answer?
If an object travels 100 feet in 2 seconds, what is the object’s approximate speed in miles per hour? (Note: 1 mile = 5280 feet)
a)
3.4
b)
3.8
c)
34
d)
38
e)
340

|
Kiran Nambiar answered |
Calculating Speed in Miles Per Hour
To find the speed of an object in miles per hour (mph) when it travels a specific distance in a certain time, follow these steps:
Step 1: Determine the Speed in Feet per Second
- Given distance: 100 feet
- Given time: 2 seconds
Calculate the speed in feet per second (fps):
\[ \text{Speed (fps)} = \frac{\text{Distance}}{\text{Time}} = \frac{100 \text{ feet}}{2 \text{ seconds}} = 50 \text{ fps} \]
Step 2: Convert Feet per Second to Miles per Hour
To convert the speed from feet per second to miles per hour, use the conversion factors:
- 1 mile = 5280 feet
- 1 hour = 3600 seconds
Use the formula:
\[ \text{Speed (mph)} = \text{Speed (fps)} \times \frac{3600 \text{ seconds}}{1 \text{ hour}} \times \frac{1 \text{ mile}}{5280 \text{ feet}} \]
Substituting the values:
\[ \text{Speed (mph)} = 50 \text{ fps} \times \frac{3600}{5280} \]
Calculating the conversion:
\[ \text{Speed (mph)} = 50 \times \frac{3600}{5280} \approx 34.09 \text{ mph} \]
Conclusion
Thus, the approximate speed of the object is around 34 mph, which corresponds to option **C**. This conversion shows how to transition from feet per second to miles per hour using fundamental unit conversions.
To find the speed of an object in miles per hour (mph) when it travels a specific distance in a certain time, follow these steps:
Step 1: Determine the Speed in Feet per Second
- Given distance: 100 feet
- Given time: 2 seconds
Calculate the speed in feet per second (fps):
\[ \text{Speed (fps)} = \frac{\text{Distance}}{\text{Time}} = \frac{100 \text{ feet}}{2 \text{ seconds}} = 50 \text{ fps} \]
Step 2: Convert Feet per Second to Miles per Hour
To convert the speed from feet per second to miles per hour, use the conversion factors:
- 1 mile = 5280 feet
- 1 hour = 3600 seconds
Use the formula:
\[ \text{Speed (mph)} = \text{Speed (fps)} \times \frac{3600 \text{ seconds}}{1 \text{ hour}} \times \frac{1 \text{ mile}}{5280 \text{ feet}} \]
Substituting the values:
\[ \text{Speed (mph)} = 50 \text{ fps} \times \frac{3600}{5280} \]
Calculating the conversion:
\[ \text{Speed (mph)} = 50 \times \frac{3600}{5280} \approx 34.09 \text{ mph} \]
Conclusion
Thus, the approximate speed of the object is around 34 mph, which corresponds to option **C**. This conversion shows how to transition from feet per second to miles per hour using fundamental unit conversions.
What is the greatest value of n such that 18n is a factor of 18! ?- a)1
- b)2
- c)3
- d)4
- e)5
Correct answer is option 'D'. Can you explain this answer?
What is the greatest value of n such that 18n is a factor of 18! ?
a)
1
b)
2
c)
3
d)
4
e)
5

|
Arjun Iyer answered |
Understanding the Problem
To determine the greatest value of \( n \) such that \( 18n \) is a factor of \( 18! \), we first need to analyze the composition of \( 18 \) and \( 18! \).
Factorization of 18
- The prime factorization of \( 18 \) is \( 2 \times 3^2 \).
- Thus, \( 18n = 2 \times 3^2 \times n \).
Finding Factors in 18!
Next, we must find out how many times the prime factors of \( 18 \) appear in \( 18! \).
Counting the Factors
1. **Counting Factor of 2 in \( 18! \)**:
- Using the formula \( \sum_{k=1}^{\infty} \left\lfloor \frac{18}{2^k} \right\rfloor \):
- \( \left\lfloor \frac{18}{2} \right\rfloor = 9 \)
- \( \left\lfloor \frac{18}{4} \right\rfloor = 4 \)
- \( \left\lfloor \frac{18}{8} \right\rfloor = 2 \)
- \( \left\lfloor \frac{18}{16} \right\rfloor = 1 \)
- Total: \( 9 + 4 + 2 + 1 = 16 \).
2. **Counting Factor of 3 in \( 18! \)**:
- Using the formula \( \sum_{k=1}^{\infty} \left\lfloor \frac{18}{3^k} \right\rfloor \):
- \( \left\lfloor \frac{18}{3} \right\rfloor = 6 \)
- \( \left\lfloor \frac{18}{9} \right\rfloor = 2 \)
- Total: \( 6 + 2 = 8 \).
Determining Maximum n
Now, we need to satisfy the condition \( 2^1 \times 3^2 \times n \) being a factor of \( 18! \).
- The factor \( n \) can contribute additional factors of \( 2 \) and \( 3 \).
- Given \( 2 \) appears 16 times and \( 3 \) appears 8 times in \( 18! \):
1. For \( 2 \):
- We can use \( 1 \) (since \( 2^1 \) is already required by \( 18 \)).
- Remaining: \( 16 - 1 = 15 \) factors of \( 2 \).
2. For \( 3 \):
- We can use \( 2 \) (since \( 3^2 \) is already required by \( 18 \)).
- Remaining: \( 8 - 2 = 6 \) factors of \( 3 \).
Calculating Maximum n
- Therefore, \( n \) can be of the form \( 2^x \times 3^y \), where:
- \( x \
To determine the greatest value of \( n \) such that \( 18n \) is a factor of \( 18! \), we first need to analyze the composition of \( 18 \) and \( 18! \).
Factorization of 18
- The prime factorization of \( 18 \) is \( 2 \times 3^2 \).
- Thus, \( 18n = 2 \times 3^2 \times n \).
Finding Factors in 18!
Next, we must find out how many times the prime factors of \( 18 \) appear in \( 18! \).
Counting the Factors
1. **Counting Factor of 2 in \( 18! \)**:
- Using the formula \( \sum_{k=1}^{\infty} \left\lfloor \frac{18}{2^k} \right\rfloor \):
- \( \left\lfloor \frac{18}{2} \right\rfloor = 9 \)
- \( \left\lfloor \frac{18}{4} \right\rfloor = 4 \)
- \( \left\lfloor \frac{18}{8} \right\rfloor = 2 \)
- \( \left\lfloor \frac{18}{16} \right\rfloor = 1 \)
- Total: \( 9 + 4 + 2 + 1 = 16 \).
2. **Counting Factor of 3 in \( 18! \)**:
- Using the formula \( \sum_{k=1}^{\infty} \left\lfloor \frac{18}{3^k} \right\rfloor \):
- \( \left\lfloor \frac{18}{3} \right\rfloor = 6 \)
- \( \left\lfloor \frac{18}{9} \right\rfloor = 2 \)
- Total: \( 6 + 2 = 8 \).
Determining Maximum n
Now, we need to satisfy the condition \( 2^1 \times 3^2 \times n \) being a factor of \( 18! \).
- The factor \( n \) can contribute additional factors of \( 2 \) and \( 3 \).
- Given \( 2 \) appears 16 times and \( 3 \) appears 8 times in \( 18! \):
1. For \( 2 \):
- We can use \( 1 \) (since \( 2^1 \) is already required by \( 18 \)).
- Remaining: \( 16 - 1 = 15 \) factors of \( 2 \).
2. For \( 3 \):
- We can use \( 2 \) (since \( 3^2 \) is already required by \( 18 \)).
- Remaining: \( 8 - 2 = 6 \) factors of \( 3 \).
Calculating Maximum n
- Therefore, \( n \) can be of the form \( 2^x \times 3^y \), where:
- \( x \
50 = 3a + 2b
7 > |–a|If a and b are both integers, how many possible solutions are there to the system above?- a)4
- b)5
- c)6
- d)7
- e)8
Correct answer is option 'D'. Can you explain this answer?
50 = 3a + 2b
7 > |–a|
7 > |–a|
If a and b are both integers, how many possible solutions are there to the system above?
a)
4
b)
5
c)
6
d)
7
e)
8

|
Athul Joshi answered |
It seems like the equation is incomplete. Could you please provide the complete equation?
If x and z are positive constants, for how many values of y is x(y)2 = z(y)4?- a)1
- b)2
- c)3
- d)4
- e)5
Correct answer is option 'C'. Can you explain this answer?
If x and z are positive constants, for how many values of y is x(y)2 = z(y)4?
a)
1
b)
2
c)
3
d)
4
e)
5

|
Notes Wala answered |
x and z are positive constants
xy2 = zy4
y2(x − zy2) = 0
Case 1: y = 0Case 2: x−zy2 = 0
x = zy2
y2 = x/z
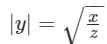
y can either take a positive or negative value.
Hence, three values of y are possible.
y2(x − zy2) = 0
Case 1: y = 0Case 2: x−zy2 = 0
x = zy2
y2 = x/z
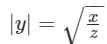
y can either take a positive or negative value.
Hence, three values of y are possible.
How many pairs (m,n) of integers satisfy the equation m + n = mn?- a)1
- b)2
- c)3
- d)4
- e)more than 4
Correct answer is option 'B'. Can you explain this answer?
How many pairs (m,n) of integers satisfy the equation m + n = mn?
a)
1
b)
2
c)
3
d)
4
e)
more than 4

|
Notes Wala answered |
To find the number of pairs (m, n) of integers that satisfy the equation m + n = mn, we can rearrange the equation as follows:
mn - m - n = 0
mn - m - n + 1 = 1
(m - 1)(n - 1) = 1
mn - m - n + 1 = 1
(m - 1)(n - 1) = 1
For the product of two integers to be 1, either both integers must be 1 or both must be -1. Therefore, we have two cases to consider:
Case 1: (m - 1) = 1 and (n - 1) = 1
This gives us m = 2 and n = 2.
This gives us m = 2 and n = 2.
Case 2: (m - 1) = -1 and (n - 1) = -1
This gives us m = 0 and n = 0.
This gives us m = 0 and n = 0.
So, there are two pairs (2, 2) and (0, 0) that satisfy the equation m + n = mn.
The answer is B: 2.
If N is a positive integer and 14N/60 is an integer, then N has how many different positive prime factors?- a)2
- b)3
- c)5
- d)6
- e)cannot be determined
Correct answer is option 'E'. Can you explain this answer?
If N is a positive integer and 14N/60 is an integer, then N has how many different positive prime factors?
a)
2
b)
3
c)
5
d)
6
e)
cannot be determined
|
|
Rahul Kapoor answered |
The given condition states that 14N/60 is an integer. We can simplify this expression further:
14N/60 = 7N/30
For 7N/30 to be an integer, N must have prime factors that cancel out the prime factors in the denominator, which are 2 and 5.
If N has additional prime factors other than 2 and 5, they would not affect the divisibility by 30 since 7N/30 can still be an integer. Therefore, the number of different positive prime factors of N cannot be determined.
Hence, the correct answer is option E: cannot be determined.
If c and d are positive integers and m is the greatest common factor of c and d, then m must be the greatest common factor of c and which of the following integers?- a)c + d
- b)2 + d
- c)cd
- d)2d
- e)d^2
Correct answer is option 'A'. Can you explain this answer?
If c and d are positive integers and m is the greatest common factor of c and d, then m must be the greatest common factor of c and which of the following integers?
a)
c + d
b)
2 + d
c)
cd
d)
2d
e)
d^2

|
Mihir Nambiar answered |
To understand why the correct answer is option 'A', let's break it down step by step:
Given:
- c and d are positive integers
- m is the greatest common factor of c and d
Definition of the Greatest Common Factor (GCF):
The greatest common factor of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder.
Step 1: Understanding the GCF of c and d
Since m is the greatest common factor of c and d, it means that m is the largest positive integer that divides both c and d without leaving a remainder.
Step 2: Considering the options
a) c and d
b) 2 and d
c) cd
d) 2d
Step 3: Analyzing option 'A'
If we choose option 'A' (c and d), we are considering the GCF of c and d itself. Since m is already defined as the GCF of c and d, it follows that m will also be the GCF of c and d. This is because the GCF of any two numbers will always be a factor of those numbers.
Step 4: Analyzing the other options
b) 2 and d: The GCF of 2 and d may or may not be equal to m. It depends on whether or not 2 is a factor of c and d.
c) cd: The GCF of cd is equal to 1, as every positive integer has 1 as a common factor. This is not necessarily equal to m.
d) 2d: The GCF of 2d may or may not be equal to m. It depends on whether or not 2 is a factor of c and d.
Step 5: Conclusion
Based on the analysis above, the only option where m is guaranteed to be the GCF is option 'A' (c and d). Therefore, the correct answer is option 'A'.
Given:
- c and d are positive integers
- m is the greatest common factor of c and d
Definition of the Greatest Common Factor (GCF):
The greatest common factor of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder.
Step 1: Understanding the GCF of c and d
Since m is the greatest common factor of c and d, it means that m is the largest positive integer that divides both c and d without leaving a remainder.
Step 2: Considering the options
a) c and d
b) 2 and d
c) cd
d) 2d
Step 3: Analyzing option 'A'
If we choose option 'A' (c and d), we are considering the GCF of c and d itself. Since m is already defined as the GCF of c and d, it follows that m will also be the GCF of c and d. This is because the GCF of any two numbers will always be a factor of those numbers.
Step 4: Analyzing the other options
b) 2 and d: The GCF of 2 and d may or may not be equal to m. It depends on whether or not 2 is a factor of c and d.
c) cd: The GCF of cd is equal to 1, as every positive integer has 1 as a common factor. This is not necessarily equal to m.
d) 2d: The GCF of 2d may or may not be equal to m. It depends on whether or not 2 is a factor of c and d.
Step 5: Conclusion
Based on the analysis above, the only option where m is guaranteed to be the GCF is option 'A' (c and d). Therefore, the correct answer is option 'A'.
Chapter doubts & questions for Problem Solving: 700 Level - Practice Questions for GMAT 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Problem Solving: 700 Level - Practice Questions for GMAT in English & Hindi are available as part of GMAT exam.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Practice Questions for GMAT
11 docs|139 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily









