All Exams >
JAMB >
Mathematics for JAMB >
All Questions
All questions of Percentages for JAMB Exam
There are three galleries in a coal mine. On the first day, two galleries are operative and after some time, the third gallery is made operative. With this, the output of the mine became half as large again. What is the capacity of the second gallery as a percentage of the first, if it is given that a four-month output of the first and the third galleries was the same as the annual output of the second gallery?
- a)60%
- b)64%
- c)65%
- d)70%
Correct answer is option 'A'. Can you explain this answer?
There are three galleries in a coal mine. On the first day, two galleries are operative and after some time, the third gallery is made operative. With this, the output of the mine became half as large again. What is the capacity of the second gallery as a percentage of the first, if it is given that a four-month output of the first and the third galleries was the same as the annual output of the second gallery?
a)
60%
b)
64%
c)
65%
d)
70%

|
Tanishq Sengupta answered |
The third gallery making the capacity ‘half as large again’ means an increase of 50%.
Further, it is given that: 4(first + third) = 12 (second) In order to get to the correct answer, try to fit in the options into this situation.
(Note here that the question is asking you to find the capacity of the second gallery as a percentage of the first.)
If we assume option (a) as correct – 70% the following solution follows:
If the second is 70, then first is 100 and the first + second is 170. Then third will be 85 (50% of first + second).
If the second is 70, then first is 100 and the first + second is 170. Then third will be 85 (50% of first + second).
Then the equation:
4 X (100 + 85) should be equal to 12 X 70
But this is not true.
4 X (100 + 85) should be equal to 12 X 70
But this is not true.
Through trial and error, you can see that the third option fits correctly.
4 X (100 + 80) = 12 X 60.
Hence, it is the correct answer.
4 X (100 + 80) = 12 X 60.
Hence, it is the correct answer.
Sailesh is working as a sales executive with a reputed FMCG Company in Hyderabad. As per the Company’s policy, Sailesh gets a commission of 6% on all sales upto Rs. 1,00,000 and 5% on all sales in excess of this amount. If Sailesh remits Rs. 2,65,000 to the FMCG company after deducting his commission, his total sales were worth:- a)Rs. 2,80,000
- b)Rs. 2,90,526
- c)Rs. 2,21,054
- d)Rs. 1,20,000
Correct answer is option 'A'. Can you explain this answer?
Sailesh is working as a sales executive with a reputed FMCG Company in Hyderabad. As per the Company’s policy, Sailesh gets a commission of 6% on all sales upto Rs. 1,00,000 and 5% on all sales in excess of this amount. If Sailesh remits Rs. 2,65,000 to the FMCG company after deducting his commission, his total sales were worth:
a)
Rs. 2,80,000
b)
Rs. 2,90,526
c)
Rs. 2,21,054
d)
Rs. 1,20,000

|
EduRev CLAT answered |
Let total sales be ‘x’
The commission that Sailesh will get is x – 265000
He gets 6% on sales upto 100000 and 5% on sales greater than that.
Calculating his commission on total sales:
0.06*100000 + 0.05(x-100000)
Equating,
0.05x + 1000 = x – 265000
0.95x = 266000
x= 280000
Hence, his sales were worth 280,000
The number of girls appearing for an admission test is twice the number of boys. If 30% of the girls and 45% of the boys get admission, the percentage of candidates who do not get admission is- a)65
- b)50
- c)60
- d)35
Correct answer is option 'A'. Can you explain this answer?
The number of girls appearing for an admission test is twice the number of boys. If 30% of the girls and 45% of the boys get admission, the percentage of candidates who do not get admission is
a)
65
b)
50
c)
60
d)
35

|
Riverdale Learning Institute answered |
Let the number of girls be 2x and number of boys be x.
Girls getting admission = 0.6x
Boys getting admission = 0.45x
Number of students not getting admission = 3x – 0.6x -0.45x = 1.95x
Percentage = (1.95x/3x) * 100 = 65%
The income of Amala is 20% more than that of Bimala and 20% less than that of Kamala. If Kamala’s income goes down by 4% and Bimala’s goes up by 10%, then the percentage by which Kamala’s income would exceed Bimala’s is nearest to- a) 31
- b) 29
- c) 28
- d) 32
Correct answer is option 'A'. Can you explain this answer?
The income of Amala is 20% more than that of Bimala and 20% less than that of Kamala. If Kamala’s income goes down by 4% and Bimala’s goes up by 10%, then the percentage by which Kamala’s income would exceed Bimala’s is nearest to
a)
31
b)
29
c)
28
d)
32
|
|
Ayushi sharma answered |
Earns x amount of income, then Bimala earns 0.8x (20% less than Kamala) and Amala earns 1.2(0.8x) = 0.96x (20% more than Bimala).
A glass of juice contains 5% fruit extract, 25% of pulp and rest of water. Find amount of water that should be added in glass of 450 ml juice to reduce pulp concentration to 15%?- a)226
- b)300
- c)224
- d)223
Correct answer is option 'B'. Can you explain this answer?
A glass of juice contains 5% fruit extract, 25% of pulp and rest of water. Find amount of water that should be added in glass of 450 ml juice to reduce pulp concentration to 15%?
a)
226
b)
300
c)
224
d)
223
|
|
Olayemi Ojo answered |
Understanding the Juice Composition
The juice contains:
- 5% fruit extract
- 25% pulp
- 70% water (100% - 5% - 25%)
In a 450 ml glass of juice, we can calculate the amounts of each component:
- Fruit extract: 5% of 450 ml = 22.5 ml
- Pulp: 25% of 450 ml = 112.5 ml
- Water: 70% of 450 ml = 315 ml
Target Concentration of Pulp
We want to reduce the pulp concentration to 15%. Let the amount of water to be added be X ml. After adding water, the new total volume of the juice will be:
- New volume = 450 ml + X ml
The pulp remains unchanged at 112.5 ml. The new pulp concentration can be expressed as:
- New pulp concentration = (Amount of pulp / New total volume) * 100
Setting this equal to 15%, we have:
- (112.5 / (450 + X)) * 100 = 15
Solving for X
Now, let's solve the equation:
1. Simplifying gives:
112.5 = 0.15 * (450 + X)
2. Expanding:
112.5 = 67.5 + 0.15X
3. Rearranging:
112.5 - 67.5 = 0.15X
45 = 0.15X
4. Dividing both sides by 0.15:
X = 45 / 0.15
X = 300 ml
Conclusion
To achieve a pulp concentration of 15% in the 450 ml juice, you need to add 300 ml of water. Thus, the correct answer is option B.
The juice contains:
- 5% fruit extract
- 25% pulp
- 70% water (100% - 5% - 25%)
In a 450 ml glass of juice, we can calculate the amounts of each component:
- Fruit extract: 5% of 450 ml = 22.5 ml
- Pulp: 25% of 450 ml = 112.5 ml
- Water: 70% of 450 ml = 315 ml
Target Concentration of Pulp
We want to reduce the pulp concentration to 15%. Let the amount of water to be added be X ml. After adding water, the new total volume of the juice will be:
- New volume = 450 ml + X ml
The pulp remains unchanged at 112.5 ml. The new pulp concentration can be expressed as:
- New pulp concentration = (Amount of pulp / New total volume) * 100
Setting this equal to 15%, we have:
- (112.5 / (450 + X)) * 100 = 15
Solving for X
Now, let's solve the equation:
1. Simplifying gives:
112.5 = 0.15 * (450 + X)
2. Expanding:
112.5 = 67.5 + 0.15X
3. Rearranging:
112.5 - 67.5 = 0.15X
45 = 0.15X
4. Dividing both sides by 0.15:
X = 45 / 0.15
X = 300 ml
Conclusion
To achieve a pulp concentration of 15% in the 450 ml juice, you need to add 300 ml of water. Thus, the correct answer is option B.
Meena scores 40% in an examination and after review, even though her score is increased by 50%, she fails by 35 marks. If her post-review score is increased by 20%, she will have 7 marks more than the passing score. The percentage score needed for passing the examination is- a)70
- b) 80
- c)60
- d) 75
Correct answer is option 'A'. Can you explain this answer?
Meena scores 40% in an examination and after review, even though her score is increased by 50%, she fails by 35 marks. If her post-review score is increased by 20%, she will have 7 marks more than the passing score. The percentage score needed for passing the examination is
a)
70
b)
80
c)
60
d)
75
|
|
Naveen Banerjee answered |
To solve this problem, let's break it down into steps:
Step 1: Find Meena's score before the review
Meena scores 40% in the examination. Let's assume the total marks in the examination are 'x'. So her score before the review is 40% of x, which is 0.4x.
Step 2: Find Meena's score after the review
After the review, her score is increased by 50%. So her new score after the review is 0.4x + 0.5(0.4x) = 0.4x + 0.2x = 0.6x.
Step 3: Find the passing score
We know that after the review, Meena fails by 35 marks. So her post-review score is less than the passing score by 35 marks. Let's assume the passing score is 'p'. Therefore, 0.6x = p - 35.
Step 4: Find Meena's score after the further increase
Meena's score after the further increase is 20% more than her post-review score. So her new score after the further increase is 0.6x + 0.2(0.6x) = 0.6x + 0.12x = 0.72x.
Step 5: Find the passing score after the further increase
We know that her post-review score after the further increase is 7 marks more than the passing score. So the passing score after the further increase is p + 7.
Step 6: Set up an equation
Now, we can set up an equation based on the information from steps 3 and 5:
0.72x = (p + 7)
Step 7: Solve the equation
From step 3, we know that 0.6x = p - 35. We can substitute this value of p from step 3 into the equation in step 6:
0.72x = (0.6x + 7) - 35
0.72x - 0.6x = -28
0.12x = -28
x = -28 / 0.12
x = -280 / 12
x = -70 / 3
Step 8: Find the passing percentage
To find the percentage score needed for passing the examination, we need to find the passing score as a percentage of the total marks. The passing score is p = 0.6x + 35.
Substituting the value of x from step 7, we get:
p = 0.6(-70/3) + 35
p = -42 + 35
p = -7
Since the passing score cannot be negative, we need to consider the absolute value of p, which is 7. Therefore, the passing score is 7 out of -70/3, which is approximately 10%.
So, the percentage score needed for passing the examination is 10%. None of the given options (a, b, c, d) match the correct answer.
Step 1: Find Meena's score before the review
Meena scores 40% in the examination. Let's assume the total marks in the examination are 'x'. So her score before the review is 40% of x, which is 0.4x.
Step 2: Find Meena's score after the review
After the review, her score is increased by 50%. So her new score after the review is 0.4x + 0.5(0.4x) = 0.4x + 0.2x = 0.6x.
Step 3: Find the passing score
We know that after the review, Meena fails by 35 marks. So her post-review score is less than the passing score by 35 marks. Let's assume the passing score is 'p'. Therefore, 0.6x = p - 35.
Step 4: Find Meena's score after the further increase
Meena's score after the further increase is 20% more than her post-review score. So her new score after the further increase is 0.6x + 0.2(0.6x) = 0.6x + 0.12x = 0.72x.
Step 5: Find the passing score after the further increase
We know that her post-review score after the further increase is 7 marks more than the passing score. So the passing score after the further increase is p + 7.
Step 6: Set up an equation
Now, we can set up an equation based on the information from steps 3 and 5:
0.72x = (p + 7)
Step 7: Solve the equation
From step 3, we know that 0.6x = p - 35. We can substitute this value of p from step 3 into the equation in step 6:
0.72x = (0.6x + 7) - 35
0.72x - 0.6x = -28
0.12x = -28
x = -28 / 0.12
x = -280 / 12
x = -70 / 3
Step 8: Find the passing percentage
To find the percentage score needed for passing the examination, we need to find the passing score as a percentage of the total marks. The passing score is p = 0.6x + 35.
Substituting the value of x from step 7, we get:
p = 0.6(-70/3) + 35
p = -42 + 35
p = -7
Since the passing score cannot be negative, we need to consider the absolute value of p, which is 7. Therefore, the passing score is 7 out of -70/3, which is approximately 10%.
So, the percentage score needed for passing the examination is 10%. None of the given options (a, b, c, d) match the correct answer.
Traders A and B buy two goods for Rs. 1000 and Rs. 2000 respectively. Trader A marks his goods up by x%, while trader B marks his goods up by 2x% and offers a discount of x%. If both make the same non-zero profit, find x.- a)25%
- b)12.5%
- c)37.5%
- d)40%
Correct answer is option 'A'. Can you explain this answer?
Traders A and B buy two goods for Rs. 1000 and Rs. 2000 respectively. Trader A marks his goods up by x%, while trader B marks his goods up by 2x% and offers a discount of x%. If both make the same non-zero profit, find x.
a)
25%
b)
12.5%
c)
37.5%
d)
40%

|
Sonal Nambiar answered |
Understanding the Problem
Traders A and B purchase goods for Rs. 1000 and Rs. 2000, respectively. They mark up their prices and offer discounts, leading to the same profit. We need to determine the value of x.
Trader A's Calculation
- Cost Price (CP): Rs. 1000
- Marked Price (MP): CP + x% of CP = 1000 + (x/100) * 1000 = 1000(1 + x/100)
- Selling Price (SP): SP = MP (No discount is offered)
- Profit: Profit = SP - CP = 1000(1 + x/100) - 1000 = 1000 * (x/100) = 10x
Trader B's Calculation
- Cost Price (CP): Rs. 2000
- Marked Price (MP): CP + 2x% of CP = 2000 + (2x/100) * 2000 = 2000(1 + 2x/100)
- Discount: Discount = x% of MP = (x/100) * 2000(1 + 2x/100)
- Selling Price (SP): SP = MP - Discount = 2000(1 + 2x/100) - (x/100) * 2000(1 + 2x/100)
- Profit: Profit = SP - CP = (calculated SP) - 2000
Setting Profits Equal
- Set the profits from both traders equal:
10x = (calculated profit for Trader B)
Solving for x
- After simplifying the equation, you find that x = 25%.
Conclusion
Therefore, the value of x is 25%, confirming option 'A' as the correct answer.
Traders A and B purchase goods for Rs. 1000 and Rs. 2000, respectively. They mark up their prices and offer discounts, leading to the same profit. We need to determine the value of x.
Trader A's Calculation
- Cost Price (CP): Rs. 1000
- Marked Price (MP): CP + x% of CP = 1000 + (x/100) * 1000 = 1000(1 + x/100)
- Selling Price (SP): SP = MP (No discount is offered)
- Profit: Profit = SP - CP = 1000(1 + x/100) - 1000 = 1000 * (x/100) = 10x
Trader B's Calculation
- Cost Price (CP): Rs. 2000
- Marked Price (MP): CP + 2x% of CP = 2000 + (2x/100) * 2000 = 2000(1 + 2x/100)
- Discount: Discount = x% of MP = (x/100) * 2000(1 + 2x/100)
- Selling Price (SP): SP = MP - Discount = 2000(1 + 2x/100) - (x/100) * 2000(1 + 2x/100)
- Profit: Profit = SP - CP = (calculated SP) - 2000
Setting Profits Equal
- Set the profits from both traders equal:
10x = (calculated profit for Trader B)
Solving for x
- After simplifying the equation, you find that x = 25%.
Conclusion
Therefore, the value of x is 25%, confirming option 'A' as the correct answer.
In a group of people, 28% of the members are young while the rest are old. If 65% of the members are literates, and 25% of the literates are young, then the percentage of old people among the illiterates is nearest to
- a)62
- b)55
- c)66
- d)59
Correct answer is option 'C'. Can you explain this answer?
In a group of people, 28% of the members are young while the rest are old. If 65% of the members are literates, and 25% of the literates are young, then the percentage of old people among the illiterates is nearest to
a)
62
b)
55
c)
66
d)
59

|
S.S Career Academy answered |
Let ‘x’ be the strength of group G. Based on the information, 0.65x constitutes of literate people {the rest 0.35x = illiterate}
Of this 0.65x , 75% are old people =(0.75)0.65x old literates.
The total number of old people in group G is 0.72x {72% of the total}.
Thus, the total number of old people who are illiterate = 0.72x - 0.4875x = 0.2325x.
This is
≈ 66& of the total number of illiterates.
Hence, Option C is the correct answer.
Of this 0.65x , 75% are old people =(0.75)0.65x old literates.
The total number of old people in group G is 0.72x {72% of the total}.
Thus, the total number of old people who are illiterate = 0.72x - 0.4875x = 0.2325x.
This is

≈ 66& of the total number of illiterates.
Hence, Option C is the correct answer.
Anil buys 12 toys and labels each with the same selling price. He sells 8 toys initially at 20% discount on the labeled price. Then he sells the remaining 4 toys at an additional 25% discount on the discounted price. Thus, he gets a total of Rs 2112, and makes a 10% profit. With no discounts, his percentage of profit would have been- a)55
- b)60
- c)54
- d)50
Correct answer is option 'D'. Can you explain this answer?
Anil buys 12 toys and labels each with the same selling price. He sells 8 toys initially at 20% discount on the labeled price. Then he sells the remaining 4 toys at an additional 25% discount on the discounted price. Thus, he gets a total of Rs 2112, and makes a 10% profit. With no discounts, his percentage of profit would have been
a)
55
b)
60
c)
54
d)
50

|
Upsc Rank Holders answered |
Let the CP of the each toy be “x”. CP of 12 toys will be “12x”. Now the shopkeeper made a 10% profit on CP. This means that
12x(1.1)= 2112 or x=160 . Hence the CP of each toy is ₹160.
Now let the SP of each toy be “m”. Now he sold 8 toys at 20% discount. This means that 8m(0.8) or 6.4m
He sold 4 toys at an additional 25% discount. 4m(0.8)(0.75)=2.4m Now 6.4m+2.4m=8.8m=2112 or m=240
Hence CP= 160 and SP=240. Hence profit percentage is 50%.
The ratio of number of male and female journalists in a newspaper office is 5:4. The newspaper has two sections, political and sports. If 30 percent of the male journalists and 40 percent of the female journalists are covering political news, what percentage of the journalists (approx.) in the newspaper is currently involved in sports reporting?- a)60 percent
- b)65 percent
- c)70 percent
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
The ratio of number of male and female journalists in a newspaper office is 5:4. The newspaper has two sections, political and sports. If 30 percent of the male journalists and 40 percent of the female journalists are covering political news, what percentage of the journalists (approx.) in the newspaper is currently involved in sports reporting?
a)
60 percent
b)
65 percent
c)
70 percent
d)
None of the above

|
Riverdale Learning Institute answered |
The ratio of number of male and female journalists in a newspaper office is 5:4.
The newspaper has two sections, political and sports.
If 30 percent of the male journalists and 40 percent of the female journalists are covering political news, what percentage of the journalists (approx.) in the newspaper is currently involved in sports reporting?
Let ‘9x’ be the number of total journalists in the office.
Then, we can say that the number of male and female journalists are ‘5x’ and ‘4x’ respectively.
Then, we can say that the number of male and female journalists are ‘5x’ and ‘4x’ respectively.
It is given that 30 percent of the male journalists and 40 percent of the female journalists are covering political news. Hence, total number of journalists who are covering political news = 0.3*5x + 0.4*4x = 3.1x
Therefore, the total number journalists who are covering sports news = 9x – 3.1x = 5.9x.
Hence, the percentage of the journalists in the newspaper is currently involved in sports reporting = 5.9x/9x x 100 ≈
Hence, the percentage of the journalists in the newspaper is currently involved in sports reporting = 5.9x/9x x 100 ≈
65 percent. Therefore, option B is the correct answer.
Instead of a metre scale, a cloth merchant uses a faulty 120 cm scale while buying, but uses a faulty 80 cm scale while selling the same cloth. If he offers a discount of 20%, what is his overall profit percentage?- a)25%
- b)20%
- c)40%
- d)15%
Correct answer is option 'B'. Can you explain this answer?
Instead of a metre scale, a cloth merchant uses a faulty 120 cm scale while buying, but uses a faulty 80 cm scale while selling the same cloth. If he offers a discount of 20%, what is his overall profit percentage?
a)
25%
b)
20%
c)
40%
d)
15%

|
Upsc Rank Holders answered |
Let’s say the cost of the cloth is x rs per metre. Because of the faulty meter, he is paying x for 120 cms when buying.
So cost of 100 cms = 100x/120.
He is selling 80 cms for x, so selling price of 100cms of cloth is 100x/80.
discount = 20%
so the effective selling price is .8*100x/80= x
profit = SP-CP= x – 100x/120 = x/6
Profit % = x/6 divided by 100x/120 = 20%
A fruit seller sells 45% of the oranges that he has along with one more orange to a customer. He then sells 20% of the remaining oranges and 2 more oranges to a second customer. He then sells 90% of the now remaining oranges to a third customer and is still left with 5 oranges. How many oranges did the fruit seller have initially?- a)121
- b)111
- c)100
- d)120
Correct answer is option 'D'. Can you explain this answer?
A fruit seller sells 45% of the oranges that he has along with one more orange to a customer. He then sells 20% of the remaining oranges and 2 more oranges to a second customer. He then sells 90% of the now remaining oranges to a third customer and is still left with 5 oranges. How many oranges did the fruit seller have initially?
a)
121
b)
111
c)
100
d)
120

|
Sun Ray Institute answered |
Let the initial oranges with the fruit seller be x.
1st selling = 0.45x + 1
Remaining = x - (0.45x + 1) = 0.55x - 1
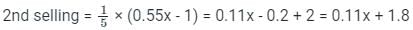
Remaining after second selling = 0.55x - 1 - (0.11x + 1.8) = 0.55x - 0.11x - 1 - 1.8 = 0.44x - 2.8
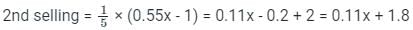
Remaining after second selling = 0.55x - 1 - (0.11x + 1.8) = 0.55x - 0.11x - 1 - 1.8 = 0.44x - 2.8
3rd selling = 90% × (0.44x - 2.8)
Remaining after 3rd selling = 0.1 × (0.44x - 2.8) = 0.044x - 0.28
According to the question-
⇒ 0.044x - 0.28 = 5
⇒ 0.044x = 5.28
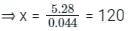
∴ The number of oranges was 120.
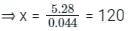
∴ The number of oranges was 120.
The weighing machine at Nathan’s shop is a faulty one. It shows 20% less than the actual weight put on it. However, it shows wrong weight only in some cases with a probability ranging between 0.4 to 0.6. Assuming that Nathan sells at cost price, what could be the maximum loss that Nathan can face? (Assume Nathan sells equal quantity in each transaction)- a)12.58%
- b)13.04%
- c)15.18%
- d)9.67%
Correct answer is option 'B'. Can you explain this answer?
The weighing machine at Nathan’s shop is a faulty one. It shows 20% less than the actual weight put on it. However, it shows wrong weight only in some cases with a probability ranging between 0.4 to 0.6. Assuming that Nathan sells at cost price, what could be the maximum loss that Nathan can face? (Assume Nathan sells equal quantity in each transaction)
a)
12.58%
b)
13.04%
c)
15.18%
d)
9.67%

|
Sun Ray Institute answered |
Machine shows 20% less than the actual weight put on it, in some of the cases. So, Nathan gives more quantity than what he charges for. And hence he goes into loss.
The loss will be maximum when the wrong weight is shown with maximum probability, that is 0.6.
Let Nathan sells T kg in each transaction, and the cost price of T kg is C.
In 60% of total cases, amount Nathan will give = T/(1 – 20/100) kg = T/0.8 kg = 1.25T kg
In remaining 40% cases, Nathan gives T kg.
⇒ Average Amount given in a transaction = 0.6 × 1.25T + 0.4 × T = 1.15T
⇒ Cost price of a transaction = 1.15TC
And, selling price of a transaction = TC
We know, Selling Price = Cost Price × (1 - (Loss %)/100)
⇒ Loss Percentage = 100 × (1 – TC/1.15TC) = 13.04
∴ Maximum loss can be 13.04%.
When 40% of a number E is added to another number R, B becomes 125% of its previous value. Then which of the following is true regarding the values of E and R?- a)Either (a) or (b) can be true depending upon the values of E and R
- b)R > E
- c)E > R
- d)R = E
Correct answer is option 'A'. Can you explain this answer?
When 40% of a number E is added to another number R, B becomes 125% of its previous value. Then which of the following is true regarding the values of E and R?
a)
Either (a) or (b) can be true depending upon the values of E and R
b)
R > E
c)
E > R
d)
R = E

|
Tanishq Shah answered |
Let's start by translating the given information into equations:
- "40% of a number E": this can be written as 0.4E
- "added to another number R": we add 0.4E to R, so we get R + 0.4E
- "B becomes 125% of its previous value": if we call the previous value of B "B0", then we have B = 1.25B0
Putting it all together, we can write:
R + 0.4E = 1.25B0
But we don't know anything about B0, so we need to find another equation to solve for E and R. We can use the fact that B is a certain percentage of its previous value:
B = 1.25B0 = 1.25(B/1.25) = B/0.8
This means that B is 0.8 times its current value. So we can write:
B = 0.8(R + 0.4E)
Now we have two equations with two unknowns, E and R:
R + 0.4E = 1.25B0
B = 0.8(R + 0.4E)
We can solve for E by substituting the second equation into the first:
R + 0.4E = 1.25(0.8(R + 0.4E))
Simplifying:
R + 0.4E = R + 1.0E
0.6E = R
So we have found that 0.6E = R. We can substitute this into either equation to solve for E or R. For example, using the second equation:
B = 0.8(R + 0.4E)
B = 0.8(0.6E + 0.4E)
B = 0.8E
So we have found that B is 0.8 times E. This means that either (a) or (b) can be true depending on the values of E and R:
(a) If E = 1 and R = 0.6, then R + 0.4E = 1 and B = 0.8E = 0.8, which satisfies the conditions.
(b) If E = 0 and R = 0, then R + 0.4E = 0 and B = 0, which also satisfies the conditions.
- "40% of a number E": this can be written as 0.4E
- "added to another number R": we add 0.4E to R, so we get R + 0.4E
- "B becomes 125% of its previous value": if we call the previous value of B "B0", then we have B = 1.25B0
Putting it all together, we can write:
R + 0.4E = 1.25B0
But we don't know anything about B0, so we need to find another equation to solve for E and R. We can use the fact that B is a certain percentage of its previous value:
B = 1.25B0 = 1.25(B/1.25) = B/0.8
This means that B is 0.8 times its current value. So we can write:
B = 0.8(R + 0.4E)
Now we have two equations with two unknowns, E and R:
R + 0.4E = 1.25B0
B = 0.8(R + 0.4E)
We can solve for E by substituting the second equation into the first:
R + 0.4E = 1.25(0.8(R + 0.4E))
Simplifying:
R + 0.4E = R + 1.0E
0.6E = R
So we have found that 0.6E = R. We can substitute this into either equation to solve for E or R. For example, using the second equation:
B = 0.8(R + 0.4E)
B = 0.8(0.6E + 0.4E)
B = 0.8E
So we have found that B is 0.8 times E. This means that either (a) or (b) can be true depending on the values of E and R:
(a) If E = 1 and R = 0.6, then R + 0.4E = 1 and B = 0.8E = 0.8, which satisfies the conditions.
(b) If E = 0 and R = 0, then R + 0.4E = 0 and B = 0, which also satisfies the conditions.
Two students appeared for an examination. One of them secured 22 marks more than the other and his marks were 55% of the sum of their marks. The marks obtained by them are _______.- a)121 and 99
- b)43 and 21
- c)58 and 36
- d)86 and 64
Correct answer is option 'A'. Can you explain this answer?
Two students appeared for an examination. One of them secured 22 marks more than the other and his marks were 55% of the sum of their marks. The marks obtained by them are _______.
a)
121 and 99
b)
43 and 21
c)
58 and 36
d)
86 and 64

|
Sun Ray Institute answered |
Given:
Two students appeared for an examination. One of them secured 22
marks more than the other and his marks were 55% of the sum of
their marks
Calculation:
Let the students be A and B
Let the marks secured by B = x
Marks secured by A = x + 22
Sum of their marks of A & B = x + x + 22 = 2x + 22
Accoring to question,
Marks of A = 55% of the sum of marks
⇒ x + 22 = 0.55 × (2x + 22)
⇒ x + 22 = 1.1x + 12.1
⇒ 0.1x = 9.9
⇒ x = 9.9/0.1 = 99 marks
Marks secured by A = 99 + 22 = 121 marks
Therefore the correct answer is 121.
Shortcut Trick:
Let us go by options.
The difference between the numbers is 22 in all cases.
So, now check the next statement.
121 = 0.55 × (121+ 99)
That is, as the first option itself satisfies the condition and since we do no have a combination of answers, it is the solution.
∴ The required numbers are 121 and 99.
John got 30% of the maximum marks in an examination and failed by 10 marks. However, Paul who took the same examination got 40% of the total marks and got 15 marks more than the passing marks. What were the passing marks in the examination?- a)75
- b)110
- c)85
- d)90
Correct answer is option 'C'. Can you explain this answer?
John got 30% of the maximum marks in an examination and failed by 10 marks. However, Paul who took the same examination got 40% of the total marks and got 15 marks more than the passing marks. What were the passing marks in the examination?
a)
75
b)
110
c)
85
d)
90

|
Sun Ray Institute answered |
Maximum mark be m
passing marks = (30/100)m + 10
marks obtained by paul = (40/100)m = [(30/100)m + 10] + 15
40m/100 = 30m/100 + 25
10m/100 = 25
m = 2500/10
m = 250
Thus passing marks = 85
passing marks = (30/100)m + 10
marks obtained by paul = (40/100)m = [(30/100)m + 10] + 15
40m/100 = 30m/100 + 25
10m/100 = 25
m = 2500/10
m = 250
Thus passing marks = 85
Which of the following is correct statement ?- a)Na2S is Sodium sulphide, Na2S03 is Sodium sulphite and Na2S04 is Sodium sulphate
- b)Na2S is Sodium sulphite, Na2S03 is Sodium sulphide and Na2S04 is Sodium sulphate
- c)Na2S is Sodium sulphite, Na2S03 is Sodium sulphate and Na2S04 is Sodium sulphide
- d)Na2S is Sodium sulphide , Na2S03 is Sodium sulphate and Na2S04 is Sodium thiosulphate
Correct answer is option 'A'. Can you explain this answer?
Which of the following is correct statement ?
a)
Na2S is Sodium sulphide, Na2S03 is Sodium sulphite and Na2S04 is Sodium sulphate
b)
Na2S is Sodium sulphite, Na2S03 is Sodium sulphide and Na2S04 is Sodium sulphate
c)
Na2S is Sodium sulphite, Na2S03 is Sodium sulphate and Na2S04 is Sodium sulphide
d)
Na2S is Sodium sulphide , Na2S03 is Sodium sulphate and Na2S04 is Sodium thiosulphate

|
Saranya Sengupta answered |
Na2S is Sodium sulphide, Na2S03 is Sodium sulphite, and Na2S04 is Sodium sulphate.
Explanation:
Sodium (Na) is a chemical element with atomic number 11. It belongs to Group 1 of the periodic table and is highly reactive. Sulfur (S) is a chemical element with atomic number 16. It belongs to Group 16 of the periodic table and can form various compounds with different elements.
Sodium sulfide (Na2S):
- Sodium sulfide is an inorganic compound with the formula Na2S.
- It is composed of two sodium (Na) ions and one sulfur (S) ion.
- Sodium sulfide is a colorless solid and it is highly soluble in water.
- It is commonly used in the leather industry for dehairing hides and in the production of dyes and pigments.
Sodium sulphite (Na2SO3):
- Sodium sulphite is an inorganic compound with the formula Na2SO3.
- It is composed of two sodium (Na) ions, one sulfur (S) ion, and three oxygen (O) ions.
- Sodium sulphite is a white crystalline solid and it is soluble in water.
- It is commonly used as a reducing agent in various chemical reactions and as a preservative in food and beverages.
Sodium sulphate (Na2SO4):
- Sodium sulphate is an inorganic compound with the formula Na2SO4.
- It is composed of two sodium (Na) ions, one sulfur (S) ion, and four oxygen (O) ions.
- Sodium sulphate is a white crystalline solid and it is soluble in water.
- It is commonly used in the manufacturing of detergents, glass, and paper.
Based on the above explanations, it can be concluded that option 'A' is the correct statement. Na2S represents sodium sulfide, Na2SO3 represents sodium sulphite, and Na2SO4 represents sodium sulphate.
Explanation:
Sodium (Na) is a chemical element with atomic number 11. It belongs to Group 1 of the periodic table and is highly reactive. Sulfur (S) is a chemical element with atomic number 16. It belongs to Group 16 of the periodic table and can form various compounds with different elements.
Sodium sulfide (Na2S):
- Sodium sulfide is an inorganic compound with the formula Na2S.
- It is composed of two sodium (Na) ions and one sulfur (S) ion.
- Sodium sulfide is a colorless solid and it is highly soluble in water.
- It is commonly used in the leather industry for dehairing hides and in the production of dyes and pigments.
Sodium sulphite (Na2SO3):
- Sodium sulphite is an inorganic compound with the formula Na2SO3.
- It is composed of two sodium (Na) ions, one sulfur (S) ion, and three oxygen (O) ions.
- Sodium sulphite is a white crystalline solid and it is soluble in water.
- It is commonly used as a reducing agent in various chemical reactions and as a preservative in food and beverages.
Sodium sulphate (Na2SO4):
- Sodium sulphate is an inorganic compound with the formula Na2SO4.
- It is composed of two sodium (Na) ions, one sulfur (S) ion, and four oxygen (O) ions.
- Sodium sulphate is a white crystalline solid and it is soluble in water.
- It is commonly used in the manufacturing of detergents, glass, and paper.
Based on the above explanations, it can be concluded that option 'A' is the correct statement. Na2S represents sodium sulfide, Na2SO3 represents sodium sulphite, and Na2SO4 represents sodium sulphate.
A solution contains 33g of common salt in 320g of water. Calculate the concentration in terms of mass, by mass percentage of the solution.- a)13.05%
- b)9.09 g
- c)9.35 g
- d)9.35%
Correct answer is option 'D'. Can you explain this answer?
A solution contains 33g of common salt in 320g of water. Calculate the concentration in terms of mass, by mass percentage of the solution.
a)
13.05%
b)
9.09 g
c)
9.35 g
d)
9.35%

|
Sun Ray Institute answered |
Formula Used:
Mass percentage in solution = Total Salt/Total Solution × 100
Calculation:
Quantity of salt = 33g
Quantity of water = 320 g
The total quantity of solution,
⇒ 33 + 320 = 353 g
Now by using the formula,
Percentage of salt in the solution
⇒ (33/353) × 100 = 9.35% (approx)
∴ Mass percentage of the solution is 9.35 %.
In a class of 450 students, 20% of students have failed in an examination, whereas another 10% students didn't appear in the exam. How many students passed the exam?- a)315
- b)210
- c)375
- d)300
Correct answer is option 'A'. Can you explain this answer?
In a class of 450 students, 20% of students have failed in an examination, whereas another 10% students didn't appear in the exam. How many students passed the exam?
a)
315
b)
210
c)
375
d)
300

|
Sun Ray Institute answered |
30% students either failed or didn't appear in the exam.
Thus the No. of students who passed the exam
= 450 - 135 = 315
Thus the No. of students who passed the exam
= 450 - 135 = 315
An alloy contains 5 kg of metal A and 20 kg of metal B. What is the percentage of metal A in the alloy?- a)40%
- b)30%
- c)20%
- d)25%
Correct answer is option 'C'. Can you explain this answer?
An alloy contains 5 kg of metal A and 20 kg of metal B. What is the percentage of metal A in the alloy?
a)
40%
b)
30%
c)
20%
d)
25%

|
Sun Ray Institute answered |
Total amount of metal in the alloy = 25 kg
5 = z% of 25
(5 x 100)/25 = z
= 20%
5 = z% of 25
(5 x 100)/25 = z
= 20%
If the price of petrol has increased from Rs. 40 per litre to Rs. 60 per litre, by how much percent a person has to decrease his consumption so that his expenditure remains same.- a)66.67%
- b)40%
- c)33.33%
- d)45%
Correct answer is option 'C'. Can you explain this answer?
If the price of petrol has increased from Rs. 40 per litre to Rs. 60 per litre, by how much percent a person has to decrease his consumption so that his expenditure remains same.
a)
66.67%
b)
40%
c)
33.33%
d)
45%

|
Sun Ray Institute answered |
Given:
If the price of petrol has increased from Rs. 40 per litre to Rs. 60 per litre
Calculation:
Let the consumption be 100 litres.
When price is Rs. 40 per litres, then, the expenditure = 100 × 40
⇒ Rs. 4,000.
At Rs. 60 per litre, the 60 × consumption = 4000
Consumption = 4,000/60 = 66.67 litres.
∴ Required decreased % = 100 - 66.67 = 33.33%
An interval of 3 hours 40 minutes is wrongly estimated as 3 hours 45.5 minutes. What is the error percentage?- a)3.2%
- b)1.5%
- c)2.5%
- d)4.1%
Correct answer is option 'C'. Can you explain this answer?
An interval of 3 hours 40 minutes is wrongly estimated as 3 hours 45.5 minutes. What is the error percentage?
a)
3.2%
b)
1.5%
c)
2.5%
d)
4.1%

|
Sun Ray Institute answered |
3 hrs 40 min = 220 min
3 hrs 45.5 min = 225.5 min
225.5 - 220 = 5.5
Now, let's assume, 225.5 is z% of 220
z = 102.5
Percentage difference = 102.5 - 100
= 2.5
3 hrs 45.5 min = 225.5 min
225.5 - 220 = 5.5
Now, let's assume, 225.5 is z% of 220
z = 102.5
Percentage difference = 102.5 - 100
= 2.5
The income of Doyel is 40% more than that of Chitra. Chitra got an 8% hike in his income, and Doyel got a 25% hike in her income. The percentage increase in their combined income is:- a)18%
- b)21%
- c)17%
- d)24%
Correct answer is option 'A'. Can you explain this answer?
The income of Doyel is 40% more than that of Chitra. Chitra got an 8% hike in his income, and Doyel got a 25% hike in her income. The percentage increase in their combined income is:
a)
18%
b)
21%
c)
17%
d)
24%

|
Sun Ray Institute answered |
Given:
The income of Doyel is 40% more than that of Chitra.
Chitra got an 8% hike in his income, and Doyel got a 25% hike in her income.
Concept used:
Incremented/Reduced value = Initial value (1 ± change%)
Calculation:
Let the income of Chitra be Rs. 500.
Income of Doyel = 500 × 1.4
⇒ Rs. 700
Income of Chitra after the hike = 500 × (1 + 8/100)
⇒ Rs. 540
Income of Doyel after the hike = 700 × (1 + 25/100)
⇒ Rs. 875
Now, percentage increase in their income combined = 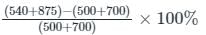
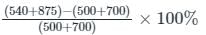
⇒ 17.916% ≈ 18%
∴ The increase in their percentage combined income is 18%.
Out of two numbers, 65% of the smaller number is equal to 45% of the larger number. If the sum of two numbers is 2574, then what is the value of the larger number?- a)1521
- b)1471
- c)1641
- d)1419
Correct answer is option 'A'. Can you explain this answer?
Out of two numbers, 65% of the smaller number is equal to 45% of the larger number. If the sum of two numbers is 2574, then what is the value of the larger number?
a)
1521
b)
1471
c)
1641
d)
1419

|
Sun Ray Institute answered |
Given:
Out of two numbers, 65% of the smaller number is equal to 45% of the larger
number. If the sum of two numbers is 2574
Calculation:
Let the smaller number be ‘x’ and the larger number be ‘y’
From the problem, it is given that
65%x = 45%y
⇒ 13x = 9y
⇒ x = (9/13)y ----(1)
Given the sum of the numbers = 2574
⇒ (x + y) = 2574 ----(2)
Substituting the value of ‘x’ from Equation 1 in Equation 2, we get
(9/13)y + y = 2574
⇒ (9y + 13y) = 2574 × 13
⇒ 22y = (2574 × 13)
⇒ y = (2574 × 13)/22 = 1521
∴ Value of the larger number is 1521
Find 8.33% of 252.- a)18
- b)21
- c)23
- d)22.5
Correct answer is option 'B'. Can you explain this answer?
Find 8.33% of 252.
a)
18
b)
21
c)
23
d)
22.5

|
Harsh Kothari answered |
It's easy first take 8% of 252 and then add 0.33% of 252 and the answer is nearby 20.9 i.e 21 option b
The price of petrol is increased by 25%. How much percent must a car owner reduce his consumption of petrol so as not to increase his expenditure on petrol?- a)20%
- b)30%
- c)35%
- d)40%
Correct answer is option 'A'. Can you explain this answer?
The price of petrol is increased by 25%. How much percent must a car owner reduce his consumption of petrol so as not to increase his expenditure on petrol?
a)
20%
b)
30%
c)
35%
d)
40%

|
Sun Ray Institute answered |
Let the original price of petrol be Rs. 100
original consumption be p litres
original expenditure be Rs. 100p
Updated price = Rs. 125
updated consumption = p - (r/100)p
updated expenditure = 125[p - (pr/100)]
original and updated expenditure must be same
Thus 125[p - (pr/100)] = 100p
solving this, we get r = 20
i.e. reduction in consumption should be 20%
original consumption be p litres
original expenditure be Rs. 100p
Updated price = Rs. 125
updated consumption = p - (r/100)p
updated expenditure = 125[p - (pr/100)]
original and updated expenditure must be same
Thus 125[p - (pr/100)] = 100p
solving this, we get r = 20
i.e. reduction in consumption should be 20%
If the average, of a given number, 50% of that number and 25% of the same number is 280, then the number is- a)280
- b)480
- c)360
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
If the average, of a given number, 50% of that number and 25% of the same number is 280, then the number is
a)
280
b)
480
c)
360
d)
None of the above

|
Sun Ray Institute answered |
Given:
Average is 280.
Formula used:
Average = sum of the observation/number of the observation
Calculation:
Let the number be x
According to the question,
⇒ (x + 50% of x + 25% of x)/3 = 280
⇒ (x + x/2 + x/4)/3 = 280
⇒ 7x/12 = 280
⇒ x = 480
∴ The number is 480.
The income of A is 25% less than the income of B and the income of C is 75% more than the income of B. If the difference in the income of A and C is Rs. 100, then find the income of B.- a)Rs. 100
- b)Rs. 70
- c)Rs. 200
- d)Rs. 500
Correct answer is option 'A'. Can you explain this answer?
The income of A is 25% less than the income of B and the income of C is 75% more than the income of B. If the difference in the income of A and C is Rs. 100, then find the income of B.
a)
Rs. 100
b)
Rs. 70
c)
Rs. 200
d)
Rs. 500

|
Sun Ray Institute answered |
Given:
The income of A is 25% less than the income of B,
The income of C is 75% more than the income of B,
The difference in the income of A and C is Rs. 100.
Calculation:
Let 'x' be the income of B.
The income of A = (100% - 25%) of B = 75% of B
The income of C = (100% + 75%) of B = 175% of B
According to the question,
⇒ 175% of B - 75% of B = Rs. 100
⇒ 100% of B = Rs. 100
⇒ B = Rs. 100
Therefore, 'Rs. 100' is the required answer.
Alternate Method
The income of A is 25% less than the income of B,
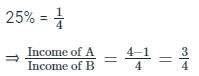
The income of C is 75% more than the income of B,
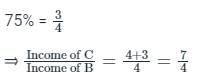
The income of A is 25% less than the income of B,
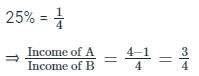
The income of C is 75% more than the income of B,
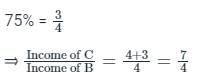
In ratio form the above finding can be written as:
Income of A : Income of B : Income of C = 3 : 4 : 7
According to the question,
⇒ 7k - 3k = 100
⇒ 4k = 100
⇒ k = 25
The income of B = 4k = Rs. 100
Therefore, 'Rs. 100' is the required answer.
If 75% of a number is added to 75, then the result is the number itself. The number is- a)490
- b)300
- c)349
- d)359
Correct answer is option 'B'. Can you explain this answer?
If 75% of a number is added to 75, then the result is the number itself. The number is
a)
490
b)
300
c)
349
d)
359

|
Sun Ray Institute answered |
Let the number be a
(75/100)a + 75 = a
75a + 7500 = 100a
7500 = 25a
a = 300
(75/100)a + 75 = a
75a + 7500 = 100a
7500 = 25a
a = 300
In an election A got 55% of the total votes and the remaining votes were casted to B. If 10,000 votes of A are given to B, there would have been a tie. Find the number of total votes polled?- a)260000
- b)240000
- c)200000
- d)220000
Correct answer is option 'C'. Can you explain this answer?
In an election A got 55% of the total votes and the remaining votes were casted to B. If 10,000 votes of A are given to B, there would have been a tie. Find the number of total votes polled?
a)
260000
b)
240000
c)
200000
d)
220000

|
Sun Ray Institute answered |
Given:
In an election A got 55% of the total votes and the remaining votes were casted to B. If 10,000 votes of A are given to B, there would have been a tie
Formula used:
A got a% votes and B got b% votes, difference in the votes = (a - b) % of Total votes
Calculation:
Let the total votes be 100x
A Gets = 55x
B gets = 45x
Given that 10,000 votes of A given to B
As per question
⇒ 55x – 10,000 = 45x + 10,000
⇒ x = 2000
Total votes polled = 100x
⇒ 100 × 2000 = 200000
∴ Total votes polled is 200000
65% of a number is more than 25% of the number by 120. What is 20% of that number?- a)60
- b)66
- c)48
- d)69
Correct answer is option 'A'. Can you explain this answer?
65% of a number is more than 25% of the number by 120. What is 20% of that number?
a)
60
b)
66
c)
48
d)
69

|
Sun Ray Institute answered |
Given:
65% of a number is more than 25% of the number by 120.
Calculations:
Let the number be x
According to question, (65x/100) - (25x/100) = 120
⇒ (65x - 25x)/100 = 120
⇒ 40x/100 = 120
⇒ x = (120 × 100)/40 = 300
But we have to find 20%, so (20/100) × 300 = 60
∴ The required number is 60.
Shortcut Trick
65% - 25% = 120
⇒ 40% = 120
⇒ 20% = 60
∴ The required number is 60
There were two candidates in an election, 10% of voters did not vote and 48 votes were found invalid. The winning candidate got 53% of all the voters in the list and won by 304 votes. Find the total number of votes enrolled.- a)1600
- b)1230
- c)4561
- d)1653
Correct answer is option 'A'. Can you explain this answer?
There were two candidates in an election, 10% of voters did not vote and 48 votes were found invalid. The winning candidate got 53% of all the voters in the list and won by 304 votes. Find the total number of votes enrolled.
a)
1600
b)
1230
c)
4561
d)
1653

|
Sun Ray Institute answered |
Given:
There were two candidates in an election, 10% of voters did not vote and 48 votes were found invalid. The winning candidate got 53% of the total votes and won by 304 votes.
Concept used:
Percentage
Calculation:
Let the total number of voters be 100x
10% of voters did not vote
Number of voters who vote = 100x - 10x = 90x
48 votes were found invalid
Valid votes = 90x - 48
Votes gained by the winning candidate 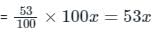
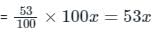
Votes gained by the loosing candidate = 90x - 48 - 53x
⇒ 37x - 48
As per the question,
⇒ 53x - (37x - 48) = 304
⇒ 16x = 304 - 48
⇒ 16x = 256
⇒ x = 16
∴ Total number of voters = 100x = 1600
Alternate Method
Let total number of votes be 100 units,
10% voters did not cast their vote
⇒ Votes polled = 90 units
The winning candidate got 53% of all the voters in the list and won by 304 votes,
⇒ Winning candidate got = 53 units votes
⇒ Other candidate got = 37 units votes
⇒ Difference in votes = 53 units votes - 37 units votes = 304 - 48 = 256 votes
⇒ 16 units = 256
∴ 100 units votes = 256/16 × 100 = 1600 votes
∴ Total number of voters = 1600.
30% apples out of 450 are rotten. How many apples are in good condition?- a)322
- b)315
- c)324
- d)344
Correct answer is option 'B'. Can you explain this answer?
30% apples out of 450 are rotten. How many apples are in good condition?
a)
322
b)
315
c)
324
d)
344

|
Sun Ray Institute answered |
Number of rotten apples = (30/100) x 450
=135
Number of apples in good condition = 450 - 135 = 315
=135
Number of apples in good condition = 450 - 135 = 315
Ted spends 55% of his income. His income increases by 28% and his expenditure also increases by 40%. The percentage of increase in his savings is:- a)12.7%
- b)13.5%
- c)13.3%
- d)12.4%
Correct answer is option 'C'. Can you explain this answer?
Ted spends 55% of his income. His income increases by 28% and his expenditure also increases by 40%. The percentage of increase in his savings is:
a)
12.7%
b)
13.5%
c)
13.3%
d)
12.4%

|
Sun Ray Institute answered |
Given:
Ted spends 55% of his income. His income increases by 28% and his expenditure also increases by 40%.
Concept used:
Income = Expenditure + Savings
Calculation:
Let the income of Ted be Rs. 100.
His expenditure = 100 × 55%
⇒ Rs. 55
His savings = 100 - 55
⇒ Rs. 45
Ted's increased income = 100 + 100 × 28%
⇒ Rs. 128
Ted's increased expenditure = 55 + 55 × 40%
⇒ Rs. 77
Ted's savings = 128 - 77
⇒ Rs. 51
Now, his savings increased by 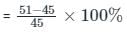
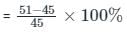
⇒ 13.3% (approx)
∴ The percentage of increase in his savings is 13.3%.
By how much percent is four-fifth of 70 lesser than five-seventh of 112?- a)15%
- b)20%
- c)30%
- d)40%
Correct answer is option 'C'. Can you explain this answer?
By how much percent is four-fifth of 70 lesser than five-seventh of 112?
a)
15%
b)
20%
c)
30%
d)
40%

|
Sun Ray Institute answered |
(5/7) x 112 = 80
(4/5) x 70 = 56
lets assume 56 is z% lesser than 80
80 - 56 =24
24 = z% of 80
(24 x 100)/80 = z
z = 30
(4/5) x 70 = 56
lets assume 56 is z% lesser than 80
80 - 56 =24
24 = z% of 80
(24 x 100)/80 = z
z = 30
An engineering student has to secure 15% marks to pass. He gets 55 marks and fails by 20 marks. Find his maximum marks.- a)300
- b)600
- c)500
- d)200
Correct answer is option 'C'. Can you explain this answer?
An engineering student has to secure 15% marks to pass. He gets 55 marks and fails by 20 marks. Find his maximum marks.
a)
300
b)
600
c)
500
d)
200

|
Sun Ray Institute answered |
Given:
An engineering student has to secure 15% marks to pass.
A student gets 55 marks and fails by 20 marks.
Calculation:
Let the total marks be x
Passing marks = x × 15%
Passing marks = 15x/100 ----(1)
According to the question,
Passing marks = 55 + 20 = 75 ----(2)
From equation (1) and (2) we get,
⇒ 15x/100 = 75
⇒ x = 7500/15
⇒ x = 500
∴ The maximum marks of the student is 500.
Shortcut Trick
Passing percentage = 15%
Passing marks = 55 + 20 = 75
Maximum marks = (75/15) × 100 = 500
∴ The maximum marks of the student is 500.
The price for a pair of bangles is Rs. 1.00. The price for a 5-pair package of the bangle is Rs. 3.40. The 5-pair package is what percent cheaper than 5 pairs purchased separately?- a)32%
- b)24%
- c)20%
- d)27%
Correct answer is option 'A'. Can you explain this answer?
The price for a pair of bangles is Rs. 1.00. The price for a 5-pair package of the bangle is Rs. 3.40. The 5-pair package is what percent cheaper than 5 pairs purchased separately?
a)
32%
b)
24%
c)
20%
d)
27%

|
Sun Ray Institute answered |
Let's assume the price of 5 pair package be p% of individual 5 pairs
3.40 = p% of 5
p = 68%
i.e (100 - 68) = 32
Thus, 5 pair package is 32% cheaper than the individual 5 pairs
3.40 = p% of 5
p = 68%
i.e (100 - 68) = 32
Thus, 5 pair package is 32% cheaper than the individual 5 pairs
A bakery shop opened with its daily supply of 40 dozen rolls. Half of the rolls were sold by noon and 60% of the remaining rolls were sold between noon and closing time. How many dozen rolls were left unsold?- a)4 Dozen
- b)8 Dozen
- c)5 Dozen
- d)6 Dozen
Correct answer is option 'B'. Can you explain this answer?
A bakery shop opened with its daily supply of 40 dozen rolls. Half of the rolls were sold by noon and 60% of the remaining rolls were sold between noon and closing time. How many dozen rolls were left unsold?
a)
4 Dozen
b)
8 Dozen
c)
5 Dozen
d)
6 Dozen

|
Sun Ray Institute answered |
Total rolls = 40 dozen
20 dozen sold by noon
Remaining rolls = 20 dozen
Rolls sold between noon and closing time (60/100)20 = 1200/100
= 12
Unsold = 20 - 12 = 8 dozen
20 dozen sold by noon
Remaining rolls = 20 dozen
Rolls sold between noon and closing time (60/100)20 = 1200/100
= 12
Unsold = 20 - 12 = 8 dozen
If 125 is subtracted from a number, it reduces to its 37.5 percent. What is 25 percent of that number?- a)65
- b)60
- c)55
- d)50
Correct answer is option 'D'. Can you explain this answer?
If 125 is subtracted from a number, it reduces to its 37.5 percent. What is 25 percent of that number?
a)
65
b)
60
c)
55
d)
50

|
Sun Ray Institute answered |
Let the number be a
a - 125 = (37.5/100) a
100a - 37.5a = 12500
a = 200
Thus 25% of 200 = 50
a - 125 = (37.5/100) a
100a - 37.5a = 12500
a = 200
Thus 25% of 200 = 50
The salary of a man was reduced by 10%. By what percent should his reduced salary be raised so as to bring it at par with his original salary?- a)19.21%
- b)15%
- c)14.21%
- d)11.11%
Correct answer is option 'D'. Can you explain this answer?
The salary of a man was reduced by 10%. By what percent should his reduced salary be raised so as to bring it at par with his original salary?
a)
19.21%
b)
15%
c)
14.21%
d)
11.11%

|
Sun Ray Institute answered |
Let the original salary be Rs. 100. New salary = Rs. 90.
Let the increase be p% of 90
[90 + (p/100)90] = 100
90 + 90p/100 = 100
9000 + 90p = 10000
90p = 10000 - 9000
p = 11.11
Let the increase be p% of 90
[90 + (p/100)90] = 100
90 + 90p/100 = 100
9000 + 90p = 10000
90p = 10000 - 9000
p = 11.11
12% of Mahesh's monthly salary is equal to 16% of Amit's monthly salary. Sonal's monthly salary is half that of Amit's. IF Sonal's annual salary is Rs. 1.08 lacs, what is Mahesh's monthly salary?- a)Rs. 30000
- b)Rs. 20000
- c)Rs. 24000
- d)Rs. 38000
Correct answer is option 'C'. Can you explain this answer?
12% of Mahesh's monthly salary is equal to 16% of Amit's monthly salary. Sonal's monthly salary is half that of Amit's. IF Sonal's annual salary is Rs. 1.08 lacs, what is Mahesh's monthly salary?
a)
Rs. 30000
b)
Rs. 20000
c)
Rs. 24000
d)
Rs. 38000

|
Sun Ray Institute answered |
Sonal's monthly salary = (1.08/12) lacs
= 9000
Thus, the monthly salary of Amit = Rs. 18000
Let's assume, the monthly salary of Mahesh = z
(12/100) z = (16/100) x 18000
z = 24000
= 9000
Thus, the monthly salary of Amit = Rs. 18000
Let's assume, the monthly salary of Mahesh = z
(12/100) z = (16/100) x 18000
z = 24000
A man's working hours a day were increased by 20% and his wages per hour were increased by 15%. By how much percent was his daily earning increased?- a)45%
- b)30%
- c)51%
- d)38%
Correct answer is option 'D'. Can you explain this answer?
A man's working hours a day were increased by 20% and his wages per hour were increased by 15%. By how much percent was his daily earning increased?
a)
45%
b)
30%
c)
51%
d)
38%

|
Sun Ray Institute answered |
Let the original number of working hours a day be p hrs.
and original wages per hour be Rs. y
Then, original daily earning = Rs. (py).
Increased working hours = p + (20p/100)
= (120p/100)
New wage per hr = y + 15y/100
= (115y/100)
New daily earning = (120p/100) x (115y/100)
= 1.38py
Assume 1.38py is z% of py
1.38py = z%(py)
z = 138
i.e. the increase in percent = 138 - 100
= 38%
and original wages per hour be Rs. y
Then, original daily earning = Rs. (py).
Increased working hours = p + (20p/100)
= (120p/100)
New wage per hr = y + 15y/100
= (115y/100)
New daily earning = (120p/100) x (115y/100)
= 1.38py
Assume 1.38py is z% of py
1.38py = z%(py)
z = 138
i.e. the increase in percent = 138 - 100
= 38%
A woman's wage was reduced by 50%. Again the reduced wage was increased by 50%. Find her loss in terms of percentage.- a)31%
- b)22%
- c)36%
- d)25%
Correct answer is option 'D'. Can you explain this answer?
A woman's wage was reduced by 50%. Again the reduced wage was increased by 50%. Find her loss in terms of percentage.
a)
31%
b)
22%
c)
36%
d)
25%

|
Sun Ray Institute answered |
Let original wage = 100.
After reduction, salary = 50.
Now 50% increase of reduced salary = 50 + [(50/100) x 50] = 75
Thus loss = 100 - 75 = 25.
25% will be the loss.
After reduction, salary = 50.
Now 50% increase of reduced salary = 50 + [(50/100) x 50] = 75
Thus loss = 100 - 75 = 25.
25% will be the loss.
Chapter doubts & questions for Percentages - Mathematics for JAMB 2025 is part of JAMB exam preparation. The chapters have been prepared according to the JAMB exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JAMB 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Percentages - Mathematics for JAMB in English & Hindi are available as part of JAMB exam.
Download more important topics, notes, lectures and mock test series for JAMB Exam by signing up for free.
Mathematics for JAMB
134 videos|94 docs|102 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









