All Exams >
JAMB >
Mathematics for JAMB >
All Questions
All questions of Logarithm for JAMB Exam
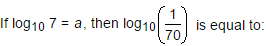
- a)- (1 + a)
- b)(1 + a)-1
- c)
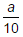
- d)
Correct answer is option 'A'. Can you explain this answer?
a)
- (1 + a)
b)
(1 + a)-1
c)
d)
|
Dia Mehta answered |
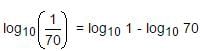
⇒ - log10 (7 x 10)
⇒ - (log10 7 + log10 10)
⇒ - (a + 1)
⇒ - (log10 7 + log10 10)
⇒ - (a + 1)
The value of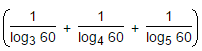 
is: - a)0
- b)1
- c)5
- d)60
Correct answer is option 'B'. Can you explain this answer?
The value of 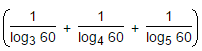is:
is:a)
0
b)
1
c)
5
d)
60
|
Shalini Patel answered |
Given expression = 1/log60 3 + 1/log60 4 + 1/log60 5
= log60 (3 x 4 x 5)
= log60 60
= 1.
= log60 (3 x 4 x 5)
= log60 60
= 1.
if log 2 = 0.30103 and log 3 = 0.4771, find the number of digits in (648)5.- a)15
- b)14
- c)13
- d)12
Correct answer is option 'A'. Can you explain this answer?
if log 2 = 0.30103 and log 3 = 0.4771, find the number of digits in (648)5.
a)
15
b)
14
c)
13
d)
12
|
Ishani Rane answered |
log(648)^5
= 5 log(648)
= 5 log(81 x 8)
= 5[log(81) + log(8)]
=5 [log(34) + log(23)]
=5[4log(3) + 3log(2)]
= 5[4 x 0.4771 + 3 x 0.30103]
= 5(1.9084 + 0.90309)
= 5 x 2.81149
approx. = 14.05
ie, log(648)^5 = 14.05 (approx.)
ie, its characteristic = 14
Hence, number of digits in (648)5 = 14+1 = 15
Which of the following statements is not correct?
- a)log10 10 = 1
- b)log (2 + 3) = log (2 x 3)
- c)log10 1 = 0
- d)log (1 + 2 + 3) = log 1 + log 2 + log 3
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is not correct?
a)
log10 10 = 1
b)
log (2 + 3) = log (2 x 3)
c)
log10 1 = 0
d)
log (1 + 2 + 3) = log 1 + log 2 + log 3
|
Prince Chaudhary answered |
According to logarithm rule . option B is never correct
If 3X+I = 6logZ3 then x is - a)2
- b)3
- c)log32
- d)log23
Correct answer is option 'D'. Can you explain this answer?
If 3X+I = 6logZ3 then x is
a)
2
b)
3
c)
log32
d)
log23
|
Anita Parida answered |
That is Z to the power of 3 or Z3?
If log 27 = 1.431, then the value of log 9 is:- a)0.934
- b)0.945
- c)0.954
- d)0.958
Correct answer is option 'C'. Can you explain this answer?
If log 27 = 1.431, then the value of log 9 is:
a)
0.934
b)
0.945
c)
0.954
d)
0.958
|
Gowri Chakraborty answered |
Log 27 = 1.431
log (33 ) = 1.431
3 log 3 = 1.431
log 3 = 0.477
log 9 = log(32 ) = 2 log 3 = (2 x 0.477) = 0.954.
log (12 - x) = -1 - a)11.6
- b)12.1
- c)11
- d)11.9
Correct answer is option 'D'. Can you explain this answer?
log (12 - x) = -1
a)
11.6
b)
12.1
c)
11
d)
11.9
|
Abhay Ghosh answered |
1/10 = 12 - x => x = 11.9
log2 (9 - 2X) = 10log (3-x) Solve for x.- a)0
- b)3
- c)Both (a) and (b)
- d)0 and 6
Correct answer is option 'A'. Can you explain this answer?
log2 (9 - 2X) = 10log (3-x) Solve for x.
a)
0
b)
3
c)
Both (a) and (b)
d)
0 and 6
|
Sameer Rane answered |
If the base of the log in the RHS is 10, then
if log 2 = 0.30103, the number of digits in 2128 is- a)38
- b)39
- c)40
- d)41
Correct answer is option 'B'. Can you explain this answer?
if log 2 = 0.30103, the number of digits in 2128 is
a)
38
b)
39
c)
40
d)
41
|
Milan Nair answered |
log(2128) = 128log(2) = 128 × 0.30103 ≈ 38.4
ie, its characteristic = 38
Hence, number of digits in 2128 = 38+1 = 39
ie, its characteristic = 38
Hence, number of digits in 2128 = 38+1 = 39
If 2 [log (x + y) - log 5] = logx + logy, then what is the value of x2 + y2?- a)20-xy
- b)23xy
- c)2 5 - xy
- d)28xy
Correct answer is option 'C'. Can you explain this answer?
If 2 [log (x + y) - log 5] = logx + logy, then what is the value of x2 + y2?
a)
20-xy
b)
23xy
c)
2 5 - xy
d)
28xy
|
Sakshi Patel answered |
2[log(x+y)-log5]=logx+logy= 2log(x+y)/5=logxy =log{(x+y)/5}^2=logxy ={(x+y)/5}^2=xy =(x+y)^2=25xy= x*x+y*y+2xy=25xy= x*x+y*y=23xy
Find x if logx =2 log 5 + 3 log 2- a)50
- b)100
- c)150
- d)200
Correct answer is option 'D'. Can you explain this answer?
Find x if logx =2 log 5 + 3 log 2
a)
50
b)
100
c)
150
d)
200
|
Jaya Gupta answered |
log x = log 25 + log 8 = log (25 x 8 ) = log 200.
What is the value of x in the following expression: log2 ( 3 - x ) + log2 ( 1 - x ) = 3?- a)1
- b)0
- c)-1
- d)Not possible
Correct answer is option 'C'. Can you explain this answer?
What is the value of x in the following expression: log2 ( 3 - x ) + log2 ( 1 - x ) = 3?
a)
1
b)
0
c)
-1
d)
Not possible
|
Aarav Sharma answered |
**Solution:**
To find the value of x in the given expression: log2 (3 - x) * log2 (1 - x) = 3, we can follow the steps below:
1. Simplify the expression:
- Using the product rule of logarithms, we can rewrite the expression as:
log2 ((3 - x) * (1 - x)) = 3
- Expanding the brackets, we get:
log2 (3 - x - 3x + x^2) = 3
- Simplifying further:
log2 (x^2 - 4x + 3) = 3
2. Convert the logarithmic equation to an exponential equation:
- In general, if log2 (a) = b, then 2^b = a.
- Applying this to our equation, we have:
x^2 - 4x + 3 = 2^3
x^2 - 4x + 3 = 8
x^2 - 4x - 5 = 0
3. Solve the quadratic equation:
- Factoring the quadratic equation, we get:
(x - 5)(x + 1) = 0
- Setting each factor equal to zero and solving for x, we have:
x - 5 = 0 or x + 1 = 0
x = 5 or x = -1
4. Check for extraneous solutions:
- Substitute the values of x back into the original equation:
log2 (3 - x) * log2 (1 - x) = 3
For x = 5: log2 (3 - 5) * log2 (1 - 5) = 3
log2 (-2) * log2 (-4) = 3
Since the logarithm of a negative number or zero is undefined, x = 5 is an extraneous solution.
For x = -1: log2 (3 - (-1)) * log2 (1 - (-1)) = 3
log2 (4) * log2 (2) = 3
2 * 1 = 3
2 = 3
Since the equation is not satisfied, x = -1 is also an extraneous solution.
5. Final Answer:
- The correct value of x in the given expression is x = -1, which is option (c).
To find the value of x in the given expression: log2 (3 - x) * log2 (1 - x) = 3, we can follow the steps below:
1. Simplify the expression:
- Using the product rule of logarithms, we can rewrite the expression as:
log2 ((3 - x) * (1 - x)) = 3
- Expanding the brackets, we get:
log2 (3 - x - 3x + x^2) = 3
- Simplifying further:
log2 (x^2 - 4x + 3) = 3
2. Convert the logarithmic equation to an exponential equation:
- In general, if log2 (a) = b, then 2^b = a.
- Applying this to our equation, we have:
x^2 - 4x + 3 = 2^3
x^2 - 4x + 3 = 8
x^2 - 4x - 5 = 0
3. Solve the quadratic equation:
- Factoring the quadratic equation, we get:
(x - 5)(x + 1) = 0
- Setting each factor equal to zero and solving for x, we have:
x - 5 = 0 or x + 1 = 0
x = 5 or x = -1
4. Check for extraneous solutions:
- Substitute the values of x back into the original equation:
log2 (3 - x) * log2 (1 - x) = 3
For x = 5: log2 (3 - 5) * log2 (1 - 5) = 3
log2 (-2) * log2 (-4) = 3
Since the logarithm of a negative number or zero is undefined, x = 5 is an extraneous solution.
For x = -1: log2 (3 - (-1)) * log2 (1 - (-1)) = 3
log2 (4) * log2 (2) = 3
2 * 1 = 3
2 = 3
Since the equation is not satisfied, x = -1 is also an extraneous solution.
5. Final Answer:
- The correct value of x in the given expression is x = -1, which is option (c).
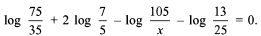
- a)90
- b)65
- c)13
- d)45
Correct answer is option 'C'. Can you explain this answer?
a)
90
b)
65
c)
13
d)
45
|
Anirudh Unni answered |
(75/35) x (49/25) x (jc/105) x (25/13) = 1 ⇒ x = 13
If log(64)= 1.806, log(16) = ?- a) 1.204
- b)0.903
- c)1.806
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If log(64)= 1.806, log(16) = ?
a)
1.204
b)
0.903
c)
1.806
d)
None of these
|
|
Gowri Chakraborty answered |
log(64)= 1.806
=> log(4^3) = 1.806
=> 3log(4) = 1.806
⇒log(4) = 1.806/3
log(16) = log (4^2) = 2log(4) = 2*1.806/3 = 2*0.062 = 1.204
Find x If logx = log 1.5 + log 12- a)12
- b)8
- c)18
- d)15
Correct answer is option 'C'. Can you explain this answer?
Find x If logx = log 1.5 + log 12
a)
12
b)
8
c)
18
d)
15
|
|
Aarav Sharma answered |
Solution:
Given, log x = log 1.5 + log 12
Using the property of logarithms, i.e., log a + log b = log ab, we can write
log x = log (1.5 × 12)
log x = log 18
Taking antilogarithm on both sides, we get
x = 18
Therefore, the correct option is C.
Explanation:
To solve this problem, we need to use the properties of logarithms. The given equation can be simplified by using the property of addition of logarithms.
We know that log a + log b = log (ab)
So, we can write log x = log (1.5 × 12)
Now, we need to simplify the expression on the right-hand side. We know that 1.5 × 12 = 18.
So, we can write log x = log 18.
To find the value of x, we need to take antilogarithm on both sides of the equation.
Antilogarithm of log 18 is equal to 18.
Therefore, the value of x is 18.
Final answer: The correct option is C.
Given, log x = log 1.5 + log 12
Using the property of logarithms, i.e., log a + log b = log ab, we can write
log x = log (1.5 × 12)
log x = log 18
Taking antilogarithm on both sides, we get
x = 18
Therefore, the correct option is C.
Explanation:
To solve this problem, we need to use the properties of logarithms. The given equation can be simplified by using the property of addition of logarithms.
We know that log a + log b = log (ab)
So, we can write log x = log (1.5 × 12)
Now, we need to simplify the expression on the right-hand side. We know that 1.5 × 12 = 18.
So, we can write log x = log 18.
To find the value of x, we need to take antilogarithm on both sides of the equation.
Antilogarithm of log 18 is equal to 18.
Therefore, the value of x is 18.
Final answer: The correct option is C.
If log 2 = 0.3010 and log 3 = 0.4771, What is the value of log51024?- a)4.31
- b)3.88
- c)3.91
- d)2.97
Correct answer is option 'A'. Can you explain this answer?
If log 2 = 0.3010 and log 3 = 0.4771, What is the value of log51024?
a)
4.31
b)
3.88
c)
3.91
d)
2.97
|
|
Gowri Chakraborty answered |
log 5 1024= log1024/log5 = log ( 2^10)/log(10/2)=10log(2)/log10−log2
=10*0.3010/1−0.3010 = 3.01/0.699 = 3010/699 = 4.31
If log10a = b, find the value of 103b in terms of a.- a) a3
- b)3a
- c)a x 1000
- d)a x 100
Correct answer is option 'A'. Can you explain this answer?
If log10a = b, find the value of 103b in terms of a.
a)
a3
b)
3a
c)
a x 1000
d)
a x 100
|
|
Harshitha Desai answered |
log10a = b ⇒ 10b = a ⇒ By definition of logs.
Thus 103b = (10b)3 = a3.
Arrange the following in an ascending order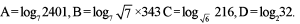
- a)ABCD
- b)BDCA
- c)BDAD
- d)BADC
Correct answer is option 'D'. Can you explain this answer?
Arrange the following in an ascending order
a)
ABCD
b)
BDCA
c)
BDAD
d)
BADC
|
KS Coaching Center answered |
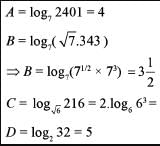
A = 4, B = 7/2, C = 6, D = 5
Arranging in ascending order: BADC
If log 2 = .301, find the number of digits in (125)25.- a)53
- b)50
- c)25
- d)63
Correct answer is option 'A'. Can you explain this answer?
If log 2 = .301, find the number of digits in (125)25.
a)
53
b)
50
c)
25
d)
63
|
|
Asha Basak answered |
logy = 25 log 125
= 25 [log 1000 - 3 log 2]
= 25 x (2.097)
= 52 +
Hence 53 digits.
Hence 53 digits.
find x If log x = log7.2 - log 2.4- a)1
- b)2
- c)3
- d)4
Correct answer is option 'C'. Can you explain this answer?
find x If log x = log7.2 - log 2.4
a)
1
b)
2
c)
3
d)
4
|
|
Jaya Gupta answered |
log x = log (7.2/2.4) = log 3 ⇒ x = 3
log153375 x log41024 = ?- a)16
- b)18
- c)12
- d)15
Correct answer is option 'D'. Can you explain this answer?
log153375 x log41024 = ?
a)
16
b)
18
c)
12
d)
15
|
|
Ankita Yadav answered |
log153375 x Log41024 = 3 log151 5 x 5 log4 4 = 3 x 5 = 15.
If log102 = .301 find log10125.- a)2.097
- b)2.301
- c)2.10
- d)2.087
Correct answer is option 'A'. Can you explain this answer?
If log102 = .301 find log10125.
a)
2.097
b)
2.301
c)
2.10
d)
2.087
|
|
Ankita Yadav answered |
log10 125 = log10( 1000/8) = log. 1000 - 31og2 = 3 - 3 x 0.301 = 2.097
?
5X = 10 - a)log 5
- b)log 10/log 2
- c)log 2
- d)1/log 5
Correct answer is option 'D'. Can you explain this answer?
5X = 10
a)
log 5
b)
log 10/log 2
c)
log 2
d)
1/log 5
|
|
Jaya Gupta answered |
x = log510 = l/log105 = 1/log 5.
3 log 5 + 2 log 4 - log 2 = ?- a)4
- b)3
- c)200
- d)1000
Correct answer is option 'B'. Can you explain this answer?
3 log 5 + 2 log 4 - log 2 = ?
a)
4
b)
3
c)
200
d)
1000
|
|
Jaya Gupta answered |
3 log 5 + 2 log 4 - log 2
= log 125 + log 16 - log 2
= log (125 x 16)/2
= log 1000 = 3.
If log10 2 = 0.3010, then log2 10 is equal to:- a)
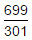
- b)
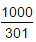
- c)0.3010
- d)0.6990
Correct answer is 'B'. Can you explain this answer?
If log10 2 = 0.3010, then log2 10 is equal to:
a)
b)
c)
0.3010
d)
0.6990
|
|
Aman Jha answered |
Log10 2=1/log2 10 therefore 0.3010=1/log2 10 log2 10=1/0.3010 so log2 10 = 1000/301
Chapter doubts & questions for Logarithm - Mathematics for JAMB 2025 is part of JAMB exam preparation. The chapters have been prepared according to the JAMB exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JAMB 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Logarithm - Mathematics for JAMB in English & Hindi are available as part of JAMB exam.
Download more important topics, notes, lectures and mock test series for JAMB Exam by signing up for free.
Mathematics for JAMB
134 videos|94 docs|102 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup
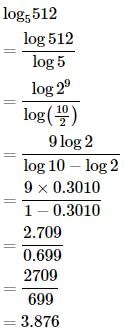
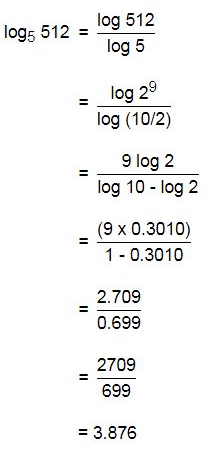
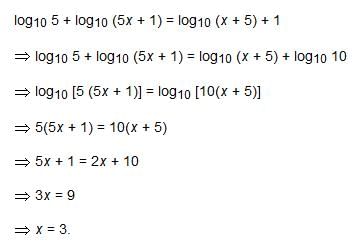
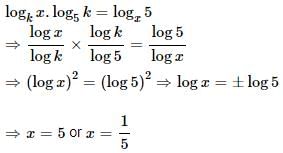
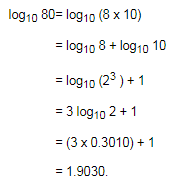
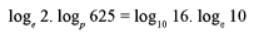