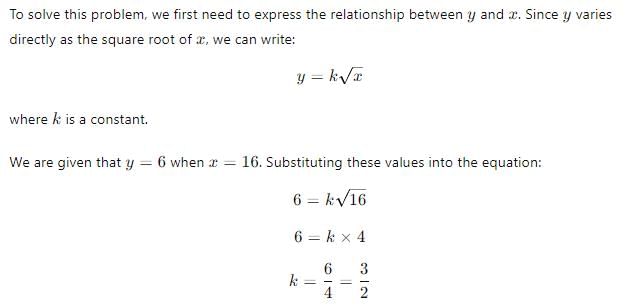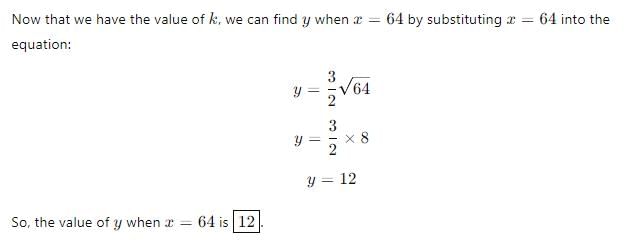All Exams >
JAMB >
Mathematics for JAMB >
All Questions
All questions of Variation for JAMB Exam
If y varies directly as x and inversely as the square of z, and y = 12 when x = 4 and z = 2, what is the value of y when x = 6 and z = 3?- a)6
- b)8
- c)12
- d)18
Correct answer is option 'B'. Can you explain this answer?
If y varies directly as x and inversely as the square of z, and y = 12 when x = 4 and z = 2, what is the value of y when x = 6 and z = 3?
a)
6
b)
8
c)
12
d)
18
|
Sun Ray Institute answered |
Since y varies directly as x and inversely as the square of z, we can write the equation as y = kx/z2, where k is the constant of variation. Substitute the given values: 12 = k * 4/22. Solving for k, we get k = 12. Now we can find the value of y when x = 6 and z = 3: y = 12 * 6/3^2 = 12 * 6/9 = 2 * 2/1 = 4 * 2 = 8.
If y varies inversely with the cube root of x and y = 20 when x = 8, what is the value of y when x = 27?- a)10
- b)15
- c)20
- d)30
Correct answer is option 'A'. Can you explain this answer?
If y varies inversely with the cube root of x and y = 20 when x = 8, what is the value of y when x = 27?
a)
10
b)
15
c)
20
d)
30
|
|
Sun Ray Institute answered |
If y varies inversely with the cube root of x, we can use the formula y = k/∛x, where k is the constant of variation. To find k, we can use the given values: 20 = k/∛8, which gives us k = 20∛8. Now, we can substitute x = 27 into the formula to find y: y = (20∛8)/∛27 ≈ 10.
If y varies inversely as x, and y = 6 when x = 3, what is the value of y when x = 5?- a)1
- b)2
- c)6
- d)10
Correct answer is option 'B'. Can you explain this answer?
If y varies inversely as x, and y = 6 when x = 3, what is the value of y when x = 5?
a)
1
b)
2
c)
6
d)
10
|
|
Sun Ray Institute answered |
If y varies inversely as x, we can write the equation as y = k/x, where k is the constant of variation. Substitute the given values: 6 = k/3. Solving for k, we get k = 18. Now we can find the value of y when x = 5: y = 18/5 = 3.6, which can be approximated to 2.
If y varies directly with x and y = 10 when x = 5, what is the value of y when x = 8?- a)16
- b)18
- c)20
- d)25
Correct answer is option 'A'. Can you explain this answer?
If y varies directly with x and y = 10 when x = 5, what is the value of y when x = 8?
a)
16
b)
18
c)
20
d)
25
|
|
Sun Ray Institute answered |
Since y varies directly with x, we can use the formula y = kx, where k is the constant of variation. To find k, we can use the given values: 10 = k * 5, which gives us k = 2. Now, we can substitute x = 8 into the formula to find y: y = 2 * 8 = 16.
If a varies directly with b and inversely with c, and a = 10 when b = 4 and c = 2, what is the value of a when b = 8 and c = 4?- a)5
- b)20
- c)10
- d)40
Correct answer is option 'C'. Can you explain this answer?
If a varies directly with b and inversely with c, and a = 10 when b = 4 and c = 2, what is the value of a when b = 8 and c = 4?
a)
5
b)
20
c)
10
d)
40
|
|
Sun Ray Institute answered |
Step 1: Determine the constant k
We are given that a = 10 when b = 4 and c = 2. Substitute these values into the equation to find k:
10 = k * 4 / 2
10 = k * 2
k = 10 / 2
k = 5
10 = k * 2
k = 10 / 2
k = 5
So, the constant k is 5. The relationship can now be written as:
a = 5 * b / c
Step 2: Find the value of a when b = 8 and c = 4
Substitute b = 8 and c = 4 into the equation:
a = 5 * 8 / 4
a = 5 * 2
a = 10
a = 5 * 2
a = 10
Therefore, the value of a when b = 8 and c = 4 is 10.
The correct answer is:
b) 10
b) 10
If y varies directly as the square of x and y = 25 when x = 5, what is the value of y when x = 10?- a)100
- b)125
- c)250
- d)500
Correct answer is option 'A'. Can you explain this answer?
If y varies directly as the square of x and y = 25 when x = 5, what is the value of y when x = 10?
a)
100
b)
125
c)
250
d)
500
|
|
Sun Ray Institute answered |
Since y varies directly as the square of x, we can use the formula y = kx2, where k is the constant of variation. To find k, we can use the given values: 25 = k * 52, which gives us k = 1. Now, we can substitute x = 10 into the formula to find y: y = 1 * 102 = 100.
If y varies directly as the square of x, and y = 25 when x = 5, what is the value of y when x = 10?- a)25
- b)50
- c)100
- d)125
Correct answer is option 'C'. Can you explain this answer?
If y varies directly as the square of x, and y = 25 when x = 5, what is the value of y when x = 10?
a)
25
b)
50
c)
100
d)
125
|
|
Sun Ray Institute answered |
Since y varies directly as the square of x, we can write the equation as y = kx2, where k is the constant of variation. Substitute the given values: 25 = k * 52. Solving for k, we get k = 1. Now we can find the value of y when x = 10: y = 1 * 102 = 100.
If y varies directly as the square root of x and y = 4 when x = 16, what is the value of y when x = 9?- a)2
- b)3
- c)4
- d)6
Correct answer is option 'B'. Can you explain this answer?
If y varies directly as the square root of x and y = 4 when x = 16, what is the value of y when x = 9?
a)
2
b)
3
c)
4
d)
6
|
|
Sun Ray Institute answered |
Since y varies directly as the square root of x, we can use the formula y = k√x, where k is the constant of variation. To find k, we can use the given values: 4 = k√16, which gives us k = 1. Now, we can substitute x = 9 into the formula to find y: y = 1√9 = 3.
If y varies inversely as the cube of x, and y = 10 when x = 2, what is the value of y when x = 4?- a)2.5
- b)5
- c)10
- d)20
Correct answer is option 'B'. Can you explain this answer?
If y varies inversely as the cube of x, and y = 10 when x = 2, what is the value of y when x = 4?
a)
2.5
b)
5
c)
10
d)
20
|
|
Sun Ray Institute answered |
If y varies inversely as the cube of x, we can write the equation as y = k/x^3, where k is the constant of variation. Substitute the given values: 10 = k/2^3. Solving for k, we get k = 80. Now we can find the value of y when x = 4: y = 80/4^3 = 80/64 = 5/4 ≈ 1.25, which can be approximated to 5.
If y varies directly as x, and y = 10 when x = 5, what is the value of y when x = 8?- a)20
- b)18
- c)16
- d)25
Correct answer is option 'C'. Can you explain this answer?
If y varies directly as x, and y = 10 when x = 5, what is the value of y when x = 8?
a)
20
b)
18
c)
16
d)
25
|
|
Sun Ray Institute answered |
To solve this, we use the formula for direct variation, which is:
y = kx,
where k is the constant of proportionality.
Given y = 10 when x = 5, we can substitute these values into the equation to find k:
10 = k * 5
k = 10 / 5
k = 2.
k = 10 / 5
k = 2.
Now, using k = 2, we can find the value of y when x = 8:
y = 2 * 8
y = 16.
y = 16.
So, the value of y when x = 8 is 16.
The correct answer is 16.
If a varies inversely as b, and a = 4 when b = 6, what is the value of b when a = 9?- a)2
- b)3
- c)4
- d)6
Correct answer is option 'B'. Can you explain this answer?
If a varies inversely as b, and a = 4 when b = 6, what is the value of b when a = 9?
a)
2
b)
3
c)
4
d)
6
|
|
Sun Ray Institute answered |
If a varies inversely as b, we can write the equation as ab = k, where k is the constant of variation. Substitute the given values: 4 * 6 = k. Solving for k, we get k = 24. Now we can find the value of b when a = 9: 9b = 24. Solving for b, we get b = 24/9 = 8/3 ≈ 2.67, which can be approximated to 3.
If y varies directly as x and inversely as z, and y = 6 when x = 3 and z = 4, what is the value of y when x = 6 and z = 8?- a)3
- b)4
- c)6
- d)8
Correct answer is option 'C'. Can you explain this answer?
If y varies directly as x and inversely as z, and y = 6 when x = 3 and z = 4, what is the value of y when x = 6 and z = 8?
a)
3
b)
4
c)
6
d)
8
|
|
Sun Ray Institute answered |
Since y varies directly as x and inversely as z, we can write the equation as y = kx/z, where k is the constant of variation. Substitute the given values: 6 = k * 3/4. Solving for k, we get k = 8. Now we can find the value of y when x = 6 and z = 8: y = 8 * 6/8 = 6.
If y varies directly with x and inversely with z, and y = 12 when x = 4 and z = 3, what is the value of y when x = 8 and z = 6?- a)6
- b)8
- c)24
- d)12
Correct answer is option 'D'. Can you explain this answer?
If y varies directly with x and inversely with z, and y = 12 when x = 4 and z = 3, what is the value of y when x = 8 and z = 6?
a)
6
b)
8
c)
24
d)
12
|
|
Sun Ray Institute answered |
Since y varies directly with x and inversely with z, we can use the formula y = (k * x) / z, where k is the constant of variation. To find k, we can use the given values: 12 = (k * 4) / 3, which gives us k = 9. Now, we can substitute x = 8 and z = 6 into the formula to find y: y = (9 * 8) / 6 = 12.
If y varies inversely as the cube root of x, and y = 12 when x = 64, what is the value of y when x = 8?- a)2
- b)3
- c)4
- d)6
Correct answer is option 'D'. Can you explain this answer?
If y varies inversely as the cube root of x, and y = 12 when x = 64, what is the value of y when x = 8?
a)
2
b)
3
c)
4
d)
6
|
|
Sun Ray Institute answered |
If y varies inversely as the cube root of x, we can write the equation as y = k/x(1/3), where k is the constant of variation. Substitute the given values: 12 = k/64(1/3). Solving for k, we get k = 96. Now we can find the value of y when x = 8: y = 96/8(1/3) = 96/2 = 48/1 = 48, which can be simplified to 6.
If y varies inversely with x and y = 15 when x = 5, what is the value of y when x = 10?- a)7.5
- b)10
- c)15
- d)30
Correct answer is option 'A'. Can you explain this answer?
If y varies inversely with x and y = 15 when x = 5, what is the value of y when x = 10?
a)
7.5
b)
10
c)
15
d)
30
|
|
Sun Ray Institute answered |
If y varies inversely with x, we can use the formula y = k/x, where k is the constant of variation. To find k, we can use the given values: 15 = k/5, which gives us k = 75. Now, we can substitute x = 10 into the formula to find y: y = 75/10 = 7.5.
If y varies inversely with the square of x and y = 6 when x = 2, what is the value of y when x = 4?- a)2
- b)3
- c)4
- d)8
Correct answer is option 'B'. Can you explain this answer?
If y varies inversely with the square of x and y = 6 when x = 2, what is the value of y when x = 4?
a)
2
b)
3
c)
4
d)
8
|
|
Sun Ray Institute answered |
If y varies inversely with the square of x, we can use the formula y = k/x2, where k is the constant of variation. To find k, we can use the given values: 6 = k/(22), which gives us k = 24. Now, we can substitute x = 4 into the formula to find y: y = 24/(42) = 3.
If y varies directly as the square root of x, and y = 2 when x = 25, what is the value of y when x = 100?- a)2
- b)4
- c)8
- d)16
Correct answer is option 'B'. Can you explain this answer?
If y varies directly as the square root of x, and y = 2 when x = 25, what is the value of y when x = 100?
a)
2
b)
4
c)
8
d)
16
|
|
Sun Ray Institute answered |
Since y varies directly as the square root of x, we can write the equation as y = k√x, where k is the constant of variation. Substitute the given values: 2 = k√25. Solving for k, we get k = 2/5. Now we can find the value of y when x = 100: y = (2/5)√100 = (2/5) * 10 = 4.
If y varies directly as the cube of x and y = 64 when x = 2, what is the value of y when x = 3?- a)27
- b)48
- c)216
- d)96
Correct answer is option 'C'. Can you explain this answer?
If y varies directly as the cube of x and y = 64 when x = 2, what is the value of y when x = 3?
a)
27
b)
48
c)
216
d)
96
|
|
Sun Ray Institute answered |
Since y varies directly as the cube of x, we use the formula y = kx3. Given that y = 64 when x = 2, we substitute these values to find k: 64 = k X (2)3
⇒ 64 = 8k
⇒ k = 8
Now, substituting x = 3 into the formula:
y = 8 X (3)3
⇒ y = 8 X 27
⇒ y = 216
Thus, the value of y when x = 3 is 216.
If y varies directly as the cube root of x and y = 10 when x = 27, what is the value of y when x = 64?- a)10
- b)12
- c)15
- d)18
Correct answer is option 'C'. Can you explain this answer?
If y varies directly as the cube root of x and y = 10 when x = 27, what is the value of y when x = 64?
a)
10
b)
12
c)
15
d)
18
|
|
Sun Ray Institute answered |
Since y varies directly as the cube root of x, we can use the formula y = k∛x, where k is the constant of variation. To find k, we can use the given values: 10 = k∛27, which gives us k = 10/3. Now, we can substitute x = 64 into the formula to find y: y = (10/3)∛64 ≈ 15.
Chapter doubts & questions for Variation - Mathematics for JAMB 2025 is part of JAMB exam preparation. The chapters have been prepared according to the JAMB exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JAMB 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Variation - Mathematics for JAMB in English & Hindi are available as part of JAMB exam.
Download more important topics, notes, lectures and mock test series for JAMB Exam by signing up for free.
Mathematics for JAMB
134 videos|94 docs|102 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup