All Exams >
JAMB >
Mathematics for JAMB >
All Questions
All questions of Angles and lines for JAMB Exam
If two angles are supplementary then the sum of their measures is ___________ .- a)45°
- b)180°
- c)90°
- d)360°
Correct answer is option 'B'. Can you explain this answer?
If two angles are supplementary then the sum of their measures is ___________ .
a)
45°
b)
180°
c)
90°
d)
360°

|
Shilpa Das answered |
Supplementary angles are two angles whose sum is equal to 180∘. In other words when you add the measure of one angle in the pair with the other angle in the pair, they equal 180 degrees.
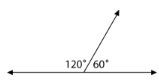
These two angles are supplementary because together they form a straight line. You can also tell that they are supplementary because when you add their angle measures the sum is equal to 180 degrees.
120+60=180degree
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Lines and Angles, Class 7, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic. Q.If two lines intersect at a point, then the vertically opposite angles are always ________- a)supplementary
- b)equal
- c)unequal
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Lines and Angles, Class 7, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic.
Q.
If two lines intersect at a point, then the vertically opposite angles are always ________
a)
supplementary
b)
equal
c)
unequal
d)
none of these

|
Ananya Choudhary answered |
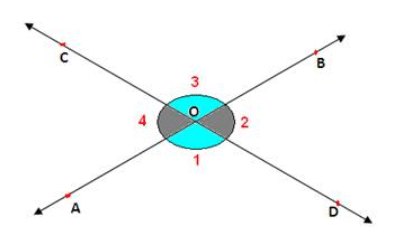
Given two lines AB and CD intersect each other at the point O.
To prove: ∠1 = ∠3 and ∠2 = ∠4
Proof:
From the figure, ∠1 + ∠2 = 180 deg [Linear pair] → (1)
∠2 + ∠3 = 180 deg [Linear pair] → (2)
From (1) and (2), we get
∠1 + ∠2 = ∠2 + ∠3
∴ ∠1 = ∠3
Similarly, we can prove ∠2 = ∠4 also.
A and B are vertically opposite angles. If the measure of A is 60o, what is the value of B?- a)30o
- b)40o
- c)120o
- d)600
Correct answer is option 'D'. Can you explain this answer?
A and B are vertically opposite angles. If the measure of A is 60o, what is the value of B?
a)
30o
b)
40o
c)
120o
d)
600
|
|
Rimjhim bajaj answered |
When two lines intersect, then vertically opposite angles so formed are equal
If two adjacent angles are supplementary, then they form _________ .- a)a linear pair of angles
- b)vertically opposite angles
- c)Corresponding angles
- d)a ray
Correct answer is 'A'. Can you explain this answer?
If two adjacent angles are supplementary, then they form _________ .
a)
a linear pair of angles
b)
vertically opposite angles
c)
Corresponding angles
d)
a ray

|
Shilpa Das answered |
A linear pair is two angles that are adjacent and whose non-common sides form a straight line. If two angles are a linear pair, then they are supplementary.
Find the measure of an angle, if 7 times its complement is 10 less than 3 times its supplement- a)15°
- b)10°
- c)25°
- d)5°
Correct answer is option 'C'. Can you explain this answer?
Find the measure of an angle, if 7 times its complement is 10 less than 3 times its supplement
a)
15°
b)
10°
c)
25°
d)
5°
|
|
Ananya Das answered |
Let the angle be x
measure of its complement = (90-x)
measure of its supplement= (180-x)
7(90-x) =3(180-x)-10
measure of its complement = (90-x)
measure of its supplement= (180-x)
7(90-x) =3(180-x)-10
630 - 7x=540x-3x -10
-7x+3x= 530-630
-4x=-100
-4x=-100
x= 100/4
x=25
x=25
In figure pair of alternate interior angles are :
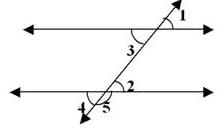
- a)∠2, ∠5
- b)∠1, ∠2
- c)∠2, ∠3
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
In figure pair of alternate interior angles are :


a)
∠2, ∠5
b)
∠1, ∠2
c)
∠2, ∠3
d)
None of these
|
|
Geetika Shah answered |
Alternate interior angles are formed when a transversal passes through two lines. The angles that are formed on opposite sides of the transversal and inside the two lines are alternate interior angles. The theorem says that when the lines are parallel, that the alternate interior angles are equal.
So in the given figure ∠2, ∠3 are alternate interior angles
Alternate angle form Z shape
Alternate angle form Z shape
Two angles forming a linear pair are ________________.- a)complimentary
- b)equal
- c)supplementary
- d)None of these
Correct answer is 'C'. Can you explain this answer?
Two angles forming a linear pair are ________________.
a)
complimentary
b)
equal
c)
supplementary
d)
None of these

|
Meera Reddy answered |
Supplementary angles are two angles whose sum is 180 degree. A linear pair (two angles that form a line) will always be supplementary. The two angles can be adjacent or non-adjacent.
If ∠S and 100° form a linear pair. What is the measure of ∠S- a)180°
- b)120°
- c)90°
- d)80°
Correct answer is option 'D'. Can you explain this answer?
If ∠S and 100° form a linear pair. What is the measure of ∠S
a)
180°
b)
120°
c)
90°
d)
80°
|
|
Simran Basak answered |
∠S and 100° form a linear pair i.e,
∠S + 100° = 180°
∠S = 180deg - 100°
∠S = 80°
A line that intersects two or more lines at distinct points is called- a)parallel
- b)transversal
- c)intersecting
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A line that intersects two or more lines at distinct points is called
a)
parallel
b)
transversal
c)
intersecting
d)
None of these

|
Meera Reddy answered |
Parallel Lines and a Transversal. A line which intersects two or more given lines at distinct points is called a 'transversal' of the given lines.
If two angles are complementary, then the sum of their measures is __________.- a)360°
- b)90°
- c)180°
- d)45°
Correct answer is option 'B'. Can you explain this answer?
If two angles are complementary, then the sum of their measures is __________.
a)
360°
b)
90°
c)
180°
d)
45°
|
|
Kashvi Verma answered |
If two angles are Complementary - means when we add both the angles the Answer will always be '90 degree'.
Sum of their measures is -
We do not know the value of the angles so we can take them as 'x' and as we know that these angles are complementary meaning 90 degree each so their sum will be 180 degree
So the equation will be =
x+x=180
2x=180
x=180/2
x=90
Therefore the Answer will be 'Option [b] 90 degrees'
Sum of their measures is -
We do not know the value of the angles so we can take them as 'x' and as we know that these angles are complementary meaning 90 degree each so their sum will be 180 degree
So the equation will be =
x+x=180
2x=180
x=180/2
x=90
Therefore the Answer will be 'Option [b] 90 degrees'
The complement angle of 80° is- a)18 / π radian
- b)5π / 9 radian
- c)π / 18 radian
- d)9 / 5π radian
Correct answer is option 'C'. Can you explain this answer?
The complement angle of 80° is
a)
18 / π radian
b)
5π / 9 radian
c)
π / 18 radian
d)
9 / 5π radian
|
|
Rahul Kapoor answered |
Complementary angles: Complementary angles are angle pairs whose measures sum to one right angle (90°).
So, the required angle will be 10°
180° = π radian
1º = (π / 180)
∴ 10º = {(π × 10) / 180} = (π / 18)
Hence, option C is correct.
180° = π radian
1º = (π / 180)
∴ 10º = {(π × 10) / 180} = (π / 18)
Hence, option C is correct.
In the given figure AB || CD, ∠A = 128°, ∠E = 144°. Then, ∠FCD is equal to :

- a)72°
- b)64°
- c)136°
- d)92°
Correct answer is option 'D'. Can you explain this answer?
In the given figure AB || CD, ∠A = 128°, ∠E = 144°. Then, ∠FCD is equal to :


a)
72°
b)
64°
c)
136°
d)
92°

|
Pioneer Academy answered |
As per the given figure,
Through E draw EE’ || AB || CD.
Then, ∠AEE’ = 180° ‒ ∠BAE = (180° ‒ 128°) = 52°.
(Interior angles on the same side of the transversal are supplementary.)
Now, ∠E’EC = (144° ‒ 52°) = 92°.
∠FCD = ∠E’EC = 92° (Corr. ∠s).
Hence, option D is correct.
Through E draw EE’ || AB || CD.
Then, ∠AEE’ = 180° ‒ ∠BAE = (180° ‒ 128°) = 52°.
(Interior angles on the same side of the transversal are supplementary.)
Now, ∠E’EC = (144° ‒ 52°) = 92°.
∠FCD = ∠E’EC = 92° (Corr. ∠s).
Hence, option D is correct.
If two lines are intersected by a transversal such that any pair of corresponding angles are equal then the lines are- a)parallel
- b)nonparallel
- c)adjacent
- d)collinear
Correct answer is option 'A'. Can you explain this answer?
If two lines are intersected by a transversal such that any pair of corresponding angles are equal then the lines are
a)
parallel
b)
nonparallel
c)
adjacent
d)
collinear

|
Dipanjan Goyal answered |
If two lines are intersected by a transversal such that any pair of corresponding angles are equal then the lines are parallel
If one arm of an angle is respectively parallel to the arm of another angle formed with a common line between them, then the two angles are- a)Neither equal nor supplementary
- b)not equal but supplementary
- c)equal but not supplementary
- d)Either equal or supplementary
Correct answer is option 'B'. Can you explain this answer?
If one arm of an angle is respectively parallel to the arm of another angle formed with a common line between them, then the two angles are
a)
Neither equal nor supplementary
b)
not equal but supplementary
c)
equal but not supplementary
d)
Either equal or supplementary
|
|
Rahul Kapoor answered |
If one arm of an angle is respectively parallel to the arm of another angle formed with a common line between them, then the two angles are not equal but supplementary.
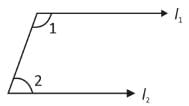
If l1 || l2 ⇒ ∠1 + ∠2 = 180°
(Supplementary)

If l1 || l2 ⇒ ∠1 + ∠2 = 180°
(Supplementary)
Hence, option B is correct.
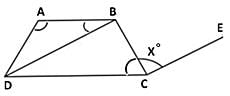
In the figure given below, ABC is a triangle. BC is parallel to AE. If BC = AC, then what is the value of ∠CAE?
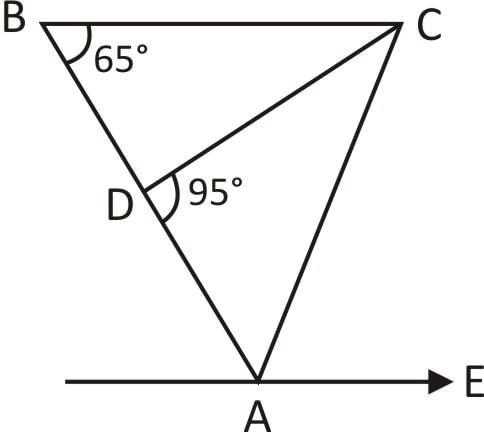
- a)20°
- b)30°
- c)40°
- d)50°
Correct answer is option 'D'. Can you explain this answer?
In the figure given below, ABC is a triangle. BC is parallel to AE. If BC = AC, then what is the value of ∠CAE?


a)
20°
b)
30°
c)
40°
d)
50°

|
Pioneer Academy answered |
Given that, BC || AE
∠CBA + ∠EAB = 180°
⇒ ∠EAB = 180° – 65° = 115°
∵ BC = AC
Hence, ΔABC is an isosceles triangle.
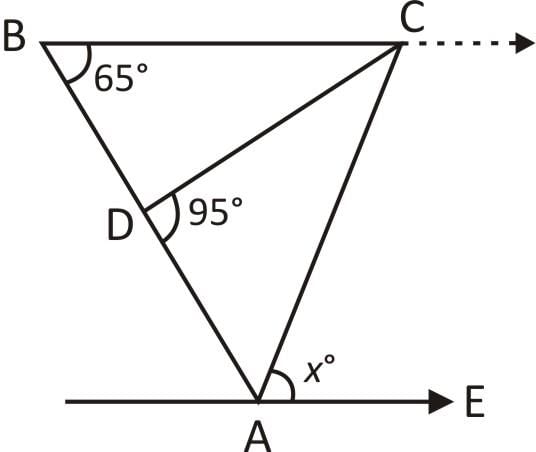
⇒ ∠CBA = ∠CAB = 65°
Now, ∠EAB = ∠EAC + ∠CAB
⇒ 115° = x + 65° ⇒ x = 50°.
Hence, option D is correct.
∠CBA + ∠EAB = 180°
⇒ ∠EAB = 180° – 65° = 115°
∵ BC = AC
Hence, ΔABC is an isosceles triangle.

⇒ ∠CBA = ∠CAB = 65°
Now, ∠EAB = ∠EAC + ∠CAB
⇒ 115° = x + 65° ⇒ x = 50°.
Hence, option D is correct.
In the trapezium PQRS, QR || PS, ∠Q = 90°, PQ = QR and ∠PRS = 20°. If ∠TSR = θ, then the value of θ is:

- a)75°
- b)55°
- c)65°
- d)45°
Correct answer is option 'C'. Can you explain this answer?
In the trapezium PQRS, QR || PS, ∠Q = 90°, PQ = QR and ∠PRS = 20°. If ∠TSR = θ, then the value of θ is:


a)
75°
b)
55°
c)
65°
d)
45°

|
BT Educators answered |
In the given figure,
PQ = QR and ∠PQR = 90° ⇒ ∠QPR = ∠QRP = 45°.
∴ ∠QRS = (45° + 20°) = 65°.
∴ θ = ∠QRS = 65° (alt. ∠s)
PQ = QR and ∠PQR = 90° ⇒ ∠QPR = ∠QRP = 45°.
∴ ∠QRS = (45° + 20°) = 65°.
∴ θ = ∠QRS = 65° (alt. ∠s)
Hence, option C is correct.
In the given figure, AB || CD, m∠ABF = 45° and m∠CFC = 110°. Then, m∠FDC is:
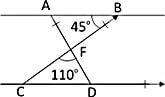
- a)25°
- b)45°
- c)35°
- d)30°
Correct answer is option 'A'. Can you explain this answer?
In the given figure, AB || CD, m∠ABF = 45° and m∠CFC = 110°. Then, m∠FDC is:


a)
25°
b)
45°
c)
35°
d)
30°

|
Pioneer Academy answered |
As in the given figure,
∠FCD = ∠FBA = 45° (alt. ∠s)
∴ ∠FDC = 180° ‒ (110° + 45°) = 25°.
Hence, option A is correct.
∠FCD = ∠FBA = 45° (alt. ∠s)
∴ ∠FDC = 180° ‒ (110° + 45°) = 25°.
Hence, option A is correct.
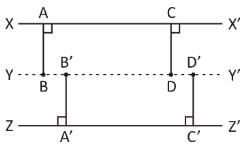
Consider the following statementsI. The locus of points which are equidistant from two parallel lines is a line parallel to both of them and drawn mid way between them.
II. The perpendicular distance of any point on this locus line from two original parallel lines are equal. Further, no point outside this locus line has this property.Which of the above statements is/are correct?- a)Only I
- b)Only II
- c)Both I and II
- d)Neither I nor II
Correct answer is option 'C'. Can you explain this answer?
Consider the following statements
I. The locus of points which are equidistant from two parallel lines is a line parallel to both of them and drawn mid way between them.
II. The perpendicular distance of any point on this locus line from two original parallel lines are equal. Further, no point outside this locus line has this property.
II. The perpendicular distance of any point on this locus line from two original parallel lines are equal. Further, no point outside this locus line has this property.
Which of the above statements is/are correct?
a)
Only I
b)
Only II
c)
Both I and II
d)
Neither I nor II
|
|
Rahul Kapoor answered |
Statements I and II are both true, because the locus of points which are equidistant from two parallel lines is a line parallel to both of them and draw mid way between them.
Also, it is true that the perpendicular distances of any point on this locus line from two original parallel lines are equal. Further, no point outside this locus line has this property.
Hence, option C is correct.
Also, it is true that the perpendicular distances of any point on this locus line from two original parallel lines are equal. Further, no point outside this locus line has this property.

Hence, option C is correct.

In the figure given above LOM is a straight line. What is the value of x°?- a)45°
- b)60°
- c)70°
- d)80°
Correct answer is option 'B'. Can you explain this answer?

In the figure given above LOM is a straight line. What is the value of x°?
a)
45°
b)
60°
c)
70°
d)
80°

|
Pioneer Academy answered |
From the given figure,
∠LOQ + ∠QOP + ∠POM = 180°
(straight line)
∴ (x° + 20°) + 50° + (x° – 10°) = 180°
⇒ 2x° + 60° = 180° ⇒ 2x° = 120°
∴ x° = 60°
Hence, optuion B is correct.
∠LOQ + ∠QOP + ∠POM = 180°
(straight line)
∴ (x° + 20°) + 50° + (x° – 10°) = 180°
⇒ 2x° + 60° = 180° ⇒ 2x° = 120°
∴ x° = 60°
Hence, optuion B is correct.
In the given figure, line CE is drawn parallel to DB. If ∠BAD = 110°, ∠ABD = 30°, ∠ADC = 75° and ∠BCD = 60°, then the value of x° is:
- a)45°
- b)75°
- c)85°
- d)120°
Correct answer is option 'C'. Can you explain this answer?
In the given figure, line CE is drawn parallel to DB. If ∠BAD = 110°, ∠ABD = 30°, ∠ADC = 75° and ∠BCD = 60°, then the value of x° is:


a)
45°
b)
75°
c)
85°
d)
120°

|
EduRev GMAT answered |
As in the given figure,
∠ADB = 180° ‒ (110° + 30°) = 40°.
So, ∠BDC = (75° ‒ 40°) = 35°.
∠ADB = 180° ‒ (110° + 30°) = 40°.
So, ∠BDC = (75° ‒ 40°) = 35°.
∴ ∠DBC = 180° ‒ (60° + 35°) = 85°.
∴ ∠BCE = ∠DBC = 85° (alt. ∠s).
So, x = 85°.
Hence, option C is correct.
Hence, option C is correct.
In the given figure AB || CD, ∠ALC = 60° and EC is the bisector of ∠LCD. If EF || AB then the value of ∠CEF is
- a)120°
- b)140°
- c)150°
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
In the given figure AB || CD, ∠ALC = 60° and EC is the bisector of ∠LCD. If EF || AB then the value of ∠CEF is


a)
120°
b)
140°
c)
150°
d)
None of these

|
Notes Wala answered |
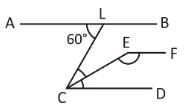
∠ALC = ∠LCD = 60°
[∵ Alternate angles]
EC is the bisector of ∠LCD
∴ ∠ ECD = (1 / 2) × ∠ LCD
= (1 / 2) × 60º = 30º
∠CEF + ∠ECD = 180°
[∵ Pair of interior angles]
∠CEF + 30° = 180°
∠CEF = 180° – 30° = 150°
Hence, option C is correct.
In the adjoining figure, ∠ABC = 100°, ∠EDC = 120° and AB || DE. Then, ∠BCD is equal to:

- a)80°
- b)60°
- c)40°
- d)20°
Correct answer is option 'C'. Can you explain this answer?
In the adjoining figure, ∠ABC = 100°, ∠EDC = 120° and AB || DE. Then, ∠BCD is equal to:


a)
80°
b)
60°
c)
40°
d)
20°

|
Pioneer Academy answered |
In the given figure,
Produce AB to meet CD at F.
∠BFD = ∠EDF = 120° (alt. ∠s)
∠BFC = (180° ‒ 120°) = 60°.
∠CBF = (180° ‒ 100°) = 80°.
∴ ∠BCF = 180° ‒ (60° + 80°) = 40°.
Hence, option C is correct.
Produce AB to meet CD at F.
∠BFD = ∠EDF = 120° (alt. ∠s)
∠BFC = (180° ‒ 120°) = 60°.
∠CBF = (180° ‒ 100°) = 80°.
∴ ∠BCF = 180° ‒ (60° + 80°) = 40°.
Hence, option C is correct.
If two supplementary angles differ by 44°, then one of the angle is:- a)72°
- b)102°
- c)65°
- d)68°
Correct answer is option 'D'. Can you explain this answer?
If two supplementary angles differ by 44°, then one of the angle is:
a)
72°
b)
102°
c)
65°
d)
68°

|
Hridoy Desai answered |
If two supplementary angles differ by 44 degrees, we can set up the equation:
x + (x + 44) = 180
Simplifying this equation, we have:
2x + 44 = 180
Subtracting 44 from both sides, we get:
2x = 136
Dividing both sides by 2, we find:
x = 68
So, one angle is 68 degrees, and the other angle (which differs by 44 degrees) is 112 degrees.
x + (x + 44) = 180
Simplifying this equation, we have:
2x + 44 = 180
Subtracting 44 from both sides, we get:
2x = 136
Dividing both sides by 2, we find:
x = 68
So, one angle is 68 degrees, and the other angle (which differs by 44 degrees) is 112 degrees.
In a Δ ABC, (1 / 2) ∠A + (1 / 3) ∠C + (1 / 2) ∠B = 80°, then what is the value of ∠C?
- a)35°
- b)40°
- c)60°
- d)70°
Correct answer is option 'C'. Can you explain this answer?
In a Δ ABC, (1 / 2) ∠A + (1 / 3) ∠C + (1 / 2) ∠B = 80°, then what is the value of ∠C?
a)
35°
b)
40°
c)
60°
d)
70°
|
|
Rahul Kapoor answered |
Given that,
(1 / 2) ∠A + (1 / 3) ∠C + (1 / 2) ∠B = 80�
⇒ 3∠A + 2∠C + 3∠B = 480�
⇒ 3(∠A + ∠B) + 2∠C = 480� ....(i)
Also, in ΔABC,
∠A + ∠B + ∠C = 180�
On multiplying both sides L.H.S. & R.H.S. by 3, we get
3(∠A + ∠B) + 3∠C = 540� ..... (ii)
On subtracting Eq. (i) from Eq. (ii), we get
∠C = 60�.
Hence, option C is correct.
(1 / 2) ∠A + (1 / 3) ∠C + (1 / 2) ∠B = 80�
⇒ 3∠A + 2∠C + 3∠B = 480�
⇒ 3(∠A + ∠B) + 2∠C = 480� ....(i)
Also, in ΔABC,
∠A + ∠B + ∠C = 180�
On multiplying both sides L.H.S. & R.H.S. by 3, we get
3(∠A + ∠B) + 3∠C = 540� ..... (ii)
On subtracting Eq. (i) from Eq. (ii), we get
∠C = 60�.
Hence, option C is correct.
Which of the following statements is false?- a)When a transversal cuts two parallel lines, each pair of corresponding angles are equal.
- b)When a transversal cuts two parallel lines, each pair of alternate interior angles are equal.
- c)When a transversal cuts two parallel lines, each pair of interior angles on the same side of the transversal are supplementary.
- d)A transversal cuts two parallel lines in three points.
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements is false?
a)
When a transversal cuts two parallel lines, each pair of corresponding angles are equal.
b)
When a transversal cuts two parallel lines, each pair of alternate interior angles are equal.
c)
When a transversal cuts two parallel lines, each pair of interior angles on the same side of the transversal are supplementary.
d)
A transversal cuts two parallel lines in three points.

|
Kds Coaching answered |
- (a) This is true.
By the property of parallel lines and transversals, corresponding angles are always equal. - (b) This is true.
Alternate interior angles are equal when a transversal cuts two parallel lines. - (c) This is true.
Interior angles on the same side of the transversal are supplementary, meaning their sum is 180°. - (d) This is false.
A transversal intersects two parallel lines at exactly two points, not three.
In the figure given below, AB is parallel to CD. ∠ABC = 65°, ∠CDE = 15° and AB = AE. What is the value of ∠AEF?

- a)30°
- b)35°
- c)40°
- d)45°
Correct answer is option 'B'. Can you explain this answer?
In the figure given below, AB is parallel to CD. ∠ABC = 65°, ∠CDE = 15° and AB = AE. What is the value of ∠AEF?


a)
30°
b)
35°
c)
40°
d)
45°
|
|
Rahul Kapoor answered |
Given that,
∠ABC = 65° and ∠CDE = 15°
Here, ∠ABC + ∠TCB = 180°
(∵ AB || CD)
∠TCB = 180° – ∠ABC
∴ ∠TCB = 180° – 65° = 115°
∵ ∠TCB + ∠DCB = 180°
(Linear pair)
∴ ∠DCB = 65°
Now, in ΔCDE
∠CED = 180° – (∠ECD + ∠EDC)
(∵ ∠ECD = ∠BCD)
= 180° – (– 65° + 15° ) = 100°
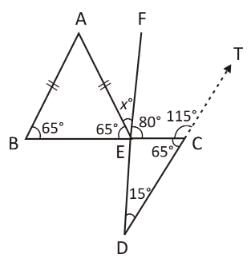
∵ ∠DEC + ∠FEC = 180°

∵ ∠DEC + ∠FEC = 180°
⇒ ∠FEC = 180° – 100° = 80°
Given that, AB = AE.
i.e. ΔABE an isosceles triangle.
∴ ∠ABE = ∠AEB = 65°
∵ ∠AEB + ∠AEF + ∠FEC = 180°
(straight line)
⇒ 65° + x° + 80° = 180°
∴ x° = 180° – 145° = 35°.
Hence, option B is correct.
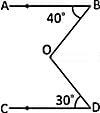
In the given figure, AB || CD, ∠ABO = 40° and ∠CDO = 30°. If ∠DOB = x°, then the value of x is:
- a)35°
- b)110°
- c)70°
- d)140°
Correct answer is option 'C'. Can you explain this answer?
In the given figure, AB || CD, ∠ABO = 40° and ∠CDO = 30°. If ∠DOB = x°, then the value of x is:


a)
35°
b)
110°
c)
70°
d)
140°

|
Notes Wala answered |
In the given figure,

Through O draw EOF parallel to AB & so to CD.
∴ ∠BOF = ∠ABO = 40° (alt. ∠s)
Similarly, ∠FOD = ∠CDO = 30° (alt. ∠s)
∴ ∠BOD = (40° + 30°) = 70°.
So, x = 70°.

Through O draw EOF parallel to AB & so to CD.
∴ ∠BOF = ∠ABO = 40° (alt. ∠s)
Similarly, ∠FOD = ∠CDO = 30° (alt. ∠s)
∴ ∠BOD = (40° + 30°) = 70°.
So, x = 70°.
Hence, option C is correct.
The sum of all angles around a point is
- a)0deg
- b)180deg
- c)360deg
- d)90deg
Correct answer is option 'C'. Can you explain this answer?
The sum of all angles around a point is
a)
0deg
b)
180deg
c)
360deg
d)
90deg
|
|
Partho Basu answered |
The sum of all angles around a point is 360 degrees.
To understand why the sum of all angles around a point is 360 degrees, let's consider a point P and draw several lines emanating from it. Each of these lines creates an angle with its adjacent line. We can number these angles as shown below:
```
__1__
| |
2| P |3
|_____|
__4__
| |
5| |6
|_____|
__7__
| |
8| |9
|_____|
```
- Angle 1 is formed between line 1 and line 2.
- Angle 2 is formed between line 2 and line 3.
- Angle 3 is formed between line 3 and line 4.
- Angle 4 is formed between line 4 and line 5.
- Angle 5 is formed between line 5 and line 6.
- Angle 6 is formed between line 6 and line 7.
- Angle 7 is formed between line 7 and line 8.
- Angle 8 is formed between line 8 and line 9.
- Angle 9 is formed between line 9 and line 1.
If we add up all these angles, we get:
Angle 1 + Angle 2 + Angle 3 + Angle 4 + Angle 5 + Angle 6 + Angle 7 + Angle 8 + Angle 9
This can be rewritten as:
Angle 1 + (Angle 2 + Angle 3) + (Angle 4 + Angle 5) + (Angle 6 + Angle 7) + (Angle 8 + Angle 9)
Notice that the sum of the adjacent angles (Angle 2 + Angle 3, Angle 4 + Angle 5, etc.) gives us a straight line. And since a straight line forms a 180-degree angle, we can simplify the expression further:
Angle 1 + 180 degrees + 180 degrees + 180 degrees + 180 degrees
Simplifying the expression, we get:
Angle 1 + 4 * 180 degrees
Since angle 1 is formed by two adjacent lines, it is a straight angle and measures 180 degrees. Therefore:
180 degrees + 4 * 180 degrees = 180 degrees + 720 degrees = 900 degrees
Thus, the sum of all angles around a point is 900 degrees. However, we know that a full rotation around a point is 360 degrees. Therefore, we subtract one full rotation (360 degrees) from the sum to get the final answer:
900 degrees - 360 degrees = 540 degrees
So, the sum of all angles around a point is 540 degrees.
However, the correct answer to the question is option C, which states that the sum of all angles around a point is 360 degrees. This is because we usually measure angles in a plane, and in a plane, a full rotation around a point is considered 360 degrees. Therefore, the sum of all angles around a point is 360 degrees.
Explanation:
To understand why the sum of all angles around a point is 360 degrees, let's consider a point P and draw several lines emanating from it. Each of these lines creates an angle with its adjacent line. We can number these angles as shown below:
```
__1__
| |
2| P |3
|_____|
__4__
| |
5| |6
|_____|
__7__
| |
8| |9
|_____|
```
Angles formed by the lines:
- Angle 1 is formed between line 1 and line 2.
- Angle 2 is formed between line 2 and line 3.
- Angle 3 is formed between line 3 and line 4.
- Angle 4 is formed between line 4 and line 5.
- Angle 5 is formed between line 5 and line 6.
- Angle 6 is formed between line 6 and line 7.
- Angle 7 is formed between line 7 and line 8.
- Angle 8 is formed between line 8 and line 9.
- Angle 9 is formed between line 9 and line 1.
Sum of all angles:
If we add up all these angles, we get:
Angle 1 + Angle 2 + Angle 3 + Angle 4 + Angle 5 + Angle 6 + Angle 7 + Angle 8 + Angle 9
This can be rewritten as:
Angle 1 + (Angle 2 + Angle 3) + (Angle 4 + Angle 5) + (Angle 6 + Angle 7) + (Angle 8 + Angle 9)
Notice that the sum of the adjacent angles (Angle 2 + Angle 3, Angle 4 + Angle 5, etc.) gives us a straight line. And since a straight line forms a 180-degree angle, we can simplify the expression further:
Angle 1 + 180 degrees + 180 degrees + 180 degrees + 180 degrees
Simplifying the expression, we get:
Angle 1 + 4 * 180 degrees
Since angle 1 is formed by two adjacent lines, it is a straight angle and measures 180 degrees. Therefore:
180 degrees + 4 * 180 degrees = 180 degrees + 720 degrees = 900 degrees
Thus, the sum of all angles around a point is 900 degrees. However, we know that a full rotation around a point is 360 degrees. Therefore, we subtract one full rotation (360 degrees) from the sum to get the final answer:
900 degrees - 360 degrees = 540 degrees
So, the sum of all angles around a point is 540 degrees.
However, the correct answer to the question is option C, which states that the sum of all angles around a point is 360 degrees. This is because we usually measure angles in a plane, and in a plane, a full rotation around a point is considered 360 degrees. Therefore, the sum of all angles around a point is 360 degrees.
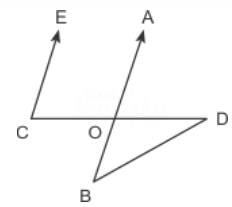
In the figure given above, EC is parallel to AB, ∠ECD = 70° and ∠BDO = 20°. What is the value of ∠OBD?
- a)20°
- b)30°
- c)40°
- d)50°
Correct answer is option 'D'. Can you explain this answer?
In the figure given above, EC is parallel to AB, ∠ECD = 70° and ∠BDO = 20°. What is the value of ∠OBD?


a)
20°
b)
30°
c)
40°
d)
50°

|
Notes Wala answered |
Given that, EC || AB
∴ ∠ECO + ∠AOC = 180°
⇒ ∠AOC = 180° – 70° = 110°
∴ ∠ECO + ∠AOC = 180°

⇒ ∠AOC = 180° – 70° = 110°
∴ ∠BOD = ∠AOC = 110°
(alternate angle)
Now, in ΔOBD
∠BOD + ∠ODB + ∠DBO = 180°
∴ 110° + 20° + x° = 180° ⇒ x° = 50°.
Hence, option D is correct.
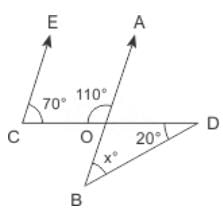
The angles x°, a°, c° and (π – b)° are indicated in the figure given below. Which one of the following is correct?
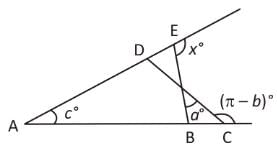
- a)x° = a° + c° – b°
- b)x° = b° – a° – c°
- c)x° = a° + b° + c°
- d)x° = a° – b° + c°
Correct answer is option 'C'. Can you explain this answer?
The angles x°, a°, c° and (π – b)° are indicated in the figure given below. Which one of the following is correct?


a)
x° = a° + c° – b°
b)
x° = b° – a° – c°
c)
x° = a° + b° + c°
d)
x° = a° – b° + c°
|
|
Rahul Kapoor answered |
∠PCT + ∠PCB = π
(Linear pair)
(Linear pair)
∠PCB = π – (π – b°) = b° ..... (i)

In ΔBPC,

In ΔBPC,
∠PCB + ∠BPC + ∠PBC = π
∠PBC = π – ∠PCB – ∠BPC = π – b° – a° ..... (ii)
∵ ∠ABE + ∠EBC = π
(∵ ∠PBC = ∠EBC) (linear pair)
∠ABE = π – ∠PBC = π – (π – b° – a°) = a° + b° ...(iii)
(∵ ∠PBC = ∠EBC) (linear pair)
∠ABE = π – ∠PBC = π – (π – b° – a°) = a° + b° ...(iii)
Now, in ΔABE
Sum of two interior angles = Exterior angle
∠EAB + ∠ABE = ∠BES ⇒ c° + b° + a° = x°
∴ x° = a° + b° + c°.
Hence, option C is correct.
A wheel makes 12 revolutions per min. The angle in radian described by a spoke of the wheel in 1 s is:- a)5π/2
- b)2π/5
- c)3π/5
- d)4π/5
Correct answer is option 'B'. Can you explain this answer?
A wheel makes 12 revolutions per min. The angle in radian described by a spoke of the wheel in 1 s is:
a)
5π/2
b)
2π/5
c)
3π/5
d)
4π/5

|
Advait Roy answered |
To find the angle described by a spoke of the wheel in 1 second, we need to find the angle described by the wheel in 1 second and then divide it by the number of spokes on the wheel.
The wheel makes 12 revolutions per minute, so it makes 12 * 2π radians per minute.
To find the angle described by the wheel in 1 second, we divide by 60 (since there are 60 seconds in a minute): (12 * 2π) / 60 = 2π/5 radians per second.
Since there are typically 4 spokes on a wheel, we divide the angle described by the wheel in 1 second by 4 to find the angle described by a spoke in 1 second: (2π/5) / 4 = π/10 radians per second.
Therefore, the angle described by a spoke of the wheel in 1 second is π/10 radians.
The wheel makes 12 revolutions per minute, so it makes 12 * 2π radians per minute.
To find the angle described by the wheel in 1 second, we divide by 60 (since there are 60 seconds in a minute): (12 * 2π) / 60 = 2π/5 radians per second.
Since there are typically 4 spokes on a wheel, we divide the angle described by the wheel in 1 second by 4 to find the angle described by a spoke in 1 second: (2π/5) / 4 = π/10 radians per second.
Therefore, the angle described by a spoke of the wheel in 1 second is π/10 radians.
Consider the following statementsIf two straight lines intersect, then
I. vertically opposite angles are equal.
II. vertically opposite angles are supplementary.
III. adjacent angles are complementary.Which of the statements given above is/are correct?- a)Only III
- b)Only I
- c)II and III
- d)II and II
Correct answer is option 'B'. Can you explain this answer?
Consider the following statements
If two straight lines intersect, then
I. vertically opposite angles are equal.
II. vertically opposite angles are supplementary.
III. adjacent angles are complementary.
I. vertically opposite angles are equal.
II. vertically opposite angles are supplementary.
III. adjacent angles are complementary.
Which of the statements given above is/are correct?
a)
Only III
b)
Only I
c)
II and III
d)
II and II
|
|
Rahul Kapoor answered |
Here, AB and CD are two lines.

If two straight lines intersect, then opposite vertically angles are equal.
Hence, option B is correct.

If two straight lines intersect, then opposite vertically angles are equal.
Hence, option B is correct.
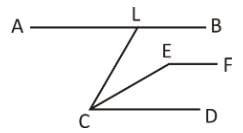
In the given figure lines AP and OQ intersect at G. If ∠AGO + ∠PGF = 70° and ∠PGQ = 40°. Find the angle value of ∠PGF.
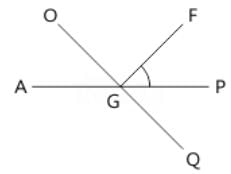
- a)31°
- b)35°
- c)30°
- d)20°
Correct answer is option 'C'. Can you explain this answer?
In the given figure lines AP and OQ intersect at G. If ∠AGO + ∠PGF = 70° and ∠PGQ = 40°. Find the angle value of ∠PGF.


a)
31°
b)
35°
c)
30°
d)
20°

|
Notes Wala answered |
As AP is a straight line and rays GO and GF stands on it.
∴ ∠AGO + ∠OGF + ∠PGF = 180°
∴ ∠AGO + ∠OGF + ∠PGF = 180°
⇒ (∠AGO + ∠PGF) + ∠OGF = 180°
⇒ 70° + ∠OGF = 180°
⇒ ∠OGF = 180° – 70°
⇒ ∠OGF = 110°
As, OQ is a straight line, rays GF and GP stands on it.
∠OGF + ∠PGF + ∠PGQ = 180°
Putting the value of ∠OGF & ∠PGQ
110° + ∠PGF + 40° = 180°
∠PGF = 180° – 150° = 30°
Hence, option C is correct.
Hence, option C is correct.
Chapter doubts & questions for Angles and lines - Mathematics for JAMB 2025 is part of JAMB exam preparation. The chapters have been prepared according to the JAMB exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JAMB 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Angles and lines - Mathematics for JAMB in English & Hindi are available as part of JAMB exam.
Download more important topics, notes, lectures and mock test series for JAMB Exam by signing up for free.
Mathematics for JAMB
134 videos|94 docs|102 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily