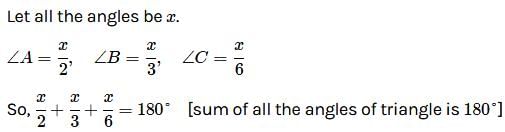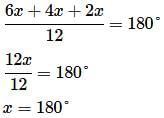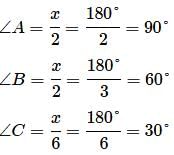All Exams >
JAMB >
Mathematics for JAMB >
All Questions
All questions of Polygons for JAMB Exam
Each of the two equal angles of an isosceles triangle is twice the third angle. Find the angles of the triangle.- a)36°, 72°, 36°
- b)45°, 60°, 75°
- c)36°, 36°, 72°
- d)72°, 72°, 36°
Correct answer is option 'D'. Can you explain this answer?
Each of the two equal angles of an isosceles triangle is twice the third angle. Find the angles of the triangle.
a)
36°, 72°, 36°
b)
45°, 60°, 75°
c)
36°, 36°, 72°
d)
72°, 72°, 36°

|
Diya Chavan answered |
Let the third angle be x°.
We know that the sum of the angles of a triangle is 180°.
∴ 2x + 2x + x = 180°
⇒ 5x = 180°
⇒ x = 36°
So, the angles are (2 × 36)°, (2 × 36)° and (x)°
Hence, the angles of the triangles are 72°, 72°, 36°.
We know that the sum of the angles of a triangle is 180°.
∴ 2x + 2x + x = 180°
⇒ 5x = 180°
⇒ x = 36°
So, the angles are (2 × 36)°, (2 × 36)° and (x)°
Hence, the angles of the triangles are 72°, 72°, 36°.
The angles of a triangle are (3x)°, (2x – 7)° and (4x – 11)°. Then x = ?- a)22
- b)18
- c)20
- d)30
Correct answer is option 'A'. Can you explain this answer?
The angles of a triangle are (3x)°, (2x – 7)° and (4x – 11)°. Then x = ?
a)
22
b)
18
c)
20
d)
30
|
|
Anita Menon answered |
According to question
3x + (2x – 7) + (4x – 11) = 180°
⇒ 9x – 18 = 180
⇒ 9x = 198
⇒ x = 22
3x + (2x – 7) + (4x – 11) = 180°
⇒ 9x – 18 = 180
⇒ 9x = 198
⇒ x = 22
A regular polygon P has 135 diagonals. Find the exterior angle of the polygon P.- a)180
- b)200
- c)250
- d)300
- e)350
Correct answer is option 'B'. Can you explain this answer?
A regular polygon P has 135 diagonals. Find the exterior angle of the polygon P.
a)
180
b)
200
c)
250
d)
300
e)
350

|
Aditya Sharma answered |
Number of diagonals in a regular polygon =nC2–n
=>nC2–n
=>nC2–n
= 135
=> n = 18
Exterior angle = 360/n
=360/18
=200
=> n = 18
Exterior angle = 360/n
=360/18
=200
Find the number of sides of a polygon if the sum of its interior angles is equal to 18000?- a)10
- b)11
- c)12
- d)13
- e)14
Correct answer is option 'C'. Can you explain this answer?
Find the number of sides of a polygon if the sum of its interior angles is equal to 18000?
a)
10
b)
11
c)
12
d)
13
e)
14
|
|
Aditya Kumar answered |
Number of sides in a polygon is 12
Explanation:
Sum of all the exterior angles of any polygon is always 360o.
As sum of every pair of interior and exterior angle is 180o,
sum of all the interior and exterior angles of a polygon with n sides, is 180o×n.
Sum of all the exterior angles of any polygon is always 360o.
As sum of every pair of interior and exterior angle is 180o,
sum of all the interior and exterior angles of a polygon with n sides, is 180o×n.
As sum of interior angles of given polygon is 1800o and sum of exterior angles is 360o. The Sum of all the angles of given polygon is 2160o.
As such 180o×n=2160o and n=2160o/ 180o = 12.
Hence, the number of sides in a polygon is 12
If the sum of interior angles of a polygon is 900 degrees, what is the number of diagonals it has?- a)9
- b)14
- c)20
- d)24
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
If the sum of interior angles of a polygon is 900 degrees, what is the number of diagonals it has?
a)
9
b)
14
c)
20
d)
24
e)
None of these

|
Atharva Chawla answered |
The sum of interior angles for an ‘n’ sided polygon is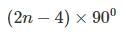
If this value is 900, then the polygon is a heptagon.
The number of diagonals for an ‘n’ sided polygon =
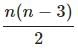
= 14 for a heptagon.
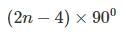
If this value is 900, then the polygon is a heptagon.
The number of diagonals for an ‘n’ sided polygon =
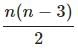
= 14 for a heptagon.
In ∆ABC, ∠B = 90°, AB = 5cm and AC = 13cm then BC = ? - a)18 cm
- b)12 cm
- c)8 cm
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
In ∆ABC, ∠B = 90°, AB = 5cm and AC = 13cm then BC = ?
a)
18 cm
b)
12 cm
c)
8 cm
d)
None of these

|
Rahul Shah answered |
By Pythagoras theorem,
AB2 + BC2 = AC2 ⇒ 52 + BC2 = 132
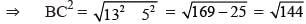
= 12 cm
AB2 + BC2 = AC2 ⇒ 52 + BC2 = 132
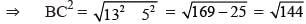
= 12 cm
What is the measure of each interior angle of a regular hexagon (in degrees)?- a)60
- b)80
- c)100
- d)120
- e)140
Correct answer is option 'D'. Can you explain this answer?
What is the measure of each interior angle of a regular hexagon (in degrees)?
a)
60
b)
80
c)
100
d)
120
e)
140
|
|
Ujwal Unni answered |
Solution:
A regular hexagon is a polygon that has six equal sides and six equal angles. To find the measure of each interior angle of a regular hexagon, we can use the formula:
Interior angle = (n-2) x 180° / n
where n is the number of sides. For a hexagon, n=6.
Using the formula, we get:
Interior angle = (6-2) x 180° / 6
Interior angle = 4 x 180° / 6
Interior angle = 720° / 6
Interior angle = 120°
Therefore, the measure of each interior angle of a regular hexagon is 120 degrees.
Hence, the correct answer is option D (120).
A regular hexagon is a polygon that has six equal sides and six equal angles. To find the measure of each interior angle of a regular hexagon, we can use the formula:
Interior angle = (n-2) x 180° / n
where n is the number of sides. For a hexagon, n=6.
Using the formula, we get:
Interior angle = (6-2) x 180° / 6
Interior angle = 4 x 180° / 6
Interior angle = 720° / 6
Interior angle = 120°
Therefore, the measure of each interior angle of a regular hexagon is 120 degrees.
Hence, the correct answer is option D (120).
If one of the interior opposite angles of an exterior angle is 45∘ and the exterior angle is 130∘, what is the measure of the second interior opposite angle?- a)75∘
- b)85∘
- c)90∘
- d)95∘
Correct answer is option 'B'. Can you explain this answer?
If one of the interior opposite angles of an exterior angle is 45∘ and the exterior angle is 130∘, what is the measure of the second interior opposite angle?
a)
75∘
b)
85∘
c)
90∘
d)
95∘

|
Learning Enablers answered |
Using the exterior angle property:
Exterior Angle = Sum of Interior Opposite Angles
130∘= 45∘+ Other Angle
Other Angle = 130∘− 45∘= 85∘
Exterior Angle = Sum of Interior Opposite Angles
130∘= 45∘+ Other Angle
Other Angle = 130∘− 45∘= 85∘
The sum of all angles of a triangle is- a)90°
- b)150°
- c)100°
- d)180°
Correct answer is option 'D'. Can you explain this answer?
The sum of all angles of a triangle is
a)
90°
b)
150°
c)
100°
d)
180°

|
Shraddha Nambiar answered |
The sum of all the angles of a triangle is 180°.
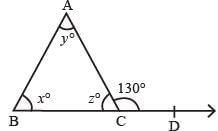
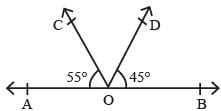
In the given figure, AOB is a straight line, ∠AOC = 68° and ∠BOC = x°, the value of x is.
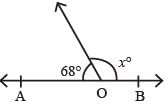
- a)112
- b)132
- c)22
- d)32
Correct answer is option 'A'. Can you explain this answer?
In the given figure, AOB is a straight line, ∠AOC = 68° and ∠BOC = x°, the value of x is.


a)
112
b)
132
c)
22
d)
32

|
गावं बोरीवली भाखर ढाणी B answered |
180 -68 =x
180 - 68 =112
that's why the value of x is 112
180 - 68 =112
that's why the value of x is 112
Two angles of a triangle are equal and the third angle measures 70°. Find the measure of each of the unknown angles.- a)50°
- b)55°
- c)70°
- d)110°
Correct answer is option 'B'. Can you explain this answer?
Two angles of a triangle are equal and the third angle measures 70°. Find the measure of each of the unknown angles.
a)
50°
b)
55°
c)
70°
d)
110°

|
Nayanika Chauhan answered |
Let the measure of each unknown angle be x°. We know that the sum of the angles of a triangle is 180°.
∴ x + x + 70 = 180°
⇒ 2x = (180° – 70°)
⇒ 2x = 110°
⇒ x = 55°
Hence each unknown angle is 55°.
∴ x + x + 70 = 180°
⇒ 2x = (180° – 70°)
⇒ 2x = 110°
⇒ x = 55°
Hence each unknown angle is 55°.
In a ∆XYZ, if ∠X = 90° and ∠Z = 48°, find ∠Y. - a)42°
- b)45°
- c)40°
- d)35°
Correct answer is option 'A'. Can you explain this answer?
In a ∆XYZ, if ∠X = 90° and ∠Z = 48°, find ∠Y.
a)
42°
b)
45°
c)
40°
d)
35°

|
Srishti Basak answered |
We know that the sum of the angles of a triangle is 180°.
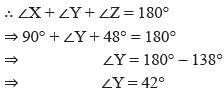
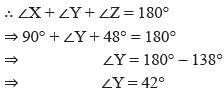
If ABCDEF is a regular hexagon and AB = 1cm, then what is the area of this regular hexagon ABCDEF?- a)
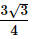
- b)√3
- c)
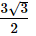
- d)2√3
- e)3√3
Correct answer is option 'C'. Can you explain this answer?
If ABCDEF is a regular hexagon and AB = 1cm, then what is the area of this regular hexagon ABCDEF?
a)
b)
√3
c)
d)
2√3
e)
3√3

|
Saanvi Reddy answered |
formula for finding the area of a hexagon is Area = (3√3 s2) / 2 where s is the length of a side of the regular hexagon
where s = 1
Hence area of hexagon will be 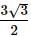
In a ∆ABC it is given that ∠B = 37° and ∠C = 29°. Then ∠A = ?- a)57°
- b)114°
- c)66°
- d)86°
Correct answer is option 'B'. Can you explain this answer?
In a ∆ABC it is given that ∠B = 37° and ∠C = 29°. Then ∠A = ?
a)
57°
b)
114°
c)
66°
d)
86°

|
Nayanika Chauhan answered |
We know that the sum of the angles of a triangle is 180°.
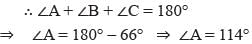
In the figure (not drawn to scale), ABCD is a square, ADE is an equilateral triangle and BFE is a straight line, find y. 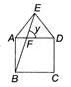
- a)90o
- b)45o
- c)75o
- d)15o
Correct answer is option 'C'. Can you explain this answer?
In the figure (not drawn to scale), ABCD is a square, ADE is an equilateral triangle and BFE is a straight line, find y.

a)
90o
b)
45o
c)
75o
d)
15o
|
|
Mrinalini Shah answered |
In ΔAEB,
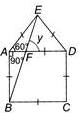
∠A=∠DAE+∠BAD ⇒ ∠A=60o+90o=15o
And, AE=AB ⇒ ∠ABE=∠AEB
[Angles opposite to equal sides are equal]
Now, ∠A+∠ABE+∠AEB=180o (Angle sum property)
⇒ 2∠AEB=180o −150o = 30o ⇒ ∠AEB = 15o
Now, ∠E=60o ⇒ ∠DEF=60o−15o = 45o
∴ In ΔEFD, ∠DEF+∠EDF+∠EFD
= 180o ⇒ 45o+60o+y = 180o
⇒ y = 180o−(45o+60o) = 75o

∠A=∠DAE+∠BAD ⇒ ∠A=60o+90o=15o
And, AE=AB ⇒ ∠ABE=∠AEB
[Angles opposite to equal sides are equal]
Now, ∠A+∠ABE+∠AEB=180o (Angle sum property)
⇒ 2∠AEB=180o −150o = 30o ⇒ ∠AEB = 15o
Now, ∠E=60o ⇒ ∠DEF=60o−15o = 45o
∴ In ΔEFD, ∠DEF+∠EDF+∠EFD
= 180o ⇒ 45o+60o+y = 180o
⇒ y = 180o−(45o+60o) = 75o
An angle is one – fifth of its supplement. The measure of the angle is- a)75°
- b)150°
- c)15°
- d)30°
Correct answer is option 'D'. Can you explain this answer?
An angle is one – fifth of its supplement. The measure of the angle is
a)
75°
b)
150°
c)
15°
d)
30°
|
|
Aryan Mukherjee answered |
Of the basic geometric shapes and is formed when two lines, line segments, or rays intersect at a common point. The common point is called the vertex of the angle, and the lines, line segments, or rays that form the angle are called the sides of the angle.
Angles are measured in degrees, with a full circle measuring 360 degrees. A right angle, which is formed when two lines or line segments intersect to form a square corner, measures 90 degrees. Angles can be classified based on their measurements as acute (less than 90 degrees), obtuse (more than 90 degrees but less than 180 degrees), straight (exactly 180 degrees), or reflex (more than 180 degrees but less than 360 degrees).
Angles have many practical applications in various fields, including mathematics, engineering, architecture, and physics. They are used to measure and describe the orientation, direction, and position of objects, as well as to calculate distances, areas, and volumes.
In addition to their geometric properties, angles can also be used to represent relationships, such as congruence (when two angles have the same measure) or supplementary (when two angles add up to 180 degrees). They can also be used to solve various types of problems, such as finding missing angles in triangles or quadrilaterals.
Overall, angles play a fundamental role in geometry and are essential for understanding and analyzing the properties and relationships of shapes and figures.
Angles are measured in degrees, with a full circle measuring 360 degrees. A right angle, which is formed when two lines or line segments intersect to form a square corner, measures 90 degrees. Angles can be classified based on their measurements as acute (less than 90 degrees), obtuse (more than 90 degrees but less than 180 degrees), straight (exactly 180 degrees), or reflex (more than 180 degrees but less than 360 degrees).
Angles have many practical applications in various fields, including mathematics, engineering, architecture, and physics. They are used to measure and describe the orientation, direction, and position of objects, as well as to calculate distances, areas, and volumes.
In addition to their geometric properties, angles can also be used to represent relationships, such as congruence (when two angles have the same measure) or supplementary (when two angles add up to 180 degrees). They can also be used to solve various types of problems, such as finding missing angles in triangles or quadrilaterals.
Overall, angles play a fundamental role in geometry and are essential for understanding and analyzing the properties and relationships of shapes and figures.
Find the measure of the angle x in the given figure.
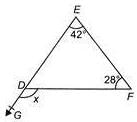
- a)50o
- b)70o
- c)60o
- d)30o
Correct answer is option 'B'. Can you explain this answer?
Find the measure of the angle x in the given figure.

a)
50o
b)
70o
c)
60o
d)
30o
|
|
Gowri Dey answered |
∠EFD+∠FED = x
(Exterior angle property of a triangle)
⇒ 28o+42o = ∠x or ∠x = 70o
(Exterior angle property of a triangle)
⇒ 28o+42o = ∠x or ∠x = 70o
A cylindrical pencil consists of a layer of wood surrounding a solid cylinder of graphite. The radius of the pencil is 6 mm, the radius of the graphite cylinder is 2 mm and the length of the pencil is 10 cm. Find the cost of the material used in a pencil, if the cost of wood is Rs. 0.70/cm3 and that of graphite is Rs. 2.80/cm3.- a)Rs. 7.85
- b)Rs. 8.76
- c)Rs. 9.36
- d)Rs. 10.56
- e)none of these
Correct answer is option 'D'. Can you explain this answer?
A cylindrical pencil consists of a layer of wood surrounding a solid cylinder of graphite. The radius of the pencil is 6 mm, the radius of the graphite cylinder is 2 mm and the length of the pencil is 10 cm. Find the cost of the material used in a pencil, if the cost of wood is Rs. 0.70/cm3 and that of graphite is Rs. 2.80/cm3.
a)
Rs. 7.85
b)
Rs. 8.76
c)
Rs. 9.36
d)
Rs. 10.56
e)
none of these

|
Saanvi Reddy answered |
Volume of the whole pencil = 3.6π cm3
Volume of graphite cylinder =0.4π cm3
Volume of wood part =3.6π−0.4π=3.2π cm3
Volume of graphite cylinder =0.4π cm3
Volume of wood part =3.6π−0.4π=3.2π cm3
Cost of the pencil = 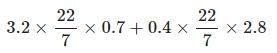
= Rs. 10.56
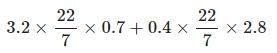
= Rs. 10.56
Two poles of height 9 cm and 14m stand upright on a plane ground. If the distance between their feet is 12 m. Find the distance between their tops.- a)12 m
- b)13 m
- c)5 m
- d)15 m
Correct answer is option 'B'. Can you explain this answer?
Two poles of height 9 cm and 14m stand upright on a plane ground. If the distance between their feet is 12 m. Find the distance between their tops.
a)
12 m
b)
13 m
c)
5 m
d)
15 m

|
Diya Chavan answered |
Let AB and CD be the given poles such that
AB = 9 m, CD = 14 m and AC = 12 m. Join BD.
From B, draw BL ⊥ CD.
DL = (CD – CL) = (CD – AB)
= (14 – 9) m = 5 m
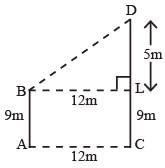
BL = AC = 12 m
Now, in right ∆BLD, by Pythagoras theorem.
We have
BD2 = BL2 + DL2 = {(12)2 + (5)2}m2
= (144 + 25) m2 = 169 m2
AB = 9 m, CD = 14 m and AC = 12 m. Join BD.
From B, draw BL ⊥ CD.
DL = (CD – CL) = (CD – AB)
= (14 – 9) m = 5 m

BL = AC = 12 m
Now, in right ∆BLD, by Pythagoras theorem.
We have
BD2 = BL2 + DL2 = {(12)2 + (5)2}m2
= (144 + 25) m2 = 169 m2
Find angle x in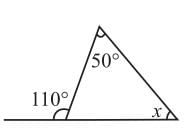
- a)60°
- b)160°
- c)80°
- d)100°
Correct answer is option 'A'. Can you explain this answer?
Find angle x in

a)
60°
b)
160°
c)
80°
d)
100°
|
|
Eduskill Classes answered |
Sum of interior opposite angles = Exterior angle
or 50° + x = 110°
or x = 60°
In a regular pentagon PQRST, what is the ratio of the area of triangle PRS to the area of the pentagon PQRST?- a)1 / (sin 72 + 4)
- b)1 / (cos 72 + 4)
- c)1 / (4 cos 72 + 1)
- d)1 / (4 sin 72 + 1)
- e)none of these
Correct answer is option 'C'. Can you explain this answer?
In a regular pentagon PQRST, what is the ratio of the area of triangle PRS to the area of the pentagon PQRST?
a)
1 / (sin 72 + 4)
b)
1 / (cos 72 + 4)
c)
1 / (4 cos 72 + 1)
d)
1 / (4 sin 72 + 1)
e)
none of these

|
Saanvi Reddy answered |
Each angle of a regular pentagon is 108 degrees. In triangle PTS, angle T = 108 degrees, and PT = TS. So, angle TPS = angle TSP = 36 degrees.
Similarly, angle QPR = 36 degrees. So, angle SPR = 108 – (36 + 36) = 36 degrees
Also, PS = PR
Area of triangle PSR = ½ * PS * PR * sin 36
Area of the pentagon = Sum of areas of the three triangles = Area of triangle PTS + Area of triangle PSR + Area of triangle PQR
= ½ * PT * PS * sin (angle TPS) + ½ * PS * PR * sin 36 + ½ * PQ * PR * sin (angle QPR)
= ½ * PT * PS * sin 36 + ½ * PS * PR * sin 36 + ½ * PQ * PR * sin 36
Required ratio = ½ * PS * PR * sin 36 / (½ * PT * PS * sin 36 + ½ * PS * PR * sin 36 + ½ * PQ * PR * sin 36)
= PR / (PT + PR + PQ)
PT = PQ = SR
SR = 2 * PR cos (angle PSR) = 2 * PR * cos 72
Ratio = PR / (2 * PR cos 72 + PR + 2 * PR cos 72) = 1 / (4 cos 72 + 1)
Similarly, angle QPR = 36 degrees. So, angle SPR = 108 – (36 + 36) = 36 degrees
Also, PS = PR
Area of triangle PSR = ½ * PS * PR * sin 36
Area of the pentagon = Sum of areas of the three triangles = Area of triangle PTS + Area of triangle PSR + Area of triangle PQR
= ½ * PT * PS * sin (angle TPS) + ½ * PS * PR * sin 36 + ½ * PQ * PR * sin (angle QPR)
= ½ * PT * PS * sin 36 + ½ * PS * PR * sin 36 + ½ * PQ * PR * sin 36
Required ratio = ½ * PS * PR * sin 36 / (½ * PT * PS * sin 36 + ½ * PS * PR * sin 36 + ½ * PQ * PR * sin 36)
= PR / (PT + PR + PQ)
PT = PQ = SR
SR = 2 * PR cos (angle PSR) = 2 * PR * cos 72
Ratio = PR / (2 * PR cos 72 + PR + 2 * PR cos 72) = 1 / (4 cos 72 + 1)
Corners of an equilateral triangle were cut off such that a regular hexagon is formed. If each side of the original triangle measures 9 cm, find the area of the hexagon in square cm. - a)(27√3)/2
- b)(81√3)/5
- c)(81√3)/4
- d)36√3
- e)54√3
Correct answer is option 'A'. Can you explain this answer?
Corners of an equilateral triangle were cut off such that a regular hexagon is formed. If each side of the original triangle measures 9 cm, find the area of the hexagon in square cm.
a)
(27√3)/2
b)
(81√3)/5
c)
(81√3)/4
d)
36√3
e)
54√3

|
Atharva Chawla answered |
Step 1: Question statement and Inferences
Since we are not given the figure, let us draw one.
Let the equilateral triangle be ABC.
∠BAC = ∠ABC = ∠BCA = 600
The corners marked in blue are cut from this triangle, thereby resulting in a regular hexagon PQRSTU.
Let each side of this hexagon be x cm
Now, we know that
Exterior angle of a n-sided regular polygon = 360o/n
Therefore,
Exterior angle of a regular hexagon
360o/6 = 60o
This means, Angle APQ = 60o
Consider Triangle APQ:
Every angle in this triangle is 60o
Therefore, BU = UP = PA = x cm
So, BA = BU + UP + PA = 3x cm
But, we are given that
Each side of triangle ABC measures 9 cm
That is, BA = 9 cm
3x = 9 cm
x = 3 cm
Thus, we have found out that each side of the regular hexagon measures 3 cm.
We need to find the area of this regular hexagon.
Step2: Finding required values
Area of hexagon = (Area of equilateral triangle ABC) -3(Area of equilateral Triangle with side 3 cm)
Area of am equilateral triangle =  ; where a is the side of the triangle
; where a is the side of the triangle
so, the area of triangle ABC = 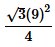
And, the area of each smaller triangle = 
Area of the hexagon =
Area of the hexagon =
Step 3: Calculating the final answer
So, the area of the hexagon is 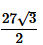 square cm.
square cm.
The figure below is a regular polygon. Find the measure of angle x (in degrees)? 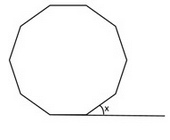
- a)36
- b)40
- c)45
- d)140
- e)144
Correct answer is option 'A'. Can you explain this answer?
The figure below is a regular polygon. Find the measure of angle x (in degrees)?
a)
36
b)
40
c)
45
d)
140
e)
144

|
Divyanshu answered |
Sum of all exterior angle of plygon = 360 degree.X+x+x+x+x+x+x+x+x+x=36010x=360X=360/10X=36
A man goes 24m due east and then 10m due north. How far is he away from his initial position?- a)24 m
- b)28 m
- c)30 m
- d)26 m
Correct answer is option 'D'. Can you explain this answer?
A man goes 24m due east and then 10m due north. How far is he away from his initial position?
a)
24 m
b)
28 m
c)
30 m
d)
26 m

|
Sneha Khanna answered |
Let O be the initial position of the man. Let he cover OA = 24m due east and then AB = 10m due north.
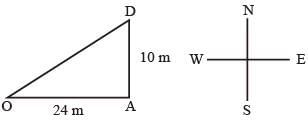
Finally, he reaches the point B. Join OB.
OB2 = (OA2 + OB2) = {(24)2 + (10)2} m2
= (576 + 100) m2 = 676 m2

Hence, the man is at a distance at 26m from his initial position.

Finally, he reaches the point B. Join OB.
OB2 = (OA2 + OB2) = {(24)2 + (10)2} m2
= (576 + 100) m2 = 676 m2

Hence, the man is at a distance at 26m from his initial position.
Find the angles of a triangle which are in the ratio 4 : 3 : 2.- a)15°, 20°, 25°
- b)20°, 20°, 40°
- c)80°, 60°, 40°
- d)40°, 80°, 60°
Correct answer is option 'C'. Can you explain this answer?
Find the angles of a triangle which are in the ratio 4 : 3 : 2.
a)
15°, 20°, 25°
b)
20°, 20°, 40°
c)
80°, 60°, 40°
d)
40°, 80°, 60°

|
Sneha Khanna answered |
Let the measure of the given angles of the triangle be (4x)°, (3x)° and (2x)° respectively.
4x + 3x + 2x = 180°
⇒ 9x = 180°
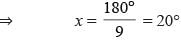
So, the angles measure (4×20)°, (3 × 20)° and (2 × 20)°
Hence, the angles of the triangle are 80°, 60°, 40°.
4x + 3x + 2x = 180°
⇒ 9x = 180°
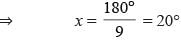
So, the angles measure (4×20)°, (3 × 20)° and (2 × 20)°
Hence, the angles of the triangle are 80°, 60°, 40°.
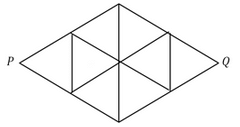 The above shape is made of eight identical equilateral triangles, each having a perimeter of 3. What is the straight-line distance between points P and Q?
The above shape is made of eight identical equilateral triangles, each having a perimeter of 3. What is the straight-line distance between points P and Q?- a)√3
- b)3
- c)4
- d)2√2
- e)2√3
Correct answer is option 'E'. Can you explain this answer?
The above shape is made of eight identical equilateral triangles, each having a perimeter of 3. What is the straight-line distance between points P and Q?
a)
√3
b)
3
c)
4
d)
2√2
e)
2√3

|
Sandeep Mehra answered |
Step 1: Question statement and Inferences
To find the straight line distance between points P and Q, calculate the height of one of the equilateral triangles.
Step 2: Finding required values
Think of the shape as two large, equilateral triangles. If each small equilateral triangle has a perimeter of 3, then it has a side of 1, and each large equilateral triangle has a side of 2.
Create a right triangle inside a large equilateral triangle, and find the third side, shown as h in the drawing.
Step 3: Calculating the final answer
The right triangle has sides 1, 2, and h, where 2 is the hypotenuse. With the Pythagorean Theorem, calculate the length of h:
You have found half the distance. Double this for the full straight-line distance of 2√3
Answer: Option (E)
In ΔABC, AC = BC and ∠C = 110°. Find ∠A and ∠B.
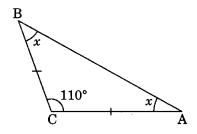
- a)35°
- b)75°
- c)45°
- d)105°
Correct answer is option 'A'. Can you explain this answer?
In ΔABC, AC = BC and ∠C = 110°. Find ∠A and ∠B.


a)
35°
b)
75°
c)
45°
d)
105°

|
Shiksha Academy answered |
In given ΔABC, ∠C = 110°
Let ∠A = ∠B = x° (Angle opposite to equal sides of a triangle are equal)
x + x + 110° = 180° (Sum of all angles in a triangle is 180°)
⇒ 2x + 110° = 180°
⇒ 2x = 180° – 110°
⇒ 2x = 70°
⇒ x = 35°
Thus, ∠A = ∠B = 35°
Let ∠A = ∠B = x° (Angle opposite to equal sides of a triangle are equal)
x + x + 110° = 180° (Sum of all angles in a triangle is 180°)
⇒ 2x + 110° = 180°
⇒ 2x = 180° – 110°
⇒ 2x = 70°
⇒ x = 35°
Thus, ∠A = ∠B = 35°
Find the measure of the angle ∠x in the given figure. 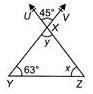
- a)72o
- b)82o
- c)90o
- d)40o
Correct answer is option 'A'. Can you explain this answer?
Find the measure of the angle ∠x in the given figure.

a)
72o
b)
82o
c)
90o
d)
40o

|
Rainbow Rise Classes answered |
∠UXV = y (Vertically opposite angles)
∴ y = 45o
∴ y = 45o
In ΔXYZ, y+x+63o = 180o (Angle sum property)
⇒ 45o+x+63o = 180o
⇒ x = 180o−(45o+63o)
⇒ x= 180o−108o = 72o
⇒ 45o+x+63o = 180o
⇒ x = 180o−(45o+63o)
⇒ x= 180o−108o = 72o
What is the measure of each angle of an equilateral triangle?- a)60°
- b)80°
- c)40°
- d)70°
Correct answer is option 'A'. Can you explain this answer?
What is the measure of each angle of an equilateral triangle?
a)
60°
b)
80°
c)
40°
d)
70°

|
Diya Chavan answered |
All the angles of equilateral triangle are equal.
In the figure (not drawn to scale), ABC is an equilateral triangle and ABD is an isosceles triangle with DA = DB, find x.
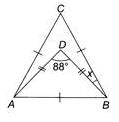
- a)14o
- b)16o
- c)12o
- d)32o
Correct answer is option 'A'. Can you explain this answer?
In the figure (not drawn to scale), ABC is an equilateral triangle and ABD is an isosceles triangle with DA = DB, find x.

a)
14o
b)
16o
c)
12o
d)
32o

|
Anmol Iyer answered |
Since ABC is an equilateral triangle.
∴ ∠CAB =∠ABC =∠BCA = 60o
And ∠DBA = ∠DAB = (60o−x)
[∵ DA = DB]
In ΔDAB, ∠DBA+∠DAB+∠ADB =180o (Angle sum Property)
⇒ 2(60o−x)+88o = 180o
⇒ 2(60o−x) = 92o
⇒ 60o−x = 46o ⇒ x = 14o
∴ ∠CAB =∠ABC =∠BCA = 60o
And ∠DBA = ∠DAB = (60o−x)
[∵ DA = DB]
In ΔDAB, ∠DBA+∠DAB+∠ADB =180o (Angle sum Property)
⇒ 2(60o−x)+88o = 180o
⇒ 2(60o−x) = 92o
⇒ 60o−x = 46o ⇒ x = 14o
ABCDE is a regular pentagon. Sides AE and ED of the pentagon are extended as shown to form triangle EFG, which is right-angled at F. Vertices A and C are joined to form the triangle ABC. What is the value of sum (x° + y°)?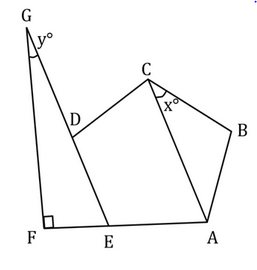
- a)30°
- b)45°
- c)54°
- d)60°
- e)72°
Correct answer is option 'C'. Can you explain this answer?
ABCDE is a regular pentagon. Sides AE and ED of the pentagon are extended as shown to form triangle EFG, which is right-angled at F. Vertices A and C are joined to form the triangle ABC. What is the value of sum (x° + y°)?
a)
30°
b)
45°
c)
54°
d)
60°
e)
72°
|
|
Mahi Gupta answered |
Step 1: Understand the question and draw inferences
To find –x°+ y°
Given – ABCDE is a regular pentagon.
This means, all sides of the pentagon are equal.
Therefore, AB = BC
In triangle ABC, two sides are equal.
Therefore, triangle ABC is an isosceles triangle.
Since angles opposite to equal sides are also equal,
Angle BAC = Angle ACB = x°
Let Angle ABC = i°
Therefore, by Angle Sum Property,
2x° + i° = 180° . . . (1)
Now, considering the right triangle EFG,
Let angle FEG = e°
Therefore, by Angle Sum Property,
e° + y° + 90° = 180°
e° + y° = 90° . . . (2)
Step 2: Finding the required values
We know that for interior angle of an n-sided regular polygon = 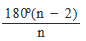
So, for n = 5, value of each interior angle = 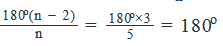
Therefore, i° = 108° . . . (3)
Also, we know that Exterior Angle of an n-sided regular polygon = 360on
So, for n = 5, the value of each exterior angle = 360o/5 = 72°
Notice that Angle FEG is an exterior angle of the regular pentagon.
Therefore, e° = 72° . . . (4)
Step 3: Calculating the final answer
From (1) and (3), we get:
2x° + 108° = 180°
Solving this equation, we get x° = 36°
From (2) and (4), we get:
72° + y° = 90°
y° = 18°
Thus, x° + y° = 36° + 18° = 54°
Correct Choice -C
 Dodger’s stadium, which is rectangular in shape, currently has one parking lot that has a maximum capacity of 2000 cars. In order to accommodate the increased demand due to District Level games, the management plans to increase the capacity of the parking lot by adding one more parking lot – parking lot 2. Assuming the shape of the structure as shown in the figure, what is the ratio of the width of parking lot 2 (w2) to the width of parking lot 1(w1). Also assume that the height of both the triangular parking lots is same as the width of the rectangle and that the allowed spacing between the cars is same in both parking lots.(1) After the addition of parking lot 2, the total parking capacity of the stadium is 6000 cars.(2) The area of parking lot 1 is 10000 m2
Dodger’s stadium, which is rectangular in shape, currently has one parking lot that has a maximum capacity of 2000 cars. In order to accommodate the increased demand due to District Level games, the management plans to increase the capacity of the parking lot by adding one more parking lot – parking lot 2. Assuming the shape of the structure as shown in the figure, what is the ratio of the width of parking lot 2 (w2) to the width of parking lot 1(w1). Also assume that the height of both the triangular parking lots is same as the width of the rectangle and that the allowed spacing between the cars is same in both parking lots.(1) After the addition of parking lot 2, the total parking capacity of the stadium is 6000 cars.(2) The area of parking lot 1 is 10000 m2- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'A'. Can you explain this answer?
Dodger’s stadium, which is rectangular in shape, currently has one parking lot that has a maximum capacity of 2000 cars. In order to accommodate the increased demand due to District Level games, the management plans to increase the capacity of the parking lot by adding one more parking lot – parking lot 2. Assuming the shape of the structure as shown in the figure, what is the ratio of the width of parking lot 2 (w2) to the width of parking lot 1(w1). Also assume that the height of both the triangular parking lots is same as the width of the rectangle and that the allowed spacing between the cars is same in both parking lots.
(1) After the addition of parking lot 2, the total parking capacity of the stadium is 6000 cars.
(2) The area of parking lot 1 is 10000 m2
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Saanvi Reddy answered |
Steps 1 and 2 – Understand the question statement and draw inferences
To find – w2 : w1
Given –
(1) Capacity of Parking Lot 1 = 2000 cars
(2) Per the figure, height of both parking lots is the same. The difference in capacity of the parking lots comes from the difference in the width of the parking lots.
Step 3 – Analyse Statement 1
Per statement 1, the total increased capacity of the parking lots is 6000 cars.
- Capacity of Parking Lot 1 = 2000
- Capacity of Parking Lot 2 = 6000 – 2000 = 4000 cars
Area Lot 2 = 2 * Area Lot 1 … (since capacity of parking lot 1 = 2000 cars and that of lot 2 = 4000 cars)
Since the height of both parking lots is the same, the ratio of area = the ratio of width
Thus, we have the value of w2 : w1
Therefore, information provided in Statement (1) is sufficient to arrive at a unique answer.
Step 4 – Analyse Statement 2
Statement 2 provides area of Parking Lot 1 – 10000 m2.
So we know that the given area can accommodate 2000 cars. But we do not know anything about the area of the parking lot 2. Thus, we do cannot find the relationship between the widths of the two parking lots.
Therefore, statement (2) does not provide sufficient information to arrive at a unique answer.
Step 5 – Analyze both Statements together
This step is not required since statement 1 helps us arrive at a unique answer.
Correct Answer – Choice A
In the given figure, the side QR of a △PQR has been produced to the point S. If ∠PRS = 115o and ∠P = 45o , then ∠Q is equal to,
- a)20o
- b)105o
- c)70o
- d)80o
Correct answer is option 'C'. Can you explain this answer?
In the given figure, the side QR of a △PQR has been produced to the point S. If ∠PRS = 115o and ∠P = 45o , then ∠Q is equal to,


a)
20o
b)
105o
c)
70o
d)
80o

|
Shiksha Academy answered |
∠PRS = ∠RPQ + ∠PQR (By exterior angle property)
⇒ 115º = 45º + ∠PQR
⇒ ∠PQR = 115º - 45º ⇒ ∠PQR = 70º
⇒ 115º = 45º + ∠PQR
⇒ ∠PQR = 115º - 45º ⇒ ∠PQR = 70º
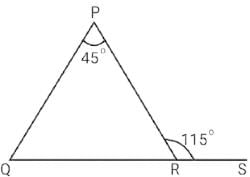
Classify the following triangle on basis of their sides 
- a)(i)scalene, (ii) isoceles, (iii) equilateral
- b)(i) isosceles, (ii) right, (iii) equilateral
- c)(i) right, (ii) isosceles, (iii) equilateral
- d)(i) equilateral, (ii) scalene, (iii) isosceles
Correct answer is option 'A'. Can you explain this answer?
Classify the following triangle on basis of their sides

a)
(i)scalene, (ii) isoceles, (iii) equilateral
b)
(i) isosceles, (ii) right, (iii) equilateral
c)
(i) right, (ii) isosceles, (iii) equilateral
d)
(i) equilateral, (ii) scalene, (iii) isosceles

|
Rainbow Rise Classes answered |
(i) PQ = 5 cm, PR = 6 cm and QR = 7 cm
PQ ≠ PR ≠ QR
Thus, ∆PQR is a scalene triangle.
(ii) AB = 4 cm, AC = 4 cm, BC = 4.5 cm
AB = AC ≠ 4.5 cm
Thus, ∆ABC is an isosceles triangle.
(iii) MN = 3 cm, ML = 3 cm and NL = 3 cm
MN = ML = NL
Thus, ∆MNL is an equilateral triangle.
PQ ≠ PR ≠ QR
Thus, ∆PQR is a scalene triangle.
(ii) AB = 4 cm, AC = 4 cm, BC = 4.5 cm
AB = AC ≠ 4.5 cm
Thus, ∆ABC is an isosceles triangle.
(iii) MN = 3 cm, ML = 3 cm and NL = 3 cm
MN = ML = NL
Thus, ∆MNL is an equilateral triangle.
∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm then AB = ?- a)5√2 cm
- b)10 cm
- c)5 cm
- d)2.5 cm
Correct answer is option 'A'. Can you explain this answer?
∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm then AB = ?
a)
5√2 cm
b)
10 cm
c)
5 cm
d)
2.5 cm

|
Dhrup Maurya answered |
Angle C is 90 so this is right angle triangle
AC= 5 then CB= 5 because it is isosceles triangle ,given in the question .Base and Parpendicular are equale and according to Pythagoras theroum
Hypothenas² = base²+parandicular²
so AB²=AC²+CB²
then AB²=5²+5²
AB²=25+25
AB²=50
AB=√50 or 5√2
So answer is 5√2
AC= 5 then CB= 5 because it is isosceles triangle ,given in the question .Base and Parpendicular are equale and according to Pythagoras theroum
Hypothenas² = base²+parandicular²
so AB²=AC²+CB²
then AB²=5²+5²
AB²=25+25
AB²=50
AB=√50 or 5√2
So answer is 5√2
The lengths of the sides of two triangles are given below. Which of them is right – angled?
(i) a = 8 cm, b = 5 cm, and c = 10 cm
(ii) a = 7 cm, b = 24 cm, and c = 25 cm- a)(i) and (ii) both
- b)(ii) is but (i) not
- c)(i) and (ii) both not
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The lengths of the sides of two triangles are given below. Which of them is right – angled?
(i) a = 8 cm, b = 5 cm, and c = 10 cm
(ii) a = 7 cm, b = 24 cm, and c = 25 cm
(i) a = 8 cm, b = 5 cm, and c = 10 cm
(ii) a = 7 cm, b = 24 cm, and c = 25 cm
a)
(i) and (ii) both
b)
(ii) is but (i) not
c)
(i) and (ii) both not
d)
None of these

|
Sreemoyee Nair answered |
(i)
Here a = 8 cm, b = 5cm and c = 10c,
The largest side is c = 10cm.
a2 + b2 = {(8)2 + (5)2} cm2
= m (64 + 25) cm2 = 89 cm2 ≠ (10)2 cm2
a2 + b2 ≠ c2
∴ Given triangle is not right angled.
(ii) Here a = 7 cm, b = 24 cm and c = 25 cm
The largest side is c = 25 cm
a2 + b2 = {(7)2 + (24)2} cm2 = (49 + 576) cm2
= 625 cm2 = (25 cm)2 = c2
⇒ a2 + b2 = c2
Given triangle is right angled.
Here a = 8 cm, b = 5cm and c = 10c,
The largest side is c = 10cm.
a2 + b2 = {(8)2 + (5)2} cm2
= m (64 + 25) cm2 = 89 cm2 ≠ (10)2 cm2
a2 + b2 ≠ c2
∴ Given triangle is not right angled.
(ii) Here a = 7 cm, b = 24 cm and c = 25 cm
The largest side is c = 25 cm
a2 + b2 = {(7)2 + (24)2} cm2 = (49 + 576) cm2
= 625 cm2 = (25 cm)2 = c2
⇒ a2 + b2 = c2
Given triangle is right angled.
Find the measure of ∠LNM in the given figure.
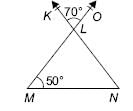
- a)30o
- b)80o
- c)70o
- d)60o
Correct answer is option 'D'. Can you explain this answer?
Find the measure of ∠LNM in the given figure.


a)
30o
b)
80o
c)
70o
d)
60o

|
Kunal Mehra answered |
∠KLO = ∠MLN
∴ ∠MLN = 70o in ∠LMN
∴ ∠MLN = 70o in ∠LMN
Also,
∠MLN+∠LNM+∠LMN = 180o (Angle sum property)
⇒ 70o+∠LNM+50o=180o
⇒ ∠LNM = 180o−(70o+50o) = 60o
⇒ 70o+∠LNM+50o=180o
⇒ ∠LNM = 180o−(70o+50o) = 60o
In the given figure, find the values of x and y.
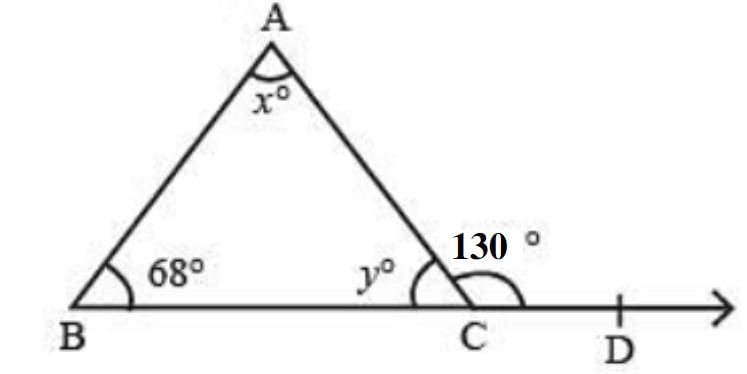
- a)y = 62°, x = 50°
- b)x = 62°, y = 50°
- c)x = 52°, y = 40°
- d)x = 50°, y = 60°
Correct answer is option 'B'. Can you explain this answer?
In the given figure, find the values of x and y.


a)
y = 62°, x = 50°
b)
x = 62°, y = 50°
c)
x = 52°, y = 40°
d)
x = 50°, y = 60°

|
Diya Chavan answered |
We know that an exterior angle of a triangle is equal to the sum of its interior opposite angles.
The sum of all the angles of a triangle is 180°.
x + y + 68 = 180° ⇒ 62° + y + 68° = 180°
⇒ 130° + y = 180°
y = 180° – 130°
= 50°
The sum of all the angles of a triangle is 180°.
x + y + 68 = 180° ⇒ 62° + y + 68° = 180°
⇒ 130° + y = 180°
y = 180° – 130°
= 50°
In the given figure, AOB is a straight line,
∠AOC = (3x – 8)°, ∠COD = 50° and ∠BOD = (x + 10)°. The value of x is
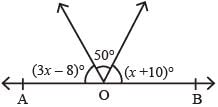
- a)42
- b)52
- c)36
- d)32
Correct answer is option 'D'. Can you explain this answer?
In the given figure, AOB is a straight line,
∠AOC = (3x – 8)°, ∠COD = 50° and ∠BOD = (x + 10)°. The value of x is

∠AOC = (3x – 8)°, ∠COD = 50° and ∠BOD = (x + 10)°. The value of x is

a)
42
b)
52
c)
36
d)
32

|
Madhavan Unni answered |
Here, (3x – 8)° + 50° + (x + 10)° = 180°
⇒ 4x + 52 = 180°
⇒ 4x = 180 – 52
⇒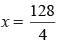
⇒ x = 32
⇒ 4x + 52 = 180°
⇒ 4x = 180 – 52
⇒
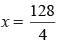
⇒ x = 32
In a ∆ABC, ∠A – ∠B = 33° and ∠B – ∠C = 18°, then ∠B = ?- a)35°
- b)55°
- c)45°
- d)57°
Correct answer is option 'B'. Can you explain this answer?
In a ∆ABC, ∠A – ∠B = 33° and ∠B – ∠C = 18°, then ∠B = ?
a)
35°
b)
55°
c)
45°
d)
57°

|
Rahul Shah answered |
∠A = 33° + ∠B and ∠C = ∠B – 18°
∴ (33° + ∠B) + ∠B + (∠B – 18°) = 180°
⇒ 3∠B = 165° 17. (d) ⇒ ∠B = 55°
∴ (33° + ∠B) + ∠B + (∠B – 18°) = 180°
⇒ 3∠B = 165° 17. (d) ⇒ ∠B = 55°
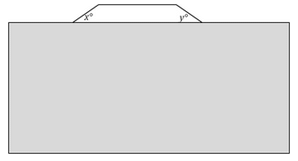 A regular polygon is partially obscured by a box. What is the sum of the angles of the polygon?(1) x°= y°(2) x°+ y°= 72°
A regular polygon is partially obscured by a box. What is the sum of the angles of the polygon?(1) x°= y°(2) x°+ y°= 72°- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'B'. Can you explain this answer?
A regular polygon is partially obscured by a box. What is the sum of the angles of the polygon?
(1) x°= y°
(2) x°+ y°= 72°
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Atharva Chawla answered |
Steps 1 & 2: Understand Question and Draw Inferences
To find the sum of the angles of the polygon, you need to know the number of angles.
Knowing that the polygon is regular, the two visible angles (and all the other hidden angles) are equal. You also know that the visible trapezoid has an angle total of 360°
Step 3: Analyze Statement 1
x°= y°
Knowing x equals y doesn’t tell you anything about the angles of the regular polygon.
Statement (1) is not sufficient.
Step 4: Analyze Statement 2
x°+ y°= 72°
The part of the regular polygon that is visible forms a quadrilateral.
This quadrilateral has 4 angles: x°, y° and two interior angles of the regular polygon.
Let each interior angle of the regular polygon = i°
Since the sum of all angles of a quadrilateral is 360°, we can write:
x° + y° + 2i° = 360°
Inserting the information given in Statement 2 in this equation, we get:
72° + 2i° = 360°
Or, 2i° = 288°
i° = 144°
Thus, we now know that every interior angle of the regular polygon measures 144°
Let the regular polygon have n sides.
Then 144°*n = (n -2)*180°
⇒ n = 10.
Therefore, sum of angles of the regular polygon = (n-2)180° = 8*180° = 1,440°.
Statement (2) is sufficient.
Step 5: Analyze Both Statements Together (if needed)
You get a unique answer in step 4, so this step is not required
Answer: Option (B)
In the given figure, find the values of x and y.
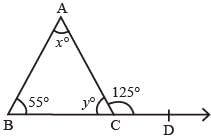
- a)x = 55°, y = 70°
- b)x = 55°, y = 55°
- c)x = 50°, y = 70°
- d)x = 70°, y = 55°
Correct answer is option 'D'. Can you explain this answer?
In the given figure, find the values of x and y.


a)
x = 55°, y = 70°
b)
x = 55°, y = 55°
c)
x = 50°, y = 70°
d)
x = 70°, y = 55°

|
Sreemoyee Nair answered |
We know that an exterior angle of a triangle is equal to the sum of its interior opposite angles.


 Two identical regular hexagons are inscribed in a rectangle whose area is 256√3 square inches. What is the perimeter of each hexagon in inches?
Two identical regular hexagons are inscribed in a rectangle whose area is 256√3 square inches. What is the perimeter of each hexagon in inches?- a)48
- b)56
- c)64
- d)56√3
- e)64√3
Correct answer is option 'A'. Can you explain this answer?
Two identical regular hexagons are inscribed in a rectangle whose area is 256√3 square inches. What is the perimeter of each hexagon in inches?
a)
48
b)
56
c)
64
d)
56√3
e)
64√3

|
Saanvi Reddy answered |
To find – Perimeter of hexagon
Given –
- The two hexagons are identical – the length of the sides are equal.
- Area of rectangle = 256√3 in2
Approach –
- Let ‘a’ be the side of the hexagon and let ‘x’ be the length of the rectangle.
- To find the perimeter of the hexagon, we need to express the sides of rectangle (x) in terms of the side of the hexagon (a).
- Then given the area we can find the measure of ‘a’
- Hence, we can find the perimeter.
Solution
- Each side of the hexagon is ‘a’ since it is a regular hexagon.
- Consider the middle shaded triangle.
- It is an equilateral triangle since each angle is 60° as explained below.
- Interior angle of the hexagon = 120°.
- The angle made by AB = 180°.
- Thus, angle of the triangle = 180 – 120 = 60°
- The purple line is a/2.
- x/2 = a/2+a+a/2 = 2a
- x = 4a
Likewise, applying Pythagoras theorem on the shaded side triangle we get the value of y in terms of a
- a2-a2/4 = y2/4
- y = a√3
We can now substitute the values of x and y in terms of a in the equation for area of the rectangle.
- xy = 256√3
- 4a2√3 = 256√3
- a = 8
- Perimeter of hexagon = 8 * 6 = 48 inches
Correct Answer = Choice A
Chapter doubts & questions for Polygons - Mathematics for JAMB 2025 is part of JAMB exam preparation. The chapters have been prepared according to the JAMB exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JAMB 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Polygons - Mathematics for JAMB in English & Hindi are available as part of JAMB exam.
Download more important topics, notes, lectures and mock test series for JAMB Exam by signing up for free.
Mathematics for JAMB
134 videos|94 docs|102 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup