All Exams >
JAMB >
Mathematics for JAMB >
All Questions
All questions of Circles for JAMB Exam
In the figure, AD is a straight line. OP is perpendicular to AD and O is the centre of both the circles. If AO = 34 cm, OB = 20 cm and OP = 16 cm, then the length of AD is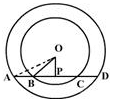
- a)20 cm
- b)50 cm
- c)60 cm
- d)43 cm
Correct answer is option 'C'. Can you explain this answer?
In the figure, AD is a straight line. OP is perpendicular to AD and O is the centre of both the circles. If AO = 34 cm, OB = 20 cm and OP = 16 cm, then the length of AD is
a)
20 cm
b)
50 cm
c)
60 cm
d)
43 cm
|
|
Sarthak Satav answered |
Here OPA is right angle triangle
given OP = 16 cm
AO = 34 cm
AP = ?
using Pythagoras theorem :
AO² = OP² + AP²
34² = 16² + AP²
1156 = 256 + AP²
1156 - 256 = AP²
900 = AP²
*√900 = AP*
30 = AP
Since AD is a straight line and O is at center of both circles
AD = AP + PD
AD = AP + AP
AD = 2AP
AD = 2 x 30
*AD = 60 CM*
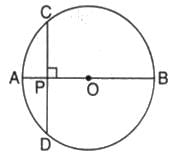
P is a point on the diameter AB of a circle and CD is a chord perpendicular to AB. If AP = 4 cm and PB = 16 cm, the length of chord CD is
- a)16 cm
- b)20 cm
- c)10 cm
- d)8 cm
Correct answer is option 'A'. Can you explain this answer?
P is a point on the diameter AB of a circle and CD is a chord perpendicular to AB. If AP = 4 cm and PB = 16 cm, the length of chord CD is

a)
16 cm
b)
20 cm
c)
10 cm
d)
8 cm

|
EduRev Class 9 answered |
AP+PB=AB [diameter of circle]
4+16=20[diameter]
so r=AO = CO=10
so clearly PO= OA-AP=10-4=6
PO=6 OC=10 So just apply pythagoreus theorem in triangle PCO
so CP will come 8 So chord CD = 2x8 = 16
4+16=20[diameter]
so r=AO = CO=10
so clearly PO= OA-AP=10-4=6
PO=6 OC=10 So just apply pythagoreus theorem in triangle PCO
so CP will come 8 So chord CD = 2x8 = 16
A rectangular enclosure 40 m x 36 m has a horse tethered to a corner with a rope of 14 m in length. What is the ratio of the respective areas it can graze, if it is outside the enclosure and if it is inside the enclosure?- a)2
- b)2:3
- c)1:4
- d)3:1
Correct answer is option 'D'. Can you explain this answer?
A rectangular enclosure 40 m x 36 m has a horse tethered to a corner with a rope of 14 m in length. What is the ratio of the respective areas it can graze, if it is outside the enclosure and if it is inside the enclosure?
a)
2
b)
2:3
c)
1:4
d)
3:1

|
Talent Skill Learning answered |
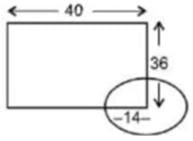
- Imagine a circle on the corner of the rectangle.
- 3 quarters of the circle lie outside the rectangle and 1 quarter lies inside.
- Hence, Required ratio = 3 : 1
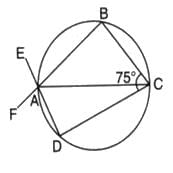
The given figure shows two intersecting circles. If ∠ABC = 75o, then the measure of ∠PAD is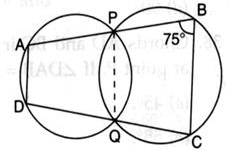
- a)75o
- b)125o
- c)105o
- d)150o
Correct answer is option 'C'. Can you explain this answer?
The given figure shows two intersecting circles. If ∠ABC = 75o, then the measure of ∠PAD is
a)
75o
b)
125o
c)
105o
d)
150o
|
|
Zachary Foster answered |
In the given figure, the points A, B, C, and D form a cyclic quadrilateral because they lie on the circumferences of the two intersecting circles.
The opposite angles of a cyclic quadrilateral are supplementary, i.e.,
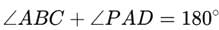
It is given that ∠ABC=75∘
Using the property of cyclic quadrilaterals:
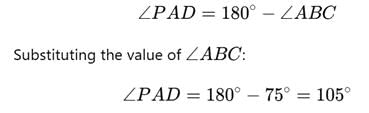
If a chord of a circle is equal to its radius, then the angle subtended by this chord in major segment is- a)45o
- b)30o
- c)60o
- d)90o
Correct answer is option 'B'. Can you explain this answer?
If a chord of a circle is equal to its radius, then the angle subtended by this chord in major segment is
a)
45o
b)
30o
c)
60o
d)
90o
|
|
Zachary Foster answered |
Let AB be the chord of the circle with center O
.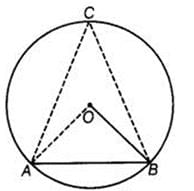

Given that AB = Radius of the circle.
Also, AO = BO = Radius
∴ ΔOAB is an equilateral triangle.
Thus, ∠AOB = ∠OBA = ∠OAB = 60°
Also, angle subtended by an arc at the center of the circle is twice the angle subtended by it at any other point in the remaining part of the circle.
∴ ∠AOB = 2∠ACB
⇒ ∠ACB = 1/2 (∠AOB)
⇒ ∠ACB = 1/2 (60°) = 30°
In the given figure, AD is the diameter of the circle and AE = DE. If ∠ABC = 115o, then the measure of ∠CAE is 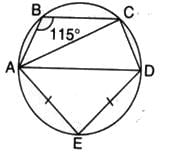
- a)70o
- b)90o
- c)80o
- d)60o
Correct answer is option 'A'. Can you explain this answer?
In the given figure, AD is the diameter of the circle and AE = DE. If ∠ABC = 115o, then the measure of ∠CAE is

a)
70o
b)
90o
c)
80o
d)
60o

|
Nclex Coaching Centre answered |
Since AD is the diameter, the angle subtended by the diameter at any point on the circle is always 90∘. Therefore:
∠ACD = 90∘
Given AE = DE, triangle ADE is isosceles. Therefore:
∠DAE =∠DEA
Since ABCD is a cyclic quadrilateral, opposite angles of a cyclic quadrilateral sum to 180∘:
∠ABC + ∠ADC = 180∘
Substituting ∠ABC=115∘
∠ADC =180∘−115∘= 65∘
In triangle ADE, since AE = DE, we have:
∠DAE=∠DEA
As ∠ADC=65∘(external angle of triangle ADE), we know that:
∠DAE = 1 / 2 × 65∘= 32.5∘
Finding ∠CAE: Since ∠CAE=∠DAE, we find:
∠CAE = 70∘
Chords AB and CD intersect at right angles. If ∠BAC = 40o, then ∠ABD is equal to
- a)45o
- b)50o
- c)60o
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
Chords AB and CD intersect at right angles. If ∠BAC = 40o, then ∠ABD is equal to
a)
45o
b)
50o
c)
60o
d)
none of these
|
|
Zachary Foster answered |
The correct answer is 50°
GIVEN: Chords AB and CD intersect at right angle. ∠BAC = 40°
TO FIND: ∠ABD
SOLUTION
We can simply solve the above problem as follows;
Let the point of intersection of the chord be 'O'.
∠AOC = 90°
Therefore,
In ΔAOC
∠AOC + ∠OAC + ∠ACO = 180°
90 + 40 + ∠ACO = 180
∠ACO = 180- 130 = 50°
Now,
AO :CO = 5:4 [since larger angle denotes shorter length]
Therefore,
Ratio of-
OB:OD=4:5 [ since they intersect and ratio gets changed]
or,
∠OBD:∠ODB=5:4 [larger length has smaller ratio]
Therefore,
∠OBD+∠ODB+90=180
5x + 4x + 90 = 180
9x + 90 = 180
x + 10 = 20
x = 10
∠OBD = 5 × 10 = 50°
Since,
∠OBD = ∠ABD
Therefore,
∠ABD = 50°
In the given figure, O is the centre of the circle ABE is a straight line,. If ∠DBE = 95o then ∠AOD is equal to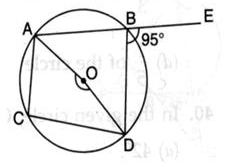
- a)190o
- b)170o
- c)180o
- d)175o
Correct answer is option 'B'. Can you explain this answer?
In the given figure, O is the centre of the circle ABE is a straight line,. If ∠DBE = 95o then ∠AOD is equal to
a)
190o
b)
170o
c)
180o
d)
175o
|
|
Zachary Foster answered |
AE is a straight line so,
angle ABD + angle EBD = 180°
angle ABD + 95° = 180°
angle ABD = 180° - 95°
angle ABD = 85°
so, it is interior angle of circle
So, angle AOD is double of angle suspended on the circle
angle AOD = 2ABD
angle AOD = 2(85°)
angle AOD = 170°
In the given figure PQ = QR = RS and ∠PTS = 75o then the measure of ∠QOR is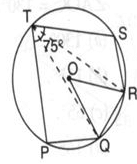
- a)25o
- b)20o
- c)50o
- d)75o
Correct answer is option 'C'. Can you explain this answer?
In the given figure PQ = QR = RS and ∠PTS = 75o then the measure of ∠QOR is
a)
25o
b)
20o
c)
50o
d)
75o

|
Kyojuro Rengoku answered |
PQ=QR=RS
PTR= 75
POS=2×75(centroid angle is double the angle suspended by any arc on remaining part of circle)
POS=150
AS PQ=QR=RS
QOR=150÷3
=50
PTR= 75
POS=2×75(centroid angle is double the angle suspended by any arc on remaining part of circle)
POS=150
AS PQ=QR=RS
QOR=150÷3
=50
ABCD is a parallelogram. A circle passes through A and D and cuts AB at E and DC at F. If ∠BEF = 80o, then ∠ABC is equal to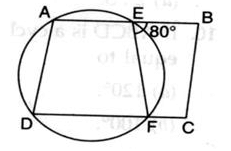
- a)120o
- b)100o
- c)80o
- d)75o
Correct answer is option 'C'. Can you explain this answer?
ABCD is a parallelogram. A circle passes through A and D and cuts AB at E and DC at F. If ∠BEF = 80o, then ∠ABC is equal to
a)
120o
b)
100o
c)
80o
d)
75o

|
Let's Tute answered |
Given, ABCD is a parallelogram and AEFD is a cyclic quadrilateral.
∠BEF=80∘
Now, ∠ADC=∠BEF=80∘ (Angle of a cyclic quadrilateral is equal to the opposite exterior angle )
Also, now in parallelogram ABCD,
∠ABC=∠ADC=80∘ (Opposite angles of a parallelogram are equal)
∠BEF=80∘
Now, ∠ADC=∠BEF=80∘ (Angle of a cyclic quadrilateral is equal to the opposite exterior angle )
Also, now in parallelogram ABCD,
∠ABC=∠ADC=80∘ (Opposite angles of a parallelogram are equal)
The region between chord and either of the arc is called- a)a sector
- b)a semicircle
- c)a segment
- d)a quarter circle
Correct answer is option 'C'. Can you explain this answer?
The region between chord and either of the arc is called
a)
a sector
b)
a semicircle
c)
a segment
d)
a quarter circle

|
Nclex Coaching Centre answered |
The region between a chord and either of its arcs is called a segment of the circular region or simply a segment of the circle. The segment formed by minor arc along with chord, is called minor segment and the segment formed by major arc, is called the major segment.
In the given figure, chords AB and CD intersect each other at right angles. Then, ∠x+∠y is equal to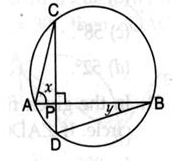
- a)75o
- b)90o
- c)45o
- d)60o
Correct answer is option 'B'. Can you explain this answer?
In the given figure, chords AB and CD intersect each other at right angles. Then, ∠x+∠y is equal to
a)
75o
b)
90o
c)
45o
d)
60o
|
|
Zachary Foster answered |
In the circle, AB and CD are two chords which intersect each other at P at right angle i.e. ∠CPB=90o.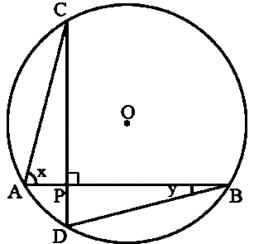

∠CAB and ∠CDB are in the same segment.
∴ ∠CDB=∠CAB=x
Now, in ΔPDB, Ext. ∠CPB=∠D+∠DBP
⇒90o = x+y (∵CD⊥AB)
Hence, x+y = 90o
BC is a diameter of the circle and ∠BAO = 60o . Then ∠ADC is equal to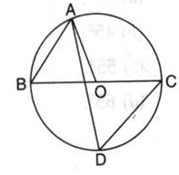
- a)45o
- b)30o
- c)60o
- d)90o
Correct answer is option 'C'. Can you explain this answer?
BC is a diameter of the circle and ∠BAO = 60o . Then ∠ADC is equal to
a)
45o
b)
30o
c)
60o
d)
90o
|
|
Swati Malkani answered |
Option C is correct i.e 60 degree
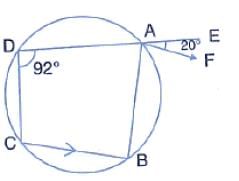
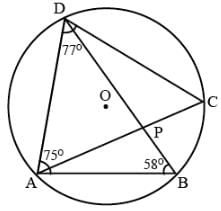
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75o, ∠ABD = 58o and ∠ADC = 77o , AC and BD intersect at P. the measure of ∠DPC is
- a)92o
- b)105o
- c)90o
- d)94o
Correct answer is option 'A'. Can you explain this answer?
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75o, ∠ABD = 58o and ∠ADC = 77o , AC and BD intersect at P. the measure of ∠DPC is

a)
92o
b)
105o
c)
90o
d)
94o

|
Varsha Pawar answered |
ANS:- let ∠PBC = x
∠ADC + ∠ABC = 180... ( opposite angles of a cyclic quadrilateral are supplementary)
77+ ∠ABD + x =180.. (∠ABC =∠ABD + x)
77+58+x =180.
135 + x =180
x = 180-135
x =45
∠PBC=45..(1)
Now , in ∆ADB,
∠ABD+∠BAD+ ∠ADB=180
58+75+ ∠ADB=180.
133+∠ADB=180.
∠ADB=180-133
∠ADB=47.
Here,. ∠ACB = ∠ADB... (angles in the same segment are equal)
Therefore,. ∠ACB=47....(2)
Now in ∆DPC,
∠DPC = ∠ACB + ∠PBC ..(exterior angle theoram.)
∠DPC= 47+45.... [from(1) and (2)]
Therefore,. ∠DPC=92.
∠ADC + ∠ABC = 180... ( opposite angles of a cyclic quadrilateral are supplementary)
77+ ∠ABD + x =180.. (∠ABC =∠ABD + x)
77+58+x =180.
135 + x =180
x = 180-135
x =45
∠PBC=45..(1)
Now , in ∆ADB,
∠ABD+∠BAD+ ∠ADB=180
58+75+ ∠ADB=180.
133+∠ADB=180.
∠ADB=180-133
∠ADB=47.
Here,. ∠ACB = ∠ADB... (angles in the same segment are equal)
Therefore,. ∠ACB=47....(2)
Now in ∆DPC,
∠DPC = ∠ACB + ∠PBC ..(exterior angle theoram.)
∠DPC= 47+45.... [from(1) and (2)]
Therefore,. ∠DPC=92.
In the given figure if ∠CAB = 49o and ∠ADC = 43o, then the measure of ∠ACB is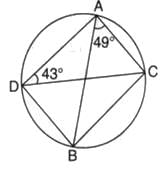
- a)92o
- b)88o
- c)74o
- d)96o
Correct answer is option 'B'. Can you explain this answer?
In the given figure if ∠CAB = 49o and ∠ADC = 43o, then the measure of ∠ACB is

a)
92o
b)
88o
c)
74o
d)
96o
|
|
Zachary Foster answered |
Angle ADC = Angle CBA(: AC is the same point that makes the angle ADC and angle CBA.)
43° = Angle CBA
In triangle ACB
Angle BAC + Angle ACB + Angle ABC = 180°
49° + Angle ACB +43° = 180°
180° - 92° = ∠ACB
88° = Angle ACB
43° = Angle CBA
In triangle ACB
Angle BAC + Angle ACB + Angle ABC = 180°
49° + Angle ACB +43° = 180°
180° - 92° = ∠ACB
88° = Angle ACB
In the given figure, O is the centre of the circle. ∠OAB and ∠OCB are 40o and 30o respectively. Then, the measure of ∠AOC is 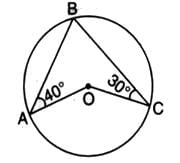
- a)170o
- b)120o
- c)110o
- d)140o
Correct answer is option 'D'. Can you explain this answer?
In the given figure, O is the centre of the circle. ∠OAB and ∠OCB are 40o and 30o respectively. Then, the measure of ∠AOC is

a)
170o
b)
120o
c)
110o
d)
140o
|
|
C K Academy answered |
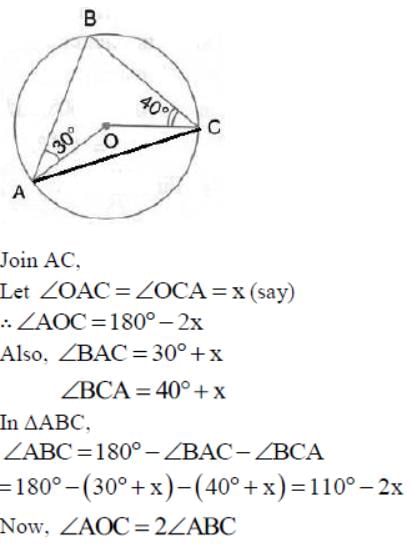
(Angle at the centre is double the angle at the circumference subtended by the same chord)
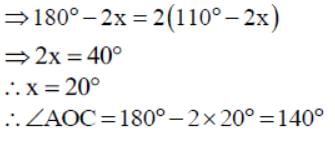
In the given figure, AB and CD are two chords of a circle intersecting at O. If AO = 4 cm and OB = 6 cm and OC = 3 cm. Find OD.
- a)4 cm
- b)6 cm
- c)8 cm
- d)10 cm
Correct answer is option 'C'. Can you explain this answer?
In the given figure, AB and CD are two chords of a circle intersecting at O. If AO = 4 cm and OB = 6 cm and OC = 3 cm. Find OD.
a)
4 cm
b)
6 cm
c)
8 cm
d)
10 cm

|
Pathways Academy answered |
By the rule of chords, cutting externally, we get:
(9 + 6) * 6 = (5 + x) * 5
90 = 25 + 5x
5x = 65
x = 13 cm
90 = 25 + 5x
5x = 65
x = 13 cm
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. The length of the common chord is- a)5 cm
- b)8 cm
- c)6 cm
- d)10 cm
Correct answer is option 'C'. Can you explain this answer?
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. The length of the common chord is
a)
5 cm
b)
8 cm
c)
6 cm
d)
10 cm
|
|
Zachary Foster answered |
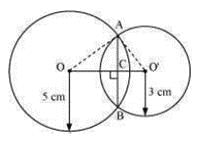
Let the radius of the circle centered at O and O' be 5 cm and 3 cm respectively.
OA = OB = 5 cm
O'A = O'B = 3 cm
OO' will be the perpendicular bisector of chord AB.
∴ AC = CB
⇒ 52 = AC2 + x2
⇒ 25 − x2 = AC2 ...(1)
In ΔO'AC,
O'A2 = AC2 + O'C2
⇒ 32 = AC2 + (4 − x)2
⇒ 9 = AC2 + 16 + x2 − 8x
⇒ AC2 = − x2 − 7 + 8x ... (2)
From equations (1) and (2), we obtain
25 − x2 = − x2 − 7 + 8x
8x = 32
x = 4
Therefore, the common chord will pass through the centre of the smaller circle i.e., O' and hence, it will be the diameter of the smaller circle.
AC2 = 25 − x2 = 25 − 42 = 25 − 16 = 9
∴ AC = 3 m
Length of the common chord AB = 2 AC = (2 × 3) m = 6 m
The perpendicular distance of a chord 8 cm long from the centre of a circle of radius 5 cm is- a)2 cm
- b)9 cm
- c)4 cm
- d)3 cm
Correct answer is option 'D'. Can you explain this answer?
The perpendicular distance of a chord 8 cm long from the centre of a circle of radius 5 cm is
a)
2 cm
b)
9 cm
c)
4 cm
d)
3 cm

|
Nclex Coaching Centre answered |
Consider a circle having center O with a chord. Let OA be the radius of the circle and AB be the chord. As given in the question, the radius of the circle is 5 cm and length of chord is 8 cm. Let the distance between the center of the circle and chord be OP. So, this can be shown diagrammatically as:
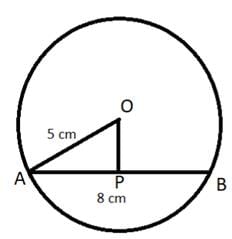
It is clear from the diagram that OP is perpendicular to AB. As OP is perpendicular to AB and passes through the center O, it will bisect the chord AB at P. Now the length of AP will be,
AP =1/2 × AB
AP =1/2 × AB
AP = 1/2 × 8
AP = 4 cm
Since, triangle OPA is a right-angle triangle, we can easily apply the Pythagoras theorem which can be stated as b2+p2 = h2 where b, p and h are base, perpendicular and hypotenuse of the respective triangle.
In ΔOPA,
Since, triangle OPA is a right-angle triangle, we can easily apply the Pythagoras theorem which can be stated as b2+p2 = h2 where b, p and h are base, perpendicular and hypotenuse of the respective triangle.
In ΔOPA,
AP2+OP2=AO2
OP2 = AO2 − AP2
OP2= 52−42
OP = 3 cm
Therefore, the distance of the chord AB from the center is 3 cm.
Therefore, the distance of the chord AB from the center is 3 cm.
Angle formed in minor segment of a circle is- a)a straight angle
- b)an acute angle
- c)a right angle
- d)an obtuse angle
Correct answer is option 'D'. Can you explain this answer?
Angle formed in minor segment of a circle is
a)
a straight angle
b)
an acute angle
c)
a right angle
d)
an obtuse angle
|
|
Zachary Foster answered |
Whenever a chord is drawn in a circle two segments are formed. One is called the minor segment while the other is called the major segment.
The angle formed by the chord in the minor segment will always be obtuse.
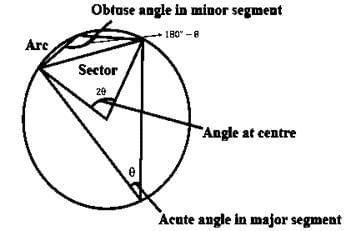
The angle formed by the chord in the minor segment will always be obtuse.

If the sum of a pair of opposite angles of a quadrilateral is 180o, the quadrilateral is:- a)square
- b)Rhombus
- c)Parallelogram
- d)Cyclic
Correct answer is option 'D'. Can you explain this answer?
If the sum of a pair of opposite angles of a quadrilateral is 180o, the quadrilateral is:
a)
square
b)
Rhombus
c)
Parallelogram
d)
Cyclic

|
Nclex Coaching Centre answered |
A quadrilateral is called cyclic if all the four vertices of it lie on a circle and the sum of either pair of opposite angles of a cyclic quadrilateral is 180∘.
Here,∠1+∠2=180∘
In the given, AB is side of regular five sided polygon and AC is a side of a regular six sided polygon inscribed in the circle with centre O. AO and CB intersect at P, then ∠APB is equal to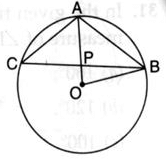
- a)72o
- b)98o
- c)90o
- d)96o
Correct answer is option 'D'. Can you explain this answer?
In the given, AB is side of regular five sided polygon and AC is a side of a regular six sided polygon inscribed in the circle with centre O. AO and CB intersect at P, then ∠APB is equal to
a)
72o
b)
98o
c)
90o
d)
96o

|
Nclex Coaching Centre answered |
For a regular n-sided polygon inscribed in a circle, the central angle subtended by each side is:
Central Angle = 360∘ / n
For the pentagon (n=5), the central angle subtended by AB is:
360∘ / 5 =72∘
For the hexagon (n=6), the central angle subtended by AC is:
360∘ / 6 = 60∘
The angle ∠APB between the two intersecting chords AB and AC can be calculated using the property of angles formed by intersecting chords: ∠APB = 1 /2 × (Sum of the arcs subtended by the opposite segments)
- Arc subtended by AB: 72∘
- Arc subtended by AC: 60∘
- The sum of the opposite arcs involved is: 72∘+120∘=192∘
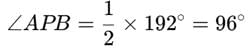
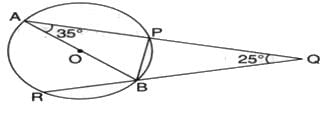
In the given figure, if ∠AOB = 80o and ∠ABC = 30o , then ∠CAO is equal to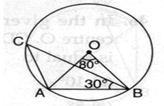
- a)30o
- b)60o
- c)80o
- d)40o
Correct answer is option 'B'. Can you explain this answer?
In the given figure, if ∠AOB = 80o and ∠ABC = 30o , then ∠CAO is equal to
a)
30o
b)
60o
c)
80o
d)
40o

|
Shiksha Academy answered |
2ACB=AOB
ACB=40
CAB+ACB+ABC=180
CAB=180-70
CAB=110
since,OA=OB(radius)
OAB=OBA
ACB=40
CAB+ACB+ABC=180
CAB=180-70
CAB=110
since,OA=OB(radius)
OAB=OBA
AOB+OAB+OBA=180
2OBA=100
OBA=50
2OBA=100
OBA=50
CAO=CAB-OBA=110-5O
CAO=60o
CAO=60o
The ratio of the sides of Δ ABC is 1:2:4. What is the ratio of the altitudes drawn onto these sides?- a)4:2:1
- b)1:2:4
- c)1:4:16
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
The ratio of the sides of Δ ABC is 1:2:4. What is the ratio of the altitudes drawn onto these sides?
a)
4:2:1
b)
1:2:4
c)
1:4:16
d)
None of these
|
|
Aakash Giery answered |
Sum of any two sides should be greater than third side.
here 1+2=3 is not less than 4 ,
1+2<4 ,so="" triangle="" is="" not="" possible.="" ,so="" triangle="" is="" not="">
here 1+2=3 is not less than 4 ,
1+2<4 ,so="" triangle="" is="" not="" possible.="" ,so="" triangle="" is="" not="">
In the given figure, a circle is centred at O. The value of x is :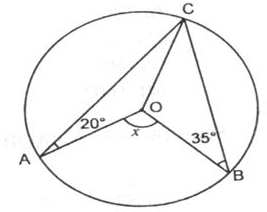
- a)55o
- b)70o
- c)110o
- d)125o
Correct answer is option 'C'. Can you explain this answer?
In the given figure, a circle is centred at O. The value of x is :
a)
55o
b)
70o
c)
110o
d)
125o

|
Nclex Coaching Centre answered |
Use the Property for Angles Subtended at the Center: The total angle subtended by the arc AB at the center O is given by:
∠AOB = 2 × ∠CAB + 2 × ∠CBA
Substitute the Given Values:
∠AOB = 2 × 20∘ + 2 × 35∘
Simplify: ∠AOB = 40∘+ 70∘= 110∘
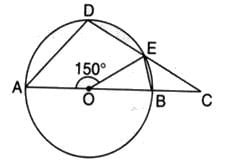
A, B, C and D are four points on a circle. AC and BD intersect at E such that angle BEC =140° and angle ECD = 25°, then angle BAC is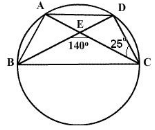
- a)90°
- b)115°
- c)100°
- d)130°
Correct answer is option 'B'. Can you explain this answer?
A, B, C and D are four points on a circle. AC and BD intersect at E such that angle BEC =140° and angle ECD = 25°, then angle BAC is
a)
90°
b)
115°
c)
100°
d)
130°

|
Nclex Coaching Centre answered |
Using the cyclic quadrilateral property:
∠BEC + ∠BAC = 180∘
Substitute the value of ∠BEC=140∘:
∠BAC = 180∘−140∘= 40∘
∠ECD is an exterior angle to triangle △CED.
- By the Exterior Angle Property:
∠ BEC = ∠BAC + ∠ECD
140∘=∠BAC+25∘
∠BAC = 140∘−25∘=115∘
Find the value of x in the given figure.
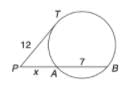
- a)16 cm
- b)7 cm
- c)12 cm
- d)9 cm
Correct answer is option 'D'. Can you explain this answer?
Find the value of x in the given figure.

a)
16 cm
b)
7 cm
c)
12 cm
d)
9 cm

|
Pooja Sen answered |
Isosceles trapezium is always cyclic The sum of opposite angles of a cyclic quadrilateral is 180°
In the given circle, O is the centre and ∠BDC = 42o. Then, ∠ACB is equal to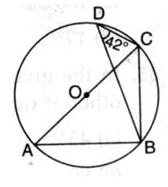
- a)58o
- b)42o
- c)52o
- d)48o
Correct answer is option 'D'. Can you explain this answer?
In the given circle, O is the centre and ∠BDC = 42o. Then, ∠ACB is equal to
a)
58o
b)
42o
c)
52o
d)
48o
|
|
Pooja Shah answered |
In ∆ BDC and ∆ BAC
Angle BAC = BDC
(angle made on same segment BC)
Since ABC is making right angle (90)
So,
In ∆ABC
ABC +BAC+ACB=180
(angle sum property of triangle)
90+42+ACB=180
ACB=180-132
ACB=48o
Angle BAC = BDC
(angle made on same segment BC)
Since ABC is making right angle (90)
So,
In ∆ABC
ABC +BAC+ACB=180
(angle sum property of triangle)
90+42+ACB=180
ACB=180-132
ACB=48o
Read the passage below and solve the questions based on it The area of a square is equal lo the area of a rectangle. Moreover, the perimeter of the square is also equal to the perimeter of the rectangle,Q.The length of the rectangle is equal to the:a)Breadth of the rectangleb)Side of the squarec)Cannot be determinedd)Both [1] and [2]Correct answer is option 'D'. Can you explain this answer?
|
|
Nikita Singh answered |
This is possible only when both the length and breadth of the rectangle are equal to the side of the square.
The radius of a circle which has a 6 cm long chord, 4 cm away from the centre of the circle is- a)9 cm
- b)8 cm
- c)10 cm
- d)5 cm
Correct answer is option 'D'. Can you explain this answer?
The radius of a circle which has a 6 cm long chord, 4 cm away from the centre of the circle is
a)
9 cm
b)
8 cm
c)
10 cm
d)
5 cm
|
|
Zachary Foster answered |
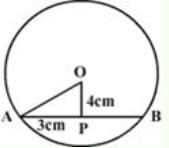
In the right triangle OAP,
OA2 = OP2 +AP2 (By Pythagoras theorem)
OA2 = 42 + 32 (perpendicular from the centre of the circle bisects the chord , AP=3cm)
OA2 = 25
OA = 5
Hence the radius of the circle is 5 cm.
The length of chord which is at a distance of 12 cm from centre of circle of radius 13 cm is:- a)12 cm
- b)13 cm
- c)5 cm
- d)10 cm
Correct answer is option 'D'. Can you explain this answer?
The length of chord which is at a distance of 12 cm from centre of circle of radius 13 cm is:
a)
12 cm
b)
13 cm
c)
5 cm
d)
10 cm
|
|
Rajput Sanjanajamwal San answered |
The drawn right triangle;
Hypotenuse H= Radius of circle =13 cm.
P= perpendicular distance =12 cm, and
′L′ be the length of half-chord
(Note that By the property of Circle, Perpendicular drawn from Centre to Chord Bisects the Chord.)
By Pythagoras theorem, in the drawn right triangle shown in figure,
H2=L2+P2
L=132–122=5 cm
Now, length of the chord is 2.L=10cm
Therefore the length of chord will be 10 cm.
So, option D will be the answer.
Hypotenuse H= Radius of circle =13 cm.
P= perpendicular distance =12 cm, and
′L′ be the length of half-chord
(Note that By the property of Circle, Perpendicular drawn from Centre to Chord Bisects the Chord.)
By Pythagoras theorem, in the drawn right triangle shown in figure,
H2=L2+P2
L=132–122=5 cm
Now, length of the chord is 2.L=10cm
Therefore the length of chord will be 10 cm.
So, option D will be the answer.
Number of circles that can be drawn through three non-collinear points is- a)3
- b)1
- c)2
- d)0
Correct answer is option 'B'. Can you explain this answer?
Number of circles that can be drawn through three non-collinear points is
a)
3
b)
1
c)
2
d)
0
|
|
Aravind Menon answered |
Explanation:
To understand the number of circles that can be drawn through three non-collinear points, let's consider the given points as A, B, and C.
Definition:
A circle can be uniquely defined by three non-collinear points.
Proof:
To prove that only one circle can be drawn through three non-collinear points, we need to show that the center and radius of the circle can be uniquely determined.
Construction:
Let's construct a circle by taking two arbitrary points A and B as the endpoints of the diameter. The center of the circle will lie on the perpendicular bisector of AB.
Case 1:
If the third point C lies on the perpendicular bisector of AB, then the circle is uniquely determined. The center of the circle will be the midpoint of AB, and the radius will be half the distance between A and B.
Case 2:
If the third point C does not lie on the perpendicular bisector of AB, then the circle is not uniquely determined. Two possible circles can be drawn through the three non-collinear points.
Proof of Case 2:
To prove that two circles can be drawn through three non-collinear points, let's consider the following scenario. Assume that the points A, B, and C are not collinear, and the circle with center O and radius r is uniquely determined.
Construction:
Let's construct a line passing through C and perpendicular to AB. This line intersects the perpendicular bisector of AB at a point D.
Case 2.1:
If C lies on the same side of AB as D, then the circle with center O and radius r can be drawn.
Case 2.2:
If C lies on the opposite side of AB as D, then another circle with center O' and radius r can be drawn. The center O' will be the reflection of O with respect to AB.
Therefore, in this case, two circles can be drawn through three non-collinear points.
Conclusion:
In conclusion, the correct answer is option B) 1. Only one circle can be drawn through three non-collinear points.
To understand the number of circles that can be drawn through three non-collinear points, let's consider the given points as A, B, and C.
Definition:
A circle can be uniquely defined by three non-collinear points.
Proof:
To prove that only one circle can be drawn through three non-collinear points, we need to show that the center and radius of the circle can be uniquely determined.
Construction:
Let's construct a circle by taking two arbitrary points A and B as the endpoints of the diameter. The center of the circle will lie on the perpendicular bisector of AB.
Case 1:
If the third point C lies on the perpendicular bisector of AB, then the circle is uniquely determined. The center of the circle will be the midpoint of AB, and the radius will be half the distance between A and B.
Case 2:
If the third point C does not lie on the perpendicular bisector of AB, then the circle is not uniquely determined. Two possible circles can be drawn through the three non-collinear points.
Proof of Case 2:
To prove that two circles can be drawn through three non-collinear points, let's consider the following scenario. Assume that the points A, B, and C are not collinear, and the circle with center O and radius r is uniquely determined.
Construction:
Let's construct a line passing through C and perpendicular to AB. This line intersects the perpendicular bisector of AB at a point D.
Case 2.1:
If C lies on the same side of AB as D, then the circle with center O and radius r can be drawn.
Case 2.2:
If C lies on the opposite side of AB as D, then another circle with center O' and radius r can be drawn. The center O' will be the reflection of O with respect to AB.
Therefore, in this case, two circles can be drawn through three non-collinear points.
Conclusion:
In conclusion, the correct answer is option B) 1. Only one circle can be drawn through three non-collinear points.
In the given figure, ∠M is 75° then ∠O is equal to.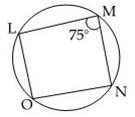
- a)110°
- b)100°
- c)105°
- d)85°
Correct answer is option 'C'. Can you explain this answer?
In the given figure, ∠M is 75° then ∠O is equal to.
a)
110°
b)
100°
c)
105°
d)
85°

|
Ravi Yadav answered |
We know that, sum of all angles of rectangle =360 so, the sum of 2 angles of rectangle = 360\2 = 180 Angle A + Angle B=180 75+B=180 or, B=180-75 or, B=105 degree.
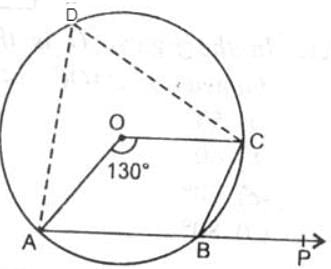
In the given figure, O is the centre of the circle and ∠AOC = 130o. Then ∠ABC is equal to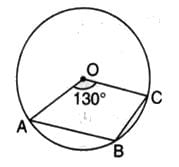
- a)115o
- b)130o
- c)65o
- d)165o
Correct answer is option 'A'. Can you explain this answer?
In the given figure, O is the centre of the circle and ∠AOC = 130o. Then ∠ABC is equal to

a)
115o
b)
130o
c)
65o
d)
165o
|
|
Astha Shukla answered |
Here is the answer
360 degree - 130 degree =230 degree
Therefore, angle ABC =1/2reflex angle AOC
Angle ABC =1/2 230 degree
So, angle ABC =115 degree
Hope it helps you
360 degree - 130 degree =230 degree
Therefore, angle ABC =1/2reflex angle AOC
Angle ABC =1/2 230 degree
So, angle ABC =115 degree
Hope it helps you
Chapter doubts & questions for Circles - Mathematics for JAMB 2025 is part of JAMB exam preparation. The chapters have been prepared according to the JAMB exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JAMB 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Circles - Mathematics for JAMB in English & Hindi are available as part of JAMB exam.
Download more important topics, notes, lectures and mock test series for JAMB Exam by signing up for free.
Mathematics for JAMB
134 videos|94 docs|102 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily