All Exams >
JAMB >
Mathematics for JAMB >
All Questions
All questions of Coordinate Geometry for JAMB Exam
The points A(0, 6), B(-5, 3) and C(3, 1) are the vertices of a triangle which is ? - a)equilateral
- b)right angled
- c)isosceles
- d)scalene
Correct answer is option 'C'. Can you explain this answer?
The points A(0, 6), B(-5, 3) and C(3, 1) are the vertices of a triangle which is ?
a)
equilateral
b)
right angled
c)
isosceles
d)
scalene
|
|
Preeti Khanna answered |
AB2= (-5 - 0)2 + (-3 - 0)2 = 25 + 9 = 34
BC2 = (3 + 5)2 + (1-3)2 = 82 + (-2)2 = 64 + 4 = 68
AC2 = (3 - 0)2 + (1 - 6)2 = 9 + 25 = 34.
AB = AC. ==> ΔABC is isosceles.
BC2 = (3 + 5)2 + (1-3)2 = 82 + (-2)2 = 64 + 4 = 68
AC2 = (3 - 0)2 + (1 - 6)2 = 9 + 25 = 34.
AB = AC. ==> ΔABC is isosceles.
In which quadrant does the point(-7, 6) lie?- a)1st
- b)2nd
- c)3rd
- d)4th
Correct answer is option 'B'. Can you explain this answer?
In which quadrant does the point(-7, 6) lie?
a)
1st
b)
2nd
c)
3rd
d)
4th
|
|
Pillu Singh answered |
Use the short tricl first draw coordinate plane then the answer comes to be B as in 2nd quad x is negative and y is postive
In which quadrant does the point(1, 5) lie? - a)1st
- b)2nd
- c)3rd
- d)4th
Correct answer is option 'A'. Can you explain this answer?
In which quadrant does the point(1, 5) lie?
a)
1st
b)
2nd
c)
3rd
d)
4th

|
Rahul Rn answered |
A quadrant because all value postive in first quadrant.
Distance between two points :If (x1, y1) and B(x2, y2) be two points, then AB = √(x2 - x1)2 + (y2 - y1)2Find the distance between the points A(-4, 7) and B(2, -5). - a)8√5 Units
- b)6√5 Units
- c)6√4 Units
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Distance between two points :
If (x1, y1) and B(x2, y2) be two points, then AB = √(x2 - x1)2 + (y2 - y1)2
Find the distance between the points A(-4, 7) and B(2, -5).
a)
8√5 Units
b)
6√5 Units
c)
6√4 Units
d)
None of these
|
|
Aisha Gupta answered |
AB = √(2+4)2 + (-5-7)2
= √62 + (-12)2
= √36+144 = √180
=√36*5 = 6√5 units.
= √62 + (-12)2
= √36+144 = √180
=√36*5 = 6√5 units.
Area of a triangle : If A(x1,y1), B(x2,y2 and C(x3, y3) be three vertices of a ΔABC, then its area is given by:Δ = 1/2 [x1(y2 - y3 + x2(y3 - y1) + x3(y1 - y2)]Find the area of ΔABC whose vertices are A(9, -5), B(3, 7) and (-2, 4). - a)29 units
- b)35.9 sq.units
- c)39 sq.units
- d) 39.5 sq.units
Correct answer is option 'C'. Can you explain this answer?
Area of a triangle :
If A(x1,y1), B(x2,y2 and C(x3, y3) be three vertices of a ΔABC, then its area is given by:
Δ = 1/2 [x1(y2 - y3 + x2(y3 - y1) + x3(y1 - y2)]
Find the area of ΔABC whose vertices are A(9, -5), B(3, 7) and (-2, 4).
a)
29 units
b)
35.9 sq.units
c)
39 sq.units
d)
39.5 sq.units
|
|
Nikita Singh answered |
Here, x1 = 9, x2 = 3, x3 = -2 and y1 = -5, y2 = 7, y3 = 4
= 1/2 [9(7-4) + 3(4+5) + (-2)(-5-7)]
= 1/2 [9(3) + 3(9) - 2(-12)]
= 1/2 [27 + 27 + 24]
= 1/2 [78]
= 39 sq.units
= 1/2 [9(7-4) + 3(4+5) + (-2)(-5-7)]
= 1/2 [9(3) + 3(9) - 2(-12)]
= 1/2 [27 + 27 + 24]
= 1/2 [78]
= 39 sq.units
The points A(-4, 0), B(1, -4), and C(5, 1) are the vertices of - a)An isosceles right angled triangle
- b)An equilateral triangle
- c)A scalene triangle
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The points A(-4, 0), B(1, -4), and C(5, 1) are the vertices of
a)
An isosceles right angled triangle
b)
An equilateral triangle
c)
A scalene triangle
d)
None of these
|
|
Ravi Singh answered |
AB2 = (1 + 4)2 + (-4 - 0)2
= 25 + 16 = 41,
BC2 = (5 - 1)2 + (1 + 4)2 = 42 + 52
= 16 + 25 = 41
AC2 = (5 + 4)2 + (1 - 0)2
= 81 + 1 = 82
AB = BC and AB2 = BC2 = AC2
ΔABC is an isosceles right angled triangle
= 25 + 16 = 41,
BC2 = (5 - 1)2 + (1 + 4)2 = 42 + 52
= 16 + 25 = 41
AC2 = (5 + 4)2 + (1 - 0)2
= 81 + 1 = 82
AB = BC and AB2 = BC2 = AC2
ΔABC is an isosceles right angled triangle
If the points (2, 3), (4, k) and (6, – 3) are collinear, then the value of ‘k’ is- a)1
- b)0
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
If the points (2, 3), (4, k) and (6, – 3) are collinear, then the value of ‘k’ is
a)
1
b)
0
c)
3
d)
4

|
Anshul Kulkarni answered |
Explanation:
Let the points A (2, 3), B(4,k) and C(6,−3) be collinear.
If the points are collinear then area of triangle ABC formed by these three points is 0.
If the points are collinear then area of triangle ABC formed by these three points is 0.
The abscissa of any point on the x – axis is- a)– 1
- b)0
- c)x
- d)1
Correct answer is option 'C'. Can you explain this answer?
The abscissa of any point on the x – axis is
a)
– 1
b)
0
c)
x
d)
1

|
Shail Jain answered |
Explanation:Since coordinates of any point on x−axis is (x,0).Therefore, abscissa is x.
Find the coordinates of the point equidistant from the points A(1, 2), B (3, –4) and C(5, –6).- a)(2, 3)
- b)(11,2)
- c)(0, 3)
- d) (1, 3)
Correct answer is option 'B'. Can you explain this answer?
Find the coordinates of the point equidistant from the points A(1, 2), B (3, –4) and C(5, –6).
a)
(2, 3)
b)
(11,2)
c)
(0, 3)
d)
(1, 3)
|
|
Ravi Singh answered |
Given three points A(1,2) B(3,-4) and C(5,-6)
we have to find the coordinates of the point equidistant from the points.
The point that is equidistant from three points is called circumcenter which can be evaluated to find the perpendicular bisectors.
To find the perpendicular bisectors of AB:

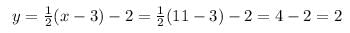
 (11,2)
(11,2)

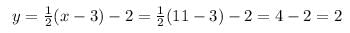
 (11,2)
(11,2)The distance of the point ( – 5, 12) from the y – axis is- a)5 units
- b)12 units
- c)- 5 units
- d)13 units
Correct answer is option 'A'. Can you explain this answer?
The distance of the point ( – 5, 12) from the y – axis is
a)
5 units
b)
12 units
c)
- 5 units
d)
13 units
|
|
Aarav Sharma answered |
Explanation:
To find the distance of a point from the y-axis, we need to measure the perpendicular distance from the point to the y-axis.
Given: Point (5, 12)
Steps to find the distance:
Step 1: Identify the coordinates of the point.
The given point is (5, 12), where 5 represents the x-coordinate and 12 represents the y-coordinate.
Step 2: Draw a line perpendicular to the y-axis passing through the point.
We draw a line from the point (5, 12) perpendicular to the y-axis. Let's call the point where the line intersects the y-axis as P.
Step 3: Measure the distance between the point and the y-axis.
The distance between the point (5, 12) and the y-axis is the length of the line segment formed by the point and point P on the y-axis.
Step 4: Calculate the distance using the Pythagorean theorem.
The distance can be calculated using the Pythagorean theorem, which states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In this case, the distance is the length of the line segment, which is the hypotenuse of a right-angled triangle. The other two sides are the x-coordinate (5) and the y-coordinate (12).
Using the Pythagorean theorem, we can calculate the distance as follows:
Distance = √((5)^2 + (12)^2)
= √(25 + 144)
= √169
= 13
Therefore, the distance of the point (5, 12) from the y-axis is 13 units.
Since none of the given options match the correct answer, it seems there is an error in the options provided. The correct answer should be option 'D' (13 units) instead of option 'A' (5 units).
To find the distance of a point from the y-axis, we need to measure the perpendicular distance from the point to the y-axis.
Given: Point (5, 12)
Steps to find the distance:
Step 1: Identify the coordinates of the point.
The given point is (5, 12), where 5 represents the x-coordinate and 12 represents the y-coordinate.
Step 2: Draw a line perpendicular to the y-axis passing through the point.
We draw a line from the point (5, 12) perpendicular to the y-axis. Let's call the point where the line intersects the y-axis as P.
Step 3: Measure the distance between the point and the y-axis.
The distance between the point (5, 12) and the y-axis is the length of the line segment formed by the point and point P on the y-axis.
Step 4: Calculate the distance using the Pythagorean theorem.
The distance can be calculated using the Pythagorean theorem, which states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In this case, the distance is the length of the line segment, which is the hypotenuse of a right-angled triangle. The other two sides are the x-coordinate (5) and the y-coordinate (12).
Using the Pythagorean theorem, we can calculate the distance as follows:
Distance = √((5)^2 + (12)^2)
= √(25 + 144)
= √169
= 13
Therefore, the distance of the point (5, 12) from the y-axis is 13 units.
Since none of the given options match the correct answer, it seems there is an error in the options provided. The correct answer should be option 'D' (13 units) instead of option 'A' (5 units).
If the vertices of a triangle are (1, 1), ( – 2, 7) and (3, – 3), then its area is- a)2 sq. units
- b)24 sq. units
- c)0 sq. units
- d)12 sq. units
Correct answer is option 'C'. Can you explain this answer?
If the vertices of a triangle are (1, 1), ( – 2, 7) and (3, – 3), then its area is
a)
2 sq. units
b)
24 sq. units
c)
0 sq. units
d)
12 sq. units

|
Aarya Patel answered |
Explanation:
Given: (x1,y1)=(1,1),(x2,y2)=(−2,7) and (x3,y3)=(3,−3)=(3,−3), then the Area of trianlge
Also therefore the three given points(vertices) are collinear
If the end points of a diameter of a circle are ( – 4, – 3) and (2, 7), then the co – ordinates of the centre are- a)( – 1, 2)
- b)(2, – 1)
- c)(0, 0)
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If the end points of a diameter of a circle are ( – 4, – 3) and (2, 7), then the co – ordinates of the centre are
a)
( – 1, 2)
b)
(2, – 1)
c)
(0, 0)
d)
none of these

|
Shail Jain answered |
Explanation:
Let the coordinates of centre O be (x,y). The end points of diameter of the circle are A (- 4, - 3) and B(2, 7).
Since centre is the midpoint of diameter.
Therefore, the coordinates of the centre O is (−1,2).
Distance of a point from the origin:The distance of a point A(x, y) from the origin O(0, 0) is given by OA = √x2 + y2Find the distance of the point A(4, -2) from the origin. - a)4√5 units
- b)2√5 units
- c)5√2 units
- d)7√2 units
Correct answer is option 'B'. Can you explain this answer?
Distance of a point from the origin:
The distance of a point A(x, y) from the origin O(0, 0) is given by OA = √x2 + y2
Find the distance of the point A(4, -2) from the origin.
a)
4√5 units
b)
2√5 units
c)
5√2 units
d)
7√2 units
|
|
Rhea Reddy answered |
OA = √4 - 02+(-2 - 0)2 = √16+4 = √20 = radic;4*5 = 2√5 units
If the co – ordinates of a point are ( – 5, 11), then its abscissa is- a)– 11
- b)5
- c)– 5
- d)11
Correct answer is option 'C'. Can you explain this answer?
If the co – ordinates of a point are ( – 5, 11), then its abscissa is
a)
– 11
b)
5
c)
– 5
d)
11
|
|
Aarav Sharma answered |
Explanation:
In mathematics, the coordinates of a point in a two-dimensional plane are represented by two numbers called the abscissa (x-coordinate) and the ordinate (y-coordinate). The abscissa represents the horizontal position of the point, while the ordinate represents the vertical position.
Given that the coordinates of the point are (5, 11), we can determine the abscissa by looking at the first number in the pair, which is 5.
So, the abscissa of the point is 5.
Key Points:
- The abscissa of a point represents its horizontal position in the coordinate plane.
- The abscissa is determined by the first number in the pair of coordinates.
- In this case, the abscissa of the point with coordinates (5, 11) is 5.
Therefore, the correct answer is option C) 5.
In mathematics, the coordinates of a point in a two-dimensional plane are represented by two numbers called the abscissa (x-coordinate) and the ordinate (y-coordinate). The abscissa represents the horizontal position of the point, while the ordinate represents the vertical position.
Given that the coordinates of the point are (5, 11), we can determine the abscissa by looking at the first number in the pair, which is 5.
So, the abscissa of the point is 5.
Key Points:
- The abscissa of a point represents its horizontal position in the coordinate plane.
- The abscissa is determined by the first number in the pair of coordinates.
- In this case, the abscissa of the point with coordinates (5, 11) is 5.
Therefore, the correct answer is option C) 5.
In which quadrant does the point(9, -2) lie?- a)1st
- b)2nd
- c)3rd
- d)4th
Correct answer is option 'D'. Can you explain this answer?
In which quadrant does the point(9, -2) lie?
a)
1st
b)
2nd
c)
3rd
d)
4th
|
|
Aisha Gupta answered |
The point (9, -2) lies in 4th quadrant.
The co – ordinates of the mid – point of the line joining the points (3p, 4) and ( – 2, 4) are (5, p). The value of ‘p’ is- a)1
- b)2
- c)3
- d)4
Correct answer is option 'D'. Can you explain this answer?
The co – ordinates of the mid – point of the line joining the points (3p, 4) and ( – 2, 4) are (5, p). The value of ‘p’ is
a)
1
b)
2
c)
3
d)
4
|
|
Aarav Sharma answered |
To find the coordinates of the midpoint of a line segment, we use the midpoint formula. The formula for finding the midpoint of a line segment with endpoints (x₁, y₁) and (x₂, y₂) is:
Midpoint = ((x₁ + x₂) / 2, (y₁ + y₂) / 2)
In this case, we are given the coordinates of two points: (3p, 4) and (2, 4). Let's use the midpoint formula to find the coordinates of the midpoint.
- Finding the x-coordinate of the midpoint:
The x-coordinate of the midpoint is given by ((x₁ + x₂) / 2). Plugging in the coordinates, we have:
((3p + 2) / 2) = 5
Simplifying the equation, we get:
3p + 2 = 10
3p = 8
p = 8/3
- Finding the y-coordinate of the midpoint:
The y-coordinate of the midpoint is given by ((y₁ + y₂) / 2). Plugging in the coordinates, we have:
(4 + 4) / 2 = 8 / 2 = 4
So, the y-coordinate of the midpoint is 4.
Therefore, the coordinates of the midpoint are (5, 4p/3).
Since we are given that the y-coordinate of the midpoint is p, we can equate it to 4p/3:
4p/3 = p
Multiplying both sides of the equation by 3, we get:
4p = 3p
p = 0
However, this contradicts with the given information that p is a non-zero value. Therefore, the only possible value for p is 0. Hence, the correct answer is option 'D' (p = 0).
Midpoint = ((x₁ + x₂) / 2, (y₁ + y₂) / 2)
In this case, we are given the coordinates of two points: (3p, 4) and (2, 4). Let's use the midpoint formula to find the coordinates of the midpoint.
- Finding the x-coordinate of the midpoint:
The x-coordinate of the midpoint is given by ((x₁ + x₂) / 2). Plugging in the coordinates, we have:
((3p + 2) / 2) = 5
Simplifying the equation, we get:
3p + 2 = 10
3p = 8
p = 8/3
- Finding the y-coordinate of the midpoint:
The y-coordinate of the midpoint is given by ((y₁ + y₂) / 2). Plugging in the coordinates, we have:
(4 + 4) / 2 = 8 / 2 = 4
So, the y-coordinate of the midpoint is 4.
Therefore, the coordinates of the midpoint are (5, 4p/3).
Since we are given that the y-coordinate of the midpoint is p, we can equate it to 4p/3:
4p/3 = p
Multiplying both sides of the equation by 3, we get:
4p = 3p
p = 0
However, this contradicts with the given information that p is a non-zero value. Therefore, the only possible value for p is 0. Hence, the correct answer is option 'D' (p = 0).
If the mid – point of the line segment joining the points (a, b – 2) and ( – 2, 4) is (2, – 3), then the values of ‘a’ and ‘b’ are- a)6, 8
- b)4, – 5
- c)6, – 8
- d)– 6, 8
Correct answer is option 'C'. Can you explain this answer?
If the mid – point of the line segment joining the points (a, b – 2) and ( – 2, 4) is (2, – 3), then the values of ‘a’ and ‘b’ are
a)
6, 8
b)
4, – 5
c)
6, – 8
d)
– 6, 8

|
Rajeev Rane answered |
Explanation:
Let the coordinates of midpoint O(2,−3) is equidistance from the points A(a,b−2) and B(−2,4).
The distance between the points A(5, -7) and B(2, 3) is:- a) 109
- b)5√7
- c)√109
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The distance between the points A(5, -7) and B(2, 3) is:
a)
109
b)
5√7
c)
√109
d)
None of these
|
|
Rhea Reddy answered |
AB2 = (2 - 5)2 + (3 + 7)2
=> (-3)2 + (10)2
=> 9 + 100 => √109
=> (-3)2 + (10)2
=> 9 + 100 => √109
Find the distance of the point A(3, -3) from the origin. - a)3√2
- b)3√6
- c) 6√2
- d)7√2
Correct answer is option 'A'. Can you explain this answer?
Find the distance of the point A(3, -3) from the origin.
a)
3√2
b)
3√6
c)
6√2
d)
7√2
|
|
Nikita Singh answered |
OA = √32+(-3)2 = √9+9 = √18 = 3√2
The distance of a point from the y – axis is called- a)none of these
- b)abscissa
- c)ordinate
- d)origin
Correct answer is option 'B'. Can you explain this answer?
The distance of a point from the y – axis is called
a)
none of these
b)
abscissa
c)
ordinate
d)
origin

|
Prasad Banerjee answered |
Explanation:
The distance of a point from the y – axis is the x (horizontal) coordinate of the point and is called abscissa.
The co – ordinates of the mid – point of the line segment joining the points ( – 2, 3) and (4, – 5) are- a)( – 1, 1)
- b)(1, – 1)
- c)( – 2, 4)
- d)(0, 0)
Correct answer is option 'B'. Can you explain this answer?
The co – ordinates of the mid – point of the line segment joining the points ( – 2, 3) and (4, – 5) are
a)
( – 1, 1)
b)
(1, – 1)
c)
( – 2, 4)
d)
(0, 0)

|
Milan Nair answered |
Explanation:
Let the coordinates of midpoint C(x,y)(x,y) of the line segment joining the points A(−2,3) and B(4,−5).
If the distance of the point P(x, y) from A(a, 0) is a + x, then y2 = ? - a)8ax
- b)6ax
- c)4ax
- d)2ax
Correct answer is option 'C'. Can you explain this answer?
If the distance of the point P(x, y) from A(a, 0) is a + x, then y2 = ?
a)
8ax
b)
6ax
c)
4ax
d)
2ax
|
|
Sagar Sharma answered |
Concept:
The distance between two points P(x1, y1) and Q(x2, y2) in a plane is given by the formula:
Distance PQ = √((x2 - x1)^2 + (y2 - y1)^2)
Given:
Point A(a, 0) and Point P(x, y) such that the distance between them is a + x.
Calculation:
To find the distance between A and P:
a + x = √((x - a)^2 + y^2)
Squaring both sides:
(a + x)^2 = (x - a)^2 + y^2
a^2 + 2ax + x^2 = x^2 - 2ax + a^2 + y^2
4ax = y^2
Therefore, y^2 = 4ax
Therefore, the correct answer is option C which is 4ax.
The distance between two points P(x1, y1) and Q(x2, y2) in a plane is given by the formula:
Distance PQ = √((x2 - x1)^2 + (y2 - y1)^2)
Given:
Point A(a, 0) and Point P(x, y) such that the distance between them is a + x.
Calculation:
To find the distance between A and P:
a + x = √((x - a)^2 + y^2)
Squaring both sides:
(a + x)^2 = (x - a)^2 + y^2
a^2 + 2ax + x^2 = x^2 - 2ax + a^2 + y^2
4ax = y^2
Therefore, y^2 = 4ax
Therefore, the correct answer is option C which is 4ax.
Find the area of ΔABC whose vertices are A(2, -5), B(4, 9) and (6, -1). - a)9 units
- b)6 sq.units
- c)7 sq.units
- d)24 sq.units
Correct answer is option 'D'. Can you explain this answer?
Find the area of ΔABC whose vertices are A(2, -5), B(4, 9) and (6, -1).
a)
9 units
b)
6 sq.units
c)
7 sq.units
d)
24 sq.units
|
|
Rajeev Kumar answered |
Here, x1 = 2, x2 = 4, x3 = 6 and y1 = -5, y2 = 9, y3 = -1
= 1/2 [2(9+1) + 4(-1+5) + 6(-5-9)]
= 1/2 [2(10) + 4(4) + 6(-14)]
= 1/2 [20 + 16 - 84]
= 1/2 [-48]
= 24 sq.units
= 1/2 [2(9+1) + 4(-1+5) + 6(-5-9)]
= 1/2 [2(10) + 4(4) + 6(-14)]
= 1/2 [20 + 16 - 84]
= 1/2 [-48]
= 24 sq.units
If the point (x, y) is equidistant from the points (5, 1) and ( – 1, 5), then the relation between ‘x’ and ‘y’ is given by- a)3x = 2y
- b)– 2x = 3y
- c)2x = 3y
- d)3x = – 2y
Correct answer is option 'A'. Can you explain this answer?
If the point (x, y) is equidistant from the points (5, 1) and ( – 1, 5), then the relation between ‘x’ and ‘y’ is given by
a)
3x = 2y
b)
– 2x = 3y
c)
2x = 3y
d)
3x = – 2y

|
Anoushka Shah answered |
Explanation:
Let the point C(x,y)is equidistant from the points A (5, 1) and B(−1,5).(−1,5).
i.e. AC = BC
The centroid of a triangle divides the median in the ratio- a)3 : 1
- b)1 : 3
- c)1:2
- d)2 : 1
Correct answer is option 'D'. Can you explain this answer?
The centroid of a triangle divides the median in the ratio
a)
3 : 1
b)
1 : 3
c)
1:2
d)
2 : 1

|
Anoushka Shah answered |
Explanation:
The centroid of a triangle is the centre of the triangle which is the point of intersection of all the three medians of the triangle and divides the median in the ratio 2 : 1The median is a line drawn from the mid-point of a side to the opposite vertix
The distance of a point from the x – axis is called- a)none of these
- b)origin
- c)abscissa
- d)ordinate
Correct answer is option 'D'. Can you explain this answer?
The distance of a point from the x – axis is called
a)
none of these
b)
origin
c)
abscissa
d)
ordinate

|
Aarya Patel answered |
Explanation:The distance of a point from the x – axis is the y (vertical) coordinate of the point and is called ordinate.
Find the value of ‘k’, if the point (0, 2) is equidistant from the points (3, k) and (k, 5)- a)1
- b)– 1
- c)0
- d)2
Correct answer is option 'A'. Can you explain this answer?
Find the value of ‘k’, if the point (0, 2) is equidistant from the points (3, k) and (k, 5)
a)
1
b)
– 1
c)
0
d)
2

|
Anoushka Shah answered |
Explanation:
Let point C (0, 2) is equidistant fromthe points A(3,k) and B(k,5).
If the point P(2, 4) lies on a circle, whose centre is C(5, 8), then the radius of the circle is- a)5 units
- b)25 units
- c)4 units
- d)8 units
Correct answer is option 'A'. Can you explain this answer?
If the point P(2, 4) lies on a circle, whose centre is C(5, 8), then the radius of the circle is
a)
5 units
b)
25 units
c)
4 units
d)
8 units

|
Aarya Patel answered |
Explanation:The point P(2 , 4) is on the circle and C(5, 8) is its centre
Hence PC will be Radius of circle.
The points A( – 1, 0), B(3, 1), C(2, 2) and D( – 2, 1) are the vertices of a- a)Square
- b)Parallelogram
- c)Rhombus
- d)Rectangle
Correct answer is option 'B'. Can you explain this answer?
The points A( – 1, 0), B(3, 1), C(2, 2) and D( – 2, 1) are the vertices of a
a)
Square
b)
Parallelogram
c)
Rhombus
d)
Rectangle
|
|
Sagar Sharma answered |
Given points:
A(1, 0), B(3, 1), C(2, 2), and D(2, 1)
Step 1: Determine the lengths of the sides of the quadrilateral.
To determine the type of quadrilateral formed by these points, we first need to find the lengths of its sides.
Distance formula: The distance between two points (x1, y1) and (x2, y2) is given by the formula:
d = √((x2 - x1)^2 + (y2 - y1)^2)
Using this formula, we can find the lengths of the sides:
AB = √((3 - 1)^2 + (1 - 0)^2) = √(2^2 + 1^2) = √5
BC = √((2 - 3)^2 + (2 - 1)^2) = √((-1)^2 + 1^2) = √2
CD = √((2 - 2)^2 + (1 - 2)^2) = √(0^2 + (-1)^2) = 1
DA = √((1 - 2)^2 + (0 - 1)^2) = √((-1)^2 + (-1)^2) = √2
Step 2: Compare the lengths of the sides.
Since the lengths of all the sides are different, the quadrilateral cannot be a square or a rhombus.
Step 3: Determine if the opposite sides are parallel.
To determine if the opposite sides are parallel, we calculate the slope of each side.
Slope formula: The slope of a line passing through two points (x1, y1) and (x2, y2) is given by the formula:
m = (y2 - y1) / (x2 - x1)
Using this formula, we can find the slopes of the sides:
AB: m = (1 - 0) / (3 - 1) = 1/2
BC: m = (2 - 1) / (2 - 3) = 1/-1 = -1
CD: m = (1 - 2) / (2 - 2) = -1/0 (undefined)
DA: m = (0 - 1) / (1 - 2) = -1/-1 = 1
Since the slopes of AB and CD are equal (1/2 = 1/2) and the slopes of BC and DA are equal (-1 = -1), the opposite sides AB and CD, as well as BC and DA, are parallel.
Conclusion:
Based on the information obtained, the quadrilateral formed by the points A(1, 0), B(3, 1), C(2, 2), and D(2, 1) is a parallelogram because its opposite sides are parallel.
A(1, 0), B(3, 1), C(2, 2), and D(2, 1)
Step 1: Determine the lengths of the sides of the quadrilateral.
To determine the type of quadrilateral formed by these points, we first need to find the lengths of its sides.
Distance formula: The distance between two points (x1, y1) and (x2, y2) is given by the formula:
d = √((x2 - x1)^2 + (y2 - y1)^2)
Using this formula, we can find the lengths of the sides:
AB = √((3 - 1)^2 + (1 - 0)^2) = √(2^2 + 1^2) = √5
BC = √((2 - 3)^2 + (2 - 1)^2) = √((-1)^2 + 1^2) = √2
CD = √((2 - 2)^2 + (1 - 2)^2) = √(0^2 + (-1)^2) = 1
DA = √((1 - 2)^2 + (0 - 1)^2) = √((-1)^2 + (-1)^2) = √2
Step 2: Compare the lengths of the sides.
Since the lengths of all the sides are different, the quadrilateral cannot be a square or a rhombus.
Step 3: Determine if the opposite sides are parallel.
To determine if the opposite sides are parallel, we calculate the slope of each side.
Slope formula: The slope of a line passing through two points (x1, y1) and (x2, y2) is given by the formula:
m = (y2 - y1) / (x2 - x1)
Using this formula, we can find the slopes of the sides:
AB: m = (1 - 0) / (3 - 1) = 1/2
BC: m = (2 - 1) / (2 - 3) = 1/-1 = -1
CD: m = (1 - 2) / (2 - 2) = -1/0 (undefined)
DA: m = (0 - 1) / (1 - 2) = -1/-1 = 1
Since the slopes of AB and CD are equal (1/2 = 1/2) and the slopes of BC and DA are equal (-1 = -1), the opposite sides AB and CD, as well as BC and DA, are parallel.
Conclusion:
Based on the information obtained, the quadrilateral formed by the points A(1, 0), B(3, 1), C(2, 2), and D(2, 1) is a parallelogram because its opposite sides are parallel.
If one end of a diameter of a circle is (4, 6) and the centre is ( – 4, 7), then the other end is- a)(8, – 12)
- b)(8, – 6)
- c)( – 12, 8)
- d)(8, 10)
Correct answer is option 'C'. Can you explain this answer?
If one end of a diameter of a circle is (4, 6) and the centre is ( – 4, 7), then the other end is
a)
(8, – 12)
b)
(8, – 6)
c)
( – 12, 8)
d)
(8, 10)

|
Shail Jain answered |
Explanation:
one end of a diameter is A(4 , 6) and the centre is O ( - 4 , 7) .... ( Given)
Let the other end be B (x,y)
Since centre is the mid-point of diameter of the circle.
Since centre is the mid-point of diameter of the circle.
therefore coordinates of centre O are x = (4 + x) / 2
Therefore, the required coordinates of other end of the diameter are (−12,8).
The distance between the points A(b, 0) and B(0, a) is. - a)√a2-b2
- b)√a2+b2
- c)√a+b
- d)a-b
Correct answer is option 'B'. Can you explain this answer?
The distance between the points A(b, 0) and B(0, a) is.
a)
√a2-b2
b)
√a2+b2
c)
√a+b
d)
a-b

|
Bank Exams India answered |
AB = √(b-0)2-(0-a)2
= √b2+a2
= √a2+b2.
= √b2+a2
= √a2+b2.
The point where the medians of a triangle meet is called the ________ of the triangle- a)none of these
- b)centroid
- c)circumcentre
- d)orthocentre
Correct answer is option 'B'. Can you explain this answer?
The point where the medians of a triangle meet is called the ________ of the triangle
a)
none of these
b)
centroid
c)
circumcentre
d)
orthocentre

|
Milan Nair answered |
Explanation:
The point where three medians of a triangle meet is called the centroid of the triangle.it is the centre of gravity of the triangle. it divides the median in the ratio 2 :1
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is- a)15 units
- b)12 units
- c)9 units
- d)10 units
Correct answer is option 'B'. Can you explain this answer?
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is
a)
15 units
b)
12 units
c)
9 units
d)
10 units

|
Pranavi Dey answered |
Explanation:
Given: the vertices of a triangle ABC, A(0, 4), B (0, 0) and C (3, 0).
∴ Perimeter of triangle ABC = AB + BC + AC
∴ Perimeter of triangle ABC = AB + BC + AC
The point of intersection of the x – axis and y – axis is called- a)quardant
- b)ordinate
- c)abscissa
- d)origin
Correct answer is option 'D'. Can you explain this answer?
The point of intersection of the x – axis and y – axis is called
a)
quardant
b)
ordinate
c)
abscissa
d)
origin

|
Anshul Kulkarni answered |
Explanation:The point of intersection of the x – axis and y – axis is called origin.The coordinates of origin are (0, 0).
The points A(4, – 1), B(6, 0), C(7, 2) and D(5, 1) are the vertices of a- a)Rectangle
- b)Parallelogram
- c)Rhombus
- d)Square
Correct answer is option 'C'. Can you explain this answer?
The points A(4, – 1), B(6, 0), C(7, 2) and D(5, 1) are the vertices of a
a)
Rectangle
b)
Parallelogram
c)
Rhombus
d)
Square

|
Avantika Basu answered |
Therefore diagonals AC and BD are not equal
Since, all sides are equal and both diagonals are not equal.
Therefore, the given quadrilateral is a rhombus.
Since, all sides are equal and both diagonals are not equal.
Therefore, the given quadrilateral is a rhombus.
If one end of a diameter of a circle is (2, 3) and the centre is ( – 2, 5), then the other end is- a)( – 6, 7)
- b)(0, 8)
- c)(0, 4)
- d)(6, – 7)
Correct answer is option 'A'. Can you explain this answer?
If one end of a diameter of a circle is (2, 3) and the centre is ( – 2, 5), then the other end is
a)
( – 6, 7)
b)
(0, 8)
c)
(0, 4)
d)
(6, – 7)

|
Rajeev Rane answered |
Explanation:
Let the coordinates of the other end be B(x2,y2).
One end of the diameter is A (2, 3) and the centre is O(−2,5).
Since the centre is midpoint of the diameter of the circle.
Since the centre is midpoint of the diameter of the circle.
Therefore, the coordinates of other end of the diameter are (−6,7).
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for "Coordinate Geometry" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations. Q. We divided the plane of the paper into four equal parts. by drawing two mutually perpendicular lines, X'OX and YOY'. These lines are called the axes. Here X'OX is called x-axis and YOY' is called y-axis. There axes divide the plane of the paper into four parts, called quadrants.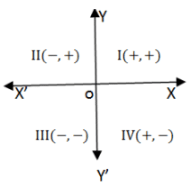 The position of a point in a plane is denoted by an ordered pair (a,b), where a is called the x co-ordinate and y is called y co-ordinate.
The position of a point in a plane is denoted by an ordered pair (a,b), where a is called the x co-ordinate and y is called y co-ordinate. In which quadrant does the point(-4, -7) lie?
In which quadrant does the point(-4, -7) lie? - a)1st
- b)2nd
- c)3rd
- d)4th
Correct answer is option 'C'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for "Coordinate Geometry" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
Q.
We divided the plane of the paper into four equal parts. by drawing two mutually perpendicular lines, X'OX and YOY'. These lines are called the axes. Here X'OX is called x-axis and YOY' is called y-axis. There axes divide the plane of the paper into four parts, called quadrants.
The position of a point in a plane is denoted by an ordered pair (a,b), where a is called the x co-ordinate and y is called y co-ordinate.
In which quadrant does the point(-4, -7) lie?
a)
1st
b)
2nd
c)
3rd
d)
4th
|
|
Ravi Singh answered |
The point (-4, -7) lies in 3rd quadrant.
The abscissa of any point on the y – axis is- a)0
- b)y
- c)– 1
- d)1
Correct answer is option 'A'. Can you explain this answer?
The abscissa of any point on the y – axis is
a)
0
b)
y
c)
– 1
d)
1

|
Rajeev Rane answered |
Explanation:Since coordinates of any point on y−axis is (0,y).Therefore, abscissa is 0.
(0, 3), (4, 0) and ( – 4, 0) are the vertices of- a)a right triangle
- b)a scalene triangle
- c)an isosceles triangle
- d)an equilateral triangle
Correct answer is option 'C'. Can you explain this answer?
(0, 3), (4, 0) and ( – 4, 0) are the vertices of
a)
a right triangle
b)
a scalene triangle
c)
an isosceles triangle
d)
an equilateral triangle

|
Prasad Banerjee answered |
Since, two sides are equal, therefore, ABC is an isosceles triangle.
Chapter doubts & questions for Coordinate Geometry - Mathematics for JAMB 2025 is part of JAMB exam preparation. The chapters have been prepared according to the JAMB exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JAMB 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Coordinate Geometry - Mathematics for JAMB in English & Hindi are available as part of JAMB exam.
Download more important topics, notes, lectures and mock test series for JAMB Exam by signing up for free.
Mathematics for JAMB
134 videos|94 docs|102 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily










