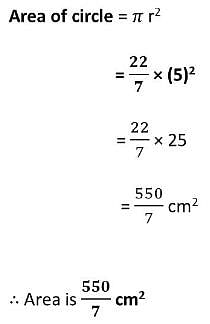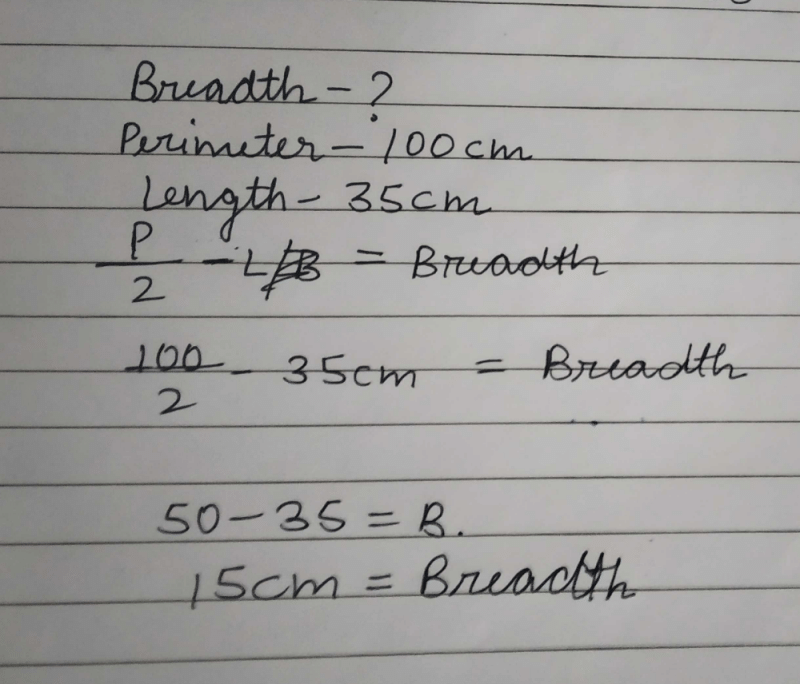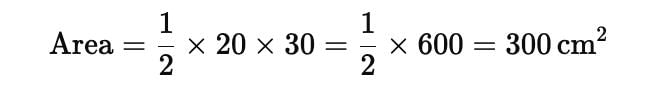All Exams >
Grade 7 >
Mathematics for Grade 7 >
All Questions
All questions of Mensuration for Grade 7 Exam
The base in the area of parallelogram is- a)area / height
- b)area × base
- c)area / base
- d)area × height
Correct answer is option 'A'. Can you explain this answer?
The base in the area of parallelogram is
a)
area / height
b)
area × base
c)
area / base
d)
area × height
|
|
Ananya Das answered |
Since area of parallelogram is base × height
So to find Base of parallelogram the formula is = Area of parallelogram / Height
So option A is the correct answer.
The height in the area of parallelogram is- a)area / base
- b)area / height
- c)area × base
- d)area × height
Correct answer is option 'A'. Can you explain this answer?
The height in the area of parallelogram is
a)
area / base
b)
area / height
c)
area × base
d)
area × height
|
|
Avantika Desai answered |
Since Area of parallelogram is base × height
So Height = Area of parallelogram / Base
So option A is the correct answer.
If the area of a circle is 2464 m2, find its diameter,
- a)56m
- b)154m
- c)176m
- d)206m
Correct answer is option 'A'. Can you explain this answer?
If the area of a circle is 2464 m2, find its diameter,
a)
56m
b)
154m
c)
176m
d)
206m

|
Sharmila Chakraborty answered |
πd2/4 = 2464
22/7xd2=2464x4
d2=2464x4x7
22
⇒ d =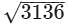 = 56m
= 56m
22/7xd2=2464x4
d2=2464x4x7
22
⇒ d =
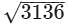 = 56m
= 56mIf the ratio of circumferences of two circles is 4:9, what is the ratio of their areas?
- a)9:4
- b)16:81
- c)4:9
- d)2:3
Correct answer is option 'B'. Can you explain this answer?
If the ratio of circumferences of two circles is 4:9, what is the ratio of their areas?
a)
9:4
b)
16:81
c)
4:9
d)
2:3

|
Shiksha Academy answered |
2πr1/2πr2 = 4/9
r1/r2 = 4/9
πr12/πr22 = r12/r22 = 16/81
r1/r2 = 4/9
πr12/πr22 = r12/r22 = 16/81
The length and the breadth of a rectangular piece of land are 400 m and 250 m respectively. What is the cost of the land at Rs. 1000 per square metre?- a)Rs.10 lakhs
- b)Rs.1 crore
- c)Rs.10 crores
- d)Rs.10 thousands
Correct answer is option 'C'. Can you explain this answer?
The length and the breadth of a rectangular piece of land are 400 m and 250 m respectively. What is the cost of the land at Rs. 1000 per square metre?
a)
Rs.10 lakhs
b)
Rs.1 crore
c)
Rs.10 crores
d)
Rs.10 thousands

|
Tanishq Kulkarni answered |
∴ Area = 400 × 250m2
= 100000 m2
Cost of the land per square metre
= Rs.1000
∴ Cost of total land
100000 × Rs.1000 = Rs.10 crores
= 100000 m2
Cost of the land per square metre
= Rs.1000
∴ Cost of total land
100000 × Rs.1000 = Rs.10 crores
Find the perimeter of a triangle with sides 4 cm, 6 cm and 10 cm
- a)20cm
- b)24cm
- c)9cm
- d)18cm
Correct answer is option 'A'. Can you explain this answer?
Find the perimeter of a triangle with sides 4 cm, 6 cm and 10 cm
a)
20cm
b)
24cm
c)
9cm
d)
18cm

|
Jaya Mukherjee answered |
Perimeter = Sum of all the sides
Perimeter of a triangle = a+b+c
Here a = 4cm , b = 6cm , c =10cm
(6+4+5)cm=15cm
So option A is the correct answer.
How many plants (approximately) will be there in a circular bed whose outer edge measures 30 cm allowing 4 cm2 for each plant?- a)18
- b)750
- c)24
- d)120
Correct answer is option 'A'. Can you explain this answer?
How many plants (approximately) will be there in a circular bed whose outer edge measures 30 cm allowing 4 cm2 for each plant?
a)
18
b)
750
c)
24
d)
120

|
Srishti Reddy answered |
Circumference = 30 cm Area
= C2/4π = 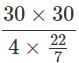 =71.6cm2
=71.6cm2
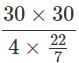 =71.6cm2
=71.6cm2Number of plants = A4 = 71.64 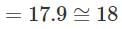
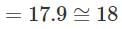
A wire bent in the form of a circle of radius 42 cm is again bent in the form of a square. What is the ratio of the regions enclosed by the circle and the square?- a)11:12
- b)21:33
- c)22:33
- d)14:11
Correct answer is option 'D'. Can you explain this answer?
A wire bent in the form of a circle of radius 42 cm is again bent in the form of a square. What is the ratio of the regions enclosed by the circle and the square?
a)
11:12
b)
21:33
c)
22:33
d)
14:11

|
Prateek Sharma answered |
Length of wire = 2π × 42 = 84πcm
Let x be the side of the square. We have, 4x = 84π ⇒ x = 21π
Area of the circle: Area of the square
= π(42)2:(21π)2
= 4:π = 4:22/7 = 14:11
Let x be the side of the square. We have, 4x = 84π ⇒ x = 21π
Area of the circle: Area of the square
= π(42)2:(21π)2
= 4:π = 4:22/7 = 14:11
A rectangular garden has a length of 12 meters and a width of 8 meters. What is the perimeter of the garden?- a)16 meters
- b)40 meters
- c)18 meters
- d)56 meters
Correct answer is option 'B'. Can you explain this answer?
A rectangular garden has a length of 12 meters and a width of 8 meters. What is the perimeter of the garden?
a)
16 meters
b)
40 meters
c)
18 meters
d)
56 meters

|
Wizius Careers answered |
Perimeter of a rectangle = 2 * (Length + Width)
Given: Length = 12 meters Width = 8 meters
Perimeter = 2 * (12 meters + 8 meters) Perimeter = 2 * (20 meters) Perimeter = 40 meters
So, the perimeter of the garden is 40 meters.
The difference between the circumference and radius of a circle is37 m. What is the circumference of the circle?- a)7m
- b)44m
- c)154m
- d)88m
Correct answer is option 'B'. Can you explain this answer?
The difference between the circumference and radius of a circle is37 m. What is the circumference of the circle?
a)
7m
b)
44m
c)
154m
d)
88m

|
Anmol Iyer answered |
2πr − r = 37
r = 37/2π−1 = 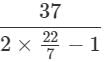 = 7m
= 7m
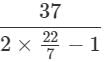 = 7m
= 7mCircumference = 2πr = 2 × 22/7 × 7 = 44m
A door frame of dimensions 4m * 5m is fixed on the wall of dimension 11m * 11m. Find the total labour charges for painting the wall if the labour charges for painting 1m2 of the wall is Rs 2.50.- a)Rs. 252.50
- b)Rs. 300
- c)Rs. 20
- d)Rs. 350
Correct answer is option 'A'. Can you explain this answer?
A door frame of dimensions 4m * 5m is fixed on the wall of dimension 11m * 11m. Find the total labour charges for painting the wall if the labour charges for painting 1m2 of the wall is Rs 2.50.
a)
Rs. 252.50
b)
Rs. 300
c)
Rs. 20
d)
Rs. 350

|
Learning Education answered |
The total area of the wall can be calculated by subtracting the area of the door from the total area of the wall.
The area of the wall is 11×11=121m2.
The area of the door is 4m×5m=20m2.
Therefore, the remaining area to be painted is 1212−202=101m2.
Now, multiply the remaining area by the labor charges per square meter to find the total labor charges:
Total labor charges=Area to be painted×Labor charges per square meter
Total labor charges=101m2×Rs 2.50/m2
Total labor charges=Rs 252.50
So, the total labor charges for painting the wall would be Rs 252.50.
The area of triangle is- a)(1/2) × base × height
- b)(1/2)× (base + height)
- c)base ´ height
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The area of triangle is
a)
(1/2) × base × height
b)
(1/2)× (base + height)
c)
base ´ height
d)
None of these

|
Shraddha Chopra answered |
Area of Triangle Calculation:
To calculate the area of a triangle, you can use the formula:
(1/2) × base × height
This formula is derived by multiplying the base of the triangle by the height of the triangle and then dividing the result by 2. This is because the area of a triangle is always half of the product of its base and height.
Example:
Let's say you have a triangle with a base of 6 units and a height of 4 units.
Using the formula: (1/2) × 6 × 4 = 12 square units.
Therefore, the area of the triangle is 12 square units.
Conclusion:
The correct formula for calculating the area of a triangle is:
(1/2) × base × height
This formula is widely used and accepted for determining the area of a triangle in various mathematical and practical applications.
The ______ is the distance around a given two-dimensional object.- a)perimeter
- b)area
- c)volume
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The ______ is the distance around a given two-dimensional object.
a)
perimeter
b)
area
c)
volume
d)
none of these

|
Ankit Jain answered |
The Concept of Perimeter
The perimeter is a fundamental concept in geometry that refers to the total distance around a two-dimensional shape. Understanding the perimeter is essential for various applications, including architecture, landscaping, and even in banking when calculating land or property boundaries.
Definition of Perimeter
- The perimeter is the sum of all the sides of a polygon.
- For regular shapes like squares and rectangles, specific formulas can be used to calculate the perimeter easily.
How to Calculate Perimeter
- For a rectangle:
- Perimeter = 2 * (length + width)
- For a square:
- Perimeter = 4 * side
- For a triangle:
- Perimeter = side1 + side2 + side3
- For a circle (circumference):
- Perimeter = 2 * π * radius
Importance of Perimeter
- Real-World Applications: Knowing the perimeter helps in planning and design, such as fencing a yard or laying out a garden.
- Measurement Skills: Understanding perimeter reinforces basic mathematical skills and promotes spatial awareness.
- Banking Relevance: In banking, accurate perimeter measurements can influence property valuations and investment decisions.
In summary, the perimeter is the total distance around a two-dimensional object, making option 'A' the correct answer. Understanding this concept is crucial across various fields, emphasizing its practical importance in both daily life and professional contexts.
The perimeter is a fundamental concept in geometry that refers to the total distance around a two-dimensional shape. Understanding the perimeter is essential for various applications, including architecture, landscaping, and even in banking when calculating land or property boundaries.
Definition of Perimeter
- The perimeter is the sum of all the sides of a polygon.
- For regular shapes like squares and rectangles, specific formulas can be used to calculate the perimeter easily.
How to Calculate Perimeter
- For a rectangle:
- Perimeter = 2 * (length + width)
- For a square:
- Perimeter = 4 * side
- For a triangle:
- Perimeter = side1 + side2 + side3
- For a circle (circumference):
- Perimeter = 2 * π * radius
Importance of Perimeter
- Real-World Applications: Knowing the perimeter helps in planning and design, such as fencing a yard or laying out a garden.
- Measurement Skills: Understanding perimeter reinforces basic mathematical skills and promotes spatial awareness.
- Banking Relevance: In banking, accurate perimeter measurements can influence property valuations and investment decisions.
In summary, the perimeter is the total distance around a two-dimensional object, making option 'A' the correct answer. Understanding this concept is crucial across various fields, emphasizing its practical importance in both daily life and professional contexts.
If we cut a square along one of its diagonals, two triangles are obtained. Area of each triangle obtained = __________.- a)(1/2)×Area of the square
- b)(1/4)×Area of the square
- c)Area of the square
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If we cut a square along one of its diagonals, two triangles are obtained. Area of each triangle obtained = __________.
a)
(1/2)×Area of the square
b)
(1/4)×Area of the square
c)
Area of the square
d)
None of these

|
Aspire Academy answered |
The correct answer is A:
When a square is cut along one of its diagonals, it forms two congruent right-angled triangles. Each of these triangles has a base and height equal to one of the sides of the square. The area of a triangle is given by the formula:
Area of a triangle=(1/2)×base×height
In this case, the base and height of each triangle are the sides of the square. Therefore, the area of each triangle is:
Area of each triangle=(1/2)×side×side
Since the side of the square is the length of the diagonal, we can write the area of each triangle as:
Area of each triangle=(1/2)×diagonal×diagonal
So, the correct option is A: (1/2)×Area of the square.
The length and breadth of a rectangular hall in a model are 0.4 m and 30 cmrespectively. What is the distance between the opposite corners of the wall in the model?- a)34.16m
- b)50m
- c)34.16 cm
- d)50cm
Correct answer is option 'D'. Can you explain this answer?
The length and breadth of a rectangular hall in a model are 0.4 m and 30 cmrespectively. What is the distance between the opposite corners of the wall in the model?
a)
34.16m
b)
50m
c)
34.16 cm
d)
50cm
|
|
Dipanjan Mukherjee answered |
Understanding the Problem
To find the distance between the opposite corners of a rectangular hall in a model, we will use the Pythagorean theorem. This theorem states that in a right-angled triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides.
Dimensions of the Hall
- Length: 0.4 m (which is equal to 40 cm since 1 m = 100 cm)
- Breadth: 30 cm
Calculating the Diagonal
To find the distance (diagonal) between opposite corners, we consider the length and breadth as the two sides of a right triangle:
- Hypotenuse (Diagonal) = √(Length² + Breadth²)
Substituting the Values
- Length = 40 cm
- Breadth = 30 cm
Now we can calculate:
- Diagonal = √(40² + 30²)
- Diagonal = √(1600 + 900)
- Diagonal = √2500
- Diagonal = 50 cm
Conclusion
The distance between the opposite corners of the hall in the model is 50 cm.
Thus, the correct answer is option 'D' (50 cm).
To find the distance between the opposite corners of a rectangular hall in a model, we will use the Pythagorean theorem. This theorem states that in a right-angled triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides.
Dimensions of the Hall
- Length: 0.4 m (which is equal to 40 cm since 1 m = 100 cm)
- Breadth: 30 cm
Calculating the Diagonal
To find the distance (diagonal) between opposite corners, we consider the length and breadth as the two sides of a right triangle:
- Hypotenuse (Diagonal) = √(Length² + Breadth²)
Substituting the Values
- Length = 40 cm
- Breadth = 30 cm
Now we can calculate:
- Diagonal = √(40² + 30²)
- Diagonal = √(1600 + 900)
- Diagonal = √2500
- Diagonal = 50 cm
Conclusion
The distance between the opposite corners of the hall in the model is 50 cm.
Thus, the correct answer is option 'D' (50 cm).
If the circumference of a circular sheet is 132 cm. Its radius and area will be _____cm and _____cm2.- a)21,1386
- b)22, 1386
- c)21,1486
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
If the circumference of a circular sheet is 132 cm. Its radius and area will be _____cm and _____cm2.
a)
21,1386
b)
22, 1386
c)
21,1486
d)
None of the above
|
|
Arnav Chatterjee answered |
Understanding Circumference
The circumference (C) of a circle is given by the formula:
C = 2 * π * r
Where:
- C is the circumference.
- r is the radius.
- π (pi) is approximately 3.14.
Given that the circumference of the circular sheet is 132 cm, we can rearrange the formula to find the radius.
Calculating the Radius
- To find the radius (r), we rearrange the formula:
r = C / (2 * π)
- Substituting the given circumference:
r = 132 / (2 * 3.14)
- This simplifies to:
r = 132 / 6.28
- Therefore:
r ≈ 21 cm
Calculating the Area
The area (A) of a circle is calculated with the formula:
A = π * r²
- Now, substituting the radius we found:
A = 3.14 * (21)²
- Calculating the square of the radius:
A = 3.14 * 441
- Thus, the area approximately equals:
A ≈ 1386 cm²
Final Values
- Radius: 21 cm
- Area: 1386 cm²
Correct Answer
The correct option is a) 21, 1386.
The circumference (C) of a circle is given by the formula:
C = 2 * π * r
Where:
- C is the circumference.
- r is the radius.
- π (pi) is approximately 3.14.
Given that the circumference of the circular sheet is 132 cm, we can rearrange the formula to find the radius.
Calculating the Radius
- To find the radius (r), we rearrange the formula:
r = C / (2 * π)
- Substituting the given circumference:
r = 132 / (2 * 3.14)
- This simplifies to:
r = 132 / 6.28
- Therefore:
r ≈ 21 cm
Calculating the Area
The area (A) of a circle is calculated with the formula:
A = π * r²
- Now, substituting the radius we found:
A = 3.14 * (21)²
- Calculating the square of the radius:
A = 3.14 * 441
- Thus, the area approximately equals:
A ≈ 1386 cm²
Final Values
- Radius: 21 cm
- Area: 1386 cm²
Correct Answer
The correct option is a) 21, 1386.
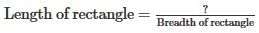
- a)breadth of rectangle
- b)Perimeter of rectangle
- c)Area of rectangle
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
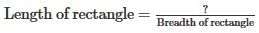
a)
breadth of rectangle
b)
Perimeter of rectangle
c)
Area of rectangle
d)
None of these
|
|
Shreya answered |
Becoz area of rectangle=length×breadth..so,if we have to find length of a rectangle then the equation is Length=Area/breadth (by cross-multiplication).....
Find the area of a triangle with a base of 20 cm and a height of 30 cm- a)300
- b)100
- c)400
- d)600
Correct answer is option 'A'. Can you explain this answer?
Find the area of a triangle with a base of 20 cm and a height of 30 cm
a)
300
b)
100
c)
400
d)
600
|
|
Mythili verma answered |
Understanding the Area of a Triangle
To find the area of a triangle, you can use the formula:
Area = (Base x Height) / 2
In this case, we have:
- Base = 20 cm
- Height = 30 cm
Calculating the Area
1. Insert the values into the formula:
- Area = (20 cm x 30 cm) / 2
2. Multiply the base and height:
- 20 cm x 30 cm = 600 cm²
3. Divide by 2:
- 600 cm² / 2 = 300 cm²
Conclusion
The area of the triangle is 300 cm². This matches option 'A', confirming that the answer is correct.
Key Points
- The area formula for a triangle is straightforward and essential for geometry.
- Always remember to measure the base and height perpendicular to each other.
- This calculation is fundamental in various applications, including construction, design, and real-life problem-solving.
By understanding these basic principles, you can confidently calculate the area of triangles in different scenarios.
To find the area of a triangle, you can use the formula:
Area = (Base x Height) / 2
In this case, we have:
- Base = 20 cm
- Height = 30 cm
Calculating the Area
1. Insert the values into the formula:
- Area = (20 cm x 30 cm) / 2
2. Multiply the base and height:
- 20 cm x 30 cm = 600 cm²
3. Divide by 2:
- 600 cm² / 2 = 300 cm²
Conclusion
The area of the triangle is 300 cm². This matches option 'A', confirming that the answer is correct.
Key Points
- The area formula for a triangle is straightforward and essential for geometry.
- Always remember to measure the base and height perpendicular to each other.
- This calculation is fundamental in various applications, including construction, design, and real-life problem-solving.
By understanding these basic principles, you can confidently calculate the area of triangles in different scenarios.
The circular grass lawn of radius 35 m has a path of width 7 m around it on the outside. What is the area of the path?- a)1496m2
- b)1450m2
- c)1576m2
- d)1694m2
Correct answer is option 'D'. Can you explain this answer?
The circular grass lawn of radius 35 m has a path of width 7 m around it on the outside. What is the area of the path?
a)
1496m2
b)
1450m2
c)
1576m2
d)
1694m2

|
Indu Gupta answered |
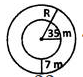
r = 35 m; R = 35+7=42 m
Formula for area of a circle:
Area = πr²
Area of inner circle:
Area = 22/7 × 35²
35² = 1225
Area = 22/7 × 1225 = 22 × 175 = 3850 m²
Area of outer circle:
Area = 22/7 × 42²
42² = 1764
Area = 22/7 × 1764 = 22 × 252 = 5544 m²
Area of path = Area of outer circle -Area of inner circle
Area of path = 5544 − 3850 = 1694m2
Find the area of following traingle: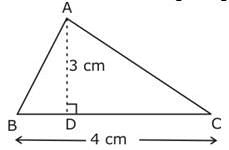
- a)6 cm2
- b)5 cm2
- c)4 cm2
- d)3 cm2
Correct answer is option 'A'. Can you explain this answer?
Find the area of following traingle:

a)
6 cm2
b)
5 cm2
c)
4 cm2
d)
3 cm2
|
|
Rohan Mehta answered |
Area of triangle= ½ *base*height
=½*4*3=6cm2
=½*4*3=6cm2
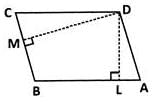
In the given figure, ABCD is a parallelogram. DL⊥AB and DM⊥BC. If AB = 18cm,BC = 12cm and DM = 10cm,find DL
- a)
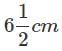
- b)6cm
- c)
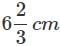
- d)
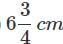
Correct answer is option 'C'. Can you explain this answer?
In the given figure, ABCD is a parallelogram. DL⊥AB and DM⊥BC. If AB = 18cm,BC = 12cm and DM = 10cm,find DL


a)
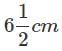
b)
6cm
c)
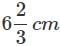
d)
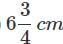

|
Anmol Iyer answered |
Here we equate the areas, i.e., AB×DL = BC×DM
⇒ 18×DL = 12×10
⇒ DL = (12×10)/18 = 20/3 =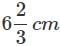
⇒ DL = (12×10)/18 = 20/3 =
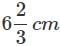
What is the circumference of a circle of diameter 10 cm?- a)35 cm
- b)30 cm
- c)31.4 cm
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
What is the circumference of a circle of diameter 10 cm?
a)
35 cm
b)
30 cm
c)
31.4 cm
d)
None of these

|
Learning Education answered |
use the formula of circumference: 2πr
given: diameter=2r=10cm
so, circumference 2πr=(3.14)10=31.4 cm
A wall hanging is in the shape given in the figure. Find its perimeter. 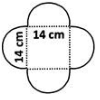
- a)176 cm
- b)146 cm
- c)44cm
- d)88cm
Correct answer is option 'D'. Can you explain this answer?
A wall hanging is in the shape given in the figure. Find its perimeter.

a)
176 cm
b)
146 cm
c)
44cm
d)
88cm

|
Abhay Menon answered |
The perimeter of the wall hanging is given by the sum of circumferences of the 4 semicircles −4 x diameter. Clearly, the diameter of each semicircle is 14 cm. The required perimeter
= 2 × circumference of circle of radius 7 cm.
= 2×2 × 22/7 × 7 = 88cm
In the following figure, ABCD is a parallelogram. DL⊥AB and AB =13 cm = AD . If the area of parallelogram is 156 cm2, find AL. 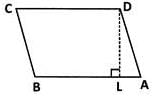
- a)5cm
- b)6cm
- c)7cm
- d)8cm
Correct answer is option 'A'. Can you explain this answer?
In the following figure, ABCD is a parallelogram. DL⊥AB and AB =13 cm = AD . If the area of parallelogram is 156 cm2, find AL.

a)
5cm
b)
6cm
c)
7cm
d)
8cm

|
Abhay Menon answered |
We have, area =156 cm2
⇒ b×h = 156
AB×DL=156
DL = 156/AB =156/13 = 12cm
In right ΔADL, AD2=DL2+LA2
AL2=AD2−DL2=132−122 = 25
∴ AL =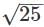 =5cm
=5cm
⇒ b×h = 156
AB×DL=156
DL = 156/AB =156/13 = 12cm
In right ΔADL, AD2=DL2+LA2
AL2=AD2−DL2=132−122 = 25
∴ AL =
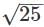 =5cm
=5cmThe height in the area of a triangle- a)(2×area)/base
- b)base/(2×area)
- c)(2×area) / height
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The height in the area of a triangle
a)
(2×area)/base
b)
base/(2×area)
c)
(2×area) / height
d)
None of these

|
Aspire Academy answered |
we know that:
area=(1/2) × base × height
so, height=(2×area)/base
so, height=(2×area)/base
Find the breadth of a rectangular plot of land, if its area is 440 m2 and the length is 22 m.- a)20 m
- b)5 m
- c)15 m
- d)10 m
Correct answer is option 'A'. Can you explain this answer?
Find the breadth of a rectangular plot of land, if its area is 440 m2 and the length is 22 m.
a)
20 m
b)
5 m
c)
15 m
d)
10 m

|
Wizius Careers answered |
The formula for the area of a rectangle is given by:
Area=Length×Breadth
In this case, the area is given as 440 m² and the length is given as 22 m. Let's denote the breadth as B. The formula can be rearranged to solve for the breadth:
Breadth=Area/Length
Substitute the given values:
Breadth=440 m2/22 m
Breadth=20 m
Chapter doubts & questions for Mensuration - Mathematics for Grade 7 2025 is part of Grade 7 exam preparation. The chapters have been prepared according to the Grade 7 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 7 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Mensuration - Mathematics for Grade 7 in English & Hindi are available as part of Grade 7 exam.
Download more important topics, notes, lectures and mock test series for Grade 7 Exam by signing up for free.
Mathematics for Grade 7
93 videos|190 docs|43 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup