All Exams >
Grade 7 >
Mathematics for Grade 7 >
All Questions
All questions of Geometry for Grade 7 Exam
Sum of the lengths of any two sides of a triangle is greater than the length of the ____.- a)first side
- b)second side
- c)third side
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Sum of the lengths of any two sides of a triangle is greater than the length of the ____.
a)
first side
b)
second side
c)
third side
d)
none of these
|
|
Ananya Das answered |
We have Triangle Inequality Theorem which states that the sum of any 2 sides of a triangle must be greater than the measure of the third side. This means that as you know the two sides greater than the third, you know what all sides will not make a triangle.
A/an _____________ connect a vertex of a triangle to the mid-point of the opposite side.- a)altitude
- b)vertex
- c)median
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A/an _____________ connect a vertex of a triangle to the mid-point of the opposite side.
a)
altitude
b)
vertex
c)
median
d)
None of these

|
Dilip Verma answered |
We can say it median as well as altitude because it makes the angle of 90 degree
Can you explain the answer of this question below:Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Practical Geometry, Class 7, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic.
Q.
The ____________ of a triangle is equal in measure to the sum of interior opposite angles.
- A:
interior angle
- B:
exterior angle
- C:
angle
- D:
None of these
The answer is B.
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Practical Geometry, Class 7, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic.
Q.
The ____________ of a triangle is equal in measure to the sum of interior opposite angles.
interior angle
exterior angle
angle
None of these
|
|
Litesh Shankar answered |
Exterior angle
Which among the following is used to construct a triangle?- a)The lengths of the three sides.
- b)The perimeter of the triangle.
- c)The measures of three angles.
- d)The names of three vertices.
Correct answer is option 'A'. Can you explain this answer?
Which among the following is used to construct a triangle?
a)
The lengths of the three sides.
b)
The perimeter of the triangle.
c)
The measures of three angles.
d)
The names of three vertices.

|
Mainak Basu answered |
S.S.S. criterion can be used indirectly to construct a triangle given the lengths of its three sides.
Satish followed the steps given in the box.
Step 1: Construct an angle of 90∘.Step 2: Bisect the 90∘ angle.
Step 3: Bisect one of the angles obtained in step 2.Which steps is not required to construct a 45o angle?.- a) Step 1
- b)Step 2
- c)Step 3
- d)Steps 2 and 3
Correct answer is option 'C'. Can you explain this answer?
Satish followed the steps given in the box.
Step 1: Construct an angle of 90∘.
Step 1: Construct an angle of 90∘.
Step 2: Bisect the 90∘ angle.
Step 3: Bisect one of the angles obtained in step 2.
Step 3: Bisect one of the angles obtained in step 2.
Which steps is not required to construct a 45o angle?.
a)
Step 1
b)
Step 2
c)
Step 3
d)
Steps 2 and 3

|
Deepak Mehra answered |
Following steps 1 and 2, an angle of 45o is constructed. So step 3 is not required.
The total measure of the three angles of a triangle is _____.- a)180°
- b)90°
- c)80°
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The total measure of the three angles of a triangle is _____.
a)
180°
b)
90°
c)
80°
d)
None of these

|
Sanjana Kumar answered |
In a Euclidean space, the sum of measures of these three angles of any triangle is invariably equal to the straight angle, also expressed as 180degree, π radians, two right angles, or a half-turn.
____ of the lengths of any two sides of a triangle is greater than the length of the third side.- a)Product
- b)Difference
- c)sum
- d)None of them
Correct answer is option 'C'. Can you explain this answer?
____ of the lengths of any two sides of a triangle is greater than the length of the third side.
a)
Product
b)
Difference
c)
sum
d)
None of them
|
|
Sameeksha Mangla answered |
Exampleif there is a triangle of sides 3,2 and 4 and if we will add 3 and 2 then it is bigger than 4
Which of the following is used to draw a line parallel to a given line?- a)A protractor
- b)A set square
- c)A ruler
- d)A ruler and compasses
Correct answer is option 'D'. Can you explain this answer?
Which of the following is used to draw a line parallel to a given line?
a)
A protractor
b)
A set square
c)
A ruler
d)
A ruler and compasses

|
Gopal Kumar answered |
A line parallel to a given line can be drawn using a ruler and a compass.
A triangle can be drawn if the hypotenuse and a _____ in the case of a right-angled triangle.- a)base
- b)hypotenuse
- c)leg
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A triangle can be drawn if the hypotenuse and a _____ in the case of a right-angled triangle.
a)
base
b)
hypotenuse
c)
leg
d)
None of these
|
|
Malini bajaj answered |
Explanation:
A right-angled triangle is a triangle in which one of the angles is a right angle (90 degrees). The side opposite to the right angle is called the hypotenuse, and the other two sides are called legs. To draw a triangle, you need at least three sides or two sides and an angle. In the case of a right-angled triangle, if you know the length of the hypotenuse and one leg, you can draw the triangle.
Why option C is correct:
The correct answer is option C, leg. This is because if you know the length of the hypotenuse and one leg, you can use the Pythagorean theorem to find the length of the other leg. The Pythagorean theorem states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides. So, if you know the length of the hypotenuse (c) and one leg (a), you can find the length of the other leg (b) using the following formula:
b = √(c^2 - a^2)
Once you know the length of all three sides, you can draw the triangle.
Example:
Suppose you want to draw a right-angled triangle with a hypotenuse of length 5 units and one leg of length 3 units. To find the length of the other leg, you can use the Pythagorean theorem:
b = √(c^2 - a^2)
b = √(5^2 - 3^2)
b = √(25 - 9)
b = √16
b = 4
So, the length of the other leg is 4 units. Now that you know the length of all three sides, you can draw the triangle.
A right-angled triangle is a triangle in which one of the angles is a right angle (90 degrees). The side opposite to the right angle is called the hypotenuse, and the other two sides are called legs. To draw a triangle, you need at least three sides or two sides and an angle. In the case of a right-angled triangle, if you know the length of the hypotenuse and one leg, you can draw the triangle.
Why option C is correct:
The correct answer is option C, leg. This is because if you know the length of the hypotenuse and one leg, you can use the Pythagorean theorem to find the length of the other leg. The Pythagorean theorem states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides. So, if you know the length of the hypotenuse (c) and one leg (a), you can find the length of the other leg (b) using the following formula:
b = √(c^2 - a^2)
Once you know the length of all three sides, you can draw the triangle.
Example:
Suppose you want to draw a right-angled triangle with a hypotenuse of length 5 units and one leg of length 3 units. To find the length of the other leg, you can use the Pythagorean theorem:
b = √(c^2 - a^2)
b = √(5^2 - 3^2)
b = √(25 - 9)
b = √16
b = 4
So, the length of the other leg is 4 units. Now that you know the length of all three sides, you can draw the triangle.
The total measure of the _____ angles of a triangle is 180°.- a)two
- b)three
- c)one
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The total measure of the _____ angles of a triangle is 180°.
a)
two
b)
three
c)
one
d)
none of these

|
Samarth Satish answered |
3 angles as Angle Sum Property states that all sid... morees of a triangle should be
In which of the following cases is the construction of a triangle not possible?- a)Measures of 3 sides are given.
- b)Measures of 2 sides and an included angle are given.
- c)Measures of 2 angles and a side are given.
- d)Measures of 3 angles are given.
Correct answer is option 'D'. Can you explain this answer?
In which of the following cases is the construction of a triangle not possible?
a)
Measures of 3 sides are given.
b)
Measures of 2 sides and an included angle are given.
c)
Measures of 2 angles and a side are given.
d)
Measures of 3 angles are given.
|
|
Varun Kapoor answered |
Unless and until you know length of one side you cannot tell at what distance the angles have to be drawn.
A triangle in which two sides are of equal lengths is called _______________.- a)equilateral
- b)scalene
- c)isosceles
- d)acute-angled
- e)
Correct answer is option 'C'. Can you explain this answer?
A triangle in which two sides are of equal lengths is called _______________.
a)
equilateral
b)
scalene
c)
isosceles
d)
acute-angled
e)
|
|
Pradyumna Rao answered |
Isosceles triangles are the triangles which two sides are equal and one is different from other. So, the answer is option C.
A simple closed curve made up of only line segments is called a _____.
- a)angle
- b)polygon
- c)quadrilateral
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A simple closed curve made up of only line segments is called a _____.
a)
angle
b)
polygon
c)
quadrilateral
d)
None of these
|
|
Kajol jain answered |
The correct answer is option 'B' - polygon.
A polygon is a simple closed curve made of three or more line segments. It is a two-dimensional shape with straight sides. The word "polygon" comes from the Greek words "poly" meaning "many" and "gonia" meaning "angle." A polygon can have any number of sides, but it must have at least three sides to be considered a polygon.
Properties of a Polygon:
1. Sides: A polygon has straight sides, which are line segments. Each side connects two vertices (corners) of the polygon.
2. Vertices: The corners of a polygon are called vertices. Each vertex is the endpoint of two sides.
3. Interior Angles: The interior angles of a polygon are the angles formed inside the shape. The sum of the interior angles of a polygon with n sides can be calculated using the formula (n-2) * 180 degrees.
4. Exterior Angles: The exterior angles of a polygon are the angles formed outside the shape. The sum of the exterior angles of any polygon is always 360 degrees.
5. Diagonals: Diagonals are line segments that connect any two non-adjacent vertices of a polygon. The number of diagonals in a polygon can be found using the formula n * (n-3) / 2, where n is the number of sides.
6. Convex and Concave: A polygon can be convex or concave. A convex polygon has all interior angles less than 180 degrees, while a concave polygon has at least one interior angle greater than 180 degrees.
Examples of Polygons:
- Triangle: A triangle is a polygon with three sides and three vertices.
- Quadrilateral: A quadrilateral is a polygon with four sides and four vertices.
- Pentagon: A pentagon is a polygon with five sides and five vertices.
- Hexagon: A hexagon is a polygon with six sides and six vertices.
- Octagon: An octagon is a polygon with eight sides and eight vertices.
In conclusion, a polygon is a simple closed curve made of three or more line segments. It is a fundamental concept in geometry and has various properties and classifications based on the number of sides and angles it possesses.
A polygon is a simple closed curve made of three or more line segments. It is a two-dimensional shape with straight sides. The word "polygon" comes from the Greek words "poly" meaning "many" and "gonia" meaning "angle." A polygon can have any number of sides, but it must have at least three sides to be considered a polygon.
Properties of a Polygon:
1. Sides: A polygon has straight sides, which are line segments. Each side connects two vertices (corners) of the polygon.
2. Vertices: The corners of a polygon are called vertices. Each vertex is the endpoint of two sides.
3. Interior Angles: The interior angles of a polygon are the angles formed inside the shape. The sum of the interior angles of a polygon with n sides can be calculated using the formula (n-2) * 180 degrees.
4. Exterior Angles: The exterior angles of a polygon are the angles formed outside the shape. The sum of the exterior angles of any polygon is always 360 degrees.
5. Diagonals: Diagonals are line segments that connect any two non-adjacent vertices of a polygon. The number of diagonals in a polygon can be found using the formula n * (n-3) / 2, where n is the number of sides.
6. Convex and Concave: A polygon can be convex or concave. A convex polygon has all interior angles less than 180 degrees, while a concave polygon has at least one interior angle greater than 180 degrees.
Examples of Polygons:
- Triangle: A triangle is a polygon with three sides and three vertices.
- Quadrilateral: A quadrilateral is a polygon with four sides and four vertices.
- Pentagon: A pentagon is a polygon with five sides and five vertices.
- Hexagon: A hexagon is a polygon with six sides and six vertices.
- Octagon: An octagon is a polygon with eight sides and eight vertices.
In conclusion, a polygon is a simple closed curve made of three or more line segments. It is a fundamental concept in geometry and has various properties and classifications based on the number of sides and angles it possesses.
How many medians a triangle can have?- a)1
- b)3
- c)2
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
How many medians a triangle can have?
a)
1
b)
3
c)
2
d)
None of these

|
Kavya Rane answered |
Three mediansIn geometry, a median of a triangle i... mores a line segment joining a vertex to the midpoint of the opposing
In which of the following cases can a triangle be constructed?- a)Measures of three sides are given.
- b)Measures of two sides and an included angle are given.
- c)Measures of two angles and the side between them are given.
- d)All the above.
Correct answer is option 'D'. Can you explain this answer?
In which of the following cases can a triangle be constructed?
a)
Measures of three sides are given.
b)
Measures of two sides and an included angle are given.
c)
Measures of two angles and the side between them are given.
d)
All the above.
|
|
Ankita sengupta answered |
Introduction:
A triangle is a closed figure with three sides and three angles. In order to construct a triangle, certain conditions must be met. Let's analyze the given options to determine which conditions are sufficient for constructing a triangle.
a) Measures of three sides are given:
If the measures of all three sides of a triangle are given, a triangle can be constructed. This is because the three sides will connect to form a closed figure, satisfying the definition of a triangle. Additionally, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side according to the triangle inequality theorem.
b) Measures of two sides and an included angle are given:
If the measures of two sides and the included angle between them are given, a triangle can also be constructed. This is known as the Side-Angle-Side (SAS) condition. The two given sides can be extended from their common vertex to form the other two sides of the triangle, and the given angle can be placed between these sides. This forms a closed figure, satisfying the definition of a triangle.
c) Measures of two angles and the side between them are given:
If the measures of two angles and the side between them are given, a triangle can be constructed. This is known as the Angle-Side-Angle (ASA) condition. One of the given angles can be placed at a vertex, and the side adjacent to this angle can be drawn. Then, the other given angle can be placed adjacent to the first angle, and the remaining side can be drawn to connect the two angles. This forms a closed figure, satisfying the definition of a triangle.
Conclusion:
From the above analysis, it is evident that a triangle can be constructed in all of the given cases: when the measures of three sides are given, when the measures of two sides and an included angle are given, and when the measures of two angles and the side between them are given. Therefore, the correct answer is option 'D' - all of the above cases allow for the construction of a triangle.
A triangle is a closed figure with three sides and three angles. In order to construct a triangle, certain conditions must be met. Let's analyze the given options to determine which conditions are sufficient for constructing a triangle.
a) Measures of three sides are given:
If the measures of all three sides of a triangle are given, a triangle can be constructed. This is because the three sides will connect to form a closed figure, satisfying the definition of a triangle. Additionally, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side according to the triangle inequality theorem.
b) Measures of two sides and an included angle are given:
If the measures of two sides and the included angle between them are given, a triangle can also be constructed. This is known as the Side-Angle-Side (SAS) condition. The two given sides can be extended from their common vertex to form the other two sides of the triangle, and the given angle can be placed between these sides. This forms a closed figure, satisfying the definition of a triangle.
c) Measures of two angles and the side between them are given:
If the measures of two angles and the side between them are given, a triangle can be constructed. This is known as the Angle-Side-Angle (ASA) condition. One of the given angles can be placed at a vertex, and the side adjacent to this angle can be drawn. Then, the other given angle can be placed adjacent to the first angle, and the remaining side can be drawn to connect the two angles. This forms a closed figure, satisfying the definition of a triangle.
Conclusion:
From the above analysis, it is evident that a triangle can be constructed in all of the given cases: when the measures of three sides are given, when the measures of two sides and an included angle are given, and when the measures of two angles and the side between them are given. Therefore, the correct answer is option 'D' - all of the above cases allow for the construction of a triangle.
The exterior angle of a triangle is ______ in measure to the sum of interior opposite angles.- a)equal
- b)unequal
- c)different
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The exterior angle of a triangle is ______ in measure to the sum of interior opposite angles.
a)
equal
b)
unequal
c)
different
d)
None of these

|
Pooja Banerjee answered |
The perpendicular line segment from a vertex of a ... moretriangle to its opposite side is
A triangle can be drawn if ______ sides given.- a)3
- b)1
- c)2
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
A triangle can be drawn if ______ sides given.
a)
3
b)
1
c)
2
d)
none of these
|
|
Rwishina answered |
A triangle can be drawn if 3 sides given.,
so the correct answer is 'A'.
so the correct answer is 'A'.
ΔPQR is a triangle right-angled at P. If PQ = 3 cm and PR = 4 cm, find QR.- a)3 cm
- b)7 cm
- c)5 cm
- d)8 cm
Correct answer is option 'C'. Can you explain this answer?
ΔPQR is a triangle right-angled at P. If PQ = 3 cm and PR = 4 cm, find QR.
a)
3 cm
b)
7 cm
c)
5 cm
d)
8 cm
|
|
Swati shukla answered |
There are several possible ways to solve this equation. Here are a few methods:
1. Graphing: Plot the graphs of y = 2x and y = -x^2 + 4. The solution(s) will be the x-coordinates of the points where the two graphs intersect.
2. Substitution: Solve one equation for one variable and substitute it into the other equation. For example, solve the first equation for x: x = y/2. Substitute this expression for x into the second equation: y = -(y/2)^2 + 4. Simplify and solve for y. Once you have the value(s) of y, substitute them back into the first equation to find the corresponding x-value(s).
3. Elimination: Multiply the first equation by 2 to make the coefficients of x in both equations the same. This gives us 2x = y. Substitute this expression for y in the second equation: y = -x^2 + 4. Simplify and solve for x. Once you have the value(s) of x, substitute them back into the first equation to find the corresponding y-value(s).
Note that the solutions to this equation may be real numbers, complex numbers, or a combination of both, depending on the specific values of x and y.
1. Graphing: Plot the graphs of y = 2x and y = -x^2 + 4. The solution(s) will be the x-coordinates of the points where the two graphs intersect.
2. Substitution: Solve one equation for one variable and substitute it into the other equation. For example, solve the first equation for x: x = y/2. Substitute this expression for x into the second equation: y = -(y/2)^2 + 4. Simplify and solve for y. Once you have the value(s) of y, substitute them back into the first equation to find the corresponding x-value(s).
3. Elimination: Multiply the first equation by 2 to make the coefficients of x in both equations the same. This gives us 2x = y. Substitute this expression for y in the second equation: y = -x^2 + 4. Simplify and solve for x. Once you have the value(s) of x, substitute them back into the first equation to find the corresponding y-value(s).
Note that the solutions to this equation may be real numbers, complex numbers, or a combination of both, depending on the specific values of x and y.
ΔABC is right-angled at C. If AC = 5 cm and BC = 12 cm find the length of AB.- a)17 cm
- b)7 cm
- c)13 cm
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
ΔABC is right-angled at C. If AC = 5 cm and BC = 12 cm find the length of AB.
a)
17 cm
b)
7 cm
c)
13 cm
d)
None of these

|
Anand Choudhury answered |
Given that AC=12cm and BC=5cm,
We can find out the value of AB by using Pythagoras theorum,
that is AB^2=BC^2+AC^2
AB^2=12^2+5^2
AB^2=144+25
AB^2=169
AB=√169
AB=13cm
How many parallel lines can be drawn passing through a point not on the given line?- a)2
- b)1
- c)3
- d)0
Correct answer is option 'B'. Can you explain this answer?
How many parallel lines can be drawn passing through a point not on the given line?
a)
2
b)
1
c)
3
d)
0

|
Jaya Mukherjee answered |
Through a given point, an infinite number of lines can be drawn. But only one of them will be parallel to the given line.
A triangular sign board is isosceles. If the unequal side is 7 cm and one of the equal sides is 6 cm, what is the measure of the third side?- a) 5cm
- b) 6cm
- c) 7cm
- d) Either [a] or [c]
Correct answer is option 'B'. Can you explain this answer?
A triangular sign board is isosceles. If the unequal side is 7 cm and one of the equal sides is 6 cm, what is the measure of the third side?
a)
5cm
b)
6cm
c)
7cm
d)
Either [a] or [c]
|
|
Mansi Yadav answered |
An isosceles triangle is a triangle with (at least) two equal sides. thus the third side is 6cm.
In ΔXYZ, x, y and z denote the three sides. Which of the following is incorrect'?
- a)x−y<z
- b)x+z<y
- c)x−y>z
- d)x+y<z
Correct answer is option 'A'. Can you explain this answer?
In ΔXYZ, x, y and z denote the three sides. Which of the following is incorrect'?
a)
x−y<z
b)
x+z<y
c)
x−y>z
d)
x+y<z

|
Tanishq Kulkarni answered |
The difference of two sides of a triangle is less than its third side.
Based on the sides of a triangle, which of the following is a classification of triangles?- a)A right angled triangle
- b)An acute angled triangle
- c)An obtuse angled triangle
- d)An isosceles triangle
Correct answer is option 'D'. Can you explain this answer?
Based on the sides of a triangle, which of the following is a classification of triangles?
a)
A right angled triangle
b)
An acute angled triangle
c)
An obtuse angled triangle
d)
An isosceles triangle
|
|
Ashwin Shah answered |
**Answer:**
To classify a triangle based on its sides, we need to consider the lengths of the sides. The different classifications of triangles based on their sides are:
a) Right-angled Triangle: In a right-angled triangle, one of the angles is a right angle, which measures 90 degrees. The sides opposite the right angle are called the legs, and the side opposite the right angle is called the hypotenuse.
b) Acute-angled Triangle: In an acute-angled triangle, all three angles are acute angles, which means they are less than 90 degrees.
c) Obtuse-angled Triangle: In an obtuse-angled triangle, one of the angles is an obtuse angle, which measures greater than 90 degrees but less than 180 degrees.
d) Isosceles Triangle: In an isosceles triangle, at least two sides have the same length. The angles opposite the equal sides are also equal.
Based on the given classifications, option 'D' - An isosceles triangle is the correct answer because it is the only option that classifies a triangle based on its sides. The other options describe the types of angles in a triangle, not the sides.
Additional Information:
- Equilateral Triangle: In an equilateral triangle, all three sides are equal in length, and all three angles are equal, measuring 60 degrees.
- Scalene Triangle: In a scalene triangle, all three sides have different lengths, and all three angles are different.
To classify a triangle based on its sides, we need to consider the lengths of the sides. The different classifications of triangles based on their sides are:
a) Right-angled Triangle: In a right-angled triangle, one of the angles is a right angle, which measures 90 degrees. The sides opposite the right angle are called the legs, and the side opposite the right angle is called the hypotenuse.
b) Acute-angled Triangle: In an acute-angled triangle, all three angles are acute angles, which means they are less than 90 degrees.
c) Obtuse-angled Triangle: In an obtuse-angled triangle, one of the angles is an obtuse angle, which measures greater than 90 degrees but less than 180 degrees.
d) Isosceles Triangle: In an isosceles triangle, at least two sides have the same length. The angles opposite the equal sides are also equal.
Based on the given classifications, option 'D' - An isosceles triangle is the correct answer because it is the only option that classifies a triangle based on its sides. The other options describe the types of angles in a triangle, not the sides.
Additional Information:
- Equilateral Triangle: In an equilateral triangle, all three sides are equal in length, and all three angles are equal, measuring 60 degrees.
- Scalene Triangle: In a scalene triangle, all three sides have different lengths, and all three angles are different.
The sum of the lengths of any two sides of a triangle is _____________ the third side of the triangle.- a)less than
- b)doubled
- c)greater than
- d)half
Correct answer is option 'C'. Can you explain this answer?
The sum of the lengths of any two sides of a triangle is _____________ the third side of the triangle.
a)
less than
b)
doubled
c)
greater than
d)
half
|
|
Shadow 😇🤍 answered |
The sum of the lengths of any two sides of a triangle is greater than the length of the third side. C is correct
Which of the following statements is incorrect?- a)The sum of angles in a triangle is 2 right angles.
- b)The exterior angle of a triangle is equal to the interior angle of the triangle.
- c)The hypotenuse is the longest side of a right angled triangle.
- d)All the above.
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is incorrect?
a)
The sum of angles in a triangle is 2 right angles.
b)
The exterior angle of a triangle is equal to the interior angle of the triangle.
c)
The hypotenuse is the longest side of a right angled triangle.
d)
All the above.
|
|
Shehnaz Menon answered |
**Incorrect Statement: The exterior angle of a triangle is equal to the interior angle of the triangle.**
**Explanation:**
To understand why this statement is incorrect, let's first define what an exterior angle and an interior angle of a triangle are.
- **Exterior Angle:** An exterior angle of a triangle is formed by extending one of the sides of the triangle.
- **Interior Angle:** An interior angle of a triangle is an angle formed by two sides of the triangle.
Now, let's examine the given statement and determine its correctness.
**a) The sum of angles in a triangle is 2 right angles:**
This statement is correct. The sum of all three angles in a triangle is always equal to 180 degrees, which is equivalent to 2 right angles (90 degrees each).
**b) The exterior angle of a triangle is equal to the interior angle of the triangle:**
This statement is incorrect. The exterior angle of a triangle is always greater than any of its interior angles. In fact, the exterior angle is equal to the sum of the two opposite interior angles of the triangle. This is known as the Exterior Angle Theorem.
**c) The hypotenuse is the longest side of a right-angled triangle:**
This statement is correct. In a right-angled triangle, the hypotenuse is the side opposite the right angle. It is the longest side of the triangle and is always opposite the largest angle.
Based on the analysis above, we can conclude that option 'B' is the incorrect statement. The exterior angle of a triangle is not equal to the interior angle of the triangle.
**Explanation:**
To understand why this statement is incorrect, let's first define what an exterior angle and an interior angle of a triangle are.
- **Exterior Angle:** An exterior angle of a triangle is formed by extending one of the sides of the triangle.
- **Interior Angle:** An interior angle of a triangle is an angle formed by two sides of the triangle.
Now, let's examine the given statement and determine its correctness.
**a) The sum of angles in a triangle is 2 right angles:**
This statement is correct. The sum of all three angles in a triangle is always equal to 180 degrees, which is equivalent to 2 right angles (90 degrees each).
**b) The exterior angle of a triangle is equal to the interior angle of the triangle:**
This statement is incorrect. The exterior angle of a triangle is always greater than any of its interior angles. In fact, the exterior angle is equal to the sum of the two opposite interior angles of the triangle. This is known as the Exterior Angle Theorem.
**c) The hypotenuse is the longest side of a right-angled triangle:**
This statement is correct. In a right-angled triangle, the hypotenuse is the side opposite the right angle. It is the longest side of the triangle and is always opposite the largest angle.
Based on the analysis above, we can conclude that option 'B' is the incorrect statement. The exterior angle of a triangle is not equal to the interior angle of the triangle.
In any right-angled triangle, the square of the length of hypotenuse is equal to the ____ of the squares of the lengths of the other two sides.- a)product
- b)sum
- c)diffrence
- d)quotient
Correct answer is option 'B'. Can you explain this answer?
In any right-angled triangle, the square of the length of hypotenuse is equal to the ____ of the squares of the lengths of the other two sides.
a)
product
b)
sum
c)
diffrence
d)
quotient

|
Shabnam Shabnam answered |
In any right-angled triangle, the square of the length of hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
For example a right angled triangle is there with sides 3,4 and 5 cm. 5 cm is the hypotenuse and 3 and 4 cm are the legs.
So, 3 cm=9 square cm
4cm= 16 square cm
5 cm= 25 square cm
9 square cm + 16 square cm = 25 square cm
Hence, it is a right angled triangle and the sum of the sqares of the two sides of the triangle other than hypotenuse is equal to square of hypotenuse.
For example a right angled triangle is there with sides 3,4 and 5 cm. 5 cm is the hypotenuse and 3 and 4 cm are the legs.
So, 3 cm=9 square cm
4cm= 16 square cm
5 cm= 25 square cm
9 square cm + 16 square cm = 25 square cm
Hence, it is a right angled triangle and the sum of the sqares of the two sides of the triangle other than hypotenuse is equal to square of hypotenuse.
Direction: David folds a sheet of paper. The dotted lines as shown in the figure are the creases formed, which are named as l, m and n. 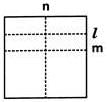 What can you say about lines I and n?
What can you say about lines I and n?- a)l//n
- b)l⊥n
- c)I is the same line as n
- d)Neither [a] nor [b]
Correct answer is option 'B'. Can you explain this answer?
Direction: David folds a sheet of paper. The dotted lines as shown in the figure are the creases formed, which are named as l, m and n.  What can you say about lines I and n?
What can you say about lines I and n?
 What can you say about lines I and n?
What can you say about lines I and n?a)
l//n
b)
l⊥n
c)
I is the same line as n
d)
Neither [a] nor [b]

|
Krish Desai answered |
A 90o angle is formed at the intersection of l and n. So l⊥n
Which is the longest side in the triangle PQR right angled at P?- a)PR
- b)PQ
- c)QR
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Which is the longest side in the triangle PQR right angled at P?
a)
PR
b)
PQ
c)
QR
d)
None of these
|
|
Rajat Singh answered |
The side opposite to greater angle is greater, and in a right angled triangle, the right angle is the largest angle. So side opposite to it is the largest and known as hypotenuse. In our question, since right angle is at P so the side opposite to it will be QR.
Identify the true statement.- a) A triangle with 3 equal sides is isosceles.
- b) A triangle with a 110o angle is right angled.
- c) A triangle with 3 acute angles is acute angled.
- d) A triangle with 2 equal sides is equilateral.
Correct answer is option 'C'. Can you explain this answer?
Identify the true statement.
a)
A triangle with 3 equal sides is isosceles.
b)
A triangle with a 110o angle is right angled.
c)
A triangle with 3 acute angles is acute angled.
d)
A triangle with 2 equal sides is equilateral.
|
|
Mansi Yadav answered |
C is correct
Which of the following can be used to construct a 30o angle?- a)Construct a 60o angle using compasses and bisect it.
- b)Construct a perpendicular bisector of a line segment.
- c)Construct the bisector of any angle.
- d)Construct an angle congruent to any given angle.
Correct answer is option 'A'. Can you explain this answer?
Which of the following can be used to construct a 30o angle?
a)
Construct a 60o angle using compasses and bisect it.
b)
Construct a perpendicular bisector of a line segment.
c)
Construct the bisector of any angle.
d)
Construct an angle congruent to any given angle.

|
Saikat Chawla answered |
Bisecting a 60o angle results in a 30o angle.
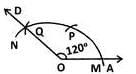
In the given figure, find the measure of ∠ROT, if PQ=QR and ∠QPR=60o.
 .
.- a)60o
- b)140o
- c)120o
- d)100o
Correct answer is option 'C'. Can you explain this answer?
In the given figure, find the measure of ∠ROT, if PQ=QR and ∠QPR=60o.


.
a)
60o
b)
140o
c)
120o
d)
100o

|
Abhiram Kulkarni answered |
ΔPQR is isosceles since PQ=QR. ∴ ∠QPR=∠QRP=60o. ∠RQT is the exterior angle of ΔPQR which is equal to the sum of interior opposite angles ∠P and ∠R . Hence, ∠RQT=60o+60o=120o.
Which type of triangle is in the classification based on angles?- a)An equilateral triangle
- b)An isosceles triangle
- c)A right angled triangle
- d)A scalene triangle
Correct answer is option 'C'. Can you explain this answer?
Which type of triangle is in the classification based on angles?
a)
An equilateral triangle
b)
An isosceles triangle
c)
A right angled triangle
d)
A scalene triangle
|
|
Shambavi bajaj answered |
Right Angled Triangle
A right-angled triangle is a type of triangle that is classified based on angles. In a right-angled triangle, one of the angles measures 90 degrees. This special angle is called the right angle and is formed by the intersection of the two shorter sides of the triangle, known as the legs. The side opposite the right angle is called the hypotenuse.
Characteristics of a Right Angled Triangle:
- Has one angle measuring 90 degrees
- The sum of the other two angles is always 90 degrees
- Follows the Pythagorean theorem: a^2 + b^2 = c^2, where 'a' and 'b' are the lengths of the legs and 'c' is the length of the hypotenuse
Example:
In a right-angled triangle with angles measuring 30, 60, and 90 degrees, the side opposite the 30-degree angle would be half the length of the hypotenuse, while the side opposite the 60-degree angle would be √3 times the length of the side opposite the 30-degree angle.
In conclusion, a right-angled triangle is a specific type of triangle based on its angles, with the defining characteristic of having one angle measuring 90 degrees.
A right-angled triangle is a type of triangle that is classified based on angles. In a right-angled triangle, one of the angles measures 90 degrees. This special angle is called the right angle and is formed by the intersection of the two shorter sides of the triangle, known as the legs. The side opposite the right angle is called the hypotenuse.
Characteristics of a Right Angled Triangle:
- Has one angle measuring 90 degrees
- The sum of the other two angles is always 90 degrees
- Follows the Pythagorean theorem: a^2 + b^2 = c^2, where 'a' and 'b' are the lengths of the legs and 'c' is the length of the hypotenuse
Example:
In a right-angled triangle with angles measuring 30, 60, and 90 degrees, the side opposite the 30-degree angle would be half the length of the hypotenuse, while the side opposite the 60-degree angle would be √3 times the length of the side opposite the 30-degree angle.
In conclusion, a right-angled triangle is a specific type of triangle based on its angles, with the defining characteristic of having one angle measuring 90 degrees.
Study the steps of construction given.Step1: Draw a ray OA.
Step2: With O as centre and any convenient radius draw an arc MN to cut 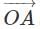 at M.
at M.
Step3: With M as centre and the same radius draw an arc to cut MN at P.
Step4: With P as centre and the same radius, draw an arc to cut MN at Q.
Step5: Draw OQ and produce it to D. An angle AOD is constructed.What is the measure of ∠AOD ?- a)60o
- b)300
- c)1200
- d)450
Correct answer is option 'C'. Can you explain this answer?
Study the steps of construction given.
Step1: Draw a ray OA.
Step2: With O as centre and any convenient radius draw an arc MN to cut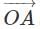 at M.
at M.
Step3: With M as centre and the same radius draw an arc to cut MN at P.
Step4: With P as centre and the same radius, draw an arc to cut MN at Q.
Step5: Draw OQ and produce it to D. An angle AOD is constructed.
Step2: With O as centre and any convenient radius draw an arc MN to cut
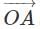 at M.
at M.Step3: With M as centre and the same radius draw an arc to cut MN at P.
Step4: With P as centre and the same radius, draw an arc to cut MN at Q.
Step5: Draw OQ and produce it to D. An angle AOD is constructed.
What is the measure of ∠AOD ?
a)
60o
b)
300
c)
1200
d)
450

|
Mahesh Sen answered |
The given steps of construction are to construct an angle of 120o.

.
Which is the longest side of a right triangle?- a)Hypotenuse
- b)Base
- c)Perpendicular
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Which is the longest side of a right triangle?
a)
Hypotenuse
b)
Base
c)
Perpendicular
d)
None of these

|
Geeta Sharma answered |
A because if we draw right triangle neeche vala base 90 vala perpendicular remain hypotenuse so it is longest
A Choose the correct option in which a triangle CANNOT be constructed with the given lengths of sides.- a)3 cm, 4 cm, 5 cm
- b)7 cm, 6 cm, 5 cm
- c)10 cm, 7 cm, 2 cm
- d)12 cm, 8 cm, 6 cm
Correct answer is option 'C'. Can you explain this answer?
A Choose the correct option in which a triangle CANNOT be constructed with the given lengths of sides.
a)
3 cm, 4 cm, 5 cm
b)
7 cm, 6 cm, 5 cm
c)
10 cm, 7 cm, 2 cm
d)
12 cm, 8 cm, 6 cm

|
Saikat Chawla answered |
The difference of any two sides of a triangle must be less than the third side. This property of triangles is not satisfied by the given measurements as 0−7=3>2 and 10−2=8>7,though 7−2=5<10 is true.
Direction: David folds a sheet of paper. The dotted lines as shown in the figure are the creases formed, which are named as l, m and n. 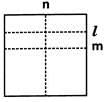 What do you call the line n with respect to the lines I and m?
What do you call the line n with respect to the lines I and m?- a)n is a line parallel to I and m.
- b)n is a line parallel to I only.
- c)n is a transversal.
- d)n is a line parallel to m only.
Correct answer is option 'C'. Can you explain this answer?
Direction: David folds a sheet of paper. The dotted lines as shown in the figure are the creases formed, which are named as l, m and n.  What do you call the line n with respect to the lines I and m?
What do you call the line n with respect to the lines I and m?
 What do you call the line n with respect to the lines I and m?
What do you call the line n with respect to the lines I and m?a)
n is a line parallel to I and m.
b)
n is a line parallel to I only.
c)
n is a transversal.
d)
n is a line parallel to m only.

|
Tanishq Nair answered |
'n? cuts I and m at distinct points and also I and m are parallel. So, n is called the transversal.
Direction: David folds a sheet of paper. The dotted lines as shown in the figure are the creases formed, which are named as l, m and n.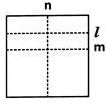 Which of the following is true?
Which of the following is true?- a)l//m
- b)l//n
- c)n//m
- d)Either [b] or [c]
Correct answer is option 'A'. Can you explain this answer?
Direction: David folds a sheet of paper. The dotted lines as shown in the figure are the creases formed, which are named as l, m and n. Which of the following is true?
Which of the following is true?
 Which of the following is true?
Which of the following is true?a)
l//m
b)
l//n
c)
n//m
d)
Either [b] or [c]

|
Gopal Kumar answered |
Clearly, l||m is true.
A triangle in which two altitudes of the triangle are two of its sides is _________.- a)obtuse-angled triangle
- b)acute-angled triangle
- c)right-angled triangle
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A triangle in which two altitudes of the triangle are two of its sides is _________.
a)
obtuse-angled triangle
b)
acute-angled triangle
c)
right-angled triangle
d)
None of these

|
Prisha Banerjee answered |
A right triangle (American English) or right-angled triangle (British English) is a triangle in which one angle is a right angle (that is, a 90-degree angle). The relation between the sides and angles of a right triangle is the basis for trigonometry.
The side opposite the right angle is called the hypotenuse (side c in the figure). The sides adjacent to the right angle are called legs (or catheti, singular: cathetus). Side a may be identified as the side adjacent to angle B and opposed to (or opposite) angle A, while side b is the side adjacent to angle A and opposed to angle B.
If the lengths of all three sides of a right triangle are integers, the triangle is said to be a Pythagorean triangle and its side lengths are collectively known as a Pythagorean triple.
The measurements of ΔDEFare EF=8.4 cm, ∠E=103o and ∠F=85o. Which of the following is correct?- a)ΔDEF can be constructed.
- b)ΔDEF is an obtuse angled triangle.
- c)ΔDEF cannot be constructed.
- d)ΔDEF is an acute angled triangle.
Correct answer is option 'C'. Can you explain this answer?
The measurements of ΔDEFare EF=8.4 cm, ∠E=103o and ∠F=85o. Which of the following is correct?
a)
ΔDEF can be constructed.
b)
ΔDEF is an obtuse angled triangle.
c)
ΔDEF cannot be constructed.
d)
ΔDEF is an acute angled triangle.

|
Krish Desai answered |
The triangle cannot be constructed as it does not satisfy the angle sum property.
How many altitude can a triangle have?- a)2
- b)3
- c)1
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
How many altitude can a triangle have?
a)
2
b)
3
c)
1
d)
None of these
|
|
Sania Arju answered |
Since all triangles have three vertices and three opposite sides, all triangles have three altitudes. The three altitudes of any triangle (or lines containing the altitudes) intersect at a common location called the orthocentre.
The orthocentre occurs inside a triangle if and only if the triangle is an acute triangle.
The orthocentre is coincidental with the vertex where the right angle occurs if and only if the triangle is a right triangle.
The orthocentre occurs outside a triangle if and only if the triangle is an obtuse triangle.
The orthocentre occurs inside a triangle if and only if the triangle is an acute triangle.
The orthocentre is coincidental with the vertex where the right angle occurs if and only if the triangle is a right triangle.
The orthocentre occurs outside a triangle if and only if the triangle is an obtuse triangle.
Chapter doubts & questions for Geometry - Mathematics for Grade 7 2025 is part of Grade 7 exam preparation. The chapters have been prepared according to the Grade 7 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 7 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Geometry - Mathematics for Grade 7 in English & Hindi are available as part of Grade 7 exam.
Download more important topics, notes, lectures and mock test series for Grade 7 Exam by signing up for free.
Mathematics for Grade 7
132 videos|250 docs|58 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup













