All Exams >
Grade 10 >
Physics for Grade 10 >
All Questions
All questions of Momentum for Grade 10 Exam
A gun of mass 5 kg fires a 50g bullet with a velocity of 200m/s. the recoil velocity of the gun is:- a)-2 m/s
- b)20 m/s
- c)Zero
- d)0.2m/s
Correct answer is option 'A'. Can you explain this answer?
A gun of mass 5 kg fires a 50g bullet with a velocity of 200m/s. the recoil velocity of the gun is:
a)
-2 m/s
b)
20 m/s
c)
Zero
d)
0.2m/s
|
|
Ravi Verma answered |
M of bullet = 50g= 50/1000 = 0.05kg
u= 200m/s , v=0m/s
m of gun = 5kg
u= 0m/s , v= ?
p of bullet before firing = 0.05x200 = 10kgm/s
p of gun before firing = 5x0 = 0kgm/s
Total p before firing = 10 + 0 = 10kgm/s
p of bullet after firing = 0.05x0 = 0kgm/s
let recoil velocity of gun = v m/s
p of gun after firing = 5v kgm/s
total p after firing = 5v + 0 = 5v kgm/s
According to law of conservation of momentum(p)
total p before firing = total p after firing
10 = 5v
10/5 = v
2 = v
∴ recoi v of gun = - 2 m/s
negative sign indicates the opp. direction of motion
When a force is applied to a body of mass 2 kg, its velocity changes from 20 ms-1 to 30 ms-1 in 2 s. The rate of change of momentum of the body is:- a)10 Kg ms-1
- b)10 N
- c)0.1 N
- d)10 Kg m
Correct answer is option 'B'. Can you explain this answer?
When a force is applied to a body of mass 2 kg, its velocity changes from 20 ms-1 to 30 ms-1 in 2 s. The rate of change of momentum of the body is:
a)
10 Kg ms-1
b)
10 N
c)
0.1 N
d)
10 Kg m
|
|
Kyra Menon answered |
Explanation:
- Mass of the body, m = 2 kg
- Initial velocity of the body, u = 20 m/s
- Final velocity of the body, v = 30 m/s
- Time taken for the change in velocity, t = 2 s
- The formula for the rate of change of momentum is given by:
Rate of change of momentum = Force applied x Time taken
- Using the formula for acceleration,
a = (v - u) / t
- Substituting the given values, we get:
a = (30 - 20) / 2 = 5 m/s2
- Using the formula for force,
F = ma
- Substituting the mass and acceleration values, we get:
F = 2 x 5 = 10 N
- Substituting the force and time values in the formula for the rate of change of momentum, we get:
Rate of change of momentum = Force applied x Time taken = 10 x 2 = 20 Ns
- However, the unit of momentum is Kg m/s. Therefore, we need to convert Ns to Kg m/s by dividing by the acceleration due to gravity (9.8 m/s2),
20 Ns / 9.8 m/s2 = 2.04 Kg m/s
- Rounding off to one decimal place, we get:
Rate of change of momentum = 2.0 Kg m/s
- Hence, the correct answer is option B, 10 N.
A machine gun of mass 24 kg fires 20g bullets at the rate of 8 bullets per second, with a speed of 250 m/s. The force required to hold the gun in position is:- a)10 N
- b)30 N
- c)40 N
- d)20 N
Correct answer is option 'C'. Can you explain this answer?
A machine gun of mass 24 kg fires 20g bullets at the rate of 8 bullets per second, with a speed of 250 m/s. The force required to hold the gun in position is:
a)
10 N
b)
30 N
c)
40 N
d)
20 N
|
|
Arvind Singh answered |
In the given problem,
mg = 24 kg ; vb = 250 m/s
mass of the bullet = 20g = 20 x 10^-3 kg
no. of bullets fired/sec = 8
F = Chnage in momentum/time = mb*vb - mb*ub/t
For t = 1 sec
Total mass of bullets in 1 second mb = (8 x 20)/1000 = 0.16 kg
F = [(0.16 x 250) - 0]/1 = 40 N
A ball of mass 5 kg moving at 3 m/s collides with another ball of mass 3 kg moving at 5 m/s in the same direction. If the balls move together after the collision in the same direction, find their common velocity.- a)5 m/s
- b)3.75 m/s
- c)6.25 m/s
- d)7.5 m/s
Correct answer is option 'B'. Can you explain this answer?
A ball of mass 5 kg moving at 3 m/s collides with another ball of mass 3 kg moving at 5 m/s in the same direction. If the balls move together after the collision in the same direction, find their common velocity.
a)
5 m/s
b)
3.75 m/s
c)
6.25 m/s
d)
7.5 m/s
|
|
Prashansa Singh answered |
Given:
Mass of ball 1 (m1) = 5 kg
Velocity of ball 1 (u1) = 3 m/s
Mass of ball 2 (m2) = 3 kg
Velocity of ball 2 (u2) = 5 m/s
After the collision, the balls move together in the same direction.
To find: Common velocity of the balls after the collision.
Solution:
1. First, we need to find the momentum of each ball before the collision using the formula:
Momentum (p) = Mass (m) x Velocity (u)
Momentum of ball 1 before the collision (p1) = m1u1 = 5 kg x 3 m/s = 15 kg m/s
Momentum of ball 2 before the collision (p2) = m2u2 = 3 kg x 5 m/s = 15 kg m/s
2. Next, we need to find the total momentum of the system before the collision (p):
Total momentum before the collision (p) = p1 + p2 = 15 kg m/s + 15 kg m/s = 30 kg m/s
3. During the collision, the balls stick together and move with a common velocity (v). Using the law of conservation of momentum, we can equate the total momentum before the collision (p) to the total momentum after the collision (p'):
Total momentum after the collision (p') = (m1 + m2) x v
4. Equating the two expressions for total momentum, we get:
p = p'
30 kg m/s = (5 kg + 3 kg) x v
5. Solving for v, we get:
v = 30 kg m/s ÷ 8 kg = 3.75 m/s
Therefore, the common velocity of the balls after the collision is 3.75 m/s.
Answer: Option B (3.75 m/s)
Mass of ball 1 (m1) = 5 kg
Velocity of ball 1 (u1) = 3 m/s
Mass of ball 2 (m2) = 3 kg
Velocity of ball 2 (u2) = 5 m/s
After the collision, the balls move together in the same direction.
To find: Common velocity of the balls after the collision.
Solution:
1. First, we need to find the momentum of each ball before the collision using the formula:
Momentum (p) = Mass (m) x Velocity (u)
Momentum of ball 1 before the collision (p1) = m1u1 = 5 kg x 3 m/s = 15 kg m/s
Momentum of ball 2 before the collision (p2) = m2u2 = 3 kg x 5 m/s = 15 kg m/s
2. Next, we need to find the total momentum of the system before the collision (p):
Total momentum before the collision (p) = p1 + p2 = 15 kg m/s + 15 kg m/s = 30 kg m/s
3. During the collision, the balls stick together and move with a common velocity (v). Using the law of conservation of momentum, we can equate the total momentum before the collision (p) to the total momentum after the collision (p'):
Total momentum after the collision (p') = (m1 + m2) x v
4. Equating the two expressions for total momentum, we get:
p = p'
30 kg m/s = (5 kg + 3 kg) x v
5. Solving for v, we get:
v = 30 kg m/s ÷ 8 kg = 3.75 m/s
Therefore, the common velocity of the balls after the collision is 3.75 m/s.
Answer: Option B (3.75 m/s)
Two objects each of mass 1.5 Kg are moving in the same straight line but in opposite directions. The velocity of each object is 2.5m/s before the collision during which they stick together. What will be the velocity of the combined object after the collision?- a)2.5m/s
- b)Zero
- c)5m/s2
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
Two objects each of mass 1.5 Kg are moving in the same straight line but in opposite directions. The velocity of each object is 2.5m/s before the collision during which they stick together. What will be the velocity of the combined object after the collision?
a)
2.5m/s
b)
Zero
c)
5m/s2
d)
none of these
|
|
Arjun Sharma answered |
Mass ofone of the objects,m1= 1.5 kg
Mass of the other object,m2= 1.5 kg
Velocity ofm1before collision,v1= 2.5 m/s
Velocity ofm2, moving in opposite direction before collision,v2= 2.5' m/s
(Negative sign arises because massm2is moving in an opposite direction)
After collision, the two objects stick together.
Total mass of the combined object =m1+m2
Velocity of the combined object =v
According to the law of conservation of momentum:
Total momentum before collision = Total momentum after collision
m1v1+m2v1= (m1+m2)v
1.5(2.5) + 1.5 (2.5') = (1.5 + 1.5)v
3.75' + 3.75 = 3v
v= 0
Hence, the velocity of the combined object after collision is 0 m/s.
The law of conservation of momentum states that the sum of momenta of two objects before collision is equal to the sum of momenta after the collision provided that ______- a)No internal unbalanced force acts on them.
- b)No external unbalanced force acts on them.
- c)No external balanced force acts on them.
- d)No internal balanced force acts on them.
Correct answer is option 'B'. Can you explain this answer?
The law of conservation of momentum states that the sum of momenta of two objects before collision is equal to the sum of momenta after the collision provided that ______
a)
No internal unbalanced force acts on them.
b)
No external unbalanced force acts on them.
c)
No external balanced force acts on them.
d)
No internal balanced force acts on them.
|
|
Jyoti Kapoor answered |
The law of conservation of momentum states that for two objects colliding in an isolated system, the total momentum before and after the collision is equal. This is because the momentum lost by one object is equal to the momentum gained by the other.
Conservation of momentum is derived from Newton's laws of motion. Newton's third law states that every action has an equal but opposite reaction; the force that one object A exerts on object B is equal but opposite to the force that object B exerts on object A. By Newton's second law, this force is equal to the product of the mass and the acceleration of the objects, so the product of the mass and acceleration of object A is equal but opposite to the product between the mass and acceleration of object B.
Rockets work on the principle of conservation of:- a)Mass
- b)Momentum
- c)Energy
- d)Impulse
Correct answer is option 'B'. Can you explain this answer?
Rockets work on the principle of conservation of:
a)
Mass
b)
Momentum
c)
Energy
d)
Impulse
|
|
Ravi Verma answered |
Rocket works on the conservation of momentum. In a rocket, the fuel burns and produces gas at high temperature. These gases are ejected out of the rocket from a nozzle at the back side of the rocket. The ejecting gas exerts a forward force on the rocket which help in accelerating. Through the mass of gases escaping per second is very small and their momentum is very large due to their tremendous velocity of escape. An equal and opposite momentum is imparted to the rocket which despite its large mass builds up a high velocity.
A point mass of 1 kg collides elastically with a stationary point mass of 5 kg. After their collision, the 1 kg mass reverses its direction and moves with a speed of 2 ms–1. Which of the following statement(s) is (are) correct for the system of these two masses?- a)Total momentum of the system is 3 kg ms–1
- b)Momentum of 5 kg mass after collision is 4 kg ms–1
- c)Kinetic energy of the centre of mass is 0.75 J
- d)Total kinetic energy of the system is 4J
Correct answer is option 'A,C'. Can you explain this answer?
A point mass of 1 kg collides elastically with a stationary point mass of 5 kg. After their collision, the 1 kg mass reverses its direction and moves with a speed of 2 ms–1. Which of the following statement(s) is (are) correct for the system of these two masses?
a)
Total momentum of the system is 3 kg ms–1
b)
Momentum of 5 kg mass after collision is 4 kg ms–1
c)
Kinetic energy of the centre of mass is 0.75 J
d)
Total kinetic energy of the system is 4J

|
Akash Shah answered |
According to law of conservation of linear momentum 1 × u1 + 5 × 0 = 1 (–2) + 5 (v2)
⇒ u1 = – 2 + 5 v2 ...(i)
⇒ u1 = – 2 + 5 v2 ...(i)
The coefficient of restituition
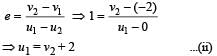
On solving (i) & (ii) we get desired results.
The momentum of a body of given mass is proportional to:- a)Its colour
- b)Its velocity
- c)Its volume
- d)Its shape
Correct answer is option 'B'. Can you explain this answer?
The momentum of a body of given mass is proportional to:
a)
Its colour
b)
Its velocity
c)
Its volume
d)
Its shape

|
Arpita Basu answered |
The correct answer is option B: the momentum of a body is proportional to its velocity.
Explanation:
1. Understanding momentum:
- Momentum is a property of a moving object that describes its motion.
- It is defined as the product of an object's mass and its velocity.
- Mathematically, momentum (p) is given by the equation p = m * v, where m is the mass of the object and v is its velocity.
2. Proportional relationship:
- When two quantities are said to be proportional to each other, it means that they vary in direct proportion.
- In this case, the momentum is proportional to the velocity, which means that as the velocity increases, the momentum also increases, and vice versa.
- This relationship can be expressed as p ∝ v.
3. Understanding mass and volume:
- Mass refers to the amount of matter contained in an object, and it remains constant regardless of the object's location or state of motion.
- Volume, on the other hand, refers to the amount of space occupied by an object.
- While both mass and volume are important properties of matter, they do not directly affect the momentum of an object.
4. Color and shape:
- The color of an object and its shape do not have any influence on its momentum.
- These characteristics are related to the object's physical appearance and do not affect its motion or the forces acting upon it.
5. Velocity and momentum:
- Velocity is a measure of how fast an object is moving in a particular direction.
- The greater the velocity of an object, the greater its momentum.
- This relationship can be understood intuitively by considering a moving car: a car traveling at a higher velocity will have more momentum and will be harder to stop compared to a car traveling at a lower velocity.
In conclusion, the momentum of a body is proportional to its velocity. This means that as the velocity of an object increases, its momentum also increases, and as the velocity decreases, the momentum decreases. The mass of the object remains constant in this relationship. The color, volume, and shape of an object do not have any influence on its momentum.
Explanation:
1. Understanding momentum:
- Momentum is a property of a moving object that describes its motion.
- It is defined as the product of an object's mass and its velocity.
- Mathematically, momentum (p) is given by the equation p = m * v, where m is the mass of the object and v is its velocity.
2. Proportional relationship:
- When two quantities are said to be proportional to each other, it means that they vary in direct proportion.
- In this case, the momentum is proportional to the velocity, which means that as the velocity increases, the momentum also increases, and vice versa.
- This relationship can be expressed as p ∝ v.
3. Understanding mass and volume:
- Mass refers to the amount of matter contained in an object, and it remains constant regardless of the object's location or state of motion.
- Volume, on the other hand, refers to the amount of space occupied by an object.
- While both mass and volume are important properties of matter, they do not directly affect the momentum of an object.
4. Color and shape:
- The color of an object and its shape do not have any influence on its momentum.
- These characteristics are related to the object's physical appearance and do not affect its motion or the forces acting upon it.
5. Velocity and momentum:
- Velocity is a measure of how fast an object is moving in a particular direction.
- The greater the velocity of an object, the greater its momentum.
- This relationship can be understood intuitively by considering a moving car: a car traveling at a higher velocity will have more momentum and will be harder to stop compared to a car traveling at a lower velocity.
In conclusion, the momentum of a body is proportional to its velocity. This means that as the velocity of an object increases, its momentum also increases, and as the velocity decreases, the momentum decreases. The mass of the object remains constant in this relationship. The color, volume, and shape of an object do not have any influence on its momentum.
The law of conservation of momentum holds for:- a)Individual particles
- b)Only for two particles
- c)A system of particles
- d)Only for three particles
Correct answer is option 'C'. Can you explain this answer?
The law of conservation of momentum holds for:
a)
Individual particles
b)
Only for two particles
c)
A system of particles
d)
Only for three particles
|
|
Ananya Sharma answered |
Conservation of momentum. A conservation law stating that the total linear momentum of a closed system remains constant through time, regardless of other possible changes within the system.
A particle of mass m is projected from the ground with an initial speed u0 at an angle α with the horizontal. At the highest point of its trajectory, it makes a completely inelastic collision with another identical particle, which was thrown vertically upward from the ground with the same initial speed u0. The angle that the composite system makes with the horizontal immediately after the collision is- a)
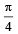
- b)
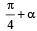
- c)
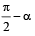
- d)
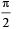
Correct answer is option 'A'. Can you explain this answer?
A particle of mass m is projected from the ground with an initial speed u0 at an angle α with the horizontal. At the highest point of its trajectory, it makes a completely inelastic collision with another identical particle, which was thrown vertically upward from the ground with the same initial speed u0. The angle that the composite system makes with the horizontal immediately after the collision is
a)
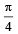
b)
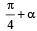
c)
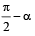
d)
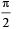

|
Devika Banerjee answered |
Activity B to M for particle thrown upwards
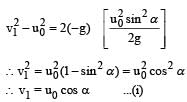
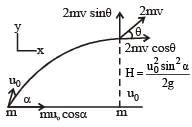
Applying conservation of linear momentum in Y-direction
2mv sinθ = mv1 = mu0cosα ...(ii) [from (i)]
Applying conservation of linear momentum in X-direction
2mv cosθ = mu0 cosα ...(iii)
on dividing (ii) and (iii) we get
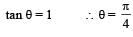
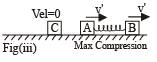
Two blocks A and B, each of mass m, are connected by a massless spring of natural length L and spring constant K.
The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in fig.. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides elastically with A. Then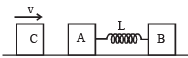
- a)the kinetic energy of the A-B system, at maximum compression of the spring, is zero.
- b)the kinetic energy of the A-B system, at maximum compression of the spring, is mv2/4.
- c)the maximum compression of the spring is
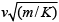
- d)the maximum compression of the spring is
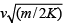
Correct answer is option 'B,D'. Can you explain this answer?
Two blocks A and B, each of mass m, are connected by a massless spring of natural length L and spring constant K.
The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in fig.. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides elastically with A. Then
The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in fig.. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides elastically with A. Then

a)
the kinetic energy of the A-B system, at maximum compression of the spring, is zero.
b)
the kinetic energy of the A-B system, at maximum compression of the spring, is mv2/4.
c)
the maximum compression of the spring is 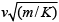
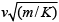
d)
the maximum compression of the spring is 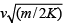

|
Ritika Kulkarni answered |
In situation 1, mass C is moving towards right with velocity v. A and B are at rest.
In situation 2, which is just after the collision of C with A, C stop and A acquires a velocity v. [head-on elastic collision between identical masses]
When A starts moving towards right, the spring suffer a compression due to which B also starts moving towards right. The compression of the spring continues till there is relative velocity between A and B. When this relative velocity becomes zero, both A and B move with the same velocity v' and the spring is in a state of maximum compression.
Applying momentum conservation in situation 1 and 3,
In situation 2, which is just after the collision of C with A, C stop and A acquires a velocity v. [head-on elastic collision between identical masses]
When A starts moving towards right, the spring suffer a compression due to which B also starts moving towards right. The compression of the spring continues till there is relative velocity between A and B. When this relative velocity becomes zero, both A and B move with the same velocity v' and the spring is in a state of maximum compression.
Applying momentum conservation in situation 1 and 3,


∴ K.E. of the system in situation 3 is
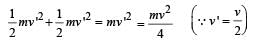
This is the kinetic energy possessed by A – B system (since, C is at rest).
Let x be the maximum compression of the spring.
Applying energy conservation
Let x be the maximum compression of the spring.
Applying energy conservation
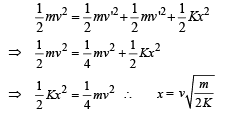
The momentum of an isolated system remains conserved provided:- a)Net final momentum of the system is zero.
- b)Net external force of the system is non zero.
- c)Net initial momentum of the system is zero.
- d)Net external force on the system is zero.
Correct answer is option 'D'. Can you explain this answer?
The momentum of an isolated system remains conserved provided:
a)
Net final momentum of the system is zero.
b)
Net external force of the system is non zero.
c)
Net initial momentum of the system is zero.
d)
Net external force on the system is zero.

|
Infinite Brains answered |
If there is no force acting on the system, then there will be no change in the moment of the system, Hence the total momentum will remain conserved
The balls, having linear momenta 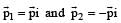 undergo a collision in free space. There is no external force acting on the balls. Let
undergo a collision in free space. There is no external force acting on the balls. Let 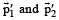 be their final momenta. The following option (s) is (are) NOT ALLOWED for any non-zero value of p, a1, a2, b1, b2, c1 and c2.
be their final momenta. The following option (s) is (are) NOT ALLOWED for any non-zero value of p, a1, a2, b1, b2, c1 and c2.- a)
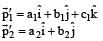
- b)
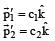
- c)
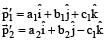
- d)
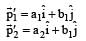
Correct answer is option 'A,D'. Can you explain this answer?
The balls, having linear momenta 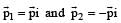 undergo a collision in free space. There is no external force acting on the balls. Let
undergo a collision in free space. There is no external force acting on the balls. Let 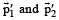 be their final momenta. The following option (s) is (are) NOT ALLOWED for any non-zero value of p, a1, a2, b1, b2, c1 and c2.
be their final momenta. The following option (s) is (are) NOT ALLOWED for any non-zero value of p, a1, a2, b1, b2, c1 and c2.
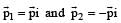 undergo a collision in free space. There is no external force acting on the balls. Let
undergo a collision in free space. There is no external force acting on the balls. Let 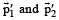 be their final momenta. The following option (s) is (are) NOT ALLOWED for any non-zero value of p, a1, a2, b1, b2, c1 and c2.
be their final momenta. The following option (s) is (are) NOT ALLOWED for any non-zero value of p, a1, a2, b1, b2, c1 and c2.a)
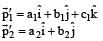
b)
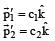
c)
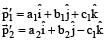
d)
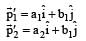

|
Rounak Desai answered |
KEY CONCEPT Use law of conservation of linear momentum.
The initial linear momentum of the system is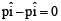 Therefore the final linear momentum should also be zero.
Therefore the final linear momentum should also be zero.
Option a :
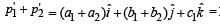 Final momentum.
Final momentum.
It is given that a1, b1, c1, a2, b2 and c2 have non-zero values. If a1 = x and a2 = – x. Also if b1 = y and b2 = – y then the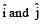 components become zero. But the third term having
components become zero. But the third term having  component is non-zero. This gives a definite final momentum to the system which violates conservation of linear momentum, so this is an incorrect option.
component is non-zero. This gives a definite final momentum to the system which violates conservation of linear momentum, so this is an incorrect option.
The initial linear momentum of the system is
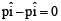 Therefore the final linear momentum should also be zero.
Therefore the final linear momentum should also be zero.Option a :
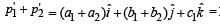 Final momentum.
Final momentum.It is given that a1, b1, c1, a2, b2 and c2 have non-zero values. If a1 = x and a2 = – x. Also if b1 = y and b2 = – y then the
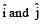 components become zero. But the third term having
components become zero. But the third term having 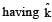 component is non-zero. This gives a definite final momentum to the system which violates conservation of linear momentum, so this is an incorrect option.
component is non-zero. This gives a definite final momentum to the system which violates conservation of linear momentum, so this is an incorrect option.Option d:
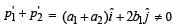 because b1 ≠ 0
because b1 ≠ 0Following the same reasoning as above this option is also ruled ou
A particle of mass m is attached to one end of a mass-less spring of force constant k, lying on a frictionless horizontal plane. The other end of the spring is fixed. The particle starts moving horizontally from its equilibrium position at time t = 0 with an initial velocity u0. When the speed of the particle is 0.5 u0, it collides elastically with a rigid wall. After this collision- a)The speed of the particle when it returns to its equilibrium position is u0
- b)The time at which the particle passes through the equilibrium position for the first time is
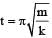
- c)The time at which the maximum compression of the spring occurs is
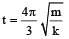
- d)The time at which the particle passes through the equilibrium position for the second time is
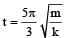
Correct answer is option 'A,D'. Can you explain this answer?
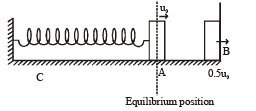
A particle of mass m is attached to one end of a mass-less spring of force constant k, lying on a frictionless horizontal plane. The other end of the spring is fixed. The particle starts moving horizontally from its equilibrium position at time t = 0 with an initial velocity u0. When the speed of the particle is 0.5 u0, it collides elastically with a rigid wall. After this collision
a)
The speed of the particle when it returns to its equilibrium position is u0
b)
The time at which the particle passes through the equilibrium position for the first time is 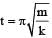
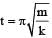
c)
The time at which the maximum compression of the spring occurs is 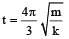
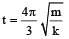
d)
The time at which the particle passes through the equilibrium position for the second time is 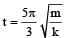

|
Athira Datta answered |
The particle collides elastically with rigid wall. Here
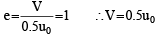
i.e. the particle rebounds with the same speed. Therefore the particle will return to its equilibrium position with speed u0. option (a) is correct.
The velocity of the particle becomes 0.5u0 after time t.
Then using the equation V = Vmax cos wt we get 0.5u0 = u0 cos wt
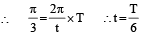
The time period
The time taken by the particle to pass through the equilibrium for the first time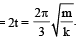 Therefore option (b) is incorrect
Therefore option (b) is incorrect
The time taken for the maximum compression
The velocity of the particle becomes 0.5u0 after time t.
Then using the equation V = Vmax cos wt we get 0.5u0 = u0 cos wt
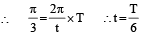
The time period

The time taken by the particle to pass through the equilibrium for the first time
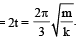 Therefore option (b) is incorrect
Therefore option (b) is incorrectThe time taken for the maximum compression

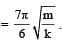 Therefore option c is incorrect.
Therefore option c is incorrect.The time taken for particle to pass through the equilibrium position second time
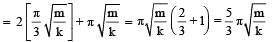
option (d) is correct.
Two particles of masses m1 and m2 in projectile motion have velocities 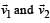 respectively at time t = 0. They collide at time to. Their velocities become
respectively at time t = 0. They collide at time to. Their velocities become 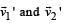 at time 2to while still moving in air. The value of
at time 2to while still moving in air. The value of 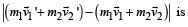
- a)zero
- b)
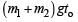
- c)
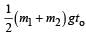
- d)
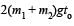
Correct answer is option 'D'. Can you explain this answer?
Two particles of masses m1 and m2 in projectile motion have velocities 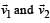 respectively at time t = 0. They collide at time to. Their velocities become
respectively at time t = 0. They collide at time to. Their velocities become 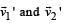 at time 2t
at time 2t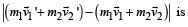
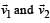 respectively at time t = 0. They collide at time to. Their velocities become
respectively at time t = 0. They collide at time to. Their velocities become 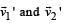 at time 2t
at time 2to
while still moving in air. The value of 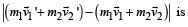
a)
zero
b)
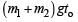
c)
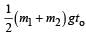
d)
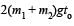

|
Athira Datta answered |
If we consider the two particles as a system then the external force acting on the system is the gravitational pull (m1 + m2) g.
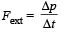
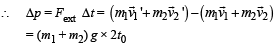
A ball of mass 0.2 kg rests on a vertical post of height 5 m. A bullet of mass 0.01 kg, traveling with a velocity V m/s in a horizontal direction, hits the centre of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of 20 m and the bullet at a distance of 100 m from the foot of the post. The velocity V of the bullet is
- a)250 m/s
- b)250√2 m/s
- c)400 m/s
- d)500 m/s
Correct answer is option 'D'. Can you explain this answer?
A ball of mass 0.2 kg rests on a vertical post of height 5 m. A bullet of mass 0.01 kg, traveling with a velocity V m/s in a horizontal direction, hits the centre of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of 20 m and the bullet at a distance of 100 m from the foot of the post. The velocity V of the bullet is

a)
250 m/s
b)
250√2 m/s
c)
400 m/s
d)
500 m/s

|
Rounak Desai answered |
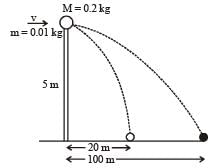
For vertical motion of bullet or ball
u = 0, s = 5m, t = ? , a = 10m/s2
u = 0, s = 5m, t = ? , a = 10m/s2
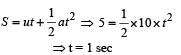
For horizontal motion of ball
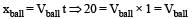
For horizontal motion of bullet
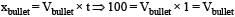
Applying conservation of linear momentum during collision, w e get
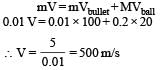
Two blocks of masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14 m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is- a)30 m/s
- b)20 m/s
- c)10 m/s
- d)5 m/s
Correct answer is option 'C'. Can you explain this answer?
Two blocks of masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14 m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is
a)
30 m/s
b)
20 m/s
c)
10 m/s
d)
5 m/s

|
Avi Chawla answered |
Just after collision
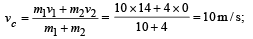
Note : Spring force is an internal force, it cannot change the linear momentum of the (two mass + spring) system.
Therefore vc remains the same.
Therefore vc remains the same.
A ball hits the floor and rebounds after an inelastic collision. In this case- a)the momentum of the ball just after the collision is the same as that just before the collision.
- b)the mechanical energy of the ball remains the same in the collision
- c)the total momen tum of the ball and the earth is conserved
- d)the total energy of the ball and the earth is conserved
Correct answer is option 'C,D'. Can you explain this answer?
A ball hits the floor and rebounds after an inelastic collision. In this case
a)
the momentum of the ball just after the collision is the same as that just before the collision.
b)
the mechanical energy of the ball remains the same in the collision
c)
the total momen tum of the ball and the earth is conserved
d)
the total energy of the ball and the earth is conserved

|
Devika Banerjee answered |
(a) is wrong because the momentum of ball changes in magnitude as well as direction.
(b) is wrong because on collision, some mechanical energy is converted into heat, sound energy.
(b) is wrong because on collision, some mechanical energy is converted into heat, sound energy.
(c) is correct because for earth + ball system the impact force is an internal force.
(d) is correct.
(d) is correct.
A shell is fired from a cannon with a velocity v (m/sec.) at an angle θ with the horizontal direction. At the highest point in its path it explodes into two pieces of equal mass. One of the pieces retraces its path to the cannon and the speed (in m/sec.) of the other piece immediately after the explosion is- a)3v cos θ
- b)2v cos θ
- c)
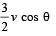
- d)
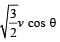
Correct answer is option 'A'. Can you explain this answer?
A shell is fired from a cannon with a velocity v (m/sec.) at an angle θ with the horizontal direction. At the highest point in its path it explodes into two pieces of equal mass. One of the pieces retraces its path to the cannon and the speed (in m/sec.) of the other piece immediately after the explosion is
a)
3v cos θ
b)
2v cos θ
c)
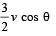
d)
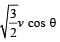

|
Lekshmi Bose answered |
As one piece retraces its path, the speed of this piece just after explosion should be v cos θ
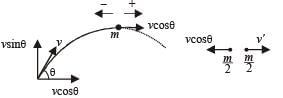
(At highest point just after explosion) NOTE THIS STEP
Applying conservation of linear momentum at the highest point;
Applying conservation of linear momentum at the highest point;
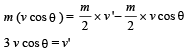
Chapter doubts & questions for Momentum - Physics for Grade 10 2025 is part of Grade 10 exam preparation. The chapters have been prepared according to the Grade 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Momentum - Physics for Grade 10 in English & Hindi are available as part of Grade 10 exam.
Download more important topics, notes, lectures and mock test series for Grade 10 Exam by signing up for free.
Physics for Grade 10
122 videos|152 docs|40 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily









