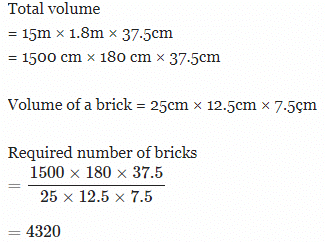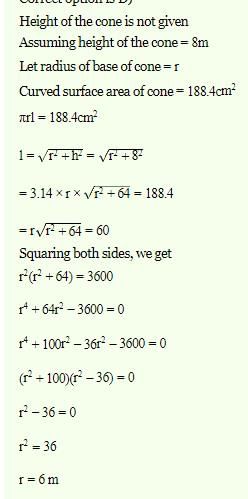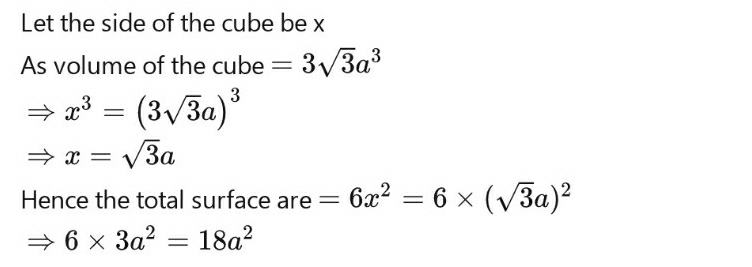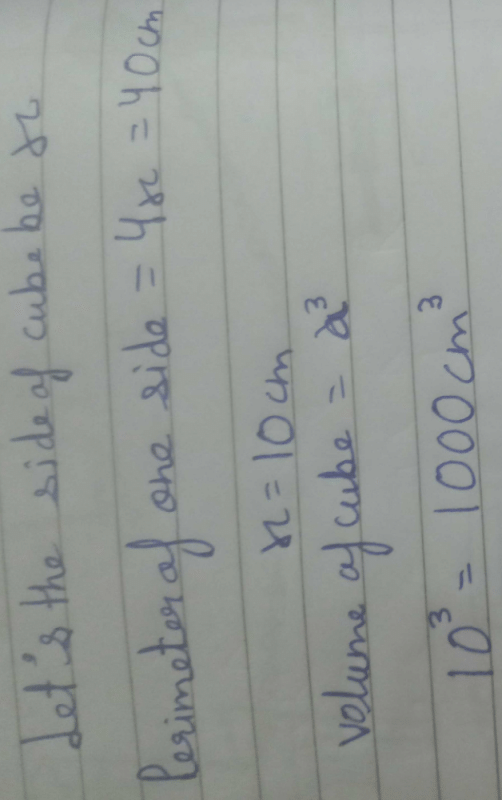All Exams >
EmSAT Achieve >
Mathematics for EmSAT Achieve >
All Questions
All questions of Surface Area & Volumes for EmSAT Achieve Exam
A rectangular sand box is 5 m wide and 2 m long. How many cubic metres of sand are needed to fill the box upto a depth of 10 cm ?- a)1
- b)10
- c)100
- d)1000
Correct answer is option 'A'. Can you explain this answer?
A rectangular sand box is 5 m wide and 2 m long. How many cubic metres of sand are needed to fill the box upto a depth of 10 cm ?
a)
1
b)
10
c)
100
d)
1000
|
Arizona Academy answered |
To calculate the volume of sand needed to fill the rectangular sandbox, we can use the formula:Volume = Length × Width × DepthGiven:
Length = 2 m
Width = 5 m
Depth = 10 cm = 0.1 mSubstituting the values into the formula:Volume = 2 m × 5 m × 0.1 m
Volume = 1 cubic meterTherefore, the correct answer is A: 1 cubic meter.
Length = 2 m
Width = 5 m
Depth = 10 cm = 0.1 mSubstituting the values into the formula:Volume = 2 m × 5 m × 0.1 m
Volume = 1 cubic meterTherefore, the correct answer is A: 1 cubic meter.
A cuboid of dimension 24cm * 9cm * 8 cm is melted and smaller cubers are of side 3 cm is formed.find how many such cubes can be formed ?- a)64
- b)56
- c)48
- d) 40
Correct answer is option 'A'. Can you explain this answer?
A cuboid of dimension 24cm * 9cm * 8 cm is melted and smaller cubers are of side 3 cm is formed.find how many such cubes can be formed ?
a)
64
b)
56
c)
48
d)
40
|
Geetika Shah answered |
Volume of cuboid = (24 * 9 * 8) cm = 1728 cu.cm
Volume of small cube = (3 * 3 * 3) cm = 27 cu.cm
Volume of small cube = (3 * 3 * 3) cm = 27 cu.cm
So, No. of small cubes formed = 1728/27 = 64.
If the lateral surface area of a cube is 1600 cm2, then its edge is:- a)20 cm
- b)15 cm
- c)18 cm
- d)25 cm
Correct answer is option 'A'. Can you explain this answer?
If the lateral surface area of a cube is 1600 cm2, then its edge is:
a)
20 cm
b)
15 cm
c)
18 cm
d)
25 cm
|
Anchal Singh answered |
Lateral surface area is the surface area of an object excluding it's base and top. A cube has 6 faces, subtracting the base and top is 4.
1600 / 4 = 400 so each side has an area of 400 cm squared.
The square root of 400 is 20 so the edge of the cube is 20 cm.
A conical tomb of base diameter 24m and height 16 m. What is the curved surface area?
- a)200π sq m
- b)240π sq m
- c)300π sq m
- d)64π sq m
Correct answer is option 'B'. Can you explain this answer?
A conical tomb of base diameter 24m and height 16 m. What is the curved surface area?
a)
200π sq m
b)
240π sq m
c)
300π sq m
d)
64π sq m
|
Sagnik Menon answered |
The formula for the curved surface area of a cone is πrs, where r is the radius of the base and s is the slant height. To find the slant height, we can use the Pythagorean theorem: s² = r² + h², where h is the height of the cone.
In this case, the radius is half of the base diameter, so r = 12m. Using the Pythagorean theorem, we get:
s² = 12² + 16²
s² = 144 + 256
s² = 400
s = 20m
Now we can calculate the curved surface area:
A = πrs
A = π(12)(20)
A = 240π
Using a calculator, we can approximate this to:
A ≈ 753.98
Therefore, the curved surface area of the conical tomb is approximately 753.98 square meters.
In this case, the radius is half of the base diameter, so r = 12m. Using the Pythagorean theorem, we get:
s² = 12² + 16²
s² = 144 + 256
s² = 400
s = 20m
Now we can calculate the curved surface area:
A = πrs
A = π(12)(20)
A = 240π
Using a calculator, we can approximate this to:
A ≈ 753.98
Therefore, the curved surface area of the conical tomb is approximately 753.98 square meters.
A beam 9 m long, 40 cm wide and 20 cm deep is made up of iron which weighs 50 kg per cubic metre.The weight of the beam is :- a)27 kg
- b)36 kg
- c)48 kg
- d)56 kg
Correct answer is option 'B'. Can you explain this answer?
A beam 9 m long, 40 cm wide and 20 cm deep is made up of iron which weighs 50 kg per cubic metre.
The weight of the beam is :
a)
27 kg
b)
36 kg
c)
48 kg
d)
56 kg
|
|
Arizona Academy answered |
To find the weight of the iron beam, we need to calculate its volume and then multiply it by the weight of 1 cubic meter of iron, which is given as 50 kg.Given:
Length of beam (l) = 9 m
Breadth (b) = 40 cm = 0.4 m
Height (h) = 20 cm = 0.2 m
Weight of 1 cubic meter of iron = 50 kgVolume of the beam = l × b × h = 9 m × 0.4 m × 0.2 m = 0.72 cubic metersWeight of the beam = Volume × Weight of 1 cubic meter of iron = 0.72 cubic meters × 50 kg/cubic meter = 36 kg
Length of beam (l) = 9 m
Breadth (b) = 40 cm = 0.4 m
Height (h) = 20 cm = 0.2 m
Weight of 1 cubic meter of iron = 50 kgVolume of the beam = l × b × h = 9 m × 0.4 m × 0.2 m = 0.72 cubic metersWeight of the beam = Volume × Weight of 1 cubic meter of iron = 0.72 cubic meters × 50 kg/cubic meter = 36 kg
Therefore, the weight of the iron beam is 36 kg, which corresponds to option B.
The curved surface area of a right circular cone whose slant height is 14 cm and base radius is 21 cm is- a)308 cm2
- b)924 cm2
- c)232 cm2
- d)446 cm2
Correct answer is option 'B'. Can you explain this answer?
The curved surface area of a right circular cone whose slant height is 14 cm and base radius is 21 cm is
a)
308 cm2
b)
924 cm2
c)
232 cm2
d)
446 cm2
|
Krish Grover answered |
( b ) 924
L = 14 cm
R = 21 cm
C S A of Cone = πRL
22 / 7 * 21 * 14 cm
22 * 21 * 2 cm
462 * 2 cm
924 centimetre square
L = 14 cm
R = 21 cm
C S A of Cone = πRL
22 / 7 * 21 * 14 cm
22 * 21 * 2 cm
462 * 2 cm
924 centimetre square
The surface area of a cube of edge 1.5 cm is- a)9.50 cm2
- b)9 cm2
- c)15.50 cm2
- d)13.50 cm2
Correct answer is option 'D'. Can you explain this answer?
The surface area of a cube of edge 1.5 cm is
a)
9.50 cm2
b)
9 cm2
c)
15.50 cm2
d)
13.50 cm2
|
Ankita Choudhary. answered |
Surface area of cube =6a^2
surface area of cube=6×(1.5)^2
surface area of cube=6×2.25
surface area of cube=13.50 answer...
surface area of cube=6×(1.5)^2
surface area of cube=6×2.25
surface area of cube=13.50 answer...
The surface area of a cube of side 27 cm is :- a)2916 cm2
- b)729 cm2
- c)4374 cm2
- d)19683 cm2
Correct answer is option 'C'. Can you explain this answer?
The surface area of a cube of side 27 cm is :
a)
2916 cm2
b)
729 cm2
c)
4374 cm2
d)
19683 cm2
|
|
Arizona Academy answered |
The surface area of a cube of side 27 cm can be found using the formula:Surface area of a cube = 6a^2, where a is the length of the side of the cube.Given:
Length of side of the cube = 27 cmSubstituting the value into the formula:Surface area of the cube = 6 × 27^2
Surface area of the cube = 6 × 729
Surface area of the cube = 4374 cm^2Therefore, the surface area of the cube of side 27 cm is 4374 cm^2, which corresponds to option C
Length of side of the cube = 27 cmSubstituting the value into the formula:Surface area of the cube = 6 × 27^2
Surface area of the cube = 6 × 729
Surface area of the cube = 4374 cm^2Therefore, the surface area of the cube of side 27 cm is 4374 cm^2, which corresponds to option C
Find the height of the right circular cylinder if its curved surface area is 176 cm2 and radius of the base is 4 cm.
- a)3.5 cm
- b)14 cm
- c)7 cm
- d)21 cm
Correct answer is option 'C'. Can you explain this answer?
Find the height of the right circular cylinder if its curved surface area is 176 cm2 and radius of the base is 4 cm.
a)
3.5 cm
b)
14 cm
c)
7 cm
d)
21 cm
|
Rahul Kumar answered |
We know CSA of cylinder=2πrh
2×22/7×4×h=176
2×22/7×4×h=176
h=176×7/(44*4)
h=1232/(44*4)
h=7 cm
h=1232/(44*4)
h=7 cm
A cube is 7 cm on an edge and another cube is 14 cm on an edge. The ratios of their curved surface areas are- a)4:1
- b)1:4
- c)1:2
- d)2:1
Correct answer is option 'B'. Can you explain this answer?
A cube is 7 cm on an edge and another cube is 14 cm on an edge. The ratios of their curved surface areas are
a)
4:1
b)
1:4
c)
1:2
d)
2:1
|
Sakki Chaudhary answered |
Curved surface area of 1st cube =6a^2
6×7×7=294
curved surface area of 2nd cube=6a^2
6×14×14=1176
ratio = 284/1176
=1:4
6×7×7=294
curved surface area of 2nd cube=6a^2
6×14×14=1176
ratio = 284/1176
=1:4
Dean has a cardboard box whose length, breadth and height are in the ratio 1:2:3. He makes a new box such that the length, breadth and height got increased by 100%, 200% and 200% respectively. How much less is volume of old box than the new box? - a) 12 times less
- b) 16 times less
- c) 17 times less
- d) 24 times less
Correct answer is option 'C'. Can you explain this answer?
Dean has a cardboard box whose length, breadth and height are in the ratio 1:2:3. He makes a new box such that the length, breadth and height got increased by 100%, 200% and 200% respectively. How much less is volume of old box than the new box?
a)
12 times less
b)
16 times less
c)
17 times less
d)
24 times less
|
Ravi Verma answered |
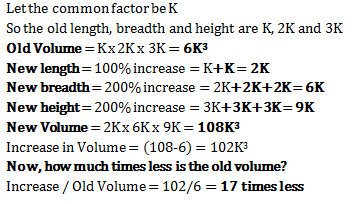
If the outer diameter of a pipe 21 m long is 1 m, then its curved surface area is- a)66 m2
- b)21 m2
- c)42 m2
- d)63 m2
Correct answer is option 'A'. Can you explain this answer?
If the outer diameter of a pipe 21 m long is 1 m, then its curved surface area is
a)
66 m2
b)
21 m2
c)
42 m2
d)
63 m2
|
|
Prateek Kushwaha answered |
Use formula of corved surface area..
2¶rh
2¶rh
The radius of two similar right circular cones are 2 cm and 6 cm. The ratio of their volumes is- a)1 : 3
- b)1 : 9
- c)9 : 1
- d)1 : 27
Correct answer is option 'D'. Can you explain this answer?
The radius of two similar right circular cones are 2 cm and 6 cm. The ratio of their volumes is
a)
1 : 3
b)
1 : 9
c)
9 : 1
d)
1 : 27
|
Nilanjan Sharma answered |
Let the volume two cones be v1 & v2 & r1 and r2 be the radii of the two right circular cones & height of the two cones be h.
Ratio of base radii = r1:r2= 3 : 5
Volume of cone = 1/3πr^2h
Volume of first cone (v1)1/Volume of second cone (v2)
=(1/3�π�r1^2�h)/(1/3�π�r2^2�h)
= (1/3�π�3^2�h)/(1/3�π�5^2�h)
= r1^2/r2^2
= 3^2/5^2
= 9/25
= 9 : 25
Hence, the ratio of their volumes is 9 : 25
Nikita has to make her project on 'Monument in India'. She decided to make her project on Gol Gumbaz monument. She already knows following things about it : - It is located in a small town in Northern Karnataka.
- It reaches up to 51 meters in height while the giant dome has an external diameter of 44 meters, making it one of the largest domes ever built.
- At each of the four corners of the cube is a dome shaped octagonal tower seven stories high with a staircase inside.
Help her in making project by answering the following questions :Q. What is the height of the cuboidal part?- a)14 m
- b)7 m
- c)29 m
- d)18 m
Correct answer is option 'C'. Can you explain this answer?
Nikita has to make her project on 'Monument in India'. She decided to make her project on Gol Gumbaz monument. She already knows following things about it :
- It is located in a small town in Northern Karnataka.
- It reaches up to 51 meters in height while the giant dome has an external diameter of 44 meters, making it one of the largest domes ever built.
- At each of the four corners of the cube is a dome shaped octagonal tower seven stories high with a staircase inside.
Help her in making project by answering the following questions :
Q. What is the height of the cuboidal part?
a)
14 m
b)
7 m
c)
29 m
d)
18 m
|
Swati Verma answered |
Total height of monument = 51 m
Radius of hemispherical dome part = height of hemispherical dome = 22 m
Height of the cuboidal part = 51 m – 22m
= 29 m
The area surrounded by a conical tent is 4526 m2. If the cost of canvas is Rs. 17 per square meter, then find the total cost of canvas.- a)Rs. 52100
- b)Rs. 76942
- c)Rs. 65000
- d)Rs. 85246
Correct answer is option 'B'. Can you explain this answer?
The area surrounded by a conical tent is 4526 m2. If the cost of canvas is Rs. 17 per square meter, then find the total cost of canvas.
a)
Rs. 52100
b)
Rs. 76942
c)
Rs. 65000
d)
Rs. 85246
|
Arun Sharma answered |
total cost = area of canvas used x cost of per meter square canvas
= 4526 x 17
= Rs. 76942
The cost of cementing the inner curved surface of a 14 m deep well of radius 2 m at the rate of Rs 2 per m2 is- a)Rs 352.
- b)Rs 176.
- c)Rs 56.
- d)Rs 112.
Correct answer is option 'A'. Can you explain this answer?
The cost of cementing the inner curved surface of a 14 m deep well of radius 2 m at the rate of Rs 2 per m2 is
a)
Rs 352.
b)
Rs 176.
c)
Rs 56.
d)
Rs 112.
|
Kamna Science Academy answered |
Depth of well(h) = 14m
radius of well(r) = 2m
radius of well(r) = 2m
Inner surface area of well(like a cylinder) = 2πrh
surface area= 2 x 22/7 x 2 x 14 = 176 m2
cost of cementing = ₹2 per m2
Total Cost = 176 x 2 = ₹352
If the ratio of volumes of two spheres is 1 : 8, then the ratio of their surface areas is :- a)1 : 2
- b)1 : 4
- c)1 : 8
- d)1 : 16
Correct answer is option 'B'. Can you explain this answer?
If the ratio of volumes of two spheres is 1 : 8, then the ratio of their surface areas is :
a)
1 : 2
b)
1 : 4
c)
1 : 8
d)
1 : 16
|
|
Sarita Reddy answered |
The correct answer is option 'B', the ratio of surface areas is 1:4.
The ratio of the surface areas of two spheres is the square of the ratio of their radii. If the ratio of volumes of two spheres is 1:8, then the ratio of their radii is 3:2 . Therefore, the ratio of the surface areas of the two spheres is (3/2)^2 = 9/4 = 1:4
The volume of a spherical shell whose internal and external diameters are 8 cm and 10 cm respectively (in cubic cm) is:- a)122π/3
- b)244π/3
- c)212
- d)257
Correct answer is option 'B'. Can you explain this answer?
The volume of a spherical shell whose internal and external diameters are 8 cm and 10 cm respectively (in cubic cm) is:
a)
122π/3
b)
244π/3
c)
212
d)
257
|
|
Sarita Reddy answered |
The volume of a spherical shell is the difference between the volumes of the two spheres that make up the shell. The internal sphere has a diameter of 8 cm, and the external sphere has a diameter of 10 cm. To find the volume of the spherical shell, we can first find the volume of each of the two spheres and then subtract the volume of the smaller sphere from the volume of the larger sphere.
The volume of a sphere is given by the formula V = (4/3)πr^3, where V is the volume, r is the radius of the sphere, and π is a mathematical constant approximately equal to 3.14159. The radius of the internal sphere is 4 cm (half of the diameter), and the radius of the external sphere is 5 cm (half of the diameter). Therefore, the volume of the internal sphere is (4/3)π(4^3) = (4/3)π64 = 256π/3 cubic cm, and the volume of the external sphere is (4/3)π(5^3) = (4/3)π125 = 500π/3 cubic cm.
To find the volume of the spherical shell, we subtract the volume of the internal sphere from the volume of the external sphere: 500π/3 - 256π/3 = 244π/3 cubic cm. Therefore, the volume of the spherical shell is 244π/3 cubic cm, which corresponds to answer choice (b).
The dimensions of the room are 7 m × 6m × 5 m. The cost of white washing the walls of the room and the ceiling at the rate of Rs 10.50 per m2 is- a)Rs 1866
- b)Rs 1860
- c)Rs 1806
- d)Rs 1800
Correct answer is option 'C'. Can you explain this answer?
The dimensions of the room are 7 m × 6m × 5 m. The cost of white washing the walls of the room and the ceiling at the rate of Rs 10.50 per m2 is
a)
Rs 1866
b)
Rs 1860
c)
Rs 1806
d)
Rs 1800
|
Mad Sister. answered |
CSA of room +area of base
so 2(l+b)*h+l*b
2(7+6)*5+7*6
2(13)*5+42.
26*5+42
130+42
172
cost =area * rate
cost =172*10.50
=1806 ANSWER...
so 2(l+b)*h+l*b
2(7+6)*5+7*6
2(13)*5+42.
26*5+42
130+42
172
cost =area * rate
cost =172*10.50
=1806 ANSWER...
If the curved surface area of a cylinder is 1760 sq. cm and its base radius is 14 cm, then its height is :- a)10 cm
- b)15 cm
- c)20 cm
- d)40 cm
Correct answer is option 'C'. Can you explain this answer?
If the curved surface area of a cylinder is 1760 sq. cm and its base radius is 14 cm, then its height is :
a)
10 cm
b)
15 cm
c)
20 cm
d)
40 cm
|
|
Sarthak Satav answered |
I think answer is 40 cm because
C.S.A. OF CYLINDER = 2πrh
1760 cm² = 2 x 22/7 x 14 x h
(1760 x 7 ) / 22 x 2 x 14 = h
that is
40 cm
C.S.A. OF CYLINDER = 2πrh
1760 cm² = 2 x 22/7 x 14 x h
(1760 x 7 ) / 22 x 2 x 14 = h
that is
40 cm
If the radius of a sphere is reduced by a factor of 3. Its volume is- a)reduced by 1/9 of the former volume.
- b)increased by 1/9 of the former volume
- c)reduced by 1/27 of the former volume.
- d)increased by 1/27 of the former volume
Correct answer is option 'C'. Can you explain this answer?
If the radius of a sphere is reduced by a factor of 3. Its volume is
a)
reduced by 1/9 of the former volume.
b)
increased by 1/9 of the former volume
c)
reduced by 1/27 of the former volume.
d)
increased by 1/27 of the former volume
|
|
Ankita answered |
Reduced by 1/27 of the former volume, Option C.
The total surface area of a hemispherical bowl of diameter 28 cm is- a)1848 cm2
- b)1800 cm2
- c)1600 cm2
- d)1648 cm2
Correct answer is option 'A'. Can you explain this answer?
The total surface area of a hemispherical bowl of diameter 28 cm is
a)
1848 cm2
b)
1800 cm2
c)
1600 cm2
d)
1648 cm2
|
|
Sarita Reddy answered |
Correct, option 'A' is the correct answer.
The total surface area of a hemispherical bowl can be calculated by using the formula 4πr^2, where r is the radius of the bowl.
Given the diameter of the bowl is 28 cm, the radius of the bowl is 14cm.
So, the total surface area of the hemispherical bowl of diameter 28 cm is 4π(14)^2 = 4π*196 =784π = 1848 cm^2 (approximately)
Alternatively, we can also use the formula 2πr^2 + 2πrr (r being the radius of the bowl) to calculate the total surface area of the hemispherical bowl.
In this case, 2π(14)^2 + 2π(14) 14 = 2π196 + 2π196 = 392π = 1848 cm^2 (approximately)
Hence the answer is A. 1848 cm2
If a hemi-spherical dome has an inner diameter of 28 m, then its volume (in m3) is :- a)6186.60
- b)5749.33
- c)7099.33
- d)7459.33
Correct answer is option 'B'. Can you explain this answer?
If a hemi-spherical dome has an inner diameter of 28 m, then its volume (in m3) is :
a)
6186.60
b)
5749.33
c)
7099.33
d)
7459.33
|
|
Sarita Reddy answered |
Correct, option 'B' is the correct answer.
The volume of a hemisphere can be calculated using the formula, V = 2/3 * π * r^3, where r is the radius of the hemisphere.
A hemi-spherical dome has an inner diameter of 28 m, so the radius of the hemisphere is half of the diameter which is 14m.
So, the volume of the hemi-spherical dome is: 2/3 * π * (14)^3 = 2/3 * π * 2744 = 5749.33 m^3 (approximately)
Hence the answer is B. 5749.33 m^3
A cubical tank has an edge equal to 6 m. The amount of water it will contain when it is one-third filled is- a)64000 litres
- b)72000 litres
- c)54000 litres
- d)36000 litres
Correct answer is option 'B'. Can you explain this answer?
A cubical tank has an edge equal to 6 m. The amount of water it will contain when it is one-third filled is
a)
64000 litres
b)
72000 litres
c)
54000 litres
d)
36000 litres
|
|
Nishanth Das answered |
Given:
Edge of cubic tank = 6 m
The tank is one-third filled.
To find:
The amount of water in the tank.
Solution:
Volume of the tank = (Edge)^3
= (6)^3
= 216 m^3
The tank is one-third filled.
So, the amount of water in the tank = (1/3) * 216 m^3
= 72 m^3
1 m^3 = 1000 litres
Therefore, 72 m^3 = 72 * 1000 litres
= <72*1000=72000>>72000 litres
Hence, the amount of water in the tank when it is one-third filled is 72000 litres.
Therefore, option (b) is the correct answer.
Edge of cubic tank = 6 m
The tank is one-third filled.
To find:
The amount of water in the tank.
Solution:
Volume of the tank = (Edge)^3
= (6)^3
= 216 m^3
The tank is one-third filled.
So, the amount of water in the tank = (1/3) * 216 m^3
= 72 m^3
1 m^3 = 1000 litres
Therefore, 72 m^3 = 72 * 1000 litres
= <72*1000=72000>>72000 litres
Hence, the amount of water in the tank when it is one-third filled is 72000 litres.
Therefore, option (b) is the correct answer.
Chapter doubts & questions for Surface Area & Volumes - Mathematics for EmSAT Achieve 2025 is part of EmSAT Achieve exam preparation. The chapters have been prepared according to the EmSAT Achieve exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Surface Area & Volumes - Mathematics for EmSAT Achieve in English & Hindi are available as part of EmSAT Achieve exam.
Download more important topics, notes, lectures and mock test series for EmSAT Achieve Exam by signing up for free.
Mathematics for EmSAT Achieve
146 videos|222 docs|220 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily