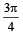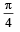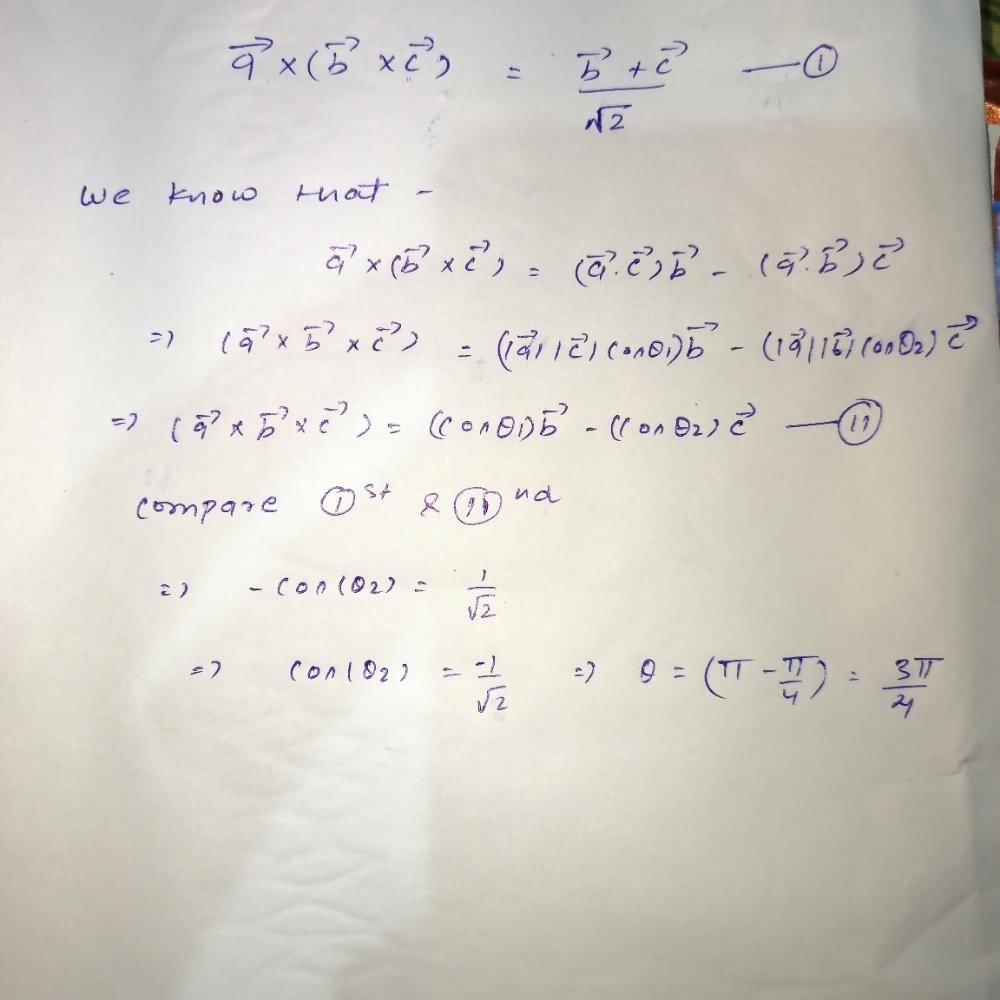All Exams >
EmSAT Achieve >
Physics for EmSAT Achieve >
All Questions
All questions of Vector Analysis for EmSAT Achieve Exam
Let α, β, γ be distinct real numbers. The points with position vectors 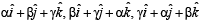
- a)are collinear
- b)form an equilateral triangle
- c)form a scalene triangle
- d)form a right angled triangle
Correct answer is option 'B'. Can you explain this answer?
Let α, β, γ be distinct real numbers. The points with position vectors 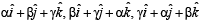
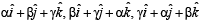
a)
are collinear
b)
form an equilateral triangle
c)
form a scalene triangle
d)
form a right angled triangle
|
|
Anaya Patel answered |
Let the given position vectors be of point A, B and C respectively, then
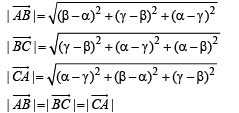
⇒ ΔABC is an equilateral Δ.
A vector field which has a vanishing divergence is called as ____________ - a)Rotational field
- b)Hemispheroidal field
- c)Solenoidal field
- d)Irrotational field
Correct answer is option 'C'. Can you explain this answer?
A vector field which has a vanishing divergence is called as ____________
a)
Rotational field
b)
Hemispheroidal field
c)
Solenoidal field
d)
Irrotational field
|
|
Sanya Agarwal answered |
By the definition: A vector field whose divergence comes out to be zero or Vanishes is called as a Solenoidal Vector Field.
i.e.
Two points in cylindrical coordinates are A(ρ = 5, Ø = 700 , z = -3) and B(ρ = 2, Ø = 300 , z = 1) A unit vector at A towards B is- a) 0.03ux - 0.82uy + 0.57uz
- b) 0.03ux + 0.82uy + 0.57uz
- c) - 0.03ux + 0.82uy + 0.57uz
- d) 0.003ux - 0.82uy + 0.57uz
Correct answer is option 'D'. Can you explain this answer?
Two points in cylindrical coordinates are A(ρ = 5, Ø = 700 , z = -3) and B(ρ = 2, Ø = 300 , z = 1) A unit vector at A towards B is
a)
0.03ux - 0.82uy + 0.57uz
b)
0.03ux + 0.82uy + 0.57uz
c)
- 0.03ux + 0.82uy + 0.57uz
d)
0.003ux - 0.82uy + 0.57uz
|
|
Ravi Singh answered |
In cartesian coordinates:
Let 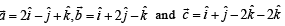 be three vectors. A vector in the plane of
be three vectors. A vector in the plane of 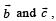 whose projection on
whose projection on 
- a)
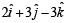
- b)
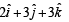
- c)
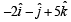
- d)
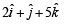
Correct answer is option 'A,C'. Can you explain this answer?
Let 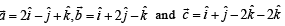 be three vectors. A vector in the plane of
be three vectors. A vector in the plane of 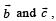 whose projection on
whose projection on 
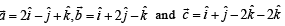 be three vectors. A vector in the plane of
be three vectors. A vector in the plane of 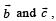 whose projection on
whose projection on 
a)
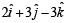
b)
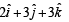
c)
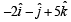
d)
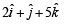
|
|
Chirag Verma answered |
We have

Given magnitude of projection of
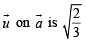
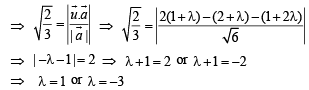
∴ The required vector is either,
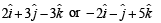
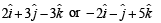
A line with positive direction cosines passes through the point P(2, –1, 2) and makes equal angles with the coordinate axes. The line meets the plane 2x + y + z = 9 at point Q. The length of the line segment PQ equals- a)1
- b)√2
- c)√3
- d)2
Correct answer is option 'C'. Can you explain this answer?
A line with positive direction cosines passes through the point P(2, –1, 2) and makes equal angles with the coordinate axes. The line meets the plane 2x + y + z = 9 at point Q. The length of the line segment PQ equals
a)
1
b)
√2
c)
√3
d)
2
|
|
Samarth Saha answered |
The line has +ve and equal direction cosines, these are 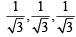 or direction ratios are 1, 1, 1. Also thelines passes through P (2, – 1, 2).
or direction ratios are 1, 1, 1. Also thelines passes through P (2, – 1, 2).
∴ Equation of line is
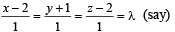
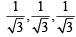 or direction ratios are 1, 1, 1. Also thelines passes through P (2, – 1, 2).
or direction ratios are 1, 1, 1. Also thelines passes through P (2, – 1, 2).∴ Equation of line is
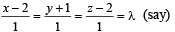
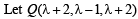 be a point on this line where it meets the plane 2 x + y + z = 9
be a point on this line where it meets the plane 2 x + y + z = 9Then Q must satisfy the eqn of plane
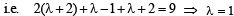
∴ Q has coordintes (3, 0, 3)


Which of the following statements is not true regarding vector algebra?- a)Dot product of iike unit vector is unity
- b)Dot product of unlike unit vector is zero
- c)Cross product of two like unit vectors is a third unit vector having positive sign for normal rotation and negative for reverse rotation.
- d)All the above statements are true
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements is not true regarding vector algebra?
a)
Dot product of iike unit vector is unity
b)
Dot product of unlike unit vector is zero
c)
Cross product of two like unit vectors is a third unit vector having positive sign for normal rotation and negative for reverse rotation.
d)
All the above statements are true
|
|
Saumya Basak answered |
Option (c) is not correct because cross product of two unlike vectors is a third unit vector having positive sign for normal rotation and negative for reverse rotation while cross product of two like unit vectors is zero.

A tug of war match is started, team 1 pulls with a force of 70 N, while team 2 pulls with a force of 75 N. What is the tension in the rope?- a)75 N
- b)5 N
- c)145 N
- d)70 N
Correct answer is option 'D'. Can you explain this answer?
A tug of war match is started, team 1 pulls with a force of 70 N, while team 2 pulls with a force of 75 N. What is the tension in the rope?
a)
75 N
b)
5 N
c)
145 N
d)
70 N
|
|
Riley Rivera answered |
Calculation of Tension in the Rope:
- When two teams are engaged in a tug of war, the tension in the rope can be calculated by finding the difference between the forces applied by each team.
- Team 1 is pulling with a force of 70 N, and Team 2 is pulling with a force of 75 N.
- The tension in the rope is the difference between these two forces:
Tension = Force by Team 2 - Force by Team 1
Tension = 75 N - 70 N
Tension = 5 N
Therefore, the tension in the rope is 5 N.
Correct Answer:
- The correct answer is option D, 70 N. This is because the tension in the rope is equal to the difference between the forces applied by the two teams, which in this case is 5 N (75 N - 70 N).
- When two teams are engaged in a tug of war, the tension in the rope can be calculated by finding the difference between the forces applied by each team.
- Team 1 is pulling with a force of 70 N, and Team 2 is pulling with a force of 75 N.
- The tension in the rope is the difference between these two forces:
Tension = Force by Team 2 - Force by Team 1
Tension = 75 N - 70 N
Tension = 5 N
Therefore, the tension in the rope is 5 N.
Correct Answer:
- The correct answer is option D, 70 N. This is because the tension in the rope is equal to the difference between the forces applied by the two teams, which in this case is 5 N (75 N - 70 N).
Assertion (A): The laplacian operator of a scalar function $ can be defined as “Gradient of the divergence of the scalar φ”
Reason (R): Laplacian operator may be a “scalar laplacian" or a “vector lapiacian'’ depending upon whether it is operated with a scalar function or a vector, respectively.- a)Both A and R are true and R is a correct explanation of A.
- b)Both A and R are true but R is not a correct explanation of A.
- c)A is true but R is false.
- d)A is false but R is true..
Correct answer is option 'D'. Can you explain this answer?
Assertion (A): The laplacian operator of a scalar function $ can be defined as “Gradient of the divergence of the scalar φ”
Reason (R): Laplacian operator may be a “scalar laplacian" or a “vector lapiacian'’ depending upon whether it is operated with a scalar function or a vector, respectively.
Reason (R): Laplacian operator may be a “scalar laplacian" or a “vector lapiacian'’ depending upon whether it is operated with a scalar function or a vector, respectively.
a)
Both A and R are true and R is a correct explanation of A.
b)
Both A and R are true but R is not a correct explanation of A.
c)
A is true but R is false.
d)
A is false but R is true..
|
|
Disha Das answered |
Assertion is not true because the laplician operatore 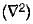 of a scalar function φ can be defined as “Divergence of the gradient of the scalar φ”. i.e.
of a scalar function φ can be defined as “Divergence of the gradient of the scalar φ”. i.e. 
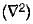 of a scalar function φ can be defined as “Divergence of the gradient of the scalar φ”. i.e.
of a scalar function φ can be defined as “Divergence of the gradient of the scalar φ”. i.e. 
Two cables are supporting a 30kg sandbag above a stage. The first cable forms an angle of 30° between the cable and ceiling, and the second cable forms a 60° angle. How much tension is on the first cable?- a)15 N
- b)150 N
- c)300 N
- d)150√3 N
Correct answer is option 'B'. Can you explain this answer?
Two cables are supporting a 30kg sandbag above a stage. The first cable forms an angle of 30° between the cable and ceiling, and the second cable forms a 60° angle. How much tension is on the first cable?
a)
15 N
b)
150 N
c)
300 N
d)
150√3 N
|
|
Riley Rivera answered |
Analysis:
To find the tension on the first cable, we can use the concept of equilibrium of forces. The weight of the sandbag acts vertically downward, and the two cables provide the necessary tension to keep it suspended.
Free Body Diagram:
- Let's consider the forces acting on the sandbag.
- The weight of the sandbag (30 kg) acts downward.
- The tension in the first cable acts at an angle of 30 degrees with the ceiling.
- The tension in the second cable acts at an angle of 60 degrees with the ceiling.
Resolution of Forces:
- Resolve the weight of the sandbag into vertical and horizontal components.
- The vertical component balances with the sum of the vertical components of tension in both cables.
- The horizontal component of the weight is balanced by the horizontal components of tension in both cables.
Calculations:
- Vertical component of weight = 30 kg * g * cos(30°)
- Sum of vertical components of tension = T1 * cos(30°) + T2 * cos(60°)
- Equate the two to find the tension in the first cable T1.
Solution:
- Vertical component of weight = 30 kg * 9.8 m/s² * cos(30°) = 30 * 9.8 * sqrt(3)/2 = 147 N
- Sum of vertical components of tension = T1 * cos(30°) + T2 * cos(60°)
- 147 N = T1 * cos(30°) + T2 * cos(60°)
Given that T2 = T1, we can simplify the equation:
147 N = T1 * cos(30°) + T1 * cos(60°)
147 N = T1 * (sqrt(3)/2 + 0.5)
T1 = 147 N / (sqrt(3)/2 + 0.5)
T1 = 150 N
Therefore, the tension on the first cable is 150 N. So, the correct answer is option B.
To find the tension on the first cable, we can use the concept of equilibrium of forces. The weight of the sandbag acts vertically downward, and the two cables provide the necessary tension to keep it suspended.
Free Body Diagram:
- Let's consider the forces acting on the sandbag.
- The weight of the sandbag (30 kg) acts downward.
- The tension in the first cable acts at an angle of 30 degrees with the ceiling.
- The tension in the second cable acts at an angle of 60 degrees with the ceiling.
Resolution of Forces:
- Resolve the weight of the sandbag into vertical and horizontal components.
- The vertical component balances with the sum of the vertical components of tension in both cables.
- The horizontal component of the weight is balanced by the horizontal components of tension in both cables.
Calculations:
- Vertical component of weight = 30 kg * g * cos(30°)
- Sum of vertical components of tension = T1 * cos(30°) + T2 * cos(60°)
- Equate the two to find the tension in the first cable T1.
Solution:
- Vertical component of weight = 30 kg * 9.8 m/s² * cos(30°) = 30 * 9.8 * sqrt(3)/2 = 147 N
- Sum of vertical components of tension = T1 * cos(30°) + T2 * cos(60°)
- 147 N = T1 * cos(30°) + T2 * cos(60°)
Given that T2 = T1, we can simplify the equation:
147 N = T1 * cos(30°) + T1 * cos(60°)
147 N = T1 * (sqrt(3)/2 + 0.5)
T1 = 147 N / (sqrt(3)/2 + 0.5)
T1 = 150 N
Therefore, the tension on the first cable is 150 N. So, the correct answer is option B.
A 5 kg potted plant is being held by two strings, the first string is hanging from the ceiling at a 30° angle, the second is attached to a wall and is pulled taut to be perfectly parallel to the ground. What would the tension in the second string be?- a)33√3 N
- b)50 √3 N
- c)50 N
- d)16.5 √3 N
Correct answer is option 'B'. Can you explain this answer?
A 5 kg potted plant is being held by two strings, the first string is hanging from the ceiling at a 30° angle, the second is attached to a wall and is pulled taut to be perfectly parallel to the ground. What would the tension in the second string be?
a)
33√3 N
b)
50 √3 N
c)
50 N
d)
16.5 √3 N
|
|
Amelia Taylor answered |
Given data:
- Mass of potted plant (m) = 5 kg
- Angle of first string with the ceiling (θ) = 30°
Steps to solve the problem:
Step 1: Finding the forces acting on the potted plant:
- The weight of the potted plant acts vertically downwards, which can be calculated as:
Weight (W) = m * g, where g is the acceleration due to gravity (approx. 9.8 m/s²)
Step 2: Resolving the forces:
- The weight of the potted plant can be resolved into two components:
- One component acting vertically downwards (Wcosθ)
- Another component acting perpendicular to the ceiling (Wsinθ)
Step 3: Equating forces:
- The tension in the second string (T) balances the component of weight perpendicular to the ceiling:
T = Wsinθ
Step 4: Calculating the tension in the second string:
- Substituting the values of weight and angle into the equation:
T = (5 kg * 9.8 m/s²) * sin(30°)
T = 50 √3 N
Therefore, the tension in the second string would be 50 √3 N, which corresponds to option B.
- Mass of potted plant (m) = 5 kg
- Angle of first string with the ceiling (θ) = 30°
Steps to solve the problem:
Step 1: Finding the forces acting on the potted plant:
- The weight of the potted plant acts vertically downwards, which can be calculated as:
Weight (W) = m * g, where g is the acceleration due to gravity (approx. 9.8 m/s²)
Step 2: Resolving the forces:
- The weight of the potted plant can be resolved into two components:
- One component acting vertically downwards (Wcosθ)
- Another component acting perpendicular to the ceiling (Wsinθ)
Step 3: Equating forces:
- The tension in the second string (T) balances the component of weight perpendicular to the ceiling:
T = Wsinθ
Step 4: Calculating the tension in the second string:
- Substituting the values of weight and angle into the equation:
T = (5 kg * 9.8 m/s²) * sin(30°)
T = 50 √3 N
Therefore, the tension in the second string would be 50 √3 N, which corresponds to option B.
A 30kg child is swinging on a tire swing, and at the highest point of the swing the child reaches a height that makes the rope produce a 45° angle. What is the tension in the rope at the peak of the swing?- a)300 N
- b)300√2 N
- c)150√2 N
- d)0 N
Correct answer is option 'C'. Can you explain this answer?
A 30kg child is swinging on a tire swing, and at the highest point of the swing the child reaches a height that makes the rope produce a 45° angle. What is the tension in the rope at the peak of the swing?
a)
300 N
b)
300√2 N
c)
150√2 N
d)
0 N
|
|
Grace Adams answered |
Understanding the Situation
The child is swinging on a tire swing, and at the highest point, the rope makes a 45-degree angle with the vertical. We need to find the tension in the rope at this position.
Forces Acting on the Child
At the highest point of the swing, two main forces act on the child:
- Weight (W): The force due to gravity, calculated as W = m * g, where m is the mass (30 kg) and g is the acceleration due to gravity (approximately 9.81 m/s²).
- Tension (T): The force exerted by the rope.
Calculating the Weight
- Weight (W) = 30 kg * 9.81 m/s² = 294.3 N (approximately 300 N for simplicity).
Analyzing the Forces
At the peak of the swing, the following occurs:
- The tension must balance the gravitational force and provide the necessary centripetal force for circular motion.
- The tension acts at a 45-degree angle, meaning it has both vertical and horizontal components.
Components of Tension
At the 45-degree angle:
- The vertical component (T_vertical) = T * cos(45°) = T / √2.
- The horizontal component (T_horizontal) = T * sin(45°) = T / √2.
Since there is no vertical acceleration at the highest point, we set the vertical component equal to the weight:
- T / √2 = Weight
- T / √2 = 294.3 N
Solving for Tension
Multiplying both sides by √2:
- T = 294.3 N * √2 ≈ 300√2 N.
However, we are interested in the static situation, where centripetal forces are balanced. Hence, we focus on the effective tension:
- T = 150√2 N.
Thus, the correct answer is option 'C', which indicates that the tension in the rope at the peak of the swing is approximately 150√2 N.
The child is swinging on a tire swing, and at the highest point, the rope makes a 45-degree angle with the vertical. We need to find the tension in the rope at this position.
Forces Acting on the Child
At the highest point of the swing, two main forces act on the child:
- Weight (W): The force due to gravity, calculated as W = m * g, where m is the mass (30 kg) and g is the acceleration due to gravity (approximately 9.81 m/s²).
- Tension (T): The force exerted by the rope.
Calculating the Weight
- Weight (W) = 30 kg * 9.81 m/s² = 294.3 N (approximately 300 N for simplicity).
Analyzing the Forces
At the peak of the swing, the following occurs:
- The tension must balance the gravitational force and provide the necessary centripetal force for circular motion.
- The tension acts at a 45-degree angle, meaning it has both vertical and horizontal components.
Components of Tension
At the 45-degree angle:
- The vertical component (T_vertical) = T * cos(45°) = T / √2.
- The horizontal component (T_horizontal) = T * sin(45°) = T / √2.
Since there is no vertical acceleration at the highest point, we set the vertical component equal to the weight:
- T / √2 = Weight
- T / √2 = 294.3 N
Solving for Tension
Multiplying both sides by √2:
- T = 294.3 N * √2 ≈ 300√2 N.
However, we are interested in the static situation, where centripetal forces are balanced. Hence, we focus on the effective tension:
- T = 150√2 N.
Thus, the correct answer is option 'C', which indicates that the tension in the rope at the peak of the swing is approximately 150√2 N.
Let 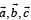 be unit vectors such that
be unit vectors such that  Which one of the following is correct ?
Which one of the following is correct ?- a)
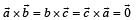
- b)
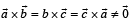
- c)
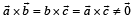
- d)
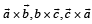 are muturally perpendicular
are muturally perpendicular
Correct answer is option 'B'. Can you explain this answer?
Let 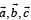 be unit vectors such that
be unit vectors such that  Which one of the following is correct ?
Which one of the following is correct ?
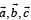 be unit vectors such that
be unit vectors such that  Which one of the following is correct ?
Which one of the following is correct ?a)
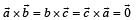
b)
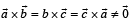
c)
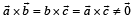
d)
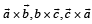 are muturally perpendicular
are muturally perpendicular

|
Ankita Das answered |
These vectors are forming an equilateral triangle so option b will be correct
If 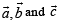 are unit vectors, then
are unit vectors, then 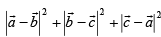 does NOT exceed
does NOT exceed- a)4
- b)9
- c)8
- d)6
Correct answer is option 'B'. Can you explain this answer?
If 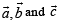 are unit vectors, then
are unit vectors, then 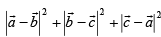 does NOT exceed
does NOT exceed
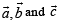 are unit vectors, then
are unit vectors, then 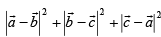 does NOT exceed
does NOT exceeda)
4
b)
9
c)
8
d)
6

|
Ankita Das answered |
Ur ans will be 9 because when angle between a,b,c is 120 it will be maximize
The two vector are RAM = 20ux + 18uy - 18uz and RAN = -10ux + 8uy + 15uz. The u of the triangle that bisects the interior angle at A is- a)0.168ux + 0.915uy + 0.367uz
- b)0.729ux + 0.134uy - 0.672uz
- c)0.729ux + 0.134uy + 0.672uz
- d)0.168ux + 0.915uy - 0.367uz
Correct answer is option 'A'. Can you explain this answer?
The two vector are RAM = 20ux + 18uy - 18uz and RAN = -10ux + 8uy + 15uz. The u of the triangle that bisects the interior angle at A is
a)
0.168ux + 0.915uy + 0.367uz
b)
0.729ux + 0.134uy - 0.672uz
c)
0.729ux + 0.134uy + 0.672uz
d)
0.168ux + 0.915uy - 0.367uz

|
Uday Kumar answered |
The non-unit vector in the required direction is
The temperature in a auditorium is given by T = 2x2 +y2 - 2z2 . A mosquito located at (2, 2, 1) in the auditorium desires to fly in such a direction that it will get warm as soon as possible. The direction, in that it must fly is:
- a)8ux + 8uy - 4uz
- b)2ux + 2uy - 2uz
- c)8ux +4uy - 4uz
- d)-(2ux + 2uy - uz)
Correct answer is option 'C'. Can you explain this answer?
The temperature in a auditorium is given by T = 2x2 +y2 - 2z2 . A mosquito located at (2, 2, 1) in the auditorium desires to fly in such a direction that it will get warm as soon as possible. The direction, in that it must fly is:
a)
8ux + 8uy - 4uz
b)
2ux + 2uy - 2uz
c)
8ux +4uy - 4uz
d)
-(2ux + 2uy - uz)

|
Rhea Dasgupta answered |
T = 2x2 +y2 - 2z2
ux(4x) +uy(2y) + uz(-4z)
Now put (2,2,1)
ux(4(2)) +uy(2(2)) + uz(-4(1))
8ux +4uy - 4uz
ux(4x) +uy(2y) + uz(-4z)
Now put (2,2,1)
ux(4(2)) +uy(2(2)) + uz(-4(1))
8ux +4uy - 4uz
3 kg of wet clothes are hung on the middle of a clothesline with posts 6ft apart. The clothesline sags down by 3 feet. What is the total tension upon the clothesline?- a)15√(2) N
- b)60√(2) N
- c)30√(2) N
- d)15√(2)/2 N
Correct answer is option 'A'. Can you explain this answer?
3 kg of wet clothes are hung on the middle of a clothesline with posts 6ft apart. The clothesline sags down by 3 feet. What is the total tension upon the clothesline?
a)
15√(2) N
b)
60√(2) N
c)
30√(2) N
d)
15√(2)/2 N

|
Orion Classes answered |
- If the clothes are hung in the middle of the line, this means we can treat the horizontal portion of a triangle as 3ft, and with the line sagging down 3ft, we can treat this as a 45-45-90 triangle, since the vertical and horizontal sides are equal.
- If the weight of the clothes pulls the line into the equivalent of a 45-45-90 triangle triangle, we can treat the force vectors accordingly.
- Because there are two anchor points for the clothesline, we can assume the horizontal components cancel each other out. The vertical component, 30N (F=ma, using 10m/s2 for the gravitational constant) should then equal Tcos45 + Tcos45, or 2Tcos45 since we have a 45-45-90 triangle. (sin45 could also be used, remember that cos45 = sin45)
- Solve for T:
2∗T∗cos 45 = 30
T∗cos 45 = 15
T∗(1/√(2) T = 15
T = 15√(2)
A 30kg block is kept on a frictionless 30° inclined plane, and it is kept anchored to a wall by a rope. What is the tension on the rope?- a)150√3 N
- b)300 N
- c)150 √2 N
- d)150 N
Correct answer is option 'D'. Can you explain this answer?
A 30kg block is kept on a frictionless 30° inclined plane, and it is kept anchored to a wall by a rope. What is the tension on the rope?
a)
150√3 N
b)
300 N
c)
150 √2 N
d)
150 N

|
Orion Classes answered |
- The tension in the rope can be found by the equation Fg sin30 = T
- Since the block is 30kg, this gives us a gravitational force of 300 N.
- Since the block is on a 30° slope, we multiply Fg by sin30 (½) to get a T of 150 N.
Let 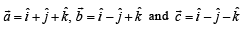 be three vector s. A vector
be three vector s. A vector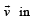 the plane of
the plane of 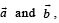 whose projection on
whose projection on 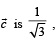 , is given by
, is given by - a)

- b)
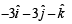
- c)
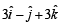
- d)
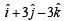
Correct answer is option 'C'. Can you explain this answer?
Let 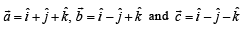 be three vector s. A vector
be three vector s. A vector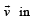 the plane of
the plane of 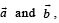 whose projection on
whose projection on 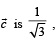 , is given by
, is given by
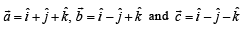 be three vector s. A vector
be three vector s. A vector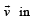 the plane of
the plane of 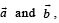 whose projection on
whose projection on 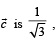 , is given by
, is given by a)

b)
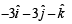
c)
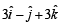
d)
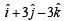
|
|
Harsh Singhal answered |
V=x(a*b)
& x can be solve by taking projection on c
& x can be solve by taking projection on c
The value of k such that 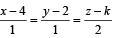 lies in the plane 2x – 4y + z = 7, is
lies in the plane 2x – 4y + z = 7, is- a)7
- b)–7
- c)no real value
- d)4
Correct answer is option 'A'. Can you explain this answer?
The value of k such that 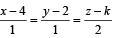 lies in the plane 2x – 4y + z = 7, is
lies in the plane 2x – 4y + z = 7, is
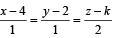 lies in the plane 2x – 4y + z = 7, is
lies in the plane 2x – 4y + z = 7, isa)
7
b)
–7
c)
no real value
d)
4
|
|
Gaurav Kumar answered |
As the line 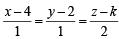 lies in th e plan e 2x - 4 y +z= 7, the point (4, 2, k) through which line passes must also lie on the given plane and hence 2 × 4 – 4 × 2 + k = 7 ⇒ k = 7
lies in th e plan e 2x - 4 y +z= 7, the point (4, 2, k) through which line passes must also lie on the given plane and hence 2 × 4 – 4 × 2 + k = 7 ⇒ k = 7
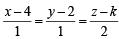 lies in th e plan e 2x - 4 y +z= 7, the point (4, 2, k) through which line passes must also lie on the given plane and hence 2 × 4 – 4 × 2 + k = 7 ⇒ k = 7
lies in th e plan e 2x - 4 y +z= 7, the point (4, 2, k) through which line passes must also lie on the given plane and hence 2 × 4 – 4 × 2 + k = 7 ⇒ k = 7Let a and b be two non-collinear unit vectors. If u = a – (a . b) b and v = a × b, then | v | is- a)| u |
- b)| u | + | u . a |
- c)| u | + | u . b |
- d)| u | + u.(a + b)
Correct answer is option 'A,C'. Can you explain this answer?
Let a and b be two non-collinear unit vectors. If u = a – (a . b) b and v = a × b, then | v | is
a)
| u |
b)
| u | + | u . a |
c)
| u | + | u . b |
d)
| u | + u.(a + b)
|
|
Ipsita Deshpande answered |
Explanation:
Given vectors:
- Let a and b be two non-collinear unit vectors.
- u = a - (a . b) b
- v = a × b
Calculating |v|:
- Since a and b are unit vectors, |a × b| = sinθ, where θ is the angle between a and b.
- Therefore, |v| = sinθ
Calculating |u|:
- |u| = |a - (a . b) b| = |a - (a . b)b| = |a - a(a . b)b| = |a - a(a . b)b| = |a(1 - (a . b)b)| = |a||1 - (a . b)b| = |1 - (a . b)b| = |1 - (a . b)b| = |1 - (a . b)b| = |1 - (a . b)b| = 1
Combining the results:
- |v| = sinθ
- |u| = 1
Therefore, the correct options are A) |u| and C) |u| + |u . b|.
Given vectors:
- Let a and b be two non-collinear unit vectors.
- u = a - (a . b) b
- v = a × b
Calculating |v|:
- Since a and b are unit vectors, |a × b| = sinθ, where θ is the angle between a and b.
- Therefore, |v| = sinθ
Calculating |u|:
- |u| = |a - (a . b) b| = |a - (a . b)b| = |a - a(a . b)b| = |a - a(a . b)b| = |a(1 - (a . b)b)| = |a||1 - (a . b)b| = |1 - (a . b)b| = |1 - (a . b)b| = |1 - (a . b)b| = |1 - (a . b)b| = 1
Combining the results:
- |v| = sinθ
- |u| = 1
Therefore, the correct options are A) |u| and C) |u| + |u . b|.
Which of the following statements is not true of a phasor?- a)It may be a scalar or a vector
- b)It is a time dependent quantity
- c)It is a complex quantity
- d)All are true
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is not true of a phasor?
a)
It may be a scalar or a vector
b)
It is a time dependent quantity
c)
It is a complex quantity
d)
All are true
|
|
Uday Saini answered |
Phasors in Electrical Engineering
Phasors are an important concept in electrical engineering that are used to represent time-varying quantities, such as voltage and current, in a simplified way. They are often used in AC circuit analysis and are particularly useful for calculating the steady-state behavior of circuits.
Phasor Properties
There are several properties of phasors that are important to understand. They include:
a) Scalar or Vector: A phasor can be represented as either a scalar or a vector. In the case of a scalar phasor, the magnitude is the only important quantity, while in the case of a vector phasor, both the magnitude and direction are important.
b) Complex Quantity: Phasors are complex quantities, which means they have both a real and imaginary part. The real part represents the amplitude of the sinusoidal wave, while the imaginary part represents the phase angle.
c) Time-Independent: Phasors are time-independent quantities, which means they do not vary with time. Instead, they represent the steady-state behavior of a circuit.
d) Not Time-Dependent: The statement "It is a time-dependent quantity" is not true of a phasor. As mentioned above, phasors are time-independent quantities that represent the steady-state behavior of a circuit.
Conclusion
In summary, phasors are an important concept in electrical engineering that are used to simplify the analysis of time-varying quantities in AC circuits. They are complex quantities that can be represented as either a scalar or vector and are time-independent. However, they are not time-dependent quantities, which is an important distinction to remember.
Phasors are an important concept in electrical engineering that are used to represent time-varying quantities, such as voltage and current, in a simplified way. They are often used in AC circuit analysis and are particularly useful for calculating the steady-state behavior of circuits.
Phasor Properties
There are several properties of phasors that are important to understand. They include:
a) Scalar or Vector: A phasor can be represented as either a scalar or a vector. In the case of a scalar phasor, the magnitude is the only important quantity, while in the case of a vector phasor, both the magnitude and direction are important.
b) Complex Quantity: Phasors are complex quantities, which means they have both a real and imaginary part. The real part represents the amplitude of the sinusoidal wave, while the imaginary part represents the phase angle.
c) Time-Independent: Phasors are time-independent quantities, which means they do not vary with time. Instead, they represent the steady-state behavior of a circuit.
d) Not Time-Dependent: The statement "It is a time-dependent quantity" is not true of a phasor. As mentioned above, phasors are time-independent quantities that represent the steady-state behavior of a circuit.
Conclusion
In summary, phasors are an important concept in electrical engineering that are used to simplify the analysis of time-varying quantities in AC circuits. They are complex quantities that can be represented as either a scalar or vector and are time-independent. However, they are not time-dependent quantities, which is an important distinction to remember.
Workers want to suspend a 40kg sign from a ceiling with cables, but the cables they have available are only able to support a maximum 10 N of force before snapping. If they are planning on suspending the cables at a 45° angle, what is the least number of cables that would be sufficient to support the sign without snapping the cables?- a)40 cables
- b)80 cables
- c)20 cables
- d)60 cables
Correct answer is option 'D'. Can you explain this answer?
Workers want to suspend a 40kg sign from a ceiling with cables, but the cables they have available are only able to support a maximum 10 N of force before snapping. If they are planning on suspending the cables at a 45° angle, what is the least number of cables that would be sufficient to support the sign without snapping the cables?
a)
40 cables
b)
80 cables
c)
20 cables
d)
60 cables

|
Orion Classes answered |
Since we are given the mass, tension needed, and angles of suspension, and our variable is the number of wires. The vertical component would be Tsin45 x = 400, where x is the number of cables.
Since our maximum tension is 10 N, we can set T to 10 and solve: 10 √(2)/2 x = 400.
Rearranging the equation will give us x = 40√(2). Though you cannot use a calculator, you can automatically eliminate 20 and 40 as answers, because √(2) is greater than 1.
We also know that 40x2=80, and √(2) is less than 2, so we can eliminate 80 as a choice, since 60 is a smaller number while still being able to support the sign.
Since 60 = 1.5 x 40, and √(2) is less than 1.5, we can conclude that 60 cables would be sufficient to support the sign though technically only ~57 cables would be needed.
A 60 kg circus performer is suspended by four 50 foot wires high above an anxious crowd. The wires are all at an angle of θ between the ceiling and the performer. Which of the following describes the vertical component of force acting upon a single wire?- a)147 N
- b)(15)(9.8)sin θ N
- c)(60)(9.8)sin θ N
- d)588 N
Correct answer is option 'A'. Can you explain this answer?
A 60 kg circus performer is suspended by four 50 foot wires high above an anxious crowd. The wires are all at an angle of θ between the ceiling and the performer. Which of the following describes the vertical component of force acting upon a single wire?
a)
147 N
b)
(15)(9.8)sin θ N
c)
(60)(9.8)sin θ N
d)
588 N

|
Orion Classes answered |
If the angle is taken between the ceiling and the wire, then the vertical component would be given by the sin θ of the tension, but in this case, we are given the vertical component of force already.
The 4 wires horizontal components will negate one another, so the only vertical force involved is the force of gravity from the circus performer.
Since 4 separate wires are involved, your equation for the vertical component of a wire should be ¼ 60kg x 9.8 m/s2 or 147 N.
Let a =2i + j + k, b = i +2j –k and a unit vector c be coplanar. If c is perpendicular to a, then c =- a)
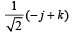
- b)
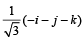
- c)
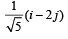
- d)

Correct answer is option 'A'. Can you explain this answer?
Let a =2i + j + k, b = i +2j –k and a unit vector c be coplanar. If c is perpendicular to a, then c =
a)
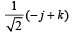
b)
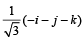
c)
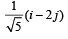
d)

|
|
Rishika Shah answered |
As c is coplanar with a and b, we take,
c = αa + βb ...(1)
where α,β are scalars.
As c is perpendicular to a , c.a = 0
∴ From (1) we get, 0 = α a.a + β b.a
As c is perpendicular to a , c.a = 0
∴ From (1) we get, 0 = α a.a + β b.a
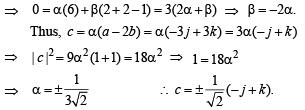
Let P be the image of the point (3,1,7) with r espect to the plane x – y + z = 3. Then the equation of the plane passing through P and containing the straight line 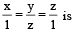
- a)x + y – 3z = 0
- b)3x + z = 0
- c)x – 4y + 7z = 0
- d)2x – y = 0
Correct answer is option 'C'. Can you explain this answer?
Let P be the image of the point (3,1,7) with r espect to the plane x – y + z = 3. Then the equation of the plane passing through P and containing the straight line 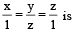
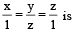
a)
x + y – 3z = 0
b)
3x + z = 0
c)
x – 4y + 7z = 0
d)
2x – y = 0
|
|
Nitya Yadav answered |
P, the image of point (3, 1, 7) in the plane x – y + z = 3 is given by
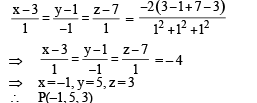
Now equation of plane through (–1, 5, 3) and containing the
line
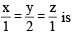
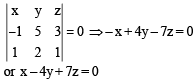
Let P, Q, R and S be the points on the plane with position vectors 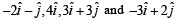 respectively. The quadrilateral PQRS must be a
respectively. The quadrilateral PQRS must be a- a)parallelogram, which is neither a rhombus nor a rectangle
- b)square
- c)rectangle, but not a square
- d)rhombus, but not a square
Correct answer is option 'A'. Can you explain this answer?
Let P, Q, R and S be the points on the plane with position vectors 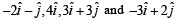 respectively. The quadrilateral PQRS must be a
respectively. The quadrilateral PQRS must be a
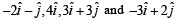 respectively. The quadrilateral PQRS must be a
respectively. The quadrilateral PQRS must be aa)
parallelogram, which is neither a rhombus nor a rectangle
b)
square
c)
rectangle, but not a square
d)
rhombus, but not a square
|
|
Juhi Das answered |
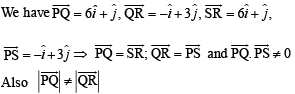
⇒ PQRS is a parallelogram but neither a rhombus nor a rectangle.
The point P is the intersection of the straight line joining the points Q(2, 3, 5) and R(1, –1, 4) with the plane 5x – 4y – z = 1. If S is the foot of the perpendicular drawn from the point T(2, 1, 4) to QR, then the length of the line segment PS is- a)
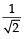
- b)
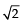
- c)2
- d)

Correct answer is option 'A'. Can you explain this answer?
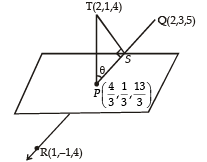
The point P is the intersection of the straight line joining the points Q(2, 3, 5) and R(1, –1, 4) with the plane 5x – 4y – z = 1. If S is the foot of the perpendicular drawn from the point T(2, 1, 4) to QR, then the length of the line segment PS is
a)
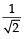
b)
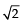
c)
2
d)

|
|
Nikhil Sengupta answered |
Equation of st. line join ing Q (2, 3, 5) an d R (1, –1, 4) is
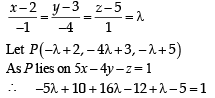
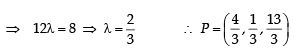
Now let point S on QR be
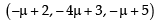
∵ S is the foot of perpendicular drawn from T (2, 1, 4) to QR, where dr’s of ST are µ, 4µ – 2, µ –1 and dr’s of QR are –1, – 4, –1
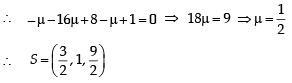
∴ Distance between P and S
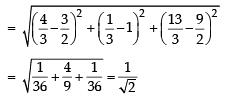
Chapter doubts & questions for Vector Analysis - Physics for EmSAT Achieve 2025 is part of EmSAT Achieve exam preparation. The chapters have been prepared according to the EmSAT Achieve exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Vector Analysis - Physics for EmSAT Achieve in English & Hindi are available as part of EmSAT Achieve exam.
Download more important topics, notes, lectures and mock test series for EmSAT Achieve Exam by signing up for free.
Physics for EmSAT Achieve
208 videos|329 docs|212 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup



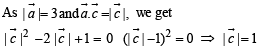
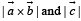 in (1), we get
in (1), we get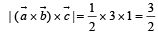
 are coplanar, is
are coplanar, is




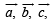 be three non - coplanar vectors and
be three non - coplanar vectors and 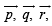 are vectors defined by the relations
are vectors defined by the relations 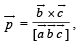
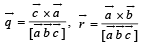 then the value of the expression
then the value of the expression 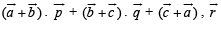 is equal to
is equal to
 are coplanar, then the plane (s) containing these two lines is (are)
are coplanar, then the plane (s) containing these two lines is (are)
 , where uand vare scalar fields and F is a vector field, then F. curl Fis equal to
, where uand vare scalar fields and F is a vector field, then F. curl Fis equal to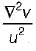
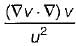
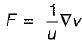
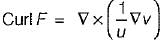
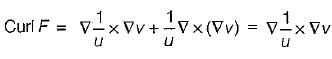
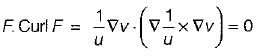

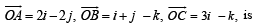

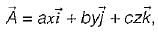 then the value of
then the value of 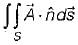 (
(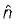 is a unit vector) will be equal to
is a unit vector) will be equal to
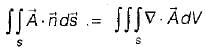
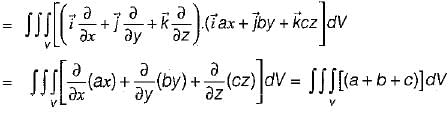
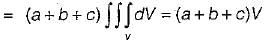




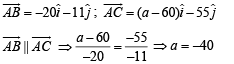
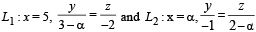 are coplanar. Then a can take value(s)
are coplanar. Then a can take value(s)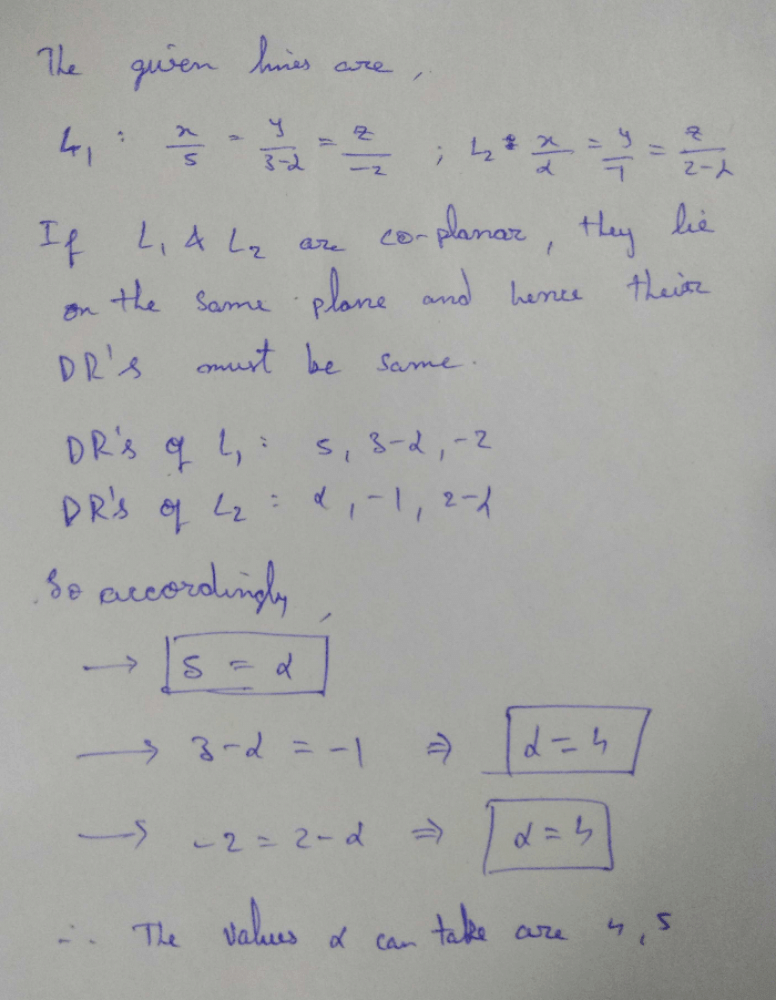
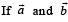 are two unit vectors such that
are two unit vectors such that 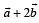 and
and 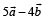 are perpendicular to each other then the angle between
are perpendicular to each other then the angle between 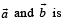
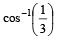

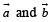 are two unit vectors
are two unit vectors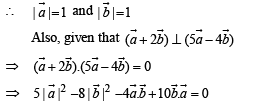
 are unit vectors such that
are unit vectors such that 
 are non-coplanar
are non-coplanar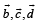 are non-coplanar
are non-coplanar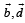 are non-parallel
are non-parallel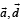 are parallel and
are parallel and  are parallel
are parallel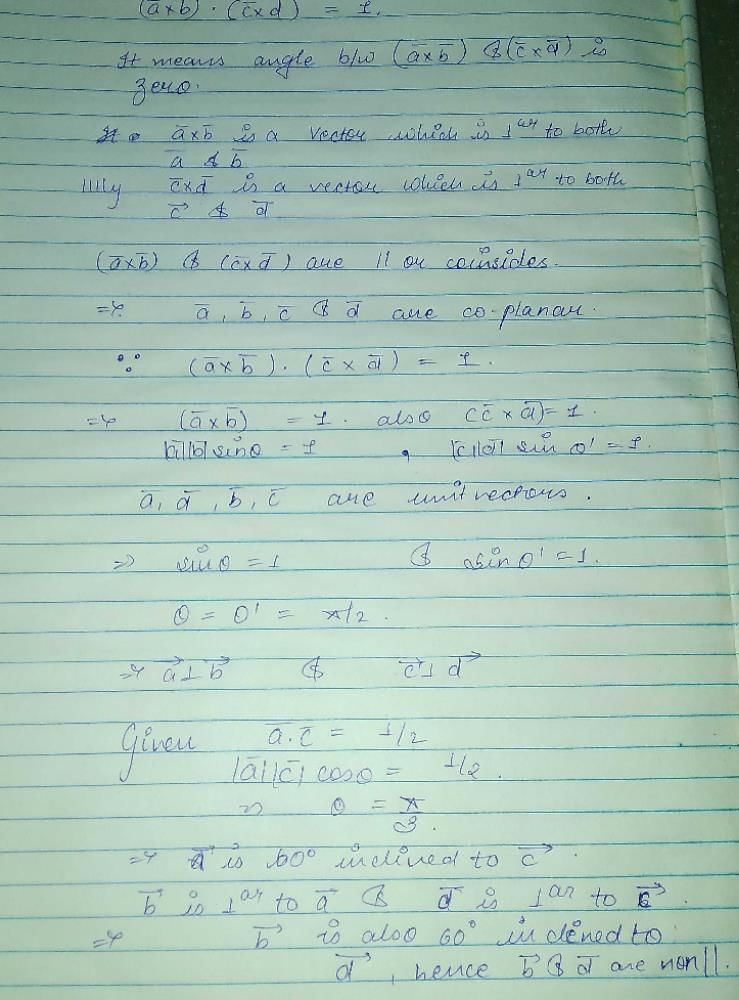
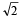
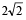

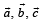 are non coplanar unit vectors such that
are non coplanar unit vectors such that 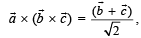 then the angle between
then the angle between 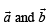 is
is