All Exams >
EmSAT Achieve >
Physics for EmSAT Achieve >
All Questions
All questions of Linear Momentum and Impulse for EmSAT Achieve Exam
The kinetic energy of a body is stated to increase by 300 percent. The corresponding increase in the momentum of the body will be ____%- a)50
- b)100
- c)200
- d)300
Correct answer is option 'B'. Can you explain this answer?
The kinetic energy of a body is stated to increase by 300 percent. The corresponding increase in the momentum of the body will be ____%
a)
50
b)
100
c)
200
d)
300
|
|
Raghav Saini answered |
Understanding Kinetic Energy and Momentum
Kinetic energy (KE) and momentum (p) are two fundamental concepts in mechanics. Their relationships can help us understand the impact of changes in one on the other.
Kinetic Energy Formula
- Kinetic energy is given by the formula: KE = (1/2)mv^2, where m is mass and v is velocity.
- If the kinetic energy increases by 300%, this means the new kinetic energy is 4 times the original (original + 3 times original).
Momentum Formula
- Momentum is given by the formula: p = mv.
- Momentum depends directly on mass and velocity.
Analyzing the Increase in Kinetic Energy
- Let the initial kinetic energy be KE1 = (1/2)mv1^2.
- The new kinetic energy after a 300% increase: KE2 = 4 * KE1 = 4 * (1/2)mv1^2 = 2mv1^2.
Relating Kinetic Energy to Momentum
- To find the new momentum, we first need to express the new velocity (v2).
- From KE2 = (1/2)mv2^2, we can deduce that: 2mv1^2 = (1/2)mv2^2, leading to v2^2 = 4v1^2, hence v2 = 2v1.
Calculating the Increase in Momentum
- Initial momentum: p1 = mv1.
- New momentum: p2 = mv2 = m(2v1) = 2mv1 = 2p1.
- The increase in momentum: Δp = p2 - p1 = 2p1 - p1 = p1.
Percentage Increase in Momentum
- The percentage increase in momentum is given by: (Δp / p1) * 100 = (p1 / p1) * 100 = 100%.
Thus, the corresponding increase in momentum is 100%, which is option B.
Kinetic energy (KE) and momentum (p) are two fundamental concepts in mechanics. Their relationships can help us understand the impact of changes in one on the other.
Kinetic Energy Formula
- Kinetic energy is given by the formula: KE = (1/2)mv^2, where m is mass and v is velocity.
- If the kinetic energy increases by 300%, this means the new kinetic energy is 4 times the original (original + 3 times original).
Momentum Formula
- Momentum is given by the formula: p = mv.
- Momentum depends directly on mass and velocity.
Analyzing the Increase in Kinetic Energy
- Let the initial kinetic energy be KE1 = (1/2)mv1^2.
- The new kinetic energy after a 300% increase: KE2 = 4 * KE1 = 4 * (1/2)mv1^2 = 2mv1^2.
Relating Kinetic Energy to Momentum
- To find the new momentum, we first need to express the new velocity (v2).
- From KE2 = (1/2)mv2^2, we can deduce that: 2mv1^2 = (1/2)mv2^2, leading to v2^2 = 4v1^2, hence v2 = 2v1.
Calculating the Increase in Momentum
- Initial momentum: p1 = mv1.
- New momentum: p2 = mv2 = m(2v1) = 2mv1 = 2p1.
- The increase in momentum: Δp = p2 - p1 = 2p1 - p1 = p1.
Percentage Increase in Momentum
- The percentage increase in momentum is given by: (Δp / p1) * 100 = (p1 / p1) * 100 = 100%.
Thus, the corresponding increase in momentum is 100%, which is option B.
Two inelastic spheres of masses 10 kg each move with velocities of 15 m/s and 5 m/s respectively in the same direction. The loss in kinetic energy when they collide- a)500 Nm
- b)0 Nm
- c)250 Nm
- d)1000 Nm
Correct answer is option 'C'. Can you explain this answer?
Two inelastic spheres of masses 10 kg each move with velocities of 15 m/s and 5 m/s respectively in the same direction. The loss in kinetic energy when they collide
a)
500 Nm
b)
0 Nm
c)
250 Nm
d)
1000 Nm
|
|
Sahil Majumdar answered |
Explanation:
Given Data:
- Mass of each sphere, m = 10 kg
- Initial velocities, u1 = 15 m/s and u2 = 5 m/s
Loss in Kinetic Energy:
- The initial total kinetic energy of the system is given by:
KE_initial = (1/2) * m1 * u1^2 + (1/2) * m2 * u2^2
= (1/2) * 10 * 15^2 + (1/2) * 10 * 5^2
= 1125 + 125
= 1250 J
- After the collision, the final total kinetic energy of the system is given by:
KE_final = (1/2) * (m1 + m2) * V^2
where V is the common final velocity of both spheres.
- Since the collision is inelastic, kinetic energy is not conserved. The loss in kinetic energy is given by:
Loss in KE = KE_initial - KE_final
- From the law of conservation of momentum:
m1 * u1 + m2 * u2 = (m1 + m2) * V
10 * 15 + 10 * 5 = 20 * V
150 + 50 = 20V
V = 10 m/s
- Substituting the value of V in the equation for KE_final:
KE_final = (1/2) * 20 * 10^2
= 1000 J
- Therefore, the loss in kinetic energy is:
Loss in KE = 1250 - 1000
= 250 J
Therefore, the correct answer is option C, 250 Nm.
Given Data:
- Mass of each sphere, m = 10 kg
- Initial velocities, u1 = 15 m/s and u2 = 5 m/s
Loss in Kinetic Energy:
- The initial total kinetic energy of the system is given by:
KE_initial = (1/2) * m1 * u1^2 + (1/2) * m2 * u2^2
= (1/2) * 10 * 15^2 + (1/2) * 10 * 5^2
= 1125 + 125
= 1250 J
- After the collision, the final total kinetic energy of the system is given by:
KE_final = (1/2) * (m1 + m2) * V^2
where V is the common final velocity of both spheres.
- Since the collision is inelastic, kinetic energy is not conserved. The loss in kinetic energy is given by:
Loss in KE = KE_initial - KE_final
- From the law of conservation of momentum:
m1 * u1 + m2 * u2 = (m1 + m2) * V
10 * 15 + 10 * 5 = 20 * V
150 + 50 = 20V
V = 10 m/s
- Substituting the value of V in the equation for KE_final:
KE_final = (1/2) * 20 * 10^2
= 1000 J
- Therefore, the loss in kinetic energy is:
Loss in KE = 1250 - 1000
= 250 J
Therefore, the correct answer is option C, 250 Nm.
A 1.0 kg ball drops vertically onto the floor with a speed of 25 m/s. It rebounds with an initial speed of 10 m/s. The impulse action on the ball during contact will be- a)15 N-s
- b)25 N-s
- c)35 N-s
- d)45 N-s
Correct answer is option 'C'. Can you explain this answer?
A 1.0 kg ball drops vertically onto the floor with a speed of 25 m/s. It rebounds with an initial speed of 10 m/s. The impulse action on the ball during contact will be
a)
15 N-s
b)
25 N-s
c)
35 N-s
d)
45 N-s

|
Anisha Chakraborty answered |
Impulse during Contact:
In order to calculate the impulse during the contact between the ball and the floor, we can use the principle of conservation of momentum. The impulse experienced by an object is equal to the change in momentum it undergoes during a collision.
Initial Momentum:
The initial momentum of the ball can be calculated using the formula:
\[p_{initial} = m \times v_{initial}\]
where
m = mass of the ball (1.0 kg)
v_{initial} = initial speed of the ball (25 m/s)
Final Momentum:
The final momentum of the ball can be calculated using the formula:
\[p_{final} = m \times v_{final}\]
where
m = mass of the ball (1.0 kg)
v_{final} = final speed of the ball (10 m/s)
Impulse:
The impulse experienced by the ball during contact is given by the formula:
\[Impulse = p_{final} - p_{initial}\]
Substitute the values into the formula to find the impulse:
\[Impulse = (1.0 \times 10) - (1.0 \times 25) = 10 - 25 = -15\,kg\,m/s\]
The negative sign indicates that the direction of the impulse is opposite to the initial direction of motion. Therefore, the magnitude of the impulse is 15 N-s.
Therefore, the correct answer is option C which is 35 N-s.
In order to calculate the impulse during the contact between the ball and the floor, we can use the principle of conservation of momentum. The impulse experienced by an object is equal to the change in momentum it undergoes during a collision.
Initial Momentum:
The initial momentum of the ball can be calculated using the formula:
\[p_{initial} = m \times v_{initial}\]
where
m = mass of the ball (1.0 kg)
v_{initial} = initial speed of the ball (25 m/s)
Final Momentum:
The final momentum of the ball can be calculated using the formula:
\[p_{final} = m \times v_{final}\]
where
m = mass of the ball (1.0 kg)
v_{final} = final speed of the ball (10 m/s)
Impulse:
The impulse experienced by the ball during contact is given by the formula:
\[Impulse = p_{final} - p_{initial}\]
Substitute the values into the formula to find the impulse:
\[Impulse = (1.0 \times 10) - (1.0 \times 25) = 10 - 25 = -15\,kg\,m/s\]
The negative sign indicates that the direction of the impulse is opposite to the initial direction of motion. Therefore, the magnitude of the impulse is 15 N-s.
Therefore, the correct answer is option C which is 35 N-s.
Calculate the velocity of a body having a mass of 9 kg and linear momentum of 63 kg m/s.- a)6 m/s
- b)7 m/s
- c)8 m/s
- d)10 m/s
Correct answer is option 'B'. Can you explain this answer?
Calculate the velocity of a body having a mass of 9 kg and linear momentum of 63 kg m/s.
a)
6 m/s
b)
7 m/s
c)
8 m/s
d)
10 m/s
|
|
Neha Joshi answered |
Linear momentum:
- It is the product of the mass and velocity of an object.
- Like velocity, linear momentum is a vector quantity possessing a direction as well as magnitude.
P = mv
where P = momentum and v = velovity.
Calculation:
Given:
Mass = 9 kg, P = 63 kg-m/sec
P = mv
63 = 9 × v
v = 7 m/s
where P = momentum and v = velovity.
Calculation:
Given:
Mass = 9 kg, P = 63 kg-m/sec
P = mv
63 = 9 × v
v = 7 m/s
During elastic and inelastic collision, ________ is conserved.- a)kinetic energy
- b)velocity
- c)viscosity
- d)momentum
Correct answer is option 'D'. Can you explain this answer?
During elastic and inelastic collision, ________ is conserved.
a)
kinetic energy
b)
velocity
c)
viscosity
d)
momentum
|
|
Atharva Majumdar answered |
Conservation of Momentum in Elastic and Inelastic Collisions
In both elastic and inelastic collisions, momentum is conserved. This means that the total momentum of the system before the collision is equal to the total momentum of the system after the collision.
Elastic Collision
- In an elastic collision, kinetic energy is also conserved along with momentum.
- The objects bounce off each other without any loss of kinetic energy.
- The total kinetic energy before the collision is equal to the total kinetic energy after the collision.
Inelastic Collision
- In an inelastic collision, kinetic energy is not conserved.
- Some of the kinetic energy is transformed into other forms of energy like sound, heat, or deformation of the objects.
- Despite this loss of kinetic energy, momentum is still conserved in the system.
Explanation
- Momentum is conserved in collisions because there is no external force acting on the system during the collision.
- According to Newton's third law of motion, the forces between the objects in the collision are equal and opposite, resulting in a constant total momentum.
- This conservation of momentum is a fundamental principle in physics and is used to analyze and predict the behavior of objects in collisions.
Therefore, in both elastic and inelastic collisions, momentum is conserved, making it a crucial concept in understanding the dynamics of interactions between objects.
In both elastic and inelastic collisions, momentum is conserved. This means that the total momentum of the system before the collision is equal to the total momentum of the system after the collision.
Elastic Collision
- In an elastic collision, kinetic energy is also conserved along with momentum.
- The objects bounce off each other without any loss of kinetic energy.
- The total kinetic energy before the collision is equal to the total kinetic energy after the collision.
Inelastic Collision
- In an inelastic collision, kinetic energy is not conserved.
- Some of the kinetic energy is transformed into other forms of energy like sound, heat, or deformation of the objects.
- Despite this loss of kinetic energy, momentum is still conserved in the system.
Explanation
- Momentum is conserved in collisions because there is no external force acting on the system during the collision.
- According to Newton's third law of motion, the forces between the objects in the collision are equal and opposite, resulting in a constant total momentum.
- This conservation of momentum is a fundamental principle in physics and is used to analyze and predict the behavior of objects in collisions.
Therefore, in both elastic and inelastic collisions, momentum is conserved, making it a crucial concept in understanding the dynamics of interactions between objects.
During Perfectly Elastic Collision between two bodies, which of the following quantities always remains conserved?- a)Total Kinetic Energy
- b)Total Linear Momentum
- c)Both total kinetic energy and linear momentum
- d)Neither Kinetic energy nor linear momentum
Correct answer is option 'C'. Can you explain this answer?
During Perfectly Elastic Collision between two bodies, which of the following quantities always remains conserved?
a)
Total Kinetic Energy
b)
Total Linear Momentum
c)
Both total kinetic energy and linear momentum
d)
Neither Kinetic energy nor linear momentum
|
|
Neha Joshi answered |
The correct answer is Both total kinetic energy and total linear momentum
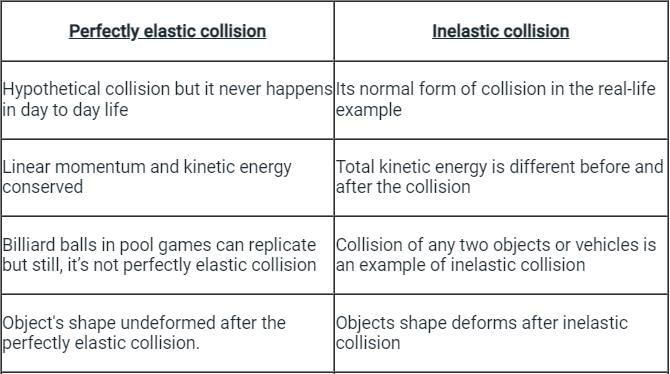
- A perfectly inelastic collision is a hypothetical collision in which two objects collide and energy is not wasted and momentum is conserved.
- While Perfectly elastic collision happens then the object’s shape remains unchanged or not deformed.
- Most of the collisions in daily life are inelastic in nature.
Important Points

The rate of change of momentum is equal to the applied force and it takes place in the direction of the force is a statement of:- a)Continuity equation
- b)Pascal’s equation
- c)Impulse – Momentum equation
- d)Darcy’s equation
Correct answer is option 'C'. Can you explain this answer?
The rate of change of momentum is equal to the applied force and it takes place in the direction of the force is a statement of:
a)
Continuity equation
b)
Pascal’s equation
c)
Impulse – Momentum equation
d)
Darcy’s equation
|
|
Neha Joshi answered |
Newton’s Second law of motion: The rate of change of momentum of any object is directly proportional to the applied force on the body.
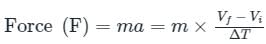
F × ΔT = ΔP
Where Δ P = Change in momentum and Δ T = change in time taken
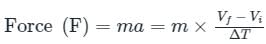
F × ΔT = ΔP
Where Δ P = Change in momentum and Δ T = change in time taken
- The above equation is known as Impulse Momentum equation and states that the impulse or force intensity is equal to change in momentum.
- According to the impulse-momentum equation, the change in momentum of an object depends on both the net force acting on the object and duration of the net force.
Two balls of equal mass and of Perfectly elastic material are lying on the floor. One of the balls with velocity V is made to strike the second ball. Both the balls after impact will move with a velocity- a)v
- b)v/2
- c)v/4
- d)v/8
Correct answer is option 'B'. Can you explain this answer?
Two balls of equal mass and of Perfectly elastic material are lying on the floor. One of the balls with velocity V is made to strike the second ball. Both the balls after impact will move with a velocity
a)
v
b)
v/2
c)
v/4
d)
v/8
|
|
Neha Joshi answered |
This is the perfectly inelastic collision/impact of the case of two bodies/balls as both the balls stick after the collision.
Perfect Inelastic Collision:
Perfect Inelastic Collision:
- Two bodies move together with the same velocity.
- The coefficient of Restitution will be 0.
- Momentum is Conserved.
- Kinetic Energy will not be Conserved.
Calculation:
Given:
Let two balls A and B have mass mA, mB respectively, and their initial velocities are uA and uB. After the collision, they will move with the same velocity, vo.
Given that mass of both balls are same.
So mA = mB = m
uA = V, uB = 0
From the Concept of Momentum Conservation:
mAuA + mBuB = (m+m)vo
mV = 2mvo
vo = V/2
Both the balls after impact will move with velocity v/2.
Given:
Let two balls A and B have mass mA, mB respectively, and their initial velocities are uA and uB. After the collision, they will move with the same velocity, vo.
Given that mass of both balls are same.
So mA = mB = m
uA = V, uB = 0
From the Concept of Momentum Conservation:
mAuA + mBuB = (m+m)vo
mV = 2mvo
vo = V/2
Both the balls after impact will move with velocity v/2.
If the momentum of a body increases from 10 units to 25 units in 5 sec, then the force acting on it is- a)1 unit
- b)2 units
- c)3 units
- d)4 units
Correct answer is option 'C'. Can you explain this answer?
If the momentum of a body increases from 10 units to 25 units in 5 sec, then the force acting on it is
a)
1 unit
b)
2 units
c)
3 units
d)
4 units
|
|
Neha Joshi answered |
The correct answer is 3 units.
- Newton's 2nd law of motion says the rate change of momentum is called force.
- The equation for the change in momentum is F × t = m × Δv
- If the momentum of a body increases from 10 units to 25 units in 5 seconds.
- Then the change in the momentum is 25 – 10 = 15 units in time 5 seconds.
- So the Force extract from this is 15/5 = 3 Newton.
Key Points
- Momentum is a vector quantity that is the product of the mass (weight) of a particle and its velocity (speed).
- SI unit: kilogram meter per second (kg⋅m/s).
- A spinning object has angular momentum.
- An object travelling with a velocity has linear momentum.
- A change in momentum may result from an acceleration or a force or an impulse.
A rigid homogeneous uniform block of mass 1 kg, height h = 0.4 m and width b = 0.3 m is pinned at one corner and placed upright in a uniform gravitational field (g = 9.81 m/s2), supported by a roller in the configuration shown in the figure. A short duration (impulsive) force F, producing an impulse IF is applied at a height of d = 0.3 m from the bottom as shown. Assume all joints to be frictionless. The minimum value of IF required to topple the block is
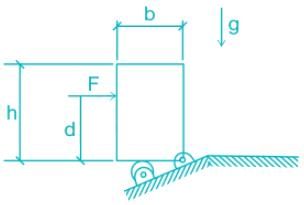
- a)0.953 Ns
- b)1.403 Ns
- c)0.814 Ns
- d)1.172 Ns
Correct answer is option 'A'. Can you explain this answer?
A rigid homogeneous uniform block of mass 1 kg, height h = 0.4 m and width b = 0.3 m is pinned at one corner and placed upright in a uniform gravitational field (g = 9.81 m/s2), supported by a roller in the configuration shown in the figure. A short duration (impulsive) force F, producing an impulse IF is applied at a height of d = 0.3 m from the bottom as shown. Assume all joints to be frictionless. The minimum value of IF required to topple the block is


a)
0.953 Ns
b)
1.403 Ns
c)
0.814 Ns
d)
1.172 Ns
|
|
Neha Joshi answered |
To topple the block we need an impulse force such that the weight will generate a clockwise moment about point O.
This will happen only when a minimum impulse that can rotate the block such that the Centre of gravity of the body will pass through the point O or beyond.
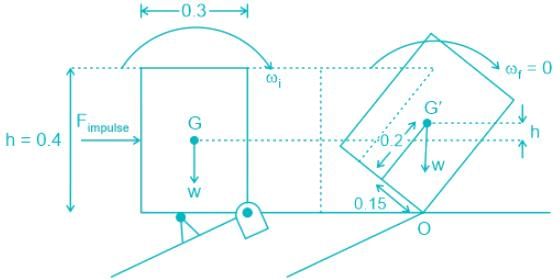
h = 0.4m, b = 0.3 m, m =1kg
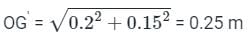
h' = OG' - h/2 = 0.25 - 0.2 = 0.05 m
Due to force F, the block will topple about A
So By energy balance

ω2 = 2 × 12 × 9.81 × 0.05
ω = 3.43 rad/s
Now,
Angular impulse = change in angular momentum
IF × d = Io × (ωi - ωf)
IF × 0.3 = 1/12 × ( 3.43 - 0)
IF = 0.953 Ns
This will happen only when a minimum impulse that can rotate the block such that the Centre of gravity of the body will pass through the point O or beyond.

h = 0.4m, b = 0.3 m, m =1kg
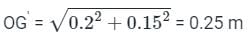
h' = OG' - h/2 = 0.25 - 0.2 = 0.05 m
Due to force F, the block will topple about A
So By energy balance

ω2 = 2 × 12 × 9.81 × 0.05
ω = 3.43 rad/s
Now,
Angular impulse = change in angular momentum
IF × d = Io × (ωi - ωf)
IF × 0.3 = 1/12 × ( 3.43 - 0)
IF = 0.953 Ns
Chapter doubts & questions for Linear Momentum and Impulse - Physics for EmSAT Achieve 2025 is part of EmSAT Achieve exam preparation. The chapters have been prepared according to the EmSAT Achieve exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Linear Momentum and Impulse - Physics for EmSAT Achieve in English & Hindi are available as part of EmSAT Achieve exam.
Download more important topics, notes, lectures and mock test series for EmSAT Achieve Exam by signing up for free.
Physics for EmSAT Achieve
208 videos|329 docs|212 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









