All Exams >
EmSAT Achieve >
Physics for EmSAT Achieve >
All Questions
All questions of Moment of Inertia for EmSAT Achieve Exam
The moment of inertia of two spheres of equal masses is equal. If one of the spheres is solid of radius 
m and the other is a hollow sphere. What is the radius of the hollow sphere?- a)5 m
- b)√3 m
- c)3√3 m
- d)3 m
Correct answer is option 'C'. Can you explain this answer?
The moment of inertia of two spheres of equal masses is equal. If one of the spheres is solid of radius m and the other is a hollow sphere. What is the radius of the hollow sphere?
m and the other is a hollow sphere. What is the radius of the hollow sphere?a)
5 m
b)
√3 m
c)
3√3 m
d)
3 m
|
Sushil Kumar answered |
Moment of inertia of solid sphere Is= 2/5MR2
moment of inertia of hollow sphere Ih =2/3MR2
given mass of solid sphere =√45 kg.
Is=Ih
2MR2/5=2MR2/3
given their masses are equal 2 (√45)2/5= 2 R2/3
45/5=R2/3
9=R2/3
9×3=R2
27=R2
√27=R
√3×9=R
3√3 m=R.
moment of inertia of hollow sphere Ih =2/3MR2
given mass of solid sphere =√45 kg.
Is=Ih
2MR2/5=2MR2/3
given their masses are equal 2 (√45)2/5= 2 R2/3
45/5=R2/3
9=R2/3
9×3=R2
27=R2
√27=R
√3×9=R
3√3 m=R.
Two rings have their moment of inertia in the ratio 2:1 and their diameters are in the ratio 2:1. The ratio of their masses will be:- a)1:2
- b)2:1
- c)1:4
- d)1:1
Correct answer is option 'A'. Can you explain this answer?
Two rings have their moment of inertia in the ratio 2:1 and their diameters are in the ratio 2:1. The ratio of their masses will be:
a)
1:2
b)
2:1
c)
1:4
d)
1:1
|
Suresh Reddy answered |
We know that MI of a ring is mr2
Where m is mass of the ring and r is its radius
When we have ratio of I = 2:1
And ratio of r = 2:1
We get ratio of r2 = 4:1
Thus to make this ratio 2:1 , that ratio of masses must be 1:2
Where m is mass of the ring and r is its radius
When we have ratio of I = 2:1
And ratio of r = 2:1
We get ratio of r2 = 4:1
Thus to make this ratio 2:1 , that ratio of masses must be 1:2
There are two circular iron discs A and B having masses in the ratio 1:2 and diameter in the ratio 2:1. The ratio of their moment of inertia is- a)4:1
- b)1:3
- c)2:1
- d)8:1
Correct answer is option 'C'. Can you explain this answer?
There are two circular iron discs A and B having masses in the ratio 1:2 and diameter in the ratio 2:1. The ratio of their moment of inertia is
a)
4:1
b)
1:3
c)
2:1
d)
8:1
|
Preeti Iyer answered |
Given,
Mass of A=1,
Mass of B=2.
diameter if A=2,
diameter if B=1.
radius (r) of A=d/2=2/2=1.
radius (r) of B=d/2=1/2.
we know ,
moment of inertia of disc=MR2/2.
moment of inertia (I)of A/moment of inertia (I)of B=MR2/2/MR2/2.
(I) of A/(I) of B=1×12/2/2×(1/2)2/2.
=1×1/2/2×(1/4)/2.
=1/2/(1/2)/2.
=1/2/1/4.
=4/2.
=2/1.
Mass of A=1,
Mass of B=2.
diameter if A=2,
diameter if B=1.
radius (r) of A=d/2=2/2=1.
radius (r) of B=d/2=1/2.
we know ,
moment of inertia of disc=MR2/2.
moment of inertia (I)of A/moment of inertia (I)of B=MR2/2/MR2/2.
(I) of A/(I) of B=1×12/2/2×(1/2)2/2.
=1×1/2/2×(1/4)/2.
=1/2/(1/2)/2.
=1/2/1/4.
=4/2.
=2/1.
Moment of inertia of a thin spherical shell of mass M and radius R about a diameter is- a)2/5 MR2
- b)4/5 MR2
- c)2/3 MR2
- d)3/5 MR2
Correct answer is option 'C'. Can you explain this answer?
Moment of inertia of a thin spherical shell of mass M and radius R about a diameter is
a)
2/5 MR2
b)
4/5 MR2
c)
2/3 MR2
d)
3/5 MR2
|
Ambition Institute answered |
A moment of inertia is a measure of the resistance of a body to angular acceleration about a given axis that is equal to the sum of the products of each element of mass in the body and the square of the element’s distance from the axis.
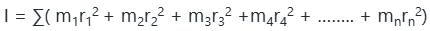
Moment of inertia of a thin spherical shell of mass M and radius R about its diameter.
I = 2/3 MR2
For a rigid body system, the moment of inertia is the sum of the moments of inertia of all its particles taken about the same axis.
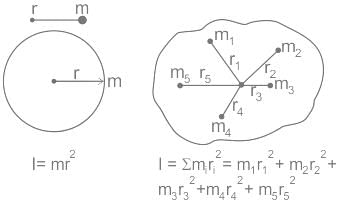
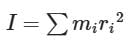
where I is the Moment of Inertia, m is point mass, r is the perpendicular distance from the axis of rotation.
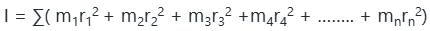
Moment of inertia of a thin spherical shell of mass M and radius R about its diameter.
I = 2/3 MR2
For a rigid body system, the moment of inertia is the sum of the moments of inertia of all its particles taken about the same axis.
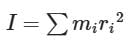
where I is the Moment of Inertia, m is point mass, r is the perpendicular distance from the axis of rotation.
A circular disc of radius R and thickness R/6 has moment of inertia I about an axis passing through its centre and perpendicular to its plane. It is melted and recasted into a solid sphere. The moment of inertia of the sphere about its diameter as axis of rotation is :- a)I
- b)2I/3
- c)I/5
- d)I/10
Correct answer is option 'C'. Can you explain this answer?
A circular disc of radius R and thickness R/6 has moment of inertia I about an axis passing through its centre and perpendicular to its plane. It is melted and recasted into a solid sphere. The moment of inertia of the sphere about its diameter as axis of rotation is :
a)
I
b)
2I/3
c)
I/5
d)
I/10
|
Ananya Basak answered |
Understanding Moment of Inertia
The moment of inertia (I) of an object quantifies its resistance to rotational motion. For a circular disc and a solid sphere, the formulas differ based on their geometry.
Step 1: Moment of Inertia of the Disc
- A circular disc of radius R and thickness R/6 has a moment of inertia about its center (I) given by the formula:
I = (1/2) * M * R², where M is the mass of the disc.
- The volume (V) of the disc can be calculated as:
V = π * R² * (R/6) = (π/6) * R³.
- The density (ρ) of the disc is:
ρ = M/V.
- From density, we can express mass (M) in terms of volume and density.
Step 2: Melting and Recasting
- When the disc is melted and recast into a solid sphere, the mass remains the same.
- The volume of the sphere (V_sphere) is:
V_sphere = (4/3) * π * r³, where r is the radius of the sphere.
- Setting the volumes equal gives:
(π/6) * R³ = (4/3) * π * r³.
- From this, we can find the radius (r) of the sphere in terms of R.
Step 3: Moment of Inertia of the Sphere
- The moment of inertia (I_sphere) of a solid sphere about its diameter is given by:
I_sphere = (2/5) * M * r².
- Since the mass (M) is the same for both the disc and the sphere, substituting r into this formula allows us to express I_sphere in terms of I.
Final Calculation
- After substituting and simplifying, we find that:
I_sphere = I/5.
Thus, the correct answer is option 'C'.
The moment of inertia (I) of an object quantifies its resistance to rotational motion. For a circular disc and a solid sphere, the formulas differ based on their geometry.
Step 1: Moment of Inertia of the Disc
- A circular disc of radius R and thickness R/6 has a moment of inertia about its center (I) given by the formula:
I = (1/2) * M * R², where M is the mass of the disc.
- The volume (V) of the disc can be calculated as:
V = π * R² * (R/6) = (π/6) * R³.
- The density (ρ) of the disc is:
ρ = M/V.
- From density, we can express mass (M) in terms of volume and density.
Step 2: Melting and Recasting
- When the disc is melted and recast into a solid sphere, the mass remains the same.
- The volume of the sphere (V_sphere) is:
V_sphere = (4/3) * π * r³, where r is the radius of the sphere.
- Setting the volumes equal gives:
(π/6) * R³ = (4/3) * π * r³.
- From this, we can find the radius (r) of the sphere in terms of R.
Step 3: Moment of Inertia of the Sphere
- The moment of inertia (I_sphere) of a solid sphere about its diameter is given by:
I_sphere = (2/5) * M * r².
- Since the mass (M) is the same for both the disc and the sphere, substituting r into this formula allows us to express I_sphere in terms of I.
Final Calculation
- After substituting and simplifying, we find that:
I_sphere = I/5.
Thus, the correct answer is option 'C'.
The moment of inertia of a solid cone of mass m and base radius r about its vertical axis is- a)3mr2/5
- b)2mr2/5
- c)3mr2/10
- d)4mr2/5
Correct answer is option 'C'. Can you explain this answer?
The moment of inertia of a solid cone of mass m and base radius r about its vertical axis is
a)
3mr2/5
b)
2mr2/5
c)
3mr2/10
d)
4mr2/5
|
Stepway Academy answered |
The moment of inertia of a rigid body about a fixed axis is defined as the sum of the product of the masses of the particles constituting the body and the square of their respective distances from the axis of the rotation.
The moment of inertia of a body is given by I = m R2
where m = Mass and R = Distance from the axis
The moment of inertia of a solid cone
m is the mass of the cone and r is the base radius of the cone and h is the height of the cone.
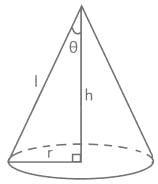
About the vertical axis
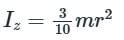
where m = Mass and R = Distance from the axis
The moment of inertia of a solid cone
m is the mass of the cone and r is the base radius of the cone and h is the height of the cone.
About the vertical axis
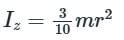
A particle of mass m is attached to a thin uniform rod of length a and mass 4m. The distance of the particle from the centre of mass of the rod is a/4. The moment of inertia of the combination about an axis passing through O normal to the rod is
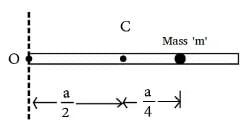
- a)
- b)
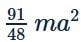
- c)
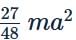
- d)
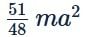
Correct answer is option 'B'. Can you explain this answer?
A particle of mass m is attached to a thin uniform rod of length a and mass 4m. The distance of the particle from the centre of mass of the rod is a/4. The moment of inertia of the combination about an axis passing through O normal to the rod is
a)
b)
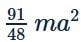
c)
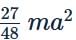
d)
|
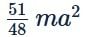
Infinity Academy answered |
Moment of inertia
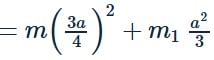
For the centre of rod
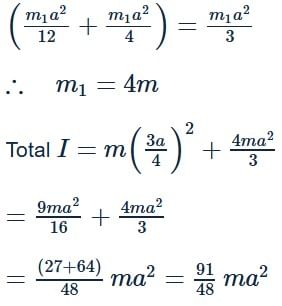
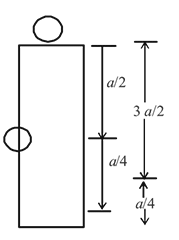
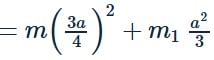
For the centre of rod
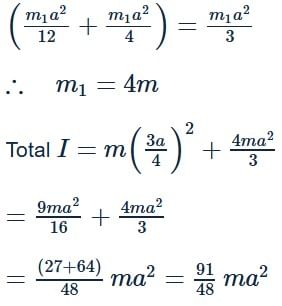
The moment of inertia of a body does not depend on- a)Mass of the body
- b)The distribution of the mass in the body
- c)Position of axis of rotation of the body.
- d)None of the above
Correct answer is option 'D'. Can you explain this answer?
The moment of inertia of a body does not depend on
a)
Mass of the body
b)
The distribution of the mass in the body
c)
Position of axis of rotation of the body.
d)
None of the above
|
|
Ambition Institute answered |
Moment of inertia of a body depends on the mass of the body, distribution of mass in the body, position of axis of rotation of the body and also depends on the distance of body from the axis of rotation.
Area moment of inertia for the quadrant shown below is:
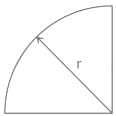
- a) π r4/ 2
- b) π r4/ 4
- c) π r4/ 8
- d) π r4/ 16
Correct answer is option 'D'. Can you explain this answer?
Area moment of inertia for the quadrant shown below is:
a)
π r4/ 2
b)
π r4/ 4
c)
π r4/ 8
d)
π r4/ 16
|
|
Ambition Institute answered |
Concept:
Area moment of inertia is given by, I = A × k2
where A is an area of section and k is radius of gyration of the section.
For circular section, k = D/4
Calculation:
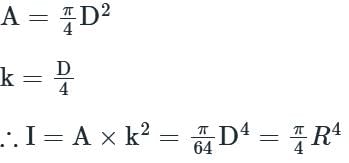
here, the area moment of inertia for the quadrant is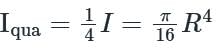
Area moment of inertia is given by, I = A × k2
where A is an area of section and k is radius of gyration of the section.
For circular section, k = D/4
Calculation:
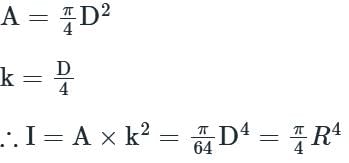
here, the area moment of inertia for the quadrant is
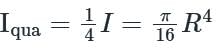
Moment of inertia of a disc of radius R about a diametric axis is 25 kg m2. The moment of inertia of the disc about a parallel axis at a distance R/2 from the centre is- a)31.25 kg m2
- b)37.5 kg m2
- c)50 kg m2
- d)62.5 kg m2
Correct answer is option 'C'. Can you explain this answer?
Moment of inertia of a disc of radius R about a diametric axis is 25 kg m2. The moment of inertia of the disc about a parallel axis at a distance R/2 from the centre is
a)
31.25 kg m2
b)
37.5 kg m2
c)
50 kg m2
d)
62.5 kg m2
|
Top Rankers answered |
From the perpendicular axis theorem, we have
Iz = Ix + Iy
where, Iz is moment of inertia about Z-axis, Ix is moment of inertia about X-axis and Iy is moment of inertia about Y-axis.
Moment of inertia of a disc, Iz = 1/2MR2
Now, Ix = Iy, because two perpendicular diameters are equivalent.
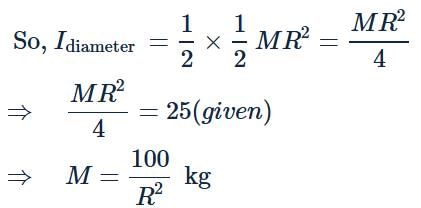
Also every diameter passes through centre of mass.
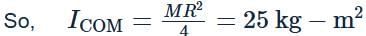
Using parallel axis theorem,
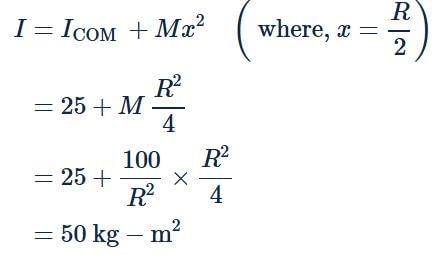
Iz = Ix + Iy
where, Iz is moment of inertia about Z-axis, Ix is moment of inertia about X-axis and Iy is moment of inertia about Y-axis.
Moment of inertia of a disc, Iz = 1/2MR2
Now, Ix = Iy, because two perpendicular diameters are equivalent.
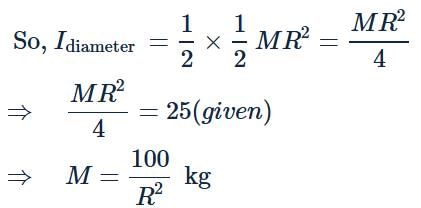
Also every diameter passes through centre of mass.
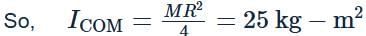
Using parallel axis theorem,
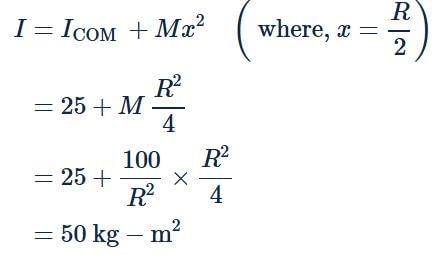
A thin circular disk is in the xy plane as shown in the figure. The ratio of its moment of inertia about z and z' axes will be: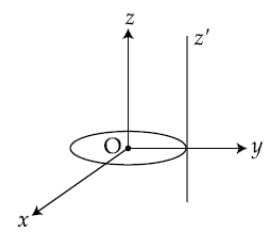
- a)1 : 3
- b)1 : 4
- c)1 : 5
- d)1 : 2
Correct answer is option 'A'. Can you explain this answer?
A thin circular disk is in the xy plane as shown in the figure. The ratio of its moment of inertia about z and z' axes will be:
a)
1 : 3
b)
1 : 4
c)
1 : 5
d)
1 : 2
|
|
Stepway Academy answered |
The problem involves a thin circular disk in the xy plane, and we need to find the ratio of its moment of inertia about the z and z' axes.
- The moment of inertia about the z-axis is calculated using the formula for a circular disk, which is (1/2)MR².
- For the z' axis, which is the axis through the centre parallel to the plane, the formula is (1/4)MR² + (1/12)MR².
- Simplifying, the moment of inertia about the z' axis becomes (1/3)MR².
- The ratio of the moment of inertia about the z and z' axes is therefore 1 : 3.
Chapter doubts & questions for Moment of Inertia - Physics for EmSAT Achieve 2025 is part of EmSAT Achieve exam preparation. The chapters have been prepared according to the EmSAT Achieve exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Moment of Inertia - Physics for EmSAT Achieve in English & Hindi are available as part of EmSAT Achieve exam.
Download more important topics, notes, lectures and mock test series for EmSAT Achieve Exam by signing up for free.
Physics for EmSAT Achieve
208 videos|329 docs|212 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup