All Exams >
EmSAT Achieve >
Physics for EmSAT Achieve >
All Questions
All questions of Heisenberg Uncertainty Principle for EmSAT Achieve Exam
Mass of a photon is given by 3.313 x 10-34 kg. Find it’s wavelength.- a)0.67A°
- b)0.67nm
- c)0.37A°
- d)1.67A°
Correct answer is option 'A'. Can you explain this answer?
Mass of a photon is given by 3.313 x 10-34 kg. Find it’s wavelength.
a)
0.67A°
b)
0.67nm
c)
0.37A°
d)
1.67A°

|
Arien Instructors answered |
Louis de Brogie gave the realation between momentum and wavelength as λ = h/p.
Here h is Planck’s constant, whose value is 6.626 x 10-34 J/s.
Wavelength = h/mc = 6.626 x 10-34 Js/(3.313 x 10-34 kg x 3 x 108 m/s) = 0.67A°.
A ball of mass 0.5kg is moving with velocity 6.626 m/s. What’s the wavelength of that ball?- a)1 x 10-34 m
- b)2 x 10-34 m
- c)2 x 10-32 m
- d)2 x 10-3 m
Correct answer is option 'B'. Can you explain this answer?
A ball of mass 0.5kg is moving with velocity 6.626 m/s. What’s the wavelength of that ball?
a)
1 x 10-34 m
b)
2 x 10-34 m
c)
2 x 10-32 m
d)
2 x 10-3 m

|
Arien Instructors answered |
Louis de Brogie gave the realation between momentum and wavelength as λ = h/p.
Here h is Planck’s constant, whose value is 6.626 x 10-34 J/s.
Wavelength = h/mv = 2 x 10-34 m (momentum p = mass m x velocity v).
Uncertainty in the position of an electron moving with a velocity 300 m/s accurate up to 0.001%, will be- a)1.93 × 10-3 m
- b)1.93 × 10-2 m
- c)3.86 × 10-2 m
- d)3.86 × 10-3 m
Correct answer is option 'B'. Can you explain this answer?
Uncertainty in the position of an electron moving with a velocity 300 m/s accurate up to 0.001%, will be
a)
1.93 × 10-3 m
b)
1.93 × 10-2 m
c)
3.86 × 10-2 m
d)
3.86 × 10-3 m
|
|
Issa Al Ghafri answered |
Calculating Uncertainty in Position of Electron
- Given: Velocity of electron = 300 m/s, Accuracy = 0.001%
Step 1: Calculate the uncertainty in velocity
- Uncertainty in velocity = 0.001% of 300 m/s
- Uncertainty in velocity = (0.001/100) * 300 = 0.003 m/s
Step 2: Use Heisenberg's Uncertainty Principle
- According to Heisenberg's Uncertainty Principle, Δx * Δp ≥ h/(4π), where h is the reduced Planck's constant.
- Since we are given the velocity, we can find the momentum using the formula p = mv, where m is the mass of the electron.
Step 3: Calculate the uncertainty in position
- Uncertainty in momentum = mass * uncertainty in velocity
- Uncertainty in position = h/(4π * uncertainty in momentum)
Therefore, the uncertainty in the position of the electron moving with a velocity of 300 m/s accurate up to 0.001% is 1.93 × 10^-2 m.
- Given: Velocity of electron = 300 m/s, Accuracy = 0.001%
Step 1: Calculate the uncertainty in velocity
- Uncertainty in velocity = 0.001% of 300 m/s
- Uncertainty in velocity = (0.001/100) * 300 = 0.003 m/s
Step 2: Use Heisenberg's Uncertainty Principle
- According to Heisenberg's Uncertainty Principle, Δx * Δp ≥ h/(4π), where h is the reduced Planck's constant.
- Since we are given the velocity, we can find the momentum using the formula p = mv, where m is the mass of the electron.
Step 3: Calculate the uncertainty in position
- Uncertainty in momentum = mass * uncertainty in velocity
- Uncertainty in position = h/(4π * uncertainty in momentum)
Therefore, the uncertainty in the position of the electron moving with a velocity of 300 m/s accurate up to 0.001% is 1.93 × 10^-2 m.
Which law found the corelation between the lifetime of the half-life of the alpha emitter and the alpha energies?- a)Bose-Einstein Distribution Law
- b)Fermi Dirac Distribution Law
- c)Geiger's law
- d)Maxwell Boltzmann Law
Correct answer is option 'C'. Can you explain this answer?
Which law found the corelation between the lifetime of the half-life of the alpha emitter and the alpha energies?
a)
Bose-Einstein Distribution Law
b)
Fermi Dirac Distribution Law
c)
Geiger's law
d)
Maxwell Boltzmann Law

|
Arien Instructors answered |
According to this law:
⇒ Range (R) = (m/3k) v3
Where m is mass, k is a constant and v is velocity.
The kinetic energy (E) is given by:
⇒ E = (1/2)m v2
The above equation can be written for v as,
⇒ v = (2E/m)1/2
So the range is given by:
⇒ R = (m/3k) × (2E/m)3/2 = (23/3 m-1/2/3k) E3/2
- From the above, it is clear that Geiger's law found the correlation between the decay constant (λ =0.693/T) and the alpha energies. Therefore option 3 is correct.
Which other variable pairs (other than momentum and position) are important observables in Heisenberg’s uncertainty principle?- a)Momentum and velocity
- b)Time and position
- c)Energy and momentum
- d)Energy and time
Correct answer is option 'D'. Can you explain this answer?
Which other variable pairs (other than momentum and position) are important observables in Heisenberg’s uncertainty principle?
a)
Momentum and velocity
b)
Time and position
c)
Energy and momentum
d)
Energy and time

|
Arien Instructors answered |
Substituting E = hv in Heisenberg’s uncertainty principle for position and momentum gives an expression in terms of energy and time as another variable pair that appears in this uncertainty principle. Momentum and velocity, time and position, and energy and momentum are not complementary pairs in this regard.
The uncertainty in measuring velocity of a proton is 4×103 m/s. The minimum uncertainty involved in measuring the position of proton will be?- a)7.9 × 10-9 m
- b)7.9 × 10-12 m
- c)3.9× 10-12 m
- d)3.9 × 10-9 m
Correct answer is option 'B'. Can you explain this answer?
The uncertainty in measuring velocity of a proton is 4×103 m/s. The minimum uncertainty involved in measuring the position of proton will be?
a)
7.9 × 10-9 m
b)
7.9 × 10-12 m
c)
3.9× 10-12 m
d)
3.9 × 10-9 m

|
Arien Instructors answered |
Δvx = 4 × 103 m/s, h = 6.63 × 10-34 J-s;
Mass of the proton = 1.67 × 10-27 kg;
From the uncertainty principle,
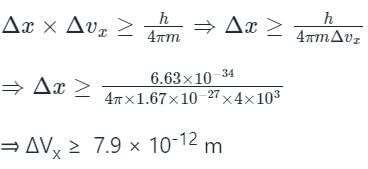
∴ minimum uncertainity involved in measuring the position will be 7.9 × 10-12 m.
Mass of the proton = 1.67 × 10-27 kg;
From the uncertainty principle,
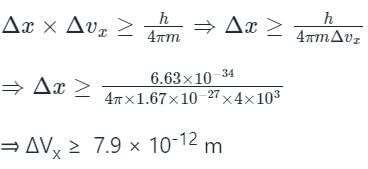
∴ minimum uncertainity involved in measuring the position will be 7.9 × 10-12 m.
The particles that are indistingishable and obey both Heisenberg's uncertainty principle and Pauli's exclusion principle obey- a)Fermi-Dirac statistics
- b)Bose-Einstein statistics
- c)Maxwell Boltzmann distribution
- d)Sigmund distribution
Correct answer is option 'A'. Can you explain this answer?
The particles that are indistingishable and obey both Heisenberg's uncertainty principle and Pauli's exclusion principle obey
a)
Fermi-Dirac statistics
b)
Bose-Einstein statistics
c)
Maxwell Boltzmann distribution
d)
Sigmund distribution

|
Arien Instructors answered |
- From the above, it is clear that, the particles that are indistinguishable and obey both Heisenberg's uncertainty principle and Pauli's exclusion principle are Fermi-Dirac statistics.
The error in the measurement of lifetime of an atom is 2 × 10-2 sec. What is the minimum uncertainty in its energy in eV?- a)2 × 10-15 eV
- b)8 × 10-15 eV
- c)1.6 × 10-14 eV
- d)4 × 10-15 eV
Correct answer is option 'C'. Can you explain this answer?
The error in the measurement of lifetime of an atom is 2 × 10-2 sec. What is the minimum uncertainty in its energy in eV?
a)
2 × 10-15 eV
b)
8 × 10-15 eV
c)
1.6 × 10-14 eV
d)
4 × 10-15 eV

|
Arien Instructors answered |
Given Δt = 2 × 10-2 sec;
From the second equation,

Therefore, minimum uncertainty in energy is
ΔE = 2.638 × 10-33 J;
Converting in eV,
ΔE = (2.638 × 10-33)/(1.6 × 10-19) eV = 1.6 × 10-14 eV;
From the second equation,

Therefore, minimum uncertainty in energy is
ΔE = 2.638 × 10-33 J;
Converting in eV,
ΔE = (2.638 × 10-33)/(1.6 × 10-19) eV = 1.6 × 10-14 eV;
Which of the following statements are correct?- a)The Heisenberg Uncertainty Principle applies to electrons, but not to protons.
- b)It is impossible to determine simultaneously both the position and time of an electron with accuracy.
- c)It is impossible to determine simultaneously both the time and mass of an electron with accuracy.
- d)It is impossible to determine simultaneously both the time and energy of an electron with accuracy.
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements are correct?
a)
The Heisenberg Uncertainty Principle applies to electrons, but not to protons.
b)
It is impossible to determine simultaneously both the position and time of an electron with accuracy.
c)
It is impossible to determine simultaneously both the time and mass of an electron with accuracy.
d)
It is impossible to determine simultaneously both the time and energy of an electron with accuracy.

|
Arien Instructors answered |
Heisenberg’s uncertainty principle is a key principle in quantum mechanics.
Very roughly, it states that if we know everything about where a particle is located (the uncertainty of position is small), we know nothing about its momentum (the uncertainty of momentum is large), and vice versa.
Versions of the uncertainty principle also exist for other quantities as well, such as energy and time.
We discuss the momentum-position and energy-time uncertainty principles separately.
The Heisenberg Uncertainty Principle applies to electrons and protons as well, it is applicable for all small particles.
Heisenberg’s uncertainty principle is given by
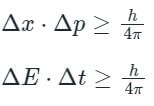
Heisenberg's uncertainty principle talks about either position, momentum pair or energy, time pair.
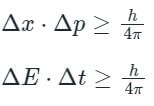
Heisenberg's uncertainty principle talks about either position, momentum pair or energy, time pair.
Fermion particles obey- a)Maxwell-Boltzmann statistics
- b)Base-Einstein statistics
- c)Pauli’s exclusion principle
- d)Heisenberg’s uncertainty principle
Correct answer is option 'C'. Can you explain this answer?
Fermion particles obey
a)
Maxwell-Boltzmann statistics
b)
Base-Einstein statistics
c)
Pauli’s exclusion principle
d)
Heisenberg’s uncertainty principle

|
Arien Instructors answered |
- Pauli exclusion principle states that in a single atom no two electrons will have an identical set or the same quantum numbers i.e. every electron should have or be in its own unique state (singlet state).
- There are two salient rules that the Pauli Exclusion Principle follows:
- Only two electrons can occupy the same orbital.
- The two electrons that are present in the same orbital must have opposite spins or it should be antiparallel.
- However, Pauli Exclusion Principle does not only apply to electrons.
- It applies to other particles of half-integer spin such as fermions. It is not relevant for particles with an integer spin such as bosons which have symmetric wave functions.
Chapter doubts & questions for Heisenberg Uncertainty Principle - Physics for EmSAT Achieve 2025 is part of EmSAT Achieve exam preparation. The chapters have been prepared according to the EmSAT Achieve exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Heisenberg Uncertainty Principle - Physics for EmSAT Achieve in English & Hindi are available as part of EmSAT Achieve exam.
Download more important topics, notes, lectures and mock test series for EmSAT Achieve Exam by signing up for free.
Physics for EmSAT Achieve
208 videos|329 docs|212 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









