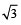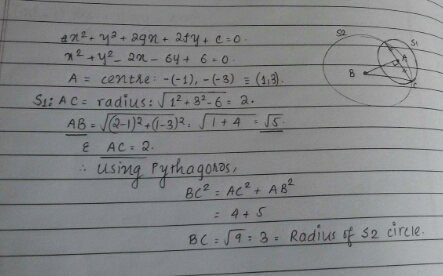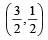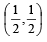All Exams >
Class 10 >
Mathematics for GCSE/IGCSE >
All Questions
All questions of Circle Theorems for Class 10 Exam
The locus of the centre of a circle, which touches externally the circle x2 + y2 – 6x – 6y + 14 = 0 and also touches the y-axis, is given by the equation: (1993 - 1 Marks)- a)x2 – 6x – 10y + 14 = 0
- b)x2 – 10x – 6y + 14 = 0
- c)y2 – 6x – 10y + 14 = 0
- d)y2 – 10x – 6y + 14 = 0
Correct answer is option 'D'. Can you explain this answer?
The locus of the centre of a circle, which touches externally the circle x2 + y2 – 6x – 6y + 14 = 0 and also touches the y-axis, is given by the equation: (1993 - 1 Marks)
a)
x2 – 6x – 10y + 14 = 0
b)
x2 – 10x – 6y + 14 = 0
c)
y2 – 6x – 10y + 14 = 0
d)
y2 – 10x – 6y + 14 = 0
|
Hansa Sharma answered |
The given circle is x2 + y2 – 6x + 14 = 0, centre (3, 3), radius = 2
Let (h, k) be the centre of touching circle.
Let (h, k) be the centre of touching circle.
Then radius of touching circle = h [as it touches y-axis also]
∴ Distance between centres of two circles = sum of the radii of two circles
⇒ (h – 3)2 + (k – 3)2 = (2 + h)2
⇒ k2 – 10h – 6k + 14 = 0
∴ locus of (h, k) is y2 – 10x – 6y + 14 = 0
If the two circles (x – 1)2 + (y – 3)2 = r2 and x2 + y2 – 8x + 2y + 8 = 0 intersect in two distinct points, then (1989 - 2 Marks)- a)2 < r < 8
- b)r < 2
- c)r = 2
- d)r > 2
Correct answer is option 'A'. Can you explain this answer?
If the two circles (x – 1)2 + (y – 3)2 = r2 and x2 + y2 – 8x + 2y + 8 = 0 intersect in two distinct points, then (1989 - 2 Marks)
a)
2 < r < 8
b)
r < 2
c)
r = 2
d)
r > 2
|
Jaideep Basu answered |
We have two circles (x – 1)2 + (y – 3)2 = r2
Centre (1, 3), radius = r and x2 + y2 – 8x + 2y + 8 = 0
Centre (1, 3), radius = r and x2 + y2 – 8x + 2y + 8 = 0
Centre (4, – 1), radius =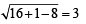 
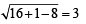
As the two circles intersect each other in two distinct points we should have
C1 C2 < r1 + r2 and C1 C2 > | r1 – r2 |
⇒ C1 C2 < r + 3 and C1 C2 < | r1 – r2|
and 5 > |r – 3 |⇒ 5 < r + 3 ⇒ | r – 3 | < 5 ⇒ r > 2 … (i)
⇒ – 5 < r – 3 < 5 ⇒ – 2 < r < 8 … (ii)
Combining (i) and (ii), we get 2 < r < 8
Let RS be the diameter of the circle x2 + y2 = 1, where S is the point (1, 0). Let P be a variable point (other than R and S) on the circle and tangents to the circle at S and P meet at the point Q. The normal to the circle at P intersects a line drawn through Q parallel to RS at point E. Then the locus of E passes through the point(s) (JEE Adv. 2016)- a)
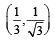
- b)
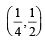
- c)
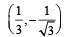
- d)
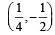
Correct answer is option 'A,C'. Can you explain this answer?
Let RS be the diameter of the circle x2 + y2 = 1, where S is the point (1, 0). Let P be a variable point (other than R and S) on the circle and tangents to the circle at S and P meet at the point Q. The normal to the circle at P intersects a line drawn through Q parallel to RS at point E. Then the locus of E passes through the point(s) (JEE Adv. 2016)
a)
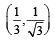
b)
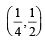
c)
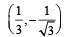
d)
|
|
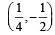
Hansa Sharma answered |
Circle : x2 + y2 = 1
Equation of tangent at P(cosθ, sinθ) x cosθ + y sinθ = 1 ...(1)
Equation of normal at P y = x tanθ ...(2)
Equation of tangent at S is x = 1
Equation of tangent at P(cosθ, sinθ) x cosθ + y sinθ = 1 ...(1)
Equation of normal at P y = x tanθ ...(2)
Equation of tangent at S is x = 1
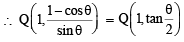
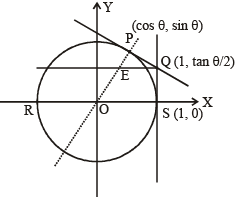
∴ Equation of line through Q and parallel to RS is
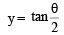
∴ Intersection point E of normal and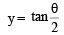
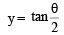
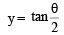= x tanθ ⇒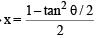 
∴ Locus of E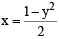 
or y2 = 1 – 2x
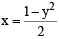or y2 = 1 – 2xIt is satisfied by the points 
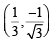
and
and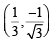Which theorem states that parallelograms on the same base and between the same parallels have equal areas?- a) Theorem of Equal Figures
- b) Theorem of Areas of Triangles
- c) Theorem 19
- d) Theorem of Congruent Figures
Correct answer is option 'C'. Can you explain this answer?
Which theorem states that parallelograms on the same base and between the same parallels have equal areas?
a)
Theorem of Equal Figures
b)
Theorem of Areas of Triangles
c)
Theorem 19
d)
Theorem of Congruent Figures
|
Let's Tute answered |
Theorem 19 states that parallelograms sharing the same base and lying between the same parallel lines have equal areas. This theorem can be proven using the properties of congruent triangles formed within the parallelograms.
The angle between a pair of tangents drawn from a point P to the circle x2 + y2 + 4x – 6y + 9 sin2α + 13 cos2α = 0 is 2α.The equation of the locus of the point P is (1996 - 1 Mark)- a)x2 + y2 + 4x – 6y + 4 = 0
- b)x2 + y2 + 4x – 6y – 9 = 0
- c)x2 + y2 + 4x – 6y – 4 = 0
- d)x2 + y2 + 4x – 6y + 9 = 0
Correct answer is option 'D'. Can you explain this answer?
The angle between a pair of tangents drawn from a point P to the circle x2 + y2 + 4x – 6y + 9 sin2α + 13 cos2α = 0 is 2α.The equation of the locus of the point P is (1996 - 1 Mark)
a)
x2 + y2 + 4x – 6y + 4 = 0
b)
x2 + y2 + 4x – 6y – 9 = 0
c)
x2 + y2 + 4x – 6y – 4 = 0
d)
x2 + y2 + 4x – 6y + 9 = 0
|
Geetika Shah answered |
Centre of the circle x2 + y2 + 4x – 6y + 9 sin2α + 13 cos2α = 0 is C (– 2, 3) and its radius is
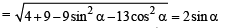
Let P (h, k) be any point on the locus. The ∠ APC =α
Also ∠ PAC =
That is, triangle APC is a right triangle.
Thus, 
⇒ (h + 2)2 + (k – 3)2 = 4 or h2 + k2 + 4h – 6k + 9 = 0
Thus required equation of the locus is x2 + y2 + 4x – 6y + 9 = 0
The equation of the circle passing through (1, 1) and the points of intersection of x2 + y2 + 13x – 3y = 0 and 2x2 + 2y2 + 4x – 7y – 25 = 0 is (1983 - 1 Mark)- a)4x2 + 4y2 – 30x – 10y – 25 = 0
- b)4x2 + 4y2 + 30x – 13y – 25 = 0
- c)4x2 + 4y2 – 17x – 10y + 25 = 0
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The equation of the circle passing through (1, 1) and the points of intersection of x2 + y2 + 13x – 3y = 0 and 2x2 + 2y2 + 4x – 7y – 25 = 0 is (1983 - 1 Mark)
a)
4x2 + 4y2 – 30x – 10y – 25 = 0
b)
4x2 + 4y2 + 30x – 13y – 25 = 0
c)
4x2 + 4y2 – 17x – 10y + 25 = 0
d)
none of these
|
Uday Ghoshal answered |
KEY CONCEPT
Circle through pts. of intersection of two circles S1 = 0 and S2 = 0 is S1 + λS2 = 0
∴ Req. circle is, (x2 + y2 + 13x – 3y) + λ (x2 + y2 + 2x
Circle through pts. of intersection of two circles S1 = 0 and S2 = 0 is S1 + λS2 = 0
∴ Req. circle is, (x2 + y2 + 13x – 3y) + λ (x2 + y2 + 2x
⇒ (1 + λ) x2 + (1 +λ) y2 + (13 + 2λ)
As it passes through (1, 1)
∴ 1 + λ + 1 + λ + 13 + 2λ – 3 –
⇒ – 12λ + 12 = 0 ⇒ λ = 1
∴ Req. circle is,
2x2 + 2y2 + 15 x - 
or4x2 + 4y2 + 30x –13 y – 25 = 0
The circles x2 + y2 – 10x + 16 = 0 and x2 + y2 = r2 intersect each other in two distinct points if (1994)- a)r < 2
- b)r > 8
- c)2 < r < 8
- d)2 ≤ r ≤ 8
Correct answer is option 'C'. Can you explain this answer?
The circles x2 + y2 – 10x + 16 = 0 and x2 + y2 = r2 intersect each other in two distinct points if (1994)
a)
r < 2
b)
r > 8
c)
2 < r < 8
d)
2 ≤ r ≤ 8
|
Sagarika Das answered |
Centres and radii of two circles are C1 (5, 0); 3 = r1 and C2 (0, 0); r = r2
As circles intersect each other in two distinct points,
|r1 – r2| < C1C2 < r1 + r2
⇒ | r – 3 | < 5 < r + 3 ⇒ 2 < r < 8
A circle is given by x2 + (y–1)2 = 1, another circle C touches it externally and also the x-axis, then the locus of its centre is (2005S)- a){(x, y) : x2 = 4y} ∪ {(x, y) : y ≤ 0}
- b){(x, y) : x2 + (y – 1)2 = 4}∪ {(x, y) : y ≤ 0}
- c){(x, y) : x2 = y} ∪ {(0, y) : y ≤ 0}
- d){(x, y) : x2 = 4y} ∪ {(0, y) : y ≤ 0}
Correct answer is option 'D'. Can you explain this answer?
A circle is given by x2 + (y–1)2 = 1, another circle C touches it externally and also the x-axis, then the locus of its centre is (2005S)
a)
{(x, y) : x2 = 4y} ∪ {(x, y) : y ≤ 0}
b)
{(x, y) : x2 + (y – 1)2 = 4}∪ {(x, y) : y ≤ 0}
c)
{(x, y) : x2 = y} ∪ {(0, y) : y ≤ 0}
d)
{(x, y) : x2 = 4y} ∪ {(0, y) : y ≤ 0}
|
|
Mahesh Mehra answered |
Let the centre of circle C be (h, k). Then as this circle touches axis of x, its radius = | k |
Also it touches the given circle x2 + (y – 1)2 = 1, centre (0, 1) radius 1, externally
Therefore, the distance between centres = sum of radii
⇒ h2 + k2 – 2k + 1 = (1 + | k |)2
⇒ h2 + k2 – 2k + 1 = 1 + 2 | k | + k2
⇒ h2 = 2k + 2 | k |
∴ Locus of (h, k) is, x2 = 2y + 2 | y |
Now if y > 0, it becomes x2 = 4y and if y < 0, it becomes x = 0
∴ Combining the two, the required locus is {(x, y) : x2 = 4y} ∪ {(0, y) : y < 0}
⇒ h2 + k2 – 2k + 1 = 1 + 2 | k | + k2
⇒ h2 = 2k + 2 | k |
∴ Locus of (h, k) is, x2 = 2y + 2 | y |
Now if y > 0, it becomes x2 = 4y and if y < 0, it becomes x = 0
∴ Combining the two, the required locus is {(x, y) : x2 = 4y} ∪ {(0, y) : y < 0}
The number of common tangents to the circles x2 + y2 = 4 and x2 + y2 – 6x – 8y = 24 is (1998 - 2 Marks)- a)0
- b)1
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
The number of common tangents to the circles x2 + y2 = 4 and x2 + y2 – 6x – 8y = 24 is (1998 - 2 Marks)
a)
0
b)
1
c)
3
d)
4
|
Sneha Sarkar answered |
x2 + y2 = 4 (given) Centre C1 ≡ (0, 0) and R1 = 2.
Also for circle x2 + y2 – 6x – 8y – 24 = 0 C2 ≡ (3, 4) and R2 = 7.
Again C1 C2 = 5 = R2 – R1
Also for circle x2 + y2 – 6x – 8y – 24 = 0 C2 ≡ (3, 4) and R2 = 7.
Again C1 C2 = 5 = R2 – R1
Therefore, the given circles touch internally such that they can have just one common tangent at the point of contact.
The locus of th e mid-point of the ch or d of con tact of tangents drawn from points lying on the straight line 4x – 5y = 20 to the circle x2 + y2 = 9 is (2012)- a)20 (x2 + y2) – 36x + 45 y = 0
- b)20 (x2 + y2) + 36x – 45 y = 0
- c)36 (x2 + y2) – 20x + 45 y = 0
- d)36 (x2 + y2) + 20x – 45 y = 0
Correct answer is option 'A'. Can you explain this answer?
The locus of th e mid-point of the ch or d of con tact of tangents drawn from points lying on the straight line 4x – 5y = 20 to the circle x2 + y2 = 9 is (2012)
a)
20 (x2 + y2) – 36x + 45 y = 0
b)
20 (x2 + y2) + 36x – 45 y = 0
c)
36 (x2 + y2) – 20x + 45 y = 0
d)
36 (x2 + y2) + 20x – 45 y = 0
|
|
Sagarika Choudhury answered |
Understanding the Problem
The problem involves finding the locus of the mid-point of the chord of contact of tangents drawn from points on the line 4x - 5y = 20 to the circle x² + y² = 9.
Circle and Line Equations
- Circle: x² + y² = 9
- Line: 4x - 5y - 20 = 0
Chord of Contact Formula
The equation of the chord of contact from point (x₁, y₁) to the circle is given by:
x*x₁ + y*y₁ = 9
Finding Midpoints
If we take a point (x₁, y₁) on the line, we can express y₁ in terms of x₁ as follows:
y₁ = (4/5)x₁ - 4
Substituting y₁ into the chord of contact equation:
x*x₁ + y*((4/5)x₁ - 4) = 9
Transforming to Midpoint Coordinates
Let the midpoint coordinates be (h, k). Thus, we have:
x = h and y = k.
Now replace x and y in the chord of contact equation:
h*x₁ + k*((4/5)x₁ - 4) = 9
This can be rearranged to express h and k in terms of each other.
Final Locus Equation
After simplifying, we find the locus of the mid-point leads to:
20(x² + y²) - 36x + 45y = 0
Thus, the correct answer is option (a).
Conclusion
The locus of the mid-point of the chord of contact is described by the equation derived from the conditions given by the circle and the line, confirming the answer as option (a).
The problem involves finding the locus of the mid-point of the chord of contact of tangents drawn from points on the line 4x - 5y = 20 to the circle x² + y² = 9.
Circle and Line Equations
- Circle: x² + y² = 9
- Line: 4x - 5y - 20 = 0
Chord of Contact Formula
The equation of the chord of contact from point (x₁, y₁) to the circle is given by:
x*x₁ + y*y₁ = 9
Finding Midpoints
If we take a point (x₁, y₁) on the line, we can express y₁ in terms of x₁ as follows:
y₁ = (4/5)x₁ - 4
Substituting y₁ into the chord of contact equation:
x*x₁ + y*((4/5)x₁ - 4) = 9
Transforming to Midpoint Coordinates
Let the midpoint coordinates be (h, k). Thus, we have:
x = h and y = k.
Now replace x and y in the chord of contact equation:
h*x₁ + k*((4/5)x₁ - 4) = 9
This can be rearranged to express h and k in terms of each other.
Final Locus Equation
After simplifying, we find the locus of the mid-point leads to:
20(x² + y²) - 36x + 45y = 0
Thus, the correct answer is option (a).
Conclusion
The locus of the mid-point of the chord of contact is described by the equation derived from the conditions given by the circle and the line, confirming the answer as option (a).
Let PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then 2r equals (2001S)- a)
- b)(PQ + RS)/2
- c)2PQ.RS/(PQ + RS)
- d)
Correct answer is option 'A'. Can you explain this answer?
Let PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then 2r equals (2001S)
a)
b)
(PQ + RS)/2
c)
2PQ.RS/(PQ + RS)
d)
|
|
Shubham Pillai answered |
Let ∠RPS = θ
∠XPQ = 90° – θ
∴∠PQX = θ (∵ ∠PXQ = 90°)
∴ΔPRS ~ ΔQPR (AA similarity)
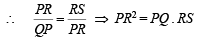
If two distinct chords, drawn from the point (p, q) on the circle x2 + y2 = px + qy (where pq ≠ 0) are bisected by the x –axis, then (1999 - 2 Marks)- a)p2 = q2
- b)p2 = 8q2
- c)P2 < 8q2
- d)p2 > 8q2.
Correct answer is option 'D'. Can you explain this answer?
If two distinct chords, drawn from the point (p, q) on the circle x2 + y2 = px + qy (where pq ≠ 0) are bisected by the x –axis, then (1999 - 2 Marks)
a)
p2 = q2
b)
p2 = 8q2
c)
P2 < 8q2
d)
p2 > 8q2.
|
Swara Chavan answered |
The given equation of the circle is x2 + y2 – px – qy = 0, pq ≠ 0 Let the chord drawn from (p, q) is bisected by x-axis at point (x1, 0).
Then equation of chord is
Then equation of chord is
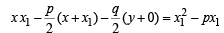(using T = S1)As it passes through (p, q), therefore,
As through (p,q) two distinct chords can be drawn.
∴ Roots of above equation be real and distinct, i.e., D > 0.
⇒ 9p2 – 4 × 2 (p2 + q2) > 0 ⇒ p2 > 8q2
If the radius of a circle is 7 cm, what is the circumference of the circle?- a)42 cm
- b)14π cm
- c)21 cm
- d)7π cm
Correct answer is option 'B'. Can you explain this answer?
If the radius of a circle is 7 cm, what is the circumference of the circle?
a)
42 cm
b)
14π cm
c)
21 cm
d)
7π cm
|
EduRev Class 9 answered |
The circumference of a circle is calculated using the formula C = 2πr. For a radius of 7 cm, the circumference would be C = 2π(7) = 14π cm. This formula is fundamental in circle geometry and helps in various practical applications.
Which of the following statements is true concerning inscribed and circumscribed circles?- a)Both circles are identical in size
- b)An inscribed circle touches all vertices of a polygon
- c)An inscribed circle cannot exist within a polygon
- d)A circumscribed circle is always larger than the inscribed circle
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements is true concerning inscribed and circumscribed circles?
a)
Both circles are identical in size
b)
An inscribed circle touches all vertices of a polygon
c)
An inscribed circle cannot exist within a polygon
d)
A circumscribed circle is always larger than the inscribed circle
|
|
Namrata Desai answered |
Understanding Circles in Polygons
When discussing inscribed and circumscribed circles, it's crucial to understand their definitions and properties.
Inscribed Circle
- An inscribed circle (or incircle) is a circle that is tangent to all sides of a polygon.
- It exists only in polygons that are tangential, meaning their sides can touch a single circle.
Circumscribed Circle
- A circumscribed circle (or circumcircle) is a circle that passes through all vertices of a polygon.
- It encompasses the entire polygon and is defined by its vertices.
Key Relationship between the Two Circles
- The circumradius (radius of the circumscribed circle) is always greater than or equal to the inradius (radius of the inscribed circle) for any polygon.
- This is because the circumcircle must extend to the vertices, while the incircle fits snugly within the polygon.
Why Option D is Correct
- The statement "A circumscribed circle is always larger than the inscribed circle" is true because:
- The circumcircle surrounds the polygon, while the incircle is contained within it.
- In most cases (except for certain degenerate cases), the circumradius will be larger than the inradius.
Conclusion
- In summary, the relationship between the inscribed and circumscribed circles illustrates fundamental geometric principles, confirming that option 'D' is indeed correct.
When discussing inscribed and circumscribed circles, it's crucial to understand their definitions and properties.
Inscribed Circle
- An inscribed circle (or incircle) is a circle that is tangent to all sides of a polygon.
- It exists only in polygons that are tangential, meaning their sides can touch a single circle.
Circumscribed Circle
- A circumscribed circle (or circumcircle) is a circle that passes through all vertices of a polygon.
- It encompasses the entire polygon and is defined by its vertices.
Key Relationship between the Two Circles
- The circumradius (radius of the circumscribed circle) is always greater than or equal to the inradius (radius of the inscribed circle) for any polygon.
- This is because the circumcircle must extend to the vertices, while the incircle fits snugly within the polygon.
Why Option D is Correct
- The statement "A circumscribed circle is always larger than the inscribed circle" is true because:
- The circumcircle surrounds the polygon, while the incircle is contained within it.
- In most cases (except for certain degenerate cases), the circumradius will be larger than the inradius.
Conclusion
- In summary, the relationship between the inscribed and circumscribed circles illustrates fundamental geometric principles, confirming that option 'D' is indeed correct.
If the circles x2 + y2 + 2x + 2ky + 6 = 0, x2 + y2 + 2ky + k = 0 intersect orthogonally, then k is (2000S)- a)
- b)
- c)
- d)
Correct answer is option 'A'. Can you explain this answer?
If the circles x2 + y2 + 2x + 2ky + 6 = 0, x2 + y2 + 2ky + k = 0 intersect orthogonally, then k is (2000S)
a)
b)
c)
d)
|
|
Md Sajid answered |
2(g1g2+f1f2)= C1+C2 orthogonal ke liye
In triangle ABC, if point D divides side BC in the ratio 1:4, what is the area ratio of triangles ABD and ADC?- a) 1:4
- b) 1:2
- c) 1:3
- d) 1:5
Correct answer is option 'A'. Can you explain this answer?
In triangle ABC, if point D divides side BC in the ratio 1:4, what is the area ratio of triangles ABD and ADC?
a)
1:4
b)
1:2
c)
1:3
d)
1:5
|
|
Let's Tute answered |
The area ratio of triangles ABD and ADC is 1:4 because the areas of the triangles are proportional to the lengths of their respective bases. Since D divides BC in a ratio of 1:4, the area of triangle ABD is one part while the area of triangle ADC is four parts.
If triangle DEF has a base DE of 12 cm and height from F perpendicular to DE of 5 cm, what is its area?- a) 20 cm²
- b) 40 cm²
- c) 30 cm²
- d) 60 cm²
Correct answer is option 'C'. Can you explain this answer?
If triangle DEF has a base DE of 12 cm and height from F perpendicular to DE of 5 cm, what is its area?
a)
20 cm²
b)
40 cm²
c)
30 cm²
d)
60 cm²
|
|
Let's Tute answered |
The area of triangle DEF can be calculated as follows: Area = 1/2 × base × height = 1/2 × 12 × 5 = 30 cm².
What is the area of triangle ABC if point D divides side BC in a ratio of 1:2?- a) 1/2 of the area of triangle ABC
- b) 1/3 of the area of triangle ABC
- c) 1/4 of the area of triangle ABC
- d) 2/3 of the area of triangle ABC
Correct answer is option 'B'. Can you explain this answer?
What is the area of triangle ABC if point D divides side BC in a ratio of 1:2?
a)
1/2 of the area of triangle ABC
b)
1/3 of the area of triangle ABC
c)
1/4 of the area of triangle ABC
d)
2/3 of the area of triangle ABC
|
|
EduRev Class 9 answered |
If point D divides side BC in a ratio of 1:2, then triangle ABD will have an area that is 1/3 of triangle ABC, while triangle ACD will have an area of 2/3 of triangle ABC. This is due to the proportionality of the bases, which directly affects the area.
If a quadrilateral is divided into triangles by its diagonals, what can be said about the areas of these triangles?- a) The areas cannot be determined without specific measurements.
- b) The areas relate to the lengths of the diagonals.
- c) The areas are always equal.
- d) The areas can be compared using the ratios of their bases.
Correct answer is option 'D'. Can you explain this answer?
If a quadrilateral is divided into triangles by its diagonals, what can be said about the areas of these triangles?
a)
The areas cannot be determined without specific measurements.
b)
The areas relate to the lengths of the diagonals.
c)
The areas are always equal.
d)
The areas can be compared using the ratios of their bases.
|
|
EduRev Class 9 answered |
The areas of the triangles formed by the diagonals of a quadrilateral can be compared using the ratios of their bases. This is due to the properties of triangle areas depending on their respective bases and heights relative to the diagonals.
In the theorem regarding triangles on the same base and between the same parallels, what conclusion can be drawn?- a) The areas are equal.
- b) The triangles are always similar.
- c) The triangles must be congruent.
- d) The areas are always unequal.
Correct answer is option 'A'. Can you explain this answer?
In the theorem regarding triangles on the same base and between the same parallels, what conclusion can be drawn?
a)
The areas are equal.
b)
The triangles are always similar.
c)
The triangles must be congruent.
d)
The areas are always unequal.
|
|
Let's Tute answered |
The theorem states that triangles on the same base and between the same parallels have equal areas. This conclusion arises from the fact that both triangles share identical base lengths and heights, leading to equal area calculations.
The centre of the circle passing through the point (0, 1) and touching the curve y = x2 at (2, 4) is (1983 - 1 Mark)- a)
- b)
- c)
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The centre of the circle passing through the point (0, 1) and touching the curve y = x2 at (2, 4) is (1983 - 1 Mark)
a)
b)
c)
d)
none of these
|
|
Ishani Menon answered |
Let C (h, k) be the centre of circle touching x2 = y at B (2, 4). Then equation of common tangent at B is
i.e., 4x – y = 4Radius is perpendicular to this tangent
= -1 ⇒ 4k = 18… (1) Also AC = BC ⇒ h2 + (k – 1)2 = (h – 2)2 + (k – 4)2
⇒ 4h + 6k = 19 … (2)
⇒ 4h + 6k = 19 … (2)
Solving (1) and (2) we get the centre as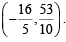 
Which theorem states that one and only one circle can pass through three non-collinear points?- a)Theorem 27
- b)Theorem 25
- c)Theorem 26
- d)Theorem 28
Correct answer is option 'C'. Can you explain this answer?
Which theorem states that one and only one circle can pass through three non-collinear points?
a)
Theorem 27
b)
Theorem 25
c)
Theorem 26
d)
Theorem 28
|
|
EduRev Class 9 answered |
Theorem 26 asserts that one unique circle can be drawn through three non-collinear points. This theorem is significant in geometry, particularly in constructions and proofs involving triangles and polygons.
What is the definition of a circle?- a)A closed curve where every point is equidistant from a fixed point
- b)A polygon with three sides
- c)A shape that has at least one angle greater than 90 degrees
- d)A straight line that divides a plane into two parts
Correct answer is option 'A'. Can you explain this answer?
What is the definition of a circle?
a)
A closed curve where every point is equidistant from a fixed point
b)
A polygon with three sides
c)
A shape that has at least one angle greater than 90 degrees
d)
A straight line that divides a plane into two parts
|
|
Let's Tute answered |
A circle is defined as a closed curve in which every point is equidistant from a fixed point known as the center. This fundamental property distinguishes circles from other geometric shapes and is pivotal in various geometric concepts and applications.
If two circles are equal, what does that mean about their radii?- a)They have different centers
- b)Their radii are equal
- c)They have different diameters
- d)One is larger than the other
Correct answer is option 'B'. Can you explain this answer?
If two circles are equal, what does that mean about their radii?
a)
They have different centers
b)
Their radii are equal
c)
They have different diameters
d)
One is larger than the other
|
|
Let's Tute answered |
Two circles are considered equal or congruent when their radii are equal. This property is essential when determining the relationships between different circles in geometry, such as in constructions and proofs.
Which theorem states that a line from the center of a circle bisecting a chord is perpendicular to that chord?- a)Theorem 23
- b)Theorem 24
- c)Theorem 22
- d)Theorem 21
Correct answer is option 'C'. Can you explain this answer?
Which theorem states that a line from the center of a circle bisecting a chord is perpendicular to that chord?
a)
Theorem 23
b)
Theorem 24
c)
Theorem 22
d)
Theorem 21
|
|
EduRev Class 9 answered |
Theorem 22 states that a line drawn from the center of a circle that bisects a chord (which is not a diameter) will be perpendicular to that chord. This theorem is fundamental in proving various properties related to chords and their relationships within circles.
In the context of circle geometry, what does the term "locus" refer to?- a)The area enclosed by a circle
- b)The center of the circle
- c)The path traced by a point moving at a constant distance from a fixed point
- d)The measurement of the circumference
Correct answer is option 'C'. Can you explain this answer?
In the context of circle geometry, what does the term "locus" refer to?
a)
The area enclosed by a circle
b)
The center of the circle
c)
The path traced by a point moving at a constant distance from a fixed point
d)
The measurement of the circumference
|
C K Academy answered |
The term "locus" refers to the path traced by a point that maintains a constant distance from a fixed point, which is the center of the circle. This concept is fundamental in defining circles and understanding their geometric properties.
Circle(s) touching x-axis at a distance 3 from the origin and having an intercept of length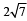 
on y-axis is (are) (JEE Adv. 2013)- a)x2 + y2 – 6x + 8y + 9 = 0
- b)x2 + y2 – 6x + 7y + 9 = 0
- c)x2 + y2 – 6x – 8y + 9 = 0
- d)x2 + y2 – 6x – 7y + 9 = 0
Correct answer is option 'A,C'. Can you explain this answer?
Circle(s) touching x-axis at a distance 3 from the origin and having an intercept of length 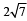on y-axis is (are) (JEE Adv. 2013)
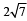on y-axis is (are) (JEE Adv. 2013)a)
x2 + y2 – 6x + 8y + 9 = 0
b)
x2 + y2 – 6x + 7y + 9 = 0
c)
x2 + y2 – 6x – 8y + 9 = 0
d)
x2 + y2 – 6x – 7y + 9 = 0
|
|
Rajiv Reddy answered |
There can be two possibilites for the given circle as shown in the figure
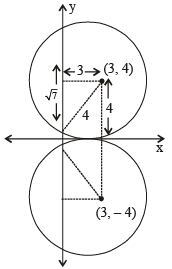
∴ The equations of circles can be (x – 3)2 + (y – 4)2 = 42
or (x – 3)2 + (y + 4)2 = 42
i.e. x2 + y2 – 6x – 8y + 9 = 0
or x2 + y2 – 6x + 8y + 9 = 0
or (x – 3)2 + (y + 4)2 = 42
i.e. x2 + y2 – 6x – 8y + 9 = 0
or x2 + y2 – 6x + 8y + 9 = 0
The equations of the tangents drawn from the origin to the circle x2 + y2 – 2rx – 2hy + h2 = 0, are (1988 - 2 Marks)- a)x = 0
- b)y = 0
- c)(h2 – r2)x – 2rhy = 0
- d)(h2 – r2)x + 2rhy = 0
Correct answer is option 'A,C'. Can you explain this answer?
The equations of the tangents drawn from the origin to the circle x2 + y2 – 2rx – 2hy + h2 = 0, are (1988 - 2 Marks)
a)
x = 0
b)
y = 0
c)
(h2 – r2)x – 2rhy = 0
d)
(h2 – r2)x + 2rhy = 0
|
Bhavya Nair answered |
The given circle is x2 + y2 – 2rx – 2hy + h2 = 0 with centre (r, h) and radius = r.
Clearly circle touches y-axis so one of its tangent is x = 0.
Clearly circle touches y-axis so one of its tangent is x = 0.
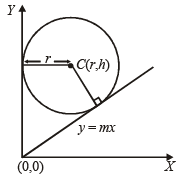
Let y = mx be the other tangent through origin.
Then length of perpendicular from C (r, h) to y = mx should be equal to r.
Then length of perpendicular from C (r, h) to y = mx should be equal to r.
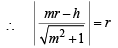
⇒ m2r2 – 2mrh + h2 = m2r2 + r2
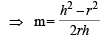
∴ Other tangent is y = 
or (h2 – r2) x – 2rhy = 0
The lines 2x – 3y = 5 and 3x – 4y = 7 are diameters of a circle of area 154 sq. units. Then the equation of this circle is- a)x2 + y2 + 2x – 2y = 62 (1989 - 2 Marks)
- b)x2 + y2 + 2x – 2y = 47
- c)x2 + y2 – 2x + 2y = 47
- d)x2 + y2 – 2x + 2y = 62
Correct answer is option 'C'. Can you explain this answer?
The lines 2x – 3y = 5 and 3x – 4y = 7 are diameters of a circle of area 154 sq. units. Then the equation of this circle is
a)
x2 + y2 + 2x – 2y = 62 (1989 - 2 Marks)
b)
x2 + y2 + 2x – 2y = 47
c)
x2 + y2 – 2x + 2y = 47
d)
x2 + y2 – 2x + 2y = 62
|
Geetika Mishra answered |
As 2x – 3y – 5 = 0 and 3x – 4y – 7 = 0 are diameters of circles.
∴ Centre of circle is solution of these two eq. ' s, i.e.
⇒ x = 1, y = – 1
∴ C (1, –1)
Also area of circle, πr2 = 154
Also area of circle, πr2 = 154
∴ Equation of required circle is
(x – 1)2 + (y + 1)2 = 72
⇒ x2 + y2 – 2x + 2y = 47
A square is inscribed in the circle x2 + y2 – 2x + 4y + 3 = 0. Its sides are parallel to the coordinate axes. The one vertex of the square is (1980)- a)(1 +
, – 2) - b)(1 – , – 2)
- c)(1, – 2 + )
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
A square is inscribed in the circle x2 + y2 – 2x + 4y + 3 = 0. Its sides are parallel to the coordinate axes. The one vertex of the square is (1980)
a)
(1 + , – 2)
, – 2)b)
(1 – , – 2)
, – 2)c)
(1, – 2 + )
)d)
none of these
|
Mihir Sharma answered |
The given circle is x2 + y2 – 2x + 4y + 3 = 0. Centre (1, – 2). Lines through centre (1, – 2) and parallel to axes are x = 1 and y = – 2.
Let the side of square be 2k.
Then sides of square are x = 1 – k and x = 1 + k and y = – 2 – k and y = – 2 + k
∴ Co-ordinates of P, Q, R, S are (1 + k, – 2 + k), (1 – k, – 2 + k), (1 – k, – 2 – k), (1 + k, – 2 – k) respectively.
Also P (1 + k, – 2 + k) lies on circle
∴ (1 + k)2 + (– 2 + k)2 – 2 (1 + k) + 4 (–2 + k) + 3 = 0 ⇒ 2k2 = 2
⇒ k = 1 or – 1 If k = 1, P (2, – 1), Q (0, – 1), R (0, – 3), S (2, – 3)
If k = – 1, P (0, – 3), Q (2, – 3), R (2, – 1), S(0, – 1)
Then sides of square are x = 1 – k and x = 1 + k and y = – 2 – k and y = – 2 + k
∴ Co-ordinates of P, Q, R, S are (1 + k, – 2 + k), (1 – k, – 2 + k), (1 – k, – 2 – k), (1 + k, – 2 – k) respectively.
Also P (1 + k, – 2 + k) lies on circle
∴ (1 + k)2 + (– 2 + k)2 – 2 (1 + k) + 4 (–2 + k) + 3 = 0 ⇒ 2k2 = 2
⇒ k = 1 or – 1 If k = 1, P (2, – 1), Q (0, – 1), R (0, – 3), S (2, – 3)
If k = – 1, P (0, – 3), Q (2, – 3), R (2, – 1), S(0, – 1)
The circle passing through the point (– 1, 0) and touching the y-axis at (0, 2) also passes through the point. (2011)- a)
- b)
- c)
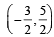
- d)(– 4, 0)
Correct answer is option 'D'. Can you explain this answer?
The circle passing through the point (– 1, 0) and touching the y-axis at (0, 2) also passes through the point. (2011)
a)
b)
c)
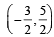
d)
(– 4, 0)
|
|
Upasana Deshpande answered |
Let centre of the circle be (h, 2) then radius = |h|
∴ Equation of circle becomes (x – h)2 + (y – 2)2 = h2
As it passes through (–1, 0)
⇒ (–1 – h)2 + 4 = h2 ⇒ h =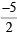 
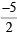
Distance of centre from (–4, 0) is 
∴ It lies on the circle.
What is the relationship between the area of a triangle and the area of a parallelogram sharing the same base and height?- a) The area of the triangle is double that of the parallelogram.
- b) The area of the triangle is one-fourth that of the parallelogram.
- c) The area of the triangle is equal to the area of the parallelogram.
- d) The area of the triangle is half that of the parallelogram.
Correct answer is option 'D'. Can you explain this answer?
What is the relationship between the area of a triangle and the area of a parallelogram sharing the same base and height?
a)
The area of the triangle is double that of the parallelogram.
b)
The area of the triangle is one-fourth that of the parallelogram.
c)
The area of the triangle is equal to the area of the parallelogram.
d)
The area of the triangle is half that of the parallelogram.
|
Imk Pathshala answered |
The area of a triangle is half that of a parallelogram on the same base and between the same parallels. This relationship highlights the geometric principle that a triangle occupies half the area of a parallelogram when both share the same base and height.
What is the formula for calculating the area of a triangle?- a) Area = 1/2 × base × height
- b) Area = base × height
- c) Area = length × breadth
- d) Area = base + height
Correct answer is option 'A'. Can you explain this answer?
What is the formula for calculating the area of a triangle?
a)
Area = 1/2 × base × height
b)
Area = base × height
c)
Area = length × breadth
d)
Area = base + height
|
|
EduRev Class 9 answered |
The area of a triangle is calculated using the formula Area = 1/2 × base × height. This formula reflects that the area of a triangle is half that of a rectangle with the same base and height, which provides a geometric visualization of the concept.
If a triangle has a base of 8 cm and a height of 5 cm, what is its area?- a) 30 cm²
- b) 50 cm²
- c) 20 cm²
- d) 40 cm²
Correct answer is option 'C'. Can you explain this answer?
If a triangle has a base of 8 cm and a height of 5 cm, what is its area?
a)
30 cm²
b)
50 cm²
c)
20 cm²
d)
40 cm²
|
|
EduRev Class 9 answered |
The area of the triangle can be calculated using the formula Area = 1/2 × base × height. Plugging in the values, we get Area = 1/2 × 8 × 5 = 20 cm².
In a parallelogram, if segments are drawn from a point inside to the vertices, what can we infer about the areas of the triangles formed?- a) They are zero.
- b) They are all equal.
- c) They must be congruent.
- d) They can be different based on the location of the point.
Correct answer is option 'D'. Can you explain this answer?
In a parallelogram, if segments are drawn from a point inside to the vertices, what can we infer about the areas of the triangles formed?
a)
They are zero.
b)
They are all equal.
c)
They must be congruent.
d)
They can be different based on the location of the point.
|
|
Let's Tute answered |
The areas of the triangles formed by drawing segments from a point inside a parallelogram to its vertices can differ based on the location of that point. This illustrates how the position of a point affects area calculations in geometric figures.
In a parallelogram, if point P is located inside, what happens to the areas of triangles formed by lines connecting point P to the vertices?- a) All triangles have equal areas.
- b) Areas are always zero.
- c) All triangles are congruent.
- d) The areas relate to the position of P.
Correct answer is option 'D'. Can you explain this answer?
In a parallelogram, if point P is located inside, what happens to the areas of triangles formed by lines connecting point P to the vertices?
a)
All triangles have equal areas.
b)
Areas are always zero.
c)
All triangles are congruent.
d)
The areas relate to the position of P.
|
|
Imk Pathshala answered |
The areas of the triangles formed by connecting point P to the vertices of the parallelogram depend on the position of point P. If P is closer to one pair of sides, the areas of the triangles will differ according to their respective bases and heights.
What type of angle is subtended by a chord at the center of a circle?- a)Central angle
- b)Obtuse angle
- c)Acute angle
- d)Right angle
Correct answer is option 'A'. Can you explain this answer?
What type of angle is subtended by a chord at the center of a circle?
a)
Central angle
b)
Obtuse angle
c)
Acute angle
d)
Right angle
|
|
Imk Pathshala answered |
The angle subtended by a chord at the center of a circle is referred to as a central angle. This angle is crucial for understanding the relationships between chords, arcs, and angles in a circle, particularly in theorems related to circle geometry.
In a right triangle formed by a radius, a chord, and a perpendicular distance from the center, what can be said about the sides?- a)The triangle is not a right triangle
- b)The radius is always the longest side
- c)The chord is the longest side
- d)The perpendicular distance equals the radius
Correct answer is option 'B'. Can you explain this answer?
In a right triangle formed by a radius, a chord, and a perpendicular distance from the center, what can be said about the sides?
a)
The triangle is not a right triangle
b)
The radius is always the longest side
c)
The chord is the longest side
d)
The perpendicular distance equals the radius
|
|
Imk Pathshala answered |
In a right triangle formed in this context, the radius is always the longest side, according to the Pythagorean theorem. This relationship is critical for solving problems related to circles and chords.
If the radius of a circle is doubled, how is the circumference affected?- a)It triples
- b)It quadruples
- c)It doubles
- d)It remains the same
Correct answer is option 'C'. Can you explain this answer?
If the radius of a circle is doubled, how is the circumference affected?
a)
It triples
b)
It quadruples
c)
It doubles
d)
It remains the same
|
|
Imk Pathshala answered |
If the radius of a circle is doubled, the circumference also doubles, as the circumference is directly proportional to the radius. This relationship is captured by the formula C = 2πr, emphasizing the importance of understanding these fundamental properties.
If the tangent at the point P on the circle x2 + y2 + 6x + 6y = 2 meets a straight line 5x –2y + 6 = 0 at a point Q on the y - axis, then the length of PQ is (2002S)- a)4
- b)
- c)5
- d)
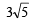
Correct answer is option 'C'. Can you explain this answer?
If the tangent at the point P on the circle x2 + y2 + 6x + 6y = 2 meets a straight line 5x –2y + 6 = 0 at a point Q on the y - axis, then the length of PQ is (2002S)
a)
4
b)
c)
5
d)
|
|
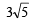
Abhiram Sen answered |
Line 5x – 2y + 6 = 0 is intersected by tangent at P to circle x2 + y2 + 6x + 6y – 2 = 0 on y-axis at Q (0, 3).
In other words tangent passes through (0, 3)
∴ PQ = length of tangent to circle from (0, 3)
In other words tangent passes through (0, 3)
∴ PQ = length of tangent to circle from (0, 3)
The triangle PQR is inscribed in the circle x2 + y2 = 25. If Q and R have co-ordinates (3,4) and (–4, 3) respectively, then ∠QPR is equal to (2000S)- a)
- b)
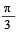
- c)
- d)
Correct answer is option 'C'. Can you explain this answer?
The triangle PQR is inscribed in the circle x2 + y2 = 25. If Q and R have co-ordinates (3,4) and (–4, 3) respectively, then ∠QPR is equal to (2000S)
a)
b)
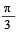
c)
d)
|
|
Jatin Verma answered |
O is the point at centre and P is the point at circumference. Therefore, angle QOR is double the angle QPR.
So, it sufficient to find the angle QOR. Now slope of OQ = 4/3
Slope of OR = – 3/4
Again m1 m2 = – 1
Therefore, ∠QOR = 90° which implies that ∠QPR = 45°.
Slope of OR = – 3/4
Again m1 m2 = – 1
Therefore, ∠QOR = 90° which implies that ∠QPR = 45°.
What is an arc in a circle?- a)The distance around the circle
- b)A line segment connecting two points on the circumference
- c)The area enclosed by two radii
- d)A portion of the circumference of the circle
Correct answer is option 'D'. Can you explain this answer?
What is an arc in a circle?
a)
The distance around the circle
b)
A line segment connecting two points on the circumference
c)
The area enclosed by two radii
d)
A portion of the circumference of the circle
|
|
Imk Pathshala answered |
An arc is defined as a portion of the circumference of a circle. Arcs can be classified as minor arcs, which are smaller than a semicircle, and major arcs, which are larger than a semicircle. This distinction is important in understanding the relationships between angles and arcs in circle geometry.
If two arcs are equal, what can be inferred about the chords they subtend?- a)The chords are parallel
- b)The chords are unequal
- c)The chords are perpendicular
- d)The chords are equal
Correct answer is option 'D'. Can you explain this answer?
If two arcs are equal, what can be inferred about the chords they subtend?
a)
The chords are parallel
b)
The chords are unequal
c)
The chords are perpendicular
d)
The chords are equal
|
|
Imk Pathshala answered |
If two arcs are equal, it follows that the chords subtended by those arcs are also equal. This relationship is fundamental in circle geometry, providing insight into how arcs and chords interact.
In a circle, if a chord is bisected by a line from the center, what can be concluded about the chord?- a)It is divided into two equal segments
- b)It is perpendicular to the radius
- c)It is the longest chord
- d)It is equal to the diameter
Correct answer is option 'A'. Can you explain this answer?
In a circle, if a chord is bisected by a line from the center, what can be concluded about the chord?
a)
It is divided into two equal segments
b)
It is perpendicular to the radius
c)
It is the longest chord
d)
It is equal to the diameter
|
|
EduRev Class 9 answered |
If a line from the center of the circle bisects a chord, it divides the chord into two equal segments. This property is essential in proving various theorems related to chords and their relationships within circles.
Which of the following describes a concentric circle?- a)Circles with different centers
- b)Circles that are equal in radius
- c)Circles with the same center but different radii
- d)Circles that intersect at two points
Correct answer is option 'C'. Can you explain this answer?
Which of the following describes a concentric circle?
a)
Circles with different centers
b)
Circles that are equal in radius
c)
Circles with the same center but different radii
d)
Circles that intersect at two points
|
|
EduRev Class 9 answered |
Concentric circles are those that have the same center point but differ in radii. This concept is often used in various applications, such as in design and architecture, where multiple circular patterns are created around a central point.
What is true about the angles subtended by equal arcs at the center of a circle?- a)They are equal
- b)They are supplementary
- c)They are unequal
- d)They are complementary
Correct answer is option 'A'. Can you explain this answer?
What is true about the angles subtended by equal arcs at the center of a circle?
a)
They are equal
b)
They are supplementary
c)
They are unequal
d)
They are complementary
|
|
Imk Pathshala answered |
The angles subtended by equal arcs at the center of a circle are equal. This property is essential for understanding the relationships between arcs and angles in circle geometry.
Let AB be a chord of the circle x2 + y2 = r2 subtending a right angle at the centre. Then the locus of the centroid of the triangle PAB as P moves on the circle is (2001S)- a)a parabola
- b)a circle
- c)an ellipse
- d)a pair of straight lines
Correct answer is option 'B'. Can you explain this answer?
Let AB be a chord of the circle x2 + y2 = r2 subtending a right angle at the centre. Then the locus of the centroid of the triangle PAB as P moves on the circle is (2001S)
a)
a parabola
b)
a circle
c)
an ellipse
d)
a pair of straight lines
|
|
Diya Roy answered |
x2 + y2 = r2 is a circle with centre at (0, 0) and radius r units.
Any arbitrary pt P on it is (r cosθ , r sinθ ) Choosing A and B as (– r, 0) and (0, – r).
[So that ∠AOB = 90°]
For locus of centriod of ΔABP
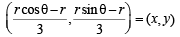
⇒ r cosθ – r = 3x
r sinθ – r = 3y
r sinθ – r = 3y
⇒ r cosθ = 3x + r
r sinθ = 3y + r
r sinθ = 3y + r
Squaring and adding (3x + r)2 + (3y + r)2 = r2 which is a circle.
Chapter doubts & questions for Circle Theorems - Mathematics for GCSE/IGCSE 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Circle Theorems - Mathematics for GCSE/IGCSE in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Mathematics for GCSE/IGCSE
38 videos|395 docs|19 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup