All Exams >
Class 10 >
Mathematics for GCSE/IGCSE >
All Questions
All questions of Cumulative Frequency for Class 10 Exam
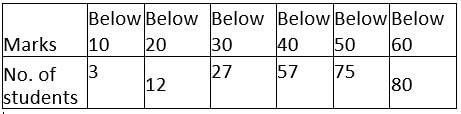
The following table gives the marks obtained by 80 students in a selection test:
The median marks is- a)34.3
- b)45.5
- c)20
- d)28.5
Correct answer is option 'A'. Can you explain this answer?
The following table gives the marks obtained by 80 students in a selection test:
The median marks is
The median marks is
a)
34.3
b)
45.5
c)
20
d)
28.5
|
Subset Academy answered |
Median =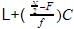 
First change the table into continuous data.
Middle of the frequencies=40 which will lie in 30-40. So
L=30
N/2=80/2=40
F=27
f=30
c=10
Median =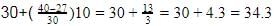
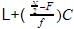
First change the table into continuous data.
Middle of the frequencies=40 which will lie in 30-40. So
L=30
N/2=80/2=40
F=27
f=30
c=10
Median =
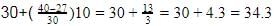
Mode is not affected by- a)Maximum value
- b)Minimum value
- c)Extreme values
- d)All of the above
Correct answer is option 'D'. Can you explain this answer?
Mode is not affected by
a)
Maximum value
b)
Minimum value
c)
Extreme values
d)
All of the above
|
|
Himaja Ammu answered |
Yaa.....mode is not affected by any of them
The mean of the marks obtained by 7 students in a group is 226. If the marks obtained by six of them are 340, 180, 260, 56, 275, 307, then the marks obtained by the seventh student are- a)200
- b)125
- c)174
- d)164
Correct answer is option 'D'. Can you explain this answer?
The mean of the marks obtained by 7 students in a group is 226. If the marks obtained by six of them are 340, 180, 260, 56, 275, 307, then the marks obtained by the seventh student are
a)
200
b)
125
c)
174
d)
164
|
Deepak trivedi answered |
Let's start by finding the sum of the marks obtained by the six students:
Sum of marks = 340 + 180 + 260 + 56 + 275 + 307 = 1418
We can then use the formula for the mean to find the total marks obtained by all seven students:
Mean = (Total marks) / (Number of students)
226 = (Total marks) / 7
Total marks = 1582
Finally, we can find the marks obtained by the seventh student by subtracting the sum of the marks obtained by the six students from the total marks obtained by all seven students:
Marks obtained by seventh student = Total marks - Sum of marks
Marks obtained by seventh student = 1582 - 1418
Marks obtained by seventh student = 164
Therefore, the answer is (d) 164.
Sum of marks = 340 + 180 + 260 + 56 + 275 + 307 = 1418
We can then use the formula for the mean to find the total marks obtained by all seven students:
Mean = (Total marks) / (Number of students)
226 = (Total marks) / 7
Total marks = 1582
Finally, we can find the marks obtained by the seventh student by subtracting the sum of the marks obtained by the six students from the total marks obtained by all seven students:
Marks obtained by seventh student = Total marks - Sum of marks
Marks obtained by seventh student = 1582 - 1418
Marks obtained by seventh student = 164
Therefore, the answer is (d) 164.
The measure of central tendency that is most suitable to find the average male or female height of the region is- a)Mode
- b)Median
- c)Mean
- d)Mean and mode
Correct answer is option 'C'. Can you explain this answer?
The measure of central tendency that is most suitable to find the average male or female height of the region is
a)
Mode
b)
Median
c)
Mean
d)
Mean and mode
|
Krishna Iyer answered |
Mean also called the expected value or average, is the central value of a discrete set of numbers. Median is the middle value of the data. Mode is the highest occurring observation. So mean is accurate to calculate average.
The mean of 15 numbers is 25. If each number is multiplied by 4, mean of the new numbers is- a)100
- b)60
- c)10
- d)40
Correct answer is option 'A'. Can you explain this answer?
The mean of 15 numbers is 25. If each number is multiplied by 4, mean of the new numbers is
a)
100
b)
60
c)
10
d)
40
|
Ishan Choudhury answered |
We have So, Mean =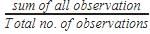 
So Mean =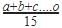
=25
If 4 is multiplied by each observation
So Mean =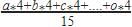
Taking common 4 from numerator=4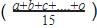
=4*25=100
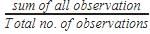
So Mean =
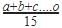=25If 4 is multiplied by each observation
So Mean =
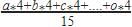
Taking common 4 from numerator=4
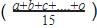=4*25=100
The median of a distribution divides it into- a)Three equal parts
- b)Does not divide into any parts.
- c)Two equal parts
- d)Four equal parts
Correct answer is option 'C'. Can you explain this answer?
The median of a distribution divides it into
a)
Three equal parts
b)
Does not divide into any parts.
c)
Two equal parts
d)
Four equal parts
|
Pranavi Joshi answered |
The median of a distribution is the middle value when the data is arranged in ascending or descending order. It is a measure of central tendency that helps us understand the central value of a dataset. When we say that the median divides the distribution into two equal parts, it means that half of the data points are smaller than the median and half are larger than the median.
To understand why the correct answer is option 'C' (the median divides the distribution into two equal parts), let's consider an example. Suppose we have a dataset of 7 numbers: 1, 3, 5, 7, 9, 11, 13. If we arrange these numbers in ascending order, we get: 1, 3, 5, 7, 9, 11, 13.
In this case, the median is the middle value, which is 7. Now, let's see how the distribution is divided by the median:
- Numbers smaller than the median: 1, 3, 5
- Median: 7
- Numbers larger than the median: 9, 11, 13
As we can see, there are three numbers smaller than the median and three numbers larger than the median. Therefore, the median divides the distribution into two equal parts.
In general, if the dataset has an odd number of values, the median will be the middle value, and it will divide the distribution into two equal parts. However, if the dataset has an even number of values, the median will be the average of the two middle values, and it will still divide the distribution into two equal parts.
Therefore, the correct answer is option 'C' (the median divides the distribution into two equal parts).
To understand why the correct answer is option 'C' (the median divides the distribution into two equal parts), let's consider an example. Suppose we have a dataset of 7 numbers: 1, 3, 5, 7, 9, 11, 13. If we arrange these numbers in ascending order, we get: 1, 3, 5, 7, 9, 11, 13.
In this case, the median is the middle value, which is 7. Now, let's see how the distribution is divided by the median:
- Numbers smaller than the median: 1, 3, 5
- Median: 7
- Numbers larger than the median: 9, 11, 13
As we can see, there are three numbers smaller than the median and three numbers larger than the median. Therefore, the median divides the distribution into two equal parts.
In general, if the dataset has an odd number of values, the median will be the middle value, and it will divide the distribution into two equal parts. However, if the dataset has an even number of values, the median will be the average of the two middle values, and it will still divide the distribution into two equal parts.
Therefore, the correct answer is option 'C' (the median divides the distribution into two equal parts).
In a shooting competition the scores of a competitor were as given below:
His median score will be- a)5
- b)3
- c)6
- d)2
Correct answer is option 'B'. Can you explain this answer?
In a shooting competition the scores of a competitor were as given below:
His median score will be
a)
5
b)
3
c)
6
d)
2
|
Hemasri Ramachandiran answered |
First arrange the data given in ascending order as
1, 2, 3, 4, 5.
Then, find the number in the mid in this order. Obviously, its 3 because its the only number in the centre among the arranged order.
Chapter doubts & questions for Cumulative Frequency - Mathematics for GCSE/IGCSE 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Cumulative Frequency - Mathematics for GCSE/IGCSE in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Mathematics for GCSE/IGCSE
38 videos|395 docs|19 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup