All Exams >
Grade 12 >
Mathematics for Grade 12 >
All Questions
All questions of Polynomial Equations and Inequalities for Grade 12 Exam
If R is a relation from a non – empty set A to a non – empty set B, then- a)R⊂A×B.
- b)R=A∪B
- c)R=A∩B
- d)R=A×B
Correct answer is option 'A'. Can you explain this answer?
If R is a relation from a non – empty set A to a non – empty set B, then
a)
R⊂A×B.
b)
R=A∪B
c)
R=A∩B
d)
R=A×B
|
|
Anaya Patel answered |
Let A and B be two sets. Then a relation R from set A to set B is a subset of A × B. Thus, R is a relation from A to B ⇔ R ⊆ A × B.
If f be a mapping defined by f(x) = x2 + 5, then 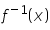 is:
is:- a)(x - 5)1/2
- b)(x2 + 5)1/2
- c)(x + 5)1/2
- d)
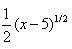
Correct answer is option 'A'. Can you explain this answer?
If f be a mapping defined by f(x) = x2 + 5, then 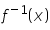 is:
is:
a)
(x - 5)1/2
b)
(x2 + 5)1/2
c)
(x + 5)1/2
d)

|
Kaia Patil answered |
F(x)=x^2+5
y=x^2+5
interchange x and y
x=y^2+5
y=(x-5)^1/2
y is the inverse of f(x)
y=x^2+5
interchange x and y
x=y^2+5
y=(x-5)^1/2
y is the inverse of f(x)
Can you explain the answer of this question below:Let R = {(P,Q) : OP = OQ , O being the origin} be an equivalence relation on A. The equivalence class [(1,2)] is
- A:
{(x,y) : x2+y2 = 5}
- B:
{(x,y) : x2 = y2}
- C:
{(x,y) : x2+y2 = 1}
- D:
{(x,y) : x2+y2 = 4}
The answer is a.
Let R = {(P,Q) : OP = OQ , O being the origin} be an equivalence relation on A. The equivalence class [(1,2)] is
{(x,y) : x2+y2 = 5}
{(x,y) : x2 = y2}
{(x,y) : x2+y2 = 1}
{(x,y) : x2+y2 = 4}
|
|
Om Desai answered |
Correct Answer : a
Explanation : A = {(x,y) : x2 + y2 = 5}
=> (1,2) {(1)2 + (4)2 = 5}
=> {1 + 4 = 5}
=> {5 = 5}
If ƒ(x) = xsecx, then ƒ(0) =- a)−1
- b)0
- c)1
- d)√(2)
Correct answer is option 'B'. Can you explain this answer?
If ƒ(x) = xsecx, then ƒ(0) =
a)
−1
b)
0
c)
1
d)
√(2)
|
|
Nabanita Bajaj answered |
You could have any superpower, what would it be?
A relation R from C to R is defined by x Ry if f |x| = y. Which of the following is correct?- a)iR1
- b)3R(–3)
- c)(2 + 3 i)R13
- d)(1 + i)R2
Correct answer is option 'A'. Can you explain this answer?
A relation R from C to R is defined by x Ry if f |x| = y. Which of the following is correct?
a)
iR1
b)
3R(–3)
c)
(2 + 3 i)R13
d)
(1 + i)R2
|
|
Preeti Iyer answered |
|2+3i| = sqroot( square(2) + square(3) ) = sqroot(13) which is not equal to 13
so, (2+3i)R 13 is wrong.
|3| = sqroot( square(3) + square(0) ) = sqroot(9) = 3 which is not equal to -3
so, 3R (-3) is wrong.
|1+i| = sqroot( square(1) + square(1) ) = sqroot(2) which is not equal to 2
so, (1+i)R 2 is wrong.
|i| =sqroot( square(0) + square(1) ) = sqroot(1) which is equal to 1
so, iR1 is correct.
A function f: X → Y is injective if and only if- a)
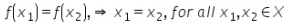
- b)
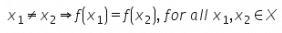
- c)f(X) = Y
- d)X = Y
Correct answer is option 'A'. Can you explain this answer?
A function f: X → Y is injective if and only if
a)
b)
c)
f(X) = Y
d)
X = Y

|
Gunjan Lakhani answered |
Let X, Y be sets, and let f : X → Y be a function. We say that f is injective (sometimes called one-to-one) if ∀x1, x2 ∈ X, f(x1) = f(x2)
⇒ x1 = x2.
⇒ x1 = x2.
Let f and g be the function from the set of integers to itself, defined by f(x) = 2x + 1 and g(x) = 3x + 4. Then the composition of f and g is ____________- a)6x + 9
- b)6x + 7
- c)6x + 6
- d)6x + 8
Correct answer is option 'A'. Can you explain this answer?
Let f and g be the function from the set of integers to itself, defined by f(x) = 2x + 1 and g(x) = 3x + 4. Then the composition of f and g is ____________
a)
6x + 9
b)
6x + 7
c)
6x + 6
d)
6x + 8
|
|
Arjun Singhania answered |
The composition of f and g is given by f(g(x)) which is equal to 2(3x + 4) + 1.
Let f : A→B and g : B→C be one-one functions. Then, gof: A→C is- a)one-one
- b)does not exist
- c)not onto
- d)onto
Correct answer is option 'A'. Can you explain this answer?
Let f : A→B and g : B→C be one-one functions. Then, gof: A→C is
a)
one-one
b)
does not exist
c)
not onto
d)
onto
|
|
Naina Bansal answered |
f is one-one g is one-oneIf f(x1) = f(x2) If g(x2) = g(x2)then x1 = x2 then x1= x2C
Let A = {1, 2, 3} and B = {5, 6, 7, 8, 9} and let f(x) = {(1, 8), (2, 7), (3, 6)} then f is- a)Surjective
- b)Not a function
- c)Injective
- d)Bijective
Correct answer is option 'C'. Can you explain this answer?
Let A = {1, 2, 3} and B = {5, 6, 7, 8, 9} and let f(x) = {(1, 8), (2, 7), (3, 6)} then f is
a)
Surjective
b)
Not a function
c)
Injective
d)
Bijective
|
|
Sharmila Choudhury answered |
Solution:
To determine whether f is surjective, injective, or bijective, we need to understand what these terms mean.
- Surjective: A function f from set A to set B is surjective (onto) if for every element y in set B, there is an element x in set A such that f(x) = y. In other words, every element in set B has at least one preimage in set A.
- Injective: A function f from set A to set B is injective (one-to-one) if for every pair of distinct elements x₁ and x₂ in set A, f(x₁) and f(x₂) are distinct in set B. In other words, no two distinct elements in set A have the same image in set B.
- Bijective: A function f from set A to set B is bijective if it is both surjective and injective. In other words, every element in set B has exactly one preimage in set A, and no two distinct elements in set A have the same image in set B.
Now, let's look at the given function f(x) = {(1, 8), (2, 7), (3, 6)}.
- f is not surjective because set B has elements 5 and 9 that do not have any preimages in set A.
- f is not a function if there is an element in set A that has more than one image in set B. However, this is not the case for f, so it is a function.
- f is injective because no two distinct elements in set A have the same image in set B. For example, f(1) = 8, f(2) = 7, and f(3) = 6, so no two distinct elements in set A have the same image in set B.
- Since f is injective but not surjective, it is not bijective.
Therefore, the correct answer is option 'C' - f is injective.
To determine whether f is surjective, injective, or bijective, we need to understand what these terms mean.
- Surjective: A function f from set A to set B is surjective (onto) if for every element y in set B, there is an element x in set A such that f(x) = y. In other words, every element in set B has at least one preimage in set A.
- Injective: A function f from set A to set B is injective (one-to-one) if for every pair of distinct elements x₁ and x₂ in set A, f(x₁) and f(x₂) are distinct in set B. In other words, no two distinct elements in set A have the same image in set B.
- Bijective: A function f from set A to set B is bijective if it is both surjective and injective. In other words, every element in set B has exactly one preimage in set A, and no two distinct elements in set A have the same image in set B.
Now, let's look at the given function f(x) = {(1, 8), (2, 7), (3, 6)}.
- f is not surjective because set B has elements 5 and 9 that do not have any preimages in set A.
- f is not a function if there is an element in set A that has more than one image in set B. However, this is not the case for f, so it is a function.
- f is injective because no two distinct elements in set A have the same image in set B. For example, f(1) = 8, f(2) = 7, and f(3) = 6, so no two distinct elements in set A have the same image in set B.
- Since f is injective but not surjective, it is not bijective.
Therefore, the correct answer is option 'C' - f is injective.
Let g(x) = 1 + x – [x] and 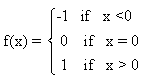 Then f{g(x)} for all x, is equal to:
Then f{g(x)} for all x, is equal to:- a)g(x)
- b)x
- c)1
- d)f(x)
Correct answer is option 'C'. Can you explain this answer?
Let g(x) = 1 + x – [x] and 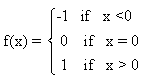
Then f{g(x)} for all x, is equal to:
a)
g(x)
b)
x
c)
1
d)
f(x)
|
|
Om Desai answered |
g(x) = 1 + x - [x]
f(x) = {-1, x<0 0, x=0 1, x>0}
f(g(x)) = f[1 + x - [x]]
= f[1 + x - 1]
= f(x)
f(g(x)) is equal to f(x)
f(x) = {-1, x<0 0, x=0 1, x>0}
f(g(x)) = f[1 + x - [x]]
= f[1 + x - 1]
= f(x)
f(g(x)) is equal to f(x)
Which one of the following relations on set of real numbers is an equivalence relation?- a)
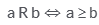
- b)
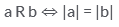
- c)

- d)

Correct answer is option 'B'. Can you explain this answer?
Which one of the following relations on set of real numbers is an equivalence relation?
a)
b)
c)
d)

|
Kumari Sakshi answered |
Equivalence relation is symmetric reflexive and transitive now see option A a>=b but in this case relation will not be symmetric now see option B if |a|=|b | then |b|=|a| so this is symmetric as well as reflexive and if |a|=|b| and |b|=|c| then|c|=|a | then it is transitive as well so it is an equivalence relation you can check yourself for the rest two
Let A = {1,2,3,4} and B = { x,y,z}. Then R = {(1,x) , ( 2,z), (1,y), (3,x)} is- a)relation from B to A
- b)Is not a relation
- c)relation from A to B
- d)relation from B to B
Correct answer is option 'C'. Can you explain this answer?
Let A = {1,2,3,4} and B = { x,y,z}. Then R = {(1,x) , ( 2,z), (1,y), (3,x)} is
a)
relation from B to A
b)
Is not a relation
c)
relation from A to B
d)
relation from B to B
|
|
Om Desai answered |
Let a set of A = (1, 2, 3, 4) and set B (x, y, z) so. set A of all elements in set B then the relation of A to B
The function, f(x) = 2x - 1 is
- a)It is not surjective
- b)It is surjective
- c)It is surjective in some intervals of the domain
- d)Insufficient information
Correct answer is option 'B'. Can you explain this answer?
The function, f(x) = 2x - 1 is
a)
It is not surjective
b)
It is surjective
c)
It is surjective in some intervals of the domain
d)
Insufficient information
|
|
Vivek Patel answered |
The function f(x) = 2x - 1 is surjective.
Explanation:
A function is surjective (also called onto) if for every element y in the codomain, there exists an element x in the domain such that f(x) = y.
In this case, the function f(x) = 2x - 1 is a linear function. For any given y value, we can find an x value such that f(x) = y:
y = 2x - 1
x = (y + 1) / 2
So, for any y value, there exists an x value that satisfies the equation. Therefore, the function is surjective.
Explanation:
A function is surjective (also called onto) if for every element y in the codomain, there exists an element x in the domain such that f(x) = y.
In this case, the function f(x) = 2x - 1 is a linear function. For any given y value, we can find an x value such that f(x) = y:
y = 2x - 1
x = (y + 1) / 2
So, for any y value, there exists an x value that satisfies the equation. Therefore, the function is surjective.
Which of the following is not an equivalence relation on I, the set of integers ; x, y- a)x R y x + y is an even integer
- b)x R y x = y
- c)x R y x < y
- d)x R y x – y is an even integer
Correct answer is option 'C'. Can you explain this answer?
Which of the following is not an equivalence relation on I, the set of integers ; x, y
a)
x R y x + y is an even integer
b)
x R y x = y
c)
x R y x < y
d)
x R y x – y is an even integer

|
Aravind Nambiar answered |
If R is a relation defined by xRy : ifx ⩽ y,then R is reflexive and transitive .But , it is not symmetric. Hence , R is not an equivalence relation.
The binary relation S = Φ (empty set) on set A = {1, 2,3} is- a)transitive and relexive
- b)symmetric and relexive
- c)transitive and symmetric
- d)neither reflexive nor symmetric
Correct answer is option 'C'. Can you explain this answer?
The binary relation S = Φ (empty set) on set A = {1, 2,3} is
a)
transitive and relexive
b)
symmetric and relexive
c)
transitive and symmetric
d)
neither reflexive nor symmetric
|
|
Rohit Jain answered |
Reflexive : A relation is reflexive if every element of set is paired with itself. Here none of the element of A is paired with themselves, so S is not reflexive.
Symmetric : This property says that if there is a pair (a, b) in S, then there must be a pair (b, a) in S. Since there is no pair here in S, this is trivially true, so S is symmetric.
Transitive : This says that if there are pairs (a, b) and (b, c) in S, then there must be pair (a,c) in S. Again, this condition is trivially true, so S is transitive.
Symmetric : This property says that if there is a pair (a, b) in S, then there must be a pair (b, a) in S. Since there is no pair here in S, this is trivially true, so S is symmetric.
Transitive : This says that if there are pairs (a, b) and (b, c) in S, then there must be pair (a,c) in S. Again, this condition is trivially true, so S is transitive.
Given below is binary composition table a* b = LCM of a and b on S = { 1,2,3,4}. Then, from the table determine which one of these options is correct.
- a)a* b is a distributive binary operation
- b)a* b is an associative binary operation
- c)a* b is not a binary operation
- d)a* b is a commutative binary operation
Correct answer is option 'C'. Can you explain this answer?
Given below is binary composition table a* b = LCM of a and b on S = { 1,2,3,4}. Then, from the table determine which one of these options is correct.
a)
a* b is a distributive binary operation
b)
a* b is an associative binary operation
c)
a* b is not a binary operation
d)
a* b is a commutative binary operation
|
|
Lavanya Menon answered |
We have ∗ is defined on the set {1,2,3,4,5} by a∗b = LCM of a and b
Now, 3∗4 = LCM of 3 and 4=12
But, 12 does not belong to {1,2,3,4,5}.
Hence, ′∗′ is not a binary operation.
Now, 3∗4 = LCM of 3 and 4=12
But, 12 does not belong to {1,2,3,4,5}.
Hence, ′∗′ is not a binary operation.
Let R be the relation on the set {1, 2, 3, 4} given by R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3,3), (3,2)}. then R is- a)R is reflexive and symmetric but not transitive.
- b)R is symmetric and transitive but not reflexive.
- c)R is an equivalence relation.
- d)R is reflexive and transitive but not symmetric.
Correct answer is option 'D'. Can you explain this answer?
Let R be the relation on the set {1, 2, 3, 4} given by R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3,3), (3,2)}. then R is
a)
R is reflexive and symmetric but not transitive.
b)
R is symmetric and transitive but not reflexive.
c)
R is an equivalence relation.
d)
R is reflexive and transitive but not symmetric.

|
Pragati Dey answered |
R be the relation in the set {1,2,3,4] given by R ={(1,2),(2,2),(1,1),(4,4),(1,3),(3,3),(3,2)}
it is seen that (a,a)∈ R for every a∈{1,2,3,4}
so,R is feflexive.
it is seen that (a,b) = (b,a) ∈ R
because, (1,2)∈ R but (2,1) ∉R
so, R is not symmetric.
it is seen that (a, b), (b, c) ∈ R ⇒ (a, c) ∈ R for all a, b, c ∈ {1, 2, 3, 4}.
so, R is transitive.
Hence, R is reflexive and transitive but not symmetric.
A function f: X → Y is surjective if and only if- a)X = Y
- b)f(X) = Y
- c)X is a singleton set
- d)Y is a singleton set
Correct answer is option 'B'. Can you explain this answer?
A function f: X → Y is surjective if and only if
a)
X = Y
b)
f(X) = Y
c)
X is a singleton set
d)
Y is a singleton set
|
|
Aqsa Kibria answered |
Hiii Saumya!!! Surjective function is one which is onto which means there is a value of y corresponding to every x in the domain..and which is option B f(X)=Y Regards
The void relation (a subset of A x A) on a non empty set A is :- a)Anti symmetric
- b)transitive
- c)Reflexive
- d)Transitive and symmetric
Correct answer is option 'D'. Can you explain this answer?
The void relation (a subset of A x A) on a non empty set A is :
a)
Anti symmetric
b)
transitive
c)
Reflexive
d)
Transitive and symmetric

|
Tejas Chawla answered |
The relation { }⊂ A x A on a is surely not reflexive.However ,neither symmetry nor transitivity is contradicted .So { } is a transitive and symmetry relation on A.
Let A = {1,2,3,4,5,6,7}. P = {1,2}, Q = {3, 7}. Write the elements of the set R so that P, Q and R form a partition that results in equivalence relation.- a){4,5,6}
- b){0}
- c){1,2,3,4,5,6,7}
- d){ }
Correct answer is option 'A'. Can you explain this answer?
Let A = {1,2,3,4,5,6,7}. P = {1,2}, Q = {3, 7}. Write the elements of the set R so that P, Q and R form a partition that results in equivalence relation.
a)
{4,5,6}
b)
{0}
c)
{1,2,3,4,5,6,7}
d)
{ }
|
|
Rajdeep Singh answered |
Solution:
Equivalence relation is a relation that is reflexive, symmetric and transitive. A partition of a set is a collection of non-empty subsets whose union is the original set and whose members are pairwise disjoint. Let's find the set R so that P, Q and R form a partition that results in equivalence relation.
Reflexive property: Every element is related to itself.
Symmetric property: If a is related to b, then b is related to a.
Transitive property: If a is related to b and b is related to c, then a is related to c.
Partition: P, Q and R are pairwise disjoint. Their union is A.
Elements of the set R: {4, 5, 6}
Explanation:
We can choose the set R as {4, 5, 6} because it is disjoint from both P and Q. This means that the sets P, Q and R are pairwise disjoint. Also, their union is A, which means that every element of A belongs to exactly one of the sets P, Q and R.
Now, let's check whether the partition formed by P, Q and R results in an equivalence relation.
Reflexive property: Every element is related to itself.
- For any element x in A, x belongs to exactly one of the sets P, Q and R.
- If x belongs to P or Q, then x is related to itself because P and Q are both reflexive.
- If x belongs to R, then x is related to itself because R is a set of elements.
Symmetric property: If a is related to b, then b is related to a.
- For any elements a and b in A, a belongs to exactly one of the sets P, Q and R, and b belongs to exactly one of the sets P, Q and R.
- If a and b belong to the same set (P, Q or R), then the relation between them is symmetric because P, Q and R are all symmetric.
- If a and b belong to different sets, then they are not related. Therefore, the relation between them is trivially symmetric.
Transitive property: If a is related to b and b is related to c, then a is related to c.
- For any elements a, b and c in A, a belongs to exactly one of the sets P, Q and R, b belongs to exactly one of the sets P, Q and R, and c belongs to exactly one of the sets P, Q and R.
- If a and b belong to the same set and b and c belong to the same set, then a and c belong to the same set by the transitive property of P, Q and R.
- If a and b belong to different sets or b and c belong to different sets, then a and c are not related. Therefore, the relation between them is trivially transitive.
Therefore, the partition formed by P, Q and R results in an equivalence relation.
Equivalence relation is a relation that is reflexive, symmetric and transitive. A partition of a set is a collection of non-empty subsets whose union is the original set and whose members are pairwise disjoint. Let's find the set R so that P, Q and R form a partition that results in equivalence relation.
Reflexive property: Every element is related to itself.
Symmetric property: If a is related to b, then b is related to a.
Transitive property: If a is related to b and b is related to c, then a is related to c.
Partition: P, Q and R are pairwise disjoint. Their union is A.
Elements of the set R: {4, 5, 6}
Explanation:
We can choose the set R as {4, 5, 6} because it is disjoint from both P and Q. This means that the sets P, Q and R are pairwise disjoint. Also, their union is A, which means that every element of A belongs to exactly one of the sets P, Q and R.
Now, let's check whether the partition formed by P, Q and R results in an equivalence relation.
Reflexive property: Every element is related to itself.
- For any element x in A, x belongs to exactly one of the sets P, Q and R.
- If x belongs to P or Q, then x is related to itself because P and Q are both reflexive.
- If x belongs to R, then x is related to itself because R is a set of elements.
Symmetric property: If a is related to b, then b is related to a.
- For any elements a and b in A, a belongs to exactly one of the sets P, Q and R, and b belongs to exactly one of the sets P, Q and R.
- If a and b belong to the same set (P, Q or R), then the relation between them is symmetric because P, Q and R are all symmetric.
- If a and b belong to different sets, then they are not related. Therefore, the relation between them is trivially symmetric.
Transitive property: If a is related to b and b is related to c, then a is related to c.
- For any elements a, b and c in A, a belongs to exactly one of the sets P, Q and R, b belongs to exactly one of the sets P, Q and R, and c belongs to exactly one of the sets P, Q and R.
- If a and b belong to the same set and b and c belong to the same set, then a and c belong to the same set by the transitive property of P, Q and R.
- If a and b belong to different sets or b and c belong to different sets, then a and c are not related. Therefore, the relation between them is trivially transitive.
Therefore, the partition formed by P, Q and R results in an equivalence relation.
Let A = {a, b, c} and R = {(a, a), (b, b), (c, c), (b, c)} be a relation on A. Here, R is- a)Transitive
- b)anti – symmetric
- c)symmetric
- d)reflexive
Correct answer is option 'D'. Can you explain this answer?
Let A = {a, b, c} and R = {(a, a), (b, b), (c, c), (b, c)} be a relation on A. Here, R is
a)
Transitive
b)
anti – symmetric
c)
symmetric
d)
reflexive

|
Anjali Deshpande answered |
Any relation R is reflexive if fx Rx for all x ∈ R. Here ,(a, a), (b, b), (c, c) ∈ R. Therefore , R is reflexive.
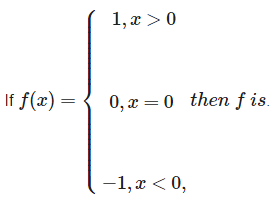
- a)the greatest integer function
- b)a constant function.
- c)the absolute value function
- d)The signum function
Correct answer is option 'D'. Can you explain this answer?
a)
the greatest integer function
b)
a constant function.
c)
the absolute value function
d)
The signum function
|
|
Om Desai answered |
By definition, The Signum function =
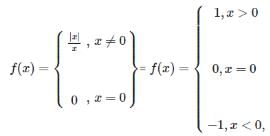
If f : A→B and g : B →C be two functions. Then, composition of f and g, gof : A→C is defined a- a)(gof)(x) = f(g(x)), for all x ∈ A
- b)(gof)(x) = g(f(x)), for all x ∈ A
- c)(gof)(x) = g(x), for all x ∈ A
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
If f : A→B and g : B →C be two functions. Then, composition of f and g, gof : A→C is defined a
a)
(gof)(x) = f(g(x)), for all x ∈ A
b)
(gof)(x) = g(f(x)), for all x ∈ A
c)
(gof)(x) = g(x), for all x ∈ A
d)
None of the above
|
|
Rashi Nair answered |
Please provide additional details or context for me to assist you better.
f: R → R is defined by 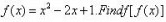
- a)x4 + 4x3 - 4x2
- b)x4 - 4x3 + 4x2
- c)x4 + 4x3 + 4x2
- d)x4 - 4x3 - 4x2
Correct answer is option 'B'. Can you explain this answer?
f: R → R is defined by 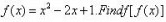
a)
x4 + 4x3 - 4x2
b)
x4 - 4x3 + 4x2
c)
x4 + 4x3 + 4x2
d)
x4 - 4x3 - 4x2
|
|
Sounak Pillai answered |
I'm sorry, could you please provide more context or a specific question related to the variable "f:R"?
Let a relation T on the set R of real numbers be T = {(a,b) : 1 + ab < 0, a,∈ R}. Then from among the ordered pairs (1,1) (1,2)(1,-2)(2,2), the only pair that belongs to T is________.- a)(2,2),
- b)(1,1),
- c)(1,-2)
- d)(1,2)
Correct answer is option 'C'. Can you explain this answer?
Let a relation T on the set R of real numbers be T = {(a,b) : 1 + ab < 0, a,∈ R}. Then from among the ordered pairs (1,1) (1,2)(1,-2)(2,2), the only pair that belongs to T is________.
a)
(2,2),
b)
(1,1),
c)
(1,-2)
d)
(1,2)
|
|
Keerthana Deshpande answered |
Relation T on R of real numbers
Definition of Relation T: T is a relation on the set R of real numbers and it is defined as T = {(a,b) : 1 ≤ ab ≤ 0, a ε R}
Explanation: This means that T is a set of ordered pairs (a,b) such that a is a real number and b is a real number, and the product of a and b is between 1 and 0, inclusive. In other words, either a and b are both negative or one of them is negative and the other is between 0 and 1.
Given ordered pairs: (1,1), (1,2), (1,-2), (2,2)
Checking which pairs belong to T:
- (1,1): 1 ≤ 1*1 ≤ 0 is false, so (1,1) does not belong to T
- (1,2): 1 ≤ 1*2 ≤ 0 is false, so (1,2) does not belong to T
- (1,-2): 1 ≤ 1*(-2) ≤ 0 is true, so (1,-2) belongs to T
- (2,2): 1 ≤ 2*2 ≤ 0 is false, so (2,2) does not belong to T
Conclusion: The only ordered pair that belongs to T is (1,-2). Therefore, the correct answer is option C, (1,-2).
Definition of Relation T: T is a relation on the set R of real numbers and it is defined as T = {(a,b) : 1 ≤ ab ≤ 0, a ε R}
Explanation: This means that T is a set of ordered pairs (a,b) such that a is a real number and b is a real number, and the product of a and b is between 1 and 0, inclusive. In other words, either a and b are both negative or one of them is negative and the other is between 0 and 1.
Given ordered pairs: (1,1), (1,2), (1,-2), (2,2)
Checking which pairs belong to T:
- (1,1): 1 ≤ 1*1 ≤ 0 is false, so (1,1) does not belong to T
- (1,2): 1 ≤ 1*2 ≤ 0 is false, so (1,2) does not belong to T
- (1,-2): 1 ≤ 1*(-2) ≤ 0 is true, so (1,-2) belongs to T
- (2,2): 1 ≤ 2*2 ≤ 0 is false, so (2,2) does not belong to T
Conclusion: The only ordered pair that belongs to T is (1,-2). Therefore, the correct answer is option C, (1,-2).
Chapter doubts & questions for Polynomial Equations and Inequalities - Mathematics for Grade 12 2025 is part of Grade 12 exam preparation. The chapters have been prepared according to the Grade 12 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 12 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Polynomial Equations and Inequalities - Mathematics for Grade 12 in English & Hindi are available as part of Grade 12 exam.
Download more important topics, notes, lectures and mock test series for Grade 12 Exam by signing up for free.
Mathematics for Grade 12
99 videos|124 docs|82 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev












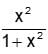 . Then f is
. Then f is














