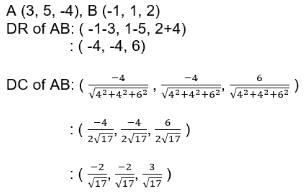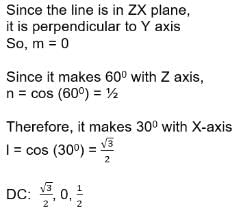All Exams >
Grade 12 >
Mathematics for Grade 12 >
All Questions
All questions of Equations of Lines and Planes for Grade 12 Exam
Find the equation of the set of points which are equidistant from the points (1, 2 , 3) and (3, 2, -1)
a) x + 2z = 0
b) y + 2z = 0
c) x – 2z = 0
d) x – 2y = 0
Correct answer is option 'C'. Can you explain this answer?
|
|
Aryan Khanna answered |
Pt. A(1, 2 , 3)
Pt. B(3, 2, -1)
Let P(x,y,z)
So, AP = BP
((x-1)2 + (y-2)2 + (z-3)2)1/2 = ((x-3)2 + (y-2)2 + (z+1)2)1/2
(x-1)2 + (y-2)2 + (z-3)2) = (x-3)2 + (y-2)2 + (z+1)2
x2 +1 -2x + y2 + 4 - 4y + z2 + 9 – 6z = x2 +9 -6x + y2 + 4 - 4y + z2 + 1 + 2z
4x – 8z = 0
x – 2z = 0
Pt. B(3, 2, -1)
Let P(x,y,z)
So, AP = BP
((x-1)2 + (y-2)2 + (z-3)2)1/2 = ((x-3)2 + (y-2)2 + (z+1)2)1/2
(x-1)2 + (y-2)2 + (z-3)2) = (x-3)2 + (y-2)2 + (z+1)2
x2 +1 -2x + y2 + 4 - 4y + z2 + 9 – 6z = x2 +9 -6x + y2 + 4 - 4y + z2 + 1 + 2z
4x – 8z = 0
x – 2z = 0
The direction cosines of the line joining the points (2, -1, 8) and (-4, -3, 5) are:- a)
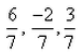
- b)
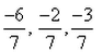
- c)
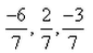
- d)
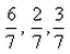
Correct answer is option 'B'. Can you explain this answer?
The direction cosines of the line joining the points (2, -1, 8) and (-4, -3, 5) are:
a)
b)
c)
d)
|
|
Geetika Shah answered |
Pt. A(2, -1, 8)
Pt. B(-4, -3, 5)
Direction Ratio DR of AB : ( -4-2 , -3+1 , 5-8 )
: (-6,-2,-3)
Direction cosine of AB : ( -6/(62+22+32)1/2 , -2/(62+22+32)1/2 , -3/(62+22+32)1/2)
: ( -6/7, -2/7, -3/7)
Pt. B(-4, -3, 5)
Direction Ratio DR of AB : ( -4-2 , -3+1 , 5-8 )
: (-6,-2,-3)
Direction cosine of AB : ( -6/(62+22+32)1/2 , -2/(62+22+32)1/2 , -3/(62+22+32)1/2)
: ( -6/7, -2/7, -3/7)
The signs of the X,Y and Z coordinates of a point that lies in the octant OXYZ’ is- a)(- , + , +)
- b)(-, – , +)
- c)( + , – , -)
- d)( + , + , -)
Correct answer is option 'D'. Can you explain this answer?
The signs of the X,Y and Z coordinates of a point that lies in the octant OXYZ’ is
a)
(- , + , +)
b)
(-, – , +)
c)
( + , – , -)
d)
( + , + , -)
|
|
Vikas Kapoor answered |
X,Y,Z imply positive X,Y,Z axis & X’,Y’,Z’ imply negative X,Y,Z axis.
So, OXYZ’ will have a point of signs (+, +, -).
So, OXYZ’ will have a point of signs (+, +, -).
The equation of the plane passing through the intersection of the planes 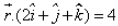 and
and 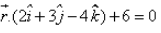 and the point (1, 2, 1) is:
and the point (1, 2, 1) is:- a)18x+6y+14z-23=0
- b)18x+7y+14z-46=0
- c)9x+3y+7z-23=0
- d)18x+7y+14z-38=0
Correct answer is option 'B'. Can you explain this answer?
The equation of the plane passing through the intersection of the planes 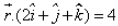 and
and 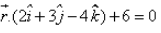 and the point (1, 2, 1) is:
and the point (1, 2, 1) is:
a)
18x+6y+14z-23=0
b)
18x+7y+14z-46=0
c)
9x+3y+7z-23=0
d)
18x+7y+14z-38=0
|
|
Aryan Khanna answered |
n1 = 2i + j + k
n2 = 2i + 3j - 4k
p1 = 4, p2 = -6
r.(n1 + λn2) = p1 + λp2
=> r . [2i + j + k + λ(2i + 3j - 4k)] = 4 - 6λ
=> r . [ i(2 + 2λ) + j(1 + 3λ) + k(1 - 4k)] = 4 - 6λ
Taking r = xi + yj + zk
(2 + 2λ)x + (1 + 3λ)y + (1 - 4k)z = 4 - 6λ
(2x + y + - z - 4) + λ(2x + 3y - 4k + 6) = 0
Given points are (1,2,1)
(2 + 2 - 1 - 4) + λ(2 + 6 - 4 + 6) = 0
-1 + λ(10) = 0
λ = 1/10
Substitute λ = 1/10, we get
18x + 7y + 14z - 46=0
n2 = 2i + 3j - 4k
p1 = 4, p2 = -6
r.(n1 + λn2) = p1 + λp2
=> r . [2i + j + k + λ(2i + 3j - 4k)] = 4 - 6λ
=> r . [ i(2 + 2λ) + j(1 + 3λ) + k(1 - 4k)] = 4 - 6λ
Taking r = xi + yj + zk
(2 + 2λ)x + (1 + 3λ)y + (1 - 4k)z = 4 - 6λ
(2x + y + - z - 4) + λ(2x + 3y - 4k + 6) = 0
Given points are (1,2,1)
(2 + 2 - 1 - 4) + λ(2 + 6 - 4 + 6) = 0
-1 + λ(10) = 0
λ = 1/10
Substitute λ = 1/10, we get
18x + 7y + 14z - 46=0
If the sum of the squares of the distances of a point from the three coordinate axes be 36, then its distance from the origin is- a)6
- b)3√2
- c)2√3
- d)6√2
Correct answer is option 'B'. Can you explain this answer?
If the sum of the squares of the distances of a point from the three coordinate axes be 36, then its distance from the origin is
a)
6
b)
3√2
c)
2√3
d)
6√2
|
|
Yash Patel answered |
Let (x,y,z) be the point.
Given sum of the squares of distance from point to the axes is 36.
⇒(x2+y2)+(y2+z2)+(z2+x2)=36
⇒2(x2+y2+z2)=36⇒x2+y2+z2=18
So the distance of the point from the origin is =3(2)1/2
Given sum of the squares of distance from point to the axes is 36.
⇒(x2+y2)+(y2+z2)+(z2+x2)=36
⇒2(x2+y2+z2)=36⇒x2+y2+z2=18
So the distance of the point from the origin is =3(2)1/2
The distance of the point (2, 3, – 5) from the plane x + 2y – 2z = 9 is:- a)2 units
- b)3/2 units
- c)3 units
- d)10/3 units
Correct answer is option 'C'. Can you explain this answer?
The distance of the point (2, 3, – 5) from the plane x + 2y – 2z = 9 is:
a)
2 units
b)
3/2 units
c)
3 units
d)
10/3 units
|
|
Nikita Singh answered |
Length of perpendicular from (2,3,-5) to the plane x + 2y − 2z − 9 = 0.
= |(2 + 2×3 −2×(−5) − 9)|√12 + 22 + (−2)2
= |2 + 6 + 10 − 9|/√9
= 9/3
= 3 units.
= |(2 + 2×3 −2×(−5) − 9)|√12 + 22 + (−2)2
= |2 + 6 + 10 − 9|/√9
= 9/3
= 3 units.
The angle between the lines x = 2y = – 3z and – 4x = 6y = – z is:- a)0°
- b)cos-1(1/√3)
- c)90°
- d)180°
Correct answer is option 'C'. Can you explain this answer?
The angle between the lines x = 2y = – 3z and – 4x = 6y = – z is:
a)
0°
b)
cos-1(1/√3)
c)
90°
d)
180°

|
Sushil Kumar answered |
x = 2y = -3z -4x = 6y = -z
x/1 = y/(½) = z(-⅓) x/(-¼) = y/(⅙) = z/(-1)
Cosθ = [(a1a2 + b1b2 + c1c2)/(a1 + b1 + c1)½ * (a2 + b2 + c2)½]
Cosθ ={[(1*(-¼)) + (½)(⅙) + (-⅓)(-1)]/[(1)2 + (½)2 + (-⅓)2]1/2 * [(-¼)2 + (⅙)2 + (-1)2]1/2}
= {[(-¼ + 1/12 - ⅓)]/[2 + 1 - ⅔]1/2 * [ -½ + ⅓ -½]½}
Cosθ = 0
θ = 90deg
x/1 = y/(½) = z(-⅓) x/(-¼) = y/(⅙) = z/(-1)
Cosθ = [(a1a2 + b1b2 + c1c2)/(a1 + b1 + c1)½ * (a2 + b2 + c2)½]
Cosθ ={[(1*(-¼)) + (½)(⅙) + (-⅓)(-1)]/[(1)2 + (½)2 + (-⅓)2]1/2 * [(-¼)2 + (⅙)2 + (-1)2]1/2}
= {[(-¼ + 1/12 - ⅓)]/[2 + 1 - ⅔]1/2 * [ -½ + ⅓ -½]½}
Cosθ = 0
θ = 90deg
If a line has the direction ratios -4, 18, -12 then what are its direction cosines?- a)-2, 9, -6
- b)-4, 18, -12
- c)2/11, 9/11, 6/11
- d)-2/11, 9/11, -6/11
Correct answer is option 'D'. Can you explain this answer?
If a line has the direction ratios -4, 18, -12 then what are its direction cosines?
a)
-2, 9, -6
b)
-4, 18, -12
c)
2/11, 9/11, 6/11
d)
-2/11, 9/11, -6/11
|
|
Vikas Kapoor answered |
DR of the line : (-4, 18 -12)
DC of the line : (-4/k, 18/k, -12/k)
where k = ((42) + (182) + (12)2)1/2
= (16 + 324 + 144)1/2
= (484)1/2
= 22
So, DC : (-4/22, 18/22, -12/22)
: (-2/11 , 9/11 , -6/11)
DC of the line : (-4/k, 18/k, -12/k)
where k = ((42) + (182) + (12)2)1/2
= (16 + 324 + 144)1/2
= (484)1/2
= 22
So, DC : (-4/22, 18/22, -12/22)
: (-2/11 , 9/11 , -6/11)
The equation of the plane passing through the line of intersection of the planes x-2y+3z+8=0 and 2x-7y+4z-3=0 and the point (3, 1, -2) is:- a)6x-15y+12z+29=0
- b)6x-15y+16z+29=0
- c)6x-15y+12z+32=0
- d)2x-5y+4z+9=0
Correct answer is option 'B'. Can you explain this answer?
The equation of the plane passing through the line of intersection of the planes x-2y+3z+8=0 and 2x-7y+4z-3=0 and the point (3, 1, -2) is:
a)
6x-15y+12z+29=0
b)
6x-15y+16z+29=0
c)
6x-15y+12z+32=0
d)
2x-5y+4z+9=0
|
|
Tejas Verma answered |
(x - 2y + 3z + 8) + μ(2x - 7y + 4z - 3) = 0
i.e, (1 + 2μ)x - (2 + 7μ)y + (3 + 4μ)z + (8 - 3μ) = 0......(1)
the required plane is passing through (3, 1, -2)
so, 3(1 + 2μ) - (1)(2 + 7μ) + (-2)(3 + 4μ)+ (8 - 3μ) = 0
3 + 6μ - 2 - 7μ -6 -8μ + 8 - 3μ = 0
by solving, μ = 1/4
putting μ in equation (1)
we get the required equation of plane as :- 6x - 15y + 16z + 29 = 0
i.e, (1 + 2μ)x - (2 + 7μ)y + (3 + 4μ)z + (8 - 3μ) = 0......(1)
the required plane is passing through (3, 1, -2)
so, 3(1 + 2μ) - (1)(2 + 7μ) + (-2)(3 + 4μ)+ (8 - 3μ) = 0
3 + 6μ - 2 - 7μ -6 -8μ + 8 - 3μ = 0
by solving, μ = 1/4
putting μ in equation (1)
we get the required equation of plane as :- 6x - 15y + 16z + 29 = 0
The Cartesian form of the equation of the plane 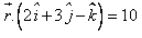 is:
is:- a)2x+3y-z=10
- b)2x+3y-z= √14
- c)2x+3y-z+√14=0
- d)2x+3y-z+10=0
Correct answer is option 'A'. Can you explain this answer?
The Cartesian form of the equation of the plane 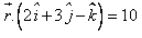 is:
is:
a)
2x+3y-z=10
b)
2x+3y-z= √14
c)
2x+3y-z+√14=0
d)
2x+3y-z+10=0
|
|
Deepak Kapoor answered |
Let r = xi + yj + zk
(xi + yj + zk) . (2i + 3j - k) = 10
2x + 3y - k = 10
If a line makes angles 45°,150°, 135°, with x, y and z-axes respectively, find its direction cosines.- a)
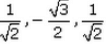
- b)
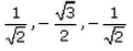
- c)
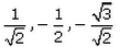
- d)
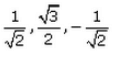
Correct answer is option 'B'. Can you explain this answer?
If a line makes angles 45°,150°, 135°, with x, y and z-axes respectively, find its direction cosines.
a)
b)
c)
d)
|
|
Leelu Bhai answered |
Direction cosines of this line are cos 45, cos150 & cos135....i.e, 1/√2, -√3/2 & -1/√2
The length of the perpendicular from the origin to the plane 3x + 2y – 6z = 21 is:- a)3
- b)14
- c)21
- d)7
Correct answer is option 'A'. Can you explain this answer?
The length of the perpendicular from the origin to the plane 3x + 2y – 6z = 21 is:
a)
3
b)
14
c)
21
d)
7
|
|
Leelu Bhai answered |
Given equation of plane is : 3x + 2y - 6z - 21= 0
the length of perpendicular from a given point
(x' , y', z') on a plane ax + by + cz + d = 0 is given as :-
d = modulus of [{ax' + by' + cz' + d}/{√(a² + b² + c)²}]
so, d = modulus of [{(3*0) + (2*0) + (-6*0) + (-21)}/{√(3² + 2² + (-6)²)}]
d= modulus of (-21/√49) = (-21/7) = 3 units
hence option A is correct....
the length of perpendicular from a given point
(x' , y', z') on a plane ax + by + cz + d = 0 is given as :-
d = modulus of [{ax' + by' + cz' + d}/{√(a² + b² + c)²}]
so, d = modulus of [{(3*0) + (2*0) + (-6*0) + (-21)}/{√(3² + 2² + (-6)²)}]
d= modulus of (-21/√49) = (-21/7) = 3 units
hence option A is correct....
If plane cuts off intercepts OA = a, OB = b, OC = c from the coordinate axes, then the area of the triangle ABC equal to- a)
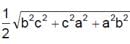
- b)
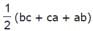
- c)
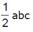
- d)
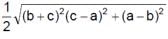
Correct answer is option 'A'. Can you explain this answer?
If plane cuts off intercepts OA = a, OB = b, OC = c from the coordinate axes, then the area of the triangle ABC equal to
a)
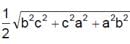
b)
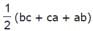
c)
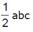
d)
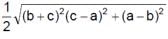
|
|
Neha Joshi answered |
=AC = −ai^ + ck^
AB = −ai^ + bj^
Area of △ABC= ½|AB × AC∣
|AB × AC∣ =
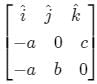
−(bc)i^− (ac)j^ − (ab)k^
∣AB × AC∣ = (b2c2 + a2c2 + a2b2)1/2
Area = 1/2(a2b2 + b2c2 + c2a2)1/2
AB = −ai^ + bj^
Area of △ABC= ½|AB × AC∣
|AB × AC∣ =
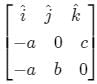
−(bc)i^− (ac)j^ − (ab)k^
∣AB × AC∣ = (b2c2 + a2c2 + a2b2)1/2
Area = 1/2(a2b2 + b2c2 + c2a2)1/2
The equation of the plane passing through the point (3, – 3, 1) and perpendicular to the line joining the points (3, 4, – 1) and (2, – 1, 5) is:- a)– x – 5y + 6z + 18 = 0
- b)x – 5y + 6z + 18 = 0
- c)x + 5y – 6z + 18 = 0
- d)– x – 5y – 6z + 18 = 0
Correct answer is 'C'. Can you explain this answer?
The equation of the plane passing through the point (3, – 3, 1) and perpendicular to the line joining the points (3, 4, – 1) and (2, – 1, 5) is:
a)
– x – 5y + 6z + 18 = 0
b)
x – 5y + 6z + 18 = 0
c)
x + 5y – 6z + 18 = 0
d)
– x – 5y – 6z + 18 = 0
|
|
Leelu Bhai answered |

If the distance of the point P(1, -2, 1) from the plane x + 2y - 2z = a, where a > 0 is 5, then foot of perpendicular from P to the plane is- a)
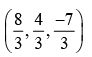
- b)
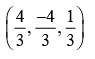
- c)
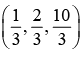
- d)
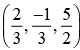
Correct answer is option 'A'. Can you explain this answer?
If the distance of the point P(1, -2, 1) from the plane x + 2y - 2z = a, where a > 0 is 5, then foot of perpendicular from P to the plane is
a)
b)
c)
d)
|
|
Lavanya Menon answered |
Distance of pt P from plane = 5
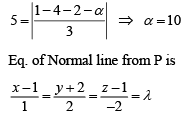
Gen. pt. on line is (λ + 1, 2λ - 2, -2λ + 1)
This pt line on plane
(λ + 1 + 2 2λ - 2) - 2 (-2λ + 1) = 10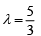
Gen. pt. on line is (λ + 1, 2λ - 2, -2λ + 1)
This pt line on plane
(λ + 1 + 2 2λ - 2) - 2 (-2λ + 1) = 10
A line makes angles α,β,γ with the coordinates axes. If α+β = 90°, then (gamma) equal to- a)0
- b)90°
- c)180°
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A line makes angles α,β,γ with the coordinates axes. If α+β = 90°, then (gamma) equal to
a)
0
b)
90°
c)
180°
d)
None of these
|
|
Lavanya Menon answered |
If a line makes the angles α,β,γ,
Then, cos2 α+cos2 β+cos2 γ=1
It is given that, α+β=90°
⇒ α=β−90°
⇒ cosα=cos(90o−β)
⇒ cosα=sinβ
⇒ cos2 α = sin2 β=1−cos2 β
⇒ cos2α+cos2β=1
As, cos2 α+cos2 β+cos^2γ=1
⇒ 1+cos2 γ=1
⇒ cos2 γ=0
hence, γ=π/2=90°
Then, cos2 α+cos2 β+cos2 γ=1
It is given that, α+β=90°
⇒ α=β−90°
⇒ cosα=cos(90o−β)
⇒ cosα=sinβ
⇒ cos2 α = sin2 β=1−cos2 β
⇒ cos2α+cos2β=1
As, cos2 α+cos2 β+cos^2γ=1
⇒ 1+cos2 γ=1
⇒ cos2 γ=0
hence, γ=π/2=90°
The equation of plane through the intersection of planes (x+y+z =1) and (2x +3y – z+4) =0 is- a)x(1 + 2k) + y(1 + 3k) + z(1 – k) + (-1 + 4k) = 0
- b)x(1+2k)+y(1-3k)+z(1-k)+(-1+4k) = 0
- c)x(1+2k) +y(1+3k)+z(1-k) +(-1 – 4k) = 0
- d)x (1-2k) + y(1+3k) +z(1-k) +(-1+4k) = 0
Correct answer is option 'A'. Can you explain this answer?
The equation of plane through the intersection of planes (x+y+z =1) and (2x +3y – z+4) =0 is
a)
x(1 + 2k) + y(1 + 3k) + z(1 – k) + (-1 + 4k) = 0
b)
x(1+2k)+y(1-3k)+z(1-k)+(-1+4k) = 0
c)
x(1+2k) +y(1+3k)+z(1-k) +(-1 – 4k) = 0
d)
x (1-2k) + y(1+3k) +z(1-k) +(-1+4k) = 0
|
|
Kritika Sarkar answered |
To find the equation of the plane through the intersection of two given planes, we need to first determine the line of intersection and then find a normal vector for the plane.
1. Finding the line of intersection:
The two given planes are:
Plane 1: x + y + z = 1
Plane 2: 2x + 3y + z + 4 = 0
To find the line of intersection, we can set the equations of the two planes equal to each other:
x + y + z = 1
2x + 3y + z + 4 = 0
By subtracting the second equation from the first equation, we can eliminate z:
x + y + z - (2x + 3y + z + 4) = 1 - 0
-x - 2y - 4 = -1
Simplifying the equation, we get:
x + 2y = 3
This equation represents the line of intersection of the two planes.
2. Finding a normal vector for the plane:
Since the line of intersection lies on both planes, the normal vector of the required plane should be perpendicular to this line. Therefore, we can choose the direction ratios of the line, -1 and 2, as coefficients of the normal vector.
The normal vector of the required plane is given by the cross product of the direction ratios of the line of intersection:
n = (1, 2, 0) x (-1, 2, 0) = (0, 0, -4)
3. Writing the equation of the plane:
Now we have a point on the plane, (1, 0, 0), and a normal vector, (0, 0, -4). We can use the point-normal form of the equation of a plane to write the equation of the required plane.
The equation of the plane is given by:
0(x - 1) + 0(y - 0) + (-4)(z - 0) = 0
Simplifying the equation, we get:
-4z + 4 = 0
z = 1
Therefore, the equation of the plane through the intersection of the given planes is:
x + 2y - 4z + 4 = 0
Comparing this equation with the options provided, we see that option A is the correct answer:
x(1 2k) + y(1 3k) + z(1 k) + (-1 4k) = 0
1. Finding the line of intersection:
The two given planes are:
Plane 1: x + y + z = 1
Plane 2: 2x + 3y + z + 4 = 0
To find the line of intersection, we can set the equations of the two planes equal to each other:
x + y + z = 1
2x + 3y + z + 4 = 0
By subtracting the second equation from the first equation, we can eliminate z:
x + y + z - (2x + 3y + z + 4) = 1 - 0
-x - 2y - 4 = -1
Simplifying the equation, we get:
x + 2y = 3
This equation represents the line of intersection of the two planes.
2. Finding a normal vector for the plane:
Since the line of intersection lies on both planes, the normal vector of the required plane should be perpendicular to this line. Therefore, we can choose the direction ratios of the line, -1 and 2, as coefficients of the normal vector.
The normal vector of the required plane is given by the cross product of the direction ratios of the line of intersection:
n = (1, 2, 0) x (-1, 2, 0) = (0, 0, -4)
3. Writing the equation of the plane:
Now we have a point on the plane, (1, 0, 0), and a normal vector, (0, 0, -4). We can use the point-normal form of the equation of a plane to write the equation of the required plane.
The equation of the plane is given by:
0(x - 1) + 0(y - 0) + (-4)(z - 0) = 0
Simplifying the equation, we get:
-4z + 4 = 0
z = 1
Therefore, the equation of the plane through the intersection of the given planes is:
x + 2y - 4z + 4 = 0
Comparing this equation with the options provided, we see that option A is the correct answer:
x(1 2k) + y(1 3k) + z(1 k) + (-1 4k) = 0
Direction: Read the following text and answer the following questions on the basis of the same:A mobile tower stands at the top of a hill. Consider the surface on which the tower stands as a plane having points A(1, 0, 2), B(3, –1, 1) and C(1, 2, 1) on it. The mobile tower is tied with 3 cables from the points A, B and C such that it stands vertically on the ground. The top of the tower is at the point (2, 3, 1) as shown in the figure.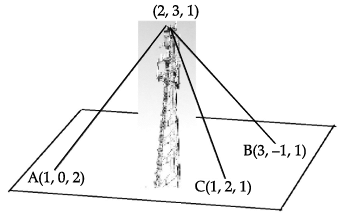 Q. The equation of the plane passing through the points A, B and C is
Q. The equation of the plane passing through the points A, B and C is- a)3x – 2y + 4z = –11
- b)3x + 2y + 4z = 11
- c)3x – 2y – 4z = 11
- d)–3x + 2y + 4z = –11
Correct answer is option 'B'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
A mobile tower stands at the top of a hill. Consider the surface on which the tower stands as a plane having points A(1, 0, 2), B(3, –1, 1) and C(1, 2, 1) on it. The mobile tower is tied with 3 cables from the points A, B and C such that it stands vertically on the ground. The top of the tower is at the point (2, 3, 1) as shown in the figure.

Q. The equation of the plane passing through the points A, B and C is
a)
3x – 2y + 4z = –11
b)
3x + 2y + 4z = 11
c)
3x – 2y – 4z = 11
d)
–3x + 2y + 4z = –11
|
|
Krishna Iyer answered |
A(1, 0, 2), B(3, –1, 1) and C(1, 2, 1)

(x - 1)(1 + 2) -y (-2, 0) + (z - 2) (4 - 0)
3x - 3 + 2y + 4z - 8 = 0
3x + 2y + 4z = 11
A point moves so that the sum of the squares of its distances from the six faces of a cube given by x = ± 1, y = ± 1, z = ± 1 is 10 units. The locus of the point is- a)x2 + y2 + z2 = 1
- b)x2 + y2 + z2 = 2
- c)x + y + z = 1
- d)x + y + z = 2
Correct answer is option 'B'. Can you explain this answer?
A point moves so that the sum of the squares of its distances from the six faces of a cube given by x = ± 1, y = ± 1, z = ± 1 is 10 units. The locus of the point is
a)
x2 + y2 + z2 = 1
b)
x2 + y2 + z2 = 2
c)
x + y + z = 1
d)
x + y + z = 2
|
|
Ram Mohith answered |
Let the point be (x,y,z)
Distance of this point from x = 1 is |x -1| and from x = +1 is |x + 1|. Similarly you can find the distance from the other faces. The sum of squares of distances will be,
(x - 1)^2 + (x + 1)^2 + (y - 1)^2 + (y + 1)^2 + (z - 1)^2 + (z + 1)^2 = 10
2(x^2 + y^2 + z^2 ) + 6 = 10
x^2 + y^2 + z^2 = 2
Distance of this point from x = 1 is |x -1| and from x = +1 is |x + 1|. Similarly you can find the distance from the other faces. The sum of squares of distances will be,
(x - 1)^2 + (x + 1)^2 + (y - 1)^2 + (y + 1)^2 + (z - 1)^2 + (z + 1)^2 = 10
2(x^2 + y^2 + z^2 ) + 6 = 10
x^2 + y^2 + z^2 = 2
If the vector equation of a line is 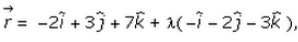 find its caryesian equation.
find its caryesian equation.- a)
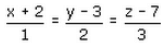
- b)
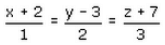
- c)
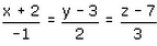
- d)
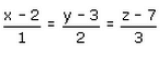
Correct answer is option 'A'. Can you explain this answer?
If the vector equation of a line is 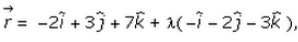 find its caryesian equation.
find its caryesian equation.
a)
b)
c)
d)
|
|
Gaurav Kumar answered |
r = -2i + 3j + 7k + λ( -i - 2j - 3k)
xi + yj + zk = (-2-λ)i + (3-2λ)j + (7-3λ)k
Equating the terms, we get
x = -2-λ y = 3-2λ z = 7-3λ
(x+2)/(-1) = λ, (y-3)/(-2) = λ, (z-7)/(-3) = λ
(x+2)/(1) = (y-3)/(2) = (z-7)/(3)
xi + yj + zk = (-2-λ)i + (3-2λ)j + (7-3λ)k
Equating the terms, we get
x = -2-λ y = 3-2λ z = 7-3λ
(x+2)/(-1) = λ, (y-3)/(-2) = λ, (z-7)/(-3) = λ
(x+2)/(1) = (y-3)/(2) = (z-7)/(3)
A variable plane passes through a fixed point (a, b, c) and meets the coordinate axes in A, B, C. Locus of the point common to the planes through A, B, C and parallel to coordinate plane, is- a)
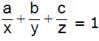
- b)
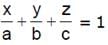
- c)ax + by + cz = 1
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
A variable plane passes through a fixed point (a, b, c) and meets the coordinate axes in A, B, C. Locus of the point common to the planes through A, B, C and parallel to coordinate plane, is
a)
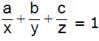
b)
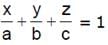
c)
ax + by + cz = 1
d)
None of these
|
|
Silent Nisarg answered |
Option a is correct
Find the direction cosines of the x axis.- a)1, 0, 0
- b)0, 0, 0
- c)0, 1, 0
- d)0, 0, 1
Correct answer is option 'A'. Can you explain this answer?
Find the direction cosines of the x axis.
a)
1, 0, 0
b)
0, 0, 0
c)
0, 1, 0
d)
0, 0, 1

|
Infinity Academy answered |
To find Direction Cosines of X-axis.
Take any two points on X-axis : A(a,0,0) & B(b,0,0)
DR of AB : (b-a,0,0)
DC of AB : ((b-a)/(((b-a)2 + 0 + 0)1/2), 0, 0)
: ((b-a)/(b-a) , 0 , 0)
: (1,0,0)
Take any two points on X-axis : A(a,0,0) & B(b,0,0)
DR of AB : (b-a,0,0)
DC of AB : ((b-a)/(((b-a)2 + 0 + 0)1/2), 0, 0)
: ((b-a)/(b-a) , 0 , 0)
: (1,0,0)
In the following case, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them. 2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0- a)The planes are perpendicular
- b)The planes are parallel
- c)The planes are at 45∘
- d)The planes are at 55∘
Correct answer is option 'B'. Can you explain this answer?
In the following case, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them. 2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0
a)
The planes are perpendicular
b)
The planes are parallel
c)
The planes are at 45∘
d)
The planes are at 55∘

|
Pranavi Iyer answered |
A variable plane passes through a fixed point (1, 2, 3). The locus of the foot of the perpendicular drawn from origin to this plane is- a)x2 + y2 + z2 – x – 2y – 3z = 0
- b)x2 + 2y2 + 3z2 – x – 2y – 3z = 0
- c)x2 + 4y2 + 9z2 + x + 2y + 3 = 0
- d)x2 + y2 + z2 + x + 2y + 3z = 0
Correct answer is option 'A'. Can you explain this answer?
A variable plane passes through a fixed point (1, 2, 3). The locus of the foot of the perpendicular drawn from origin to this plane is
a)
x2 + y2 + z2 – x – 2y – 3z = 0
b)
x2 + 2y2 + 3z2 – x – 2y – 3z = 0
c)
x2 + 4y2 + 9z2 + x + 2y + 3 = 0
d)
x2 + y2 + z2 + x + 2y + 3z = 0
|
|
Neha Joshi answered |
α(x − α) + β(y − β) + γ(z − γ) = 0
α(1 − α) + β (2 − β) + γ ( 3 − γ) = 0
α + 2β + 3γ = α2 + β2 + γ2
α2 + β2 + γ2 − α − 2β − 3γ = 0
x2 + y2 + z2 − x − 2y− 3z = 0
α(1 − α) + β (2 − β) + γ ( 3 − γ) = 0
α + 2β + 3γ = α2 + β2 + γ2
α2 + β2 + γ2 − α − 2β − 3γ = 0
x2 + y2 + z2 − x − 2y− 3z = 0
The equation of the plane, which is at a distance of 5 unit from the origin and has 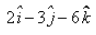 as a normal vector, is:
as a normal vector, is:- a)
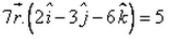
- b)
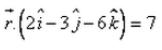
- c)
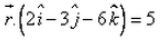
- d)
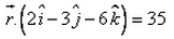
Correct answer is option 'D'. Can you explain this answer?
The equation of the plane, which is at a distance of 5 unit from the origin and has 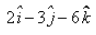 as a normal vector, is:
as a normal vector, is:
a)
b)
c)
d)
|
|
Preeti Iyer answered |
x = 3i - 2j - 6k
|x| = ((3)2 + (2)2 + (6)2)
|x| = (49)½
|x| = 7
x = x/|x|
= (3i - 2j - 6k)/7
The required equation of plane is r.x = d
⇒ r.(3i - 2j - 6k)/7 = 5
⇒ r.(3i - 2j - 6k) = 35
|x| = ((3)2 + (2)2 + (6)2)
|x| = (49)½
|x| = 7
x = x/|x|
= (3i - 2j - 6k)/7
The required equation of plane is r.x = d
⇒ r.(3i - 2j - 6k)/7 = 5
⇒ r.(3i - 2j - 6k) = 35
For which value of a lines 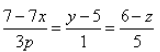 and
and 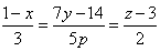 are perpendicular?
are perpendicular?
- a)11/70
- b)5
- c)1
- d)70/11
Correct answer is option 'B'. Can you explain this answer?
For which value of a lines 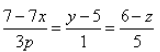 and
and 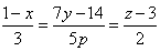 are perpendicular?
are perpendicular?
a)
11/70
b)
5
c)
1
d)
70/11
|
|
Tejas Verma answered |
(x-1)/(-3) = (y-2)/(2p/7) = (z-3)/2
(x-1)(-3p/7) = (y - 5)/1 = (z - 6)/(-5)
The direction ratio of the line are -3, 2p/7, -2 and (-3p)/7, 1, -5
Two lines with direction ratios, a1, b1, c1 and a2, b2, c2 are perpendicular to each other if a1a2 + b1b2 + c1c2 = 0
Therefore, (-3)(-3p/7) + (2p/7)(1) + 2(-5) = 0
(9p/7) + (2p/7) = 10
11p = 70
p = 70/1
(x-1)(-3p/7) = (y - 5)/1 = (z - 6)/(-5)
The direction ratio of the line are -3, 2p/7, -2 and (-3p)/7, 1, -5
Two lines with direction ratios, a1, b1, c1 and a2, b2, c2 are perpendicular to each other if a1a2 + b1b2 + c1c2 = 0
Therefore, (-3)(-3p/7) + (2p/7)(1) + 2(-5) = 0
(9p/7) + (2p/7) = 10
11p = 70
p = 70/1
The equation of the plane passing through the point (3, – 3, 1) and perpendicular to the line joining the points (3, 4, – 1) and (2, – 1, 5) is:- a)– x – 5y + 6z + 18 = 0
- b)x – 5y + 6z + 18 = 0
- c)x + 5y – 6z + 18 = 0
- d)– x – 5y – 6z + 18 = 0
Correct answer is option 'C'. Can you explain this answer?
The equation of the plane passing through the point (3, – 3, 1) and perpendicular to the line joining the points (3, 4, – 1) and (2, – 1, 5) is:
a)
– x – 5y + 6z + 18 = 0
b)
x – 5y + 6z + 18 = 0
c)
x + 5y – 6z + 18 = 0
d)
– x – 5y – 6z + 18 = 0
|
|
Preeti Iyer answered |
The equation of the plane passing through the point (3, – 3, 1) is:
a(x – 3) + b(y + 3) + c(z – 1) = 0 and the direction ratios of the line joining the points
(3, 4, – 1) and (2, – 1, 5) is 2 – 3, – 1 – 4, 5 + 1, i.e., – 1, – 5, 6.
Since the plane is perpendicular to the line whose direction ratios are – 1, – 5, 6, therefore, direction ratios of the normal to the plane is – 1, – 5, 6.
So, required equation of plane is: – 1(x – 3) – 5(y + 3) + 6(z – 1) = 0
i.e., x + 5y – 6z + 18 = 0.
a(x – 3) + b(y + 3) + c(z – 1) = 0 and the direction ratios of the line joining the points
(3, 4, – 1) and (2, – 1, 5) is 2 – 3, – 1 – 4, 5 + 1, i.e., – 1, – 5, 6.
Since the plane is perpendicular to the line whose direction ratios are – 1, – 5, 6, therefore, direction ratios of the normal to the plane is – 1, – 5, 6.
So, required equation of plane is: – 1(x – 3) – 5(y + 3) + 6(z – 1) = 0
i.e., x + 5y – 6z + 18 = 0.
The Cartesian equation of plane passing through (1, 1, 1) and containing the x-axis is- a)z – x = 0
- b)y – z = 0
- c)x – y = 0
- d)2x – y – z = 0
Correct answer is option 'B'. Can you explain this answer?
The Cartesian equation of plane passing through (1, 1, 1) and containing the x-axis is
a)
z – x = 0
b)
y – z = 0
c)
x – y = 0
d)
2x – y – z = 0
|
|
Naina Sharma answered |
Eq. of x-axis is
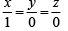
Equation of plane passing through (1, 1, 1) and containing
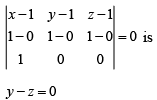
Equation of plane passing through (1, 1, 1) and containing
The coplanar points A, B, C, D are (2 – x, 2, 2), (2, 2 – y, 2), (2, 2, 2 – z) and (1, 1, 1) respectively. Then- a)
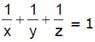
- b)x + y + z = 1
- c)
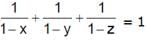
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The coplanar points A, B, C, D are (2 – x, 2, 2), (2, 2 – y, 2), (2, 2, 2 – z) and (1, 1, 1) respectively. Then
a)
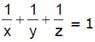
b)
x + y + z = 1
c)
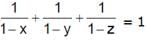
d)
None of these
|
|
Neha Joshi answered |
We have four coplanar points.
The three vectors connecting two of them at a time are thus coplanar.
⇒{(−x, y, 0) (-x, 0, z) (1−x, 1, 1)} = 0
⇒−x (−z) −y (−x−z+xz)+0=0
⇒xz + xy + yz = xyz
⇒1/y + 1/z + 1/x = 1
The three vectors connecting two of them at a time are thus coplanar.
⇒{(−x, y, 0) (-x, 0, z) (1−x, 1, 1)} = 0
⇒−x (−z) −y (−x−z+xz)+0=0
⇒xz + xy + yz = xyz
⇒1/y + 1/z + 1/x = 1
Direction: Read the following text and answer the following questions on the basis of the same:The Indian coast guard, while patrolling, saw a suspicious boat with people. They were nowhere looking like fishermen. The coast guard were closely observing the movement of the boat for an opportunity to seize the boat. They observed that the boat is moving along a planar surface. At an instant of time, the coordinates of the position of the coast guard helicopter and the boat is (1, 3, 5) and (2, 5, 3) respectively. Q. If the coast guard decides to shoot the boat at that given instant of time, when the speed of bullet is 36 m/sec, then what is the time taken for the bullet to travel and hit the boat?
Q. If the coast guard decides to shoot the boat at that given instant of time, when the speed of bullet is 36 m/sec, then what is the time taken for the bullet to travel and hit the boat?- a)1/8 second
- b)1/14 second
- c)1/10 second
- d)1/12 second
Correct answer is option 'D'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
The Indian coast guard, while patrolling, saw a suspicious boat with people. They were nowhere looking like fishermen. The coast guard were closely observing the movement of the boat for an opportunity to seize the boat. They observed that the boat is moving along a planar surface. At an instant of time, the coordinates of the position of the coast guard helicopter and the boat is (1, 3, 5) and (2, 5, 3) respectively.

Q. If the coast guard decides to shoot the boat at that given instant of time, when the speed of bullet is 36 m/sec, then what is the time taken for the bullet to travel and hit the boat?
a)
1/8 second
b)
1/14 second
c)
1/10 second
d)
1/12 second
|
|
Nandini Iyer answered |
Time taken for the bullet to travel and hit the boat

The equation of plane which passes through (2, –3, 1) & is normal to the line joining the points (3, 4, –1) & (2, – 1, 5) is given by- a)x + 5y – 6z + 19 = 0
- b)x – 5y + 6z – 19 =0
- c)x + 5y + 3z + 19 = 0
- d)x – 5y – 6z – 19 = 0
Correct answer is option 'A'. Can you explain this answer?
The equation of plane which passes through (2, –3, 1) & is normal to the line joining the points (3, 4, –1) & (2, – 1, 5) is given by
a)
x + 5y – 6z + 19 = 0
b)
x – 5y + 6z – 19 =0
c)
x + 5y + 3z + 19 = 0
d)
x – 5y – 6z – 19 = 0
|
|
Aarya Shah answered |
A(3,4,−1) and B(2,−1,5)
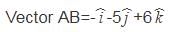
Vector AB is normal to the required plane
⇒ Directions of normal (−1,−5,6)
∴ Equation ,−x−5y+6z=k
Point (2,−3,1) passes through the plane,
∴ −2+15+6=k⇒k=19
∴ −x−5y+6z = 19
x+5y−6z+19 = 0
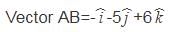
Vector AB is normal to the required plane
⇒ Directions of normal (−1,−5,6)
∴ Equation ,−x−5y+6z=k
Point (2,−3,1) passes through the plane,
∴ −2+15+6=k⇒k=19
∴ −x−5y+6z = 19
x+5y−6z+19 = 0
In the following case, determine whether the given planes are parallel orperpendicular, and in case they are neither, find the angles between them. 2x + y + 3z – 2 = 0 and x – 2y + 5 = 0- a)The planes are parallel
- b)The planes are at 45∘
- c)The planes are at 55∘
- d)The planes are perpendicular
Correct answer is option 'D'. Can you explain this answer?
In the following case, determine whether the given planes are parallel orperpendicular, and in case they are neither, find the angles between them. 2x + y + 3z – 2 = 0 and x – 2y + 5 = 0
a)
The planes are parallel
b)
The planes are at 45∘
c)
The planes are at 55∘
d)
The planes are perpendicular

|
Preethi Kaur answered |
We have ,
2x + y + 3z – 2 = 0 and x – 2y + 5 = 0. Let θ be the angle between the planes , then

2x + y + 3z – 2 = 0 and x – 2y + 5 = 0. Let θ be the angle between the planes , then
Direction: Read the following text and answer the following questions on the basis of the same:A cricket match is organized between two Clubs A and B for which a team from each club is chosen. Remaining players of Club A and Club B are respectively sitting on the plane represented by the equation 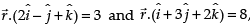 to cheer the team of their own clubs.
to cheer the team of their own clubs. Q. The intercept form of the equation of the plane on which players of Club B are seated is
Q. The intercept form of the equation of the plane on which players of Club B are seated is- a)
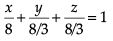
- b)
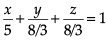
- c)
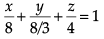
- d)
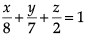
Correct answer is option 'C'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
A cricket match is organized between two Clubs A and B for which a team from each club is chosen. Remaining players of Club A and Club B are respectively sitting on the plane represented by the equation 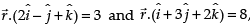 to cheer the team of their own clubs.
to cheer the team of their own clubs.
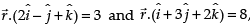 to cheer the team of their own clubs.
to cheer the team of their own clubs.
Q. The intercept form of the equation of the plane on which players of Club B are seated is
a)
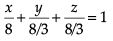
b)
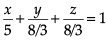
c)
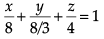
d)
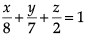
|
|
Hansa Sharma answered |
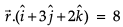
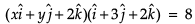
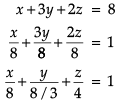
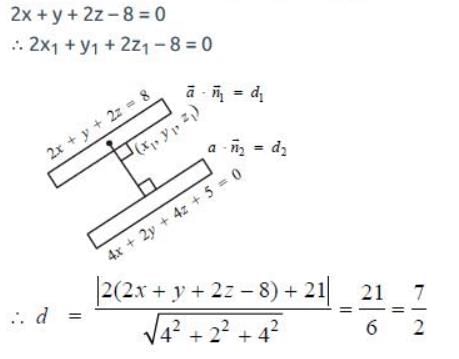
Distance between two parallel planes 2x + y + 2z = 8 and 4x + 2y + 4z + 5 = 0 is- a)3/2
- b)5/2
- c)7/2
- d)9/2
Correct answer is option 'C'. Can you explain this answer?
Distance between two parallel planes 2x + y + 2z = 8 and 4x + 2y + 4z + 5 = 0 is
a)
3/2
b)
5/2
c)
7/2
d)
9/2
|
|
Sanaya Nambiar answered |
Let x1, y1, z1 be any point on the plane

Find the equations of the planes that passes through three points (1, 1, 0), (1, 2, 1), (– 2, 2, – 1)- a)2x + 3y – 7z = 5
- b)2x + 5y – 3z = 5
- c)3x + 3y – 3z = 5
- d)2x + 3y – 3z = 5
Correct answer is option 'D'. Can you explain this answer?
Find the equations of the planes that passes through three points (1, 1, 0), (1, 2, 1), (– 2, 2, – 1)
a)
2x + 3y – 7z = 5
b)
2x + 5y – 3z = 5
c)
3x + 3y – 3z = 5
d)
2x + 3y – 3z = 5

|
Anand Khanna answered |
In cartesian co-ordinate system :
Equation of a plane passing through three non collinear
Equation of a plane passing through three non collinear
Points (x1, y1, z1) , (x2, y2, z2) and (x3, y3, z3) is given by :
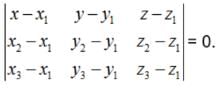
Therefore, the equations of the planes that passes through three points (1,1,0), (1,2,1), (-2,2,-1) is given by :
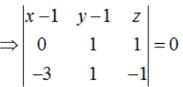
⇒ (x-1)(-2) - (y-1) (3) + 3z = 0
⇒ 2x+3y - 3z = 5
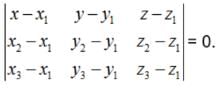
Therefore, the equations of the planes that passes through three points (1,1,0), (1,2,1), (-2,2,-1) is given by :
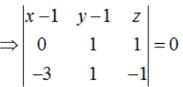
⇒ (x-1)(-2) - (y-1) (3) + 3z = 0
⇒ 2x+3y - 3z = 5
Chapter doubts & questions for Equations of Lines and Planes - Mathematics for Grade 12 2025 is part of Grade 12 exam preparation. The chapters have been prepared according to the Grade 12 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 12 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Equations of Lines and Planes - Mathematics for Grade 12 in English & Hindi are available as part of Grade 12 exam.
Download more important topics, notes, lectures and mock test series for Grade 12 Exam by signing up for free.
Mathematics for Grade 12
99 videos|133 docs|90 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup







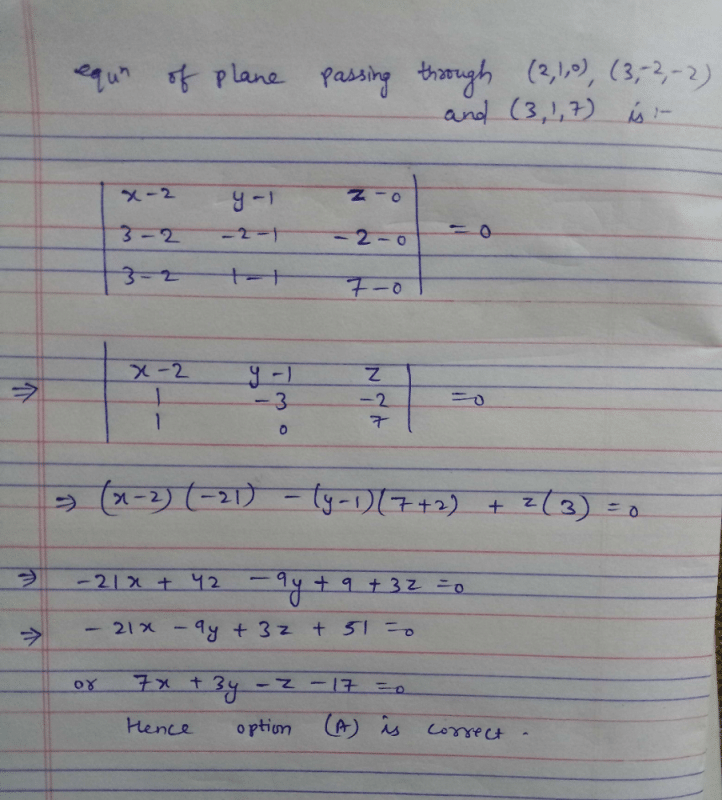


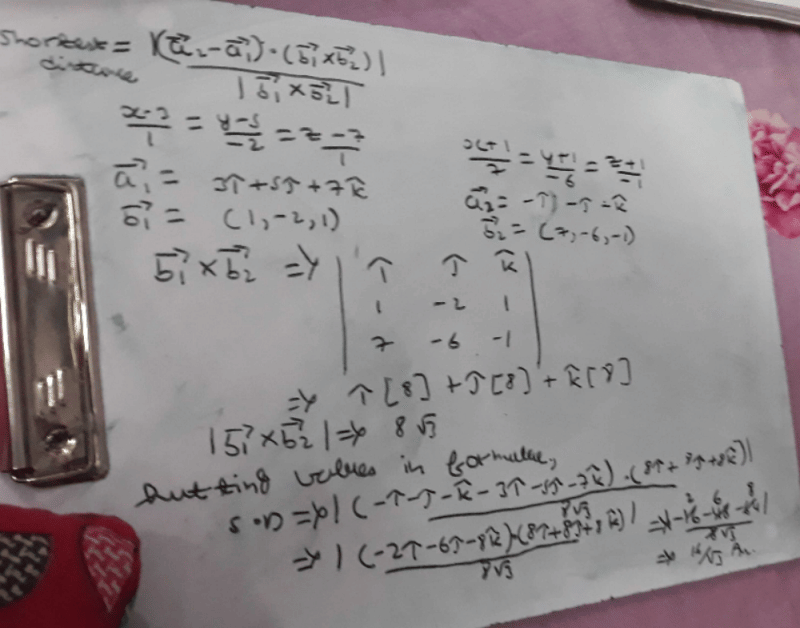

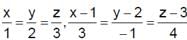 and
and 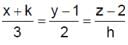 are concurrent then
are concurrent then