All Exams >
GMAT >
Quantitative for GMAT >
All Questions
All questions of Percentages for GMAT Exam
Find the value of y % of x? - x = 5
- x % of y = 2
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question ask
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
Find the value of y % of x?
- x = 5
- x % of y = 2
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question ask
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Gauri Iyer answered |
Statement (1) alone is not sufficient to answer the question asked.
Statement (1) provides the value of x as 5, but there is no information about the value of y. Therefore, we cannot determine the value of y % of x using statement (1) alone.
Statement (2) alone is sufficient to answer the question asked.
Statement (2) provides the value of x % of y as 2. We can use this information to set up an equation:
x % of y = 2
(5/100) * y = 2
y = (2 * 100)/5
y = 40
Therefore, the value of y is 40 when x is 5 and x % of y is 2. Statement (2) alone is sufficient to answer the question asked.
The correct answer is option (B).
Statement (1) provides the value of x as 5, but there is no information about the value of y. Therefore, we cannot determine the value of y % of x using statement (1) alone.
Statement (2) alone is sufficient to answer the question asked.
Statement (2) provides the value of x % of y as 2. We can use this information to set up an equation:
x % of y = 2
(5/100) * y = 2
y = (2 * 100)/5
y = 40
Therefore, the value of y is 40 when x is 5 and x % of y is 2. Statement (2) alone is sufficient to answer the question asked.
The correct answer is option (B).
A toy manufacturer runs his plant for 30 days in a month such that his daily output is constant during the month. He undertakes the maintenance of his plant every 6 months for 5 days in a month, during which period no toys are produced. As he has to undertake the maintenance of the plant this month, he increases his constant daily output of toys by 10 percent compared to the last month’s constant daily output. If the manufacturer wants to keep his monthly revenue unchanged as compared to last month, by approximately what percentage should be increase the price per toy?- a)7%
- b)8%
- c)9%
- d)10%
- e)11%
Correct answer is option 'C'. Can you explain this answer?
A toy manufacturer runs his plant for 30 days in a month such that his daily output is constant during the month. He undertakes the maintenance of his plant every 6 months for 5 days in a month, during which period no toys are produced. As he has to undertake the maintenance of the plant this month, he increases his constant daily output of toys by 10 percent compared to the last month’s constant daily output. If the manufacturer wants to keep his monthly revenue unchanged as compared to last month, by approximately what percentage should be increase the price per toy?
a)
7%
b)
8%
c)
9%
d)
10%
e)
11%
|
|
Aarav Sharma answered |
Given:
Earlier Month
- Total running duration of the plant in the month = 30 days
- Let the daily output during the month = n toys
- Let the total monthly revenue be P
This Month
- Maintenance Period during the month= 5 days
- Total running duration of the plant in the month = 30 - 5 = 25 days
- Let the total monthly revenue be Q
To Find: To keep P = Q, by what percentage should the manufacturer increase the price per toy?
Approach:
- The percentage increase in the selling price needed
- x is the selling price per toy in the Earlier Month
- And, y is the selling price per toy in This Month
- Calculating monthly revenue of the Earlier Month (P)
- Number of toys produced in 1 day = n
- Total number of days = 30
- Therefore, total number of toys produced in the Earlier Month = 30n
- As assumed above, the selling price per toy be x
- Hence, monthly revenue P = (30n) * x = 30nx
- Calculating monthly revenue of This Month(Q)
- Number of toys produced in 1 day = 1.1n
- Total number of days = 25
- Therefore, total number of toys produced This Month = 1.1n*25
- As assumed above, the selling price per toy be y
- Hence, monthly revenue Q = (1.1n * 25) * y = 1.1*25ny
Working out:
- Equating the monthly revenue of both the months, we have
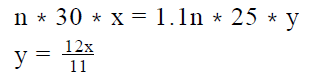
2. So, the percentage increase in the price can be calculated as:
Answer : C
There are 25 students in the class and 60% of them are boys. How many boys are there?
- a)5
- b)10
- c)15
- d)25
- e)50
Correct answer is option 'E'. Can you explain this answer?
There are 25 students in the class and 60% of them are boys. How many boys are there?
a)
5
b)
10
c)
15
d)
25
e)
50
|
|
Aditya Kumar answered |
There are a number of ways to work the math on this.
60% = 60/100 = 3/5
3/5 * 25 or (3 * 25)/5 =
75/5 = 15
So the exact number is 15 boys, but the way the question is worded, it could be a trick question. It says 60% are boys, but does not specify that the other 40% are all not boys. In that case the answer would be:
15 <= number of boys <= 25
During a housing slump, the number of houses for sale increases by 50% every month. What is the percentage increase in the number of houses on sale after 3 months?- a)150%
- b)175%
- c)187.5%
- d)212.5%
- e)237.5%
Correct answer is option 'E'. Can you explain this answer?
During a housing slump, the number of houses for sale increases by 50% every month. What is the percentage increase in the number of houses on sale after 3 months?
a)
150%
b)
175%
c)
187.5%
d)
212.5%
e)
237.5%

|
Future Foundation Institute answered |
Step 1: Question statement and Inferences
We are given that during a housing slump, the number of houses for sale increases by 50% every month.
Let the initial number of houses for sale = x
We need to find the number of houses for sale at the end of 3 months to be able to calculate the required percentage increase.
Step 2: Finding required values
Therefore number of houses for sale at the end of the first month = x + 50 % of x=1.5x
Similarly number of houses for sale at the end of the second month = 1.5×(1.5x)=(1.5)2x
Similarly number of houses for sale at the end of the third month = (1.5)3 x = 3.375x
Step 3: Calculating the final answer
Therefore absolute increase in the number of houses = 3.375x−x=2.375x
Therefore the percentage increase in the number of houses compared to the initial number = 2.375x/x×100=237.5%
Correct Answer: E
What is 1/10 % of 50?- a)0.005
- b)0.05
- c)0.5
- d)5
- e)500
Correct answer is option 'B'. Can you explain this answer?
What is 1/10 % of 50?
a)
0.005
b)
0.05
c)
0.5
d)
5
e)
500
|
|
Yash Patel answered |
⇒ 1/10 % of 50
= 1/10 x 1/100 x 50
= 0.05
A soccer team played 25% more matches year-on-year in the second year of its formation. It won 84% of the matches it played in the second year, which was an improvement of 5% over the percentage of matches won in the first year. In the third year, the team played 4% fewer matches year-on-year but lost only 12.5% of the matches it played, which was one less than the number of matches lost by the team in the second year. Which of the following statements must be correct? - The team lost the same number of matches in the first yea and the second year
- The team won the same number of matches in the second year and the third year
- The team played five more matches in the third year than the first year
- a)I only
- b)II only
- c)III only
- d)I, II and III
- e)None of the above
Correct answer is option 'E'. Can you explain this answer?
A soccer team played 25% more matches year-on-year in the second year of its formation. It won 84% of the matches it played in the second year, which was an improvement of 5% over the percentage of matches won in the first year. In the third year, the team played 4% fewer matches year-on-year but lost only 12.5% of the matches it played, which was one less than the number of matches lost by the team in the second year. Which of the following statements must be correct?
- The team lost the same number of matches in the first yea and the second year
- The team won the same number of matches in the second year and the third year
- The team played five more matches in the third year than the first year
a)
I only
b)
II only
c)
III only
d)
I, II and III
e)
None of the above

|
Ameya Yadav answered |
Given:
- So, in Year 1, the number of matches won = 80% of (Number of matches played in Year 1)
- Number of matches played in Year 3 = 4% less than the number of matches played in Year 2
To Find: Which of the 3 statements are correct?
Approach:
- In order to answer the question, we need to know the values (either the exact values or the values in terms of X) for the number of matches Played, Won and Lost in all the 3 years.
- To make sense of the given information, we’ll represent it visually and then work towards calculating the values that we do not yet know.
Working out:
- Representing the given information visually
- We can represent the given (and inferred) information discussed above in a table as under:
- As we see, there are currently 3 unknown values in the table above.
- Finding the unknown values
- Number of matches Lost in Year 1 = (Total matches played in Year
- Number of matches Lost in Year 2 = (Total matches played in Year
- Number of matches Won in Year 3 = (Total matches played in Year
- So, the complete table will look as under:
- So, after substituting X = 20, the values in the table will look as under:
- Evaluating the 3 statements
- St-I: The team lost the same number of matches in the first year and the second year
- Statement I is correct
- St-II: The team won the same number of matches in the second year and the third year
- St-I: The team lost the same number of matches in the first year and the second year
- Statement II is also correct
- St-III: The team played five more matches in the third year than the first year
- Statement III is not correct because the team played four more matches in Year 3 than Year 1, not five more matches
- St-III: The team played five more matches in the third year than the first year
Looking at the answer choices, we see that the correct answer is Option E
In a competitive examination in State A, 6% candidates got selected from the total appeared candidates. State B had an equal number of candidates appeared and 7% candidates got selected with 80 more candidates got selected than A. What was the number of candidates appeared from each State?- a)8200
- b)7500
- c)7000
- d)8000
- e)8500
Correct answer is option 'D'. Can you explain this answer?
In a competitive examination in State A, 6% candidates got selected from the total appeared candidates. State B had an equal number of candidates appeared and 7% candidates got selected with 80 more candidates got selected than A. What was the number of candidates appeared from each State?
a)
8200
b)
7500
c)
7000
d)
8000
e)
8500

|
Devika Yadav answered |
State A and State B had an equal number of candidates appeared.
In state A, 6% candidates got selected from the total appeared candidates
In state B, 7% candidates got selected from the total appeared candidates
But in State B, 80 more candidates got selected than State A
From these, it is clear that 1% of the total appeared candidates in State B = 80
=> total appeared candidates in State B = 80 x 100 = 8000
=> total appeared candidates in State A = total appeared candidates in State B = 8000
In state A, 6% candidates got selected from the total appeared candidates
In state B, 7% candidates got selected from the total appeared candidates
But in State B, 80 more candidates got selected than State A
From these, it is clear that 1% of the total appeared candidates in State B = 80
=> total appeared candidates in State B = 80 x 100 = 8000
=> total appeared candidates in State A = total appeared candidates in State B = 8000
Tom’s salary has increased by 10% to $11,000. Mike’s salary has reduced by 5%. What is Mike’s current salary if his old salary was two times Tom’s old salary?- a)$18,000
- b)$19,000
- c)$20,000
- d)$21,000
- e)$22,000
Correct answer is option 'B'. Can you explain this answer?
Tom’s salary has increased by 10% to $11,000. Mike’s salary has reduced by 5%. What is Mike’s current salary if his old salary was two times Tom’s old salary?
a)
$18,000
b)
$19,000
c)
$20,000
d)
$21,000
e)
$22,000

|
Saumya Sharma answered |
Step 1: Question statement and Inferences
We are given that the salary of Tom has increased by 10%, and now it has become $11,000, whereas the salary of Mike has decreased by 5%.
It is also given that the old salary of Mike was twice that of Tom's old salary.
Let Tom’s old salary = TO
Let Mike’s old salary = MO and Mike’s new salary = MN
We need to find the value of MN
Step 2: Finding required values
TO + 10% of TO = 11000
⇒ 1.1* TO = 11000
⇒ TO = 10000
Therefore Tom’s old salary = $10,000
It is also given that Mike’s old salary is twice Tom’s old salary.
⇒ MO = 2 * TO = 20000
Mike’s current salary is 5% less than his old salary.
MN = MO – 5% of MO
⇒ MN = 0.95*MO
⇒ MN = 0.95 * 20000 = 19000
Step 3: Calculating final answer
Therefore Mike’s current salary = $19,000
Correct Answer: B
A company had 1000 employees at the beginning of the year 2011. If p percent of the employees present at the beginning of the year left the company during the year and the number of employees at the end of the year was r percent greater than the number of employees at the beginning of the year, how many employees joined the company during the year 2011?(1) p + r = 30
(2) Had the number of employees leaving the company been r percent of the employees at the beginning of the year and the number of employees at the end of the year been p percent greater than the number of employees at the beginning of the year, the number of employees who joined the company would have remained the same.- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
A company had 1000 employees at the beginning of the year 2011. If p percent of the employees present at the beginning of the year left the company during the year and the number of employees at the end of the year was r percent greater than the number of employees at the beginning of the year, how many employees joined the company during the year 2011?
(1) p + r = 30
(2) Had the number of employees leaving the company been r percent of the employees at the beginning of the year and the number of employees at the end of the year been p percent greater than the number of employees at the beginning of the year, the number of employees who joined the company would have remained the same.
(2) Had the number of employees leaving the company been r percent of the employees at the beginning of the year and the number of employees at the end of the year been p percent greater than the number of employees at the beginning of the year, the number of employees who joined the company would have remained the same.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed.
answer the question asked, and additional data specific to the problem are needed.

|
Saumya Shah answered |
Understanding the Problem
To determine how many employees joined the company in 2011, we start with the following information:
- Initial employees: 1000
- Employees who left: p% of 1000
- Employees at the end of the year: 1000 + (r% of 1000)
Let's denote:
- Number of employees who left: (p/100) * 1000 = 10p
- Employees at the end of the year: 1000 + (r/100) * 1000 = 1000 + 10r
The number of employees who joined the company can be calculated as:
Employees Joined = Employees at the end - Employees at the beginning + Employees who left.
This leads to the equation:
Employees Joined = (1000 + 10r) - 1000 + 10p = 10r + 10p
Analyzing Statement (1)
- From Statement (1), we have p + r = 30.
- We can express r as (30 - p).
- Substituting this back into our equation for Employees Joined gives us:
Employees Joined = 10(30) = 300.
This statement alone is sufficient to determine the number of employees who joined.
Analyzing Statement (2)
- Statement (2) provides a condition about leaving and joining percentages.
- Although it gives a relationship, it does not provide specific values for p or r.
- Therefore, we cannot uniquely determine how many employees joined based solely on this statement.
Conclusion
- Statement (1) alone gives a clear answer regarding the number of employees who joined.
- Statement (2) lacks specific values and cannot answer the question on its own.
Thus, the correct answer is option 'A': Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
To determine how many employees joined the company in 2011, we start with the following information:
- Initial employees: 1000
- Employees who left: p% of 1000
- Employees at the end of the year: 1000 + (r% of 1000)
Let's denote:
- Number of employees who left: (p/100) * 1000 = 10p
- Employees at the end of the year: 1000 + (r/100) * 1000 = 1000 + 10r
The number of employees who joined the company can be calculated as:
Employees Joined = Employees at the end - Employees at the beginning + Employees who left.
This leads to the equation:
Employees Joined = (1000 + 10r) - 1000 + 10p = 10r + 10p
Analyzing Statement (1)
- From Statement (1), we have p + r = 30.
- We can express r as (30 - p).
- Substituting this back into our equation for Employees Joined gives us:
Employees Joined = 10(30) = 300.
This statement alone is sufficient to determine the number of employees who joined.
Analyzing Statement (2)
- Statement (2) provides a condition about leaving and joining percentages.
- Although it gives a relationship, it does not provide specific values for p or r.
- Therefore, we cannot uniquely determine how many employees joined based solely on this statement.
Conclusion
- Statement (1) alone gives a clear answer regarding the number of employees who joined.
- Statement (2) lacks specific values and cannot answer the question on its own.
Thus, the correct answer is option 'A': Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
Which of the following statements are true?I. If a positive number X is increased by 20% the resulting number would be 1.2XII.If a positive number X is decreased by 20 % the resulting number would be 0.8XIII.32% of 24 is less than 24% of 32.- a)I only
- b)II only
- c)III only
- d)I and II only
- e)I, II, and III
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements are true?
I. If a positive number X is increased by 20% the resulting number would be 1.2X
II.If a positive number X is decreased by 20 % the resulting number would be 0.8X
III.32% of 24 is less than 24% of 32.
a)
I only
b)
II only
c)
III only
d)
I and II only
e)
I, II, and III

|
Sharmila Singh answered |
Solution:
I. If a positive number X is increased by 20%, the resulting number would be 1.2X.
This statement is true. When a positive number is increased by a percentage, we multiply the original number by the decimal equivalent of that percentage and add it to the original number. In this case, increasing X by 20% means adding 0.2X to X, which gives us 1.2X.
II. If a positive number X is decreased by 20%, the resulting number would be 0.8X.
This statement is also true. When a positive number is decreased by a percentage, we multiply the original number by the decimal equivalent of that percentage and subtract it from the original number. In this case, decreasing X by 20% means subtracting 0.2X from X, which gives us 0.8X.
III. 32% of 24 is less than 24% of 32.
This statement is true. To compare 32% of 24 and 24% of 32, we can calculate both and compare the results.
32% of 24 = (32/100) * 24 = 7.68
24% of 32 = (24/100) * 32 = 7.68
Both values are equal. However, the question asks whether 32% of 24 is less than 24% of 32. Since both values are equal, the statement is false.
Therefore, the correct answer is option D, I and II only.
I. If a positive number X is increased by 20%, the resulting number would be 1.2X.
This statement is true. When a positive number is increased by a percentage, we multiply the original number by the decimal equivalent of that percentage and add it to the original number. In this case, increasing X by 20% means adding 0.2X to X, which gives us 1.2X.
II. If a positive number X is decreased by 20%, the resulting number would be 0.8X.
This statement is also true. When a positive number is decreased by a percentage, we multiply the original number by the decimal equivalent of that percentage and subtract it from the original number. In this case, decreasing X by 20% means subtracting 0.2X from X, which gives us 0.8X.
III. 32% of 24 is less than 24% of 32.
This statement is true. To compare 32% of 24 and 24% of 32, we can calculate both and compare the results.
32% of 24 = (32/100) * 24 = 7.68
24% of 32 = (24/100) * 32 = 7.68
Both values are equal. However, the question asks whether 32% of 24 is less than 24% of 32. Since both values are equal, the statement is false.
Therefore, the correct answer is option D, I and II only.
If b is a prime number, what percent of 3 is b?
(1) b is more than 200% greater than 2 and less than 40% of 32 (2) 3b/7 is 40% less than 5- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
If b is a prime number, what percent of 3 is b?
(1) b is more than 200% greater than 2 and less than 40% of 32
(1) b is more than 200% greater than 2 and less than 40% of 32
(2) 3b/7 is 40% less than 5
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed.
answer the question asked, and additional data specific to the problem are needed.

|
Yash Rane answered |
Step 1 & 2: Understand Question and Draw Inference
Given: Prime number b
To find: What percent of 3 is b?
Let b be x percent of 3
To find: What percent of 3 is b?
Let b be x percent of 3
Therefore, in order to find the value of x, we need to find the value of b
Step 3 : Analyze Statement 1 independent
Statement 1 says that ‘b is more than 200% greater than 2 and less than 40% of 32’
- Therefore, as per Statement 1, b is a prime number that lies between 6 and 12.8, exclusive
- So, possible values of b = {7, 11}
- Since Statement 1 doesn’t lead to a unique value of b, it is not sufficient
Step 4 : Analyze Statement 2 independent
Statement 2 says that ‘ 3b/7 is 40% less than 5'
So, b = 7
Since Statement 2 leads to a unique value of b, it is sufficient to answer the question
Since Statement 2 leads to a unique value of b, it is sufficient to answer the question
Step 5: Analyze Both Statements Together (if needed)
Since we get a unique answer in Step 4, this step is not required
Answer: Option B
Answer: Option B
Five friends Adi, Brian, Close, Derek and Eli appeared in two aptitude tests. In the first aptitude test, Derek’s score was 50 percent less than the average (arithmetic mean) score of the five people. In the second aptitude test, Derek scored 50 percent more than what he scored on the first aptitude test. If the scores of his friends in the second aptitude test were same as their scores in the first aptitude test, by approximately what percentage was Derek’s score less than the average (arithmetic mean) score of the 5 people in the second aptitude test?- a)25%
- b)28%
- c)33%
- d)40%
- e)50%
Correct answer is option 'B'. Can you explain this answer?
Five friends Adi, Brian, Close, Derek and Eli appeared in two aptitude tests. In the first aptitude test, Derek’s score was 50 percent less than the average (arithmetic mean) score of the five people. In the second aptitude test, Derek scored 50 percent more than what he scored on the first aptitude test. If the scores of his friends in the second aptitude test were same as their scores in the first aptitude test, by approximately what percentage was Derek’s score less than the average (arithmetic mean) score of the 5 people in the second aptitude test?
a)
25%
b)
28%
c)
33%
d)
40%
e)
50%

|
Mihir Ghoshal answered |
Given:
- 1st Aptitude Test
- Let the scores of Adi, Brian, Close, Derek and Eli be a, b, c, d and e respectively
- Let the average score be x
- d = x – 50% of x = 0.5x
- 2nd Aptitude Test
- Adi, Brian, Close and Eli scored a, b, c and e respectively
- Derek’s score = d + 50% of d = 1.5d
- Let the average score be y
To Find: By approximately what percentage was Derek’s score less than the average (arithmetic mean) score of the 5 people in the second aptitude test?
Approach:
We can see from the expression above that if we could express y or d in terms of a common variable, we will be able to calculate our answer
- Expression of y: As y is the average score of the 2 aptitude test, we can express y in terms of a, b, c, d and e.
- Expression of x: Also, in the 1 aptitude test, as x is the average score, we can express x in terms of a, b, c, d, and e.
- Using (2) and (3), we can express y in terms of x and d( We cannot express y solely in terms of x, because in, the coefficient of d is different to the coefficient of d in x.)
- Expression of d : Using the relation “Derek’s score was 50 percent less than the average (arithmetic mean) score of the five people “ in the 1 aptitude test, we can also express d in terms of x.
- Using (2.a) and (3), we can express y in terms of x only.
- As in (3), we have already expressed d in terms of x only, we have achieved our objective of expressing y and d in terms of a common variable i.e. x, which will give us the answer
Working out:
- Expression of y: Average score in the 2nd aptitude test
- Expression of x: Average score in the 1st aptitude test
- Using (1) and (2), we can
- Expression of d: As “Derek’s score was 50 percent less than the average (arithmetic mean) score of the five people” in the 1 aptitude test, we can write d = 0.5x
Answer B
if A = x% of y and B = y% of x, then which of the following is true?- a)A is smaller than B.
- b)A is greater than B
- c)Relationship between A and B cannot be determined.
- d)If x is smaller than y, then A is greater than B.
- e)None of these
Correct answer is option 'E'. Can you explain this answer?
if A = x% of y and B = y% of x, then which of the following is true?
a)
A is smaller than B.
b)
A is greater than B
c)
Relationship between A and B cannot be determined.
d)
If x is smaller than y, then A is greater than B.
e)
None of these

|
Soumya Iyer answered |

Restaurant A and Restaurant B decides to roll out a new plan which they believe will get them new customers. Restaurant A decides to give a 10% discount on the original bill amount, and then applies 15% tax on the discounted bill. Restaurant B, on the other hand applies a 15% tax on the original bill amount and then gives a 10% discount on the taxed bill.If the original bill amount is same for both restaurants, which of the following must be true?- a)Restaurant A will be 5% cheaper than Restaurant B
- b)Restaurant B will be 5% cheaper than Restaurant A
- c)Restaurant A will be 10% cheaper than Restaurant B
- d)Restaurant B will be 10% cheaper than Restaurant A
- e)Both Restaurants will charge an equal final bill.
Correct answer is option 'E'. Can you explain this answer?
Restaurant A and Restaurant B decides to roll out a new plan which they believe will get them new customers. Restaurant A decides to give a 10% discount on the original bill amount, and then applies 15% tax on the discounted bill. Restaurant B, on the other hand applies a 15% tax on the original bill amount and then gives a 10% discount on the taxed bill.
If the original bill amount is same for both restaurants, which of the following must be true?
a)
Restaurant A will be 5% cheaper than Restaurant B
b)
Restaurant B will be 5% cheaper than Restaurant A
c)
Restaurant A will be 10% cheaper than Restaurant B
d)
Restaurant B will be 10% cheaper than Restaurant A
e)
Both Restaurants will charge an equal final bill.

|
Mihir Ghoshal answered |
Let X be the original bill amount for both the restaurants.
Restaurant A:
- Original bill amount = X
A 10% discount is given on the original bill amount.
i.e.
On this discounted price a 15% tax is applied.
i.e.
Therefore, the final bill amount in Restaurant A is 0.9X (1.15)
Restaurant B:
- Original bill amount = X
A 15% tax is applied on the original bill amount.
i.e.
On this taxed bill, a 10% discount is applied.
i.e.
Therefore, the final bill amount in Restaurant B is 1.15X (0.9)
Comparing the final bills at both Restaurant A and Restaurant B, we see that
Both Restaurants will charge an equal final bill.
Correct Answer: Option E
Abe and Beth both start from a common point and travel in different directions towards their respective destinations. Abe’s
average speed is 25% greater than Beth’s average speed but Abe needs to cover 50% greater distance than Beth. Which of the
following is closest to the percentage by which the travel time of Beth lesser than that of Abe?- a)17%
- b)20%
- c)25%
- d)40%
- e)60%
Correct answer is option 'A'. Can you explain this answer?
Abe and Beth both start from a common point and travel in different directions towards their respective destinations. Abe’s
average speed is 25% greater than Beth’s average speed but Abe needs to cover 50% greater distance than Beth. Which of the
following is closest to the percentage by which the travel time of Beth lesser than that of Abe?
average speed is 25% greater than Beth’s average speed but Abe needs to cover 50% greater distance than Beth. Which of the
following is closest to the percentage by which the travel time of Beth lesser than that of Abe?
a)
17%
b)
20%
c)
25%
d)
40%
e)
60%

|
Anirban Das answered |
Given:
- Let Abe’s Average Speed, Distance covered and Time taken be S , D and T respectively
- Let Beth’s Average Speed, Distance covered and Time taken be S , D and T respectively
To Find: approx. % by which TB is lesser than
Approach:
- % by which T is lesser than
- So, to answer the question, we need to find:
- Either the values of TA and TB
- Or TA in terms of TB
- Using the given relations between S and S , and between DA and DB , we’ll express T in terms of T and hence, answer the question
Working out:
- So, % by which TA is lesser than TB =
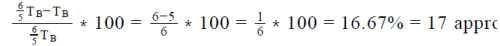
Looking at the answer choices, we see that Option A is correct
An airline allowed free baggage only up to 20 kilograms of weight. Each extra kilogram of weight cost a passenger $5 per kilogram. Of the total weight of the baggage that Roger was carrying, 60 percent of the weight was more than the free baggage allowance. If the total ticket cost of Roger including the excess baggage fare was $600, by what percentage did his ticket cost increase because of the excess baggage that he was carrying?- a)20%
- b)25%
- c)33%
- d)40%
- e)45%
Correct answer is option 'C'. Can you explain this answer?
An airline allowed free baggage only up to 20 kilograms of weight. Each extra kilogram of weight cost a passenger $5 per kilogram. Of the total weight of the baggage that Roger was carrying, 60 percent of the weight was more than the free baggage allowance. If the total ticket cost of Roger including the excess baggage fare was $600, by what percentage did his ticket cost increase because of the excess baggage that he was carrying?
a)
20%
b)
25%
c)
33%
d)
40%
e)
45%

|
Maya Khanna answered |
Given information:
- Free baggage allowance: 20 kilograms
- Cost for each extra kilogram: $5
- Total ticket cost including excess baggage fare: $600
- 60% of the total weight carried by Roger was more than the free baggage allowance
To find: The percentage increase in Roger's ticket cost due to excess baggage
Let's assume the total weight of Roger's baggage as 'x' kilograms. Since 60% of the weight is more than the free baggage allowance, the weight of the excess baggage can be calculated as 0.6x kilograms.
Cost calculation:
- The cost for the free baggage allowance of 20 kilograms is $0, as it is within the limit.
- The cost for the excess baggage can be calculated as the product of the excess weight and the cost per kilogram: 0.6x * $5 = $3x.
The total ticket cost, including the excess baggage fare, is given as $600. So we can write the equation as:
$0 + $3x = $600
Solving the equation:
$3x = $600
Dividing both sides by 3:
x = $200
Therefore, the total weight of Roger's baggage is 200 kilograms.
Percentage increase calculation:
- The cost for the excess baggage is $3x, which in this case is $3 * 200 = $600.
- The original ticket cost without excess baggage is $600 - $600 = $0.
- The percentage increase in the ticket cost due to excess baggage can be calculated as (excess baggage cost / original ticket cost) * 100%:
(600 / 0) * 100% = undefined
However, since the original ticket cost is $0, we cannot calculate the percentage increase.
Hence, it seems there is an error in the question or the given information. The correct answer cannot be determined with the provided details.
- Free baggage allowance: 20 kilograms
- Cost for each extra kilogram: $5
- Total ticket cost including excess baggage fare: $600
- 60% of the total weight carried by Roger was more than the free baggage allowance
To find: The percentage increase in Roger's ticket cost due to excess baggage
Let's assume the total weight of Roger's baggage as 'x' kilograms. Since 60% of the weight is more than the free baggage allowance, the weight of the excess baggage can be calculated as 0.6x kilograms.
Cost calculation:
- The cost for the free baggage allowance of 20 kilograms is $0, as it is within the limit.
- The cost for the excess baggage can be calculated as the product of the excess weight and the cost per kilogram: 0.6x * $5 = $3x.
The total ticket cost, including the excess baggage fare, is given as $600. So we can write the equation as:
$0 + $3x = $600
Solving the equation:
$3x = $600
Dividing both sides by 3:
x = $200
Therefore, the total weight of Roger's baggage is 200 kilograms.
Percentage increase calculation:
- The cost for the excess baggage is $3x, which in this case is $3 * 200 = $600.
- The original ticket cost without excess baggage is $600 - $600 = $0.
- The percentage increase in the ticket cost due to excess baggage can be calculated as (excess baggage cost / original ticket cost) * 100%:
(600 / 0) * 100% = undefined
However, since the original ticket cost is $0, we cannot calculate the percentage increase.
Hence, it seems there is an error in the question or the given information. The correct answer cannot be determined with the provided details.
An army’s recruitment process included n rounds of selection tasks. For the first a rounds, the rejection percentage was 60 percent per round. For the next b rounds, the rejection percentage was 50 percent per round and for the remaining rounds, the selection percentage was 70 percent per round. If there were 100000 people who applied for the army and 1400 were finally selected, what was the value of n?- a)4
- b)5
- c)6
- d)8
- e)10
Correct answer is option 'C'. Can you explain this answer?
An army’s recruitment process included n rounds of selection tasks. For the first a rounds, the rejection percentage was 60 percent per round. For the next b rounds, the rejection percentage was 50 percent per round and for the remaining rounds, the selection percentage was 70 percent per round. If there were 100000 people who applied for the army and 1400 were finally selected, what was the value of n?
a)
4
b)
5
c)
6
d)
8
e)
10

|
Athul Joshi answered |
Given:
- Total number of applicants = 100000
- Total people selected = 1400
- Total number of rounds = n
- Rejection percentage of each round for the first a rounds = 60%
- Selection percentage of each round for the first n rounds = 40%
- Rejection percentage of each round for the next b rounds = 50%
- Selection percentage of each round for the next b rounds = 50%
- Selection percentage of each round for the remaining rounds(let’s say c rounds) = 70%
To Find: Value of n?
- n = a + b + c
- So, we need to find the values of either all of a, b or c or the value of sum of a , b and c.
Approach:
- As we know the number of applicants, the selection percentage of each round and the number of people finally selected, we would need to devise an expression for people finally selected in terms of a, b and c.
- So, number of people who cleared the 1st round = Total number of applicants x selection percentage of first round
- Similarly, people who cleared the first 2 rounds = Total number of applicants x selection percentage of first
round x selection percentage of second round - So, people who cleared the first a rounds = Total number of applicants x selection percentage of first round x selection percentage of second round x ...selection percentage of a round
- As the selection percentage of each of the first a rounds is the same, we can write, people who cleared the first a rounds = Total number of applicants x (selection percentage of each round till the a rounds)a
- Similarly, people who cleared the first 2 rounds = Total number of applicants x selection percentage of first
- Similarly, number of people who cleared the next b rounds as well= Total number of applicants x (selection percentage of each round till a rounds)a x selection percentage of each round till the next b rounds)b
- So, number of people who cleared the last c rounds as well= Total number of applicants x (selection percentage of each round till a rounds)a x (selection percentage of each round till next b rounds)b x (selection percentage of each round till the last c rounds)c
- (People who were finally selected) = (people who cleared all the rounds).
- Now, we will prime factorize the expression on both the sides and equate the exponents of the individual prime factors to find the values of a, b and c.
Working out:
1. Total number of applicants = 100000
2. Number of people who were selected = (Number of people who cleared all the rounds). So, we can write
3. Comparing the powers of each prime factor on the two sides of the above equation:
- Comparing powers of 7, we have c = 1
- Comparing powers of 5, we have 5 – a –c = 2. As c = 1, we have a = 2
- Comparing powers of 2, we have 5 + a – b – c = 3.
- As c = 1 and a = 2, we have b = 3
4. So, n = a+ b+ c = 2 + 3+1 = 6
Answer: C
Jack made a withdrawal from his savings account to fund a medical emergency. What was the percent decrease in his savings fund, if his savings fund post withdrawal will need to be increased by 25 percent to be restored to its initial amount?- a)10%
- b)20%
- c)25%
- d)40%
- e)50%
Correct answer is option 'B'. Can you explain this answer?
Jack made a withdrawal from his savings account to fund a medical emergency. What was the percent decrease in his savings fund, if his savings fund post withdrawal will need to be increased by 25 percent to be restored to its initial amount?
a)
10%
b)
20%
c)
25%
d)
40%
e)
50%

|
Abhishek Kapoor answered |
Step 1: Question statement and Inferences
Let the withdrawal from the fund be p%
Let the initial amount be X
Balance after withdrawal = B = X -p% of X
Step 2: Finding required values
We are also given that B needs to be increased by 25% to bring it back to X.
Step 3: Calculating the final answer
Substitute Equation (1) in Equation (2):
5(100−p)=400500–5p=4005p=100p=20%
Thus, the withdrawal from the fund was 20%
Answer: Option (B)
Last year country X won 15 gold medals in total 60 competitions. This year country X won only 5 gold medals in a total of 50 competitions. What is the percentage reduction in the percentage of gold medals won per competition this year vs last year?- a)15%
- b)40%
- c)60%
- d)80%
- e)100%
Correct answer is option 'C'. Can you explain this answer?
Last year country X won 15 gold medals in total 60 competitions. This year country X won only 5 gold medals in a total of 50 competitions. What is the percentage reduction in the percentage of gold medals won per competition this year vs last year?
a)
15%
b)
40%
c)
60%
d)
80%
e)
100%

|
Pranav Das answered |
Introduction:
The question asks us to calculate the percentage reduction in the percentage of gold medals won per competition this year compared to last year for country X.
Step 1: Calculate the percentage of gold medals won per competition last year:
To find the percentage of gold medals won per competition last year, we need to divide the total number of gold medals won by country X by the total number of competitions and then multiply by 100.
Total gold medals won last year = 15
Total competitions last year = 60
Percentage of gold medals won per competition last year = (15/60) * 100 = 25%
Step 2: Calculate the percentage of gold medals won per competition this year:
Similarly, we need to divide the total number of gold medals won this year by country X by the total number of competitions this year and multiply by 100.
Total gold medals won this year = 5
Total competitions this year = 50
Percentage of gold medals won per competition this year = (5/50) * 100 = 10%
Step 3: Calculate the percentage reduction:
To find the percentage reduction, we need to calculate the difference between the two percentages and divide it by the percentage of gold medals won per competition last year. Then multiply by 100 to get the percentage.
Percentage reduction = [(25% - 10%) / 25%] * 100 = 15/25 * 100 = 60%
Conclusion:
The percentage reduction in the percentage of gold medals won per competition this year compared to last year for country X is 60%. Therefore, the correct answer is option C.
The question asks us to calculate the percentage reduction in the percentage of gold medals won per competition this year compared to last year for country X.
Step 1: Calculate the percentage of gold medals won per competition last year:
To find the percentage of gold medals won per competition last year, we need to divide the total number of gold medals won by country X by the total number of competitions and then multiply by 100.
Total gold medals won last year = 15
Total competitions last year = 60
Percentage of gold medals won per competition last year = (15/60) * 100 = 25%
Step 2: Calculate the percentage of gold medals won per competition this year:
Similarly, we need to divide the total number of gold medals won this year by country X by the total number of competitions this year and multiply by 100.
Total gold medals won this year = 5
Total competitions this year = 50
Percentage of gold medals won per competition this year = (5/50) * 100 = 10%
Step 3: Calculate the percentage reduction:
To find the percentage reduction, we need to calculate the difference between the two percentages and divide it by the percentage of gold medals won per competition last year. Then multiply by 100 to get the percentage.
Percentage reduction = [(25% - 10%) / 25%] * 100 = 15/25 * 100 = 60%
Conclusion:
The percentage reduction in the percentage of gold medals won per competition this year compared to last year for country X is 60%. Therefore, the correct answer is option C.
In a class of 100 students, the percentage of boys in the class is equal to the percentage of students who pass in a test. If 2 out of
every 3 girls in the class pass the test and the number of boys who do not pass the test is 10 less than the total number of girls in the
class, which of the following is the closest to the percentage of boys who passed the test?- a)40%
- b)50%
- c)60%
- d)70%
- e)80%
Correct answer is option 'D'. Can you explain this answer?
In a class of 100 students, the percentage of boys in the class is equal to the percentage of students who pass in a test. If 2 out of
every 3 girls in the class pass the test and the number of boys who do not pass the test is 10 less than the total number of girls in the
class, which of the following is the closest to the percentage of boys who passed the test?
every 3 girls in the class pass the test and the number of boys who do not pass the test is 10 less than the total number of girls in the
class, which of the following is the closest to the percentage of boys who passed the test?
a)
40%
b)
50%
c)
60%
d)
70%
e)
80%

|
Anirban Das answered |
Given:
- Total students = 100
- Let the number of boys be B
- So, the number of girls = 100 – B
- Let the number of boys be B
- So, number of students who pass = B
- The number of students who don’t pass = 100 – B
To Find: The approximate % of boys who pass the test
Approach:
-
- So, to answer the question, we’ll need:
- Either the values of ‘Number of boys who pass’ and B
- Or the ratio of ‘Number of boys who pass’ and B
- We’re given information about the 100 students on 2 parameters –
- Gender (Boy, Girl)
- Test Performance (Pass, Don’t Pass)
- So, to be able to work with the information effectively, we will represent the information visually.
- Then, we’ll work towards finding the required values.
Working out:
Representing the given information visually
- Working towards the required values
- As a first step, let’s complete the empty cells in the above table:
- Girls who don’t pass = (Total number of girls) – (Girls who pass)
- As a first step, let’s complete the empty cells in the above table:
- Boys who Pass = (Total number of boys) – (Boys who don’t pass)
- = B – (90 – B) = 2B – 90
- From the above table, we can draft the following linear equation in terms of B:
- (Girls who pass) + (Boys who pass) = Total number of students who pass
- And, Number of boys who pass = 2B - 90 = 2*70 – 90 = 140 – 90 = 50
- So, the Required percentage =
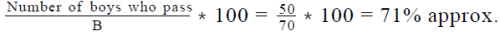
Looking at the answer choices, we see that the option that is closest to the required percentage is Option D
Two employees X and Y are paid a total of Rs. 550 per week by their employer. If X is paid 120 percent of the sum paid to Y, how much is Y paid per week?- a)Rs. 150
- b)Rs. 300
- c)Rs. 250
- d)Rs. 200
- e)Rs. 275
Correct answer is option 'C'. Can you explain this answer?
Two employees X and Y are paid a total of Rs. 550 per week by their employer. If X is paid 120 percent of the sum paid to Y, how much is Y paid per week?
a)
Rs. 150
b)
Rs. 300
c)
Rs. 250
d)
Rs. 200
e)
Rs. 275

|
Amar Chakraborty answered |
Let the amount paid to X per week = x
and the amount paid to Y per week = y
Then x + y = 550
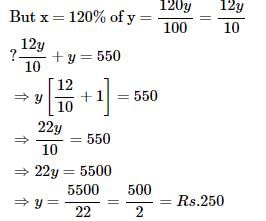
and the amount paid to Y per week = y
Then x + y = 550
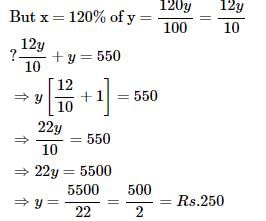
The temperature of a place at noon on a certain day is 25% higher than the temperature of the same place at midnight on the same
day. What the temperature of the place at midnight?
(1) The temperature of the place at midnight is 20% lower than the temperature of the same place at noon
(2) The temperature of the place at noon is 10 units greater than the temperature of the place at midnight- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'B'. Can you explain this answer?
The temperature of a place at noon on a certain day is 25% higher than the temperature of the same place at midnight on the same
day. What the temperature of the place at midnight?
(1) The temperature of the place at midnight is 20% lower than the temperature of the same place at noon
(2) The temperature of the place at noon is 10 units greater than the temperature of the place at midnight
day. What the temperature of the place at midnight?
(1) The temperature of the place at midnight is 20% lower than the temperature of the same place at noon
(2) The temperature of the place at noon is 10 units greater than the temperature of the place at midnight
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked
not sufficient to answer the question asked
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Devansh Shah answered |
Step 1 & 2: Understand Question and Draw Inference
Let temperature at midnight be M
And, temperature at noon be N
Given:
And, temperature at noon be N
Given:
We need to find the value of M.
We already have 1 equation between N and M. If we have one more equation between N and M, we can find a unique value of M.
We already have 1 equation between N and M. If we have one more equation between N and M, we can find a unique value of M.
Step 3 : Analyze Statement 1 independent
This equation restates what we already know from Equation (I). So, not sufficient.
Step 4 : Analyze Statement 2 independent
Statement 2 says that
N = M + 10 . . . (II)
We now have one more equation between N and M. So, Equations (I) and (II) are sufficient to find a unique value of M.
N = M + 10 . . . (II)
We now have one more equation between N and M. So, Equations (I) and (II) are sufficient to find a unique value of M.
Step 5: Analyze Both Statements Together (if needed)
Since we arrive at a unique answer in Step 4, this step is not required
Answer: B
Answer: B
A positive number Y is first increased by 10% then decreased by 50% and then increased by 100%. The series of successive changes to Y is equivalent to a single change of- a)20% decrease
- b)10% decrease
- c)10% increase
- d)20% increase
- e)No change
Correct answer is option 'C'. Can you explain this answer?
A positive number Y is first increased by 10% then decreased by 50% and then increased by 100%. The series of successive changes to Y is equivalent to a single change of
a)
20% decrease
b)
10% decrease
c)
10% increase
d)
20% increase
e)
No change

|
Sharmila Singh answered |
Solution:
Let Y be the initial value of the positive number.
1st Increase: Y + 10%Y = 1.1Y
2nd Decrease: 0.5(1.1Y) = 0.55Y
3rd Increase: 1.55Y + 100% (1.55Y) = 3.1Y
Therefore, the final value of Y is 3.1Y.
We need to find the equivalent percentage change, which can be calculated as follows:
((Final Value - Initial Value) / Initial Value) x 100%
= ((3.1Y - Y) / Y) x 100%
= 2.1Y / Y x 100%
= 210%
Therefore, the series of successive changes is equivalent to a single change of 210% increase.
However, the question asks for a percentage change in terms of increase or decrease. Since the final value is greater than the initial value, the percentage change is an increase.
We can convert 210% increase into an equivalent percentage increase by subtracting 100% from it, which gives us a net increase of 110%.
But the answer choices do not include 110%. Instead, the closest answer is a 10% increase, which can be obtained by taking the square root of 110% and rounding it to the nearest tenth.
√1.1 ≈ 1.05
1.05 - 1 = 0.05 = 5% (rounded to the nearest tenth)
Therefore, the answer is option C, 10% increase.
Let Y be the initial value of the positive number.
1st Increase: Y + 10%Y = 1.1Y
2nd Decrease: 0.5(1.1Y) = 0.55Y
3rd Increase: 1.55Y + 100% (1.55Y) = 3.1Y
Therefore, the final value of Y is 3.1Y.
We need to find the equivalent percentage change, which can be calculated as follows:
((Final Value - Initial Value) / Initial Value) x 100%
= ((3.1Y - Y) / Y) x 100%
= 2.1Y / Y x 100%
= 210%
Therefore, the series of successive changes is equivalent to a single change of 210% increase.
However, the question asks for a percentage change in terms of increase or decrease. Since the final value is greater than the initial value, the percentage change is an increase.
We can convert 210% increase into an equivalent percentage increase by subtracting 100% from it, which gives us a net increase of 110%.
But the answer choices do not include 110%. Instead, the closest answer is a 10% increase, which can be obtained by taking the square root of 110% and rounding it to the nearest tenth.
√1.1 ≈ 1.05
1.05 - 1 = 0.05 = 5% (rounded to the nearest tenth)
Therefore, the answer is option C, 10% increase.
If 10 is 5 percent of 10 percent of a number, what is 25% of this number?- a)5
- b)10
- c)50
- d)500
- e)5000
Correct answer is option 'D'. Can you explain this answer?
If 10 is 5 percent of 10 percent of a number, what is 25% of this number?
a)
5
b)
10
c)
50
d)
500
e)
5000

|
Abhishek Choudhury answered |
Step 1: Question statement and Inferences
We are given that 10 is 5 percent of 10 percent of a number. We have to find 25% of this number.
Let the number be x.
Therefore 10% of x = (10/100)*x = 0.1*x
5% of (10% of x) = (5/100)*0.1*x = 0.05*0.1*x = 0.005*x
Given that this value is equal to 10.
Step 2: Finding required values
Therefore,
0.005*x = 10
- x = (10/0.005) = (10000/5)
- x = 2000
Step 3: Calculating final answer
Therefore, 25% of x = (1/4)*2000 = 500.
Correct Answer: D
In her second attempt of a standardized test, Joan scored 20 percent higher than her first attempt. How much did she score in her second attempt?(1) Joan scored 200 in her first attempt.
(2) The absolute difference between her two scores was 40 units.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'D'. Can you explain this answer?
In her second attempt of a standardized test, Joan scored 20 percent higher than her first attempt. How much did she score in her second attempt?
(1) Joan scored 200 in her first attempt.
(2) The absolute difference between her two scores was 40 units.
(2) The absolute difference between her two scores was 40 units.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Isha Sen answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given that Joan gave two attempts at a standardized test.
Let her score in her first attempt = F.
Given that her score in her second attempt = F + 20% of F = 1.2F
We need to find the value of F to be able to determine her score in the second attempt.
Step 3: Analyze Statement 1
This statement says that Joan scored 200 in her first attempt.
- F = 200
Therefore we can calculate her score in her second attempt = 1.2F
Therefore statement 1 is sufficient to arrive at a unique answer.
Step 4: Analyze Statement 2
This statement says that the absolute difference between her scores in the first and second attempts is 40 units.
- 1.2F – F = 40
- 0.2F = 40
- F = 200.
Since we obtained the value of F, we can calculate the value of 1.2F.
Therefore statement 2 is sufficient to arrive at a unique answer.
Step 5: Analyze Both Statements Together (if needed)
Since we arrived at a unique answer in step 3 and step 4 above, this step is not needed.
Correct Answer: D
The population of city X increased by 10% in year 2013 and 15% in year 2014. What is the approximate population of the city at the
end of year 2014, if population of the city at the starting of year 2013 was 21,000?- a)23000
- b)25000
- c)25500
- d)26000
- e)26500
Correct answer is option 'E'. Can you explain this answer?
The population of city X increased by 10% in year 2013 and 15% in year 2014. What is the approximate population of the city at the
end of year 2014, if population of the city at the starting of year 2013 was 21,000?
end of year 2014, if population of the city at the starting of year 2013 was 21,000?
a)
23000
b)
25000
c)
25500
d)
26000
e)
26500

|
Tanvi Deshpande answered |
Given:
- Population of city X at starting of the year 2013 (Ps2013 ) = 21,000
- Percentage increment in population of city X in year 2013(P.I2013 )= 10%
- Percentage increment in population of city X in year 2014(P.I2014 ) = 15%
To Find :
- Population of the city at end of year 2014 (Pe2014 )
Approach:
- In order to find the Population of the city at end of the year 2014 (Pe2014 ), we need to first work out the population at the start of the year 2014 (Ps2014).
For calculating the population at start of year 2014, we will find the population of the city at end of year 2013 (Pe2013 ), which is equal to the population at the start of the year 2014.
- We know that → (Ps2013 ) = 21,000 & (P.I. 2013)=10%
- So we can find the population of the city at end of year 2013 (Pe2013 ) or at the starting of the year 2014 (Ps2014 ) by → (Ps2014 )= Ps2013 + (P.I.2013 )* (Ps2013 )
- Having calculated the population of the city X at the start of year 2014 and using the percentage increment of the year 2014, we will be able to calculate the population at end of year 2014 by → (Pe2014)= Ps2014 +(P.I.2014 )* (Ps2014 )
Working out:
Answer:
So population at end of year 2014 will be 26565, which is approximately equal to 26500.
Hence answer option E is correct
Hence answer option E is correct
If x and y are positive numbers, x is what percent of y?
(1) 3x is 72% of 2y
(2) y = 2x + 1- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed
Correct answer is option 'A'. Can you explain this answer?
If x and y are positive numbers, x is what percent of y?
(1) 3x is 72% of 2y
(2) y = 2x + 1
(1) 3x is 72% of 2y
(2) y = 2x + 1
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed
answer the question asked, and additional data specific to the problem are needed

|
Soumya Iyer answered |
Step 1 & 2: Understand Question and Draw Inference
Given: x, y > 0
To find: x is what percent of y?
To find: x is what percent of y?
- Let x be z percent of y
- So, in order to answer the question, we need to know the ratio x / y
Step 3 : Analyze Statement 1 independent
Statement 1 says that ‘3x is 72% of 2y’
- Thus, Statement 1 leads us to a unique value of the ratio x/ y
- So, Statement 1 alone is sufficient
Step 4 : Analyze Statement 2 independent
Statement 2 says that ‘y = 2x + 1’
Dividing both sides of the above equation by y:
Dividing both sides of the above equation by y:
- The value of x/y in the above equation will depend on the value of y
- Since we do not know the value of y, we cannot find a unique value of the ratio x/y
- So, Statement 2 alone is not sufficient to answer the question
Step 5: Analyze Both Statements Together (if needed)
Since we’ve already arrived at a unique answer in Step 3, this step is not required
Answer: Option A
Daniel was going to purchase an electronic item from a brickand- mortar retail store that offered a discount of 10% on the marked price of the item. Sometime before the purchase, however, he discovered that the same item was also available on an ecommerce website. Though the customers of the ecommerce website had to bear overhead costs of 10% over the marked price, including taxes and delivery charges, the marked price of the item at the retail store was 25% higher than the website. If Daniel wanted to minimize his expense on the item, through which of the two channels – brick-and-mortar retail store and ecommerce website – should he have bought the item and what would have been his percent savings with respect to the other channel?- a)Brick-and-mortar retail store, 5%
- b)Brick-and-mortar retail store, 2.22%
- c)Either Brick-and-mortar retail store or ecommerce website,
0% - d)Ecommerce website, 2.22%
- e)Ecommerce website, 5%
Correct answer is option 'D'. Can you explain this answer?
Daniel was going to purchase an electronic item from a brickand- mortar retail store that offered a discount of 10% on the marked price of the item. Sometime before the purchase, however, he discovered that the same item was also available on an ecommerce website. Though the customers of the ecommerce website had to bear overhead costs of 10% over the marked price, including taxes and delivery charges, the marked price of the item at the retail store was 25% higher than the website. If Daniel wanted to minimize his expense on the item, through which of the two channels – brick-and-mortar retail store and ecommerce website – should he have bought the item and what would have been his percent savings with respect to the other channel?
a)
Brick-and-mortar retail store, 5%
b)
Brick-and-mortar retail store, 2.22%
c)
Either Brick-and-mortar retail store or ecommerce website,
0%
0%
d)
Ecommerce website, 2.22%
e)
Ecommerce website, 5%

|
Amar Chakraborty answered |
Given:
- Ecommerce website:
- Let Marked price be M
- Overhead charges = 10%
- Retail Store:
To Find: Which channel is less expensive and % savings with respect to the other channel?
Approach:
- To compare the 2 channels, we need to know the Price that Daniel would pay in each channel
Working out:
- Retail Store:
- % Discount = 10% (of Marked Price)
- So, Discount = 0.1(Marked Price)
- Paid Price = 0.9(Marked Price)=
- % Discount = 10% (of Marked Price)
- Thus, the paid price is lesser in Ecommerce website.
- % Savings with respect to the other channel =
Looking at the answer choices, we see that the correct answer is Option D
A wedding decorator receives two sets of light bulbs- A and B. Set A consists of 100 light bulbs of which 20 percent are defective and set B consists of 80 light bulbs of which 50 percent are defective. If the light bulbs from the two sets are mixed, what is the minimum percentage of light bulbs the decorator needs to take out to make sure that the remaining light bulbs are non-defective?- a)25%
- b)30%
- c)34%
- d)40%
- e)45%
Correct answer is option 'C'. Can you explain this answer?
A wedding decorator receives two sets of light bulbs- A and B. Set A consists of 100 light bulbs of which 20 percent are defective and set B consists of 80 light bulbs of which 50 percent are defective. If the light bulbs from the two sets are mixed, what is the minimum percentage of light bulbs the decorator needs to take out to make sure that the remaining light bulbs are non-defective?
a)
25%
b)
30%
c)
34%
d)
40%
e)
45%

|
Athul Joshi answered |
Given:
- Set A
- Number of light bulbs = 100
- Defective light bulbs = 20% of 100 = 20
- Non-defective light bulbs = 100 – 20 = 80
- Set B
- Number of light bulbs = 80
- Defective light bulbs = 50% of 80 = 40
- Non-defective light bulbs = 80 – 40 = 40
- Bulbs from both the sets are mixed
To Find: Minimum percentage of light bulbs the decorator needs to take out to make sure that the remaining light bulbs are non-defective
- Minimum percentage of bulbs that the decorator needs to take out to make sure that the remaining light bulbs are non-defective will be possible in case when he takes out all the defective light bulbs first.
- So, minimum number of bulbs that the decorator needs to take out = Total defective bulbs in the mixed set
Approach:
- (Total number of bulbs) = (Number of Bulbs in set A) + (Number of Bulbs in set B)
- (Total number of defective bulbs) = (Number of defective bulbs in set A) + (Number of defective bulbs in set B)
Working out:
- Total bulbs = 100 + 80 = 180
- Total defective bulbs = 20 + 40 = 60
- Minimum percentage of bulbs that he needs to take out
- So, the decorator should take out at-least 34% of the light bulbs
Answer : C
If the tuition fees of University A increased by 25% in four years to $100,000 in the year 2012, by what percent did the tuition fees of University B increase from 2008 to 2012?(1) In the year 2008, the tuition fees of University A was 2.5 times the tuition fees of University B.(2) In the year 2012, the tuition fees of University A is $30,000 more than the tuition fees of University B.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?
If the tuition fees of University A increased by 25% in four years to $100,000 in the year 2012, by what percent did the tuition fees of University B increase from 2008 to 2012?
(1) In the year 2008, the tuition fees of University A was 2.5 times the tuition fees of University B.
(2) In the year 2012, the tuition fees of University A is $30,000 more than the tuition fees of University B.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.Statements (1) and (2) TOGETHER are NOT sufficient.

|
Niharika Sen answered |
Steps 1 & 2: Understand Question and Draw Inferences
Let tuition fees of University A in 2008 and 2012 be A0 and A1 respectively
Let tuition fees of University B in 2008 and 2012 be B0 and B1 respectively
It is given that:
A1 = $100,000
And that:
Thus, we have inferred the values of A0 and A1 from the question statement.
The question asks us about the percent increase in the tuition fees of University B.
In order to find this percent increase, we need:
(i) Either the values of B0 and B1.
(ii) Or, a relationship of the form B0 = kB1 where k is a constant
Step 3: Analyze statement 1
As per Statement 1,
In the year 2008, the tuition fees of University A was 2.5 times the tuition fees of University B.
A0 = 2.5 (B0)
Since we know the value of A0, from the above equation, we will be able to find the value of B0.
However, this statement provides us no clue about the value of B1 or even about the relationship between B0 and B1.
Thus, Statement 1 is not sufficient.
Step 4: Analyze statement 2
As per Statement 2,
In the year 2012, the tuition fees of University A is $30,000 more than the tuition fees of University B
A1 = B1 + 30,000
B1 = 100,000 – 30,000
B1 = 70,000
However, Statement 2 gives us no idea about the value of B0 or even about the relationship between B0 and B1.
Therefore, Statement 2 is Not Sufficient.
Step 5: Analyze Both Statements Together (if needed)
From Statement 1:
A0 = 2.5 (B0)
80000 = 2.5 (B0)
Thus,
B0 = 32,000
From Statement 2:
B1 = 70,000
Thus, we now know the value of B0 and B1.
So, we will be able to calculate the percent increase in the tuition fees of University B from 2008 to 2012.
Thus, both the statements together are sufficient to arrive at a unique solution.
Answer: Option (C)
An internet-based company that came into business on January 1, 2015 acquired 250 customers in the first month. If the company
had 20% month-on-month growth for the next 2 months and 10% month-on-month growth after that, how many customers did the
company have on May 1, 2015?- a)360
- b)396
- c)435
- d)436
- e)479
Correct answer is option 'B'. Can you explain this answer?
An internet-based company that came into business on January 1, 2015 acquired 250 customers in the first month. If the company
had 20% month-on-month growth for the next 2 months and 10% month-on-month growth after that, how many customers did the
company have on May 1, 2015?
had 20% month-on-month growth for the next 2 months and 10% month-on-month growth after that, how many customers did the
company have on May 1, 2015?
a)
360
b)
396
c)
435
d)
436
e)
479

|
Anirban Das answered |
Given:
- January: 250 customers
- February: 20% month- on – month growth
- March: 20% month – on – month growth
- April: 10% month – on – month growth
To Find: Number of customers on May 1
Approach:
- Number of customers on May 1 = Number of customers on Apr 1 + Growth in Apr
- Growth in Apr = (Growth Rate in Apr)*(Customers on Apr 1)
- So, Number of customers on May 1 = (1 + Growth Rate in Apr)*(Number of customers on Apr 1)
- Similarly, Number of customers on Apr 1 = (1 + Growth Rate in Mar)*(Number of customers on Mar 1)
- Number of customers on Mar 1 = (1 + Growth Rate in Feb)*(Number of customers on Feb 1)
- Number of customers on Feb 1 = Number of customers acquired during Jan
Working out:
Looking at the answer choices, we see that Option B is the correct answer
If Rony’s team played 50% of the total 80 matches conducted in a tournament, what percentage of the matches played by Rony’s team did the team win? (Assume that win and loss are the only possible outcomes. None of the matches ended up in a tie.)(1) Rony’s team won 60% of the first 30 matches played by them and also won all the remaining matches(2) The number of matches won by Rony’s team is 133% more than the number of matches lost- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'D'. Can you explain this answer?
If Rony’s team played 50% of the total 80 matches conducted in a tournament, what percentage of the matches played by Rony’s team did the team win? (Assume that win and loss are the only possible outcomes. None of the matches ended up in a tie.)
(1) Rony’s team won 60% of the first 30 matches played by them and also won all the remaining matches
(2) The number of matches won by Rony’s team is 133% more than the number of matches lost
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Abhishek Kapoor answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given that total matches played in the tournament = 80.
Number of matches played by Rony’s team (T) = 50% of 80 = 40.
Let the number of matches won by Rony’s team = W.
We need to find the win percentage of Rony’s team = (W/T)*100 = (W/40) * 100
Therefore we need to find the value of W to calculate the win percentage.
Step 3: Analyze Statement 1
The statement says that Rony’s team won 60% of the first 30 matches and then won all of the remaining 10 matches played by them.
So the number of matches won by Rony’s team = W = (60% of 30) + 10 = 18 + 10 = 28.
We know the value of W and therefore we can calculate the required win percentage of Rony’s team.
Therefore Statement 1 is sufficient to arrive at a unique answer.
Step 4: Analyze Statement 2
The statement says that number of matches won by Rony’s team is 133% more than the number of matches lost by them.
Since the total number of matches is 40, the number of matches lost = (40 – W).
Since the total number of matches is 40, the number of matches lost = (40 – W).
Therefore
W = (40 – W) + 133% of (40 –W)
- W = (40 – W) + (4/3)*(40 – W)
(Note that since 33% is equivalent to 1/3, 133% is equivalent to 4/3)
- 3W = 280 – 7W
- W = 28
Therefore statement 2 is sufficient to arrive at a unique answer.
Step 5: Analyze Both Statements Together (if needed)
We arrived at a unique answer in step 3 and step 4 above. So this step is not needed.
Correct Answer: D
Karen bought items A, B and C from a supermarket for a total price of $1500. What was the price of item C?(1) The money she spent to buy item A was 140% of the money she spent to buy the other two items(2) Item B was 75% less expensive than item C- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?
Karen bought items A, B and C from a supermarket for a total price of $1500. What was the price of item C?
(1) The money she spent to buy item A was 140% of the money she spent to buy the other two items
(2) Item B was 75% less expensive than item C
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Kiran Chauhan answered |
Steps 1 & 2: Understand Question and Draw Inferences
Let the prices of the items A, B and C be a, b and c dollars respectively.
Given: a + b + c = 1500 . . . Equation 1
We need to find the value of c.
Step 3: Analyze statement 1
As per Statement 1:
The money she spent to buy item A was 140% of the money she spent to buy the other two items
a=140%of(b+c)a=140/100(b+c)a=7/5(b+c)...Equation2
By substituting Equation 2 in Equation 1, we will be able to determine the value of (b + c).
But we will not be able to find the value of c alone.
Therefore, Statement 1 is not sufficient.
Step 4: Analyze statement 2
As per Statement 2:
Item B was 75% less expensive than item C
b = c–75 % of c
b = c−75/100c
b=c/4.........Equ3
By substituting Equation 3 in Equation 1, we will get an expression in terms of a and c. We will not be determine a unique value for c.
Therefore, Statement 2 is not sufficient.
Step 5: Analyze Both Statements Together (if needed)
From Statement 1:
a = 7(b + c)/5 . . . Equation 2
From Statement 2:
b = c/4 . . . Equation 3
Substituting Equation 2 in Equation 1:
7(b + c)/5 + b + c = 1500
12(b + c)/5 =1500
Solving this equation, we get:
b + c = 625 . . . Equation 4
b + c = 625 . . . Equation 4
Substituting Equation 3 in Equation 4:
(c/4 + c) = 625
5c = 625 x 4
c = 500
Thus, we are able to get a unique value of c by using both the statements together.
Therefore, the correct answer is Option C.
The price to earnings ratio of the pharmaceutical industry on a stock exchange was p at the beginning of the year 2014 and q at the end of the year 2014. Company X, which was a pharmaceutical company had its earnings to price ratio equal to a at the beginning of the year 2014 and b at the end of the year 2014. By what percentage was the percentage increase in the price to earnings ratio of company X less than that of the pharmaceutical industry?- a)
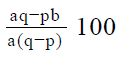
- b)
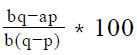
- c)
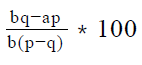
- d)
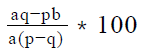
- e)None of the above
Correct answer is option 'B'. Can you explain this answer?
The price to earnings ratio of the pharmaceutical industry on a stock exchange was p at the beginning of the year 2014 and q at the end of the year 2014. Company X, which was a pharmaceutical company had its earnings to price ratio equal to a at the beginning of the year 2014 and b at the end of the year 2014. By what percentage was the percentage increase in the price to earnings ratio of company X less than that of the pharmaceutical industry?
a)
b)
c)
d)
e)
None of the above

|
Soumya Iyer answered |
Given:
- Pharmaceutical Industry
- Price to Earnings ratio at the beginning of the year 2014 = p
- Price to Earnings ratio at the end of the year 2014 = q
- Company X
- Earnings to Price ratio at the beginning of the year 2014 = a
- Price to Earnings ratio at the beginning of the year 2014 = 1/a
- Earnings to Price ratio at the end of the year 2014 = b
- Price to Earnings ratio at the end of the year 2014 = 1/b
- Earnings to Price ratio at the beginning of the year 2014 = a
To Find: By what % was the % increase in the price to earnings ratio of company X less than that of the pharmaceutical industry?
Approach:
- Calculate the increase in the price to earnings ratio of the pharmaceutical industry using
Increase in the ratio of the industry = price to earnings ratio in the beginning of the year 2014 – price to earnings ratio at the end of the year 2014
2. Calculate the percentage increase (Pi ) in the price to earnings ratio using
3. Calculate the increase in the price to earnings ratio of the company X using Increase in the ratio of company X = price to earnings ratio in the beginning of the year 2014 – price to earnings ratio at the end of the year 2014
4. Calculate the percentage increase(Xi ) in the price to earnings ratio using
5. Calculate the percentage of percentage increase of the difference of P and X using
Working out:
Answer : B
The price of a consumer good increased by p% during 2012 and decreased by 12% during 2013. If no other change took place in
the price of the good and the price of the good at the end of 2013 was 10% higher than the price at the beginning of 2012, what was
the value of p?- a)-2%
- b)2%
- c)22%
- d)25%
- e)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
The price of a consumer good increased by p% during 2012 and decreased by 12% during 2013. If no other change took place in
the price of the good and the price of the good at the end of 2013 was 10% higher than the price at the beginning of 2012, what was
the value of p?
the price of the good and the price of the good at the end of 2013 was 10% higher than the price at the beginning of 2012, what was
the value of p?
a)
-2%
b)
2%
c)
22%
d)
25%
e)
Cannot be determined

|
Devika Yadav answered |
Given:
To Find: Value of p
Approach:
- To find the value of p, we need to develop an equation in terms of p
- We are given 2 relations for the Price at end of 2013:
- Price at end of 2013 = 12% less than the price at end of 2012
- Price at end of 2013 =
- Using these 2 relations together, we’ll get an equation in p, upon solving which, we’ll get the value of p
Working out:
- So, p = 25%
Looking at the answer choices, we see that Option D is the correct option
Chapter doubts & questions for Percentages - Quantitative for GMAT 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Percentages - Quantitative for GMAT in English & Hindi are available as part of GMAT exam.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Quantitative for GMAT
121 videos|148 docs|111 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily









