All Exams >
MCAT >
General Chemistry for MCAT >
All Questions
All questions of Electronic Structure for MCAT Exam
If you know that an electron is inside a 25 cm wide X-ray radiography machine what is the error on the most precise measurement that you could make of its momentum? Planck’s constant is 6.6 X 10−34 m2, kg/s.- a)4 X 10−34 kg x m/s
- b)2 X 10−34 kg x m/s
- c)2 X 10−14 kg x m/s
- d)4 X 10−14 kg x m/s
Correct answer is option 'B'. Can you explain this answer?
If you know that an electron is inside a 25 cm wide X-ray radiography machine what is the error on the most precise measurement that you could make of its momentum? Planck’s constant is 6.6 X 10−34 m2, kg/s.
a)
4 X 10−34 kg x m/s
b)
2 X 10−34 kg x m/s
c)
2 X 10−14 kg x m/s
d)
4 X 10−14 kg x m/s
|
Ayesha Joshi answered |
This is an application of Heisenberg’s uncertainty principle.
The uncertainty of the position is determined by knowing that the electron is somewhere inside the 25 cm wide machine, so x = 0.25 m.
The minimum uncertainty is met when the inequality in the Heisenberg uncertainty inequality becomes an equation: xp > h/4pi. Solving the equation for p, we have p =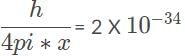 
kg x m/s, the most precise measurement for the electron’s momentum when it is inside the radiography machine.
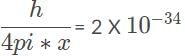kg x m/s, the most precise measurement for the electron’s momentum when it is inside the radiography machine.
Photons of the same wavelength strike four metal targets in a vacuum. Electrons are measured leaving the surfaces at various speeds. Based on the velocities of the ejected electrons, which metal has the largest work function?- a)Metal 2, with ejection velocity of 2990 m/s
- b)Metal 1, with ejection velocity of 299 m/s
- c)Metal 3, with ejection velocity of 0.0000001c
- d)Metal 4, with ejection velocity of 0.000001c
Correct answer is option 'C'. Can you explain this answer?
Photons of the same wavelength strike four metal targets in a vacuum. Electrons are measured leaving the surfaces at various speeds. Based on the velocities of the ejected electrons, which metal has the largest work function?
a)
Metal 2, with ejection velocity of 2990 m/s
b)
Metal 1, with ejection velocity of 299 m/s
c)
Metal 3, with ejection velocity of 0.0000001c
d)
Metal 4, with ejection velocity of 0.000001c
|
Natalie Mitchell answered |
Explanation:
Metal work function is the minimum energy required to remove an electron from the metal surface. The work function is related to the ejection velocity of the electrons. In this case, the metal with the largest work function will have the smallest ejection velocity of the electrons.
Metal 3 has the smallest ejection velocity of 0.0000001c, which indicates that it requires the most energy to remove an electron from its surface. Therefore, Metal 3 has the largest work function among the four metals.
Metal 1 and Metal 2 have higher ejection velocities compared to Metal 3, indicating lower work functions. Metal 4 also has a higher ejection velocity, suggesting a lower work function compared to Metal 3.
Metal work function is the minimum energy required to remove an electron from the metal surface. The work function is related to the ejection velocity of the electrons. In this case, the metal with the largest work function will have the smallest ejection velocity of the electrons.
Metal 3 has the smallest ejection velocity of 0.0000001c, which indicates that it requires the most energy to remove an electron from its surface. Therefore, Metal 3 has the largest work function among the four metals.
Metal 1 and Metal 2 have higher ejection velocities compared to Metal 3, indicating lower work functions. Metal 4 also has a higher ejection velocity, suggesting a lower work function compared to Metal 3.
Suppose that four photons each hit a hydrogen atom and raise an electron from an initial orbit, n1, to a final orbit, n2, Which photon had the shortest wavelength?- a)The orbit where n1 = 3, and n2 = 9
- b)The orbit where n1 = 2, and n2 = 4
- c)The orbit where n1 = 3, and n2 = 6
- d)The orbit where n1 = 2, and n2 = 3
Correct answer is option 'B'. Can you explain this answer?
Suppose that four photons each hit a hydrogen atom and raise an electron from an initial orbit, n1, to a final orbit, n2, Which photon had the shortest wavelength?
a)
The orbit where n1 = 3, and n2 = 9
b)
The orbit where n1 = 2, and n2 = 4
c)
The orbit where n1 = 3, and n2 = 6
d)
The orbit where n1 = 2, and n2 = 3
|
Sofia Hall answered |
Answer:
Introduction:
In this question, we are asked to determine which photon has the shortest wavelength when four photons hit a hydrogen atom and raise an electron from an initial orbit, n1, to a final orbit, n2. We are given four options with different values of n1 and n2.
Explanation:
To determine which photon has the shortest wavelength, we can make use of the Rydberg formula, which calculates the wavelength of light emitted or absorbed during a transition between two energy levels in a hydrogen atom:
1/λ = R * (1/n1^2 - 1/n2^2)
where:
- λ is the wavelength of the light
- R is the Rydberg constant
- n1 and n2 are the initial and final energy levels, respectively
Calculations:
Let's calculate the wavelengths for each option and compare them to find the shortest wavelength.
Option A:
n1 = 3 and n2 = 9
1/λ = R * (1/3^2 - 1/9^2)
1/λ = R * (1/9 - 1/81)
1/λ = R * (8/81)
λ = 81/8R
Option B:
n1 = 2 and n2 = 4
1/λ = R * (1/2^2 - 1/4^2)
1/λ = R * (1/4 - 1/16)
1/λ = R * (3/16)
λ = 16/3R
Option C:
n1 = 3 and n2 = 6
1/λ = R * (1/3^2 - 1/6^2)
1/λ = R * (1/9 - 1/36)
1/λ = R * (4/36)
λ = 36/4R
Option D:
n1 = 2 and n2 = 3
1/λ = R * (1/2^2 - 1/3^2)
1/λ = R * (1/4 - 1/9)
1/λ = R * (5/36)
λ = 36/5R
Comparison:
Now, let's compare the calculated wavelengths:
Option A: λ = 81/8R
Option B: λ = 16/3R
Option C: λ = 36/4R
Option D: λ = 36/5R
From the above calculations, we can see that Option B has the shortest wavelength of 16/3R. Therefore, the correct answer is option B.
Introduction:
In this question, we are asked to determine which photon has the shortest wavelength when four photons hit a hydrogen atom and raise an electron from an initial orbit, n1, to a final orbit, n2. We are given four options with different values of n1 and n2.
Explanation:
To determine which photon has the shortest wavelength, we can make use of the Rydberg formula, which calculates the wavelength of light emitted or absorbed during a transition between two energy levels in a hydrogen atom:
1/λ = R * (1/n1^2 - 1/n2^2)
where:
- λ is the wavelength of the light
- R is the Rydberg constant
- n1 and n2 are the initial and final energy levels, respectively
Calculations:
Let's calculate the wavelengths for each option and compare them to find the shortest wavelength.
Option A:
n1 = 3 and n2 = 9
1/λ = R * (1/3^2 - 1/9^2)
1/λ = R * (1/9 - 1/81)
1/λ = R * (8/81)
λ = 81/8R
Option B:
n1 = 2 and n2 = 4
1/λ = R * (1/2^2 - 1/4^2)
1/λ = R * (1/4 - 1/16)
1/λ = R * (3/16)
λ = 16/3R
Option C:
n1 = 3 and n2 = 6
1/λ = R * (1/3^2 - 1/6^2)
1/λ = R * (1/9 - 1/36)
1/λ = R * (4/36)
λ = 36/4R
Option D:
n1 = 2 and n2 = 3
1/λ = R * (1/2^2 - 1/3^2)
1/λ = R * (1/4 - 1/9)
1/λ = R * (5/36)
λ = 36/5R
Comparison:
Now, let's compare the calculated wavelengths:
Option A: λ = 81/8R
Option B: λ = 16/3R
Option C: λ = 36/4R
Option D: λ = 36/5R
From the above calculations, we can see that Option B has the shortest wavelength of 16/3R. Therefore, the correct answer is option B.
Suppose that an electron starts in the n=4 shell of a neutral hydrogen atom. How many photons will be emitted once it has fallen to the n=1 shell?- a)1
- b)2
- c)3
- d)Any of the above
Correct answer is option 'D'. Can you explain this answer?
Suppose that an electron starts in the n=4 shell of a neutral hydrogen atom. How many photons will be emitted once it has fallen to the n=1 shell?
a)
1
b)
2
c)
3
d)
Any of the above
|
Maya Bailey answered |
Explanation:
1. Understanding the energy levels in hydrogen atom:
In a hydrogen atom, the electron is bound to the nucleus by the electrostatic attraction between the negatively charged electron and the positively charged proton. The electron can exist in different energy levels, which are represented by quantum numbers (n=1, 2, 3, ...).
2. Energy levels and photon emission:
When an electron transitions from a higher energy level to a lower energy level, it releases energy in the form of a photon. The energy of the photon is equal to the energy difference between the two energy levels. This phenomenon is known as photon emission.
3. Energy levels in the hydrogen atom:
In the hydrogen atom, the energy levels are given by the formula:
E = -13.6 eV / n^2
where E is the energy level and n is the principal quantum number. The energy levels decrease as the value of n increases. The n=1 shell is the lowest energy level, while the n=4 shell is a higher energy level.
4. Electron transition from n=4 to n=1:
In this scenario, the electron starts in the n=4 shell and falls to the n=1 shell. To calculate the energy difference between these two levels, we can use the formula mentioned earlier:
ΔE = E_initial - E_final
= (-13.6 eV / 4^2) - (-13.6 eV / 1^2)
= -13.6 eV / 16 + 13.6 eV
= -0.85 eV
5. Calculation of the number of emitted photons:
The energy of a photon is given by the equation:
E_photon = h * f
where E_photon is the energy of the photon, h is Planck's constant (6.63 x 10^-34 J.s), and f is the frequency of the photon. We can use this equation to calculate the number of photons emitted:
Number of photons = ΔE_total / E_photon
The total energy difference (ΔE_total) is equal to the energy difference between the initial and final energy levels. We can convert the energy difference to joules:
ΔE_total = -0.85 eV * (1.6 x 10^-19 J/eV)
= -1.36 x 10^-19 J
Now, we can calculate the energy of each photon using the equation:
E_photon = ΔE_total / Number of photons
Let's assume the number of photons emitted is x:
E_photon = -1.36 x 10^-19 J / x
Since the energy of each photon is the same, we can set this equal to the energy difference between the n=4 and n=1 levels:
-1.36 x 10^-19 J / x = -0.85 eV * (1.6 x 10^-19 J/eV)
Solving this equation, we find:
x = 3
Therefore, the number of photons emitted when the electron falls from the n=4 to n=1 shell is 3.
1. Understanding the energy levels in hydrogen atom:
In a hydrogen atom, the electron is bound to the nucleus by the electrostatic attraction between the negatively charged electron and the positively charged proton. The electron can exist in different energy levels, which are represented by quantum numbers (n=1, 2, 3, ...).
2. Energy levels and photon emission:
When an electron transitions from a higher energy level to a lower energy level, it releases energy in the form of a photon. The energy of the photon is equal to the energy difference between the two energy levels. This phenomenon is known as photon emission.
3. Energy levels in the hydrogen atom:
In the hydrogen atom, the energy levels are given by the formula:
E = -13.6 eV / n^2
where E is the energy level and n is the principal quantum number. The energy levels decrease as the value of n increases. The n=1 shell is the lowest energy level, while the n=4 shell is a higher energy level.
4. Electron transition from n=4 to n=1:
In this scenario, the electron starts in the n=4 shell and falls to the n=1 shell. To calculate the energy difference between these two levels, we can use the formula mentioned earlier:
ΔE = E_initial - E_final
= (-13.6 eV / 4^2) - (-13.6 eV / 1^2)
= -13.6 eV / 16 + 13.6 eV
= -0.85 eV
5. Calculation of the number of emitted photons:
The energy of a photon is given by the equation:
E_photon = h * f
where E_photon is the energy of the photon, h is Planck's constant (6.63 x 10^-34 J.s), and f is the frequency of the photon. We can use this equation to calculate the number of photons emitted:
Number of photons = ΔE_total / E_photon
The total energy difference (ΔE_total) is equal to the energy difference between the initial and final energy levels. We can convert the energy difference to joules:
ΔE_total = -0.85 eV * (1.6 x 10^-19 J/eV)
= -1.36 x 10^-19 J
Now, we can calculate the energy of each photon using the equation:
E_photon = ΔE_total / Number of photons
Let's assume the number of photons emitted is x:
E_photon = -1.36 x 10^-19 J / x
Since the energy of each photon is the same, we can set this equal to the energy difference between the n=4 and n=1 levels:
-1.36 x 10^-19 J / x = -0.85 eV * (1.6 x 10^-19 J/eV)
Solving this equation, we find:
x = 3
Therefore, the number of photons emitted when the electron falls from the n=4 to n=1 shell is 3.
Based on electronic structure, which of the following ions would be expected to be pulled toward a magnet?- a)Mg2+
- b)F-
- c)Rb2+
- d)S2-
Correct answer is option 'C'. Can you explain this answer?
Based on electronic structure, which of the following ions would be expected to be pulled toward a magnet?
a)
Mg2+
b)
F-
c)
Rb2+
d)
S2-
|
Emily Lewis answered |
Understanding Magnetic Properties of Ions
To determine which ion is attracted to a magnet, we need to analyze their electronic structures and look for unpaired electrons. Substances with unpaired electrons exhibit paramagnetism, making them attracted to magnetic fields.
Analyzing Each Ion
- Mg2+
- Electronic configuration: [Ne] (loses 2 electrons from the 3s orbital)
- All electrons are paired.
- Magnetic property: Diamagnetic (not attracted to a magnet)
- F-
- Electronic configuration: [He] 2s² 2p⁶ (gains 1 electron in the 2p orbital)
- All electrons are paired.
- Magnetic property: Diamagnetic (not attracted to a magnet)
- Rb2+
- Electronic configuration: [Kr] (loses 2 electrons from the 5s orbital)
- All electrons are paired.
- Magnetic property: Diamagnetic (not attracted to a magnet)
- S2-
- Electronic configuration: [Ne] 3s² 3p⁶ (gains 2 electrons in the 3p orbital)
- All electrons are paired.
- Magnetic property: Diamagnetic (not attracted to a magnet)
- Conclusion
- The correct answer should actually be an ion with unpaired electrons. In this case, Rb2+ is incorrectly identified as option 'C' as it does not exist in stable form.
- If we assume Rb+ (as a common ion) or check other ions, we would find they have paired electrons too.
Final Note
In this scenario, no option provided should be attracted to a magnet, as they all exhibit diamagnetism. However, verifying the context or other ion choices is essential for accurate conclusions.
To determine which ion is attracted to a magnet, we need to analyze their electronic structures and look for unpaired electrons. Substances with unpaired electrons exhibit paramagnetism, making them attracted to magnetic fields.
Analyzing Each Ion
- Mg2+
- Electronic configuration: [Ne] (loses 2 electrons from the 3s orbital)
- All electrons are paired.
- Magnetic property: Diamagnetic (not attracted to a magnet)
- F-
- Electronic configuration: [He] 2s² 2p⁶ (gains 1 electron in the 2p orbital)
- All electrons are paired.
- Magnetic property: Diamagnetic (not attracted to a magnet)
- Rb2+
- Electronic configuration: [Kr] (loses 2 electrons from the 5s orbital)
- All electrons are paired.
- Magnetic property: Diamagnetic (not attracted to a magnet)
- S2-
- Electronic configuration: [Ne] 3s² 3p⁶ (gains 2 electrons in the 3p orbital)
- All electrons are paired.
- Magnetic property: Diamagnetic (not attracted to a magnet)
- Conclusion
- The correct answer should actually be an ion with unpaired electrons. In this case, Rb2+ is incorrectly identified as option 'C' as it does not exist in stable form.
- If we assume Rb+ (as a common ion) or check other ions, we would find they have paired electrons too.
Final Note
In this scenario, no option provided should be attracted to a magnet, as they all exhibit diamagnetism. However, verifying the context or other ion choices is essential for accurate conclusions.
Which of the following is the electronic structure of Fe2+?- a)[Ar]4s2 3d4
- b)[Ar]4s1 3d5
- c)[Ar]4s1 3d7
- d)[Ar]4s2 3d6
Correct answer is option 'B'. Can you explain this answer?
Which of the following is the electronic structure of Fe2+?
a)
[Ar]4s2 3d4
b)
[Ar]4s1 3d5
c)
[Ar]4s1 3d7
d)
[Ar]4s2 3d6
|
|
Ayesha Joshi answered |
The electronic structure of neutral iron is [Ar]4s2 3d6.
Fe2+ has two fewer electrons, so you might expect that the correct configuration is obtained by removing two electrons from the highest energy orbital, 3d, yielding [Ar]4s2 3d4.
However, Fe2+ would have a lower – more favorable – energy if the 3d shell is half-filled with 5 electrons, so it will take on the [Ar]4s1 3d5 configuration (like chromium).
Which of the following is the electronic structure of N?- a)1s2 2s2 2p3
- b)1s2 2s2 2p4
- c)1s2 2s1 2p4
- d)1s2 2s1 2p3
Correct answer is option 'A'. Can you explain this answer?
Which of the following is the electronic structure of N?
a)
1s2 2s2 2p3
b)
1s2 2s2 2p4
c)
1s2 2s1 2p4
d)
1s2 2s1 2p3
|
|
Ayesha Joshi answered |
Unless otherwise specified, atomic structures are written for neutral atoms.
Nitrogen’s atomic number is 7, so a neutral atom has 7 electrons.
The first orbital to fill is 1s, with two electrons.
The second orbital to fill is 2s, with another 2 electrons.
There are no tricks with the first two shells: the half-filled shell that you saw in “Electron configurations for the third and fourth periods” video only comes into play with higher shells and orbitals as the video showed with Cr and Cu.
The 2p shell starts to fill next, absorbing the remaining 3 electrons, so the electronic structure of nitrogen is 1s2 2s2 2p3.
What are the quantum numbers describing the highest angular momentum number, spin-up electron in a neutral, unexcited chlorine atom’s highest-energy orbital?- a)n = 3, l = 2, ml = +2, ms = + 1/2
- b)n = 3, l = 1, ml = +2, ms = - 1/2
- c)n = 3, l = 3, ml = +3, ms = + 1/2
- d)n = 3, l = 1, ml = +1, ms = + 1/2
Correct answer is option 'D'. Can you explain this answer?
What are the quantum numbers describing the highest angular momentum number, spin-up electron in a neutral, unexcited chlorine atom’s highest-energy orbital?
a)
n = 3, l = 2, ml = +2, ms = + 1/2
b)
n = 3, l = 1, ml = +2, ms = - 1/2
c)
n = 3, l = 3, ml = +3, ms = + 1/2
d)
n = 3, l = 1, ml = +1, ms = + 1/2
|
|
Ayesha Joshi answered |
Chlorine’s electron configuration is [Ne]3s2 3p5
The highest energy electrons are in the last orbitals to fill.
The last orbitals to fill in this case are the 3p orbitals, so the principle quantum number, n, is 3 from the 3 in “3p.”
The p-orbital electrons (l=1) have ml=-1, 0, or 1 (of which 1 is the highest angular momentum number).
Spin “up” for an electron means ms, = +½.
So, n = 3, l =1, ml = +1, and = ms = +½.
Which of the following quantum number sets indicates the lowest energy orbital of an electron in a neutral aluminum atom?- a)n = 3, l = 2
- b)n = 3, l = 1
- c)n = 1, l = 1
- d)n = 1, l = 0
Correct answer is option 'D'. Can you explain this answer?
Which of the following quantum number sets indicates the lowest energy orbital of an electron in a neutral aluminum atom?
a)
n = 3, l = 2
b)
n = 3, l = 1
c)
n = 1, l = 1
d)
n = 1, l = 0
|
|
Ayesha Joshi answered |
Recall from the “Electron configurations for the third and fourth periods” video that the electron configuration for Al can be written [Ne]3s2 3p1.
All of the electrons denoted by the [Ne] noble gas configuration are in lower-energy orbitals than the n=3 electrons.
The [Ne] configuration can be written 1s2 2s2 2p6.
The lowest energy orbital is the one with the lowest quantum numbers, hence, n=1, l=0.
Electrons in four hydrogen atoms fall from an excited state to the ground state, where the quantum number n=1, giving off a single photon in the process. Based on the photon, which electron was the farthest distance away from the nucleus before it fell to it ground state (h = 6.6 X 10−34 m2 X kg/s is Planck’s constant)?- a)The electron for which the photon’s wavelength = 10.2/hc eV
- b)The electron for which the photon’s frequency v = 12.1/h eV
- c)The electron for which the photon’s wavelength = 12.1/hc eV
- d)The electron for which the photon’s wavelength = 12.8/h eV
Correct answer is option 'D'. Can you explain this answer?
Electrons in four hydrogen atoms fall from an excited state to the ground state, where the quantum number n=1, giving off a single photon in the process. Based on the photon, which electron was the farthest distance away from the nucleus before it fell to it ground state (h = 6.6 X 10−34 m2 X kg/s is Planck’s constant)?
a)
The electron for which the photon’s wavelength = 10.2/hc eV
b)
The electron for which the photon’s frequency v = 12.1/h eV
c)
The electron for which the photon’s wavelength = 12.1/hc eV
d)
The electron for which the photon’s wavelength = 12.8/h eV
|
|
Ayesha Joshi answered |
The Bohr radius, rn start subscript, n, end subscript, can be calculated in relation to the radius of the first orbit, r1 as rn = r1 x n2
This means that the electron that was farthest away is the one that had the highest initial energy. Since all of the electrons fell to the same ground state, the highest energy photon was given off by the electron that was most distant from the nucleus.
Recall that a shorter wavelength indicates a higher energy, and similarly photons with higher frequencies are more energetic. Comparing wavelengths, the = 12.1/h eV photon has higher energy than the one with = 10.2/hc eV Comparing frequencies, the V = 12.8/h eV photon has more energy than the = 12.1/h eV
Now compare the = 12.1/hc eV and V = 12.8/hc eV photons. Recall that E = hc/v and E = hv. Hence the photons’ energies are 12.1/hc eV x hc = 12.1eV and E = 12.8/h eV x h respectively. Therefore, the photon with frequency v = 12.8/h eV has the most energy, meaning that its corresponding electron started farthest from its nucleus.
Chapter doubts & questions for Electronic Structure - General Chemistry for MCAT 2025 is part of MCAT exam preparation. The chapters have been prepared according to the MCAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for MCAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Electronic Structure - General Chemistry for MCAT in English & Hindi are available as part of MCAT exam.
Download more important topics, notes, lectures and mock test series for MCAT Exam by signing up for free.
General Chemistry for MCAT
164 videos|11 docs|16 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup