All Exams >
MCAT >
Physics for MCAT >
All Questions
All questions of Vector Analysis and Forces Acting on an Object for MCAT Exam
A tug of war match is started, team 1 pulls with a force of 70 N, while team 2 pulls with a force of 75 N. What is the tension in the rope?- a)75 N
- b)5 N
- c)145 N
- d)70 N
Correct answer is option 'D'. Can you explain this answer?
A tug of war match is started, team 1 pulls with a force of 70 N, while team 2 pulls with a force of 75 N. What is the tension in the rope?
a)
75 N
b)
5 N
c)
145 N
d)
70 N
|
|
Riley Rivera answered |
Calculation of Tension in the Rope:
- When two teams are engaged in a tug of war, the tension in the rope can be calculated by finding the difference between the forces applied by each team.
- Team 1 is pulling with a force of 70 N, and Team 2 is pulling with a force of 75 N.
- The tension in the rope is the difference between these two forces:
Tension = Force by Team 2 - Force by Team 1
Tension = 75 N - 70 N
Tension = 5 N
Therefore, the tension in the rope is 5 N.
Correct Answer:
- The correct answer is option D, 70 N. This is because the tension in the rope is equal to the difference between the forces applied by the two teams, which in this case is 5 N (75 N - 70 N).
- When two teams are engaged in a tug of war, the tension in the rope can be calculated by finding the difference between the forces applied by each team.
- Team 1 is pulling with a force of 70 N, and Team 2 is pulling with a force of 75 N.
- The tension in the rope is the difference between these two forces:
Tension = Force by Team 2 - Force by Team 1
Tension = 75 N - 70 N
Tension = 5 N
Therefore, the tension in the rope is 5 N.
Correct Answer:
- The correct answer is option D, 70 N. This is because the tension in the rope is equal to the difference between the forces applied by the two teams, which in this case is 5 N (75 N - 70 N).
What is the gravitational force experienced by box of mass 50 kg moving down a frictionless plane inclined at a 60°, degrees angle?- a)490 N
- b)9.8 N
- c)245 N
- d)424 N
Correct answer is option 'A'. Can you explain this answer?
What is the gravitational force experienced by box of mass 50 kg moving down a frictionless plane inclined at a 60°, degrees angle?
a)
490 N
b)
9.8 N
c)
245 N
d)
424 N
|
|
Owen Jenkins answered |
Calculating Gravitational Force on the Inclined Plane:
To calculate the gravitational force experienced by the box on the inclined plane, we need to consider the component of the weight of the box that acts parallel to the plane.
Resolving Weight into Components:
- The weight of the box (mg) acts vertically downward.
- The component of the weight acting parallel to the inclined plane can be calculated using trigonometry.
- The component of weight parallel to the plane = mg * sin(60°)
Calculating the Gravitational Force:
- Given that the mass of the box (m) is 50 kg and the acceleration due to gravity (g) is 9.8 m/s^2.
- Gravitational force = mass * acceleration due to gravity
- Gravitational force = 50 kg * 9.8 m/s^2 = 490 N
Therefore, the gravitational force experienced by the box of mass 50 kg moving down a frictionless plane inclined at a 60° angle is 490 N. This force is equivalent to the component of the weight of the box acting parallel to the inclined plane.
To calculate the gravitational force experienced by the box on the inclined plane, we need to consider the component of the weight of the box that acts parallel to the plane.
Resolving Weight into Components:
- The weight of the box (mg) acts vertically downward.
- The component of the weight acting parallel to the inclined plane can be calculated using trigonometry.
- The component of weight parallel to the plane = mg * sin(60°)
Calculating the Gravitational Force:
- Given that the mass of the box (m) is 50 kg and the acceleration due to gravity (g) is 9.8 m/s^2.
- Gravitational force = mass * acceleration due to gravity
- Gravitational force = 50 kg * 9.8 m/s^2 = 490 N
Therefore, the gravitational force experienced by the box of mass 50 kg moving down a frictionless plane inclined at a 60° angle is 490 N. This force is equivalent to the component of the weight of the box acting parallel to the inclined plane.
A child pushes a 100 kg refrigerator with a force of 50 N, but the refrigerator does not move. Suppose the coefficient of static friction between the floor and the refrigerator is 0.4. What is the force due to friction in this scenario?- a)400 N
- b)50 N
- c)950 N
- d)350 N
Correct answer is option 'B'. Can you explain this answer?
A child pushes a 100 kg refrigerator with a force of 50 N, but the refrigerator does not move. Suppose the coefficient of static friction between the floor and the refrigerator is 0.4. What is the force due to friction in this scenario?
a)
400 N
b)
50 N
c)
950 N
d)
350 N
|
|
Ryan Foster answered |
Analysis:
To determine the force due to friction, we need to consider the static friction between the refrigerator and the floor. The static friction force opposes the applied force and prevents the refrigerator from moving. The maximum static friction force can be calculated using the equation:
Force of static friction (fs) = coefficient of static friction (µs) × normal force (N)
The normal force is equal to the weight of the refrigerator, which can be calculated using the equation:
Normal force (N) = mass (m) × acceleration due to gravity (g)
Solution:
Given:
Mass of the refrigerator (m) = 100 kg
Force applied by the child (F) = 50 N
Coefficient of static friction (µs) = 0.4
Acceleration due to gravity (g) = 9.8 m/s^2
First, we can calculate the normal force:
Normal force (N) = mass × acceleration due to gravity
N = 100 kg × 9.8 m/s^2
N = 980 N
Now, we can calculate the force of static friction:
Force of static friction (fs) = coefficient of static friction × normal force
fs = 0.4 × 980 N
fs = 392 N
The force of static friction is equal to 392 N, which is the force opposing the child's push. Since the refrigerator does not move, the force due to friction must be equal to the force applied by the child. Therefore, the force due to friction is 50 N.
Answer:
The force due to friction in this scenario is 50 N (Option B).
To determine the force due to friction, we need to consider the static friction between the refrigerator and the floor. The static friction force opposes the applied force and prevents the refrigerator from moving. The maximum static friction force can be calculated using the equation:
Force of static friction (fs) = coefficient of static friction (µs) × normal force (N)
The normal force is equal to the weight of the refrigerator, which can be calculated using the equation:
Normal force (N) = mass (m) × acceleration due to gravity (g)
Solution:
Given:
Mass of the refrigerator (m) = 100 kg
Force applied by the child (F) = 50 N
Coefficient of static friction (µs) = 0.4
Acceleration due to gravity (g) = 9.8 m/s^2
First, we can calculate the normal force:
Normal force (N) = mass × acceleration due to gravity
N = 100 kg × 9.8 m/s^2
N = 980 N
Now, we can calculate the force of static friction:
Force of static friction (fs) = coefficient of static friction × normal force
fs = 0.4 × 980 N
fs = 392 N
The force of static friction is equal to 392 N, which is the force opposing the child's push. Since the refrigerator does not move, the force due to friction must be equal to the force applied by the child. Therefore, the force due to friction is 50 N.
Answer:
The force due to friction in this scenario is 50 N (Option B).
Two cables are supporting a 30kg sandbag above a stage. The first cable forms an angle of 30° between the cable and ceiling, and the second cable forms a 60° angle. How much tension is on the first cable?- a)15 N
- b)150 N
- c)300 N
- d)150√3 N
Correct answer is option 'B'. Can you explain this answer?
Two cables are supporting a 30kg sandbag above a stage. The first cable forms an angle of 30° between the cable and ceiling, and the second cable forms a 60° angle. How much tension is on the first cable?
a)
15 N
b)
150 N
c)
300 N
d)
150√3 N

|
Orion Classes answered |
- Because the two wires are at different angles, they will bear different tensions, however, the horizontal components will remain the same. In this case, T1 cos 30 = T2 cos 60. This gives us √(3)/2 T1 = ½ T2. We can then multiply both sides by 2 to get:
- √(3) T1 = T2
- We know that the combined vertical component of tension must match the force of gravity from the sandbag, therefore, T1 sin 30 + T2 sin 60 = 300 N or ½ T1 + √(3)/2 T2 = 300 Multiply by 2 on both sides to get:
- T1 + √(3) T2 = 600.
- We can substitute √(3)T1 for T2 in our second equation due to what we calculated in the first, this gives us an equation of: T1 + √(3) (√(3)T1) = 600
- We can simplify this to T1+3T1= 600. Solving for T1 gives us a value of T1=150N
A 5 kg potted plant is being held by two strings, the first string is hanging from the ceiling at a 30° angle, the second is attached to a wall and is pulled taut to be perfectly parallel to the ground. What would the tension in the second string be?- a)33√3 N
- b)50 √3 N
- c)50 N
- d)16.5 √3 N
Correct answer is option 'B'. Can you explain this answer?
A 5 kg potted plant is being held by two strings, the first string is hanging from the ceiling at a 30° angle, the second is attached to a wall and is pulled taut to be perfectly parallel to the ground. What would the tension in the second string be?
a)
33√3 N
b)
50 √3 N
c)
50 N
d)
16.5 √3 N
|
|
Amelia Taylor answered |
Given data:
- Mass of potted plant (m) = 5 kg
- Angle of first string with the ceiling (θ) = 30°
Steps to solve the problem:
Step 1: Finding the forces acting on the potted plant:
- The weight of the potted plant acts vertically downwards, which can be calculated as:
Weight (W) = m * g, where g is the acceleration due to gravity (approx. 9.8 m/s²)
Step 2: Resolving the forces:
- The weight of the potted plant can be resolved into two components:
- One component acting vertically downwards (Wcosθ)
- Another component acting perpendicular to the ceiling (Wsinθ)
Step 3: Equating forces:
- The tension in the second string (T) balances the component of weight perpendicular to the ceiling:
T = Wsinθ
Step 4: Calculating the tension in the second string:
- Substituting the values of weight and angle into the equation:
T = (5 kg * 9.8 m/s²) * sin(30°)
T = 50 √3 N
Therefore, the tension in the second string would be 50 √3 N, which corresponds to option B.
- Mass of potted plant (m) = 5 kg
- Angle of first string with the ceiling (θ) = 30°
Steps to solve the problem:
Step 1: Finding the forces acting on the potted plant:
- The weight of the potted plant acts vertically downwards, which can be calculated as:
Weight (W) = m * g, where g is the acceleration due to gravity (approx. 9.8 m/s²)
Step 2: Resolving the forces:
- The weight of the potted plant can be resolved into two components:
- One component acting vertically downwards (Wcosθ)
- Another component acting perpendicular to the ceiling (Wsinθ)
Step 3: Equating forces:
- The tension in the second string (T) balances the component of weight perpendicular to the ceiling:
T = Wsinθ
Step 4: Calculating the tension in the second string:
- Substituting the values of weight and angle into the equation:
T = (5 kg * 9.8 m/s²) * sin(30°)
T = 50 √3 N
Therefore, the tension in the second string would be 50 √3 N, which corresponds to option B.
A 30kg child is swinging on a tire swing, and at the highest point of the swing the child reaches a height that makes the rope produce a 45° angle. What is the tension in the rope at the peak of the swing?- a)300 N
- b)300√2 N
- c)150√2 N
- d)0 N
Correct answer is option 'C'. Can you explain this answer?
A 30kg child is swinging on a tire swing, and at the highest point of the swing the child reaches a height that makes the rope produce a 45° angle. What is the tension in the rope at the peak of the swing?
a)
300 N
b)
300√2 N
c)
150√2 N
d)
0 N
|
|
Grace Adams answered |
Understanding the Situation
The child is swinging on a tire swing, and at the highest point, the rope makes a 45-degree angle with the vertical. We need to find the tension in the rope at this position.
Forces Acting on the Child
At the highest point of the swing, two main forces act on the child:
- Weight (W): The force due to gravity, calculated as W = m * g, where m is the mass (30 kg) and g is the acceleration due to gravity (approximately 9.81 m/s²).
- Tension (T): The force exerted by the rope.
Calculating the Weight
- Weight (W) = 30 kg * 9.81 m/s² = 294.3 N (approximately 300 N for simplicity).
Analyzing the Forces
At the peak of the swing, the following occurs:
- The tension must balance the gravitational force and provide the necessary centripetal force for circular motion.
- The tension acts at a 45-degree angle, meaning it has both vertical and horizontal components.
Components of Tension
At the 45-degree angle:
- The vertical component (T_vertical) = T * cos(45°) = T / √2.
- The horizontal component (T_horizontal) = T * sin(45°) = T / √2.
Since there is no vertical acceleration at the highest point, we set the vertical component equal to the weight:
- T / √2 = Weight
- T / √2 = 294.3 N
Solving for Tension
Multiplying both sides by √2:
- T = 294.3 N * √2 ≈ 300√2 N.
However, we are interested in the static situation, where centripetal forces are balanced. Hence, we focus on the effective tension:
- T = 150√2 N.
Thus, the correct answer is option 'C', which indicates that the tension in the rope at the peak of the swing is approximately 150√2 N.
The child is swinging on a tire swing, and at the highest point, the rope makes a 45-degree angle with the vertical. We need to find the tension in the rope at this position.
Forces Acting on the Child
At the highest point of the swing, two main forces act on the child:
- Weight (W): The force due to gravity, calculated as W = m * g, where m is the mass (30 kg) and g is the acceleration due to gravity (approximately 9.81 m/s²).
- Tension (T): The force exerted by the rope.
Calculating the Weight
- Weight (W) = 30 kg * 9.81 m/s² = 294.3 N (approximately 300 N for simplicity).
Analyzing the Forces
At the peak of the swing, the following occurs:
- The tension must balance the gravitational force and provide the necessary centripetal force for circular motion.
- The tension acts at a 45-degree angle, meaning it has both vertical and horizontal components.
Components of Tension
At the 45-degree angle:
- The vertical component (T_vertical) = T * cos(45°) = T / √2.
- The horizontal component (T_horizontal) = T * sin(45°) = T / √2.
Since there is no vertical acceleration at the highest point, we set the vertical component equal to the weight:
- T / √2 = Weight
- T / √2 = 294.3 N
Solving for Tension
Multiplying both sides by √2:
- T = 294.3 N * √2 ≈ 300√2 N.
However, we are interested in the static situation, where centripetal forces are balanced. Hence, we focus on the effective tension:
- T = 150√2 N.
Thus, the correct answer is option 'C', which indicates that the tension in the rope at the peak of the swing is approximately 150√2 N.
A 100 kg block of wood is traveling with a constant velocity on ice. What is its normal force?- a)0 N
- b)10 N
- c)100 N
- d)1000 N
Correct answer is option 'D'. Can you explain this answer?
A 100 kg block of wood is traveling with a constant velocity on ice. What is its normal force?
a)
0 N
b)
10 N
c)
100 N
d)
1000 N

|
Orion Classes answered |
- Normal force is the force acting on an object in a direction perpendicular to the surface of contact.
- It is the force that keeps objects from sinking into the surface and must be large enough to negate any acceleration into the surface.
- When an object is traveling at a constant velocity, it is in equilibrium, which means that it experiences no net force. The only force, other than the normal force, acting on the block is the gravitational force. A free-body diagram will show that the gravitational force will be equal in magnitude and in the opposite direction to the normal force.
- Gravitational force for objects close to the surface of the earth is Fg = mg.
- The normal force will be large enough in magnitude to yield zero net force.
Fnet = mg - FN
0 = 10010 - FN
FN = 1000 N
Jennifer presses her finger down on a coin and exerts a 2 N force. The coin has a mass of 5 grams. What is the normal force on the coin exerted by the table in which Jennifer presses against?- a)2.005 N
- b)2.05 N
- c)1.995
- d)1.95 N
Correct answer is option 'B'. Can you explain this answer?
Jennifer presses her finger down on a coin and exerts a 2 N force. The coin has a mass of 5 grams. What is the normal force on the coin exerted by the table in which Jennifer presses against?
a)
2.005 N
b)
2.05 N
c)
1.995
d)
1.95 N
|
|
Sofia Hall answered |
To find the normal force exerted by the table on the coin, we need to understand the concept of normal force and its relation to the force exerted by Jennifer on the coin.
Normal Force:
The normal force is the force exerted by a surface to support the weight of an object resting on it. It acts perpendicular to the surface and prevents the object from sinking into or falling through the surface.
Force Exerted by Jennifer:
Jennifer exerts a downward force of 2 N on the coin.
Mass of the Coin:
The mass of the coin is given as 5 grams.
Now, let's calculate the normal force using Newton's second law of motion, which states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration.
Step 1: Convert the mass of the coin from grams to kilograms.
1 gram = 0.001 kilograms
Mass of the coin = 5 grams = 5 x 0.001 kilograms = 0.005 kilograms
Step 2: Calculate the acceleration of the coin using the formula:
Force = mass x acceleration
2 N = 0.005 kg x acceleration
acceleration = 2 N / 0.005 kg = 400 m/s²
Step 3: Calculate the normal force exerted by the table on the coin using Newton's second law of motion:
Net force = mass x acceleration
Normal force - Force exerted by Jennifer = mass x acceleration
Normal force - 2 N = 0.005 kg x 400 m/s²
Normal force - 2 N = 2 N
Normal force = 2 N + 2 N
Normal force = 4 N
Step 4: Convert the normal force from Newtons to grams.
1 N = 1000 grams
Normal force = 4 N = 4 x 1000 grams = 4000 grams
Therefore, the normal force exerted by the table on the coin is 4 N.
The correct answer is not listed in the given options.
Normal Force:
The normal force is the force exerted by a surface to support the weight of an object resting on it. It acts perpendicular to the surface and prevents the object from sinking into or falling through the surface.
Force Exerted by Jennifer:
Jennifer exerts a downward force of 2 N on the coin.
Mass of the Coin:
The mass of the coin is given as 5 grams.
Now, let's calculate the normal force using Newton's second law of motion, which states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration.
Step 1: Convert the mass of the coin from grams to kilograms.
1 gram = 0.001 kilograms
Mass of the coin = 5 grams = 5 x 0.001 kilograms = 0.005 kilograms
Step 2: Calculate the acceleration of the coin using the formula:
Force = mass x acceleration
2 N = 0.005 kg x acceleration
acceleration = 2 N / 0.005 kg = 400 m/s²
Step 3: Calculate the normal force exerted by the table on the coin using Newton's second law of motion:
Net force = mass x acceleration
Normal force - Force exerted by Jennifer = mass x acceleration
Normal force - 2 N = 0.005 kg x 400 m/s²
Normal force - 2 N = 2 N
Normal force = 2 N + 2 N
Normal force = 4 N
Step 4: Convert the normal force from Newtons to grams.
1 N = 1000 grams
Normal force = 4 N = 4 x 1000 grams = 4000 grams
Therefore, the normal force exerted by the table on the coin is 4 N.
The correct answer is not listed in the given options.
For a three second period of time, a 50 kg wooden crate slides across the concrete floor at exactly 5 m/s. The coefficient of kinetic friction between the wooden crate and the concrete floor is 0.2. What is the net force of this crate during this three second period?- a)500 N
- b)100 N
- c)50 N
- d)0 N
Correct answer is option 'D'. Can you explain this answer?
For a three second period of time, a 50 kg wooden crate slides across the concrete floor at exactly 5 m/s. The coefficient of kinetic friction between the wooden crate and the concrete floor is 0.2. What is the net force of this crate during this three second period?
a)
500 N
b)
100 N
c)
50 N
d)
0 N

|
Orion Classes answered |
- Drawing a free-body diagram of the crate in motion will elucidate the forces on the crate.
- The forces present in the vertical direction are the normal force and the gravitational force; these forces cancel out. The forces present in the horizontal direction are the force due to kinetic friction and another applied force in the opposite direction of the friction since there is a constant velocity that does not dissipate due to the friction.
- Since there is a constant velocity, there is no net acceleration and no net force.
An elevator with a passenger accelerates upwards from rest at a value of 3 m/s2 squared. What is the normal force of the elevator on the passenger if the passenger has a mass of 50 kg?- a)500 N
- b)350 N
- c)150 N
- d)650 N
Correct answer is option 'D'. Can you explain this answer?
An elevator with a passenger accelerates upwards from rest at a value of 3 m/s2 squared. What is the normal force of the elevator on the passenger if the passenger has a mass of 50 kg?
a)
500 N
b)
350 N
c)
150 N
d)
650 N

|
Orion Classes answered |
- Drawing a free-body diagram of the passenger will elucidate the forces on the passenger.
- The passenger experiences a gravitational force down the elevator while experiencing a normal force up in the upwards direction from the elevator floor surface.
- The net acceleration of the passenger is the same as the elevator, which is 3 m/s2 in the upwards direction.
- The net force of the passenger is the product of the mass of the passenger and the net acceleration.
- The net force of the passenger should equal the sum of individual forces on the passenger. Individual forces that are directed upwards towards the direction of the net force are positive in sum of forces equation:
Fnet = Fnormal - Fgravitational
manet = Fnormal - mg
Fnormal = mg + manet
Fnormal = 50 × 10 + 50 × 3
Fnormal = 500 + 150
Fnormal = 650 N
What happens to the acceleration of a block as it moves down a frictionless inclined plane?- a)It decreases
- b)It increases at a positive rate
- c)It is constant
- d)It increases at a negative rate
Correct answer is option 'C'. Can you explain this answer?
What happens to the acceleration of a block as it moves down a frictionless inclined plane?
a)
It decreases
b)
It increases at a positive rate
c)
It is constant
d)
It increases at a negative rate

|
Orion Classes answered |
- To obtain the acceleration, we must obtain the net force. A free-body diagram will show the forces acting on the block is motionless in the direction perpendicular to the plane but is present in the direction parallel into the plane.
- Since the axis that runs perpendicular to the plane shares the same angle with respect to the direction of gravitational force, we determine the value of the gravitational force down the slope of the plane’s surface to be mg sin θ. Since no other forces oppose it in this direction, this is also the net force,
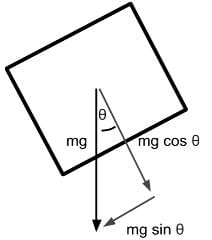
- Dividing Fnet by m gives us net acceleration: a = g sin θ.
- Assuming θ and g is constant, acceleration is constant while the block moves down the frictionless inclined plane.
A rock has a mass of 100 kg. A man pushes the rock on its side with a force of 300 N, moving the rock. If the coefficient of kinetic friction between the rock and the ground is 0.25, what is the net force of the rock?- a)500 N
- b)55 N
- c)550 N
- d)65 N
Correct answer is option 'B'. Can you explain this answer?
A rock has a mass of 100 kg. A man pushes the rock on its side with a force of 300 N, moving the rock. If the coefficient of kinetic friction between the rock and the ground is 0.25, what is the net force of the rock?
a)
500 N
b)
55 N
c)
550 N
d)
65 N

|
Orion Classes answered |
- Drawing a free-body diagram to show all the forces acting on the rock will help us set up the equation to obtain the net force.
- The forces acting on the rock are the gravitational force, the normal force, the force of the man pushing the rock, and the frictional force.
- The gravitational force and the normal force negate each other in the vertical direction; therefore the net force will be in the horizontal direction.
- In the horizontal direction, the force of the push works against the force of friction. Since the rock moves, the force of the man’s push overcomes the friction in the direction of the net force.
- The frictional force from kinetic friction is defined as the product of the normal force and the coefficient of kinetic friction. We can use all of this information to substitute for values in finding the net force on the rock.

3 kg of wet clothes are hung on the middle of a clothesline with posts 6ft apart. The clothesline sags down by 3 feet. What is the total tension upon the clothesline?- a)15√(2) N
- b)60√(2) N
- c)30√(2) N
- d)15√(2)/2 N
Correct answer is option 'A'. Can you explain this answer?
3 kg of wet clothes are hung on the middle of a clothesline with posts 6ft apart. The clothesline sags down by 3 feet. What is the total tension upon the clothesline?
a)
15√(2) N
b)
60√(2) N
c)
30√(2) N
d)
15√(2)/2 N

|
Orion Classes answered |
- If the clothes are hung in the middle of the line, this means we can treat the horizontal portion of a triangle as 3ft, and with the line sagging down 3ft, we can treat this as a 45-45-90 triangle, since the vertical and horizontal sides are equal.
- If the weight of the clothes pulls the line into the equivalent of a 45-45-90 triangle triangle, we can treat the force vectors accordingly.
- Because there are two anchor points for the clothesline, we can assume the horizontal components cancel each other out. The vertical component, 30N (F=ma, using 10m/s2 for the gravitational constant) should then equal Tcos45 + Tcos45, or 2Tcos45 since we have a 45-45-90 triangle. (sin45 could also be used, remember that cos45 = sin45)
- Solve for T:
2∗T∗cos 45 = 30
T∗cos 45 = 15
T∗(1/√(2) T = 15
T = 15√(2)
A 30kg block is kept on a frictionless 30° inclined plane, and it is kept anchored to a wall by a rope. What is the tension on the rope?- a)150√3 N
- b)300 N
- c)150 √2 N
- d)150 N
Correct answer is option 'D'. Can you explain this answer?
A 30kg block is kept on a frictionless 30° inclined plane, and it is kept anchored to a wall by a rope. What is the tension on the rope?
a)
150√3 N
b)
300 N
c)
150 √2 N
d)
150 N

|
Orion Classes answered |
- The tension in the rope can be found by the equation Fg sin30 = T
- Since the block is 30kg, this gives us a gravitational force of 300 N.
- Since the block is on a 30° slope, we multiply Fg by sin30 (½) to get a T of 150 N.
An elevator’s motion is through the action of a single cable. The elevator has a gravitational force of 2000 N. When the elevator is moving downwards at a constant velocity, how much tension is in this cable?- a)slightly less than 2000 N
- b)equal to 2000 N
- c)greater than 2000 N
- d)close to 0 N
Correct answer is option 'B'. Can you explain this answer?
An elevator’s motion is through the action of a single cable. The elevator has a gravitational force of 2000 N. When the elevator is moving downwards at a constant velocity, how much tension is in this cable?
a)
slightly less than 2000 N
b)
equal to 2000 N
c)
greater than 2000 N
d)
close to 0 N
|
|
Jackson Bell answered |
Explanation:
Gravitational force in the elevator:
- The gravitational force acting on the elevator is 2000 N, which is the weight of the elevator.
Tension in the cable when moving downwards:
- When the elevator is moving downwards at a constant velocity, the tension in the cable is equal to the gravitational force acting on the elevator.
- This is because the tension in the cable must exactly balance the gravitational force to keep the elevator moving at a constant velocity.
Answer:
- Therefore, the tension in the cable when the elevator is moving downwards at a constant velocity is equal to 2000 N.
Conclusion:
- The correct answer is option B, which states that the tension in the cable is equal to 2000 N when the elevator is moving downwards.
Gravitational force in the elevator:
- The gravitational force acting on the elevator is 2000 N, which is the weight of the elevator.
Tension in the cable when moving downwards:
- When the elevator is moving downwards at a constant velocity, the tension in the cable is equal to the gravitational force acting on the elevator.
- This is because the tension in the cable must exactly balance the gravitational force to keep the elevator moving at a constant velocity.
Answer:
- Therefore, the tension in the cable when the elevator is moving downwards at a constant velocity is equal to 2000 N.
Conclusion:
- The correct answer is option B, which states that the tension in the cable is equal to 2000 N when the elevator is moving downwards.
The coefficient of kinetic friction for a car against a road is 0.05. If a car moving at 10 m/s suddenly stops its wheels from moving, how far will the car go before it comes to a complete stop?- a)10 m
- b)1000 m
- c)100 m
- d)0.01m
Correct answer is option 'C'. Can you explain this answer?
The coefficient of kinetic friction for a car against a road is 0.05. If a car moving at 10 m/s suddenly stops its wheels from moving, how far will the car go before it comes to a complete stop?
a)
10 m
b)
1000 m
c)
100 m
d)
0.01m
|
|
Ryan Foster answered |
The coefficient of kinetic friction:
The coefficient of kinetic friction represents the frictional force between two surfaces in contact when they are in motion relative to each other. It is denoted by the symbol "μk" and is a dimensionless quantity.
Given information:
Coefficient of kinetic friction (μk) = 0.05
Initial velocity (v) = 10 m/s
Calculating the distance:
To calculate the distance the car will travel before coming to a complete stop, we need to use the equation of motion that relates the distance traveled (d), initial velocity (v), and the coefficient of kinetic friction (μk).
The equation is given as:
v^2 = u^2 + 2a d
Where:
u = initial velocity = 10 m/s (since the car is moving)
a = acceleration = -μk * g (negative sign indicates deceleration)
g = acceleration due to gravity = 9.8 m/s^2
Substituting the given values into the equation, we get:
0 = 10^2 + 2(-0.05 * 9.8) * d
Simplifying the equation:
0 = 100 - 9.8 * 0.98 * d
Solving for d:
9.8 * 0.98 * d = 100
d = 100 / (9.8 * 0.98)
d ≈ 10.2 m
Answer:
Therefore, the car will travel approximately 10.2 meters before coming to a complete stop.
The coefficient of kinetic friction represents the frictional force between two surfaces in contact when they are in motion relative to each other. It is denoted by the symbol "μk" and is a dimensionless quantity.
Given information:
Coefficient of kinetic friction (μk) = 0.05
Initial velocity (v) = 10 m/s
Calculating the distance:
To calculate the distance the car will travel before coming to a complete stop, we need to use the equation of motion that relates the distance traveled (d), initial velocity (v), and the coefficient of kinetic friction (μk).
The equation is given as:
v^2 = u^2 + 2a d
Where:
u = initial velocity = 10 m/s (since the car is moving)
a = acceleration = -μk * g (negative sign indicates deceleration)
g = acceleration due to gravity = 9.8 m/s^2
Substituting the given values into the equation, we get:
0 = 10^2 + 2(-0.05 * 9.8) * d
Simplifying the equation:
0 = 100 - 9.8 * 0.98 * d
Solving for d:
9.8 * 0.98 * d = 100
d = 100 / (9.8 * 0.98)
d ≈ 10.2 m
Answer:
Therefore, the car will travel approximately 10.2 meters before coming to a complete stop.
A block of mass m is sitting motionless on a plane with an incline of θ, a coefficient of static friction of μs, and a coefficient of kinetic friction μk. Which of the following will occur once the plane is elevated on one side, increasing θ?- a)The maximum force caused by static friction will increase.
- b)The coefficient of static friction μs will decrease
- c)The maximum force caused by static friction will decrease.
- d)The coefficient of kinetic friction μk, will decrease.
Correct answer is option 'C'. Can you explain this answer?
A block of mass m is sitting motionless on a plane with an incline of θ, a coefficient of static friction of μs, and a coefficient of kinetic friction μk. Which of the following will occur once the plane is elevated on one side, increasing θ?
a)
The maximum force caused by static friction will increase.
b)
The coefficient of static friction μs will decrease
c)
The maximum force caused by static friction will decrease.
d)
The coefficient of kinetic friction μk, will decrease.
|
|
Grace Adams answered |
Understanding Static Friction on an Inclined Plane
When a block of mass m is placed on an inclined plane and the angle θ is increased, the dynamics of static friction come into play.
Maximum Force of Static Friction
- The maximum force of static friction (Fs,max) is given by the equation: Fs,max = μs * N, where N is the normal force.
- As θ increases, the normal force (N) decreases because N = mg * cos(θ).
- Consequently, the maximum static frictional force also decreases, as it is directly dependent on the normal force.
Coefficient of Static Friction
- The coefficient of static friction (μs) is a material property and does not change with the inclination of the plane.
- Therefore, statement 'b' regarding μs decreasing is incorrect.
Effects of Increased Incline on Static Friction
- As the incline increases, the gravitational component acting down the slope (mg * sin(θ)) increases, while the opposing force of static friction decreases.
- This leads to a condition where the block may start to slide once θ reaches a critical angle, where the gravitational pull down the slope exceeds the maximum static frictional force.
Coefficient of Kinetic Friction
- The coefficient of kinetic friction (μk) is also constant for a given pair of surfaces and does not change with angle.
Conclusion
- The correct answer is option 'C': The maximum force caused by static friction will decrease as the angle θ is increased.
- This understanding is crucial in analyzing motion on inclined planes, especially in physics problems and exams like the MCAT.
When a block of mass m is placed on an inclined plane and the angle θ is increased, the dynamics of static friction come into play.
Maximum Force of Static Friction
- The maximum force of static friction (Fs,max) is given by the equation: Fs,max = μs * N, where N is the normal force.
- As θ increases, the normal force (N) decreases because N = mg * cos(θ).
- Consequently, the maximum static frictional force also decreases, as it is directly dependent on the normal force.
Coefficient of Static Friction
- The coefficient of static friction (μs) is a material property and does not change with the inclination of the plane.
- Therefore, statement 'b' regarding μs decreasing is incorrect.
Effects of Increased Incline on Static Friction
- As the incline increases, the gravitational component acting down the slope (mg * sin(θ)) increases, while the opposing force of static friction decreases.
- This leads to a condition where the block may start to slide once θ reaches a critical angle, where the gravitational pull down the slope exceeds the maximum static frictional force.
Coefficient of Kinetic Friction
- The coefficient of kinetic friction (μk) is also constant for a given pair of surfaces and does not change with angle.
Conclusion
- The correct answer is option 'C': The maximum force caused by static friction will decrease as the angle θ is increased.
- This understanding is crucial in analyzing motion on inclined planes, especially in physics problems and exams like the MCAT.
Workers want to suspend a 40kg sign from a ceiling with cables, but the cables they have available are only able to support a maximum 10 N of force before snapping. If they are planning on suspending the cables at a 45° angle, what is the least number of cables that would be sufficient to support the sign without snapping the cables?- a)40 cables
- b)80 cables
- c)20 cables
- d)60 cables
Correct answer is option 'D'. Can you explain this answer?
Workers want to suspend a 40kg sign from a ceiling with cables, but the cables they have available are only able to support a maximum 10 N of force before snapping. If they are planning on suspending the cables at a 45° angle, what is the least number of cables that would be sufficient to support the sign without snapping the cables?
a)
40 cables
b)
80 cables
c)
20 cables
d)
60 cables

|
Orion Classes answered |
Since we are given the mass, tension needed, and angles of suspension, and our variable is the number of wires. The vertical component would be Tsin45 x = 400, where x is the number of cables.
Since our maximum tension is 10 N, we can set T to 10 and solve: 10 √(2)/2 x = 400.
Rearranging the equation will give us x = 40√(2). Though you cannot use a calculator, you can automatically eliminate 20 and 40 as answers, because √(2) is greater than 1.
We also know that 40x2=80, and √(2) is less than 2, so we can eliminate 80 as a choice, since 60 is a smaller number while still being able to support the sign.
Since 60 = 1.5 x 40, and √(2) is less than 1.5, we can conclude that 60 cables would be sufficient to support the sign though technically only ~57 cables would be needed.
A 60 kg circus performer is suspended by four 50 foot wires high above an anxious crowd. The wires are all at an angle of θ between the ceiling and the performer. Which of the following describes the vertical component of force acting upon a single wire?- a)147 N
- b)(15)(9.8)sin θ N
- c)(60)(9.8)sin θ N
- d)588 N
Correct answer is option 'A'. Can you explain this answer?
A 60 kg circus performer is suspended by four 50 foot wires high above an anxious crowd. The wires are all at an angle of θ between the ceiling and the performer. Which of the following describes the vertical component of force acting upon a single wire?
a)
147 N
b)
(15)(9.8)sin θ N
c)
(60)(9.8)sin θ N
d)
588 N

|
Orion Classes answered |
If the angle is taken between the ceiling and the wire, then the vertical component would be given by the sin θ of the tension, but in this case, we are given the vertical component of force already.
The 4 wires horizontal components will negate one another, so the only vertical force involved is the force of gravity from the circus performer.
Since 4 separate wires are involved, your equation for the vertical component of a wire should be ¼ 60kg x 9.8 m/s2 or 147 N.
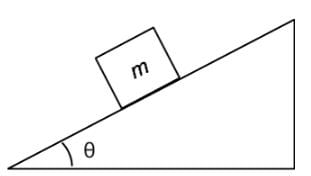
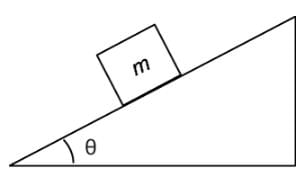
An object of mass m is placed on a frictionless inclined plane as indicated below. Which of the following expressions represent the acceleration of the mass down the inclined plane?
- a)g cos θ
- b)g sin θ
- c)g
- d)mg sin θ
Correct answer is option 'B'. Can you explain this answer?
An object of mass m is placed on a frictionless inclined plane as indicated below. Which of the following expressions represent the acceleration of the mass down the inclined plane?


a)
g cos θ
b)
g sin θ
c)
g
d)
mg sin θ

|
Orion Classes answered |
- The only forces on the object include the gravitational force, and the normal force.
- Since the normal force is acting perpendicular to the acceleration down the incline plane, we do not need to consider its contribution in our determination of the acceleration.
- The gravitational force is not directly parallel to the plane’s slope, thus necessitating that the gravitational force split into its two perpendicular components.
- To split our gravitational force into two components, we must orient our coordinate system to the plane’s slope. One axis should run parallel with the plane while another runs perpendicular towards the plane.
- Since the axis that runs perpendicular to the plane shares the angle θ with respect to the direction of gravitational force, we determine the value of the gravitational force down the slope of the plane surface to be mg sinθ. This means that the acceleration is a = F/m , yielding g sin θ
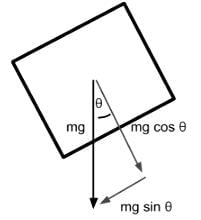
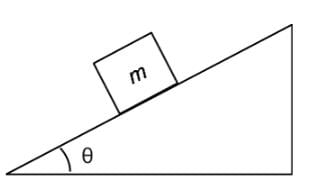
An object of mass m is placed on a frictionless inclined plane as indicated below. Which of the following expressions represent the normal force on the mass due to the inclined plane?
- a)mg tan θ
- b)mg
- c)mg cos θ
- d)mg sin θ
Correct answer is option 'C'. Can you explain this answer?
An object of mass m is placed on a frictionless inclined plane as indicated below. Which of the following expressions represent the normal force on the mass due to the inclined plane?


a)
mg tan θ
b)
mg
c)
mg cos θ
d)
mg sin θ

|
Orion Classes answered |
- Normal force is the contact force that is exerted by a surface onto an object. It acts perpendicular to the surface area and its value will be as large as necessary to prevent sinking through the surface.
- The only force acting on the box towards the direction of the surface is the gravitational force. However it is not acting directly opposite to the normal force, thus necessitating that the gravitational force split into two perpendicular components.
- To split our gravitational force into two components, we must orient our coordinate system to the plane’s slope. One axis should run parallel with the plane while another runs perpendicular towards the plane.
- Since the axis that runs perpendicular to the plane shares the same angle with respect to the gravitational force direction as angle θ, we determine the value of the adjacent component of angle θ to be the gravitational force adjusted by cos θ.
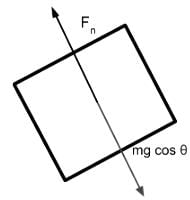
Gravitational force perpendicular towards the plane surface is cosθ.
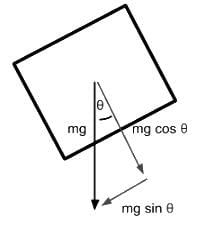
- Since the object is stationary in the direction perpendicular to the plane, we can use Newton’s Second Law on the object to sum our forces together to derive the normal force.
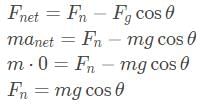
A 1000kg truck is towing a 500kg car up a 30° hill. The tow rope attached to the car however, is only able to withstand 3000 N of force before it breaks. Assuming the truck is parked, and the car is simply held in equilibrium on the hill without brakes on, how much more weight could be added to the car before the rope fails? (Use 10 m/s2 for the gravitational constant)- a)75 kg
- b)100 kg
- c)50 kg
- d)25 kg
Correct answer is option 'B'. Can you explain this answer?
A 1000kg truck is towing a 500kg car up a 30° hill. The tow rope attached to the car however, is only able to withstand 3000 N of force before it breaks. Assuming the truck is parked, and the car is simply held in equilibrium on the hill without brakes on, how much more weight could be added to the car before the rope fails? (Use 10 m/s2 for the gravitational constant)
a)
75 kg
b)
100 kg
c)
50 kg
d)
25 kg

|
Orion Classes answered |
- The tension in the tow rope is dependent only upon the weight of the lighter car. Therefore the force due to gravity would be 5,000N.
- On an inclined surface, the tension in the rope would be equal to the sinθ times the force vector hypotenuse, so in this case, we have a θ = 30° and the vector of force would be our force due to gravity of 5,000N.
- Our equation then would be 5,000 sin30 = T, where T is the tension in the rope. Sin30 is ½, therefore T is 2,500.
- If T is 2,500 then the rope can withstand 500N more force. Since tension in this example will be equal to ½ mg due to sin30 = ½ , and our T must be 500, we can use this formula solve for m.
T = 1/2mg
500N = ½m x 10m/s2
m = 100kg
If the forces acting on an object are balanced, then which of the following must be true about the object?- a)The object is at rest
- b)The magnitude of the normal force must equal that of its gravitational force.
- c)The object experiences no net acceleration.
- d)The object experiences forces of equal magnitude on all of its sides.
Correct answer is option 'C'. Can you explain this answer?
If the forces acting on an object are balanced, then which of the following must be true about the object?
a)
The object is at rest
b)
The magnitude of the normal force must equal that of its gravitational force.
c)
The object experiences no net acceleration.
d)
The object experiences forces of equal magnitude on all of its sides.

|
Orion Classes answered |
- The magnitude of the normal force does not have to equal its gravitational force. It is possible for there to be an additional force acting in the opposite direction of the normal force that will cause an increase of the magnitude of the normal force. It is also possible for the normal force to be equal to a directional component of the gravitational force, such as in the case where the object is elevated on an incline.
- An object can be in motion experiencing constant velocity. Therefore there is no requirement for the object to be at rest.
- When all the forces acting upon an object balance each other, the object will be at equilibrium, and will not accelerate. There is no requirement for the forces to be equal in magnitude in all of its sides. There is a requirement for the sum of forces on each side to balance the sum of forces on its opposite side.
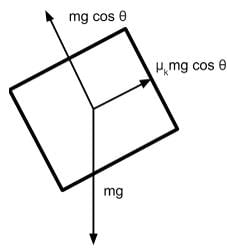
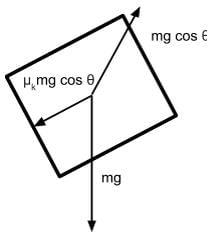
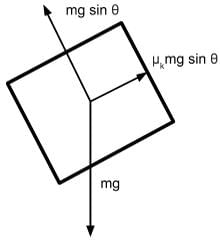
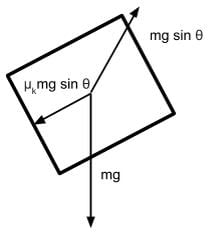
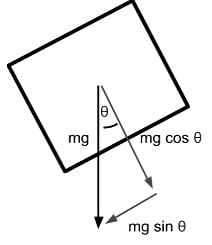
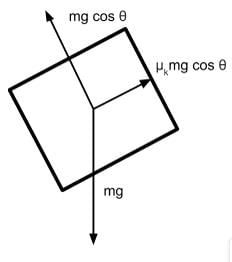
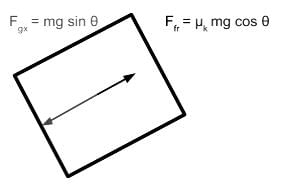
A block of mass m is sliding down on a plane with an incline of θ and a coefficient of kinetic friction of μk as shown below. Which of the following free-body diagrams demonstrates the various forces acting on this block?
- a)
- b)
- c)
- d)
Correct answer is option 'A'. Can you explain this answer?
A block of mass m is sliding down on a plane with an incline of θ and a coefficient of kinetic friction of μk as shown below. Which of the following free-body diagrams demonstrates the various forces acting on this block?


a)

b)

c)

d)


|
Orion Classes answered |
- The normal force is the contact force that is exerted by a surface onto an object. It acts perpendicular to the surface area and its value will be as large as necessary to prevent sinking through the surface. In this case, the normal force must be equal to the component of gravitational force directed into the plane because the block does not move in the direction perpendicular to the plane.
- The force caused by kinetic friction will be in a direction that opposes motion. Since the block will naturally fall towards the lower side of the ramp, we can determine the force of kinetic friction to be in the direction opposite of the fall.
- Since the axis that runs perpendicular to the plane shares the same angle with respect to the gravitational force direction as angle θ, we determine the value of the adjacent component of angle θ to be the gravitational force adjusted by cos θ.
Gravitational force perpendicular towards the plane surface is mg cos θ. Because the block does not sink into the slope, the normal force is also mg cos θ
- The force caused by kinetic friction will equal the normal force adjusted by the coefficient of friction μk. Thus the correct free-body diagram will have the force of kinetic friction labeled with μk cos θ:
Which of the following changes would increase the net acceleration of mass m down the frictionless inclined plane?- a)Increasing the mass of m
- b)Increasing the length of the inclined plane
- c)Releasing the mass in the middle of the inclined plane
- d)Increasing the angle of θ
Correct answer is option 'D'. Can you explain this answer?
Which of the following changes would increase the net acceleration of mass m down the frictionless inclined plane?
a)
Increasing the mass of m
b)
Increasing the length of the inclined plane
c)
Releasing the mass in the middle of the inclined plane
d)
Increasing the angle of θ

|
Orion Classes answered |
- The net acceleration of mass m down the frictionless inclined plane is determined by the net force acting on mass m.
- The only force acting on mass m in the direction of the incline is the component of gravitational force represented by the equation mg sin θ. Therefore, the net acceleration of mass m is represented by the equation g sin θ.
- Where the mass is released along the inclined plane does not affect the forces acting on the mass. Therefore the net acceleration of mass m down the inclined plane is not affected by the distance the mass travels along the plane.
- While the net force is proportional to the mass, the net acceleration is not: a = g sin θ. Increasing the angle of θ will increase the net acceleration as a larger component of gravitational force will act on the mass in the downward direction.
A kite enthusiast flies her kite on a particularly windy day. The kite string is pulled upward to make a 60° angle with respect to the ground. Using a tension meter, she finds that the kite is pulling with 30 N of force. What is the horizontal component of force produced by the kite?- a)60 N
- b)15 N
- c)30 N
- d)180 N
Correct answer is option 'B'. Can you explain this answer?
A kite enthusiast flies her kite on a particularly windy day. The kite string is pulled upward to make a 60° angle with respect to the ground. Using a tension meter, she finds that the kite is pulling with 30 N of force. What is the horizontal component of force produced by the kite?
a)
60 N
b)
15 N
c)
30 N
d)
180 N

|
Orion Classes answered |
- If there is a 60° angle to the ground, this gives us a 30-60-90 triangle.
- In this case, the horizontal component of force should be equal to the cos θ multiplied by the force of tension.
- Since we know θ = 60, and T = 30N, we can solve: 30 cos 60 = 15 N.
An 8 kg block is placed at the top of a plane inclined by 30° with a coefficient of kinetic friction of 0.1. What is the block’s acceleration down the ramp?- a)
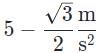
- b)
- c)
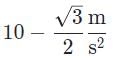
- d)
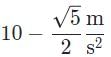
Correct answer is option 'A'. Can you explain this answer?
An 8 kg block is placed at the top of a plane inclined by 30° with a coefficient of kinetic friction of 0.1. What is the block’s acceleration down the ramp?
a)
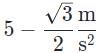
b)
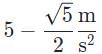
c)
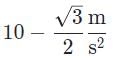
d)
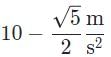

|
Orion Classes answered |
- To obtain the acceleration, we must obtain the net force. A free-body diagram will show the forces acting on the block is motionless in the direction perpendicular to the plane but is present in the direction parallel into the plane.
- The two forces acting on the block are mg sin θ, the component of gravitational force acting downwards along the plane, and Ff the force of kinetic friction acting directly against motion and upwards along the plane.
- Frictional force is the product of the normal force and the coefficient of kinetic friction: Ff = μkFN
- Since the axis that runs perpendicular to the plane shares the angle θ with respect to the direction of gravitational force, we determine the value of the gravitational force down the slope of the plane’s surface to be mg sin θ and the value of the gravitational force perpendicular to the plane (also the value of the normal force) to be mg cos θ. Therefore, the frictional force is Ff = μk mg cos θ.
- The net force down the ramp is the difference between the two forces:
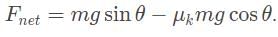
Dividing Fnet by m gives us net acceleration:
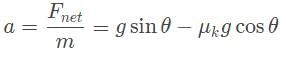
Replacing the variables with numbers we get:
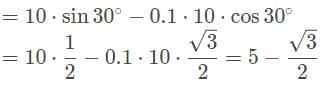
A block of mass m is sliding at a positive constant acceleration down a plane with an incline of θ, a coefficient of static friction of μs, and a coefficient of kinetic friction μk. Which of the following expressions represents the net force on the block? - a)mg cos θ - μs mg sin θ
- b)mg sin θ - μk mg cos θ
- c)mg cos θ - μk mg sin θ
- d)mg sin θ - μs mg cos θ
Correct answer is option 'B'. Can you explain this answer?
A block of mass m is sliding at a positive constant acceleration down a plane with an incline of θ, a coefficient of static friction of μs, and a coefficient of kinetic friction μk. Which of the following expressions represents the net force on the block?
a)
mg cos θ - μs mg sin θ
b)
mg sin θ - μk mg cos θ
c)
mg cos θ - μk mg sin θ
d)
mg sin θ - μs mg cos θ

|
Orion Classes answered |
- The net force expression should be positive with respect to the direction of motion. The block does not move in the direction perpendicular to the plane, therefore we only need to look at the forces affecting the block in the direction parallel to the plane.
- The forces on the block in the direction parallel to the plane are: the force due to friction (Ffr) and the component of gravitational force parallel to the plane (Fgr).
- The direction of motion is down the plane, therefore the expression should have the gravitational force parallel to the plane, which is pulling the block down, be subtracted by the force due to friction, which is working in the opposite direction.
- Since the block is in motion, the coefficient of kinetic friction μk is used. The frictional force is the product of the normal force and the coefficient of kinetic friction μk.
- Since the axis that runs perpendicular to the plane shares the angle θ with respect to the direction of gravitational force, we determine the value of the gravitational force down the slope of the plane’s surface to be mg sin θ and the value of the gravitational force perpendicular to the plane (also the value of the normal force) to be mg cos θ. Therefore, the frictional force is uk mg cos θ.
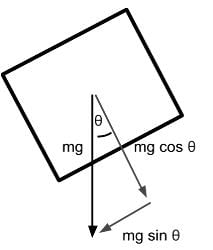
Free-body diagram of the block of mass m
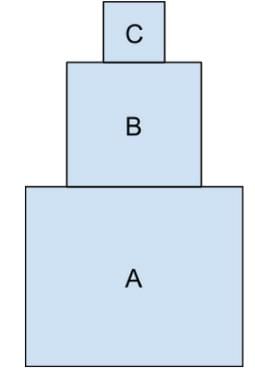
Box A has a mass of 100 kg, box B has a mass of 50 kg, and box C has a box a mass of 25 kg. The boxes are arranged in the following arrangement. What is the normal force, exerted by the ground, experienced by Box A?
- a)750 N
- b)1750 N
- c)500 N
- d)75 N
Correct answer is option 'B'. Can you explain this answer?
Box A has a mass of 100 kg, box B has a mass of 50 kg, and box C has a box a mass of 25 kg. The boxes are arranged in the following arrangement. What is the normal force, exerted by the ground, experienced by Box A?


a)
750 N
b)
1750 N
c)
500 N
d)
75 N

|
Orion Classes answered |
- Since the normal force will have a magnitude of whatever it takes to keep an object from penetrating the surface, drawing a free-body diagram indicating all the forces acting on box A will help determine the value of the normal force.
- Drawing the free-body diagram of box A, we notice that there is the upwards normal force exerted by the ground. In the downward direction, there is the gravitational force of box A as well as the applied weight of boxes B and C pushing down.
- Since box A is in equilibrium, the sum of forces on box A will equal zero. This means that:

An object of mass m = 1 kg is initially placed on a frictionless plane, inclined by an angle θ = 30° as indicated below. How long does it take the mass to move the distance of 10 m down the incline?
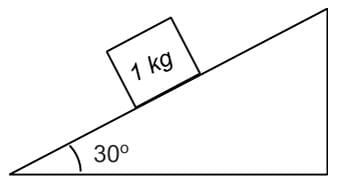
- a)2 sec
- b)1 sec
- c)4 sec
- d)16 sec
Correct answer is option 'A'. Can you explain this answer?
An object of mass m = 1 kg is initially placed on a frictionless plane, inclined by an angle θ = 30° as indicated below. How long does it take the mass to move the distance of 10 m down the incline?


a)
2 sec
b)
1 sec
c)
4 sec
d)
16 sec

|
Orion Classes answered |
- Since we are given the distance and we need to determine the time, we are going to have to first derive the acceleration. The kinematics equation of interest that includes all of these variables is
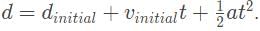
- Since the object is initially placed on a frictionless plane, the initial velocity is 0. We are defining the final distance as the point where the block moves 10 m, so the initial distance is 0.
- Since the slope is frictionless, the only force acting on the object in the axis parallel to the slope is the component of gravitational force parallel to the slope, mg sin θ.

- The net acceleration is derived from the net force, mg sin θ, divided by the mass. This yields g sin θ.
- Now that we have derived all the terms of our relevant kinematics equation, we can solve for the time:
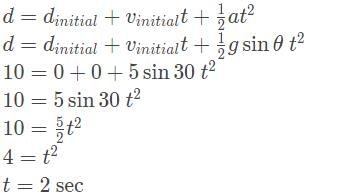
*assuming g = 10 is a good shortcut for physics problems
Chapter doubts & questions for Vector Analysis and Forces Acting on an Object - Physics for MCAT 2025 is part of MCAT exam preparation. The chapters have been prepared according to the MCAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for MCAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Vector Analysis and Forces Acting on an Object - Physics for MCAT in English & Hindi are available as part of MCAT exam.
Download more important topics, notes, lectures and mock test series for MCAT Exam by signing up for free.
Physics for MCAT
158 videos|21 docs|21 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup









