All Exams >
MCAT >
Physics for MCAT >
All Questions
All questions of Reflection and Refraction for MCAT Exam
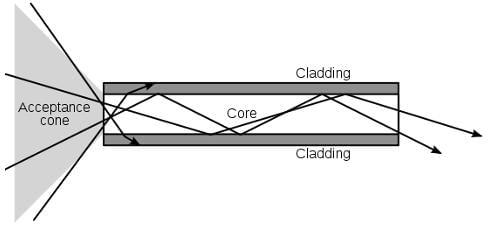Above is a schematic of a fiber optic cable, which maintains total internal reflection throughout the length of the cable. The index of refraction of the cladding of a cable is generally 1.52, while the core has an index of refraction of 1.62 Choosing from the list below, what is the smallest angle of incidence light could have to enter from the acceptance cone that would be able to ‘escape’ the fiber optic cable?- a)60°
- b)30°
- c)45°
- d)80°
Correct answer is option 'B'. Can you explain this answer?
Above is a schematic of a fiber optic cable, which maintains total internal reflection throughout the length of the cable. The index of refraction of the cladding of a cable is generally 1.52, while the core has an index of refraction of 1.62 Choosing from the list below, what is the smallest angle of incidence light could have to enter from the acceptance cone that would be able to ‘escape’ the fiber optic cable?
a)
60°
b)
30°
c)
45°
d)
80°
|
Ayesha Joshi answered |
- There are multiple ways to come to an answer. You can use the critical angle formula sin θc = n2/n1 but this requires some math gymnastics.
- One important realization to make is that the larger an angle of incidence is, the more likely it will be internally reflected. The angle of incidence is measured between the ray of light and the normal of the inside of the cable, therefore in the figure, the rays coming in from outside the acceptance cone would have the lowest angle of incidence.
- Since we’re looking for the smallest angle of incidence possible to escape the cable, we should simply pick 30°
- The harder way, if we use the formula, would give the result of sin θc = 1.52/1.62. We probably would need a calculator to solve this directly, but we should know the sine of 30°, 45°, and 60° , which are the available answer choices. Additionally, we know we want to find the smallest angle, so we can focus on 30°
- sin (30°) = 1/2, therefore sin (30°) is much smaller than the sin (θc), which is all we need to know. Remember, if an angle is smaller than the critical angle, it will not be internally reflected! Since 30° is our smallest incident angle choice, even if the other angles can ‘escape’ the cable, 30° must be the correct answer.
Which of the following is true concerning total internal reflection?
I. Light traveling from a lower index of refraction to a higher one can experience total internal refraction.
II. If the angle of incidence equals the critical angle then light will not be refracted
III. If an angle of incidence is larger than the critical angle, it will not experience total internal reflection.- a)I, II, III
- b)II only
- c)II & III
- d)None of the above are true
Correct answer is option 'D'. Can you explain this answer?
Which of the following is true concerning total internal reflection?
I. Light traveling from a lower index of refraction to a higher one can experience total internal refraction.
II. If the angle of incidence equals the critical angle then light will not be refracted
III. If an angle of incidence is larger than the critical angle, it will not experience total internal reflection.
I. Light traveling from a lower index of refraction to a higher one can experience total internal refraction.
II. If the angle of incidence equals the critical angle then light will not be refracted
III. If an angle of incidence is larger than the critical angle, it will not experience total internal reflection.
a)
I, II, III
b)
II only
c)
II & III
d)
None of the above are true
|
Evelyn Clark answered |
Explanation:
Total internal reflection occurs when light traveling from a higher index of refraction to a lower index of refraction is reflected back into the higher index material. Let's break down each statement given in the question:
I. Light traveling from a lower index of refraction to a higher one can experience total internal refraction:
- This statement is incorrect. Total internal reflection only occurs when light travels from a higher index of refraction to a lower one.
II. If the angle of incidence equals the critical angle then light will not be refracted:
- This statement is true. When the angle of incidence is equal to the critical angle, the refracted ray will travel along the interface between the two materials, resulting in no refraction.
III. If an angle of incidence is larger than the critical angle, it will not experience total internal reflection:
- This statement is also true. If the angle of incidence is greater than the critical angle, total internal reflection will not occur, and the light will be partially transmitted into the second material.
Therefore, the correct answer is option 'D' - None of the above are true.
In the figure below, from P → Q a ray of light passes from air through glass with a refraction index of 1.5. If the angle of reflection is 30° , what is sin of the angle of refraction?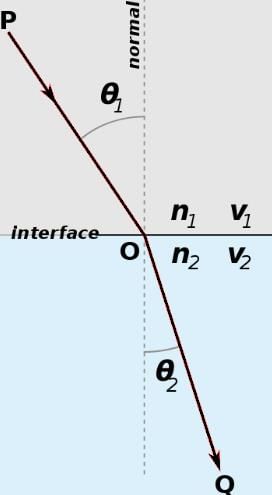
- a)1/2
- b)2/3
- c)
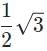
- d)1/3
Correct answer is option 'D'. Can you explain this answer?
In the figure below, from P → Q a ray of light passes from air through glass with a refraction index of 1.5. If the angle of reflection is 30° , what is sin of the angle of refraction?
a)
1/2
b)
2/3
c)
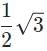
d)
1/3
|
Orion Classes answered |
- To find the sin of the angle of refraction you must use Snell’s law:
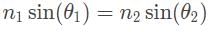
- The angle of reflection will be equal to the angle of incidence, so we can simply use 30° as θ1.
- We can basically treat the index of refraction of air (n1) as 1.
- Plugging in our values into Snell’s law we get
sin(30) = 1.5 sin θ2 therefore,
0.5 = 1.5 sin (θ2)
sin (θ2) = 1/3
Which of the following is true of reflected light rays from a surface?
I. The angle of incidence is equal to the angle of reflection for diffuse reflections.
II. The angle measured between the surface and the ray is the same magnitude as the angle of reflection
III. The angle of incidence is found by subtracting the angle made with the surface from the normal- a)I + II
- b)I + III
- c)II only
- d)I only
Correct answer is option 'B'. Can you explain this answer?
Which of the following is true of reflected light rays from a surface?
I. The angle of incidence is equal to the angle of reflection for diffuse reflections.
II. The angle measured between the surface and the ray is the same magnitude as the angle of reflection
III. The angle of incidence is found by subtracting the angle made with the surface from the normal
I. The angle of incidence is equal to the angle of reflection for diffuse reflections.
II. The angle measured between the surface and the ray is the same magnitude as the angle of reflection
III. The angle of incidence is found by subtracting the angle made with the surface from the normal
a)
I + II
b)
I + III
c)
II only
d)
I only
|
|
Ayesha Joshi answered |
- The angle of incidence is in fact found by taking the difference between the normal and the angle of reflection made at the surface
- The angle between the surface and the ray will not be equal to the angle of reflection
- The angle of incidence is always equal to the angle of reflection, even for diffuse reflections. Therefore I + III are both correct.
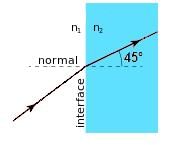A laser beam is refracted in a prism with an index of refraction (n2) of √3/√2. The angle of refraction is measured to be 45°. If the prism is in a vacuum, what is the angle between the incoming ray of light and the surface of the prism?- a)80°
- b)45°
- c)30°
- d)60°
Correct answer is option 'C'. Can you explain this answer?
A laser beam is refracted in a prism with an index of refraction (n2) of √3/√2. The angle of refraction is measured to be 45°. If the prism is in a vacuum, what is the angle between the incoming ray of light and the surface of the prism?
a)
80°
b)
45°
c)
30°
d)
60°
|
|
Orion Classes answered |
- Note that the angle of incidence is found by subtracting the angle made with the surface from the normal, and note how this is different from what the question is asking for.
- Use Snell’s law to find the angle of incidence, since it is in a vacuum, n1 = 1.
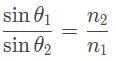
- We are trying to find θ1 Therefore:
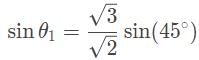
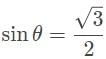
θ = 60° - Don’t let that answer fool you! That is simply our angle of incidence! Since our angle of incidence is measured from the normal of the surface, this means that the angle between the ray and the surface of the prism must be 30° (90 - 60 = 30)
A diamond has an index of refraction of 2.4, point, 4. What is the speed of light within the diamond?- a)2.25 × 108 m/s
- b)3.0 × 108 m/s
- c)7.2 × 108 m/s
- d)1.25 × 108 m/s
Correct answer is option 'D'. Can you explain this answer?
A diamond has an index of refraction of 2.4, point, 4. What is the speed of light within the diamond?
a)
2.25 × 108 m/s
b)
3.0 × 108 m/s
c)
7.2 × 108 m/s
d)
1.25 × 108 m/s
|
|
Ayesha Joshi answered |
- The formula for the index of refraction is n = c/v, where n is the index, c is the speed of light in a vacuum (3 × 108 m/s), and v is the velocity of light in the other medium.
- We can immediately disregard 7.2 × 108 m/s because that would mean light is moving faster than the speed of light in a vacuum, which isn’t possible.
- To solve, we simply divide 3.2 × 108 m/s by 2.4 A quick math trick to help solve this is to block out the extra zeroes and realize that 2.4 can’t go into 3.0 more than once, and therefore only 1.25 × 108 m/s could work as an answer.
What would the critical angle be for a flare lit underneath the surface ocean, if the index of refraction for ocean water is 1.33?- a)
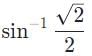
- b)
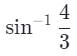
- c)
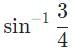
- d)
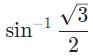
Correct answer is option 'C'. Can you explain this answer?
What would the critical angle be for a flare lit underneath the surface ocean, if the index of refraction for ocean water is 1.33?
a)
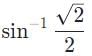
b)
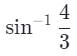
c)
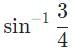
d)
|
|
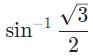
Orion Classes answered |
- To find the critical angle, we must use the formula
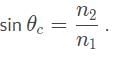
- The index of refraction for air can be considered 1, and since the example is light passing into air from water, our n2 should be 1.
- Plugging our values into the formula, we should get sin
A prism is used to separate white light into a rainbow. Which color of the visible spectrum would have the smallest angle of refraction (the angle between the ray and a line normal to the surface of the prism)?- a)Green
- b)Violet
- c)Red
- d)Orange
Correct answer is option 'B'. Can you explain this answer?
A prism is used to separate white light into a rainbow. Which color of the visible spectrum would have the smallest angle of refraction (the angle between the ray and a line normal to the surface of the prism)?
a)
Green
b)
Violet
c)
Red
d)
Orange
|
|
Ayesha Joshi answered |
- Wavelength of light and index of refraction are inversely proportional; i.e. the index of refraction increases as the wavelength of light decreases.
- Violet light would have the smallest wavelength of visible light, therefore the highest index of refraction.
- The larger the index of refraction, the smaller the angle of refraction (use Snell's Law to convince yourself of this!), therefore violet should have the smallest angle of refraction for visible light.
A ray of light refracts as it passes from glass into a vacuum. It’s angle of incidence is 30°, and its angle of refraction is 60° what is the index of refraction of the glass?- a)√3
- b)
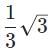
- c)1.33
- d)
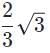
Correct answer is option 'A'. Can you explain this answer?
A ray of light refracts as it passes from glass into a vacuum. It’s angle of incidence is 30°, and its angle of refraction is 60° what is the index of refraction of the glass?
a)
√3
b)
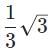
c)
1.33
d)
|
|
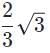
Ayesha Joshi answered |
- Use Snell’s law to calculate the index of reflection of the glass. Snell’s law: n1 sin (θ1) = n2 sin (θ2)
- The index of refraction for light in a vacuum is 1, therefore n2 = 1 and we simply must solve for n1.
- The index of refraction can never be less than 1, therefore
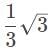cannot be an answer. - Plugging in our values:
n1 sin (30) = 1 sin (60)
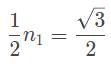
n1 = √3
A ray of light passing through a gel with an index of refraction of 1.5 has an incidence angle of 30° as it transitions through a pane of glass. The angle of refraction is 45°. What is the speed of light within the glass?- a)1.5 × 108 m/s
- b)2√2 × 108 m/s
- c)2 × 108 m/s
- d)2√3 × 108 m/s
Correct answer is option 'B'. Can you explain this answer?
A ray of light passing through a gel with an index of refraction of 1.5 has an incidence angle of 30° as it transitions through a pane of glass. The angle of refraction is 45°. What is the speed of light within the glass?
a)
1.5 × 108 m/s
b)
2√2 × 108 m/s
c)
2 × 108 m/s
d)
2√3 × 108 m/s
|
Maya Bailey answered |
The incident angle of 30 degrees is the angle between the incident ray and the normal line (a line perpendicular to the surface of the gel).
When light passes from one medium to another with different refractive indices, it bends or changes direction. This bending is known as refraction. The amount of bending depends on the incident angle and the refractive indices of the two media involved.
In this case, the incident ray is passing from air (or vacuum) into the gel, which has a refractive index of 1.5. The formula for calculating the angle of refraction is given by Snell's law:
n1 * sin(theta1) = n2 * sin(theta2)
Where:
n1 = refractive index of the first medium (air/vacuum) = 1 (approximately)
theta1 = incident angle
n2 = refractive index of the second medium (gel) = 1.5
theta2 = angle of refraction
Plugging in the values, we have:
1 * sin(30) = 1.5 * sin(theta2)
sin(theta2) = (1 * sin(30)) / 1.5
sin(theta2) = 0.5
To find theta2, we take the inverse sine (arcsine) of 0.5:
theta2 = arcsin(0.5)
theta2 ≈ 30 degrees
So, the ray of light passing through the gel with an incidence angle of 30 degrees will have an angle of refraction of approximately 30 degrees as well.
When light passes from one medium to another with different refractive indices, it bends or changes direction. This bending is known as refraction. The amount of bending depends on the incident angle and the refractive indices of the two media involved.
In this case, the incident ray is passing from air (or vacuum) into the gel, which has a refractive index of 1.5. The formula for calculating the angle of refraction is given by Snell's law:
n1 * sin(theta1) = n2 * sin(theta2)
Where:
n1 = refractive index of the first medium (air/vacuum) = 1 (approximately)
theta1 = incident angle
n2 = refractive index of the second medium (gel) = 1.5
theta2 = angle of refraction
Plugging in the values, we have:
1 * sin(30) = 1.5 * sin(theta2)
sin(theta2) = (1 * sin(30)) / 1.5
sin(theta2) = 0.5
To find theta2, we take the inverse sine (arcsine) of 0.5:
theta2 = arcsin(0.5)
theta2 ≈ 30 degrees
So, the ray of light passing through the gel with an incidence angle of 30 degrees will have an angle of refraction of approximately 30 degrees as well.
Chapter doubts & questions for Reflection and Refraction - Physics for MCAT 2025 is part of MCAT exam preparation. The chapters have been prepared according to the MCAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for MCAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Reflection and Refraction - Physics for MCAT in English & Hindi are available as part of MCAT exam.
Download more important topics, notes, lectures and mock test series for MCAT Exam by signing up for free.
Physics for MCAT
158 videos|21 docs|21 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup