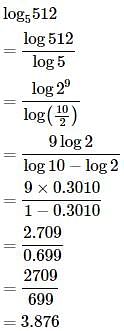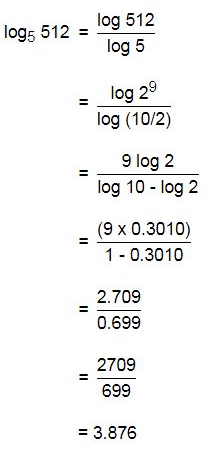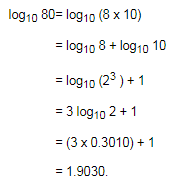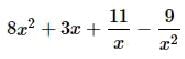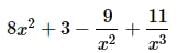All Exams >
Mechanical Engineering >
General Aptitude for GATE >
All Questions
All questions of Powers, Exponents and Logarithms for Mechanical Engineering Exam
What is the value of 225 + 225?- a)226
- b)250
- c)425
- d)450
- e)2625
Correct answer is option 'A'. Can you explain this answer?
What is the value of 225 + 225?
a)
226
b)
250
c)
425
d)
4
50
e)
2625

|
Anihegde1502 answered |
Take 2raise to25 common thjs ib bracket there will be (1+1)i.e 2raise to25 *2 thus power will get add 25+1 i.e 26 hence ans is option A
If ‘x’ and ‘y’ are non-negative integers, what is the value of x + y?(1) x4 is even, where x is a prime number.(2) xy is odd.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?
If ‘x’ and ‘y’ are non-negative integers, what is the value of x + y?
(1) x4 is even, where x is a prime number.
(2) xy is odd.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
BT Educators answered |
(1) x = 2, y is unknown. Insufficient
(2) x and y unknown. Insufficient
(1)+(2) only possibility x=2, y=0; Sufficient
C is correct
(2) x and y unknown. Insufficient
(1)+(2) only possibility x=2, y=0; Sufficient
C is correct
If a, b and x are integers such that 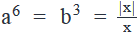 , what is the value of a - b
, what is the value of a - b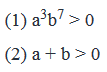
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
If a, b and x are integers such that 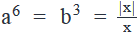 , what is the value of a - b
, what is the value of a - b
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Anaya Patel answered |
Steps 1 & 2: Understand Question and Draw Inferences
- As a6 is always positive,a6 = 1, i.e. a = 1 or -1
- So, we can reject the value of Possible values of a – b
- If a = 1 and b = 1, a – b = 0
- If a = -1 and b = 1, a- b = -2
- So, we need to find the unique value of a to find the value of a – b.Step 3: Analyze Statement 1 independently(1) a3 b7 > 0
- Rewriting a3b7 as ab(a2b6)
- Therefore, ab(a2b6)>0
- We know that a2b6 is always > 0 (even power of any number is always positive)
- So, for ab(a2b6)> 0
- ab > 0
- This tells us that a and b have same signs.
- Since b > 0, therefore a will also be greater than 0, so the value of a = 1.
- a – b = 1 -1 = 0
- Sufficient to answerStep 4: Analyze Statement 2 independently(2) a + b > 0
- If a = 1 and b = 1, a + b = 2 > 0
- If a = -1 and b = 1, a + b = 0, is not greater than zero
- Hence, we have a unique answer, where a =1 and b = 1Thus a – b = 1 – 1 = 0.Sufficient to answer.Step 5: Analyze Both Statements Together (if needed)As we have a unique answer from steps 3 and 4, this step is not required.Answer: D
Which of the following statements is not correct?
- a)log10 10 = 1
- b)log (2 + 3) = log (2 x 3)
- c)log10 1 = 0
- d)log (1 + 2 + 3) = log 1 + log 2 + log 3
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is not correct?
a)
log10 10 = 1
b)
log (2 + 3) = log (2 x 3)
c)
log10 1 = 0
d)
log (1 + 2 + 3) = log 1 + log 2 + log 3

|
Prince Chaudhary answered |
According to logarithm rule . option B is never correct
The value of 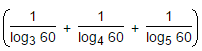 is:
is: - a)0
- b)1
- c)5
- d)60
Correct answer is option 'B'. Can you explain this answer?
The value of 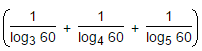 is:
is:
a)
0
b)
1
c)
5
d)
60
|
|
Shalini Patel answered |
Given expression = 1/log60 3 + 1/log60 4 + 1/log60 5
= log60 (3 x 4 x 5)
= log60 60
= 1.
= log60 (3 x 4 x 5)
= log60 60
= 1.
if log 2 = 0.30103 and log 3 = 0.4771, find the number of digits in (648)5.- a)15
- b)14
- c)13
- d)12
Correct answer is option 'A'. Can you explain this answer?
if log 2 = 0.30103 and log 3 = 0.4771, find the number of digits in (648)5.
a)
15
b)
14
c)
13
d)
12

|
Ishani Rane answered |
log(648)^5
= 5 log(648)
= 5 log(81 x 8)
= 5[log(81) + log(8)]
=5 [log(34) + log(23)]
=5[4log(3) + 3log(2)]
= 5[4 x 0.4771 + 3 x 0.30103]
= 5(1.9084 + 0.90309)
= 5 x 2.81149
approx. = 14.05
ie, log(648)^5 = 14.05 (approx.)
ie, its characteristic = 14
Hence, number of digits in (648)5 = 14+1 = 15
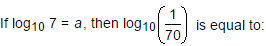
- a)- (1 + a)
- b)(1 + a)-1
- c)
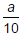
- d)
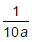
Correct answer is option 'A'. Can you explain this answer?
a)
- (1 + a)
b)
(1 + a)-1
c)
d)
|
|
Dia Mehta answered |
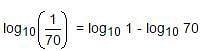
⇒ - log10 (7 x 10)
⇒ - (log10 7 + log10 10)
⇒ - (a + 1)
⇒ - (log10 7 + log10 10)
⇒ - (a + 1)
If Z is a positive integer such that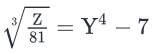
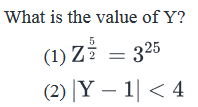
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
If Z is a positive integer such that
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Meera Rana answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given:
- Z is a positive integer
- Z = 81(Y4 – 7)3 . . . (1)
We need to find the value of Y.
Step 3: Analyze Statement 1 independently
- Squaring both sides:
- Z5 = 350
- Taking 5th root on both sides:
- Z = 310 . . . (2)
- Put (2) in (1):
- 310 = 34(Y4 – 7)3
- 36 = (Y4 – 7)3
- Taking the cube-root on both sides:
- 32 = Y4 – 7
- Y4 = 9 + 7 = 16
- Y4 = 24 = (-2)4
- Y = 2 or -2
Not sufficient to determine a unique value of Y.
Step 4: Analyze Statement 2 independently
(2) |Y-1| < 4
- Distance of Y from 1 on the number line is less than 4 units
- -3 < Y < 5
Multiple values of Y possible. Not sufficient.
Step 5: Analyze Both Statements Together (if needed)
- From St. 1, Y = 2 or – 2
- From St. 2, -3 < Y < 5
- This inequality is satisfied by both 2 and -2
So, even after combining both statements, we have 2 possible values of Y
Since we couldn’t find a unique value of Y, the correct answer. Is Option E.
if log 2 = 0.30103, the number of digits in 2128 is- a)38
- b)39
- c)40
- d)41
Correct answer is option 'B'. Can you explain this answer?
if log 2 = 0.30103, the number of digits in 2128 is
a)
38
b)
39
c)
40
d)
41

|
Gajendra Jain answered |
To find the number of digits multiply 128 with log2 and then add 1.
James deposited $1,000 each in two investment schemes X and Y. Scheme X doubles the invested amount every 7 years and scheme Y doubles the invested amount every 14 years. If James withdraws $500 from scheme X at the end of every 7th year, how many years will it take for the total amount invested in schemes X and Y to amount more than $40,000?
- a)14
- b)28
- c)42
- d)56
- e)70
Correct answer is option 'C'. Can you explain this answer?
James deposited $1,000 each in two investment schemes X and Y. Scheme X doubles the invested amount every 7 years and scheme Y doubles the invested amount every 14 years. If James withdraws $500 from scheme X at the end of every 7th year, how many years will it take for the total amount invested in schemes X and Y to amount more than $40,000?
a)
14
b)
28
c)
42
d)
56
e)
70
|
|
Meera Rana answered |
Given
- Scheme X doubles the invested amount every 7 years
- James deposited $1000 in scheme X
- James withdraws $500 from scheme X after the end of every 7 years
- Scheme Y doubles the invested amount after every 14 years
- James deposited $1,000 in scheme Y
To Find: Number of years it will take total amount deposited in schemes X and Y to grow to > $40,000?
Approach
- For finding the number of years it will take the deposits in schemes X and Y to grow to more than $40,000, we need to find the amount in both the schemes X and Y after every 7 years.(As amount in scheme X doubles after every 7 years, we will need to calculate the amount at the end of every 7 years and not at the end of 14 years).
- Scheme X
- As the amount invested in scheme X doubles every 7 years, we will need to calculate the amount in scheme X after every interval of 7 years
- However, we will need to make sure that we subtract $500 at each interval of 7 years from the final amount
- Scheme Y
- As the amount invested in scheme Y doubles after every 14 years, we will need to calculate the amount in scheme Y after every interval of 14 years.
- At each interval, we will calculate the sum of amounts in scheme X and Y to check if it exceeds $40,000.
Working Out
- Amount at the end of year 7 in scheme X = $1000 * 2 = $2000
- However James withdrew $500 at the end of 7th year, So, the amount remaining will be $2000 – $500 = $1500
- The same logic has been applied in calculating the amounts at the end of every 7 year interval
- Amount at the end of year 14 in scheme Y = $1000 * 2 = $2000
- The same logic has been applied in calculating the amounts at the end of every 14 years interval.
- The same logic has been applied in calculating the amounts at the end of every 14 years interval.
- We can see that the total amount in schemes X and Y exceed $40,000 by the end of the year 42.
Answer: C
If log 27 = 1.431, then the value of log 9 is:- a)0.934
- b)0.945
- c)0.954
- d)0.958
Correct answer is option 'C'. Can you explain this answer?
If log 27 = 1.431, then the value of log 9 is:
a)
0.934
b)
0.945
c)
0.954
d)
0.958

|
Gowri Chakraborty answered |
Log 27 = 1.431
log (33 ) = 1.431
3 log 3 = 1.431
log 3 = 0.477
log 9 = log(32 ) = 2 log 3 = (2 x 0.477) = 0.954.
If n is a positive integer greater than 2, what is the greatest prime factor of 3n + 3n + 3n – 3n-2?- a)3
- b)5
- c)7
- d)11
- e)13
Correct answer is option 'E'. Can you explain this answer?
If n is a positive integer greater than 2, what is the greatest prime factor of 3n + 3n + 3n – 3n-2?
a)
3
b)
5
c)
7
d)
11
e)
13

|
Arnab Kumar answered |
Solution:
Firstly, we can simplify the given expression by combining the exponents:
3n 3n 3n 3n-2 = 33n-2 * 33n = 36n
Now, to find the greatest prime factor of 36n, we can factorize it into prime factors:
36n = 2^2 * 3^2 * n
The greatest prime factor of 36n would be the largest prime factor of n. Since n is greater than 2, we know that it is either a prime number or a composite number with prime factors.
To find the greatest prime factor of n, we can start by dividing n by 2 repeatedly until we get an odd number. For example, if n is 60, we can divide it by 2 three times to get 15:
60 ÷ 2 = 30
30 ÷ 2 = 15
Now, we can check if 15 is a prime number or if it has any other prime factors. We can do this by dividing 15 by the smallest prime numbers, which are 2, 3, 5, 7, 11, 13, etc.
15 ÷ 3 = 5
Since 5 is a prime number, it is the greatest prime factor of n. Therefore, the greatest prime factor of 36n is 13, which is the largest prime factor of 3.
Firstly, we can simplify the given expression by combining the exponents:
3n 3n 3n 3n-2 = 33n-2 * 33n = 36n
Now, to find the greatest prime factor of 36n, we can factorize it into prime factors:
36n = 2^2 * 3^2 * n
The greatest prime factor of 36n would be the largest prime factor of n. Since n is greater than 2, we know that it is either a prime number or a composite number with prime factors.
To find the greatest prime factor of n, we can start by dividing n by 2 repeatedly until we get an odd number. For example, if n is 60, we can divide it by 2 three times to get 15:
60 ÷ 2 = 30
30 ÷ 2 = 15
Now, we can check if 15 is a prime number or if it has any other prime factors. We can do this by dividing 15 by the smallest prime numbers, which are 2, 3, 5, 7, 11, 13, etc.
15 ÷ 3 = 5
Since 5 is a prime number, it is the greatest prime factor of n. Therefore, the greatest prime factor of 36n is 13, which is the largest prime factor of 3.
Find the value of positive integer P that lies between 1 and 30 and is a perfect square.(1) P has at least one Prime factor(2) The cube of P is less than 300- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'B'. Can you explain this answer?
Find the value of positive integer P that lies between 1 and 30 and is a perfect square.
(1) P has at least one Prime factor
(2) The cube of P is less than 300
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Disha Mehta answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given that P is positive and 1 < P < 30.
It is also given that P is a perfect square.
This means, that P is the square of an integer.
Therefore the possible values of P are 4, 9, 16, and 25.
Step 3: Analyze Statement 1
Given that P has at least one prime factor.
EVERY number greater than 1 has at least one prime factor.
This statement doesn’t help us to eliminate any value out of the four possible values of P.
So statement 1 is not sufficient to arrive at a unique answer.
Step 4: Analyze Statement 2
Given that cube of P is less than 300.
Observe that only 4 satisfies this condition.
43=64
93=729
(Since 93 itself is greater than 300, it is clear that 163 and 253 will also be greater than 300.)
Therefore the only possible value for P is 4.
Statement 2 is sufficient to arrive at a unique answer.
Step 5: Analyze Both Statements Together (if needed)
We arrived at a unique answer in step 4. Hence this step is not required.
Correct Answer: B
If 3p+3p+3p=3q, what is p in terms of q?- a)q-1
- b)q/3
- c)3q
- d)q+1
- e)q/6
Correct answer is option 'A'. Can you explain this answer?
If 3p+3p+3p=3q, what is p in terms of q?
a)
q-1
b)
q/3
c)
3q
d)
q+1
e)
q/6

|
Siddharth Pillai answered |
We have 3p+3p+3p=3∗3p=3p+1=3q.
So p+1=q, and p=q−1.
What is the remainder obtained when 1010 + 105 – 24 is divided by 36?- a)5
- b)6
- c)12
- d)16
- e)32
Correct answer is option 'E'. Can you explain this answer?
What is the remainder obtained when 1010 + 105 – 24 is divided by 36?
a)
5
b)
6
c)
12
d)
16
e)
32

|
Pallabi Sengupta answered |
Given:
- Not applicable
To find: The remainder when 1010 + 105 – 24 is divided by 36
Approach:
- Let the required remainder be r. This means, we will be able to write:
1010 + 105 – 24 = 36k + r, where quotient k is an integer and 0 ≤ r < 36
The above expression is our GOAL expression. We’ll try to simplify the dividend 1010 + 105 – 24 till it is comparable to our GOAL expression, and then, by comparison, we’ll be able to find the value of r.
Working Out:
- 1010 + 105 – 24 = 1005 + 1002*10 – (36 – 12)
- =(36*3 – 8)5 + (36*3 – 8)2*10 – 36 + 12
- Now, from Binomial Theorem, we know that every term in the expansion of (36*3 – 8)5 will be divisible by 36, except the last term, and the last term will be (-8)5
- So, we can write: (36*3 – 8)5 is of the form 36a + (-8)5, where 36a is a catch-all term conveying that all the other terms in this expansion are divisible by 36
- Similarly, every term in the expansion of (36*3 – 8)2 will be divisible by 36 except the last term, and the last term will be (-8)2
- So, we can write: (36*3 – 8)2 = 36b + (-8)2
- Now, from Binomial Theorem, we know that every term in the expansion of (36*3 – 8)5 will be divisible by 36, except the last term, and the last term will be (-8)5
- So, the given expression simplifies to:
- {36a + (-8)5 } + {36b + (-8)2}*10 – 36 + 12
- = (36a + 360b – 36) + (-85 + 640 + 12)
- = (36a + 360b – 36) + (-85+ 652)
- = (36a + 360b – 36 + 648) + (-85+ 4)
- = (36a + 360b – 36 + 36*18) + (-85+ 4)
- The above expression is not comparable to our GOAL expression because the term -85 in it is still unresolved. Do we need to calculate the value of -85 to answer this question? No. We only need to express it in terms of 36. Once again, we’ll use Binomial Theorem to do so:
- -85 = -8(82)2 = -8(64)2 = -8(36*2 – 8)2
- Every term in the expansion of (36*2 – 8)2 will be divisible by 36 except the last term. The last term will be (-8)2 = 64
- So, the expression (36*2 – 8)2 can be written as: 36c + 64
- So, -8(36*2 – 8)2 = -8(36c + 64)
- =-8(36c + 36*2 – 8)
- = (-8*36c – 8*36*2) + 64
- -85 = -8(82)2 = -8(64)2 = -8(36*2 – 8)2
- So, the given expression simplifies to: (36a + 360b – 36 + 72) + {(-8*36c – 8*36*2) + 64} + 4
- = (36a + 360b – 36 + 72 – 8*36c – 8*36*2) + 68
- =(36a + 360b – 36 + 72 – 8*36c – 8*36*2 + 36) + 32
- Now, the above expression is exactly comparable to our GOAL Expression: 36k + r
- So, by comparison, we can say that Remainder r = 32
Looking at the answer choices, we see that the correct answer is Option E
If log 2 = 0.3010 and log 3 = 0.4771, What is the value of log51024?- a)4.31
- b)3.88
- c)3.91
- d)2.97
Correct answer is option 'A'. Can you explain this answer?
If log 2 = 0.3010 and log 3 = 0.4771, What is the value of log51024?
a)
4.31
b)
3.88
c)
3.91
d)
2.97

|
Gowri Chakraborty answered |
log 5 1024= log1024/log5 = log ( 2^10)/log(10/2)=10log(2)/log10−log2
=10*0.3010/1−0.3010 = 3.01/0.699 = 3010/699 = 4.31
What are the last two digits, in order, of 6789 ?Possible Answers:- a)36
- b)16
- c)56
- d)96
- e)76
Correct answer is option 'D'. Can you explain this answer?
What are the last two digits, in order, of 6789 ?
Possible Answers:
a)
36
b)
16
c)
56
d)
96
e)
76

|
Malavika Choudhury answered |
Inspect the first few powers of 6; a pattern emerges.
61=6
62=36
63=216
64=1,296
65=7,776
66=46,656
67=279,936
68=1,679,616
69=10,077,696
610=60,466,176
As you can see, the last two digits repeat in a cycle of 5.
789 divided by 5 yields a remainder of 4; the pattern that becomes apparent in the above list is that if the exponent divided by 5 yields a remainder of 4, then the power ends in the diigts 96.
Find the value of n that satisfies the equation 2(-3)4n = 18(27)n+2- a)3
- b)4
- c)6
- d)8
- e)22
Correct answer is option 'D'. Can you explain this answer?
Find the value of n that satisfies the equation 2(-3)4n = 18(27)n+2
a)
3
b)
4
c)
6
d)
8
e)
22

|
Mrinalini Dasgupta answered |
We need to find the value of n, given 2(−34n)=18(27)n+2
(Cancelling 2 on both sides. Also making use of the fact that 32k = (-3)2k)
What is the maximum possible power of 4 in the number that is obtained when the product of the first 15 positive integers is subtracted from the product of the first 20 positive integers?- a)0
- b)3
- c)5
- d)7
- e)8
Correct answer is option 'C'. Can you explain this answer?
What is the maximum possible power of 4 in the number that is obtained when the product of the first 15 positive integers is subtracted from the product of the first 20 positive integers?
a)
0
b)
3
c)
5
d)
7
e)
8

|
Sahana Mehta answered |
Given
- Product of first 15 positive integers = 1*2*3…….* 15 = 15!
- Product of first 20 positive integers = 1*2*3*…….* 20 = 20!
- So, we can write 20! = 15! * 16 * 17 * 18 * 19 * 20
To Find: Maximum power of 4 that divides (20! – 15!)
Approach
- We will first need to simplify the expression 20! – 15!
- We know that 20! = 15! * 16 * 17 * 18 * 19 * 20
- So, 20! – 15! = 15! (20*19*18….*16 – 1) = 15! * odd integer
- Since 20 *19*…..16 is even, and 1 is odd, 20*19*……16 -1 will be odd
- Therefore, we only need to find the maximum power of 4 that divides 15!
2. To find the maximum power of 4 in 15!, we will first need to find the maximum power of 2 in 15!, as 4 = 22
- Let’s take a simple example to understand how we can find this. Consider a number p = 1*2*3*4. We need to find the power of 2 in p.
- Now, powers of 2 will occur in multiples of 2. So, we should first find the multiples of 2 in p. They are 2 and 4. However all multiples of 2 will not contain only 21. Some of them may contain higher powers of 2. For example, here 4 contains 22.
- So, when we are finding multiples of 2, we should also find the multiples of higher powers of 2 in p.
- Hence, 2 will occur 2 + 1 = 3 times in p.
3. We will use the same logic to find out the power of 2 in 15!
- Once we know the power of 2 in 15!, we can find the power of 4 in 15!
Working Out
If log(64)= 1.806, log(16) = ?- a) 1.204
- b)0.903
- c)1.806
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If log(64)= 1.806, log(16) = ?
a)
1.204
b)
0.903
c)
1.806
d)
None of these

|
Gowri Chakraborty answered |
log(64)= 1.806
=> log(4^3) = 1.806
=> 3log(4) = 1.806
⇒log(4) = 1.806/3
log(16) = log (4^2) = 2log(4) = 2*1.806/3 = 2*0.062 = 1.204
Positive integer P lies between 1 and 30. What is the value of P?(1) P has at least two prime factors(2) The cube of P is less than 300- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?
Positive integer P lies between 1 and 30. What is the value of P?
(1) P has at least two prime factors
(2) The cube of P is less than 300
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Soumya Iyer answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given that P is a positive integer and that 1 < P < 30.
We need to find the value of P
Step 3: Analyze Statement 1
Given that P has at least two prime factors.
- P is a composite number with two or more prime factors.
However, there are more than one composite number between 1 and 30. The possible values of P are:
Clearly, Statement (1) doesn’t lead us to a unique value of P.
Not Sufficient.
Step 4: Analyze Statement 2
Statement 2 says that the cube of P is less than 300.
Let us list out the cubes of natural numbers.
There are 5 natural numbers between 1 and 30 whose cubes are less than 300.
Statement 2 alone is not sufficient to arrive at a unique answer.
Step 5: Analyze Both Statements Together (if needed)
From Statement 1,
Possible values of P: 6, 10, 14, 15, 21, 22, 26
From Statement 2,
Possible values of P: 2, 3, 4, 5, 6
By combining the two statements, we get:
P = 6
Therefore statement 1 and statement 2 combined are sufficient to arrive at a unique answer.
Correct Answer: C
The intensity of radiation emanating from a nuclear event is measured on an exponential scale where the second and fourth points indicate intensities of 25 and 625, respectively. On that scale, what would the intensity at the third point be?- a)50
- b)75
- c)125
- d)250
- e)312.5
Correct answer is option 'C'. Can you explain this answer?
The intensity of radiation emanating from a nuclear event is measured on an exponential scale where the second and fourth points indicate intensities of 25 and 625, respectively. On that scale, what would the intensity at the third point be?
a)
50
b)
75
c)
125
d)
250
e)
312.5

|
Siddharth Pillai answered |
Step 1: Question statement and Inferences
We are given that the scale is an exponential scale. This means that every term on this scale is equal to the previous term multiplied by a fixed value.
Step 2 & 3: Simplifying the fraction and calculating the final answer
We are given that 2nd term on the scale = 25 = 52
4th term on the scale = 625 = 54
From here, we can discern the pattern that:
The nth term on the scale = 5n
Thus, the 3rd term on the scale = 53 = 125
Answer: Option (C)
A function 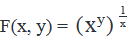 for positive integers x and y. Is F(a, b) > a, where a and b are positive integers?
for positive integers x and y. Is F(a, b) > a, where a and b are positive integers?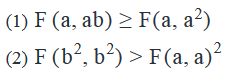
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
A function 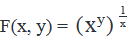 for positive integers x and y. Is F(a, b) > a, where a and b are positive integers?
for positive integers x and y. Is F(a, b) > a, where a and b are positive integers?
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Sahana Mehta answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Since a is a positive integer, multiplying both sides of the inequality doesn’t impact the sign of inequality
- So, the question simplifies to: is b > a?
Step 3: Analyze Statement 1 independently
Using the definition of this function, we can write: 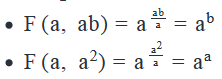
So as per Statement 1:
As a is a positive integer,aa > 0. So, we can divide both sides of the inequality by aa without changing the sign of the inequality.
So, b > a or b = a.
Hence, we can not say for sure if b > a. Insufficient to answer.
Step 4: Analyze Statement 2 independently
Using the definition of this function, we can write:
So, as per statement-2, 
- As a > 0, - a < 0. So b < -a is not possible as it will mean that b is negative.
- So, the only possible case is b > a
Sufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
As we have a unique answer from step – 4, this step is not required.
Answer: B
Does ab lie between 0 and 1, exclusive?(1) |a| < 1(2) b is a positive odd integer- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
Does ab lie between 0 and 1, exclusive?
(1) |a| < 1
(2) b is a positive odd integer
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Pallabi Sengupta answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given: Two numbers a and b
To Find: Is 0 < ab < 1
Following cases are possible:
- a ≥ 1 →
- If b≥ 0, then ab ≥ 1. So, the answer to the question is NO
- If b < 0, then 0 < ab < 1. So, the answer to the question is YES
2. 0 < a < 1 → Irrespective of the value of b, 0 < ab < 1 So, the answer to the question is YES
3. If a = 0 → Irrespective of the value of b, ab = 0. So, the answer to the question is NO.
4. -1 < a < 0 →
- If b is even, 0 < ab < 1 So, the answer to the question is YES.
- If b is odd, -1 < ab < 0. So, the answer to the question is NO.
5. a ≤ -1 →
- If b is even,ab≥1. So, the answer to the question is NO.
- If b is odd, ab≤1. So, the answer to the question is NO
So, the answer to the question will be YES, if:
- a ≥ 1 and b < 0 OR
- 0 < a < 1 OR
- -1 < a < 0 and b is even
And the answer to the question will be NO, if:
- a ≥ 1 and b ≥ 0 OR
- a = 0 OR
- -1 < a < 0 and b is odd OR
- a ≤ -1
So, we can answer the given question with a unique answer for the above cases.
Step 3: Analyze Statement 1 independently
(1) |a| < 1
- This means, -1 < a < 1. So, following cases can occur:
- -1 < a < 0 → As we have seen from our analysis above that in this case the answer to the question may be YES or NO
- Now, we don’t need to analyse other cases as we do not have unique from this case itself, but we will do so for the sake of completing the analysis.
- a = 0 → The answer to the question is NO in this case
- 0 < a < 1 → The answer to the question is YES in this case.
- As we do not have a unique answer , we cannot say for sure if 0 < ab < 1
- -1 < a < 0 → As we have seen from our analysis above that in this case the answer to the question may be YES or NO
Insufficient to answer
Step 4: Analyze Statement 2 independently
(2) b is a positive odd integer
- We have seen from our analysis in steps 1&2 that we need to find the range of values of a to answer this question.
- As we do not know the value of a, the statement is insufficient to tell if 0 < ab < 1
Insufficient to answer
Step 5: Analyze Both Statements Together (if needed)
(1)From Statement 1, -1 < a < 1
(2) From Statement 2, b > 0
Following cases are possible:
- -1 < a < 0 → We have seen from our analysis in steps 1&2 that if b is odd, the answer to the question is NO.
- a = 0 → We have seen from our analysis in steps 1&2 that in this case the answer to the question is NO.
- 0 < a < 1 → We have seen from our analysis in steps 1&2 that in this case the answer to the question is YES
As we do not have a unique answer, the combination of statements is insufficient to answer.
Answer: E
If 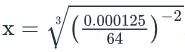 , what is the value of x?
, what is the value of x?- a)6400
- b)8000
- c)12500
- d)15625
- e)22500
Correct answer is option 'A'. Can you explain this answer?
If 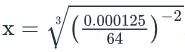 , what is the value of x?
, what is the value of x?
a)
6400
b)
8000
c)
12500
d)
15625
e)
22500

|
Arya Yadav answered |
Given:
To find: Value of x
Working Out:
Looking at the answer choices, we see that the correct answer is Option A
Is the sum of xy and yx positive?(1) xy > 0(2) x + y > 0- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
Is the sum of xy and yx positive?
(1) xy > 0
(2) x + y > 0
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Sahana Mehta answered |
Steps 1 & 2: Understand Question and Draw Inferences
To Find: If xy + yx > 0
Step 3: Analyze Statement 1 independently
(1) xy > 0
- Tells that x and y are of the same sign. Two cases arise:
- x, y > 0
- In this case xy, yx > 0. So, xy + yx > 0
- x, y < 0
- In this case, xy + yx may or may not be positive, depending on the values of x and y. Following cases can arise:
- Both x, y are even → In this case xy,yx > 0. So, xy+yx > 0
- Both x and y are odd → In this case xy,yx < 0. So, xy+yx < 0
- x is even and y is odd → In this case xy < 0, yx > 0. Cannot comment on the value of xy+yx
- x is odd and y is even → In this case xy < 0, yx > 0. Cannot comment on the value of xy+yx
- x, y > 0
Insufficient to answer.
Step 4: Analyze Statement 2 independently
(2) x + y > 0
- Considering the constraint x + y > 0, following cases are possible:
- x, y > 0. So, x + y > 0. In this case, xy, yx > 0. So, xy + yx > 0
- x < 0, y > 0 and |y| > |x|. So, x + y > 0. In this case xy + yx may or may not be positive.
- If y is odd, then xy < 0 , yx > 0 as y is positive. In this case, we cannot comment on the value of xy + yx
- If y is even , then xy > 0 , yx > 0 as y is positive. In this case, xy + yx > 0
- x > 0, y < 0 and |x| > |y|. So, x + y > 0. In this case xy + yx may or may not be positive.
Insufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
- From Statement 1, xy > 0
- From Statement 2, x + y > 0
Statement-1 tells us that x and y have the same signs. Following cases are possible:
- If x & y > 0, xy > 0 and x + y > 0. In this case xy + yx > 0
- If x & y < 0, x+ y < 0. Not possible. (If x & y both are negative, the x + y cannot be > 0)
The only possible case is when x, y > 0 and hence xy + yx > 0
Sufficient to answer.
Answer: C
If x and y are positive integers, what is the remainder when y is divided by x?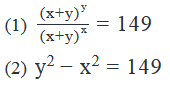
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
If x and y are positive integers, what is the remainder when y is divided by x?
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Gitanjali Kumar answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Given: x, y are integers > 0
- y = ax + r , where a is a positive integer and r is an integer such that 0 ≤ r < x
To Find: Value of r for which we need to find the value of x and y.
Step 3: Analyze Statement 1 independently
- As 149 is expressed as an integer raised to a power, we need to find that integer. As this integer will be a factor of 149, we need to find if 149 can be expressed as a factor raised to its power. So, let’s check its divisibility by the prime numbers.
- Divisibility by 2: As 149 is odd, it is not divisible by 2
- Divisibility by 3: As the sum of the digits of 149 (i.e. 14) is not divisible by 3, 149 will not be divisible by 3
- Divisibility by 5: As the units digit of 149 is neither 0 nor 5, it is not divisible by 5
- Divisibility by 7: We can see that 149 when divided by 7, leaves a remainder 2. So, it is not divisible by 7
- Divisibility by 11: 149 when divided by 11 leaves a remainder 4. So, it is not divisible by 11
- Divisibility by 13: We see that 149 when divided by 13 leaves a remainder 6. So, it is not divisible by 13.
- Since 122 < 149 < 132 and 149 is not divisible by any prime number till 13, we can say that 149 is a prime number.
- As 149 is a prime number, any integer apart from 149 raised to any power will not result in 149.
- Only possible option is x + y = 149 and y – x = 1
- 2 equations, 2 variables, we can find unique values of x and y and hence find the remainder.
Sufficient to answer.
Step 4: Analyze Statement 2 independently
- So, we need to express 149 as a product of 2 integers. For expressing 149 as a product of 2 integers, we need to find the factors of 149.
- As we have found above that 149 is a prime number, the only possible case of expressing 149 as a product of 2 integers is 149 * 1
- y + x = 149 and y – x = 1
- 2 equations, 2 variables, we can find unique values of x and y and hence find the remainder.
Sufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
As we have a unique answer from steps 3 and 4, this step is not required.
Answer: D
Simplify the following expression without a calculator:
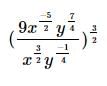
- a)
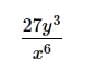
- b)
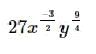
- c)
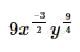
- d)
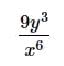
- e)
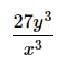
Correct answer is option 'E'. Can you explain this answer?
Simplify the following expression without a calculator:
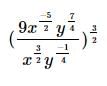
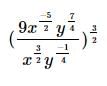
a)
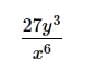
b)
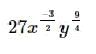
c)
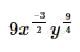
d)
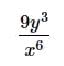
e)
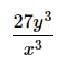

|
Sharmila Singh answered |
he easiest way to simplify is to work from the inside out. We should first get rid of the negatives in the exponents. Remember that variables with negative exponents are equal to the inverse of the expression with the opposite sign. For example
 So using this, we simplify:
So using this, we simplify:
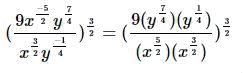
Now when we multiply variables with exponents, to combine them, we add the exponents together. For example, (a2)(a2)=a2+2=a4 Doing this to our expression we get it simplified to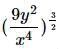
The next step is taking the inside expression and exponentiating it. When taking an exponent of a variable with an exponent, we actually multiply the exponents. For example, (a2)4=a(2∗4)=a8.
The other rule we must know that is an exponent of one half is the same as taking the square root. So for the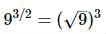 So using these rules,
So using these rules,
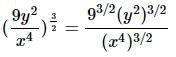
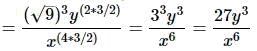
 So using this, we simplify:
So using this, we simplify: 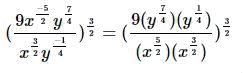
Now when we multiply variables with exponents, to combine them, we add the exponents together. For example, (a2)(a2)=a2+2=a4 Doing this to our expression we get it simplified to
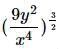
The next step is taking the inside expression and exponentiating it. When taking an exponent of a variable with an exponent, we actually multiply the exponents. For example, (a2)4=a(2∗4)=a8.
The other rule we must know that is an exponent of one half is the same as taking the square root. So for the
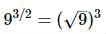 So using these rules,
So using these rules,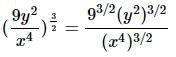
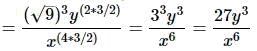
If x is a positive integer less than 100 such that x is divisible by 2y, where y is a positive integer, what is the value of y?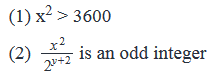
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
If x is a positive integer less than 100 such that x is divisible by 2y, where y is a positive integer, what is the value of y?
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Abhishek Choudhury answered |
Steps 1 & 2: Understand Question and Draw Inferences
- x is an integer such that 0 < x < 100
- x is divisible by 2y, where y is a positive integer
- Since y > 0, this means 2 is definitely a prime factor 2
- Since x is a positive integer, we can write the Prime-factorized form of x as:
- are integers > 0, z ≥ y and are prime numbers other than 2.
- As x < 100, 2z < 100
- So, z = { 1, 2, 3, 4, 5, 6} as 27 = 128 > 100
- Since x is completely divisible by 2y, z ≥ y. So, y can take any value of z, i.e. 1 ≤ y ≤ 6
- To Find: Unique value of y
Step 3: Analyze Statement 1 independently
- As x is a positive integer, x < -60 is not possible.
- So, x > 60, i.e. 60 < x < 100.
However, we do not know if 2 is the only prime factor or x. So, we cannot find a unique value of y.
- For example, if 2 is the only prime factor of x, then y can have only 1 value: 6
- But if x has other prime factors, then multiple values of y are possible. For example, x could be 22*3*7 (y = 2) or 23*11 (y = 3) etc.
Insufficient to answer.
Step 4: Analyze Statement 2 independently
- Using the prime factorized expression of x, we can write:
- Since the integer resulting from this division is odd, the powers of 2 in the numerator and the denominator should cancel out each other.
- Hence 22z = 2y+2
- z=y/2+1 ….(1). So, y must be even as z is an integer
- Also, from our discussion in Steps 1 and 2, we know that z ≥ y
- Substituting (1) in the above inequality, we get:
Using (2), along with the inference that y must be even, we have y = 2 as the only possible option.
Sufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
As we have a unique answer from step 4, this step is not required.
Answer: B
Solve for N:
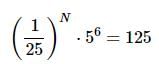
- a)N= -2
- b)N= -1/2
- c)N= 3/2
- d)N= -1/4
- e)The equation has no solution.
Correct answer is option 'C'. Can you explain this answer?
Solve for N:
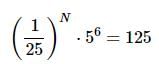
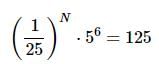
a)
N= -2
b)
N= -1/2
c)
N= 3/2
d)
N= -1/4
e)
The equation has no solution.

|
Arya Yadav answered |
(1/25)N ⋅ 56=125
(5−2)N ⋅ 56=53
5−2⋅N ⋅ 56=53
5−2N + 6=53
−2N+6=3
−2N+6−6=3−6
−2N=−3
−2N÷(−2)=−3÷(−2)
N=3/2
3x4 x x2+x2-x = - a)3x9
- b)x(3x5-x+1)
- c) 3x5+x−1
- d)x(3x5+x−1)
- e) 3x7
Correct answer is option 'D'. Can you explain this answer?
3x4 x x2+x2-x =
a)
3x9
b)
x(3x5-x+1)
c)
3x5+x−1
d)
x(3x5+x−1)
e)
3x7

|
Mrinalini Dasgupta answered |
3x4 x x2 = 3x6
then
3x4 x x2 + x2 - x = 3x6+x2 - x=x(3x5+x-1)
then
3x4 x x2 + x2 - x = 3x6+x2 - x=x(3x5+x-1)
If x and y are non-zero numbers, what is the value of y?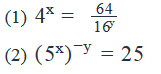
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
If x and y are non-zero numbers, what is the value of y?
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Arka Basu answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given: x ≠ 0, y ≠ 0
To find: y = ?
Step 3: Analyze Statement 1 independently
Equating the powers of 2 on both sides:
2x = 6 – 4y
x + 2y = 3
1 Linear Equation with 2 unknowns. Not sufficient to find a unique value of y.
Step 4: Analyze Statement 2 independently
Not sufficient to find a unique value of y.
Step 5: Analyze Both Statements Together (if needed)
- From Statement 1: x + 2y = 3 . . . (1)
- From Statement 2: xy = -2
Substituting (2) in (1):
- This quadratic equation gives 2 values of y
- The only constraint on y: y ≠ 0
- Since 0 is not a root of the above quadratic equation, this constraint doesn’t help eliminate one of the two roots of y
- Thus, 2 values of y are obtained from the combination of the two statements
Not sufficient to obtain a unique value of y.
Answer: Option E
if, 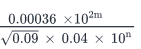 = 3 x 107 , then 4m - 2n =
= 3 x 107 , then 4m - 2n =- a)9
- b)10
- c)14
- d)16
- e)18
Correct answer is option 'E'. Can you explain this answer?
if, 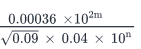 = 3 x 107 , then 4m - 2n =
= 3 x 107 , then 4m - 2n =
a)
9
b)
10
c)
14
d)
16
e)
18

|
Soumya Iyer answered |
We need to find the value of 4m – 2n.
Given expression:
Therefore, 4m -2n =2 * (2m -n) =18
Correct Answer: E
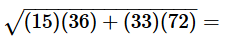
- a)18
- b)
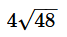
- c)54
- d)
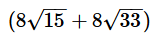
- e)

Correct answer is option 'C'. Can you explain this answer?
a)
18
b)
c)
54
d)
e)

|
Hridoy Gupta answered |
Given expression is:
Note that 15 = 3*5
36 = 62
33 = 3*11
72 = 36*2 = 62*2
Therefore
Correct Answer: C
For any integer z, the function PODD(z) is defined as the product of all odd integers between –z and z, inclusive. Which of the following numbers will not divide PODD (-15) completely?I. 38II. 55III. 73 - a)I only
- b)II only
- c)III only
- d)I and II only
- e)II and III only
Correct answer is option 'E'. Can you explain this answer?
For any integer z, the function PODD(z) is defined as the product of all odd integers between –z and z, inclusive. Which of the following numbers will not divide PODD (-15) completely?
I. 38
II. 55
III. 73
a)
I only
b)
II only
c)
III only
d)
I and II only
e)
II and III only

|
Arya Yadav answered |
Given:
To find: PODD(-15) will not be divisible by which of the given 3 options?
Approach:
- The given 3 options involve powers of 3, 5 and 7. So, to answer the question, we’ll find the powers of 3, 5 and 7 in the prime-factorized expression of PODD(-15)
- The answer for an option will be YES (meaning that option will not divide PODD(-15) completely) if the power of the prime factor in that option is greater than the power of that prime factor in the prime-factorized expression for PODD(-15)
(For example, 25 will not divide a number of the form 24*3)
Working Out:
- Finding the power of 3 in PODD(-15) and evaluating Option I

- Look again at the expression for PODD(-15):
- PODD(-15) = (-1)8(1*3*5*7*9*11*13*15)2
- Note that each of the above multiples of 3 occurs twice in PODD(-15)
- So, power of 3 in PODD(-15) = (1+2+1)*2= 4*2 = 8
- Since the power of 3 in Option I is equal to the power of 3 in PODD(-15), 38 will divide PODD(-15) completely.
Finding the power of 5 in PODD(-15) and evaluating Option II
-
- Since the multiples of 5 and 15 occurs twice in PODD(-15), power of 5 in PODD(-15) = (1+1)*2 = 4
- Since the power of 5 in Option II is greater than the power of 5 in PODD(-15), 55 will not divide PODD(-15) completely.
- Finding the power of 7 in PODD(-15) and evaluating Option III
- The only multiple of 7 in PODD(-15) is 7 itself.
- Since 7 occurs twice in PODD(-15), the power of 7 in PODD(-15) = 1*2 = 2
- Since the power of 7 in Option III is greater than the power of 5 in PODD(-15), 73 will not divide PODD(-15) completely.
- Thus we see that only Options II and III will not divide PODD(-15) completely.
Looking at the answer choices, we see that the correct answer is Option E
Simplify the given expression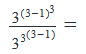
- a)1/9
- b)1/3
- c)1
- d)3
- e)9
Correct answer is option 'B'. Can you explain this answer?
Simplify the given expression
a)
1/9
b)
1/3
c)
1
d)
3
e)
9

|
Gitanjali Kumar answered |
Correct Answer: Option B
Chapter doubts & questions for Powers, Exponents and Logarithms - General Aptitude for GATE 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Powers, Exponents and Logarithms - General Aptitude for GATE in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
General Aptitude for GATE
194 videos|167 docs|152 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup