All Exams >
Mechanical Engineering >
General Aptitude for GATE >
All Questions
All questions of Rotation of shapes for Mechanical Engineering Exam
We have 2 rectangular sheets of paper. M and N, of dimensions 6 cm x 1 cm each. Sheet M is rolled to from an open cylinder by bringing the short edges of the sheet together. Sheet N is cut into equal patches and assembled to from the largest closed cube. Assuming the ends of the cylinder are closed, the ratio of the volume of the cylinder to that cube is ______- a)3/π
- b)9/π
- c)π/2
- d)3π
Correct answer is option 'B'. Can you explain this answer?
We have 2 rectangular sheets of paper. M and N, of dimensions 6 cm x 1 cm each. Sheet M is rolled to from an open cylinder by bringing the short edges of the sheet together. Sheet N is cut into equal patches and assembled to from the largest closed cube. Assuming the ends of the cylinder are closed, the ratio of the volume of the cylinder to that cube is ______
a)
3/π
b)
9/π
c)
π/2
d)
3π

|
Crack Gate answered |
Given:
Two rectangular sheets M and N have the dimension 6 cm × 1 cm each, in which cylinder will be formed by bringing the short edges of the sheet together. Given that ends of the cylinder are closed.
Concept:
Volume of cylinder = π x r2 x h
The volume of the cube = a3
The volume of the cube = a3
Calculation:
Let be assume the side of the cube is a,
⇒ The area of the sheet N = 6 x a2
⇒ 6 × 1 = 6 x a2
⇒ a = 1
⇒ Volume of the cube = a3 = 13 = 1
⇒ The circumference = 6
⇒ 2 × π × r = 6, r = 3/π and height of the cylinder = 1 cm
⇒ Volume of the cylinder = π x (3/π)2 x 1 = 9/π
⇒ The required ratio = 9/π : 1
∴ The required result will be 9/π .
⇒ The area of the sheet N = 6 x a2
⇒ 6 × 1 = 6 x a2
⇒ a = 1
⇒ Volume of the cube = a3 = 13 = 1
⇒ The circumference = 6
⇒ 2 × π × r = 6, r = 3/π and height of the cylinder = 1 cm
⇒ Volume of the cylinder = π x (3/π)2 x 1 = 9/π
⇒ The required ratio = 9/π : 1
∴ The required result will be 9/π .
Consider a square sheet of side 1 unit. In the first step, it is cut along the main diagonal to get two triangles. In the next step, one of the cut triangles is revolved about its short edge to form a solid cone. The volume of the resulting cone, in cubic units, is ________- a)π/3
- b)2π/3
- c)3π/3
- d)3π
Correct answer is option 'A'. Can you explain this answer?
Consider a square sheet of side 1 unit. In the first step, it is cut along the main diagonal to get two triangles. In the next step, one of the cut triangles is revolved about its short edge to form a solid cone. The volume of the resulting cone, in cubic units, is ________
a)
π/3
b)
2π/3
c)
3π/3
d)
3π

|
Mehul Choudhury answered |
Understanding the Problem
To find the volume of the cone formed by revolving one of the triangles, we first need to analyze the shape and dimensions of the triangles.
Step 1: Triangle Dimensions
- The square has a side length of 1 unit.
- Cutting it along the main diagonal divides the square into two right-angled triangles.
- Each triangle has a base and height of 1 unit.
Step 2: Selecting the Triangle
- We can choose either of the two triangles; the result will be the same.
- For the purpose of this explanation, let's select the triangle with vertices at (0, 0), (1, 0), and (0, 1).
Step 3: Revolving the Triangle
- When we revolve this triangle about its short edge (the edge along the y-axis, from (0, 0) to (0, 1)), we create a cone.
- The height of the cone is the length of the edge we are revolving around, which is 1 unit.
- The radius of the cone is the length of the base of the triangle, which is also 1 unit.
Step 4: Volume of the Cone
- The formula for the volume of a cone is given by:
Volume = (1/3) * π * r^2 * h
- Substituting the values:
- r = 1 unit (radius)
- h = 1 unit (height)
- Thus, the volume becomes:
Volume = (1/3) * π * (1^2) * 1 = (1/3) * π = π/3 cubic units.
Final Answer
The volume of the resulting cone is π/3 cubic units, which corresponds to option 'A'.
To find the volume of the cone formed by revolving one of the triangles, we first need to analyze the shape and dimensions of the triangles.
Step 1: Triangle Dimensions
- The square has a side length of 1 unit.
- Cutting it along the main diagonal divides the square into two right-angled triangles.
- Each triangle has a base and height of 1 unit.
Step 2: Selecting the Triangle
- We can choose either of the two triangles; the result will be the same.
- For the purpose of this explanation, let's select the triangle with vertices at (0, 0), (1, 0), and (0, 1).
Step 3: Revolving the Triangle
- When we revolve this triangle about its short edge (the edge along the y-axis, from (0, 0) to (0, 1)), we create a cone.
- The height of the cone is the length of the edge we are revolving around, which is 1 unit.
- The radius of the cone is the length of the base of the triangle, which is also 1 unit.
Step 4: Volume of the Cone
- The formula for the volume of a cone is given by:
Volume = (1/3) * π * r^2 * h
- Substituting the values:
- r = 1 unit (radius)
- h = 1 unit (height)
- Thus, the volume becomes:
Volume = (1/3) * π * (1^2) * 1 = (1/3) * π = π/3 cubic units.
Final Answer
The volume of the resulting cone is π/3 cubic units, which corresponds to option 'A'.
Consider a square sheet of side 1 unit. The sheet is first folded along the main diagonal. This is followed by a fold along its line of symmetry. The resulting folded shape is again folded along its line of symmetry. The area of each face of the final folded shape, in square units, equal to _____.- a)1/4
- b)1/8
- c)1/32
- d)1/16
Correct answer is option 'B'. Can you explain this answer?
Consider a square sheet of side 1 unit. The sheet is first folded along the main diagonal. This is followed by a fold along its line of symmetry. The resulting folded shape is again folded along its line of symmetry. The area of each face of the final folded shape, in square units, equal to _____.
a)
1/4
b)
1/8
c)
1/32
d)
1/16
|
|
Gaurav Kapoor answered |
Understanding the Folding Process
To solve the problem, we need to analyze the sequence of folds on the square sheet.
Step 1: First Fold along the Main Diagonal
- When the square sheet (1 unit by 1 unit) is folded along the main diagonal, it forms a right triangle.
- The area of the triangle is half of the original square's area:
- Area = 1/2 square units.
Step 2: Second Fold along the Line of Symmetry
- After the first fold, the triangle is folded again along its line of symmetry (the vertical line through the right angle).
- This fold creates a smaller triangle, which has half the area of the already folded triangle:
- Area = (1/2) * (1/2) = 1/4 square units.
Step 3: Third Fold along the Line of Symmetry
- The final fold is again along the line of symmetry of the current shape (the smaller triangle).
- This results in an even smaller triangle, reducing the area by half once more:
- Area = (1/2) * (1/4) = 1/8 square units.
Final Area of Each Face
- After completing all three folds, the area of each face of the final folded shape is 1/8 square units.
Thus, the correct answer is option 'B': 1/8 square units.
To solve the problem, we need to analyze the sequence of folds on the square sheet.
Step 1: First Fold along the Main Diagonal
- When the square sheet (1 unit by 1 unit) is folded along the main diagonal, it forms a right triangle.
- The area of the triangle is half of the original square's area:
- Area = 1/2 square units.
Step 2: Second Fold along the Line of Symmetry
- After the first fold, the triangle is folded again along its line of symmetry (the vertical line through the right angle).
- This fold creates a smaller triangle, which has half the area of the already folded triangle:
- Area = (1/2) * (1/2) = 1/4 square units.
Step 3: Third Fold along the Line of Symmetry
- The final fold is again along the line of symmetry of the current shape (the smaller triangle).
- This results in an even smaller triangle, reducing the area by half once more:
- Area = (1/2) * (1/4) = 1/8 square units.
Final Area of Each Face
- After completing all three folds, the area of each face of the final folded shape is 1/8 square units.
Thus, the correct answer is option 'B': 1/8 square units.
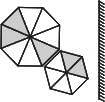
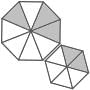
 Which one of the groups given below can be assembled to get the shape that is shown above using each piece only once without overlapping with each other? (rotation and translation operations may be used).
Which one of the groups given below can be assembled to get the shape that is shown above using each piece only once without overlapping with each other? (rotation and translation operations may be used).- a)
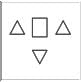
- b)
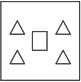
- c)

- d)
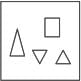
Correct answer is option 'B'. Can you explain this answer?

Which one of the groups given below can be assembled to get the shape that is shown above using each piece only once without overlapping with each other? (rotation and translation operations may be used).
a)

b)

c)

d)


|
Telecom Tuners answered |
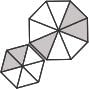
option 1:
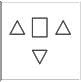
The above-given image will not be able to produce

The above-given image will be able to produce

The above-given image will not be able to produce

The above-given image will be able to produce

as three triangles will make the bottom part whereas the remaining two will make the above part.
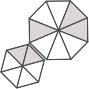
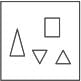
Option 3:

The above-given image will not be able to produce

as there is no scope for trapezium to fit in it.
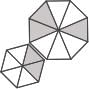
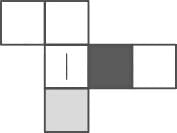
Option 4:
The above-given image will not be able to produce

as one more triangle is required.

as one more triangle is required.
Thus option 2 is the correct answer here.
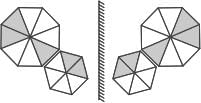
 Consider a cube made by folding a single sheet of paper of appropriate shape. The interior faces of the cube are all blank. However, the exterior faces that are not visible in the above view may not be blank.Which one of the following represents a possible unfolding of the cube?
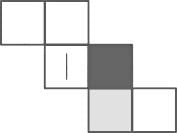
Consider a cube made by folding a single sheet of paper of appropriate shape. The interior faces of the cube are all blank. However, the exterior faces that are not visible in the above view may not be blank.Which one of the following represents a possible unfolding of the cube?- a)
- b)
- c)

- d)

Correct answer is option 'D'. Can you explain this answer?

Consider a cube made by folding a single sheet of paper of appropriate shape. The interior faces of the cube are all blank. However, the exterior faces that are not visible in the above view may not be blank.
Which one of the following represents a possible unfolding of the cube?
a)

b)

c)

d)


|
Telecom Tuners answered |
The Dark Shaded edge is perpendicular to a given line and the Light shaded edge is parallel to the given line so it can be assumed that option 4 is correct but there is no sign of + represented anywhere in the Question.
Hence, the correct answer is "Option 4".
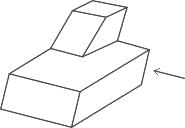
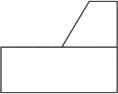
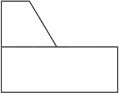
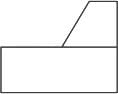
A block with a trapezoidal cross-section is placed over a block with rectangular cross section as shown above.Which one of the following is the correct drawing of the view of the 3D object as viewed in the direction indicated by an arrow in the above figure?- a)
- b)

- c)
- d)

Correct answer is option 'A'. Can you explain this answer?

A block with a trapezoidal cross-section is placed over a block with rectangular cross section as shown above.
Which one of the following is the correct drawing of the view of the 3D object as viewed in the direction indicated by an arrow in the above figure?
a)

b)

c)

d)


|
Telecom Tuners answered |
If we view the given figure from the direction of the arrow mentioned in the question we will see a trapezium on the right side placed above the rectangle.
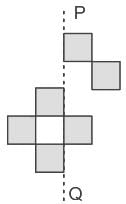 The least number of squares that must be added so that the line P-Q becomes the line of symmetry is ________.
The least number of squares that must be added so that the line P-Q becomes the line of symmetry is ________.- a)4
- b)3
- c)6
- d)7
Correct answer is option 'C'. Can you explain this answer?

The least number of squares that must be added so that the line P-Q becomes the line of symmetry is ________.
a)
4
b)
3
c)
6
d)
7

|
Crack Gate answered |
For symmetry we have to add some squares

After combining the obtained figure we get

Hence for making the P-Q line symmetry 6 squares must be added
 Corners are cut from an equilateral triangle to produce a regular convex hexagon as shown in the figure above. The ratio of the area of the regular convex hexagon to the area of the original equilateral triangle is
Corners are cut from an equilateral triangle to produce a regular convex hexagon as shown in the figure above. The ratio of the area of the regular convex hexagon to the area of the original equilateral triangle is- a)2 : 3
- b)3 : 4
- c)4 : 5
- d)5 : 6
Correct answer is option 'A'. Can you explain this answer?

Corners are cut from an equilateral triangle to produce a regular convex hexagon as shown in the figure above. The ratio of the area of the regular convex hexagon to the area of the original equilateral triangle is
a)
2 : 3
b)
3 : 4
c)
4 : 5
d)
5 : 6

|
Gate Funda answered |
Concept:
Area of an equilateral triangle
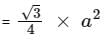
where a = side of the triangle.
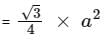
where a = side of the triangle.
Calculation:
Given:
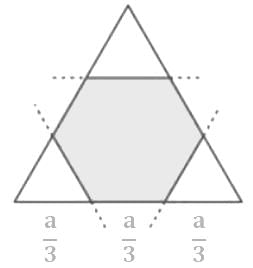
Let the side of the large triangle is 'a' then the side of the regular hexagon is a/3
If each triangle's area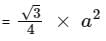
then the area of regular hexagon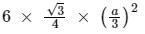
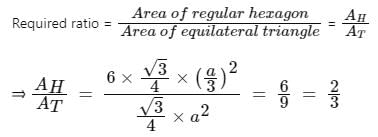
If each triangle's area
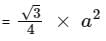
then the area of regular hexagon
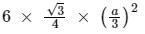
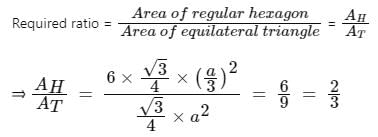
∴ The ratio of the area of the regular convex hexagon to the area of the original equilateral triangle is 2/3
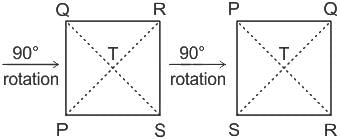
Consider the following square with the four corners and the center marked as P, Q, R, S and T respectively.Let X, Y and Z represent the following operations:X: rotation of the square by 180 degree with respect to the S-Q axis.
Y: rotation of the square by 180 degree with respect to the P-R axis.
Z: rotation of the square by 90 degree clockwise with respect to the axis perpendicular, going into the screen and passing through the point T.Consider the following three distinct sequences of operation (which are applied in the left to right order).
(1) XYZZ
(2) XY
(3) ZZZZWhich one of the following statements is correct as per the information provided above?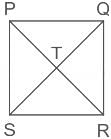
- a)The sequence of operations (1) and (2) are equivalent
- b)The sequence of operations (1) and (3) are equivalent
- c)The sequence of operations (2) and (3) are equivalent
- d)The sequence of operations (1), (2) and (3) are equivalent
Correct answer is option 'B'. Can you explain this answer?
Consider the following square with the four corners and the center marked as P, Q, R, S and T respectively.
Let X, Y and Z represent the following operations:
X: rotation of the square by 180 degree with respect to the S-Q axis.
Y: rotation of the square by 180 degree with respect to the P-R axis.
Z: rotation of the square by 90 degree clockwise with respect to the axis perpendicular, going into the screen and passing through the point T.
Y: rotation of the square by 180 degree with respect to the P-R axis.
Z: rotation of the square by 90 degree clockwise with respect to the axis perpendicular, going into the screen and passing through the point T.
Consider the following three distinct sequences of operation (which are applied in the left to right order).
(1) XYZZ
(2) XY
(3) ZZZZ
(1) XYZZ
(2) XY
(3) ZZZZ
Which one of the following statements is correct as per the information provided above?

a)
The sequence of operations (1) and (2) are equivalent
b)
The sequence of operations (1) and (3) are equivalent
c)
The sequence of operations (2) and (3) are equivalent
d)
The sequence of operations (1), (2) and (3) are equivalent

|
Telecom Tuners answered |
1) For XYZZ
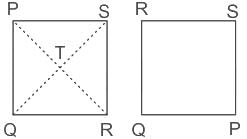
and ZZ

and ZZ

3) ZZZZ
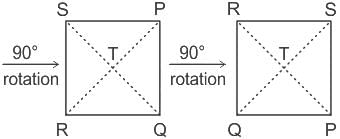

Chapter doubts & questions for Rotation of shapes - General Aptitude for GATE 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Rotation of shapes - General Aptitude for GATE in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
General Aptitude for GATE
229 videos|191 docs|158 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup