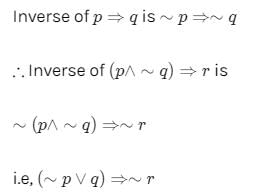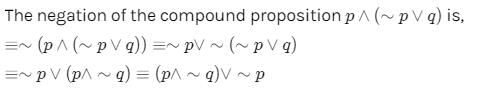All Exams >
JEE >
Chapter-wise Tests for JEE Main & Advanced >
All Questions
All questions of Mathematical Reasoning for JEE Exam
The quantifier used in the statement “For every real number x, x is less than x + 5” is:- a)For every
- b)And
- c)There exist
- d)Or
Correct answer is option 'A'. Can you explain this answer?
The quantifier used in the statement “For every real number x, x is less than x + 5” is:
a)
For every
b)
And
c)
There exist
d)
Or
|
|
Gaurav Kumar answered |
Quantifier is “For Every”
Negotiation of statement is : There exist a real number x such that x is not less than x+5
Negotiation of statement is : There exist a real number x such that x is not less than x+5
In order to prove the statement “If p then q” we need to show that:- a)By assuming that p is true, prove that q must be true.
- b)By assuming that p is true, prove that q must be false.
- c)By assuming that p is false, prove that q must be true
- d)By assuming that p is not true, prove that q must be true.
Correct answer is option 'C'. Can you explain this answer?
In order to prove the statement “If p then q” we need to show that:
a)
By assuming that p is true, prove that q must be true.
b)
By assuming that p is true, prove that q must be false.
c)
By assuming that p is false, prove that q must be true
d)
By assuming that p is not true, prove that q must be true.
|
|
Krishna Iyer answered |
Case 1: By assuming that p is true, prove that q must be true.(Direct method)
Case 2 : By assuming that q is false, prove that p must be false.(Contrapositive Method)
Case 2 : By assuming that q is false, prove that p must be false.(Contrapositive Method)
Which of the following is not a statement?- a)Mathematics is an easy subject
- b)The product of 8 and 12 is 100
- c)All integers are real numbers
- d)India is a part of SAARC
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not a statement?
a)
Mathematics is an easy subject
b)
The product of 8 and 12 is 100
c)
All integers are real numbers
d)
India is a part of SAARC
|
|
Hansa Sharma answered |
Mathematics is difficult for some but not for other.
Hence this statement can be true or false.
So it is not a statement.
Hence this statement can be true or false.
So it is not a statement.
Name the technique used in the solution of the problems below :
Question: Show that the following statement is false: If n is an odd integer, then n is prime.
Solution: The given statement is in the form “if p then q” we have to show that this is false, If p then ~q.
n= 99 is odd integer which is not a prime number. Thus, we conclude that the given statement is false.- a)Counter example
- b)Contrapositive method
- c)Direct method
- d)By Contradiction
Correct answer is option 'A'. Can you explain this answer?
Name the technique used in the solution of the problems below :
Question: Show that the following statement is false: If n is an odd integer, then n is prime.
Solution: The given statement is in the form “if p then q” we have to show that this is false, If p then ~q.
n= 99 is odd integer which is not a prime number. Thus, we conclude that the given statement is false.
Question: Show that the following statement is false: If n is an odd integer, then n is prime.
Solution: The given statement is in the form “if p then q” we have to show that this is false, If p then ~q.
n= 99 is odd integer which is not a prime number. Thus, we conclude that the given statement is false.
a)
Counter example
b)
Contrapositive method
c)
Direct method
d)
By Contradiction
|
|
Suresh Reddy answered |
Here n = 99 is a counter example of the given statement.
Therefore,
Option A
Therefore,
Option A
If x = 5 and y = - 2, then x – 2y = 9. The contrapositive of this proposition is
- a)x – 2y = 9 if x = 5 and y = - 2
- b)If x – 2y = 9, then x ≠ 5 or y ≠ - 2
- c)If x – 2y ≠ 9 then x ≠ 5 and y ≠ 2
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If x = 5 and y = - 2, then x – 2y = 9. The contrapositive of this proposition is
a)
x – 2y = 9 if x = 5 and y = - 2
b)
If x – 2y = 9, then x ≠ 5 or y ≠ - 2
c)
If x – 2y ≠ 9 then x ≠ 5 and y ≠ 2
d)
none of these
|
|
Lavanya Menon answered |
Let p,q and r be three propositions given by
p:x=5; q:y=−2 and r:x−2y=9
Then, the given statement is (p∧q)→r
Its contrapositive is
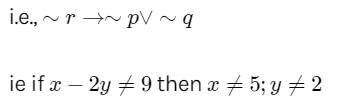
p:x=5; q:y=−2 and r:x−2y=9
Then, the given statement is (p∧q)→r
Its contrapositive is
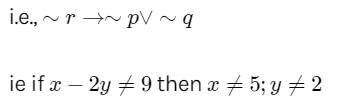
In order to prove the statement “p if and only if q” we need to show:- a)If p is false, then q is false.
- b)If p is true, then q is false
- c)If p is false, then q is true
- d)If p is true, then q is true
Correct answer is option 'D'. Can you explain this answer?
In order to prove the statement “p if and only if q” we need to show:
a)
If p is false, then q is false.
b)
If p is true, then q is false
c)
If p is false, then q is true
d)
If p is true, then q is true
|
|
Srestha Choudhary answered |
It is necessary to provide evidence or logical reasoning that supports the truth of the statement. This can be done through various means, such as conducting experiments, analyzing data, presenting empirical evidence, or providing logical arguments based on facts and principles. The proof should be objective and verifiable, so that it can be accepted by others as valid and reliable. Additionally, it is important to consider counterarguments and address any potential objections or alternative explanations to strengthen the proof.
Name the technique used in the first step of the soluntion of the problem below :
Verify that √5 is irrational
Solution ; Let us assume that √5 is rational- a)Counter example
- b)Direct method
- c)By Contradiction
- d)Contrapositive method
Correct answer is option 'C'. Can you explain this answer?
Name the technique used in the first step of the soluntion of the problem below :
Verify that √5 is irrational
Solution ; Let us assume that √5 is rational
Verify that √5 is irrational
Solution ; Let us assume that √5 is rational
a)
Counter example
b)
Direct method
c)
By Contradiction
d)
Contrapositive method

|
Drisri Jha answered |
It can only solve with contradiction method Because underroot 5 is rational no.
The negation of the statement “p: For every real number x, x3 > x2.” is:- a)There exists real number c such that x3 = x2.
- b)There exists real number c such that x2 > x.
- c)There exists real number c such that x3 > x.
- d)There exists a real number x such that x3 < x2.
Correct answer is option 'D'. Can you explain this answer?
The negation of the statement “p: For every real number x, x3 > x2.” is:
a)
There exists real number c such that x3 = x2.
b)
There exists real number c such that x2 > x.
c)
There exists real number c such that x3 > x.
d)
There exists a real number x such that x3 < x2.
|
|
Gaurav Kumar answered |
Negation of p :
There exists a real number x such that x3 < x2.
There exists a real number x such that x3 < x2.
A compound statement with an ‘Or’ is false when both the component statements are ……- a)Same
- b)True
- c)Different
- d)False
Correct answer is option 'D'. Can you explain this answer?
A compound statement with an ‘Or’ is false when both the component statements are ……
a)
Same
b)
True
c)
Different
d)
False

|
Dinesh Kotha answered |
Any compound statement which has And as the connecting word is said to be false if all its component statements are false. A compound statement which has Or as the connecting word is said to be true if one of its component statement orboth the component statements is true.
The connecting word used in the compound statement “Cube of an integer is positive or negative” is:- a)There exist
- b)And
- c)Or
- d)For all
Correct answer is option 'C'. Can you explain this answer?
The connecting word used in the compound statement “Cube of an integer is positive or negative” is:
a)
There exist
b)
And
c)
Or
d)
For all
|
|
Gaurav Kumar answered |
Cube of an integer is +ve or -ve.
p: Cube of an integer is +ve
q: Cube of an integer is -ve
p: Cube of an integer is +ve
q: Cube of an integer is -ve
Which of the following is a compound statement- a)Sun is a star
- b)I am a very strong boy
- c)7 is both odd and prime number
- d)There is something wrong in the room
Correct answer is option 'C'. Can you explain this answer?
Which of the following is a compound statement
a)
Sun is a star
b)
I am a very strong boy
c)
7 is both odd and prime number
d)
There is something wrong in the room
|
|
Tanuja Kapoor answered |
Compound statement is connected with And , or , etc.
So, the statement 7 is both odd and prime number is a compound statement.
So, the statement 7 is both odd and prime number is a compound statement.
Two pairs of statement are:p: If a quadrilateral is a rectangle, then its opposite sides are equal.q: If opposite sides of a quadrilateral are equal, then the quadrilateral is a rectangle.The combined statement of these pairs using “If and only if” is:- a)A quadrilateral is a rectangle if and only if its all sides are equal.
- b)A quadrilateral is a rectangle if and only if its opposite sides are equal.
- c)A quadrilateral is a square if and only if its opposite sides are equal.
- d)A quadrilateral is not a rectangle if and only if its opposite sides are equal.
Correct answer is option 'B'. Can you explain this answer?
Two pairs of statement are:
p: If a quadrilateral is a rectangle, then its opposite sides are equal.
q: If opposite sides of a quadrilateral are equal, then the quadrilateral is a rectangle.
The combined statement of these pairs using “If and only if” is:
a)
A quadrilateral is a rectangle if and only if its all sides are equal.
b)
A quadrilateral is a rectangle if and only if its opposite sides are equal.
c)
A quadrilateral is a square if and only if its opposite sides are equal.
d)
A quadrilateral is not a rectangle if and only if its opposite sides are equal.
|
|
Arun Yadav answered |
p: If a quadrilateral is a rectangle, then its opposite sides are equal.
q: If opposite sides of a quadrilateral are equal, then the quadrilateral is a rectangle.
Combined statement using “if and only if” is ‘A quadrilateral is a rectangle if and only if its opposite sides are equal’ because statements p & q are satisfied in this combined statement.
q: If opposite sides of a quadrilateral are equal, then the quadrilateral is a rectangle.
Combined statement using “if and only if” is ‘A quadrilateral is a rectangle if and only if its opposite sides are equal’ because statements p & q are satisfied in this combined statement.
The component statements ‘p’ and ‘q’ of the given compound statement ‘All integers are either even or odd.; are- a)P : All non integers are even,q: All non integers are odd
- b)P : All integers are not even,q: All integers are notodd
- c)P : All integers are even,q: All integers are not odd
- d)P : All integers are even,q: All integers are odd
Correct answer is option 'D'. Can you explain this answer?
The component statements ‘p’ and ‘q’ of the given compound statement ‘All integers are either even or odd.; are
a)
P : All non integers are even,q: All non integers are odd
b)
P : All integers are not even,q: All integers are notodd
c)
P : All integers are even,q: All integers are not odd
d)
P : All integers are even,q: All integers are odd
|
|
Sagar Kapoor answered |
Component statements of ‘All integers are either even or odd’ are:
P: All integers are even
Q: All integers are odd
P: All integers are even
Q: All integers are odd
Let p and q be two prepositions given by p : I play cricket during the holidays, q : I just sleep throughout the day then , the compound statement p ∧ q is- a)I play cricket during the holidays or I just sleep throughout the day
- b)If I play cricket during the holidays, I just sleep throughout the day
- c)I play cricket during the holidays and just sleep throughout the day
- d)I just sleep throughout the day if and only if I play cricket during the holidays
Correct answer is option 'A'. Can you explain this answer?
Let p and q be two prepositions given by p : I play cricket during the holidays, q : I just sleep throughout the day then , the compound statement p ∧ q is
a)
I play cricket during the holidays or I just sleep throughout the day
b)
If I play cricket during the holidays, I just sleep throughout the day
c)
I play cricket during the holidays and just sleep throughout the day
d)
I just sleep throughout the day if and only if I play cricket during the holidays

|
Peter Parker answered |
Option A is correct.
Negation of the statement p→(q ∨ r) is- a)∼p→∼(q ∨ r)
- b)∼p→∼(q ∧ r)
- c)(q ∨ r)→ p
- d)p ∧ (∼q ∧∼r )
Correct answer is option 'D'. Can you explain this answer?
Negation of the statement p→(q ∨ r) is
a)
∼p→∼(q ∨ r)
b)
∼p→∼(q ∧ r)
c)
(q ∨ r)→ p
d)
p ∧ (∼q ∧∼r )

|
Manish Aggarwal answered |
The correct option is D p ∧ (∼q ∧∼r)
We know that, ∼(p → q)≡ p ∧ (∼q)
Also, negation of (q ∨ r) is (∼q∧∼r)
So, ∼(p→(q ∨ r))≡ p ∧(∼q∧∼r)
We know that, ∼(p → q)≡ p ∧ (∼q)
Also, negation of (q ∨ r) is (∼q∧∼r)
So, ∼(p→(q ∨ r))≡ p ∧(∼q∧∼r)
A sentence is called a mathematically accepted statement if- a)it’s true
- b)it’s either true or false but not both.
- c)it’s false
- d)it’s neither true or false
Correct answer is option 'B'. Can you explain this answer?
A sentence is called a mathematically accepted statement if
a)
it’s true
b)
it’s either true or false but not both.
c)
it’s false
d)
it’s neither true or false
|
|
Siddharth Roy answered |
In mathematical reasoning, a statement is called a mathematically acceptable statement if it is either true or false but not both.
Let p and q be two propositions. Then the implication p↔∼q is true ,when
- a)p is true and q is true
- b)p is true and q is false
- c)p is false and q is true
- d)both p and q are false
Correct answer is option 'C'. Can you explain this answer?
Let p and q be two propositions. Then the implication p↔∼q is true ,when
a)
p is true and q is true
b)
p is true and q is false
c)
p is false and q is true
d)
both p and q are false
|
|
Niharika Deshpande answered |
Notation: Negation is denoted by the symbol ~
Bi-conditional:
Let, p and q are two simple propositions. If p and q both the propositions are either True or False then Bi-conditional gives the output as True otherwise if anyone is False then the output is False.
Notation: Bi-conditional is denoted by the symbol ⇔
Step-2: Truth Table:
The truth table is used to perform logical operations on given propositions. It is used to check whether the given propositional statement is either True or False. Using some of the logical operations like AND, OR, NOR, Conditional, and Bi-conditional.
Given p and q are both simple propositions
The truth table for p⇔~q is given below
pq~qp⇔~q
TT F F
TFT T
FTF T
FFT F
TT F F
TFT T
FTF T
FFT F
Where T is True and F is False.
From the above table, we can conclude p⇔~q is True if p is False and q is True.
Hence option 'C' is the correct answer.
The contra positive of a statement p ⇒ q, is the statement- a)~q ⇒ ~p
- b)~ q ⇒ p
- c)q ⇒ p
- d)q⇒ ~ p
Correct answer is option 'A'. Can you explain this answer?
The contra positive of a statement p ⇒ q, is the statement
a)
~q ⇒ ~p
b)
~ q ⇒ p
c)
q ⇒ p
d)
q⇒ ~ p
|
|
Rajat Patel answered |
The contrapositive of a conditional statement of the form "If p then q" is "If ~q then ~p". . A conditional statement is not logically equivalent to its converse. Inverse: Suppose a conditional statement of the form "If p then q" is given.
For any three propositions p, q, and r, the proposition (p∧q)∧(q∧r) is true, when- a)p is true and q, r are false
- b)p, q, r are all true
- c)p, q are true and r is false
- d)p, q, r are all false
Correct answer is option 'B'. Can you explain this answer?
For any three propositions p, q, and r, the proposition (p∧q)∧(q∧r) is true, when
a)
p is true and q, r are false
b)
p, q, r are all true
c)
p, q are true and r is false
d)
p, q, r are all false
|
|
Priyanka Basak answered |
Q) ∨ (p ∧ r) is logically equivalent to the proposition (p ∨ r) ∧ (q ∨ r).
To show this, we can use a truth table:
| p | q | r | p ∨ q | p ∧ r | (p ∨ q) ∨ (p ∧ r) | (p ∨ r) ∧ (q ∨ r) |
|---|---|---|-------|-------|-------------------|-------------------|
| T | T | T | T | T | T | T |
| T | T | F | T | F | T | T |
| T | F | T | T | T | T | T |
| T | F | F | T | F | T | T |
| F | T | T | T | F | T | T |
| F | T | F | T | F | T | T |
| F | F | T | T | F | F | F |
| F | F | F | F | F | F | F |
As we can see from the truth table, the two propositions have the same truth values for all possible truth values of p, q, and r. Therefore, they are logically equivalent.
To show this, we can use a truth table:
| p | q | r | p ∨ q | p ∧ r | (p ∨ q) ∨ (p ∧ r) | (p ∨ r) ∧ (q ∨ r) |
|---|---|---|-------|-------|-------------------|-------------------|
| T | T | T | T | T | T | T |
| T | T | F | T | F | T | T |
| T | F | T | T | T | T | T |
| T | F | F | T | F | T | T |
| F | T | T | T | F | T | T |
| F | T | F | T | F | T | T |
| F | F | T | T | F | F | F |
| F | F | F | F | F | F | F |
As we can see from the truth table, the two propositions have the same truth values for all possible truth values of p, q, and r. Therefore, they are logically equivalent.
The contrapositive of (p∨q)→ r is- a)∼r→(p∧q)
- b)∼r→∼(p∨q)
- c)p→(p∧q)
- d)∼r→(∼p∧∼q)
Correct answer is option 'D'. Can you explain this answer?
The contrapositive of (p∨q)→ r is
a)
∼r→(p∧q)
b)
∼r→∼(p∨q)
c)
p→(p∧q)
d)
∼r→(∼p∧∼q)
|
|
Nishanth Gupta answered |
Contrapositive of p→q is ∼q→∼p.
∴ Contrapositive of (p∨q)⇒r is ∼r⇒∼(p∨q) i.e. ∼r⇒(∼p∧∼q).
∴ Contrapositive of (p∨q)⇒r is ∼r⇒∼(p∨q) i.e. ∼r⇒(∼p∧∼q).
If p→(q∨r) is false , then the truth values of p , q and r, are respectively- a)T,F,F
- b)F,T,T
- c)F,F,F
- d)T,T,T
Correct answer is option 'A'. Can you explain this answer?
If p→(q∨r) is false , then the truth values of p , q and r, are respectively
a)
T,F,F
b)
F,T,T
c)
F,F,F
d)
T,T,T
|
|
Hiral Pillai answered |
I'm sorry, but I do not understand what "Ifp" means. Can you please provide more context or information?
Let p and q be two propositions given by P : The sky is blue, q : Milk is white, Then , p^q is- a)The sky is blue and milk is white
- b)The sky is blue or milk is white
- c)if the sky is blue then, milk is white
- d)The sky is white and milk is blue
Correct answer is option 'A'. Can you explain this answer?
Let p and q be two propositions given by P : The sky is blue, q : Milk is white, Then , p^q is
a)
The sky is blue and milk is white
b)
The sky is blue or milk is white
c)
if the sky is blue then, milk is white
d)
The sky is white and milk is blue
|
|
Geetika Mishra answered |
p∧q means statement p and q
=> The sky is blue and milk is white.
p∧(q∧r) is logically equivalent to- a)(p∨q)∧r
- b)(p∧q)∧r
- c)p→(q∧r)
- d)(p∨q)∨r
Correct answer is option 'B'. Can you explain this answer?
p∧(q∧r) is logically equivalent to
a)
(p∨q)∧r
b)
(p∧q)∧r
c)
p→(q∧r)
d)
(p∨q)∨r

|
Maulik Verma answered |
There are many words that begin with the letter "p." Here are a few examples:
1. Pizza
2. Penguin
3. Pencil
4. Party
5. Paint
6. Phone
7. Park
8. Puppy
9. Peach
10. Potato
1. Pizza
2. Penguin
3. Pencil
4. Party
5. Paint
6. Phone
7. Park
8. Puppy
9. Peach
10. Potato
The component statements are:
p: You are wet when it rains.
q: You are wet when you are in river.
The compound statement of these component statements using appropriate connective is:- a)You are not wet when you are in river or it rains.
- b)You are wet when you are in river and it rains.
- c)You are wet when it rains and you are in a river
- d)You are wet when it rains or you are in a river.
Correct answer is option 'D'. Can you explain this answer?
The component statements are:
p: You are wet when it rains.
q: You are wet when you are in river.
The compound statement of these component statements using appropriate connective is:
p: You are wet when it rains.
q: You are wet when you are in river.
The compound statement of these component statements using appropriate connective is:
a)
You are not wet when you are in river or it rains.
b)
You are wet when you are in river and it rains.
c)
You are wet when it rains and you are in a river
d)
You are wet when it rains or you are in a river.

|
Suhani Dangarh answered |
Yes d is correct 1st one not is written 2nd one says you are wet only when you are in river and that time rain comes 3rd says you are wet when rain and you must be in river at that time so 4th is correct which says you are wet either when you are in river or it rains
The contrapositive of the inverse of p⇒ ~q is- a)p ⇒ q
- b)~q ⇒ ~p
- c)~q ⇒ p
- d)~p ⇒ ~q
Correct answer is option 'C'. Can you explain this answer?
The contrapositive of the inverse of p⇒ ~q is
a)
p ⇒ q
b)
~q ⇒ ~p
c)
~q ⇒ p
d)
~p ⇒ ~q
|
|
Neha Sharma answered |
The inverse of p ⇒ ∼q is ∼p ⇒ q
The contrapositive of ∼p ⇒ q is ∼q ⇒ p. [∴ Contrapositive of p ⇒ q is∼q ⇒ p.]
The contrapositive of ∼p ⇒ q is ∼q ⇒ p. [∴ Contrapositive of p ⇒ q is∼q ⇒ p.]
The contrapositive of 2x + 3 = 9 ⇒ x ≠ 4 is- a)x ≠ 4, 2x+3 ≠ 9
- b)x = 4, 2x+3 ≠ 9
- c)x = 4, 2x+3 = 9
- d)x ≠ 4, 2x+3 = 9
Correct answer is option 'B'. Can you explain this answer?
The contrapositive of 2x + 3 = 9 ⇒ x ≠ 4 is
a)
x ≠ 4, 2x+3 ≠ 9
b)
x = 4, 2x+3 ≠ 9
c)
x = 4, 2x+3 = 9
d)
x ≠ 4, 2x+3 = 9
|
|
Bhavana Gupta answered |
Explanation:
Contrapositive:
The contrapositive of a statement is formed by negating both the hypothesis and conclusion of the original statement and switching their order.
Given Statement:
2x + 3 = 9 → x ≠ 4
Contrapositive:
x = 4 → 2x + 3 ≠ 9
Explanation:
- The original statement states that if 2x + 3 = 9, then x is not equal to 4.
- The contrapositive of this statement states that if x is equal to 4, then 2x + 3 is not equal to 9.
- Therefore, the correct contrapositive of the given statement is option B: x = 4, 2x + 3 ≠ 9.
Conclusion:
The contrapositive of the given statement is correctly represented in option B.
Contrapositive:
The contrapositive of a statement is formed by negating both the hypothesis and conclusion of the original statement and switching their order.
Given Statement:
2x + 3 = 9 → x ≠ 4
Contrapositive:
x = 4 → 2x + 3 ≠ 9
Explanation:
- The original statement states that if 2x + 3 = 9, then x is not equal to 4.
- The contrapositive of this statement states that if x is equal to 4, then 2x + 3 is not equal to 9.
- Therefore, the correct contrapositive of the given statement is option B: x = 4, 2x + 3 ≠ 9.
Conclusion:
The contrapositive of the given statement is correctly represented in option B.
Which of the following pairs is logically equivalent ?- a)Contrapositive, Converse
- b)Conditional, Inverse
- c)Inverse, Contrapositive
- d)Conditional, Contrapositive
Correct answer is option 'D'. Can you explain this answer?
Which of the following pairs is logically equivalent ?
a)
Contrapositive, Converse
b)
Conditional, Inverse
c)
Inverse, Contrapositive
d)
Conditional, Contrapositive
|
|
Akanksha Nair answered |
Understanding Logical Equivalence
In logic, understanding the relationships between different forms of statements is crucial. The terms involved are:
- Conditional Statement: If P, then Q (P → Q)
- Contrapositive: If not Q, then not P (¬Q → ¬P)
- Converse: If Q, then P (Q → P)
- Inverse: If not P, then not Q (¬P → ¬Q)
Logically Equivalent Statements
Two statements are logically equivalent if they always yield the same truth value.
Relationship Between Conditional and Contrapositive
- The contrapositive of a conditional statement is always logically equivalent to the original conditional.
- This means that if the conditional statement (P → Q) is true, then its contrapositive (¬Q → ¬P) is also true, and vice versa.
Why Option D is Correct
- Conditional (P → Q): This asserts that if P is true, Q must also be true.
- Contrapositive (¬Q → ¬P): This asserts that if Q is false, P must also be false.
Both statements convey the same logical relationship, thus confirming their logical equivalence.
Other Options Explained
- Option A (Contrapositive, Converse): Not equivalent. The converse (Q → P) does not logically follow from the contrapositive.
- Option B (Conditional, Inverse): Not equivalent. The inverse (¬P → ¬Q) is not necessarily true if the conditional is true.
- Option C (Inverse, Contrapositive): Not equivalent. The inverse does not share the same truth value as the contrapositive.
Conclusion
Thus, option D, which pairs the Conditional and the Contrapositive, is the only correct answer as they are logically equivalent. Understanding these relationships is essential for mastering logical reasoning in mathematics and related fields.
In logic, understanding the relationships between different forms of statements is crucial. The terms involved are:
- Conditional Statement: If P, then Q (P → Q)
- Contrapositive: If not Q, then not P (¬Q → ¬P)
- Converse: If Q, then P (Q → P)
- Inverse: If not P, then not Q (¬P → ¬Q)
Logically Equivalent Statements
Two statements are logically equivalent if they always yield the same truth value.
Relationship Between Conditional and Contrapositive
- The contrapositive of a conditional statement is always logically equivalent to the original conditional.
- This means that if the conditional statement (P → Q) is true, then its contrapositive (¬Q → ¬P) is also true, and vice versa.
Why Option D is Correct
- Conditional (P → Q): This asserts that if P is true, Q must also be true.
- Contrapositive (¬Q → ¬P): This asserts that if Q is false, P must also be false.
Both statements convey the same logical relationship, thus confirming their logical equivalence.
Other Options Explained
- Option A (Contrapositive, Converse): Not equivalent. The converse (Q → P) does not logically follow from the contrapositive.
- Option B (Conditional, Inverse): Not equivalent. The inverse (¬P → ¬Q) is not necessarily true if the conditional is true.
- Option C (Inverse, Contrapositive): Not equivalent. The inverse does not share the same truth value as the contrapositive.
Conclusion
Thus, option D, which pairs the Conditional and the Contrapositive, is the only correct answer as they are logically equivalent. Understanding these relationships is essential for mastering logical reasoning in mathematics and related fields.
The negation of the proposition “if a quadrilateral is a square, then it is a rhombus “ is- a)if a quadrilateral is not a square , then it is a rhombus
- b)a quadrilateral is not a square and it is a rhombus
- c)if a quadrilateral is a square , then it is not a rhombus
- d)a quadrilateral is a square and it is not a rhombus
Correct answer is option 'D'. Can you explain this answer?
The negation of the proposition “if a quadrilateral is a square, then it is a rhombus “ is
a)
if a quadrilateral is not a square , then it is a rhombus
b)
a quadrilateral is not a square and it is a rhombus
c)
if a quadrilateral is a square , then it is not a rhombus
d)
a quadrilateral is a square and it is not a rhombus

|
Seelam Yogitha answered |
P-->Q=~p ^ Q .Negation of P-->Q=~(~P ^ Q) = P V ~Q
Logical equivalent proposition to the proposition ∼(p∨q) is- a)∼p↔∼q
- b)∼p∧∼q
- c)∼p∨∼q
- d)∼p→∼q
Correct answer is option 'B'. Can you explain this answer?
Logical equivalent proposition to the proposition ∼(p∨q) is
a)
∼p↔∼q
b)
∼p∧∼q
c)
∼p∨∼q
d)
∼p→∼q

|
Nisha Banerjee answered |
The logical equivalent proposition to a given proposition depends on the specific proposition in question. Please provide the proposition for which you would like to find the logical equivalent.
Which of the following is logically equivalent to ∼(p↔q) ?- a)(p∨q)∨(q∧p)
- b)(p∨q)∨(q∧∼p)
- c)(p∨∼q)∨(q∧∼p)
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Which of the following is logically equivalent to ∼(p↔q) ?
a)
(p∨q)∨(q∧p)
b)
(p∨q)∨(q∧∼p)
c)
(p∨∼q)∨(q∧∼p)
d)
none of these
|
|
Sanaya Patel answered |
Logical Equivalence Explanation:
Logical equivalence means two statements have the same truth values in all possible scenarios. In this case, we are looking for a statement that is logically equivalent to ∼(p↔q).
Option Analysis:
a) (p∨q)∨(q∧p)
This statement is not logically equivalent to ∼(p↔q) as it involves both OR and AND operations.
b) (p∨q)∨(q∧¬p)
This statement is not logically equivalent to ∼(p↔q) as it has a negation on p which is not present in the original statement.
c) (p∨¬q)∨(q∧¬p)
This statement is logically equivalent to ∼(p↔q) as it represents the exclusive OR operation. The exclusive OR (XOR) operation is true when the inputs are different, which is the same as the biconditional statement.
d) none of these
This option is incorrect as we have found a logically equivalent statement in option c.
Therefore, the correct answer is option c) (p∨¬q)∨(q∧¬p).
Write the compound statement of the following component statements:
p: A rectangle is a quadrilateral.
q: The opposite sides of a rectangle are equal.- a)A rectangle is a quadrilateral and its opposite sides are equal.
- b)A rectangle is a quadrilateral and its opposite sides are not equal.
- c)A rectangle is not a quadrilateral and its opposite sides are equal.
- d)A rectangle is a figure and its opposite sides are of different length.
Correct answer is option 'A'. Can you explain this answer?
Write the compound statement of the following component statements:
p: A rectangle is a quadrilateral.
q: The opposite sides of a rectangle are equal.
p: A rectangle is a quadrilateral.
q: The opposite sides of a rectangle are equal.
a)
A rectangle is a quadrilateral and its opposite sides are equal.
b)
A rectangle is a quadrilateral and its opposite sides are not equal.
c)
A rectangle is not a quadrilateral and its opposite sides are equal.
d)
A rectangle is a figure and its opposite sides are of different length.
|
|
Sagarika Choudhury answered |
p: A rectangle is a quadrilateral.
q: The opposite sides of a rectangle are equal.
Compound statement using connecting word: ‘and’
A rectangle is a quadrilateral and its opposite sides are equal.
q: The opposite sides of a rectangle are equal.
Compound statement using connecting word: ‘and’
A rectangle is a quadrilateral and its opposite sides are equal.
Which of the following is a proposition ?- a)Logic is an interesting subject
- b)I am a lion
- c)A half open door is half closed
- d)A triangle is a circle and 10 is a prime number
Correct answer is option 'D'. Can you explain this answer?
Which of the following is a proposition ?
a)
Logic is an interesting subject
b)
I am a lion
c)
A half open door is half closed
d)
A triangle is a circle and 10 is a prime number
|
|
Kritika Khanna answered |
Proposition in Logic
Definition of Proposition:
A proposition is a statement that is either true or false.
Examples of Statements:
- Logic is an interesting subject.
- I am a lion.
- A half-open door is half closed.
- A triangle is a circle and 10 is a prime number.
Explanation:
Out of the four given statements, only option 'D' is a proposition because it can be evaluated as either true or false. A triangle cannot be a circle and 10 is not a prime number, so the statement is false.
Option 'A' is not a proposition because it is a subjective statement and cannot be evaluated as true or false. It may be interesting to some people and not to others.
Option 'B' is not a proposition because it is a false statement. The speaker is not actually a lion.
Option 'C' is not a proposition because it is an ambiguous statement. The meaning of "half-open" can vary depending on the context, so it cannot be evaluated as true or false.
Therefore, the only proposition in the given options is option 'D'.
Definition of Proposition:
A proposition is a statement that is either true or false.
Examples of Statements:
- Logic is an interesting subject.
- I am a lion.
- A half-open door is half closed.
- A triangle is a circle and 10 is a prime number.
Explanation:
Out of the four given statements, only option 'D' is a proposition because it can be evaluated as either true or false. A triangle cannot be a circle and 10 is not a prime number, so the statement is false.
Option 'A' is not a proposition because it is a subjective statement and cannot be evaluated as true or false. It may be interesting to some people and not to others.
Option 'B' is not a proposition because it is a false statement. The speaker is not actually a lion.
Option 'C' is not a proposition because it is an ambiguous statement. The meaning of "half-open" can vary depending on the context, so it cannot be evaluated as true or false.
Therefore, the only proposition in the given options is option 'D'.
The contrapositive of p→(∼q→∼r) is- a)(q∧∼r)→p
- b)(q∨∼r)∨p
- c)(∼q∧r)→∼p
- d)(q∧∼r)→∼p
Correct answer is option 'C'. Can you explain this answer?
The contrapositive of p→(∼q→∼r) is
a)
(q∧∼r)→p
b)
(q∨∼r)∨p
c)
(∼q∧r)→∼p
d)
(q∧∼r)→∼p
|
|
Shraddha Roy answered |
The contrapositive of p is "If not q, then not p."
Let p and q be two propositions. Then the contrapositive of the implication p→q is- a)∼q→∼p
- b)∼p→∼q
- c)∼q→p
- d)p↔q
Correct answer is option 'A'. Can you explain this answer?
Let p and q be two propositions. Then the contrapositive of the implication p→q is
a)
∼q→∼p
b)
∼p→∼q
c)
∼q→p
d)
p↔q

|
Rohit Joshi answered |
The contrapositive of the implication "p implies q" is "not q implies not p."
The statement p ⇒ p∨q is- a)a contradiction
- b)both a tautology and contradiction
- c)neither a contradiction nor a tautology
- d)a tautology
Correct answer is option 'D'. Can you explain this answer?
The statement p ⇒ p∨q is
a)
a contradiction
b)
both a tautology and contradiction
c)
neither a contradiction nor a tautology
d)
a tautology
|
|
Ujwal Ghosh answered |
A tautology is a proposition is always true.
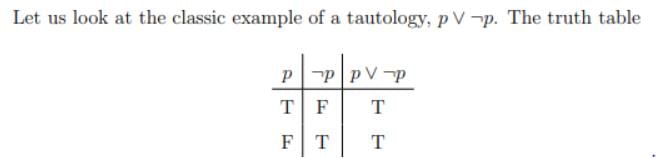
Which of the following sentences is a statement ?- a)2 is the smallest prime number
- b)Aarushi is a pretty girl
- c)What are you doing
- d)Oh ! It is amazing
Correct answer is option 'A'. Can you explain this answer?
Which of the following sentences is a statement ?
a)
2 is the smallest prime number
b)
Aarushi is a pretty girl
c)
What are you doing
d)
Oh ! It is amazing
|
|
Samridhi Sarkar answered |
Explanation:
A statement is a declarative sentence that can be either true or false. It gives some information or makes some assertion about the subject. The subject can be a person, place, thing, or idea. Let's analyze the given options to identify which one is a statement.
a) 2 is the smallest prime number - This is a declarative sentence that gives some information about the number 2. It is a statement.
b) Aarushi is a pretty girl - This is also a declarative sentence that makes an assertion about a person named Aarushi. It is a statement.
c) What are you doing? - This is an interrogative sentence that asks a question. It is not a statement.
d) Oh! It is amazing - This is an exclamatory sentence that expresses a strong emotion. It is not a statement.
Therefore, the correct answer is option 'A' - 2 is the smallest prime number, which is a statement.
A statement is a declarative sentence that can be either true or false. It gives some information or makes some assertion about the subject. The subject can be a person, place, thing, or idea. Let's analyze the given options to identify which one is a statement.
a) 2 is the smallest prime number - This is a declarative sentence that gives some information about the number 2. It is a statement.
b) Aarushi is a pretty girl - This is also a declarative sentence that makes an assertion about a person named Aarushi. It is a statement.
c) What are you doing? - This is an interrogative sentence that asks a question. It is not a statement.
d) Oh! It is amazing - This is an exclamatory sentence that expresses a strong emotion. It is not a statement.
Therefore, the correct answer is option 'A' - 2 is the smallest prime number, which is a statement.
Consider the proposition: “If we control population growth, we prosper “. Negative of this proposition is- a)If we do not control population growth but we prosper
- b)We control population but we do not prosper
- c)If we control population, we do not prosper
- d)We do not control population but we prosper
Correct answer is option 'B'. Can you explain this answer?
Consider the proposition: “If we control population growth, we prosper “. Negative of this proposition is
a)
If we do not control population growth but we prosper
b)
We control population but we do not prosper
c)
If we control population, we do not prosper
d)
We do not control population but we prosper

|
Sravya Banerjee answered |
"Everyone loves pizza."
This proposition is a general statement that claims that every person loves pizza. However, it is not necessarily true as not everyone may love pizza. People have different preferences when it comes to food, and there may be individuals who do not enjoy or love pizza. Therefore, this proposition is not accurate.
This proposition is a general statement that claims that every person loves pizza. However, it is not necessarily true as not everyone may love pizza. People have different preferences when it comes to food, and there may be individuals who do not enjoy or love pizza. Therefore, this proposition is not accurate.
Which option is not same as “if p then q”?- a)~p implies q.
- b)p is a sufficient condition for q.
- c)~q implies ~p
- d)p only if q.
Correct answer is option 'A'. Can you explain this answer?
Which option is not same as “if p then q”?
a)
~p implies q.
b)
p is a sufficient condition for q.
c)
~q implies ~p
d)
p only if q.

|
Srishti Roy answered |
Your question is not clear. Please provide more information or rephrase your question.
Chapter doubts & questions for Mathematical Reasoning - Chapter-wise Tests for JEE Main & Advanced 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Mathematical Reasoning - Chapter-wise Tests for JEE Main & Advanced in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup