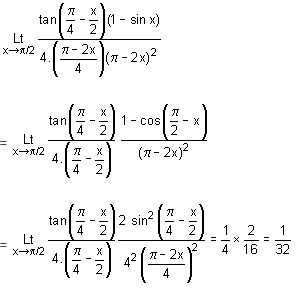All Exams >
JEE >
Mock Tests for JEE Main and Advanced 2026 >
All Questions
All questions of JEE Main Additional Practice Mock Tests for JEE Exam
Water is filled up to a height h in a cylindrical vessel. It takes time t to completely drain the vessel by means of a small hole at the bottom. If water is filled up to a height 4h then the time it takes to completely drain the vessel is- a)t
- b)4t
- c)2t
- d)t/4
Correct answer is option 'C'. Can you explain this answer?
Water is filled up to a height h in a cylindrical vessel. It takes time t to completely drain the vessel by means of a small hole at the bottom. If water is filled up to a height 4h then the time it takes to completely drain the vessel is
a)
t
b)
4t
c)
2t
d)
t/4

|
Amit Yadav answered |
B
If the pairs of straight lines x2 - 2pxy - y2 = 0 and x2 - 2qxy - y2 = 0 be such that each pair bisects the angle between the other pair, then pq is equal to
Correct answer is '-1'. Can you explain this answer?
If the pairs of straight lines x2 - 2pxy - y2 = 0 and x2 - 2qxy - y2 = 0 be such that each pair bisects the angle between the other pair, then pq is equal to
|
|
Krishna Iyer answered |
Given equations are
x2 - 2qxy - y2 = 0 ... (1)
x2 - 2pxy - y2 = 0 ... (2)
Joint equations of angle bisector of the lines (i) and (ii) are same.
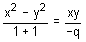
qx2 + 2xy - qy2 = 0 ... (3)
Now, (2) and (3) are same.
Taking ratio of their coefficients.
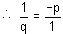
⇒ pq = -1
If the binding energy of an electron in a hydrogen atom is 13.6 eV, then the energy required to remove the electron from the first excited state of Li++ is- a)30.6 eV
- b)13.6 eV
- c)3.4 eV
- d)122.4 eV
Correct answer is option 'A'. Can you explain this answer?
If the binding energy of an electron in a hydrogen atom is 13.6 eV, then the energy required to remove the electron from the first excited state of Li++ is
a)
30.6 eV
b)
13.6 eV
c)
3.4 eV
d)
122.4 eV
|
|
Krishna Iyer answered |
Binding energy of the electron,
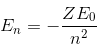
Hence, for n = 2:
Binding energy, E2 = 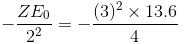
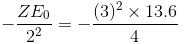
E2 = -30.6 eV
Energy required to remove the electron from the first excited state of Li++ = 30.6 eV
The number of values of a for which the pair of lines represented by 3ax2 + 5xy + (a2 - 2)y2 = 0, perpendicular to each other, is
Correct answer is '2'. Can you explain this answer?
The number of values of a for which the pair of lines represented by 3ax2 + 5xy + (a2 - 2)y2 = 0, perpendicular to each other, is
|
|
Neha Pillai answered |
Perpendicular Lines:
In order to determine the number of values of 'a' for which the pair of lines represented by the given equation are perpendicular, we need to understand the conditions for two lines to be perpendicular.
Two lines are perpendicular if the product of their slopes is -1. The slope of a line is given by the coefficient of x divided by the coefficient of y in the equation of the line.
Equation Analysis:
The given equation is: 3ax^2 + 5xy + (a^2 - 2)y^2 = 0
To find the slopes of the lines represented by this equation, we need to convert it into the standard form of a line equation, which is in the form of ax + by + c = 0.
Converting the Equation:
Let's convert the given equation into the standard form by rearranging the terms:
3ax^2 + 5xy + (a^2 - 2)y^2 = 0
3ax^2 + 5xy + a^2y^2 - 2y^2 = 0
3ax^2 + 5xy + a^2y^2 = 2y^2
Now, let's divide the entire equation by y^2 to get rid of the quadratic terms:
(3ax^2 + 5xy + a^2y^2) / y^2 = 2y^2 / y^2
3ax^2 / y^2 + 5xy / y^2 + a^2 = 2
Simplifying further:
3a(x/y)^2 + 5(x/y) + a^2 = 2
Now, let's consider x/y as a new variable, say 'm':
3am^2 + 5m + a^2 - 2 = 0
Conditions for Perpendicular Lines:
For two lines to be perpendicular, the product of their slopes should be -1. Therefore, we need to find the values of 'a' for which the slopes of the lines represented by the given equation satisfy this condition.
Calculating the Slopes:
The slope of the line represented by the given equation can be found by differentiating the equation with respect to x/y and solving for m.
Differentiating the equation 3am^2 + 5m + a^2 - 2 = 0 with respect to m:
6am + 5 = 0
m = -5/6a
Product of Slopes:
Now, let's find the product of the slopes of the two lines represented by the given equation:
m1 * m2 = (-5/6a) * (-5/6a) = 25/36a^2
Condition for Perpendicular Lines:
To find the values of 'a' for which the lines are perpendicular, we need the product of their slopes to be -1.
Therefore, 25/36a^2 = -1
36a^2 = -25
a^2 = -25/36
Solution:
The equation a^2 = -25/36 has no real solutions since the square of a real number cannot be negative.
Therefore, there are no values of 'a' for which
In order to determine the number of values of 'a' for which the pair of lines represented by the given equation are perpendicular, we need to understand the conditions for two lines to be perpendicular.
Two lines are perpendicular if the product of their slopes is -1. The slope of a line is given by the coefficient of x divided by the coefficient of y in the equation of the line.
Equation Analysis:
The given equation is: 3ax^2 + 5xy + (a^2 - 2)y^2 = 0
To find the slopes of the lines represented by this equation, we need to convert it into the standard form of a line equation, which is in the form of ax + by + c = 0.
Converting the Equation:
Let's convert the given equation into the standard form by rearranging the terms:
3ax^2 + 5xy + (a^2 - 2)y^2 = 0
3ax^2 + 5xy + a^2y^2 - 2y^2 = 0
3ax^2 + 5xy + a^2y^2 = 2y^2
Now, let's divide the entire equation by y^2 to get rid of the quadratic terms:
(3ax^2 + 5xy + a^2y^2) / y^2 = 2y^2 / y^2
3ax^2 / y^2 + 5xy / y^2 + a^2 = 2
Simplifying further:
3a(x/y)^2 + 5(x/y) + a^2 = 2
Now, let's consider x/y as a new variable, say 'm':
3am^2 + 5m + a^2 - 2 = 0
Conditions for Perpendicular Lines:
For two lines to be perpendicular, the product of their slopes should be -1. Therefore, we need to find the values of 'a' for which the slopes of the lines represented by the given equation satisfy this condition.
Calculating the Slopes:
The slope of the line represented by the given equation can be found by differentiating the equation with respect to x/y and solving for m.
Differentiating the equation 3am^2 + 5m + a^2 - 2 = 0 with respect to m:
6am + 5 = 0
m = -5/6a
Product of Slopes:
Now, let's find the product of the slopes of the two lines represented by the given equation:
m1 * m2 = (-5/6a) * (-5/6a) = 25/36a^2
Condition for Perpendicular Lines:
To find the values of 'a' for which the lines are perpendicular, we need the product of their slopes to be -1.
Therefore, 25/36a^2 = -1
36a^2 = -25
a^2 = -25/36
Solution:
The equation a^2 = -25/36 has no real solutions since the square of a real number cannot be negative.
Therefore, there are no values of 'a' for which
According to the kinetic theory of gases, between two successive collisions, a gas molecule travels- a)In a circular path
- b)In a wavy path
- c)In a straight line path
- d)With an accelerated velocity
Correct answer is option 'C'. Can you explain this answer?
According to the kinetic theory of gases, between two successive collisions, a gas molecule travels
a)
In a circular path
b)
In a wavy path
c)
In a straight line path
d)
With an accelerated velocity
|
|
Varun Kapoor answered |
According to kinetic theory, the gas molecules are in a state of constant rapid motion in all possible directions colliding in a random manner with one another and with the walls of the container and between two successive collisions, molecules travel in a straight line path but show haphazard motion due to collisions.
A circular disc of radius r and thickness r/6 has moment of inertia I about an axis passing through its centre and perpendicular to its plane. It is melted and recasted to a solid sphere. The moment of inertia of the sphere about its diameter as axis of rotation is- a)I/2
- b)2I/11
- c)I/10
- d)I/5
Correct answer is option 'D'. Can you explain this answer?
A circular disc of radius r and thickness r/6 has moment of inertia I about an axis passing through its centre and perpendicular to its plane. It is melted and recasted to a solid sphere. The moment of inertia of the sphere about its diameter as axis of rotation is
a)
I/2
b)
2I/11
c)
I/10
d)
I/5

|
Akshita Nair answered |
Volume oc circular disc = surface of area x thickness
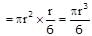
The mass of the circular disc and sphere are the same
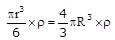
where R is the radius of the sphere,
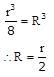
Moment of interia of a circluar disc

Moment of interia of solid sphere
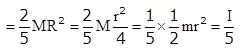
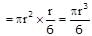
The mass of the circular disc and sphere are the same
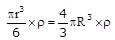
where R is the radius of the sphere,
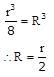
Moment of interia of a circluar disc

Moment of interia of solid sphere
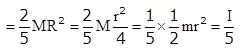
The number of P-O-P bridges in the structures of phosphorus pentoxide and phosphorus trioxide is- a)6, 6
- b)5, 5
- c)5, 6
- d)6, 5
Correct answer is option 'A'. Can you explain this answer?
The number of P-O-P bridges in the structures of phosphorus pentoxide and phosphorus trioxide is
a)
6, 6
b)
5, 5
c)
5, 6
d)
6, 5
|
|
Deepika Sen answered |
Understanding P-O-P Bridges in Phosphorus Compounds
Phosphorus pentoxide (P2O5) and phosphorus trioxide (P2O3) are two important phosphorus oxides that exhibit different bonding structures. The concept of P-O-P (phosphorus-oxygen-phosphorus) bridges is crucial in understanding their molecular frameworks.
Phosphorus Pentoxide (P2O5)
- P2O5 is known to have a dimeric structure consisting of two phosphorus atoms connected by oxygen atoms.
- In its anhydrous form, it primarily exists as a cyclic structure with multiple bridging oxygens.
- The number of P-O-P bridges in P2O5 is 6, as it forms a network with six oxygen atoms linking the phosphorus centers.
Phosphorus Trioxide (P2O3)
- P2O3 features a different structural arrangement compared to P2O5.
- It has a more polymeric structure with fewer bridging oxygens.
- The number of P-O-P bridges in P2O3 is 5, due to the presence of fewer oxygen linkages between the phosphorus atoms.
Summary of Bridges
- Phosphorus Pentoxide (P2O5): 6 P-O-P bridges
- Phosphorus Trioxide (P2O3): 5 P-O-P bridges
Conclusion
The correct answer to the question regarding the number of P-O-P bridges in phosphorus pentoxide and phosphorus trioxide is option 'A': 6 bridges in P2O5 and 5 bridges in P2O3. This understanding of the structural differences underscores the significance of bridging oxygens in determining the properties of these phosphorus oxides.
Phosphorus pentoxide (P2O5) and phosphorus trioxide (P2O3) are two important phosphorus oxides that exhibit different bonding structures. The concept of P-O-P (phosphorus-oxygen-phosphorus) bridges is crucial in understanding their molecular frameworks.
Phosphorus Pentoxide (P2O5)
- P2O5 is known to have a dimeric structure consisting of two phosphorus atoms connected by oxygen atoms.
- In its anhydrous form, it primarily exists as a cyclic structure with multiple bridging oxygens.
- The number of P-O-P bridges in P2O5 is 6, as it forms a network with six oxygen atoms linking the phosphorus centers.
Phosphorus Trioxide (P2O3)
- P2O3 features a different structural arrangement compared to P2O5.
- It has a more polymeric structure with fewer bridging oxygens.
- The number of P-O-P bridges in P2O3 is 5, due to the presence of fewer oxygen linkages between the phosphorus atoms.
Summary of Bridges
- Phosphorus Pentoxide (P2O5): 6 P-O-P bridges
- Phosphorus Trioxide (P2O3): 5 P-O-P bridges
Conclusion
The correct answer to the question regarding the number of P-O-P bridges in phosphorus pentoxide and phosphorus trioxide is option 'A': 6 bridges in P2O5 and 5 bridges in P2O3. This understanding of the structural differences underscores the significance of bridging oxygens in determining the properties of these phosphorus oxides.
A metal conductor of length 1 m rotates vertically about one of its ends at angular velocity 5 radian per second. If the horizontal component of Earth's magnetic field is 0.2 x 10-4 T, then the emf developed between the two ends of the conductor is- a)5 μV
- b)50 μV
- c)5 mV
- d)50 mV
Correct answer is option 'B'. Can you explain this answer?
A metal conductor of length 1 m rotates vertically about one of its ends at angular velocity 5 radian per second. If the horizontal component of Earth's magnetic field is 0.2 x 10-4 T, then the emf developed between the two ends of the conductor is
a)
5 μV
b)
50 μV
c)
5 mV
d)
50 mV
|
|
Chirag Verma answered |
Induced e.m.f. = 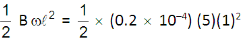
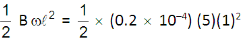
∴ Induced e.m.f = 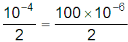
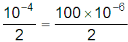
= 50 μV
Which is the most volatile?- a)CH3CH2CH2NH2
- b)(CH3)3N
- c)CH3CH2NHCH3
- d)CH3–CH2–OH
Correct answer is option 'B'. Can you explain this answer?
Which is the most volatile?
a)
CH3CH2CH2NH2
b)
(CH3)3N
c)
CH3CH2NHCH3
d)
CH3–CH2–OH
|
|
Maya Sharma answered |
The most volatile compound among the given options is (CH3)3N, or trimethylamine.
Explanation:
Volatile compounds are substances that have a relatively low boiling point and evaporate easily at room temperature. The volatility of a compound is influenced by several factors, including molecular weight, intermolecular forces, and functional groups.
1. Molecular weight:
Generally, as the molecular weight of a compound increases, its volatility decreases. This is because larger molecules have stronger intermolecular forces, which require more energy to overcome and evaporate. Among the given options, trimethylamine [(CH3)3N] has the lowest molecular weight (59.11 g/mol), making it more volatile than the other compounds.
2. Intermolecular forces:
Intermolecular forces, such as hydrogen bonding, dipole-dipole interactions, and London dispersion forces, also affect the volatility of a compound. Stronger intermolecular forces tend to increase boiling points and decrease volatility.
a) CH3CH2CH2NH2 (ethylamine): This compound can form hydrogen bonds through the nitrogen atom, increasing its boiling point and reducing its volatility compared to non-hydrogen bonding compounds. However, it is less volatile than trimethylamine due to its higher molecular weight (45.08 g/mol) and fewer methyl groups.
c) CH3CH2NHCH3 (dimethylamine): Similar to ethylamine, this compound can also form hydrogen bonds. However, it has a higher molecular weight (59.11 g/mol) and only one methyl group, making it less volatile than trimethylamine.
d) CH3–CH2–OH (ethanol): This compound can form hydrogen bonds through the hydroxyl group. It has a higher molecular weight (46.07 g/mol) than trimethylamine and fewer methyl groups, making it less volatile.
Therefore, among the given options, (CH3)3N (trimethylamine) is the most volatile compound due to its low molecular weight and lack of strong intermolecular forces.
Explanation:
Volatile compounds are substances that have a relatively low boiling point and evaporate easily at room temperature. The volatility of a compound is influenced by several factors, including molecular weight, intermolecular forces, and functional groups.
1. Molecular weight:
Generally, as the molecular weight of a compound increases, its volatility decreases. This is because larger molecules have stronger intermolecular forces, which require more energy to overcome and evaporate. Among the given options, trimethylamine [(CH3)3N] has the lowest molecular weight (59.11 g/mol), making it more volatile than the other compounds.
2. Intermolecular forces:
Intermolecular forces, such as hydrogen bonding, dipole-dipole interactions, and London dispersion forces, also affect the volatility of a compound. Stronger intermolecular forces tend to increase boiling points and decrease volatility.
a) CH3CH2CH2NH2 (ethylamine): This compound can form hydrogen bonds through the nitrogen atom, increasing its boiling point and reducing its volatility compared to non-hydrogen bonding compounds. However, it is less volatile than trimethylamine due to its higher molecular weight (45.08 g/mol) and fewer methyl groups.
c) CH3CH2NHCH3 (dimethylamine): Similar to ethylamine, this compound can also form hydrogen bonds. However, it has a higher molecular weight (59.11 g/mol) and only one methyl group, making it less volatile than trimethylamine.
d) CH3–CH2–OH (ethanol): This compound can form hydrogen bonds through the hydroxyl group. It has a higher molecular weight (46.07 g/mol) than trimethylamine and fewer methyl groups, making it less volatile.
Therefore, among the given options, (CH3)3N (trimethylamine) is the most volatile compound due to its low molecular weight and lack of strong intermolecular forces.
The coefficient of x5 in the expansion of (1 + x)21 + (1 + x)22 +...+(1 + x)30 is- a)51C5
- b)9C5
- c)31C6 - 21C6
- d)30C5 + 20C5
Correct answer is option 'C'. Can you explain this answer?
The coefficient of x5 in the expansion of (1 + x)21 + (1 + x)22 +...+(1 + x)30 is
a)
51C5
b)
9C5
c)
31C6 - 21C6
d)
30C5 + 20C5
|
|
Ananya Das answered |
(1 + x)21 + (1 + x)22 +...+(1 + x)30
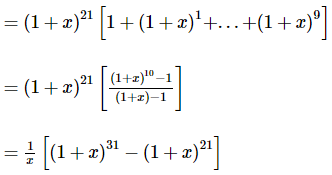
∴ Coefficient of x5 in the given expression
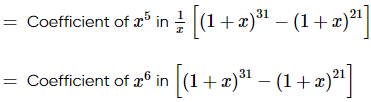
= 31C6 - 21C6
Three point charges Q, +q and +q are placed at the vertices of a right-angled isosceles triangle as shown in the figure. If the net electrostatic energy of the configuration is zero, then what is the value of 10×∣Q/q∣? [Take √2 =1.4]
Correct answer is '6'. Can you explain this answer?
Three point charges Q, +q and +q are placed at the vertices of a right-angled isosceles triangle as shown in the figure. If the net electrostatic energy of the configuration is zero, then what is the value of 10×∣Q/q∣? [Take √2 =1.4]
|
|
Neha Sharma answered |
Net electrostatic energy of the configuration will be
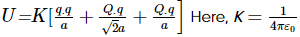
Putting U = 0, we get
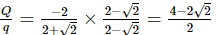
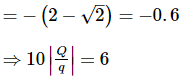
The total number of isotopes of hydrogen and number of radioactive isotopes among them, respectively, are:- a)2 and 0
- b)3 and 2
- c)3 and 1
- d)2 and 1
Correct answer is option 'C'. Can you explain this answer?
The total number of isotopes of hydrogen and number of radioactive isotopes among them, respectively, are:
a)
2 and 0
b)
3 and 2
c)
3 and 1
d)
2 and 1
|
|
Lavanya Menon answered |
Total number of isotopes of hydrogen is 3
⇒ 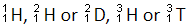
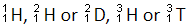
and only 13H or 13T is an Radioactive element.
In which one of the following pairs is the radius of the second species greater than that of the first?- a)Na, Mg
- b)Li+, Be2+
- c)Ba2+, Sr2+
- d)O2−, N3−
Correct answer is option 'D'. Can you explain this answer?
In which one of the following pairs is the radius of the second species greater than that of the first?
a)
Na, Mg
b)
Li+, Be2+
c)
Ba2+, Sr2+
d)
O2−, N3−
|
|
Meera Bajaj answered |
Explanation:
Species Comparison:
- The radius of an ion is determined by its electron configuration and the number of protons in its nucleus.
- In general, as you move down a group in the periodic table, the radius of the ions increases due to the addition of new electron shells.
Comparison of Species in each Pair:
a) Na, Mg
- Na is a neutral atom with 11 electrons and Mg is a neutral atom with 12 electrons.
- Mg has a greater number of protons in its nucleus compared to Na, so Mg has a smaller radius than Na.
b) Li+, Be2+
- Li+ has lost one electron compared to the neutral atom Li, so it has a smaller radius.
- Be2+ has lost two electrons compared to the neutral atom Be, so it has an even smaller radius than Li+.
c) Ba2+, Sr2+
- Both Ba and Sr are in the same group in the periodic table, meaning they have the same number of electron shells.
- Since Ba2+ has a greater nuclear charge due to its higher number of protons compared to Sr2+, Ba2+ has a smaller radius.
d) O2-, N3-
- O2- has gained two electrons compared to the neutral atom O, resulting in a larger radius for O2-.
- N3- has gained three electrons compared to the neutral atom N, resulting in a larger radius for N3-.
- Therefore, in this pair, the radius of the second species (N3-) is greater than that of the first species (O2-).
Therefore, the correct answer is option 'D' - O2-, N3-.
Species Comparison:
- The radius of an ion is determined by its electron configuration and the number of protons in its nucleus.
- In general, as you move down a group in the periodic table, the radius of the ions increases due to the addition of new electron shells.
Comparison of Species in each Pair:
a) Na, Mg
- Na is a neutral atom with 11 electrons and Mg is a neutral atom with 12 electrons.
- Mg has a greater number of protons in its nucleus compared to Na, so Mg has a smaller radius than Na.
b) Li+, Be2+
- Li+ has lost one electron compared to the neutral atom Li, so it has a smaller radius.
- Be2+ has lost two electrons compared to the neutral atom Be, so it has an even smaller radius than Li+.
c) Ba2+, Sr2+
- Both Ba and Sr are in the same group in the periodic table, meaning they have the same number of electron shells.
- Since Ba2+ has a greater nuclear charge due to its higher number of protons compared to Sr2+, Ba2+ has a smaller radius.
d) O2-, N3-
- O2- has gained two electrons compared to the neutral atom O, resulting in a larger radius for O2-.
- N3- has gained three electrons compared to the neutral atom N, resulting in a larger radius for N3-.
- Therefore, in this pair, the radius of the second species (N3-) is greater than that of the first species (O2-).
Therefore, the correct answer is option 'D' - O2-, N3-.
The half-life of a radioisotope is six hours. If the initial mass of the isotope is 200 g, then the mass (in g) remaining after 24 hours undecayed will be (Nearest integer)
Correct answer is '13'. Can you explain this answer?
The half-life of a radioisotope is six hours. If the initial mass of the isotope is 200 g, then the mass (in g) remaining after 24 hours undecayed will be (Nearest integer)
|
|
Neha Joshi answered |
Radioactive decay follows first order kinetics.
Number of half-lives (t1/2) = 24/6 = 4
Nt = N0(1/2)4 = N0/16.
1 g of the element will reduce to 1/16g.
Therefore, mass of the radioisotope remaining 1/16 x 200 = 12.5 g = 13 g
Which of the following are substituted purines?A. AdenineB. UracilC. GuanineD. Cytosine- a)Only A and B
- b)Only A and C
- c)Only A and D
- d)Only B and C
Correct answer is option 'B'. Can you explain this answer?
Which of the following are substituted purines?
A. Adenine
B. Uracil
C. Guanine
D. Cytosine
a)
Only A and B
b)
Only A and C
c)
Only A and D
d)
Only B and C
|
|
Pranavi Kumar answered |
Understanding Substituted Purines
To clarify why the correct answer is option 'B', let’s first define what purines are and what is meant by substituted purines.
What are Purines?
- Purines are one of the two types of nitrogenous bases found in nucleic acids (DNA and RNA).
- The two primary purines are adenine (A) and guanine (G).
What are Substituted Purines?
- Substituted purines are purine derivatives that have additional functional groups or atoms attached to the basic purine structure.
- Common examples include hypoxanthine (a derivative of adenine) and xanthine (a derivative of guanine).
Analysis of the Options
- A. Adenine:
- This is a purine itself, but not a substituted purine in its basic form.
- B. Uracil:
- Uracil is not a purine; it is a pyrimidine. However, it can be considered in certain contexts as a derivative in RNA, but not as a substituted purine.
- C. Guanine:
- Like adenine, guanine is a purine but not a substituted one in its standard form.
- D. Cytosine:
- Cytosine is another pyrimidine and does not belong to the purine category.
Conclusion
- The question is misleading since none of the options listed are strictly classified as substituted purines.
- However, the correct interpretation could be that adenine and guanine, when modified, can be viewed as potential candidates in certain biochemical pathways.
- Thus, the confusion arises from the context of the question, but strictly speaking, option 'B' identified uracil as a non-purine, diverging from purine classification.
To clarify why the correct answer is option 'B', let’s first define what purines are and what is meant by substituted purines.
What are Purines?
- Purines are one of the two types of nitrogenous bases found in nucleic acids (DNA and RNA).
- The two primary purines are adenine (A) and guanine (G).
What are Substituted Purines?
- Substituted purines are purine derivatives that have additional functional groups or atoms attached to the basic purine structure.
- Common examples include hypoxanthine (a derivative of adenine) and xanthine (a derivative of guanine).
Analysis of the Options
- A. Adenine:
- This is a purine itself, but not a substituted purine in its basic form.
- B. Uracil:
- Uracil is not a purine; it is a pyrimidine. However, it can be considered in certain contexts as a derivative in RNA, but not as a substituted purine.
- C. Guanine:
- Like adenine, guanine is a purine but not a substituted one in its standard form.
- D. Cytosine:
- Cytosine is another pyrimidine and does not belong to the purine category.
Conclusion
- The question is misleading since none of the options listed are strictly classified as substituted purines.
- However, the correct interpretation could be that adenine and guanine, when modified, can be viewed as potential candidates in certain biochemical pathways.
- Thus, the confusion arises from the context of the question, but strictly speaking, option 'B' identified uracil as a non-purine, diverging from purine classification.
An alternating voltage having frequency of 50 cycles/sec and maximum voltage 220 V is supplied to a circuit containing a pure inductance of 0.02 H and a pure resistance of 10 Ω in series. The value of maximum current in circuit is-- a)16.52 A
- b)18.64 A
- c)20.18 A
- d)22. 73 A
Correct answer is option 'B'. Can you explain this answer?
An alternating voltage having frequency of 50 cycles/sec and maximum voltage 220 V is supplied to a circuit containing a pure inductance of 0.02 H and a pure resistance of 10 Ω in series. The value of maximum current in circuit is-
a)
16.52 A
b)
18.64 A
c)
20.18 A
d)
22. 73 A

|
Harshitha Nambiar answered |
Impendance of L.R series circut
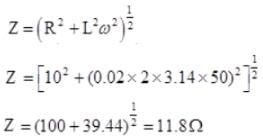
Value of current
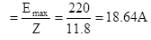
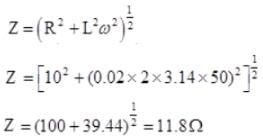
Value of current
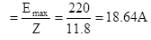
A steel ball of mass 60 g falls from a height 0.8 m on the horizontal surface of a massive slab. The coefficient of restitution between the ball and the slab is e = 0.4; the total momentum imparted to the slab by the ball after numerous bounces is- a)0.56 Ns
- b)0.64 Ns
- c)0.72 Ns
- d)0.78 Ns
Correct answer is option 'A'. Can you explain this answer?
A steel ball of mass 60 g falls from a height 0.8 m on the horizontal surface of a massive slab. The coefficient of restitution between the ball and the slab is e = 0.4; the total momentum imparted to the slab by the ball after numerous bounces is
a)
0.56 Ns
b)
0.64 Ns
c)
0.72 Ns
d)
0.78 Ns

|
Roshni Chavan answered |
Let v be the velocity of the ball on reaching the slab.
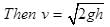
By Newton's law of collision, the velocity v ' after the first im pact is v ' = ev (upward direction).
Similarly, v"=ev' = e2v; v' " = e3v an d so on.
Mom entum im parted to the slab after the first im pact
= mv - (-mv') = m (v + v')
= mv (1 + e )
Similarly, the momentum imparted in the second impact = m(v ' + v ") = m (v ' + e v')
= mv'( 1 + e) = m ( l + e) ev
Momentum im parted to the slab in the third impact
= m (v" + v' " )
= m (v " + ev" )
= m ( 1 + e )v "
= m ( 1 + e ) e2v and so on.
∴ total momentum imparted
= mv ( 1 + e) + mve ( 1 + e)+ mve2( 1 + e) + ...
= mv ( 1 + e) (1 + e + e2 + e3 + ....)
as e < 1
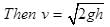
By Newton's law of collision, the velocity v ' after the first im pact is v ' = ev (upward direction).
Similarly, v"=ev' = e2v; v' " = e3v an d so on.
Mom entum im parted to the slab after the first im pact
= mv - (-mv') = m (v + v')
= mv (1 + e )
Similarly, the momentum imparted in the second impact = m(v ' + v ") = m (v ' + e v')
= mv'( 1 + e) = m ( l + e) ev
Momentum im parted to the slab in the third impact
= m (v" + v' " )
= m (v " + ev" )
= m ( 1 + e )v "
= m ( 1 + e ) e2v and so on.
∴ total momentum imparted
= mv ( 1 + e) + mve ( 1 + e)+ mve2( 1 + e) + ...
= mv ( 1 + e) (1 + e + e2 + e3 + ....)
as e < 1
Which of the following pairs of physical quantities does not have same dimensional formula ?- a)Work and torque
- b)Angular momentum and Planck's constant
- c)Tension and surface tension
- d)Impulse and linear momentum
Correct answer is option 'C'. Can you explain this answer?
Which of the following pairs of physical quantities does not have same dimensional formula ?
a)
Work and torque
b)
Angular momentum and Planck's constant
c)
Tension and surface tension
d)
Impulse and linear momentum
|
|
Divyansh Choudhary answered |
Explanation:
To determine which pair of physical quantities does not have the same dimensional formula, we need to compare the dimensions of each quantity.
Let's analyze each pair:
a) Work and torque:
- Work is defined as the product of force and displacement. Its dimensions can be expressed as [M^1 L^2 T^-2].
- Torque is defined as the product of force and perpendicular distance from the axis of rotation. Its dimensions can be expressed as [M^1 L^2 T^-2].
- The dimensional formulas of work and torque are the same, [M^1 L^2 T^-2]. Therefore, option 'a' is not the correct answer.
b) Angular momentum and Planck's constant:
- Angular momentum is defined as the product of moment of inertia and angular velocity. Its dimensions can be expressed as [M^1 L^2 T^-1].
- Planck's constant is a fundamental constant in quantum mechanics and its dimensions can be expressed as [M^1 L^2 T^-1].
- The dimensional formulas of angular momentum and Planck's constant are the same, [M^1 L^2 T^-1]. Therefore, option 'b' is not the correct answer.
c) Tension and surface tension:
- Tension is the force transmitted through a string, rope, cable, or any other type of flexible connector. Its dimensions can be expressed as [M^1 L^1 T^-2].
- Surface tension is the force per unit length acting perpendicular to an imaginary line drawn on the surface of a liquid. Its dimensions can be expressed as [M^1 T^-2].
- The dimensional formulas of tension and surface tension are different. Therefore, option 'c' is the correct answer.
d) Impulse and linear momentum:
- Impulse is defined as the change in momentum of an object. Its dimensions can be expressed as [M^1 L^1 T^-1].
- Linear momentum is defined as the product of mass and velocity. Its dimensions can be expressed as [M^1 L^1 T^-1].
- The dimensional formulas of impulse and linear momentum are the same, [M^1 L^1 T^-1]. Therefore, option 'd' is not the correct answer.
Therefore, the correct answer is option 'C' - Tension and surface tension.
To determine which pair of physical quantities does not have the same dimensional formula, we need to compare the dimensions of each quantity.
Let's analyze each pair:
a) Work and torque:
- Work is defined as the product of force and displacement. Its dimensions can be expressed as [M^1 L^2 T^-2].
- Torque is defined as the product of force and perpendicular distance from the axis of rotation. Its dimensions can be expressed as [M^1 L^2 T^-2].
- The dimensional formulas of work and torque are the same, [M^1 L^2 T^-2]. Therefore, option 'a' is not the correct answer.
b) Angular momentum and Planck's constant:
- Angular momentum is defined as the product of moment of inertia and angular velocity. Its dimensions can be expressed as [M^1 L^2 T^-1].
- Planck's constant is a fundamental constant in quantum mechanics and its dimensions can be expressed as [M^1 L^2 T^-1].
- The dimensional formulas of angular momentum and Planck's constant are the same, [M^1 L^2 T^-1]. Therefore, option 'b' is not the correct answer.
c) Tension and surface tension:
- Tension is the force transmitted through a string, rope, cable, or any other type of flexible connector. Its dimensions can be expressed as [M^1 L^1 T^-2].
- Surface tension is the force per unit length acting perpendicular to an imaginary line drawn on the surface of a liquid. Its dimensions can be expressed as [M^1 T^-2].
- The dimensional formulas of tension and surface tension are different. Therefore, option 'c' is the correct answer.
d) Impulse and linear momentum:
- Impulse is defined as the change in momentum of an object. Its dimensions can be expressed as [M^1 L^1 T^-1].
- Linear momentum is defined as the product of mass and velocity. Its dimensions can be expressed as [M^1 L^1 T^-1].
- The dimensional formulas of impulse and linear momentum are the same, [M^1 L^1 T^-1]. Therefore, option 'd' is not the correct answer.
Therefore, the correct answer is option 'C' - Tension and surface tension.
The number of positive integral values of x satisfying the equation [x/13] = [x/17] is n, where [⋅] denotes the greatest integer function, then n/3 is equal to
Correct answer is '9'. Can you explain this answer?
The number of positive integral values of x satisfying the equation [x/13] = [x/17] is n, where [⋅] denotes the greatest integer function, then n/3 is equal to
|
|
Rajeev Choudhary answered |
[x] represents the greatest integer less than or equal to x. We can rewrite the equation as follows:
[x/13] = [x/17]
This equation can be rewritten as:
13([x/13]) = 17([x/17])
13([x/13]) = 17([x/13] + [x/17])
13([x/13]) = 17([x/13] + 1)
13([x/13]) = 17([x/13]) + 17
-4([x/13]) = 17
([x/13]) = -17/4
Since the greatest integer less than or equal to -17/4 is -5, there are no positive integral values of x satisfying the equation. Therefore, n = 0.
[x/13] = [x/17]
This equation can be rewritten as:
13([x/13]) = 17([x/17])
13([x/13]) = 17([x/13] + [x/17])
13([x/13]) = 17([x/13] + 1)
13([x/13]) = 17([x/13]) + 17
-4([x/13]) = 17
([x/13]) = -17/4
Since the greatest integer less than or equal to -17/4 is -5, there are no positive integral values of x satisfying the equation. Therefore, n = 0.
Two vertical poles AL and BM of heights 20 m and 80 m respectively stand apart on a horizontal plane. If A and B be the feet of the poles and AM and BL intersect at P, then the height of P is equal to- a)50 m
- b)18 m
- c)16 m
- d)15 m
Correct answer is option 'C'. Can you explain this answer?
Two vertical poles AL and BM of heights 20 m and 80 m respectively stand apart on a horizontal plane. If A and B be the feet of the poles and AM and BL intersect at P, then the height of P is equal to
a)
50 m
b)
18 m
c)
16 m
d)
15 m
|
|
Sanaya Patel answered |
Given information:
- Heights of poles AL and BM are 20 m and 80 m respectively.
- P is the point where AM and BL intersect.
- We need to find the height of point P.
Solution:
Step 1: Find the distance AP and BP
- Using similar triangles, we can find the distance AP and BP.
- Let x be the distance AP and y be the distance BP.
- By similar triangles, we have x/20 = (x+y)/80.
- Solving this equation, we get x = 16 m and y = 64 m.
Step 2: Find the height of point P
- The height of point P is the sum of the heights of poles AL and BM at point P.
- Height of P = 20 + (80 - 64) = 20 + 16 = 36 m.
Therefore, the height of point P is 36 m, which is option 'C'.
A beam of light traveling in water strikes a glass plate which is also immersed in water. When the angle of incidence is 50 ° the reflected beam is found to be plane polarised. The refractive index of water is 4/3. The refractive index of the glass plate is (Given tan 50 ° = 1.198)- a)1.54
- b)1.57
- c)1.60
- d)1.63
Correct answer is option 'C'. Can you explain this answer?
A beam of light traveling in water strikes a glass plate which is also immersed in water. When the angle of incidence is 50 ° the reflected beam is found to be plane polarised. The refractive index of water is 4/3. The refractive index of the glass plate is (Given tan 50 ° = 1.198)
a)
1.54
b)
1.57
c)
1.60
d)
1.63

|
Amrita Sarkar answered |
by brewster's law,
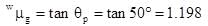
This is the refractive index of glass w.r.to water.
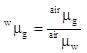
∴ refractive index of glass
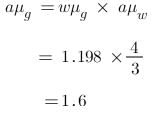
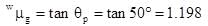
This is the refractive index of glass w.r.to water.
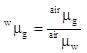
∴ refractive index of glass
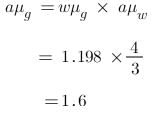
Find the angular speed of the meter stick, when a person throws it such that the centre of the stick is moving with a speed of 10 m s-1 vertically upwards & left end of stick with a speed of 20 m s-1 vertically upwards.- a)20 rad s-1
- b)10 rad s-1
- c)30 rad s-1
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Find the angular speed of the meter stick, when a person throws it such that the centre of the stick is moving with a speed of 10 m s-1 vertically upwards & left end of stick with a speed of 20 m s-1 vertically upwards.
a)
20 rad s-1
b)
10 rad s-1
c)
30 rad s-1
d)
None of these
|
|
Gaurav Kumar answered |
Given velocity of centre C of the rod, vC = 10 m s−1
and velocity of end A of the rod vA = 20 m s−1
Let ω be the angular velocity of the rod.
Since vA > vC, thus the stick will rotate in clockwise direction.
Now using the relation, vA − vC = ωr, we get,
⇒ 20 − 10 = ω(l/2)
⇒10 = ω/2 rad s−1
⇒ ω = 20 rad s-1
Hence, the angular speed of the stick is 20 rad s−1.
One ticket is selected at random from 50 tickets numbered 00, 01, 02, ..., 49. Then, the probability that the sum of the digits on the selected ticket is 8, given that the product of these digits is zero, equals- a)1/7
- b)5/14
- c)1/50
- d)1/14
Correct answer is option 'D'. Can you explain this answer?
One ticket is selected at random from 50 tickets numbered 00, 01, 02, ..., 49. Then, the probability that the sum of the digits on the selected ticket is 8, given that the product of these digits is zero, equals
a)
1/7
b)
5/14
c)
1/50
d)
1/14
|
|
Neha Joshi answered |
Any number in the set, S = {00, 01, 02, ...., 49} is of the form ab, where a ∈ {0, 1, 2, 3, 4} and b ∈ {0, 1, 2, ..., 9}
For the product of digits to be zero, the numbers must be of the form either a0, which are 5 in number because a ∈ {0, 1, 2, 3, 4} or of the form 0b, which are 10 in number because b ∈ {0, 1, 2, ..., 9}.
The only number common to both = 00
Thus, the number of numbers in S, the product of which is zero = 10 + 5 - 1 = 14
Of these, the number whose sum of digits is 8 is just one i.e. 08.
The required probability = 1/14
The vapour pressure of water at 20 °C is 17.5 torr. What will be the no. of moles of water present in one litre of air at 20 °C and 40% relative humidity.(R =0.082 L atm/mol-k)- a)4.2 x 10-4 mole
- b)4.2 x 10-6 mole
- c)3.82 X 10-4 mole
- d)3.82 X 10-6 mole
Correct answer is option 'C'. Can you explain this answer?
The vapour pressure of water at 20 °C is 17.5 torr. What will be the no. of moles of water present in one litre of air at 20 °C and 40% relative humidity.(R =0.082 L atm/mol-k)
a)
4.2 x 10-4 mole
b)
4.2 x 10-6 mole
c)
3.82 X 10-4 mole
d)
3.82 X 10-6 mole

|
Dipika Choudhury answered |
Relative humidity (RH) = 
∴ Partial pressure of H2O = RH × Vapour pressure of H2O


∴ Partial pressure of H2O = RH × Vapour pressure of H2O

The electrical conductivity of a semiconductor increases when electromagnetic radiation of wavelength shorter than 2480 nm is incident on it. The band gap (in eV) for the semiconductor is (Nearest integer)
Correct answer is '1'. Can you explain this answer?
The electrical conductivity of a semiconductor increases when electromagnetic radiation of wavelength shorter than 2480 nm is incident on it. The band gap (in eV) for the semiconductor is (Nearest integer)
|
|
Ritu Singh answered |
Band gap = Energy of photon of wavelength (λ) 2480 nm
Energy = 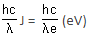
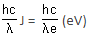
Band gap = 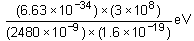
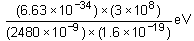
= 0.5 eV ≈ 1 eV
Consider all possible isomeric ketones including stereoisomers of molecular formula 'C5H10O'. All these isomers are independently reacted with LiAlH4 (NOTE: stereoisomers are also reacted separately) The, total number of ketones that give a racemic product(s) is/are.
Correct answer is '2'. Can you explain this answer?
Consider all possible isomeric ketones including stereoisomers of molecular formula 'C5H10O'. All these isomers are independently reacted with LiAlH4 (NOTE: stereoisomers are also reacted separately) The, total number of ketones that give a racemic product(s) is/are.
|
|
Sakshi Sen answered |
Isomeric Ketones of C5H10O
To determine the number of ketones that give a racemic product when reacted with LiAlH4, we first need to identify all the possible isomeric ketones with the molecular formula C5H10O.
The general formula for a ketone is R-CO-R', where R and R' can be any alkyl or aryl groups. In this case, we have 5 carbon atoms, so the ketone group will be attached to one of the carbon atoms, leaving 4 carbon atoms to form the alkyl or aryl groups.
Step 1: Determine the Number of Carbon Atoms Attached to the Ketone Group
To identify the possible isomers, we need to determine the number of carbon atoms attached to the ketone group. This can be done by counting the remaining carbon atoms after attaching the ketone group to one of the carbons.
In this case, we have 5 carbon atoms, so there are four possibilities for the number of carbon atoms attached to the ketone group: 1, 2, 3, or 4.
Step 2: Generate Isomeric Structures
Using the number of carbon atoms attached to the ketone group, we can now generate the isomeric structures.
Case 1: Ketone with 1 Carbon Atom Attached
In this case, the ketone will be attached to one of the four remaining carbon atoms, and the other three carbon atoms will form alkyl or aryl groups.
Possible structure: CH3-CH2-CH2-CO-CH3
Case 2: Ketone with 2 Carbon Atoms Attached
In this case, the ketone will be attached to two of the four remaining carbon atoms, and the other two carbon atoms will form alkyl or aryl groups.
Possible structures:
1. CH3-CH2-CO-CH2-CH3
2. CH3-CO-CH2-CH2-CH3
Case 3: Ketone with 3 Carbon Atoms Attached
In this case, the ketone will be attached to three of the four remaining carbon atoms, and the remaining carbon atom will form an alkyl or aryl group.
Possible structures:
1. CH3-CO-CH(CH3)-CH3
2. CH3-CH2-CO-CH(CH3)-CH2-CH3
Case 4: Ketone with 4 Carbon Atoms Attached
In this case, the ketone will be attached to all four remaining carbon atoms.
Possible structure: CH3-CH2-CO-CH2-CH2-CH3
Step 3: Reacting with LiAlH4
When the isomeric ketones are reacted with LiAlH4, they undergo reduction to form alcohols. The stereoisomers of the ketones will react independently, meaning that each stereoisomer will give a separate product.
Step 4: Identifying Racemic Products
A racemic product is one that contains equal amounts of both enantiomers. In the case of ketones, the reduction by LiAlH4 can result in the formation of a chiral center, leading to the possibility of en
To determine the number of ketones that give a racemic product when reacted with LiAlH4, we first need to identify all the possible isomeric ketones with the molecular formula C5H10O.
The general formula for a ketone is R-CO-R', where R and R' can be any alkyl or aryl groups. In this case, we have 5 carbon atoms, so the ketone group will be attached to one of the carbon atoms, leaving 4 carbon atoms to form the alkyl or aryl groups.
Step 1: Determine the Number of Carbon Atoms Attached to the Ketone Group
To identify the possible isomers, we need to determine the number of carbon atoms attached to the ketone group. This can be done by counting the remaining carbon atoms after attaching the ketone group to one of the carbons.
In this case, we have 5 carbon atoms, so there are four possibilities for the number of carbon atoms attached to the ketone group: 1, 2, 3, or 4.
Step 2: Generate Isomeric Structures
Using the number of carbon atoms attached to the ketone group, we can now generate the isomeric structures.
Case 1: Ketone with 1 Carbon Atom Attached
In this case, the ketone will be attached to one of the four remaining carbon atoms, and the other three carbon atoms will form alkyl or aryl groups.
Possible structure: CH3-CH2-CH2-CO-CH3
Case 2: Ketone with 2 Carbon Atoms Attached
In this case, the ketone will be attached to two of the four remaining carbon atoms, and the other two carbon atoms will form alkyl or aryl groups.
Possible structures:
1. CH3-CH2-CO-CH2-CH3
2. CH3-CO-CH2-CH2-CH3
Case 3: Ketone with 3 Carbon Atoms Attached
In this case, the ketone will be attached to three of the four remaining carbon atoms, and the remaining carbon atom will form an alkyl or aryl group.
Possible structures:
1. CH3-CO-CH(CH3)-CH3
2. CH3-CH2-CO-CH(CH3)-CH2-CH3
Case 4: Ketone with 4 Carbon Atoms Attached
In this case, the ketone will be attached to all four remaining carbon atoms.
Possible structure: CH3-CH2-CO-CH2-CH2-CH3
Step 3: Reacting with LiAlH4
When the isomeric ketones are reacted with LiAlH4, they undergo reduction to form alcohols. The stereoisomers of the ketones will react independently, meaning that each stereoisomer will give a separate product.
Step 4: Identifying Racemic Products
A racemic product is one that contains equal amounts of both enantiomers. In the case of ketones, the reduction by LiAlH4 can result in the formation of a chiral center, leading to the possibility of en
A is a set containing n elements, subset P of A is chosen. The set A is reconstructed by replacing the elements of P, subset Q of A is chosen. The number of ways of selecting P and Q so that P and Q are non intersecting, is- a)2n − 1
- b)3n − 1
- c)3n − 2
- d)3n + 1
Correct answer is option 'B'. Can you explain this answer?
A is a set containing n elements, subset P of A is chosen. The set A is reconstructed by replacing the elements of P, subset Q of A is chosen. The number of ways of selecting P and Q so that P and Q are non intersecting, is
a)
2n − 1
b)
3n − 1
c)
3n − 2
d)
3n + 1
|
|
Pallabi Nambiar answered |
Problem:
Given a set A with n elements, we need to choose two subsets P and Q such that P and Q are non-intersecting.
Approach:
To solve this problem, we can use the concept of Inclusion-Exclusion Principle.
Inclusion-Exclusion Principle:
The Inclusion-Exclusion Principle is a counting technique used to calculate the size of a union of sets. It states that the size of the union of sets is equal to the sum of the sizes of individual sets, minus the sum of the sizes of all possible intersections of pairs of sets, plus the sum of the sizes of all possible intersections of triples of sets, and so on.
Step 1: Selecting the subset P
- We have n elements in set A.
- For each element in A, we have two choices - either include it in P or exclude it from P.
- So, the total number of ways to select P is 2^n.
Step 2: Selecting the subset Q
- After selecting P, the remaining elements in set A are (n - |P|), where |P| denotes the number of elements in P.
- For each element in the remaining set, we have three choices - include it in Q, exclude it from Q, or include it in P and Q (which is not allowed as per the problem).
- So, the total number of ways to select Q is 3^(n - |P|).
Step 3: Counting the number of non-intersecting subsets
- For each selection of P, we have 2^n choices for P and 3^(n - |P|) choices for Q.
- However, we need to ensure that P and Q are non-intersecting.
- To count the number of non-intersecting subsets, we need to subtract the cases where P and Q intersect.
- The number of ways P and Q can intersect is the number of ways to select a subset from P.
- Since P can have |P| elements, the number of ways to select a subset from P is 2^|P|.
- Therefore, the number of non-intersecting subsets is 2^n - 2^|P|.
Step 4: Simplifying the expression
- Since we need to find the total number of ways to select P and Q, we can sum the number of non-intersecting subsets over all possible values of |P|.
- The value of |P| can range from 0 to n.
- So, the total number of ways to select P and Q is given by the sum of (2^n - 2^|P|) for |P| from 0 to n.
- This can be simplified as follows:
- 2^n - 2^0 + 2^n - 2^1 + 2^n - 2^2 + ... + 2^n - 2^n
- = n * 2^n - (2^0 + 2^1 + 2^2 + ... + 2^n)
- = n * 2^n - (2^(n+1) - 1)
- = n * 2^n - 2^(n+1) + 1
-
Given a set A with n elements, we need to choose two subsets P and Q such that P and Q are non-intersecting.
Approach:
To solve this problem, we can use the concept of Inclusion-Exclusion Principle.
Inclusion-Exclusion Principle:
The Inclusion-Exclusion Principle is a counting technique used to calculate the size of a union of sets. It states that the size of the union of sets is equal to the sum of the sizes of individual sets, minus the sum of the sizes of all possible intersections of pairs of sets, plus the sum of the sizes of all possible intersections of triples of sets, and so on.
Step 1: Selecting the subset P
- We have n elements in set A.
- For each element in A, we have two choices - either include it in P or exclude it from P.
- So, the total number of ways to select P is 2^n.
Step 2: Selecting the subset Q
- After selecting P, the remaining elements in set A are (n - |P|), where |P| denotes the number of elements in P.
- For each element in the remaining set, we have three choices - include it in Q, exclude it from Q, or include it in P and Q (which is not allowed as per the problem).
- So, the total number of ways to select Q is 3^(n - |P|).
Step 3: Counting the number of non-intersecting subsets
- For each selection of P, we have 2^n choices for P and 3^(n - |P|) choices for Q.
- However, we need to ensure that P and Q are non-intersecting.
- To count the number of non-intersecting subsets, we need to subtract the cases where P and Q intersect.
- The number of ways P and Q can intersect is the number of ways to select a subset from P.
- Since P can have |P| elements, the number of ways to select a subset from P is 2^|P|.
- Therefore, the number of non-intersecting subsets is 2^n - 2^|P|.
Step 4: Simplifying the expression
- Since we need to find the total number of ways to select P and Q, we can sum the number of non-intersecting subsets over all possible values of |P|.
- The value of |P| can range from 0 to n.
- So, the total number of ways to select P and Q is given by the sum of (2^n - 2^|P|) for |P| from 0 to n.
- This can be simplified as follows:
- 2^n - 2^0 + 2^n - 2^1 + 2^n - 2^2 + ... + 2^n - 2^n
- = n * 2^n - (2^0 + 2^1 + 2^2 + ... + 2^n)
- = n * 2^n - (2^(n+1) - 1)
- = n * 2^n - 2^(n+1) + 1
-
Two pi and half sigma bonds are present in:- a)N2+
- b)N2
- c)O2+
- d)O2
Correct answer is option 'A'. Can you explain this answer?
Two pi and half sigma bonds are present in:
a)
N2+
b)
N2
c)
O2+
d)
O2
|
|
Maulik Majumdar answered |
Explanation:
N2 molecule:
- The N2 molecule has a triple bond between the two nitrogen atoms.
- This triple bond consists of one sigma bond and two pi bonds.
- Therefore, in the N2 molecule, there are two pi bonds present.
Sigma and Pi bonds:
- Sigma bonds are formed by the head-on overlap of atomic orbitals.
- Pi bonds are formed by the side-ways overlap of atomic orbitals.
Answer:
- In the N2 molecule, there are two pi bonds present, along with one sigma bond.
- Therefore, the correct answer is option 'A'.
N2 molecule:
- The N2 molecule has a triple bond between the two nitrogen atoms.
- This triple bond consists of one sigma bond and two pi bonds.
- Therefore, in the N2 molecule, there are two pi bonds present.
Sigma and Pi bonds:
- Sigma bonds are formed by the head-on overlap of atomic orbitals.
- Pi bonds are formed by the side-ways overlap of atomic orbitals.
Answer:
- In the N2 molecule, there are two pi bonds present, along with one sigma bond.
- Therefore, the correct answer is option 'A'.
Which of these is correct in regard to a magnet?- a)Geometric length = 0.8 times the magnetic length
- b)Magnetic length = 0.8 times the geometric length
- c)Magnetic length= Geometric length
- d)Geometric length = 10/9 of magnetic length
Correct answer is option 'B'. Can you explain this answer?
Which of these is correct in regard to a magnet?
a)
Geometric length = 0.8 times the magnetic length
b)
Magnetic length = 0.8 times the geometric length
c)
Magnetic length= Geometric length
d)
Geometric length = 10/9 of magnetic length
|
|
Mayank Choudhary answered |
Explanation:
In regard to a magnet, the correct statement is option B: Magnetic length = 0.8 times the geometric length.
Understanding the terms:
1. Geometric length: It refers to the physical length or size of the magnet, which can be measured using a ruler or any other measuring instrument.
2. Magnetic length: It refers to the effective length of the magnet where the magnetic field is concentrated and has a significant influence.
Explanation of option B:
The statement "Magnetic length = 0.8 times the geometric length" means that the effective length of the magnet, where the magnetic field is concentrated, is 0.8 times the physical length of the magnet.
Reasoning:
The magnetic field of a magnet is not uniformly distributed throughout its entire length. Rather, it is concentrated near the ends of the magnet. These concentrated regions are known as the magnetic poles.
When a magnet is magnetized, the magnetic domains within it align in a specific pattern. The alignment of these domains is responsible for the creation of the magnetic field. The magnetic field lines emerge from one pole (north) and enter the other pole (south).
Since the magnetic field is concentrated near the poles, the effective length of the magnet, where the magnetic field lines are significant, is less than the actual physical length of the magnet. This effective length is known as the magnetic length.
The statement in option B implies that the magnetic length is 0.8 times the geometric length. In other words, the magnetic field is concentrated within 80% of the physical length of the magnet, leaving the remaining 20% as non-magnetic regions.
This concept is important in various applications of magnets, such as magnetic separators, magnetic resonance imaging (MRI) machines, and magnetic levitation systems. Understanding the relationship between the geometric length and magnetic length helps in designing and optimizing these applications.
In regard to a magnet, the correct statement is option B: Magnetic length = 0.8 times the geometric length.
Understanding the terms:
1. Geometric length: It refers to the physical length or size of the magnet, which can be measured using a ruler or any other measuring instrument.
2. Magnetic length: It refers to the effective length of the magnet where the magnetic field is concentrated and has a significant influence.
Explanation of option B:
The statement "Magnetic length = 0.8 times the geometric length" means that the effective length of the magnet, where the magnetic field is concentrated, is 0.8 times the physical length of the magnet.
Reasoning:
The magnetic field of a magnet is not uniformly distributed throughout its entire length. Rather, it is concentrated near the ends of the magnet. These concentrated regions are known as the magnetic poles.
When a magnet is magnetized, the magnetic domains within it align in a specific pattern. The alignment of these domains is responsible for the creation of the magnetic field. The magnetic field lines emerge from one pole (north) and enter the other pole (south).
Since the magnetic field is concentrated near the poles, the effective length of the magnet, where the magnetic field lines are significant, is less than the actual physical length of the magnet. This effective length is known as the magnetic length.
The statement in option B implies that the magnetic length is 0.8 times the geometric length. In other words, the magnetic field is concentrated within 80% of the physical length of the magnet, leaving the remaining 20% as non-magnetic regions.
This concept is important in various applications of magnets, such as magnetic separators, magnetic resonance imaging (MRI) machines, and magnetic levitation systems. Understanding the relationship between the geometric length and magnetic length helps in designing and optimizing these applications.
The volume of a cube is increasing at the rate of 18 cm3 per second. When the edge of the cube is 12 cm, then the rate in cm2/s at which the surface area of the cube increases, is
Correct answer is '6'. Can you explain this answer?
The volume of a cube is increasing at the rate of 18 cm3 per second. When the edge of the cube is 12 cm, then the rate in cm2/s at which the surface area of the cube increases, is
|
|
Bhavya Kulkarni answered |
Given Data:
- Volume of the cube is increasing at the rate of 18 cm3 per second.
- The edge of the cube is 12 cm.
To Find:
- The rate at which the surface area of the cube increases in cm2/s.
Formula:
- The volume of a cube is given by V = a3, where a is the length of the edge.
- The surface area of a cube is given by A = 6a2.
Explanation:
Step 1: Find the rate of change of edge length (da/dt)
- We are given that the volume of the cube is increasing at the rate of 18 cm3 per second.
- Since the volume of a cube is given by V = a3, we can differentiate both sides with respect to time to find the rate of change of the edge length (da/dt).
- dV/dt = 3a2 * da/dt
- Given dV/dt = 18 cm3/s and a = 12 cm, we can solve for da/dt.
Step 2: Find the rate of change of surface area (dA/dt)
- The surface area of a cube is given by A = 6a2.
- We can differentiate both sides with respect to time to find the rate of change of the surface area (dA/dt).
- dA/dt = 12a * da/dt
- Given da/dt from step 1, we can solve for dA/dt.
Step 3: Calculate the rate at which the surface area of the cube increases
- Plug in the values for a and da/dt into the formula dA/dt = 12a * da/dt.
- Given a = 12 cm and da/dt = 0.25 cm/s (from step 1), we can calculate dA/dt.
Final Answer:
- The rate at which the surface area of the cube increases is 6 cm2/s.
- Volume of the cube is increasing at the rate of 18 cm3 per second.
- The edge of the cube is 12 cm.
To Find:
- The rate at which the surface area of the cube increases in cm2/s.
Formula:
- The volume of a cube is given by V = a3, where a is the length of the edge.
- The surface area of a cube is given by A = 6a2.
Explanation:
Step 1: Find the rate of change of edge length (da/dt)
- We are given that the volume of the cube is increasing at the rate of 18 cm3 per second.
- Since the volume of a cube is given by V = a3, we can differentiate both sides with respect to time to find the rate of change of the edge length (da/dt).
- dV/dt = 3a2 * da/dt
- Given dV/dt = 18 cm3/s and a = 12 cm, we can solve for da/dt.
Step 2: Find the rate of change of surface area (dA/dt)
- The surface area of a cube is given by A = 6a2.
- We can differentiate both sides with respect to time to find the rate of change of the surface area (dA/dt).
- dA/dt = 12a * da/dt
- Given da/dt from step 1, we can solve for dA/dt.
Step 3: Calculate the rate at which the surface area of the cube increases
- Plug in the values for a and da/dt into the formula dA/dt = 12a * da/dt.
- Given a = 12 cm and da/dt = 0.25 cm/s (from step 1), we can calculate dA/dt.
Final Answer:
- The rate at which the surface area of the cube increases is 6 cm2/s.
Statement -1 : Two stones are simultaneously projected from level ground from same point with same speed but different angles with horizontal. Both stones move in same vertical plane. Then the two stones may collide in mid air.Statement - 2 For two stones projected simultaneously from same point with same speed at different angles with horizontal, their trajectories may intersect at some point.- a)Statement - 1 is True, statement -2 is True; Statement- 2 is a correct explanation for statement -1
- b)Statement - 1 is True, statement -2 is true; Statement- 2 is Not a correct explanation for statement -1
- c)Statement - 1 is True, statement -2 is False
- d)Statement - 1 is False, statement -2 is True
Correct answer is option 'D'. Can you explain this answer?
Statement -1 : Two stones are simultaneously projected from level ground from same point with same speed but different angles with horizontal. Both stones move in same vertical plane. Then the two stones may collide in mid air.
Statement - 2 For two stones projected simultaneously from same point with same speed at different angles with horizontal, their trajectories may intersect at some point.
a)
Statement - 1 is True, statement -2 is True; Statement- 2 is a correct explanation for statement -1
b)
Statement - 1 is True, statement -2 is true; Statement- 2 is Not a correct explanation for statement -1
c)
Statement - 1 is True, statement -2 is False
d)
Statement - 1 is False, statement -2 is True
|
|
Athira Kaur answered |
Statement-1: Two stones are simultaneously projected from level ground from the same point with the same speed but different angles with the horizontal. Both stones move in the same vertical plane. Then the two stones may collide in mid-air.
Statement-2: For two stones projected simultaneously from the same point with the same speed at different angles with the horizontal, their trajectories may intersect at some point.
To determine the validity of the given statements, let's analyze each one separately.
Analysis of Statement-1:
When two stones are simultaneously projected from the same point with the same speed but different angles with the horizontal, their trajectories will differ due to the difference in the angle of projection. However, both stones move in the same vertical plane.
If the stones are projected with certain angles such that their trajectories intersect at some point, there is a possibility of collision in mid-air. This can happen when the stones are projected at specific angles and speeds where their paths cross each other. Therefore, Statement-1 is true.
Analysis of Statement-2:
When two stones are simultaneously projected from the same point with the same speed but different angles with the horizontal, their trajectories will differ due to the difference in the angle of projection. The paths followed by the stones are determined by the initial velocity, angle of projection, and the force of gravity.
The trajectories of the stones can be determined using projectile motion equations. If the angles of projection and initial velocities are chosen in such a way that their paths intersect at some point, the stones will indeed cross each other's paths. Therefore, Statement-2 is true.
Relationship between Statement-1 and Statement-2:
Statement-2 provides the explanation for the possibility of collision mentioned in Statement-1. The collision can occur if the trajectories of the stones intersect at some point.
Therefore, the correct option is option D: Statement-1 is false, statement-2 is true.
Statement-2: For two stones projected simultaneously from the same point with the same speed at different angles with the horizontal, their trajectories may intersect at some point.
To determine the validity of the given statements, let's analyze each one separately.
Analysis of Statement-1:
When two stones are simultaneously projected from the same point with the same speed but different angles with the horizontal, their trajectories will differ due to the difference in the angle of projection. However, both stones move in the same vertical plane.
If the stones are projected with certain angles such that their trajectories intersect at some point, there is a possibility of collision in mid-air. This can happen when the stones are projected at specific angles and speeds where their paths cross each other. Therefore, Statement-1 is true.
Analysis of Statement-2:
When two stones are simultaneously projected from the same point with the same speed but different angles with the horizontal, their trajectories will differ due to the difference in the angle of projection. The paths followed by the stones are determined by the initial velocity, angle of projection, and the force of gravity.
The trajectories of the stones can be determined using projectile motion equations. If the angles of projection and initial velocities are chosen in such a way that their paths intersect at some point, the stones will indeed cross each other's paths. Therefore, Statement-2 is true.
Relationship between Statement-1 and Statement-2:
Statement-2 provides the explanation for the possibility of collision mentioned in Statement-1. The collision can occur if the trajectories of the stones intersect at some point.
Therefore, the correct option is option D: Statement-1 is false, statement-2 is true.
The number of seven digit integers, with sum of the digits equal to 10 and formed by using the digits 1, 2 and 3 only, is
Correct answer is '77'. Can you explain this answer?
The number of seven digit integers, with sum of the digits equal to 10 and formed by using the digits 1, 2 and 3 only, is
|
|
Gaurav Kumar answered |
To form a 77 digit number
There are two possible cases
Case 1: Five 1's, one 2's, one 3's
⇒1, 1, 1, 1, 1, 2, 3
Number of numbers = 7! / 5! = 42
Case 2: Four 1's, three 2's
⇒1, 1, 1, 1, 2, 2, 2
Number of numbers=7! / 4!3! = 35
Total number of such numbers 42 + 35 = 77
∴ Arrangement of nn number out of which pp are identical, qq are identical and rest are different is given by
To get maximum current through a resistance of 2.5 Ω, one can use mm rows of cells, each row having n cells. The internal resistance of each cell is 0.5 Ω. What are the values of n & m, if the total number of cells is 45?.
- a)3, 15
- b)5, 9
- c)9, 5
- d)15, 3
Correct answer is option 'D'. Can you explain this answer?
To get maximum current through a resistance of 2.5 Ω, one can use mm rows of cells, each row having n cells. The internal resistance of each cell is 0.5 Ω. What are the values of n & m, if the total number of cells is 45?.
a)
3, 15
b)
5, 9
c)
9, 5
d)
15, 3
|
|
Muskaan Sharma answered |
To get the maximum current through a resistance of 2.5 ohms, you would need to apply the maximum voltage across the resistor.
Ohm's Law states that the current flowing through a resistor is directly proportional to the voltage applied across it and inversely proportional to the resistance. The formula for Ohm's Law is:
I = V / R
Where:
I = current (in amperes)
V = voltage (in volts)
R = resistance (in ohms)
In this case, the resistance is 2.5 ohms. To get the maximum current, you would need to apply the maximum voltage across the resistor. However, you haven't provided the maximum voltage value. Without knowing the maximum voltage, it is not possible to calculate the maximum current.
Ohm's Law states that the current flowing through a resistor is directly proportional to the voltage applied across it and inversely proportional to the resistance. The formula for Ohm's Law is:
I = V / R
Where:
I = current (in amperes)
V = voltage (in volts)
R = resistance (in ohms)
In this case, the resistance is 2.5 ohms. To get the maximum current, you would need to apply the maximum voltage across the resistor. However, you haven't provided the maximum voltage value. Without knowing the maximum voltage, it is not possible to calculate the maximum current.
A ring of mass m, radius r having charge q uniformly distributed over it and free to rotate about it's own axis is placed in a region having a magnetic field B parallel to its axis. If the magnetic field is suddenly switched off, the angular velocity acquired by the ring is- a)qB/m
- b)2qB/m
- c)qB/2m
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A ring of mass m, radius r having charge q uniformly distributed over it and free to rotate about it's own axis is placed in a region having a magnetic field B parallel to its axis. If the magnetic field is suddenly switched off, the angular velocity acquired by the ring is
a)
qB/m
b)
2qB/m
c)
qB/2m
d)
None of these
|
|
Samarth Saha answered |
Angular Momentum Conservation
---------------------------
When the magnetic field is suddenly switched off, the ring will experience a change in its angular momentum. According to the principle of conservation of angular momentum, the initial angular momentum of the ring must be equal to the final angular momentum.
Initial Angular Momentum
-----------------------
The initial angular momentum of the ring is given by:
L_initial = I_initial * ω_initial
where I_initial is the moment of inertia of the ring and ω_initial is its initial angular velocity.
Final Angular Momentum
---------------------
After the magnetic field is switched off, the ring will stop rotating. Therefore, its final angular velocity ω_final will be zero. The final angular momentum of the ring is given by:
L_final = I_final * ω_final
where I_final is the moment of inertia of the ring when it is not rotating.
Moment of Inertia of the Ring
----------------------------
The moment of inertia of a ring rotating about its own axis is given by:
I = m * r^2
where m is the mass of the ring and r is its radius.
Equating Initial and Final Angular Momentum
------------------------------------------
Using the principle of conservation of angular momentum, we can equate the initial and final angular momentum:
L_initial = L_final
I_initial * ω_initial = I_final * ω_final
m * r^2 * ω_initial = I_final * 0
m * r^2 * ω_initial = 0
Since the final angular velocity ω_final is zero, the term I_final * ω_final is also zero.
Simplifying the equation, we get:
m * r^2 * ω_initial = 0
Solving for ω_initial, we find:
ω_initial = 0
Therefore, the angular velocity acquired by the ring when the magnetic field is suddenly switched off is zero.
Correct Answer
--------------
The correct answer is option 'D' (None of these), as the angular velocity acquired by the ring is zero.
---------------------------
When the magnetic field is suddenly switched off, the ring will experience a change in its angular momentum. According to the principle of conservation of angular momentum, the initial angular momentum of the ring must be equal to the final angular momentum.
Initial Angular Momentum
-----------------------
The initial angular momentum of the ring is given by:
L_initial = I_initial * ω_initial
where I_initial is the moment of inertia of the ring and ω_initial is its initial angular velocity.
Final Angular Momentum
---------------------
After the magnetic field is switched off, the ring will stop rotating. Therefore, its final angular velocity ω_final will be zero. The final angular momentum of the ring is given by:
L_final = I_final * ω_final
where I_final is the moment of inertia of the ring when it is not rotating.
Moment of Inertia of the Ring
----------------------------
The moment of inertia of a ring rotating about its own axis is given by:
I = m * r^2
where m is the mass of the ring and r is its radius.
Equating Initial and Final Angular Momentum
------------------------------------------
Using the principle of conservation of angular momentum, we can equate the initial and final angular momentum:
L_initial = L_final
I_initial * ω_initial = I_final * ω_final
m * r^2 * ω_initial = I_final * 0
m * r^2 * ω_initial = 0
Since the final angular velocity ω_final is zero, the term I_final * ω_final is also zero.
Simplifying the equation, we get:
m * r^2 * ω_initial = 0
Solving for ω_initial, we find:
ω_initial = 0
Therefore, the angular velocity acquired by the ring when the magnetic field is suddenly switched off is zero.
Correct Answer
--------------
The correct answer is option 'D' (None of these), as the angular velocity acquired by the ring is zero.
An uncharged capacitor of capacitance 4 μF and a resistance of 2.5 MΩ are connected in series with 12 V battery at t = 0. Find the time in seconds (approximate to the nearest integer) after which the potential difference across the capacitor is three times the potential difference across the resistor. [Given, ln(2) = 0.693]
Correct answer is '14'. Can you explain this answer?
An uncharged capacitor of capacitance 4 μF and a resistance of 2.5 MΩ are connected in series with 12 V battery at t = 0. Find the time in seconds (approximate to the nearest integer) after which the potential difference across the capacitor is three times the potential difference across the resistor. [Given, ln(2) = 0.693]
|
|
Varun Kapoor answered |
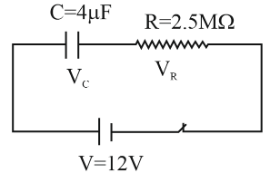
During charging voltage across capacitor with time is given by
Vc = V(1 − e−t/T)
V = VC + VR
Here, V is the applied potential.
Given that VC = 3VR = 3(V−VC)
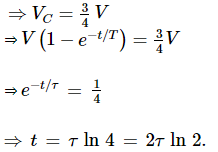
Here τ = CR =10 s
⇒ t = 2 × 10 × 0.693 = 13.86 s ≃ 14 s
How many EDTA (ethylenediaminetetraacetic acid) molecules are required to make an octahedral complex with a Ca2+
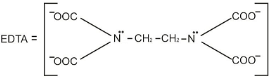
Correct answer is '1'. Can you explain this answer?
How many EDTA (ethylenediaminetetraacetic acid) molecules are required to make an octahedral complex with a Ca2+
|
|
Ritu Singh answered |
EDTA, which has four lone pairs of donor oxygen atoms and two lone pair donor nitrogen atoms in each molecule forms complex with Ca2+ ion. EDTA is hexadentate, and hence, only 1 EDTA will be required to form an octahedral complex with Ca2+
A coil having n turns and resistance RΩ is connected with a galvanometer of resistance 4RΩ. This combination is moved in time t seconds from a magnetic field W1 weber to W2 weber. The induced current in the circuit is- a)
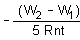
- b)
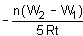
- c)
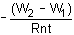
- d)
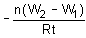
Correct answer is option 'B'. Can you explain this answer?
A coil having n turns and resistance RΩ is connected with a galvanometer of resistance 4RΩ. This combination is moved in time t seconds from a magnetic field W1 weber to W2 weber. The induced current in the circuit is
a)
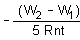
b)
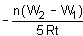
c)
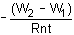
d)
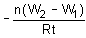
|
|
Neha Sharma answered |
Induced current,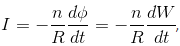
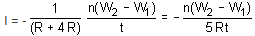
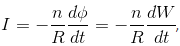
where ф = W = Flux x Per unit turn of the coil
Total resistance of the coil and the meter = R + 4R
Therefore,
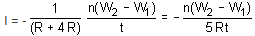
More number of oxidation states are exhibited by the actinoids than those by the Lanthanoids, the main reason being- a)More reactive nature of the actinoids than the Lanthanoids.
- b)4f orbitals more diffused than the 5f orbitals
- c)More energy difference between 5f and 6d than between 4f and 5d orbitals
- d)Lesser energy difference between 5f and 6d than between 4f and 5d orbitals
Correct answer is option 'D'. Can you explain this answer?
More number of oxidation states are exhibited by the actinoids than those by the Lanthanoids, the main reason being
a)
More reactive nature of the actinoids than the Lanthanoids.
b)
4f orbitals more diffused than the 5f orbitals
c)
More energy difference between 5f and 6d than between 4f and 5d orbitals
d)
Lesser energy difference between 5f and 6d than between 4f and 5d orbitals
|
|
Varun Kapoor answered |
Actinoids show different oxidation states such as +2, +3, +4, +5, +6 and +7. However, +3 oxidation state is most common among all the lanthanoids. The wide range of oxidation states of actinoids is attributed to the fact that the 5f ,6d and 7s energy levels are of comparable energies. Therefore, all these three subshells can participate.
The coefficient of x5 in (1+2x+3x2+……….up to infinite term)-3/2 is- a)21
- b)25
- c)26
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
The coefficient of x5 in (1+2x+3x2+……….up to infinite term)-3/2 is
a)
21
b)
25
c)
26
d)
None of these

|
Nandini Choudhury answered |
(1+2x+3x2+………)–3/2
=((1–x)–2)–3/2
= (1 − x)3 = 1 − 3x + 3x2 − x3
∴ coefficient of x5 = 0.
=((1–x)–2)–3/2
= (1 − x)3 = 1 − 3x + 3x2 − x3
∴ coefficient of x5 = 0.
If pH of a saturated solution of Ba(OH)2 is 12, the value of its K(sp) is found to be n×10-7M3. find the value of ‘n’ here?
Correct answer is '5'. Can you explain this answer?
If pH of a saturated solution of Ba(OH)2 is 12, the value of its K(sp) is found to be n×10-7M3. find the value of ‘n’ here?
|
|
Yash Patel answered |
As pH = 12
pOH = 14 − 12 = 2
[OH] = 10 − 2M = 0.01M/L
In case of Ba(OH)s2 ⇌ Ba2s+ + 2OH2s−
As 2s = 0.01m/L
s = 0.01 / 2 = 5×10−3m/L
Ksp for Ba(OH)2 = 4s3 = 4(5 × 10−3)3 = 5 × 10−7M3
Hence ‘n’ = 5
In general, the properties that decrease and increase down a group in the periodic table, respectively, are:- a)electronegativity and electron gain enthalpy.
- b)electronegativity and atomic radius.
- c)atomic radius and electronegativity.
- d)electron gain enthalpy and electronegativity.
Correct answer is option 'B'. Can you explain this answer?
In general, the properties that decrease and increase down a group in the periodic table, respectively, are:
a)
electronegativity and electron gain enthalpy.
b)
electronegativity and atomic radius.
c)
atomic radius and electronegativity.
d)
electron gain enthalpy and electronegativity.
|
|
Tarun Roy answered |
Explanation:
Atomic Radius:
- Atomic radius increases down a group in the periodic table. This is because as you move down a group, new energy levels are being added which increases the distance between the nucleus and the outermost electrons.
Electronegativity:
- Electronegativity decreases down a group in the periodic table. This is because as you move down a group, the outermost electrons are further away from the nucleus, making it harder for the atom to attract additional electrons.
Therefore, the correct answer is option 'B' - Electronegativity and Atomic Radius.
Atomic Radius:
- Atomic radius increases down a group in the periodic table. This is because as you move down a group, new energy levels are being added which increases the distance between the nucleus and the outermost electrons.
Electronegativity:
- Electronegativity decreases down a group in the periodic table. This is because as you move down a group, the outermost electrons are further away from the nucleus, making it harder for the atom to attract additional electrons.
Therefore, the correct answer is option 'B' - Electronegativity and Atomic Radius.
If (1, 5, 35),(7, 5, 5),(1, λ, 7 and (2λ,1,2) are coplanar, then the sum of all possible values of λ is:- a)44/5
- b)-44/5
- c)39/5
- d)-39/5
Correct answer is option 'A'. Can you explain this answer?
If (1, 5, 35),(7, 5, 5),(1, λ, 7 and (2λ,1,2) are coplanar, then the sum of all possible values of λ is:
a)
44/5
b)
-44/5
c)
39/5
d)
-39/5
|
|
Yash Chawla answered |
To determine if the given points are coplanar, we can check if the determinant of a matrix formed by the coordinates of the points is equal to zero.
The matrix formed by the coordinates of the points is:
| 1 5 35 |
| 7 5 5 |
| 1 λ 7 |
| 2λ 1 2 |
To find the determinant, we can expand along the first row:
Det = 1 * (5 * 7 - 5 * λ) - 5 * (7 * 7 - 1 * λ) + 35 * (7 * λ - 1 * 5)
= 35 - 35λ - 245 + 5λ + 245λ - 175
= -44λ
For the points to be coplanar, the determinant must be equal to zero:
-44λ = 0
Solving for λ, we have:
λ = 0
Therefore, the only possible value of λ is 0.
However, we need to check if this value satisfies the condition that the points are coplanar. To do this, we can substitute λ = 0 into the matrix and check if the determinant is indeed equal to zero.
The matrix with λ = 0 is:
| 1 5 35 |
| 7 5 5 |
| 1 0 7 |
| 0 1 2 |
Calculating the determinant of this matrix, we get:
Det = 1 * (5 * 7 - 5 * 0) - 5 * (7 * 7 - 1 * 0) + 35 * (7 * 0 - 1 * 5)
= 35 - 0 + 0
= 35
Since the determinant is not equal to zero, the points (1, 5, 35), (7, 5, 5), (1, 0, 7), and (0, 1, 2) are not coplanar.
Therefore, there are no possible values of λ that make the given points coplanar. Hence, the sum of all possible values of λ is 0.
The correct answer is option 'A'.
The matrix formed by the coordinates of the points is:
| 1 5 35 |
| 7 5 5 |
| 1 λ 7 |
| 2λ 1 2 |
To find the determinant, we can expand along the first row:
Det = 1 * (5 * 7 - 5 * λ) - 5 * (7 * 7 - 1 * λ) + 35 * (7 * λ - 1 * 5)
= 35 - 35λ - 245 + 5λ + 245λ - 175
= -44λ
For the points to be coplanar, the determinant must be equal to zero:
-44λ = 0
Solving for λ, we have:
λ = 0
Therefore, the only possible value of λ is 0.
However, we need to check if this value satisfies the condition that the points are coplanar. To do this, we can substitute λ = 0 into the matrix and check if the determinant is indeed equal to zero.
The matrix with λ = 0 is:
| 1 5 35 |
| 7 5 5 |
| 1 0 7 |
| 0 1 2 |
Calculating the determinant of this matrix, we get:
Det = 1 * (5 * 7 - 5 * 0) - 5 * (7 * 7 - 1 * 0) + 35 * (7 * 0 - 1 * 5)
= 35 - 0 + 0
= 35
Since the determinant is not equal to zero, the points (1, 5, 35), (7, 5, 5), (1, 0, 7), and (0, 1, 2) are not coplanar.
Therefore, there are no possible values of λ that make the given points coplanar. Hence, the sum of all possible values of λ is 0.
The correct answer is option 'A'.
Chapter doubts & questions for JEE Main Additional Practice Mock Tests - Mock Tests for JEE Main and Advanced 2026 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of JEE Main Additional Practice Mock Tests - Mock Tests for JEE Main and Advanced 2026 in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup