All Exams >
Bank Exams >
RBI Assistant Preparation Course >
All Questions
All questions of Mensuration for Bank Exams Exam
Find the perimeter of the a square with side 4cm.- a)16 cm
- b)12 cm
- c)10 cm
- d)8 cm
Correct answer is option 'A'. Can you explain this answer?
Find the perimeter of the a square with side 4cm.
a)
16 cm
b)
12 cm
c)
10 cm
d)
8 cm

|
Sreesha Phalod answered |
Sol. perimeter of square=4* sides
=4*4 (sides is 4)
=16.
=4*4 (sides is 4)
=16.
Find the volume of a cuboid whose length is 8 cm, width is 3 cm and height is 5 cm. - a)135 cm3
- b)125 cm3
- c)120 cm3
- d)130 cm3
Correct answer is option 'C'. Can you explain this answer?
Find the volume of a cuboid whose length is 8 cm, width is 3 cm and height is 5 cm.
a)
135 cm3
b)
125 cm3
c)
120 cm3
d)
130 cm3
|
|
Tanishq Joshi answered |
Finding Volume of a Cuboid
Given: length = 8 cm, width = 3 cm, height = 5 cm
To find: Volume of the cuboid
Formula: Volume of a cuboid = length x width x height
Substituting the given values in the formula, we get:
Volume = 8 cm x 3 cm x 5 cm
Volume = 120 cm3
Therefore, the correct answer is option C, 120 cm3.
Given: length = 8 cm, width = 3 cm, height = 5 cm
To find: Volume of the cuboid
Formula: Volume of a cuboid = length x width x height
Substituting the given values in the formula, we get:
Volume = 8 cm x 3 cm x 5 cm
Volume = 120 cm3
Therefore, the correct answer is option C, 120 cm3.
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Mensuration, Class 8, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic. Q.Find the volume of a cuboid whose length is 8 cm, breadth 6 cm and height 3.5 cm. - a)215 cm3
- b)172 cm3
- c)150 cm3
- d)168 cm3
Correct answer is option 'D'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Mensuration, Class 8, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic.
Q.
Find the volume of a cuboid whose length is 8 cm, breadth 6 cm and height 3.5 cm.
a)
215 cm3
b)
172 cm3
c)
150 cm3
d)
168 cm3
|
|
Ankita Shah answered |
Given,
Length (l) = 8 cm
Breadth (b) = 6 cm
Height (h) = 3.5 cm
We know that the volume of a cuboid is given by the formula:
Volume = length × breadth × height
Substituting the given values, we get:
Volume = 8 cm × 6 cm × 3.5 cm
Volume = 168 cm³
Therefore, the volume of the given cuboid is 168 cm³.
Hence, the correct option is (d) 168 cm³.
Length (l) = 8 cm
Breadth (b) = 6 cm
Height (h) = 3.5 cm
We know that the volume of a cuboid is given by the formula:
Volume = length × breadth × height
Substituting the given values, we get:
Volume = 8 cm × 6 cm × 3.5 cm
Volume = 168 cm³
Therefore, the volume of the given cuboid is 168 cm³.
Hence, the correct option is (d) 168 cm³.
Find the area of a triangle whose base is 4 cm and altitude is 6 cm.- a)10 cm2
- b)14 cm2
- c)16 cm2
- d)12 cm2
Correct answer is option 'D'. Can you explain this answer?
Find the area of a triangle whose base is 4 cm and altitude is 6 cm.
a)
10 cm2
b)
14 cm2
c)
16 cm2
d)
12 cm2
|
|
Kavya Saxena answered |
We know that area of triangle is equals to 1/2 base × altitude.
Here, base = 4 cm and altitude = 6 cm.
So, area = 1/2 × 4 × 6= 24 /2= 12 cm2.
Here, base = 4 cm and altitude = 6 cm.
So, area = 1/2 × 4 × 6= 24 /2= 12 cm2.
Cylindrical cans of cricket balls are to be packed in a box. Each can has a radius of 7 cm and height of 30 cm. Dimension of the box is l = 76 cm, b = 46 cm, h = 45 cm. What is the maximum number of cans that can fit in the box?- a)15
- b)17
- c)22
- d)21
Correct answer is option 'D'. Can you explain this answer?
Cylindrical cans of cricket balls are to be packed in a box. Each can has a radius of 7 cm and height of 30 cm. Dimension of the box is l = 76 cm, b = 46 cm, h = 45 cm. What is the maximum number of cans that can fit in the box?
a)
15
b)
17
c)
22
d)
21

|
Naroj Boda answered |
This question requires a good deal of visualization. Since, both the box and cans are hard solids, simply dividing the volume won’t work because the shape can’t be deformed.
Each cylindrical can has a diameter of 14 cm and while they are kept erect in the box will occupy height of 30 cm
Number of such cans that can be placed in a row
Number of such rows that can be placed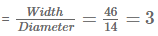
Thus 5 x 3 = 15 cans can be placed in an erect position.
However, height of box = 45cm and only 30 cm has been utilized so far
Remaining height = 15 cm > 14 cm (Diameter of the can)
So, some cans can be placed horizontally on the base.
Number of cans in horizontal row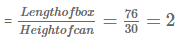
Number of such rows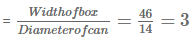
∴ 2 x 3 = 6 cans can be placed horizontally
∴ Maximum number of cans = 15+6 = 21
Choice (D) is therefore, the correct answer.
Each cylindrical can has a diameter of 14 cm and while they are kept erect in the box will occupy height of 30 cm
Number of such cans that can be placed in a row
Number of such rows that can be placed
Thus 5 x 3 = 15 cans can be placed in an erect position.
However, height of box = 45cm and only 30 cm has been utilized so far
Remaining height = 15 cm > 14 cm (Diameter of the can)
So, some cans can be placed horizontally on the base.
Number of cans in horizontal row
Number of such rows
∴ 2 x 3 = 6 cans can be placed horizontally
∴ Maximum number of cans = 15+6 = 21
Choice (D) is therefore, the correct answer.
PQRST is a pentagon in which all the interior angles are unequal. A circle of radius ‘r’ is inscribed in each of the vertices. Find the area of portion of circles falling inside the pentagon. - a)πr2
- b)1.5πr2
- c)2πr2
- d)1.25πr2
Correct answer is option 'B'. Can you explain this answer?
PQRST is a pentagon in which all the interior angles are unequal. A circle of radius ‘r’ is inscribed in each of the vertices. Find the area of portion of circles falling inside the pentagon.
a)
πr2
b)
1.5πr2
c)
2πr2
d)
1.25πr2
|
|
Preeti Khanna answered |
Since neither angles nor sides are given in the question, immediately the sum of angles of pentagon should come in mind. To use it,
We know the area of the sectors of a circle is given as,
We know the area of the sectors of a circle is given as,
Note => The above concept is applicable for a polygon of n sides.
Choice (B) is therefore, the correct answer.
Correct Answer: 1.5πr2
Choice (B) is therefore, the correct answer.
Correct Answer: 1.5πr2
An inverted right circular cone has a radius of 9 cm. This cone is partly filled with oil which is dipping from a hole in the tip at a rate of 1cm2/hour. Currently the level of oil 3 cm from top and surface area is 36π cm2. How long will it take the cone to be completely empty?- a)216π hours
- b)1 hour
- c)3 hours
- d)36π hours
Correct answer is option 'A'. Can you explain this answer?
An inverted right circular cone has a radius of 9 cm. This cone is partly filled with oil which is dipping from a hole in the tip at a rate of 1cm2/hour. Currently the level of oil 3 cm from top and surface area is 36π cm2. How long will it take the cone to be completely empty?
a)
216π hours
b)
1 hour
c)
3 hours
d)
36π hours
|
|
Aarav Sharma answered |
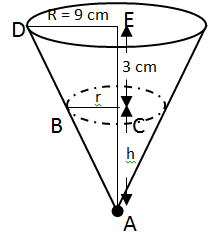
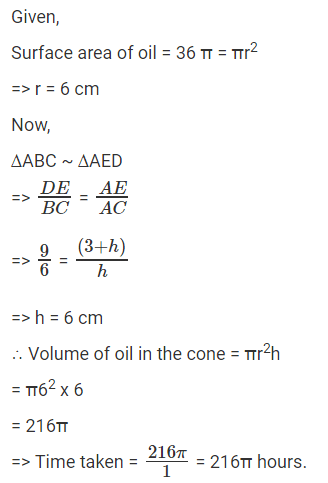
PQRS is a circle and circles are drawn with PO, QO, RO and SO as diameters. Areas A and B are marked. A/B is equal to: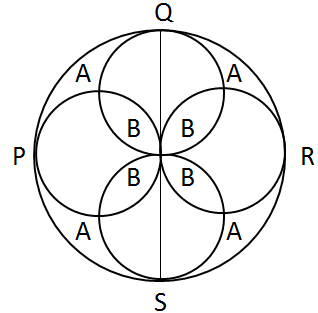
- a)π
- b)1
- c)π/4
- d)2
Correct answer is option 'B'. Can you explain this answer?
PQRS is a circle and circles are drawn with PO, QO, RO and SO as diameters. Areas A and B are marked. A/B is equal to:
a)
π
b)
1
c)
π/4
d)
2

|
Divey Sethi answered |
Such questions are all about visualization and ability to write one area in terms of others.
Here, Let the radius of PQRS be 2r
∴ Radius of each of the smaller circles = 2r/2 = r
∴ Area A can be written as:
A = π (2r)2 – 4 x π(r)2 (Area of the four smaller circles) + B (since, B has been counted twice in the previous subtraction)
Here, Let the radius of PQRS be 2r
∴ Radius of each of the smaller circles = 2r/2 = r
∴ Area A can be written as:
A = π (2r)2 – 4 x π(r)2 (Area of the four smaller circles) + B (since, B has been counted twice in the previous subtraction)
A = 4πr2 - 4πr2 + B
A = B
A/B = 1
A = B
A/B = 1
Choice (B) is therefore, the correct answer.
Correct Answer: 1
Correct Answer: 1
Figure above shows a box which has to be completely wrapped with paper. However, a single Sheet of paper need to be used without any tearing. The dimension of the required paper could be 
- a)17 cm by 4 cm
- b)12 cm by 6 cm
- c)15 cm by 4 cm
- d)13 cm by 4 cm
Correct answer is option 'B'. Can you explain this answer?
Figure above shows a box which has to be completely wrapped with paper. However, a single Sheet of paper need to be used without any tearing. The dimension of the required paper could be
a)
17 cm by 4 cm
b)
12 cm by 6 cm
c)
15 cm by 4 cm
d)
13 cm by 4 cm

|
Naroj Boda answered |
Total surface area of the box = 2(4x6 + 1x6 + 1x4)
= 2(24 + 6 + 4)
= 68 cm2
As the problem says the paper can’t be torn/cut a portion of paper will need to be fold, so, the area of paper required would be greater than 68 cm2. Only option b) gives the area greater 68 cm2
Choice (B) is therefore, the correct answer.
Correct Answer: 12 cm by 6 cm
= 2(24 + 6 + 4)
= 68 cm2
As the problem says the paper can’t be torn/cut a portion of paper will need to be fold, so, the area of paper required would be greater than 68 cm2. Only option b) gives the area greater 68 cm2
Choice (B) is therefore, the correct answer.
Correct Answer: 12 cm by 6 cm
If the edge of a cube is 1 cm then which of the following is its total surface area?- a)1 cm2
- b)4 cm2
- c)6 cm2
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If the edge of a cube is 1 cm then which of the following is its total surface area?
a)
1 cm2
b)
4 cm2
c)
6 cm2
d)
none of these
|
|
Stuti Basak answered |
Explanation:
To find the total surface area of a cube, we need to find the area of all its six faces and add them up. Since all the faces of a cube are identical squares, we can find the area of one face and multiply it by 6 to get the total surface area.
Given, the edge of the cube is 1 cm. Therefore, the area of one face of the cube is:
Area of square = side × side
Area of square = 1 cm × 1 cm
Area of square = 1 cm²
To find the total surface area of the cube, we need to multiply the area of one face by 6:
Total surface area of cube = 6 × area of one face
Total surface area of cube = 6 × 1 cm²
Total surface area of cube = 6 cm²
Therefore, the total surface area of the cube is 6 cm², which is option C.
To find the total surface area of a cube, we need to find the area of all its six faces and add them up. Since all the faces of a cube are identical squares, we can find the area of one face and multiply it by 6 to get the total surface area.
Given, the edge of the cube is 1 cm. Therefore, the area of one face of the cube is:
Area of square = side × side
Area of square = 1 cm × 1 cm
Area of square = 1 cm²
To find the total surface area of the cube, we need to multiply the area of one face by 6:
Total surface area of cube = 6 × area of one face
Total surface area of cube = 6 × 1 cm²
Total surface area of cube = 6 cm²
Therefore, the total surface area of the cube is 6 cm², which is option C.
A sphere of radius r is cut by a plane at a distance of h from its center, thereby breaking this sphere into two different pieces. The cumulative surface area of these two pieces is 25% more than that of the sphere. Find h.- a)
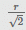
- b)
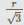
- c)
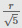
- d)

Correct answer is option 'A'. Can you explain this answer?
A sphere of radius r is cut by a plane at a distance of h from its center, thereby breaking this sphere into two different pieces. The cumulative surface area of these two pieces is 25% more than that of the sphere. Find h.
a)
b)
c)
d)
|
|
Anaya Patel answered |
Area = 4πr2
A right circular cone has height H and radius R. A small cone is cut off at the top by a plane parallel to the base. At what height above the base the section has been made?
Statement (I): H = 20 cm
Statement (II): Volume of small cone: volume of large cone : 1:15- a)If the question can be answered with statement I alone but not statement II alone, or can be answered with statement II alone but not statement I alone.
- b)If the question cannot be answered with statement I alone or with statement II alone, but can be answered if both statements are used together.
- c)If the question can be answered with either statement alone.
- d)If the question cannot be answered with the information provided.
Correct answer is option 'B'. Can you explain this answer?
A right circular cone has height H and radius R. A small cone is cut off at the top by a plane parallel to the base. At what height above the base the section has been made?
Statement (I): H = 20 cm
Statement (II): Volume of small cone: volume of large cone : 1:15
Statement (I): H = 20 cm
Statement (II): Volume of small cone: volume of large cone : 1:15
a)
If the question can be answered with statement I alone but not statement II alone, or can be answered with statement II alone but not statement I alone.
b)
If the question cannot be answered with statement I alone or with statement II alone, but can be answered if both statements are used together.
c)
If the question can be answered with either statement alone.
d)
If the question cannot be answered with the information provided.

|
Ishani Rane answered |
From statement I, we know that the height of the initial cone is 20cm. However, nothing is said about the small cone. Hence, we cannot answer the question using statement A. So, we can eliminate choices (A) and (D).
We are down to choices (A), (B) or (D).
From Statement II, we know that the ratio of the volume of the small cone to that of the large cone is 1 : 15.
i.e. *π*r2*h : *π*R2*H is 1 : 15 (r is the base radius of the smaller cone and h is the height of the smaller cone)
or r2 * h : R2 * H is 1 : 15
From this information, we will not be able to find the answer to h. Hence, we can eliminate choice (A).
Combining the information in the two statements:
When a section is made the two cones are similar triangles. so =
R =
We know H = 20
h = * r
i.e., h3 = H3. Substituting H = 20, we can get the value for h.
Choice (B) is therefore, the correct answer.
Correct Answer: If the question cannot be answered with statement I alone or with statement II alone, but can be answered if both statements are used together.
The area of a rhombus is 200 cm², and one of its diagonals is 20 cm. The length of the other diagonal is _____- a)20 cm
- b)20 m
- c)22 cm
- d)22 m
Correct answer is option 'A'. Can you explain this answer?
The area of a rhombus is 200 cm², and one of its diagonals is 20 cm. The length of the other diagonal is _____
a)
20 cm
b)
20 m
c)
22 cm
d)
22 m

|
EduRev Class 8 answered |
Let the length of one diagonal be d1 = 20 cm, and the length of the other diagonal be d2
The formula for the area of a rhombus is:
Area = 1/2 x d1 x d
Area = 1/2 x d1 x d
2
Substitute the given values:
200 cm² = 1/2 x 20 x d2
200 cm² = 10 x d2
20cm = d2
The area of the circle is 2464 cm2 and the ratio of the breadth of the rectangle to radius of the circle is 6:7. If the circumference of the circle is equal to the perimeter of the rectangle, then what is the area of the rectangle.- a)1456 cm2
- b)1536 cm2
- c)1254 cm2
- d)5678 cm2
Correct answer is option 'B'. Can you explain this answer?
The area of the circle is 2464 cm2 and the ratio of the breadth of the rectangle to radius of the circle is 6:7. If the circumference of the circle is equal to the perimeter of the rectangle, then what is the area of the rectangle.
a)
1456 cm2
b)
1536 cm2
c)
1254 cm2
d)
5678 cm2
|
|
Luminary Institute answered |
Area of the circle=πr2
2464 = 22/7 * r2
Radius of the circle=28 cm
Circumference of the circle=2 * π* r =2 * 22/7 * 28
= 176 cm
Breadth of the rectangle=6/7 * 28=24 cm
Perimeter of the rectangle=2 * (l + b)
176 = 2 * (l + 24)
Length of the rectangle = 64 cm
Area of the rectangle = l * b = 24 * 64 = 1536 cm2
Three circles with radius 2 cm touch each other as shown :- 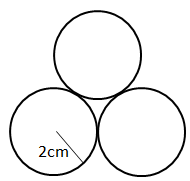
- a)3π(4+√3)2
- b)π/2(4+2√3)2
- c)π/4(4+2√3)2
- d)12π−π/2(4+2√3)2
Correct answer is option 'B'. Can you explain this answer?
Three circles with radius 2 cm touch each other as shown :-
a)
3π(4+√3)2
b)
π/2(4+2√3)2
c)
π/4(4+2√3)2
d)
12π−π/2(4+2√3)2

|
Mainak Majumdar answered |
(This can easily be derived using trigonometry. However, please remember this formula. It is useful at places)
Anil grows tomatoes in his backyard which is in the shape of a square. Each tomato takes 1 cm2 in his backyard. This year, he has been able to grow 131 more tomatoes than last year. The shape of the backyard remained a square. How many tomatoes did Anil produce this year?- a)4225
- b)4096
- c)4356
- d)Insufficient Data
Correct answer is option 'C'. Can you explain this answer?
Anil grows tomatoes in his backyard which is in the shape of a square. Each tomato takes 1 cm2 in his backyard. This year, he has been able to grow 131 more tomatoes than last year. The shape of the backyard remained a square. How many tomatoes did Anil produce this year?
a)
4225
b)
4096
c)
4356
d)
Insufficient Data

|
Naveen Jain answered |
Let the area of backyard be x2 this year and y2 last year
∴ X2- Y2 = 131
=) (X+Y) (X-Y) = 131
Now, 131 is a prime number (a unique one too. Check out its properties on Google). Also, always identify the prime number given in a question. Might be helpful in cracking the solution.
=) (X+Y) (X-Y) = 131 x 1
=) X+Y = 131
X-Y = 1
=) 2X = 132 =) X = 66
and Y = 65
∴ Number of tomatoes produced this year = 662 = 4356
Choice (C) is therefore, the correct answer.
Correct Answer: 4356
∴ X2- Y2 = 131
=) (X+Y) (X-Y) = 131
Now, 131 is a prime number (a unique one too. Check out its properties on Google). Also, always identify the prime number given in a question. Might be helpful in cracking the solution.
=) (X+Y) (X-Y) = 131 x 1
=) X+Y = 131
X-Y = 1
=) 2X = 132 =) X = 66
and Y = 65
∴ Number of tomatoes produced this year = 662 = 4356
Choice (C) is therefore, the correct answer.
Correct Answer: 4356
ABCD is a square drawn inside a square PTRS of sides 4 cm by joining midpoints of the sides PR, PT, TS, SR. Another square is drawn inside ABCD similarly. This process is repeated infinite number of times. Find the sum of all the squares.
- a)16 cm2
- b)28 cm2
- c)32 cm2
- d)Infinite
Correct answer is option 'C'. Can you explain this answer?
ABCD is a square drawn inside a square PTRS of sides 4 cm by joining midpoints of the sides PR, PT, TS, SR. Another square is drawn inside ABCD similarly. This process is repeated infinite number of times. Find the sum of all the squares.
a)
16 cm2
b)
28 cm2
c)
32 cm2
d)
Infinite

|
Rajdeep Verma answered |
If we write the infinite series of area of squares:
= 42 + (2√2)2 + 22 + ……. infinite
Since it is a decreasing series sum of infinite terms can be approximated.
= 16 + 8 + 4 +………infinite
A spherical shaped sweet is placed inside a cube of side 5 cm such that the sweet just fits the cube. A fly is sitting on one of the vertices of the cube. What is the shortest distance the fly must travel to reach the sweet?- a)2.5 cm
- b)5(√3 – 1) cm
- c)5(√2 – 1) cm
- d)2.5(√3 – 1) cm
Correct answer is option 'D'. Can you explain this answer?
A spherical shaped sweet is placed inside a cube of side 5 cm such that the sweet just fits the cube. A fly is sitting on one of the vertices of the cube. What is the shortest distance the fly must travel to reach the sweet?
a)
2.5 cm
b)
5(√3 – 1) cm
c)
5(√2 – 1) cm
d)
2.5(√3 – 1) cm

|
Ishani Rane answered |
The question demands visualization. The shortest distance required to be travelled by the fly would be diagonally and be given by:-
Distance =
= (Since diagonal of the cube is given as √3 x l)
= 2.5(√3 – 1)
A square PQRS has an equilateral triangle PTO inscribed as shown:What is the ratio of AΔPQT to AΔTRU?- a)1 : 3
- b)1 : √3
- c)1 : √2
- d)1 : 2
Correct answer is option 'D'. Can you explain this answer?
A square PQRS has an equilateral triangle PTO inscribed as shown:
What is the ratio of AΔPQT to AΔTRU?
a)
1 : 3
b)
1 : √3
c)
1 : √2
d)
1 : 2

|
Gowri Chakraborty answered |
Let PQ, a side of equilateral triangle be b
By symmetry QT=ST=z (say)

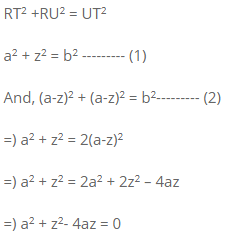
=) a^2 + z^2 – 2az = 2az (Please note how the solution is being managed here. You must always be aware of what you are looking for. Here, as equation -℗ we are looking for (a-z)2 in terms of az)
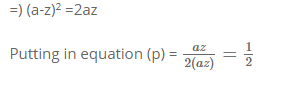
If the parallel sides of a parallelogram are 2 cm apart and their sum is 10 cm then its area is:- a)20 cm2
- b)5 cm2
- c)10 cm2
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If the parallel sides of a parallelogram are 2 cm apart and their sum is 10 cm then its area is:
a)
20 cm2
b)
5 cm2
c)
10 cm2
d)
none of these
|
|
Srestha Menon answered |
Understanding the Parallelogram Area
To find the area of a parallelogram, we can use the formula:
Area = base × height
Where:
- The base is the length of one of the parallel sides.
- The height is the perpendicular distance between the parallel sides.
Given Information
- The distance between the parallel sides (height) = 2 cm
- The sum of the lengths of the parallel sides = 10 cm
Finding the Base
Since we have the sum of the two parallel sides, we can define their lengths as follows:
Let one side be "a" and the other side be "b". According to the problem:
a + b = 10 cm
To find the area, we need the length of one of the sides. For simplicity, let's assume both sides are equal. Thus:
a = b = 10 cm / 2 = 5 cm
Calculating the Area
Now, substituting the values into the area formula:
Area = base × height
Area = 5 cm × 2 cm
Area = 10 cm²
Conclusion
The area of the parallelogram is 10 cm². Hence, the correct answer is option 'C'. This demonstrates how understanding the properties of parallelograms can help solve geometry problems effectively.
To find the area of a parallelogram, we can use the formula:
Area = base × height
Where:
- The base is the length of one of the parallel sides.
- The height is the perpendicular distance between the parallel sides.
Given Information
- The distance between the parallel sides (height) = 2 cm
- The sum of the lengths of the parallel sides = 10 cm
Finding the Base
Since we have the sum of the two parallel sides, we can define their lengths as follows:
Let one side be "a" and the other side be "b". According to the problem:
a + b = 10 cm
To find the area, we need the length of one of the sides. For simplicity, let's assume both sides are equal. Thus:
a = b = 10 cm / 2 = 5 cm
Calculating the Area
Now, substituting the values into the area formula:
Area = base × height
Area = 5 cm × 2 cm
Area = 10 cm²
Conclusion
The area of the parallelogram is 10 cm². Hence, the correct answer is option 'C'. This demonstrates how understanding the properties of parallelograms can help solve geometry problems effectively.
The length of each side of a cube is 24 cm. The volume of the cube is equal to the volume of a cuboid. If the breadth and the height of the cuboid are 32 cm and 12 cm, respectively, then what will be the length of the cuboid?- a)36
- b)27
- c)16
- d)20
Correct answer is option 'A'. Can you explain this answer?
The length of each side of a cube is 24 cm. The volume of the cube is equal to the volume of a cuboid. If the breadth and the height of the cuboid are 32 cm and 12 cm, respectively, then what will be the length of the cuboid?
a)
36
b)
27
c)
16
d)
20
|
|
C K Academy answered |
Given:
The length of each side of a cube is 24 cm.
The breadth and the height of the cuboid are 32 cm and 12 cm, respectively.
The length of each side of a cube is 24 cm.
The breadth and the height of the cuboid are 32 cm and 12 cm, respectively.
Concept used:
The volume of the cube is equal to the volume of a cuboid.
Volume of cube = a³
Volume of cuboid = lbh
The volume of the cube is equal to the volume of a cuboid.
Volume of cube = a³
Volume of cuboid = lbh
Calculation:
The volume of the cube is equal to the volume of a cuboid.
⇒ 24³ = l × 32 × 12
⇒ l = 3 × 12
⇒ l = 36
The volume of the cube is equal to the volume of a cuboid.
⇒ 24³ = l × 32 × 12
⇒ l = 3 × 12
⇒ l = 36
∴ Option 1 is the correct answer.
PQRS is a square of sides 2 cm & ST = 2 cm. Also, PT=RT. What is the area of ?PST?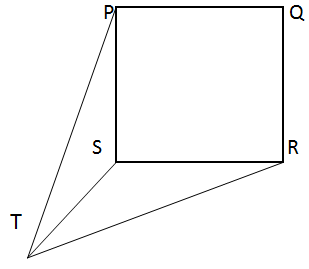
- a)2 cm2
- b)√3 cm2
- c)√2 cm2
- d)
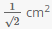
Correct answer is option 'C'. Can you explain this answer?
PQRS is a square of sides 2 cm & ST = 2 cm. Also, PT=RT. What is the area of ?PST?
a)
2 cm2
b)
√3 cm2
c)
√2 cm2
d)
|
|
Rajeev Kumar answered |
Although the figure looks like a 3D figure but on reading through the question, it is clear that the diagram is on a single plane.
Top surface of a raised platform is in the shape of regular octagon as shown in the figure. Find the area of the octagonal surface.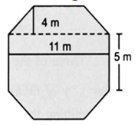
- a)11.9 cm3
- b)119 cm
- c)119 m2
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Top surface of a raised platform is in the shape of regular octagon as shown in the figure. Find the area of the octagonal surface.

a)
11.9 cm3
b)
119 cm
c)
119 m2
d)
None of these
|
|
C K Academy answered |
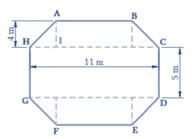
Visually, the area of the octagonal surface will be the sum of the area of two trapezia and the area of rectangular region.
Area of octagon ABCDEFGH = Area of Trapezium ABCH + Area of rectangle HCDG + Area of trapezium EFGD
Side of the regular octagon = 5 cm
Area of trapezium ABCH = Area of trapezium EFGD
Area of trapezium ABCH = 1/2 × (AB + CH) × AI
= 1/2 × (5 m + 11 m) × 4 m
= 1/2 × 16 m × 4 m
= 32 m2
Area of trapezium ABCH = Area of trapezium EFGD = 32 m2
Area of rectangle HCDG = HC × CD = 11 m × 5 m = 55 m2
Area of ABCDEFGH = Area of trapezium ABCH + Area of rectangle HCDG + Area of trapezium EFGD
= 32 m2+ 55 m2+ 32 m2
= 119 m2
Thus the area of the octagonal surface is 119 m2
A string is wound around two circular disk as shown. If the radius of the two disk are 40 cm and 30 cm respectively. What is the total length of the string?
- a)70 cm
- b) 70 + 165*π
- c) 70 + 120π
- d) 70 + 165 * π/2
Correct answer is option 'D'. Can you explain this answer?
A string is wound around two circular disk as shown. If the radius of the two disk are 40 cm and 30 cm respectively. What is the total length of the string?
a)
70 cm
b)
70 + 165*π
c)
70 + 120π
d)
70 + 165 * π/2

|
Bijoy Pillai answered |
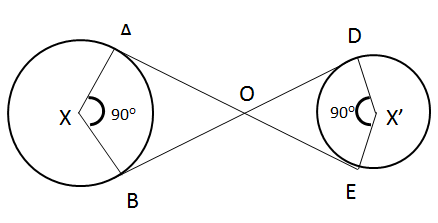
As, tangent from an exterior point makes right angle with the radius.
=) ADXB and ODX’E are squares,
∴ AO = BO = 40 cm
OD = DE = 30 cm
Chapter doubts & questions for Mensuration - RBI Assistant Preparation Course 2025 is part of Bank Exams exam preparation. The chapters have been prepared according to the Bank Exams exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Bank Exams 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Mensuration - RBI Assistant Preparation Course in English & Hindi are available as part of Bank Exams exam.
Download more important topics, notes, lectures and mock test series for Bank Exams Exam by signing up for free.
RBI Assistant Preparation Course
713 videos|966 docs|289 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









