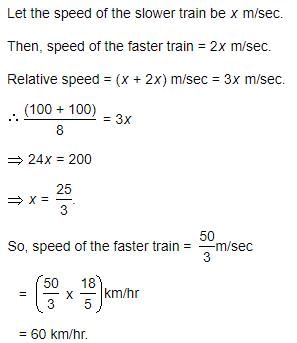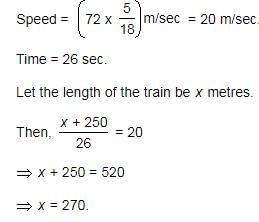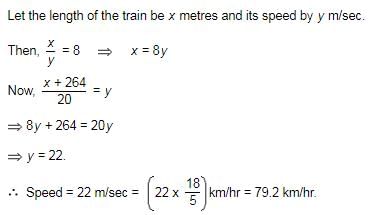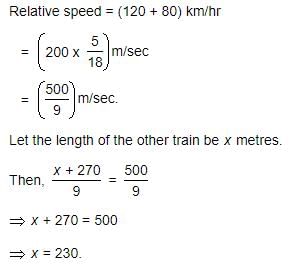All Exams >
Bank Exams >
RBI Assistant Preparation Course >
All Questions
All questions of Problems on Trains for Bank Exams Exam
Two trains, one from P to Q and the other from Q to P, start simultaneously. After they meet, the trains reach their destinations after 9 hours and 16 hours respectively. The ratio of their speeds is
- a)2 : 3
- b)2 :1
- c)4 : 3
- d) 3 : 2
Correct answer is option 'C'. Can you explain this answer?
a)
2 : 3
b)
2 :1
c)
4 : 3
d)
3 : 2
|
Manoj Ghosh answered |
Explanation:
Let us name the trains as A and B. Then,
(A's speed) : (B's speed) = b : a = 16 : 9 = 4 :
A train 360 m long runs with a speed of 45 km/hr. What time will it take to pass a platform of 140 m long?
- a)38 sec
- b)35 s
- c)44 sec
- d)40 s
Correct answer is option 'D'. Can you explain this answer?
a)
38 sec
b)
35 s
c)
44 sec
d)
40 s
|
Kiran Reddy answered |
Formula For Converting From Km/hr to m/s:
Xkm/hr = X × 5/18m/s
Therefore, Speed = 45 × 5/18m/sec
= 252m/sec
Total Distance To Be covered = (360+140)m=500m
Formula for finding
Time = Distance/Speed
∴ Requiredtime = (500×20/25sec
= 40sec.
Xkm/hr = X × 5/18m/s
Therefore, Speed = 45 × 5/18m/sec
= 252m/sec
Total Distance To Be covered = (360+140)m=500m
Formula for finding
Time = Distance/Speed
∴ Requiredtime = (500×20/25sec
= 40sec.
A jogger is running at 9 kmph alongside a railway track in 240 meters ahead of the engine of a 120 meters long train . The train is running at 45 kmph in the same direction. how much time does it take for the train to pass the jogger?
- a)46
- b)36
- c)18
- d)22
Correct answer is option 'B'. Can you explain this answer?
a)
46
b)
36
c)
18
d)
22
|
|
Kiran Reddy answered |
Speed of train relative to jogger = (45 - 9) km/hr = 36 km/hr.
= (36 x 5/18)m/sec
= 10 m/sec.
Distance to be covered = (240 + 120) m = 360 m.
Time taken = 360/10
= 36 sec.
= (36 x 5/18)m/sec
= 10 m/sec.
Distance to be covered = (240 + 120) m = 360 m.
Time taken = 360/10
= 36 sec.
A train overtakes two persons who are walking in the same direction to that of the train at 2 kmph and 4 kmph and passes them completely in 9 and 10 seconds respectively. What is the length of the train?
- a)62m
- b)54m
- c)50m
- d)55m
Correct answer is option 'C'. Can you explain this answer?
a)
62m
b)
54m
c)
50m
d)
55m
|
Ishani Rane answered |
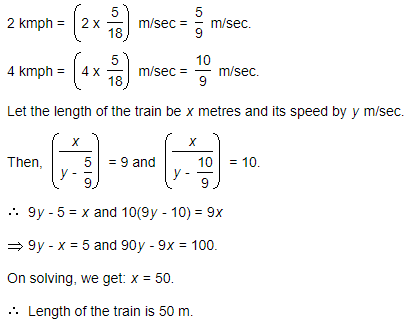
A train has a length of 150 meters . it is passing a man who is moving at 2 km/hr in the same direction of the train, in 3 seconds. Find out the speed of the train
- a)182 km/hr
- b)180 km/hr
- c)152 km/hr
- d)169 km/hr
Correct answer is option 'A'. Can you explain this answer?
a)
182 km/hr
b)
180 km/hr
c)
152 km/hr
d)
169 km/hr
|
Gowri Roy answered |
Explanation:
Length of the train, l = 150m
Speed of the man , Vm= 2 km/hr
Relative speed, Vr = total distance/time = (150/3) m/s = (150/3) x (18/5) = 180 km/hr
Relative Speed = Speed of train, Vt - Speed of man (As both are moving in the same direction)
=> 180 = Vt - 2
=> Vt = 180 + 2 = 182 km/hr
A train having a length of 240 m passes a post in 24 seconds. How long will it take to pass a platform having a length of 650 m?
- a)120 sec
- b)99 s
- c)89 s
- d)80 s
Correct answer is option 'C'. Can you explain this answer?
a)
120 sec
b)
99 s
c)
89 s
d)
80 s
|
Anu Reddy answered |
Speed = 240/24 m/sec
= 10m/sec
∴ Requiredtime = (240+650)/10sec.
= 89sec.
= 10m/sec
∴ Requiredtime = (240+650)/10sec.
= 89sec.
A train travelling at a speed of 75 mph enters a tunnel 3 1/2 miles long. The train is 1/4 mile long. How long does it take for the train to pass through the tunnel from the moment the front enters to the moment the rear emerges?
- a)3 min
- b) 4.2 min
- c)3.4 min
- d)5.5 min
Correct answer is option 'A'. Can you explain this answer?
a)
3 min
b)
4.2 min
c)
3.4 min
d)
5.5 min
|
Pallabi Deshpande answered |
A train ,130 meters long travels at a speed of 45 km/hr crosses a bridge in 30 seconds. The length of the bridge is
- a)270 m
- b)245 m
- c)235 m
- d)220 m
Correct answer is option 'B'. Can you explain this answer?
a)
270 m
b)
245 m
c)
235 m
d)
220 m
|
|
Devanshi Ahuja answered |
45*(5/18) = 12.5
=>(130+x)/12.5 = 30
=>(130+x) = 375
=> x = 375 - 130
=>x = 245
=>(130+x)/12.5 = 30
=>(130+x) = 375
=> x = 375 - 130
=>x = 245
Two trains having length of 140 m and 160 m long run at the speed of 60 km/hr and 40 km/hr respectively in opposite directions (on parallel tracks). The time which they take to cross each other, is
- a)10.8s
- b)12s
- c)9.8s
- d)8s
Correct answer is option 'A'. Can you explain this answer?
a)
10.8s
b)
12s
c)
9.8s
d)
8s
|
|
Krithika Bose answered |
Relative speed = (60+40)km/hr
= (100×5/18) m/sec
= (250/9) m/sec
Distance covered in crossing each other =(140+160)m
= 300m
Required time = Distance/Time
=> 300/(250/9)
= 300*(9/250)
= 54/5
= 10.8 sec
= (100×5/18) m/sec
= (250/9) m/sec
Distance covered in crossing each other =(140+160)m
= 300m
Required time = Distance/Time
=> 300/(250/9)
= 300*(9/250)
= 54/5
= 10.8 sec
A train passes a platform in 36 seconds. The same train passes a man standing on the platform in 20 seconds. If the speed of the train is 54 km/hr, The length of the platform is
- a) None of these
- b)280 meter
- c) 240 meter
- d)200 meter
Correct answer is option 'C'. Can you explain this answer?
a)
None of these
b)
280 meter
c)
240 meter
d)
200 meter
|
|
Ishani Rane answered |
A train is running at a speed of 40 km/hr and it crosses a post in 18 seconds. What is the length of the train?- a)190 metres
- b)160 metres
- c)200 metres
- d)120 metres
Correct answer is option 'C'. Can you explain this answer?
A train is running at a speed of 40 km/hr and it crosses a post in 18 seconds. What is the length of the train?
a)
190 metres
b)
160 metres
c)
200 metres
d)
120 metres
|
Mahesh Kapoor answered |
To find the length of the train, we can use the formula:
Length of train = Speed × Time
Given:
Speed of the train = 40 km/hr
Time taken to cross the post = 18 seconds
Converting the speed from km/hr to m/s:
We know that 1 km/hr = 5/18 m/s
So, the speed of the train in m/s = (40 × 5/18) m/s = 200/18 m/s = 100/9 m/s
Calculating the length of the train:
Length of train = (100/9) × 18
Length of train = 1800/9
Length of train = 200 meters
Therefore, the length of the train is 200 meters, which is option C.
Length of train = Speed × Time
Given:
Speed of the train = 40 km/hr
Time taken to cross the post = 18 seconds
Converting the speed from km/hr to m/s:
We know that 1 km/hr = 5/18 m/s
So, the speed of the train in m/s = (40 × 5/18) m/s = 200/18 m/s = 100/9 m/s
Calculating the length of the train:
Length of train = (100/9) × 18
Length of train = 1800/9
Length of train = 200 meters
Therefore, the length of the train is 200 meters, which is option C.
Two trains, each 100 m long are moving in opposite directions. They cross each other in 8 seconds. If one is moving twice as fast the other, the speed of the faster train is
- a)75 km/hr
- b)60 km/hr
- c)35 km/hr
- d)70 km/hr
Correct answer is option 'B'. Can you explain this answer?
a)
75 km/hr
b)
60 km/hr
c)
35 km/hr
d)
70 km/hr
|
|
Juhi Dasgupta answered |
Solution:
Given, length of each train = 100 m
Time taken to cross each other = 8 sec
Let the speed of the slower train be x m/s
Then, the speed of the faster train = 2x m/s
Relative speed of the trains = (speed of slower train + speed of faster train)
= (x + 2x) m/s
= 3x m/s
Distance covered during crossing = sum of the lengths of the trains = 100 + 100 = 200 m
Using the formula, distance = speed × time
we can find the speed of slower train as follows:
distance = speed × time
=> 200 = 3x × 8
=> x = 6.25 m/s
Converting the speed to km/hr, we get:
Speed of slower train = 6.25 × 18/5 km/hr
= 22.5 km/hr
Speed of faster train = 2x = 2 × 6.25 m/s = 12.5 m/s
Converting the speed to km/hr, we get:
Speed of faster train = 12.5 × 18/5 km/hr
= 45 km/hr
Therefore, the speed of the faster train is 45 km/hr, which is option B.
Given, length of each train = 100 m
Time taken to cross each other = 8 sec
Let the speed of the slower train be x m/s
Then, the speed of the faster train = 2x m/s
Relative speed of the trains = (speed of slower train + speed of faster train)
= (x + 2x) m/s
= 3x m/s
Distance covered during crossing = sum of the lengths of the trains = 100 + 100 = 200 m
Using the formula, distance = speed × time
we can find the speed of slower train as follows:
distance = speed × time
=> 200 = 3x × 8
=> x = 6.25 m/s
Converting the speed to km/hr, we get:
Speed of slower train = 6.25 × 18/5 km/hr
= 22.5 km/hr
Speed of faster train = 2x = 2 × 6.25 m/s = 12.5 m/s
Converting the speed to km/hr, we get:
Speed of faster train = 12.5 × 18/5 km/hr
= 45 km/hr
Therefore, the speed of the faster train is 45 km/hr, which is option B.
Two trains having equal lengths, take 10 seconds and 15 seconds respectively to cross a post. If the length of each train is 120 meters, in what time (in seconds) will they cross each other when traveling in opposite direction?
- a)10
- b)25
- c)12
- d)20
Correct answer is option 'C'. Can you explain this answer?
a)
10
b)
25
c)
12
d)
20
|
Dhruv Mehra answered |
A train is traveling at 48 kmph . It crosses another train having half of its length , traveling in opposite direction at 42 kmph, in 12 seconds. It also passes a railway platform in 45 seconds. What is the length of the platform?
- a)500 m
- b)360 m
- c)480 m
- d)400 m
Correct answer is option 'D'. Can you explain this answer?
a)
500 m
b)
360 m
c)
480 m
d)
400 m
|
Sameer Rane answered |
Let the length of the train traveling at 48 kmph be 2x meters.
And length of the platform is y meters.
Relative speed of train = (48+42) kmph
= (90*5/18) = 25 m/sec;
And 48 kmph = 48*5/18 = 40/3 m/sec.
According to the question,
(2x +x)/25 = 12;
Or, 3x = 12*25 = 300;
Or, x = 300/3 = 100m
Then, length of the train = 2x = 100*2 = 200m.
200+y/(40/3) = 45;
600+3y = 40*45;
Or, 3y = 1800-600 = 1200;
Or, y = 1200/3 = 400 m.
Length of the platform = 400 m.
Two trains running in opposite directions cross a man standing on the platform in 27 seconds and 17 seconds respectively . If they cross each other in 23 seconds, what is the ratio of their speeds?
- a)Insufficient data
- b)3 : 1
- c)1 : 3
- d)3 : 2
Correct answer is option 'D'. Can you explain this answer?
a)
Insufficient data
b)
3 : 1
c)
1 : 3
d)
3 : 2
|
Debanshi Reddy answered |
Let the speeds of the two trains be x m/sec and y m/sec respectively.
Then, length of the first train = 27x meters,
Length of the second train = 17y meters.
[distance = speed*time]
(27x+17y)/(x+y)=23
=>27x+17y=23x+23y
=>4x=6y
=>x/y=6/4=3/2=3:2
Two trains of equal length are running on parallel lines in the same direction at 46 km/hr and 36 km/hr. If the faster train passes the slower train in 36 seconds,what is the length of each train?
- a)88
- b)70
- c)62
- d)50
Correct answer is option 'D'. Can you explain this answer?
a)
88
b)
70
c)
62
d)
50
|
|
Shraddha Khanna answered |
Given:
- Two trains are running on parallel lines in the same direction.
- The speed of the faster train is 46 km/hr.
- The speed of the slower train is 36 km/hr.
- The faster train passes the slower train in 36 seconds.
To find:
The length of each train.
Approach:
Let's assume the length of each train is 'x'.
When the faster train overtakes the slower train, it covers the length of the slower train.
The relative speed between the two trains is the difference between their speeds: (46 - 36) = 10 km/hr.
We need to convert the speed from km/hr to m/s to match the time unit.
1 km/hr = (5/18) m/s
So, the relative speed between the two trains is (10 * 5/18) m/s.
The formula to find the distance covered is:
Distance = Speed * Time
Substituting the values, we have:
x = (10 * 5/18 * 36) m
Simplifying further:
x = 100 m
Therefore, the length of each train is 100 meters.
Hence, the correct answer is option D) 50 meters.
- Two trains are running on parallel lines in the same direction.
- The speed of the faster train is 46 km/hr.
- The speed of the slower train is 36 km/hr.
- The faster train passes the slower train in 36 seconds.
To find:
The length of each train.
Approach:
Let's assume the length of each train is 'x'.
When the faster train overtakes the slower train, it covers the length of the slower train.
The relative speed between the two trains is the difference between their speeds: (46 - 36) = 10 km/hr.
We need to convert the speed from km/hr to m/s to match the time unit.
1 km/hr = (5/18) m/s
So, the relative speed between the two trains is (10 * 5/18) m/s.
The formula to find the distance covered is:
Distance = Speed * Time
Substituting the values, we have:
x = (10 * 5/18 * 36) m
Simplifying further:
x = 100 m
Therefore, the length of each train is 100 meters.
Hence, the correct answer is option D) 50 meters.
Chapter doubts & questions for Problems on Trains - RBI Assistant Preparation Course 2025 is part of Bank Exams exam preparation. The chapters have been prepared according to the Bank Exams exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Bank Exams 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Problems on Trains - RBI Assistant Preparation Course in English & Hindi are available as part of Bank Exams exam.
Download more important topics, notes, lectures and mock test series for Bank Exams Exam by signing up for free.
RBI Assistant Preparation Course
713 videos|966 docs|289 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup