All Exams >
Commerce >
Applied Mathematics for Class 12 >
All Questions
All questions of Linear Programming for Commerce Exam
How many of the following points satisfy the inequality 2x – 3y > -5?
(1, 1), (-1, 1), (1, -1), (-1, -1), (-2, 1), (2, -1), (-1, 2) and (-2, -1)- a)2
- b)4
- c)6
- d)5
Correct answer is option 'D'. Can you explain this answer?
How many of the following points satisfy the inequality 2x – 3y > -5?
(1, 1), (-1, 1), (1, -1), (-1, -1), (-2, 1), (2, -1), (-1, 2) and (-2, -1)
(1, 1), (-1, 1), (1, -1), (-1, -1), (-2, 1), (2, -1), (-1, 2) and (-2, -1)
a)
2
b)
4
c)
6
d)
5
|
Megha Chopra answered |
It is not possible to answer this question without knowing the values of the points. Please provide more information.
The set of all feasible solutions of a LPP is a ____ set.- a)Concave
- b)Convex
- c)Feasible
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The set of all feasible solutions of a LPP is a ____ set.
a)
Concave
b)
Convex
c)
Feasible
d)
None of these
|
Varun Kapoor answered |
The set of feasible solutions to an LP (feasible region) forms a (possibly unbounded) convex set.
Maximize Z = 100x + 120y , subject to constraints 2x + 3y ≤ 30, 3x + y ≤ 17, x ≥ 0, y ≥ 0.- a)1260
- b)1200
- c)1300
- d)1280
Correct answer is option 'A'. Can you explain this answer?
Maximize Z = 100x + 120y , subject to constraints 2x + 3y ≤ 30, 3x + y ≤ 17, x ≥ 0, y ≥ 0.
a)
1260
b)
1200
c)
1300
d)
1280
|
Amrita Sarkar answered |
We have , Maximize Z = 100x + 120y , subject to constraints 2x + 3y ≤ 30, 3x + y ≤ 17, x ≥ 0, y ≥ 0.
Objective function of a LPP is- a)function to be optimized
- b)A constraint
- c)Relation between variables
- d)Equation in a line
Correct answer is option 'A'. Can you explain this answer?
Objective function of a LPP is
a)
function to be optimized
b)
A constraint
c)
Relation between variables
d)
Equation in a line
|
Jaideep Basu answered |
Objective function of a Linear Programming Problem (LPP)
The objective function of a Linear Programming Problem (LPP) is a mathematical function that is to be optimized or maximized. It represents the goal or objective of the problem and determines the best possible solution.
Understanding Linear Programming
Linear Programming is a mathematical technique used to determine the best possible outcome or solution in a given set of constraints. It involves optimizing a linear objective function while adhering to a set of linear constraints.
The Components of a LPP
A Linear Programming Problem consists of the following components:
1. Decision Variables: These are the variables that represent the quantities or values that we want to determine or find. They are denoted by x1, x2, x3, etc.
2. Objective Function: The objective function is a mathematical expression that defines the goal or objective of the problem. It is a linear combination of the decision variables and is either to be maximized or minimized.
3. Constraints: Constraints are the limitations or restrictions that need to be satisfied while finding the optimal solution. They are represented by a set of linear inequalities or equations.
4. Feasible Region: The feasible region is the set of all possible solutions that satisfy the given constraints.
The Objective Function
The objective function is a key component of a Linear Programming Problem. It quantifies the objective or goal in terms of the decision variables and defines the direction of optimization. The objective can be to maximize profits, minimize costs, maximize production, minimize waste, etc.
The objective function is typically a linear equation or expression that involves the decision variables. It may have coefficients that represent the importance or weightage of each decision variable in achieving the objective. The coefficients can be positive or negative depending on whether the objective is to be maximized or minimized.
Conclusion
In summary, the objective function of a Linear Programming Problem (LPP) represents the goal or objective that needs to be optimized or maximized. It is a mathematical expression involving the decision variables and determines the direction of optimization. The objective function plays a crucial role in finding the optimal solution within the given constraints.
The objective function of a Linear Programming Problem (LPP) is a mathematical function that is to be optimized or maximized. It represents the goal or objective of the problem and determines the best possible solution.
Understanding Linear Programming
Linear Programming is a mathematical technique used to determine the best possible outcome or solution in a given set of constraints. It involves optimizing a linear objective function while adhering to a set of linear constraints.
The Components of a LPP
A Linear Programming Problem consists of the following components:
1. Decision Variables: These are the variables that represent the quantities or values that we want to determine or find. They are denoted by x1, x2, x3, etc.
2. Objective Function: The objective function is a mathematical expression that defines the goal or objective of the problem. It is a linear combination of the decision variables and is either to be maximized or minimized.
3. Constraints: Constraints are the limitations or restrictions that need to be satisfied while finding the optimal solution. They are represented by a set of linear inequalities or equations.
4. Feasible Region: The feasible region is the set of all possible solutions that satisfy the given constraints.
The Objective Function
The objective function is a key component of a Linear Programming Problem. It quantifies the objective or goal in terms of the decision variables and defines the direction of optimization. The objective can be to maximize profits, minimize costs, maximize production, minimize waste, etc.
The objective function is typically a linear equation or expression that involves the decision variables. It may have coefficients that represent the importance or weightage of each decision variable in achieving the objective. The coefficients can be positive or negative depending on whether the objective is to be maximized or minimized.
Conclusion
In summary, the objective function of a Linear Programming Problem (LPP) represents the goal or objective that needs to be optimized or maximized. It is a mathematical expression involving the decision variables and determines the direction of optimization. The objective function plays a crucial role in finding the optimal solution within the given constraints.
Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px+qy, where p, q > 0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is- a)p = 2q
- b)p = q
- c)p = 3q
- d)p = q/2
Correct answer is 'D'. Can you explain this answer?
Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px+qy, where p, q > 0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is
a)
p = 2q
b)
p = q
c)
p = 3q
d)
p = q/2
|
Rohit Roy answered |
We have Z = px + qy , At (3, 0) Z = 3p ……………………………….(1) At (1 , 1) Z = p + q …………………………(2) Therefore , from (1) and (2) : We have : p = q/2 .
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman’s time in its making while a cricket bat takes 3 hour of machine time and 1 hour of craftman’s time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsman’s time. What number of rackets and bats must be made if the factory is to work at full capacity?- a)5 tennis rackets and 15 cricket bats
- b)4 tennis rackets and 12 cricket bats
- c)4 tennis rackets and 14 cricket bats
- d)3 tennis rackets and 13 cricket bats
Correct answer is option 'B'. Can you explain this answer?
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman’s time in its making while a cricket bat takes 3 hour of machine time and 1 hour of craftman’s time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsman’s time. What number of rackets and bats must be made if the factory is to work at full capacity?
a)
5 tennis rackets and 15 cricket bats
b)
4 tennis rackets and 12 cricket bats
c)
4 tennis rackets and 14 cricket bats
d)
3 tennis rackets and 13 cricket bats
|
Advait Ghoshal answered |
Let number of rackets made = x
And number of bats made = y
Therefore , the above L.P.P. is given as :
Maximise , Z = x +y , subject to the constraints : 1.5x +3y ≤ 42 and. 3x +y ≤ 24, i.e.0.5x + y ≤ 14 i.e. x +2y ≤ 28 and 3x +y ≤ 24 , x, y ≥ 0.
Here Z = 16 is maximum. i.e Maximum number of rackets = 4 and number of bats = 12.
And number of bats made = y
Therefore , the above L.P.P. is given as :
Maximise , Z = x +y , subject to the constraints : 1.5x +3y ≤ 42 and. 3x +y ≤ 24, i.e.0.5x + y ≤ 14 i.e. x +2y ≤ 28 and 3x +y ≤ 24 , x, y ≥ 0.
Here Z = 16 is maximum. i.e Maximum number of rackets = 4 and number of bats = 12.
In linear programming problems the optimum solution- a)satisfies a set of piecewise – linear inequalities (called constraints)
- b)satisfies a set of linear inequalities (called linear constraints)
- c)satisfies a set of quadratic inequalities (calledconstraints)
- d)satisfies a set of cubic inequalities (calledconstraints)
Correct answer is option 'B'. Can you explain this answer?
In linear programming problems the optimum solution
a)
satisfies a set of piecewise – linear inequalities (called constraints)
b)
satisfies a set of linear inequalities (called linear constraints)
c)
satisfies a set of quadratic inequalities (calledconstraints)
d)
satisfies a set of cubic inequalities (calledconstraints)
|
Jaideep Mukherjee answered |
Explanation:
Linear Programming Problems:
Linear programming involves optimizing a linear objective function subject to a set of linear constraints. The goal is to find the values of the decision variables that maximize or minimize the objective function while satisfying all constraints.
Optimum Solution:
The optimum solution in linear programming problems refers to the values of the decision variables that result in the maximum or minimum value of the objective function while still meeting all the constraints.
Linear Inequalities:
In linear programming, the constraints are typically represented as linear inequalities. These are mathematical statements that involve linear expressions (variables raised to the power of 1) connected by inequality symbols such as ≤, ≥, or =.
Optimum Solution and Linear Inequalities:
The optimum solution in linear programming satisfies a set of linear inequalities, also known as linear constraints. These constraints define the feasible region within which the optimal solution must lie. The optimal solution is the point within this feasible region that maximizes or minimizes the objective function.
Conclusion:
Therefore, in linear programming problems, the optimum solution always satisfies a set of linear inequalities or linear constraints. This is a fundamental aspect of linear programming and is crucial for finding the most efficient solutions to optimization problems.
Linear Programming Problems:
Linear programming involves optimizing a linear objective function subject to a set of linear constraints. The goal is to find the values of the decision variables that maximize or minimize the objective function while satisfying all constraints.
Optimum Solution:
The optimum solution in linear programming problems refers to the values of the decision variables that result in the maximum or minimum value of the objective function while still meeting all the constraints.
Linear Inequalities:
In linear programming, the constraints are typically represented as linear inequalities. These are mathematical statements that involve linear expressions (variables raised to the power of 1) connected by inequality symbols such as ≤, ≥, or =.
Optimum Solution and Linear Inequalities:
The optimum solution in linear programming satisfies a set of linear inequalities, also known as linear constraints. These constraints define the feasible region within which the optimal solution must lie. The optimal solution is the point within this feasible region that maximizes or minimizes the objective function.
Conclusion:
Therefore, in linear programming problems, the optimum solution always satisfies a set of linear inequalities or linear constraints. This is a fundamental aspect of linear programming and is crucial for finding the most efficient solutions to optimization problems.
Let R be the feasible region (convex polygon) for a linear programming problem and let Z = ax + by be the objective function. When Z has an optimal value (maximum or minimum), where the variables x and y are subject to constraints described by linear inequalities,- a)optimal value must occur at a corner point (vertex) of the feasible region.
- b)optimal value must occur at the centroid of the feasible region.
- c)optimal value must occur at the midpoints of the corner points (vertices) of the feasible region
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Let R be the feasible region (convex polygon) for a linear programming problem and let Z = ax + by be the objective function. When Z has an optimal value (maximum or minimum), where the variables x and y are subject to constraints described by linear inequalities,
a)
optimal value must occur at a corner point (vertex) of the feasible region.
b)
optimal value must occur at the centroid of the feasible region.
c)
optimal value must occur at the midpoints of the corner points (vertices) of the feasible region
d)
None of these
|
Poulomi Datta answered |
Let R be the feasible region (convex polygon) for a linear programming problem and let Z = ax + by be the objective function. When Z has an optimal value (maximum or minimum), where the variables x and y are subject to constraints described by linear inequalities,then , optimal value must occur at a corner point (vertex) of the feasible region.
Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F = 4x + 6y be the objective function. Maximum of F – Minimum of F =- a)60
- b)48
- c)42
- d)18
Correct answer is option 'A'. Can you explain this answer?
Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F = 4x + 6y be the objective function. Maximum of F – Minimum of F =
a)
60
b)
48
c)
42
d)
18
|
Rhea Joshi answered |
Here the objective function is given by : F = 4x +6y .
Maximum of F – Minimum of F = 72 – 12 = 30 .
Maximum of F – Minimum of F = 72 – 12 = 30 .
The optimum value of the objective function is attained at the points- a)Corner points of feasible region
- b)Any point of the feasible region
- c)On x-axis
- d)On y-axis
Correct answer is option 'A'. Can you explain this answer?
The optimum value of the objective function is attained at the points
a)
Corner points of feasible region
b)
Any point of the feasible region
c)
On x-axis
d)
On y-axis
|
Anjali Reddy answered |
Given that,
• There is an objective function
• There are optimal values
From the definition of optimal value of a Linear Programming Problem(LPP):
An optimal/ feasible solution is any point in the feasible region that gives a maximum or minimum value if substituted in the objective function.
Here feasible region of an LPP is defined as:
A feasible region is that common region determined by all the constraints including the non-negative constraints of the LPP.
So the Feasible region of a LPP is a convex polygon where, its vertices (or corner points) determine the optimal values (either maximum/minimum) of the objective function.
For Example,
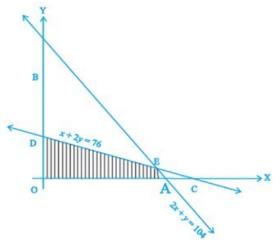
5x + y ≤ 100 ; x + y ≤ 60 ; x ≥ 0 ; y ≥ 0
The feasible solution of the LPP is given by the convex polygon OADC.
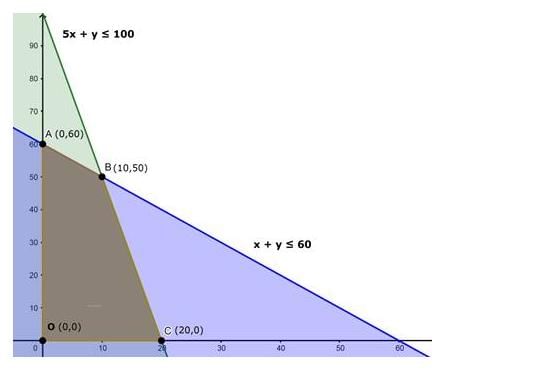
Here, points O, A ,D and C will be optimal solutions of the taken LPP
• There is an objective function
• There are optimal values
From the definition of optimal value of a Linear Programming Problem(LPP):
An optimal/ feasible solution is any point in the feasible region that gives a maximum or minimum value if substituted in the objective function.
Here feasible region of an LPP is defined as:
A feasible region is that common region determined by all the constraints including the non-negative constraints of the LPP.
So the Feasible region of a LPP is a convex polygon where, its vertices (or corner points) determine the optimal values (either maximum/minimum) of the objective function.
For Example,
5x + y ≤ 100 ; x + y ≤ 60 ; x ≥ 0 ; y ≥ 0
The feasible solution of the LPP is given by the convex polygon OADC.
Here, points O, A ,D and C will be optimal solutions of the taken LPP
Can you explain the answer of this question below:A ……… of a feasible region is a point in the region, which is the intersection of two boundary lines.
- A:
Section point
- B:
Corner point
- C:
Reasonable point
- D:
Vertex point
The answer is b.
A ……… of a feasible region is a point in the region, which is the intersection of two boundary lines.
Section point
Corner point
Reasonable point
Vertex point
|
Rahul Bansal answered |
Corner Point:
A vertex of the feasible region. Not every intersection of lines is a corner point. The corner points only occur at a vertex of the feasible region. If there is going to be an optimal solution to a linear programming problem, it will occur at one or more corner points, or on a line segment between two corner points.
In linear programming, optimal solution- a)satisfies all the constraints only
- b)is not unique
- c)satisfies all the constraints as well as the objective function
- d)maximizes the objective function only
Correct answer is option 'C'. Can you explain this answer?
In linear programming, optimal solution
a)
satisfies all the constraints only
b)
is not unique
c)
satisfies all the constraints as well as the objective function
d)
maximizes the objective function only
|
Sanchita Iyer answered |
In linear programming, optimal solution satisfies all the constraints as well as the objective function .
Maximize Z = – x + 2y, subject to the constraints: x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.- a)Maximum Z = 12 at (2, 6)
- b)Z has no maximum value
- c)Maximum Z = 10 at (2, 6)
- d)Maximum Z = 14 at (2, 6)
Correct answer is option 'B'. Can you explain this answer?
Maximize Z = – x + 2y, subject to the constraints: x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
a)
Maximum Z = 12 at (2, 6)
b)
Z has no maximum value
c)
Maximum Z = 10 at (2, 6)
d)
Maximum Z = 14 at (2, 6)
|
Sushant Khanna answered |
Objective function is Z = - x + 2 y ……………………(1).
The given constraints are : x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
The given constraints are : x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
Corner points Z = - x + 2y
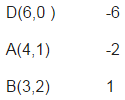
Here , the open half plane has points in common with the feasible region .
Therefore , Z has no maximum value.
Here , the open half plane has points in common with the feasible region .
Therefore , Z has no maximum value.
Shape of the feasible region formed by the following constraints is x + y ≤ 2, x + y ≥ 5, x ≥ 0, y ≥ 0- a)No feasible region
- b)Triangular region
- c)Unbounded solution
- d)Trapezium
Correct answer is option 'A'. Can you explain this answer?
Shape of the feasible region formed by the following constraints is x + y ≤ 2, x + y ≥ 5, x ≥ 0, y ≥ 0
a)
No feasible region
b)
Triangular region
c)
Unbounded solution
d)
Trapezium
|
Prajjawal Sahu answered |
No feasible region simply means that no solution
Since equation 1 and 2 have no common area
Hence Correct Answer is Option (A)
Maximise Z = 3x + 4y subject to the constraints: x + y ≤ 4, x ≥ 0, y ≥ 0.- a)Maximum Z = 18 at (1, 4)
- b)Maximum Z = 19 at (1, 5)
- c)Maximum Z = 16 at (0, 4)
- d)Maximum Z = 17 at (0, 5)
Correct answer is option 'C'. Can you explain this answer?
Maximise Z = 3x + 4y subject to the constraints: x + y ≤ 4, x ≥ 0, y ≥ 0.
a)
Maximum Z = 18 at (1, 4)
b)
Maximum Z = 19 at (1, 5)
c)
Maximum Z = 16 at (0, 4)
d)
Maximum Z = 17 at (0, 5)
|
Manisha Mehta answered |
Objective function is Z = 3x + 4 y ……(1).
The given constraints are : x + y ≤ 4, x ≥ 0, y ≥ 0.
therefore Z = 16 is maximum at ( 0 , 4 ) .
The given constraints are : x + y ≤ 4, x ≥ 0, y ≥ 0.
therefore Z = 16 is maximum at ( 0 , 4 ) .
A linear programming problem is one that is concerned with- a)finding the upper limits of a linear function of several variables
- b)finding the lower limit of a linear function of several variables
- c)finding the limiting values of a linear function of several variables
- d)finding the optimal value (maximum or minimum) of a linear function of several variables
Correct answer is option 'D'. Can you explain this answer?
A linear programming problem is one that is concerned with
a)
finding the upper limits of a linear function of several variables
b)
finding the lower limit of a linear function of several variables
c)
finding the limiting values of a linear function of several variables
d)
finding the optimal value (maximum or minimum) of a linear function of several variables
|
Manisha Choudhary answered |
A linear programming problem is one that is concerned with finding the optimal value (maximum or minimum) of a linear function of several variables .
A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1 and F2 are available. Food F1 costs Rs 4 per unit food and F2 costs Rs 6 per unit. One unit of food F1 contains 3 units of vitamin A and 4 units of minerals. One unit of food F2 contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem. Find the minimum cost for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements.- a)Minimum cost = Rs 114
- b)Minimum cost = Rs 134
- c)Minimum cost = Rs 124
- d)Minimum cost = Rs 104
Correct answer is option 'D'. Can you explain this answer?
A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1 and F2 are available. Food F1 costs Rs 4 per unit food and F2 costs Rs 6 per unit. One unit of food F1 contains 3 units of vitamin A and 4 units of minerals. One unit of food F2 contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem. Find the minimum cost for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements.
a)
Minimum cost = Rs 114
b)
Minimum cost = Rs 134
c)
Minimum cost = Rs 124
d)
Minimum cost = Rs 104
|
Devansh Joshi answered |
Let number of units of food F1 = x
And number of units of food F2 = y
Therefore , the above L.P.P. is given as :
Minimise , Z = 4x +6y , subject to the constraints : 3 x + 6y ≥ 80, 4x + 3y ≥ 100, x,y ≥ 0.
Corner points Z =4x +6 y B(80/3 , 0) 320/3 D(24,4/3 ) 104…………………(Min.) A(0,100/3) 200 Here Z = 104 is minimum. i.e. Minimum cost = Rs 104.
And number of units of food F2 = y
Therefore , the above L.P.P. is given as :
Minimise , Z = 4x +6y , subject to the constraints : 3 x + 6y ≥ 80, 4x + 3y ≥ 100, x,y ≥ 0.
Corner points Z =4x +6 y B(80/3 , 0) 320/3 D(24,4/3 ) 104…………………(Min.) A(0,100/3) 200 Here Z = 104 is minimum. i.e. Minimum cost = Rs 104.
Which of the following types of problems cannot be solved by linear programming methods- a)Diet problems
- b)Transportation problems
- c)Manufacturing problems
- d)Traffic signal control
Correct answer is option 'D'. Can you explain this answer?
Which of the following types of problems cannot be solved by linear programming methods
a)
Diet problems
b)
Transportation problems
c)
Manufacturing problems
d)
Traffic signal control
|
Nandini Choudhury answered |
Traffic signal control types of problems cannot be solved by linear programming methods .
In a LPP, the objective function is always- a)cubic
- b)quadratic
- c)Linear
- d)constant
Correct answer is option 'C'. Can you explain this answer?
In a LPP, the objective function is always
a)
cubic
b)
quadratic
c)
Linear
d)
constant
|
Pragati Patel answered |
In a LPP, the objective function is always linear.
The optimal value of the objective function Z = ax + by may or may not exist, if the feasible region for a LPP is- a)a circle
- b)a polygon
- c)Bounded
- d)Unbounded
Correct answer is option 'D'. Can you explain this answer?
The optimal value of the objective function Z = ax + by may or may not exist, if the feasible region for a LPP is
a)
a circle
b)
a polygon
c)
Bounded
d)
Unbounded
|
Avantika Joshi answered |
The optimal value of the objective function Z = ax + by may or may not exist, if the feasible region for a LPP is unbounded.
The maximum value of Z = 4x + 3y subjected to the constraints 3x + 2y ≤ 160, 5x + 2y ≤ 200, x + 2y ≤ 80 ;
x, y ≥ 0 attains at- a)x = 40, y = 0
- b)x = 40, y = 25
- c)x = 0, y = 25
- d)x = 30. y = 25
Correct answer is option 'D'. Can you explain this answer?
The maximum value of Z = 4x + 3y subjected to the constraints 3x + 2y ≤ 160, 5x + 2y ≤ 200, x + 2y ≤ 80 ;
x, y ≥ 0 attains at
x, y ≥ 0 attains at
a)
x = 40, y = 0
b)
x = 40, y = 25
c)
x = 0, y = 25
d)
x = 30. y = 25
|
Harshad Nair answered |
Given object function is
Z = 4x+3y
Constraints are
3x + 2y ≥ 160
5x + 2y ≥ 200
x + 2y ≥ 80
x ≥ 0
y≥ 0.
Consider, the inequalities as equalities for some time,
3x + 2y = 160 ; 5x + 2y = 200 and x + 2y = 80
If we convert these into intercept line format equations, we get,
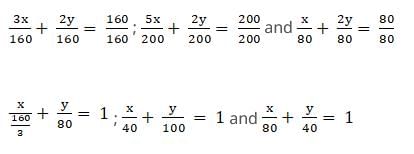
From this form of line, we can say that the line 3x + 2y = 160 meets the x-axis at (,0) and y-axis at (0,80).
This shows the inequality 3x + 2y ≥ 160 holds.
Similarly, from the intercept line format, we can say that the line 5x + 2y = 200 meets the x-axis at (40,0) and y-axis at (0,100).
This shows the inequality 5x + 2y ≥ 200 holds .
Similarly from the intercept line format, we can say that the line x + 2y = 80 meets the x-axis at (80,0) and y-axis at (0,40).
This shows the inequality x + 2y ≥ 80 holds .
Now considering the inequalities, x ≥ 0 and y ≥ 0, this clearly shows the region where both x and y are positive. This represents the 1st quadrant of the graph.
So, the solutions of the LPP are in the first quadrant where the inequalities meet.
We can clearly see that, there is no area in the 1st quadrant where all the three inequalities met.
This clearly says that there is no solution for the LPP with the given constraints.
Hence the option D, is the solution to the problem.
Z = 4x+3y
Constraints are
3x + 2y ≥ 160
5x + 2y ≥ 200
x + 2y ≥ 80
x ≥ 0
y≥ 0.
Consider, the inequalities as equalities for some time,
3x + 2y = 160 ; 5x + 2y = 200 and x + 2y = 80
If we convert these into intercept line format equations, we get,
[Dividing the whole equation with the right hand side number of the equation]
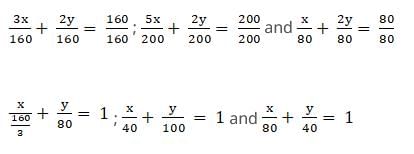
From this form of line, we can say that the line 3x + 2y = 160 meets the x-axis at (,0) and y-axis at (0,80).
This shows the inequality 3x + 2y ≥ 160 holds.
Similarly, from the intercept line format, we can say that the line 5x + 2y = 200 meets the x-axis at (40,0) and y-axis at (0,100).
This shows the inequality 5x + 2y ≥ 200 holds .
Similarly from the intercept line format, we can say that the line x + 2y = 80 meets the x-axis at (80,0) and y-axis at (0,40).
This shows the inequality x + 2y ≥ 80 holds .
Now considering the inequalities, x ≥ 0 and y ≥ 0, this clearly shows the region where both x and y are positive. This represents the 1st quadrant of the graph.
So, the solutions of the LPP are in the first quadrant where the inequalities meet.
Now by plotting all the graphs 3x + 2y ≥ 160 , 5x + 2y ≥ 200 and x + 2y ≥ 80 we get the below graph.
We can clearly see that, there is no area in the 1st quadrant where all the three inequalities met.
This clearly says that there is no solution for the LPP with the given constraints.
Hence the option D, is the solution to the problem.
In a LPP if the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same- a)Minimum value
- b)Mean value
- c)Maximum value
- d)Upper limit value
Correct answer is option 'C'. Can you explain this answer?
In a LPP if the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same
a)
Minimum value
b)
Mean value
c)
Maximum value
d)
Upper limit value
|
|
Rhea Joshi answered |
In a LPP if the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same maximum value .
In linear programming problems the function whose maxima or minima are to be found is called- a)Delta function
- b)Selection function
- c)Subjective function
- d)Objective function
Correct answer is option 'D'. Can you explain this answer?
In linear programming problems the function whose maxima or minima are to be found is called
a)
Delta function
b)
Selection function
c)
Subjective function
d)
Objective function
|
Sinjini Datta answered |
In linear programming problems the function whose maxima or minima are to be found is called Objective function .
In linear programming infeasible solutions- a)fall on the x = 0 plane
- b)fall inside the feasible region
- c)fall outside the feasible region
- d)fall inside the a regular polygon
Correct answer is option 'C'. Can you explain this answer?
In linear programming infeasible solutions
a)
fall on the x = 0 plane
b)
fall inside the feasible region
c)
fall outside the feasible region
d)
fall inside the a regular polygon
|
|
Lekshmi Bose answered |
In linear programming infeasible solutions fall outside the feasible region .
One kind of cake requires 200g of flour and 25g of fat, and another kind of cake requires 100g of flour and 50g of fat. Find the maximum number of cakes which can be made from 5kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes.- a)Maximum number of cakes = 30 , 20 of kind one and 10 cakes of another kind
- b)Maximum number of cakes = 32 , 20 of kind one and 12 cakes of another kind
- c)Maximum number of cakes = 34 , 27 of kind one and 7 cakes of another kind
- d)Maximum number of cakes = 33 , 22 of kind one and 11 cakes of another kind
Correct answer is option 'A'. Can you explain this answer?
One kind of cake requires 200g of flour and 25g of fat, and another kind of cake requires 100g of flour and 50g of fat. Find the maximum number of cakes which can be made from 5kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes.
a)
Maximum number of cakes = 30 , 20 of kind one and 10 cakes of another kind
b)
Maximum number of cakes = 32 , 20 of kind one and 12 cakes of another kind
c)
Maximum number of cakes = 34 , 27 of kind one and 7 cakes of another kind
d)
Maximum number of cakes = 33 , 22 of kind one and 11 cakes of another kind
|
|
Pragati Patel answered |
Let number of cakes of first type = x
And number of cakes of second type = y
Therefore , the above L.P.P. is given as :
Minimise , Z = x +y , subject to the constraints : 200x +100y ≤ 5000 and. 25x +50y ≤ 1000, i.e. 2x + y ≤ 50 and x +2y ≤ 40 x, y ≥ 0.
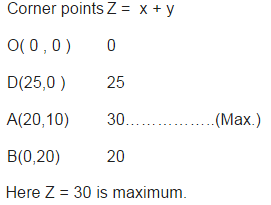
i.e Maximum number of cakes = 30 , 20 of kind one and 10 cakes of another kind .
And number of cakes of second type = y
Therefore , the above L.P.P. is given as :
Minimise , Z = x +y , subject to the constraints : 200x +100y ≤ 5000 and. 25x +50y ≤ 1000, i.e. 2x + y ≤ 50 and x +2y ≤ 40 x, y ≥ 0.
i.e Maximum number of cakes = 30 , 20 of kind one and 10 cakes of another kind .
A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs17.50 per package on nuts and Rs 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machines for at the most 12 hours a day?- a)3 packages of nuts and 3 packages of bolts; Maximum profit = Rs 73.50.
- b)4 packages of nuts and 4 packages of bolts; Maximum profit = Rs 76.50.
- c)3 packages of nuts and 4 packages of bolts; Maximum profit = Rs 74.50.
- d)4 packages of nuts and 3 packages of bolts; Maximum profit = Rs 75.50.
Correct answer is option 'A'. Can you explain this answer?
A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs17.50 per package on nuts and Rs 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machines for at the most 12 hours a day?
a)
3 packages of nuts and 3 packages of bolts; Maximum profit = Rs 73.50.
b)
4 packages of nuts and 4 packages of bolts; Maximum profit = Rs 76.50.
c)
3 packages of nuts and 4 packages of bolts; Maximum profit = Rs 74.50.
d)
4 packages of nuts and 3 packages of bolts; Maximum profit = Rs 75.50.
|
|
Lekshmi Bose answered |
Let number of packages of nuts produced = x
And number of packages of bolts produced = y
Therefore , the above L.P.P. is given as :
Maximise , Z = 17.50x +7y , subject to the constraints : x +3y ≤ 12 and. 3x +y ≤ 12, x, y ≥ 0.
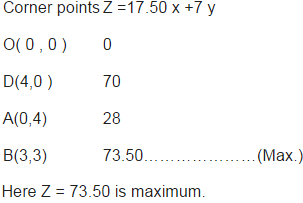
i.e 3 packages of nuts and 3 packages of bolts;
Maximum profit = Rs 73.50.
And number of packages of bolts produced = y
Therefore , the above L.P.P. is given as :
Maximise , Z = 17.50x +7y , subject to the constraints : x +3y ≤ 12 and. 3x +y ≤ 12, x, y ≥ 0.
i.e 3 packages of nuts and 3 packages of bolts;
Maximum profit = Rs 73.50.
A maximum or a minimum may not exist for a linear programming problem if- a)The feasible region is bounded
- b)if the constraints are non linear
- c)if the objective function is continuous
- d)The feasible region is unbounded
Correct answer is option 'D'. Can you explain this answer?
A maximum or a minimum may not exist for a linear programming problem if
a)
The feasible region is bounded
b)
if the constraints are non linear
c)
if the objective function is continuous
d)
The feasible region is unbounded
|
|
Arnav Datta answered |
Introduction:
Linear programming is a mathematical technique used to determine the best possible outcome in a given mathematical model with linear relationships. It involves optimizing an objective function while satisfying a set of constraints. The feasible region represents the set of all possible solutions that satisfy these constraints.
Explanation:
In linear programming, a maximum or a minimum may not exist for a problem under certain conditions. Let's analyze these conditions one by one:
1. Bounded feasible region:
If the feasible region is bounded, it means that there are finite boundaries or limits to the values that the decision variables can take. In such cases, a maximum or a minimum always exists because the feasible region is finite. Therefore, option 'A' is incorrect.
2. Nonlinear constraints:
Linear programming deals with linear constraints, which means that the constraints can be represented by linear equations or inequalities. If the constraints are nonlinear, it implies that the relationships between the decision variables are not linear. In such cases, the problem becomes a nonlinear programming problem, and linear programming techniques may not be applicable. Therefore, option 'B' is incorrect.
3. Continuous objective function:
The objective function represents the quantity that needs to be maximized or minimized. In linear programming, the objective function is always assumed to be continuous. A continuous function is one that does not have any abrupt changes or discontinuities. The continuity of the objective function ensures that a maximum or a minimum can be achieved within the feasible region. Therefore, option 'C' is incorrect.
4. Unbounded feasible region:
If the feasible region is unbounded, it means that there are no finite boundaries or limits to the values that the decision variables can take. In such cases, the solution space extends infinitely in one or more directions, and a maximum or a minimum may not exist. This happens when there are no constraints that restrict the decision variables sufficiently to achieve a finite solution. Therefore, option 'D' is correct.
Conclusion:
In summary, a maximum or a minimum may not exist for a linear programming problem if the feasible region is unbounded. This occurs when there are no constraints that limit the decision variables sufficiently to achieve a finite solution.
Linear programming is a mathematical technique used to determine the best possible outcome in a given mathematical model with linear relationships. It involves optimizing an objective function while satisfying a set of constraints. The feasible region represents the set of all possible solutions that satisfy these constraints.
Explanation:
In linear programming, a maximum or a minimum may not exist for a problem under certain conditions. Let's analyze these conditions one by one:
1. Bounded feasible region:
If the feasible region is bounded, it means that there are finite boundaries or limits to the values that the decision variables can take. In such cases, a maximum or a minimum always exists because the feasible region is finite. Therefore, option 'A' is incorrect.
2. Nonlinear constraints:
Linear programming deals with linear constraints, which means that the constraints can be represented by linear equations or inequalities. If the constraints are nonlinear, it implies that the relationships between the decision variables are not linear. In such cases, the problem becomes a nonlinear programming problem, and linear programming techniques may not be applicable. Therefore, option 'B' is incorrect.
3. Continuous objective function:
The objective function represents the quantity that needs to be maximized or minimized. In linear programming, the objective function is always assumed to be continuous. A continuous function is one that does not have any abrupt changes or discontinuities. The continuity of the objective function ensures that a maximum or a minimum can be achieved within the feasible region. Therefore, option 'C' is incorrect.
4. Unbounded feasible region:
If the feasible region is unbounded, it means that there are no finite boundaries or limits to the values that the decision variables can take. In such cases, the solution space extends infinitely in one or more directions, and a maximum or a minimum may not exist. This happens when there are no constraints that restrict the decision variables sufficiently to achieve a finite solution. Therefore, option 'D' is correct.
Conclusion:
In summary, a maximum or a minimum may not exist for a linear programming problem if the feasible region is unbounded. This occurs when there are no constraints that limit the decision variables sufficiently to achieve a finite solution.
Let R be the feasible region for a linear programming problem,and let Z = ax + by be the objective function. If R is bounded, then the objective function Z has both a maximum and a minimum value on R and- a)each of these occurs at a corner point (vertex) of R.
- b)each of these occurs at themidpoints of the edges of R
- c)each of these occurs at the centre of R.
- d)each of these occurs at some points except corner points of R.
Correct answer is option 'A'. Can you explain this answer?
Let R be the feasible region for a linear programming problem,and let Z = ax + by be the objective function. If R is bounded, then the objective function Z has both a maximum and a minimum value on R and
a)
each of these occurs at a corner point (vertex) of R.
b)
each of these occurs at themidpoints of the edges of R
c)
each of these occurs at the centre of R.
d)
each of these occurs at some points except corner points of R.
|
|
Nandini Choudhury answered |
Let R be the feasible region for a linear programming problem,and let Z = ax + by be the objective function. If R is bounded, then the objective function Z has both a maximum and a minimum value on R and each of these occurs at a corner point (vertex) of R.
A merchant plans to sell two types of personal computers – a desktop model and a portable model that will cost Rs 25000 and Rs 40000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and if his profit on the desktop model is Rs 4500 and on portable model is Rs 5000.- a)200 units of desktop model and 50 units of portable model; Maximum profit = Rs 1150000
- b)260 units of desktop model and 50 units of portable model; Maximum profit = Rs 1150400
- c)220 units of desktop model and 50 units of portable model; Maximum profit = Rs 1150020
- d)240 units of desktop model and 50 units of portable model; Maximum profit = Rs 1150040
Correct answer is option 'A'. Can you explain this answer?
A merchant plans to sell two types of personal computers – a desktop model and a portable model that will cost Rs 25000 and Rs 40000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and if his profit on the desktop model is Rs 4500 and on portable model is Rs 5000.
a)
200 units of desktop model and 50 units of portable model; Maximum profit = Rs 1150000
b)
260 units of desktop model and 50 units of portable model; Maximum profit = Rs 1150400
c)
220 units of desktop model and 50 units of portable model; Maximum profit = Rs 1150020
d)
240 units of desktop model and 50 units of portable model; Maximum profit = Rs 1150040
|
|
Sanchita Iyer answered |
Let number of desktop model computers = x
And number of portable model computers = y
Therefore , the above L.P.P. is given as :
Maximise , Z = 4500x +5000y , subject to the constraints : x +y ≤ 250 and 25000x +40000y ≤ 700000 .i.e. x +y ≤ 250 and 5x +8y ≤ 1400 , x, y ≥ 0.
Here Z = 1150000 is maximum.
i.e. 200 units of desktop model and 50 units of portable model; Maximum profit = Rs 1150000 .
And number of portable model computers = y
Therefore , the above L.P.P. is given as :
Maximise , Z = 4500x +5000y , subject to the constraints : x +y ≤ 250 and 25000x +40000y ≤ 700000 .i.e. x +y ≤ 250 and 5x +8y ≤ 1400 , x, y ≥ 0.
Here Z = 1150000 is maximum.
i.e. 200 units of desktop model and 50 units of portable model; Maximum profit = Rs 1150000 .
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman’s time in its making while a cricket bat takes 3 hour of machine time and 1 hour of craftman’s time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsman’s time. If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the maximum profit of the factory when it works at full capacity?- a)Maximum profit = Rs 220
- b)Maximum profit = Rs 210
- c)Maximum profit = Rs 200
- d)Maximum profit = Rs 230
Correct answer is option 'C'. Can you explain this answer?
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman’s time in its making while a cricket bat takes 3 hour of machine time and 1 hour of craftman’s time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsman’s time. If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the maximum profit of the factory when it works at full capacity?
a)
Maximum profit = Rs 220
b)
Maximum profit = Rs 210
c)
Maximum profit = Rs 200
d)
Maximum profit = Rs 230
|
Ujwal Chawla answered |
Let number of rackets made = x
And number of bats made = y
Therefore , the above L.P.P. is given as :
Maximise , Z = x +y , subject to the constraints : 1.5x +3y ≤ 42 and. 3x +y ≤ 24, i.e.0.5x + y ≤ 14 i.e. x +2y ≤ 28 and 3x +y ≤ 24 , x, y ≥ 0.
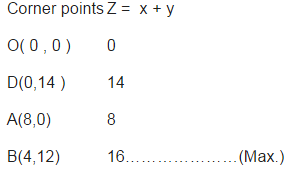
Here Z = 16 is maximum. i.e Maximum number of rackets = 4 and number of bats = 12.
Here , profit function is P = 20x + 10y
Profit is maximum at x = 4 and y = 12 .
Therefore , maximum profit = 20(4) + 10 ( 12) = 200.i.e. Rs.200.
And number of bats made = y
Therefore , the above L.P.P. is given as :
Maximise , Z = x +y , subject to the constraints : 1.5x +3y ≤ 42 and. 3x +y ≤ 24, i.e.0.5x + y ≤ 14 i.e. x +2y ≤ 28 and 3x +y ≤ 24 , x, y ≥ 0.
Here Z = 16 is maximum. i.e Maximum number of rackets = 4 and number of bats = 12.
Here , profit function is P = 20x + 10y
Profit is maximum at x = 4 and y = 12 .
Therefore , maximum profit = 20(4) + 10 ( 12) = 200.i.e. Rs.200.
A fruit grower can use two types of fertilizer in his garden, brand P and brand Q. The amounts (in kg) of nitrogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicate that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine.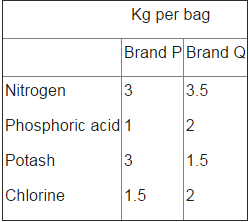
If the grower wants to maximise the amount of nitrogen added to the garden, how many bags of each brand should be added? What isthe maximum amount of nitrogen added?- a)150 bags of brand P and 50 bags of brand Q; Maximum amount of nitrogen = 625 kg
- b)160 bags of brand P and 52 bags of brand Q; Maximum amount of nitrogen = 635 kg
- c)140 bags of brand P and 50 bags of brand Q; Maximum amount of nitrogen = 595 kg
- d)145 bags of brand P and 55 bags of brand Q; Maximum amount of nitrogen = 555 kg
Correct answer is option 'C'. Can you explain this answer?
A fruit grower can use two types of fertilizer in his garden, brand P and brand Q. The amounts (in kg) of nitrogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicate that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine.
If the grower wants to maximise the amount of nitrogen added to the garden, how many bags of each brand should be added? What isthe maximum amount of nitrogen added?
a)
150 bags of brand P and 50 bags of brand Q; Maximum amount of nitrogen = 625 kg
b)
160 bags of brand P and 52 bags of brand Q; Maximum amount of nitrogen = 635 kg
c)
140 bags of brand P and 50 bags of brand Q; Maximum amount of nitrogen = 595 kg
d)
145 bags of brand P and 55 bags of brand Q; Maximum amount of nitrogen = 555 kg
|
Akash Shah answered |
Let the number of bags used for fertilizer of brand P = x And the number of bags used for fertilizer of brand Q = y . Here , Z = 3x + 3.5y subject to constraints : :1.5 x +2 y ≤ 310, x + 2y ≥ 240, 3x + 1.5y ≥ 270 , x,y ≥ 0
Here Z = 595 is maximum i.e. 140 bags of brand P and 50 bags of brand Q; Maximum amount of nitrogen = 595 kg .
Here Z = 595 is maximum i.e. 140 bags of brand P and 50 bags of brand Q; Maximum amount of nitrogen = 595 kg .
Maximize Z = 3x + 2y subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.- a)Maximum Z = 20 at (4, 3)
- b)Maximum Z = 22 at (4, 3)
- c)Maximum Z = 24 at (4, 3)
- d)Maximum Z = 18 at (4, 3)
Correct answer is option 'D'. Can you explain this answer?
Maximize Z = 3x + 2y subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
a)
Maximum Z = 20 at (4, 3)
b)
Maximum Z = 22 at (4, 3)
c)
Maximum Z = 24 at (4, 3)
d)
Maximum Z = 18 at (4, 3)
|
Dipika Choudhury answered |
Objective function is Z = 3x + 2 y ……………………(1).
The given constraints are : x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
The given constraints are : x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
The linear inequalities or equations or restrictions on the variables of a linear programming problem are called …… The conditions x ≥ 0 , y ≥ 0 are called …….- a)Objective functions, optimal value
- b)Constraints, non-negative restrictions
- c)Objective functions, non-negative restrictions
- d)Constraints, negative restrictions
Correct answer is option 'B'. Can you explain this answer?
The linear inequalities or equations or restrictions on the variables of a linear programming problem are called …… The conditions x ≥ 0 , y ≥ 0 are called …….
a)
Objective functions, optimal value
b)
Constraints, non-negative restrictions
c)
Objective functions, non-negative restrictions
d)
Constraints, negative restrictions
|
Abhay Chauhan answered |
Understanding Linear Programming Terms
Linear programming is a mathematical method used to maximize or minimize a linear objective function, subject to a set of linear inequalities or equations. In this context, it’s essential to differentiate between various components of the problem.
What are Constraints?
- Constraints are the linear inequalities or equations that limit the values of the variables in a linear programming problem.
- They define the feasible region, representing all possible solutions that satisfy these restrictions.
- For example, if we have constraints like x + y ≤ 10, this means that the sum of x and y cannot exceed 10.
What are Non-Negative Restrictions?
- The conditions x ≥ 0 and y ≥ 0 are referred to as non-negative restrictions.
- These ensure that the values of the variables are not negative, which is crucial in many real-world scenarios, such as production quantities or resource allocations.
- Non-negativity is integral to ensuring realistic and practical solutions in linear programming problems.
Why Option B is Correct?
- The correct answer is option 'B' because it appropriately labels the linear inequalities as "constraints" and the conditions x ≥ 0, y ≥ 0 as "non-negative restrictions."
- This terminology aligns with standard definitions in linear programming, making it crucial for understanding the problem structure and finding optimal solutions.
In summary, recognizing the terminology in linear programming helps clarify the problem and guides the approach to finding feasible and optimal solutions.
Linear programming is a mathematical method used to maximize or minimize a linear objective function, subject to a set of linear inequalities or equations. In this context, it’s essential to differentiate between various components of the problem.
What are Constraints?
- Constraints are the linear inequalities or equations that limit the values of the variables in a linear programming problem.
- They define the feasible region, representing all possible solutions that satisfy these restrictions.
- For example, if we have constraints like x + y ≤ 10, this means that the sum of x and y cannot exceed 10.
What are Non-Negative Restrictions?
- The conditions x ≥ 0 and y ≥ 0 are referred to as non-negative restrictions.
- These ensure that the values of the variables are not negative, which is crucial in many real-world scenarios, such as production quantities or resource allocations.
- Non-negativity is integral to ensuring realistic and practical solutions in linear programming problems.
Why Option B is Correct?
- The correct answer is option 'B' because it appropriately labels the linear inequalities as "constraints" and the conditions x ≥ 0, y ≥ 0 as "non-negative restrictions."
- This terminology aligns with standard definitions in linear programming, making it crucial for understanding the problem structure and finding optimal solutions.
In summary, recognizing the terminology in linear programming helps clarify the problem and guides the approach to finding feasible and optimal solutions.
A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4hours for assembling. The profit is Rs 5 each for type A and Rs 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize the profit?- a)8 Souvenir of types A and 27 of Souvenir of type B; Maximum profit = Rs 170
- b)9 Souvenir of types A and 21 of Souvenir of type B; Maximum profit = Rs 163
- c)8 Souvenir of types A and 20 of Souvenir of type B; Maximum profit = Rs 160
- d)7 Souvenir of types A and 210 of Souvenir of type B; Maximum profit = Rs 161
Correct answer is option 'C'. Can you explain this answer?
A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4hours for assembling. The profit is Rs 5 each for type A and Rs 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize the profit?
a)
8 Souvenir of types A and 27 of Souvenir of type B; Maximum profit = Rs 170
b)
9 Souvenir of types A and 21 of Souvenir of type B; Maximum profit = Rs 163
c)
8 Souvenir of types A and 20 of Souvenir of type B; Maximum profit = Rs 160
d)
7 Souvenir of types A and 210 of Souvenir of type B; Maximum profit = Rs 161
|
Mehul Chavan answered |
Let number of souvenirs of type A = x
And number of souvenirs of type B = y
Therefore , the above L.P.P. is given as :
Maximise , Z = 5x +6y , subject to the constraints : 5x +8y ≤ 200 and. 10x +8y ≤ 240 , x, y ≥ 0.
Here Z = 160 is maximum.
i.e. 8 Souvenir of types A and 20 of Souvenir of type B; Maximum profit = Rs 160.
And number of souvenirs of type B = y
Therefore , the above L.P.P. is given as :
Maximise , Z = 5x +6y , subject to the constraints : 5x +8y ≤ 200 and. 10x +8y ≤ 240 , x, y ≥ 0.
Here Z = 160 is maximum.
i.e. 8 Souvenir of types A and 20 of Souvenir of type B; Maximum profit = Rs 160.
Determine the maximum value of Z = 11x + 7y subject to the constraints :2x + y ≤ 6, x ≤ 2, x ≥ 0, y ≥ 0.- a)47
- b)45
- c)42
- d)43
Correct answer is option 'C'. Can you explain this answer?
Determine the maximum value of Z = 11x + 7y subject to the constraints :2x + y ≤ 6, x ≤ 2, x ≥ 0, y ≥ 0.
a)
47
b)
45
c)
42
d)
43
|
Ipsita Sen answered |
Here , maximize Z = 11x + 7y , subject to the constraints :2x + y ≤ 6, x ≤ 2, x ≥ 0, y ≥ 0.
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and a sprayer. It takes 2 hours on grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs 5 and that from a shade is Rs 3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximize his profit?- a)5 Pedestal lamps and 4 wooden shades; Maximum profit = Rs 35
- b)5 Pedestal lamps and 5 wooden shades; Maximum profit = Rs 38
- c)4 Pedestal lamps and 4 wooden shades; Maximum profit = Rs 32
- d)4 Pedestal lamps and 5 wooden shades; Maximum profit = Rs 36
Correct answer is option 'C'. Can you explain this answer?
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and a sprayer. It takes 2 hours on grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs 5 and that from a shade is Rs 3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximize his profit?
a)
5 Pedestal lamps and 4 wooden shades; Maximum profit = Rs 35
b)
5 Pedestal lamps and 5 wooden shades; Maximum profit = Rs 38
c)
4 Pedestal lamps and 4 wooden shades; Maximum profit = Rs 32
d)
4 Pedestal lamps and 5 wooden shades; Maximum profit = Rs 36
|
Bhavana Das answered |
Let number of pedestal lamps manufactured = x
And number of wooden shades manufactured = y
Therefore , the above L.P.P. is given as :
Maximise , Z = 5x +3y , subject to the constraints : 2x +y ≤ 12 and. 3x +2y ≤ 20 , x, y ≥ 0.
Here Z = 32 is maximum.
i.e 30 packages of screws A and 20 packages of screws B; Maximum profit = Rs 410.
i.e. 4 Pedestal lamps and 4 wooden shades; Maximum profit = Rs 32 .
And number of wooden shades manufactured = y
Therefore , the above L.P.P. is given as :
Maximise , Z = 5x +3y , subject to the constraints : 2x +y ≤ 12 and. 3x +2y ≤ 20 , x, y ≥ 0.
Here Z = 32 is maximum.
i.e 30 packages of screws A and 20 packages of screws B; Maximum profit = Rs 410.
i.e. 4 Pedestal lamps and 4 wooden shades; Maximum profit = Rs 32 .
A factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines tomanufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of Rs 7 and screws B at a profit of Rs 10. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximize his profit? Determine the maximum profit.- a)32 packages of screws A and 22 packages of screws B; Maximum profit = Rs 414
- b)32 packages of screws A and 20 packages of screws B; Maximum profit = Rs 412
- c)30 packages of screws A and 20 packages of screws B; Maximum profit = Rs 410
- d)30 packages of screws A and 22 packages of screws B; Maximum profit = Rs 412
Correct answer is option 'C'. Can you explain this answer?
A factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines tomanufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of Rs 7 and screws B at a profit of Rs 10. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximize his profit? Determine the maximum profit.
a)
32 packages of screws A and 22 packages of screws B; Maximum profit = Rs 414
b)
32 packages of screws A and 20 packages of screws B; Maximum profit = Rs 412
c)
30 packages of screws A and 20 packages of screws B; Maximum profit = Rs 410
d)
30 packages of screws A and 22 packages of screws B; Maximum profit = Rs 412
|
|
Akash Shah answered |
Let number of packages of screws A produced = x
And number of packages of screws B produced = y
Therefore , the above L.P.P. is given as :
Maximise , Z = 7x +10y , subject to the constraints : 4x +6y ≤ 240 and. 6x +3y ≤ 240 i.e. 2x +3y ≤ 120 and 2x +y ≤ 80 , x, y ≥ 0.
i.e 30 packages of screws A and 20 packages of screws B; Maximum profit = Rs 410.
And number of packages of screws B produced = y
Therefore , the above L.P.P. is given as :
Maximise , Z = 7x +10y , subject to the constraints : 4x +6y ≤ 240 and. 6x +3y ≤ 240 i.e. 2x +3y ≤ 120 and 2x +y ≤ 80 , x, y ≥ 0.
i.e 30 packages of screws A and 20 packages of screws B; Maximum profit = Rs 410.
In linear programming feasible region (or solution region) for the problem is- a)The common region determined by all the constraints including the non – negative constraints x ⩾ 0, y⩾ 0
- b)The common region determined by all the x ⩾ 0 and the objective function
- c)The common region determined by all the objective functions including the non – negative constraints x ⩾ 0, y ⩾ 0
- d)The common region determined by all the x ⩾ 0, y ⩾ 0 and the objective function
Correct answer is option 'A'. Can you explain this answer?
In linear programming feasible region (or solution region) for the problem is
a)
The common region determined by all the constraints including the non – negative constraints x ⩾ 0, y⩾ 0
b)
The common region determined by all the x ⩾ 0 and the objective function
c)
The common region determined by all the objective functions including the non – negative constraints x ⩾ 0, y ⩾ 0
d)
The common region determined by all the x ⩾ 0, y ⩾ 0 and the objective function
|
|
Sanchita Iyer answered |
In linear programming feasible region (or solution region) for the problem is given by The common region determined by all the constraints including the non – negative constraints x ⩾0, y ⩾ 0
An oil company has two depots A and B with capacities of 7000 L and 4000 L respectively. The company is to supply oil to three petrol pumps, D, E and F whose requirements are 4500L, 3000L and 3500L respectively. The distances (in km) between the depots and the petrol pumps is given in the following table: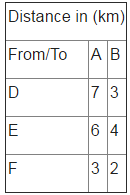
Assuming that the transportation cost of 10 litres of oil is Re 1 per km, how should the delivery be scheduled in order that the transportation cost is minimum?What is the minimum cost?- a)From A: 550, 3000 and 3500 litres; From B: 4000, 0, 0 litres to D, E and F respectively; Minimum cost = Rs 4800
- b)From A: 540, 3000 and 3500 litres; From B: 4000, 0, 0 litres to D, E and F respectively; Minimum cost = Rs 4700
- c)From A: 500, 3000 and 3500 litres; From B: 4000, 0, 0 litres to D, E and F respectively; Minimum cost = Rs 4400
- d)From A: 520, 3000 and 3500 litres; From B: 4000, 0, 0 litres to D, E and F respectively; Minimum cost = Rs 4600
Correct answer is option 'C'. Can you explain this answer?
An oil company has two depots A and B with capacities of 7000 L and 4000 L respectively. The company is to supply oil to three petrol pumps, D, E and F whose requirements are 4500L, 3000L and 3500L respectively. The distances (in km) between the depots and the petrol pumps is given in the following table:
Assuming that the transportation cost of 10 litres of oil is Re 1 per km, how should the delivery be scheduled in order that the transportation cost is minimum?What is the minimum cost?
a)
From A: 550, 3000 and 3500 litres; From B: 4000, 0, 0 litres to D, E and F respectively; Minimum cost = Rs 4800
b)
From A: 540, 3000 and 3500 litres; From B: 4000, 0, 0 litres to D, E and F respectively; Minimum cost = Rs 4700
c)
From A: 500, 3000 and 3500 litres; From B: 4000, 0, 0 litres to D, E and F respectively; Minimum cost = Rs 4400
d)
From A: 520, 3000 and 3500 litres; From B: 4000, 0, 0 litres to D, E and F respectively; Minimum cost = Rs 4600
|
Prisha Yadav answered |
Here objective function is : Z = 3x + y + 39500 , subject to constraints : : x + y ≤ 7000, x ≤ 4500, x + y ≥ 3500, , y ≤ 3000x , x,y ≥ 0
Here Z = 4400 is minimum.i.e. . From A: 500, 3000 and 3500 litres; From B: 4000, 0, 0 litres to D, E and F respectively; Minimum cost = Rs 4400 .
Here Z = 4400 is minimum.i.e. . From A: 500, 3000 and 3500 litres; From B: 4000, 0, 0 litres to D, E and F respectively; Minimum cost = Rs 4400 .
Minimize Z = 3x + 5y such that x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0.- a)Minimum Z = 7 at 3/2,1/2
- b)Minimum Z = 8 at 3/2,1/2
- c)Minimum Z = 9 at 3/2,1/2 110 V 60 Hz
- d)Minimum Z = 10 at 3/2,1/2
Correct answer is option 'A'. Can you explain this answer?
Minimize Z = 3x + 5y such that x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0.
a)
Minimum Z = 7 at 3/2,1/2
b)
Minimum Z = 8 at 3/2,1/2
c)
Minimum Z = 9 at 3/2,1/2 110 V 60 Hz
d)
Minimum Z = 10 at 3/2,1/2
|
Mira Roy answered |
Objective function is Z = 3x + 5 y ……………………(1).
The given constraints are : x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0 .
The given constraints are : x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0 .
Infeasibility means that the number of solutions to the linear programming models that satisfies all constraints is- a)At least 1
- b)An infinite number
- c)Zero
- d)At least 2
Correct answer is option 'C'. Can you explain this answer?
Infeasibility means that the number of solutions to the linear programming models that satisfies all constraints is
a)
At least 1
b)
An infinite number
c)
Zero
d)
At least 2
|
|
Ujwal Choudhury answered |
Infeasibility in linear programming models refers to a situation where there are no feasible solutions that satisfy all the constraints. Let's understand this concept in detail.
Feasible Solution:
A feasible solution in linear programming is a solution that satisfies all the given constraints. It is a point that lies within the feasible region, which is defined by the intersection of all the constraints.
Infeasible Solution:
On the other hand, an infeasible solution is a solution that violates one or more constraints. It is a point that lies outside the feasible region and cannot be achieved given the constraints.
Number of Solutions:
Now, let's discuss the number of solutions to a linear programming model that satisfies all the constraints. This can be classified into four possibilities:
1. At least 1 solution: In some cases, there may be only one feasible solution that satisfies all the constraints. This means that there is a unique optimal solution to the linear programming problem.
2. An infinite number of solutions: In certain situations, there might be an infinite number of feasible solutions that satisfy all the constraints. This occurs when the constraints are not restrictive enough to define a unique solution.
3. Zero solutions (Infeasible): Infeasibility occurs when there are no feasible solutions that satisfy all the constraints. This happens when the constraints are contradictory or when they overlap in such a way that no feasible region exists.
4. At least 2 solutions: It is possible to have multiple feasible solutions that satisfy all the constraints. In such cases, the objective function may have multiple optimal solutions, and the decision-maker can choose any of them.
Correct Answer:
In the given question, the correct answer is option 'C', which states that the number of solutions to the linear programming models that satisfy all the constraints is zero. This means that the given constraints are contradictory or overlapping in such a way that no feasible solution exists.
By understanding the concept of infeasibility and the possible number of solutions in linear programming, we can analyze the feasibility of a problem and determine whether it is solvable or not.
Feasible Solution:
A feasible solution in linear programming is a solution that satisfies all the given constraints. It is a point that lies within the feasible region, which is defined by the intersection of all the constraints.
Infeasible Solution:
On the other hand, an infeasible solution is a solution that violates one or more constraints. It is a point that lies outside the feasible region and cannot be achieved given the constraints.
Number of Solutions:
Now, let's discuss the number of solutions to a linear programming model that satisfies all the constraints. This can be classified into four possibilities:
1. At least 1 solution: In some cases, there may be only one feasible solution that satisfies all the constraints. This means that there is a unique optimal solution to the linear programming problem.
2. An infinite number of solutions: In certain situations, there might be an infinite number of feasible solutions that satisfy all the constraints. This occurs when the constraints are not restrictive enough to define a unique solution.
3. Zero solutions (Infeasible): Infeasibility occurs when there are no feasible solutions that satisfy all the constraints. This happens when the constraints are contradictory or when they overlap in such a way that no feasible region exists.
4. At least 2 solutions: It is possible to have multiple feasible solutions that satisfy all the constraints. In such cases, the objective function may have multiple optimal solutions, and the decision-maker can choose any of them.
Correct Answer:
In the given question, the correct answer is option 'C', which states that the number of solutions to the linear programming models that satisfy all the constraints is zero. This means that the given constraints are contradictory or overlapping in such a way that no feasible solution exists.
By understanding the concept of infeasibility and the possible number of solutions in linear programming, we can analyze the feasibility of a problem and determine whether it is solvable or not.
In a LPP, the linear inequalities or restrictions on the variables are called- a)Inequalities
- b)Linear constraints
- c)Constraints
- d)Limits
Correct answer is option 'B'. Can you explain this answer?
In a LPP, the linear inequalities or restrictions on the variables are called
a)
Inequalities
b)
Linear constraints
c)
Constraints
d)
Limits
|
|
Sushant Khanna answered |
In a LPP, the linear inequalities or restrictions on the variables are called Linear constraints
Two godowns A and B have grain capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:
How should the supplies be transported in order that the transportation cost is minimum? What is the minimum cost?- a)From A : 12,52, 40 units; From B: 50,0,0 units to D, E and F respectively and minimum cost = Rs 530
- b)From A : 10,52, 42 units; From B: 50,0,0 units to D, E and F respectively and minimum cost = Rs 550
- c)From A : 10,50, 40 units; From B: 50,0,0 units to D, E and F respectively and minimum cost = Rs 510
- d)From A : 10,53, 44 units; From B: 50,0,0 units to D, E and F respectively and minimum cost = Rs 570
Correct answer is option 'C'. Can you explain this answer?
Two godowns A and B have grain capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:
How should the supplies be transported in order that the transportation cost is minimum? What is the minimum cost?
a)
From A : 12,52, 40 units; From B: 50,0,0 units to D, E and F respectively and minimum cost = Rs 530
b)
From A : 10,52, 42 units; From B: 50,0,0 units to D, E and F respectively and minimum cost = Rs 550
c)
From A : 10,50, 40 units; From B: 50,0,0 units to D, E and F respectively and minimum cost = Rs 510
d)
From A : 10,53, 44 units; From B: 50,0,0 units to D, E and F respectively and minimum cost = Rs 570
|
|
Ujwal Chawla answered |
Let the number of units of grain transported from godown A to D = x And the number of units of grain transported from godown A to E = y Therefore , the number of units of grain transported from godown A to F = 100 – (x+y) Therefore , the number of units of grain transported from godown B to D = 60 – x The number of units of grain transported from godown B to E = 50 – y The number of units of grain transported from godown B to F = x + y – 60 . Here , the objective function is :Minimise Z = 2.5x + 1.5y + 410 . , subject to constraints : 60 - x ≥ 0,50 - y ≥ 0 ,100 – (x + y) ≥ 0 , (x + y) - 60 ≥ 0 , x,y ≥ 0.
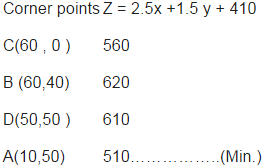
Here Z = 510 is minimum.i.e. From A : 10,50, 40 units; From B: 50,0,0 units to D, E and F respectively and minimum cost = Rs 510 .
Here Z = 510 is minimum.i.e. From A : 10,50, 40 units; From B: 50,0,0 units to D, E and F respectively and minimum cost = Rs 510 .
Shape of feasible region formed by following constraints is 4x + y ≥ 20, 2x + 3y ≥ 30, x, y ≥ 0.- a)Trapezium
- b)Triangular region
- c)Unbounded region and shape is not fixed
- d)No feasible region
Correct answer is option 'C'. Can you explain this answer?
Shape of feasible region formed by following constraints is 4x + y ≥ 20, 2x + 3y ≥ 30, x, y ≥ 0.
a)
Trapezium
b)
Triangular region
c)
Unbounded region and shape is not fixed
d)
No feasible region
|
Divyansh Mukherjee answered |
Understanding the Constraints
To analyze the feasible region formed by the constraints:
1. 4x + y ≤ 20
2. 2x + 3y ≤ 30
3. x ≥ 0
4. y ≥ 0
We must first examine each constraint graphically.
Graphical Representation
- The line 4x + y = 20 intersects the axes at points (5, 0) and (0, 20).
- The line 2x + 3y = 30 intersects the axes at points (15, 0) and (0, 10).
Feasible Region Analysis
- The feasible region is the area where all constraints overlap and is bounded by these lines and the axes.
- Both constraints, when graphed, create a region that is not fully enclosed due to the nature of the lines and the positive quadrant restrictions.
Unbounded Region
- As you continue to extend the lines, you will notice that the feasible region expands infinitely in at least one direction.
- The region is unbounded because the lines do not intersect in a way that closes off the area completely.
Conclusion
- Since the feasible region does not form a complete and closed shape, it is classified as an unbounded region.
- Thus, the correct answer is option 'C': Unbounded region and shape is not fixed.
This means that while the constraints limit the values of x and y, they do not create a bounded area, confirming the nature of the feasible region.
To analyze the feasible region formed by the constraints:
1. 4x + y ≤ 20
2. 2x + 3y ≤ 30
3. x ≥ 0
4. y ≥ 0
We must first examine each constraint graphically.
Graphical Representation
- The line 4x + y = 20 intersects the axes at points (5, 0) and (0, 20).
- The line 2x + 3y = 30 intersects the axes at points (15, 0) and (0, 10).
Feasible Region Analysis
- The feasible region is the area where all constraints overlap and is bounded by these lines and the axes.
- Both constraints, when graphed, create a region that is not fully enclosed due to the nature of the lines and the positive quadrant restrictions.
Unbounded Region
- As you continue to extend the lines, you will notice that the feasible region expands infinitely in at least one direction.
- The region is unbounded because the lines do not intersect in a way that closes off the area completely.
Conclusion
- Since the feasible region does not form a complete and closed shape, it is classified as an unbounded region.
- Thus, the correct answer is option 'C': Unbounded region and shape is not fixed.
This means that while the constraints limit the values of x and y, they do not create a bounded area, confirming the nature of the feasible region.
Chapter doubts & questions for Linear Programming - Applied Mathematics for Class 12 2025 is part of Commerce exam preparation. The chapters have been prepared according to the Commerce exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Commerce 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Linear Programming - Applied Mathematics for Class 12 in English & Hindi are available as part of Commerce exam.
Download more important topics, notes, lectures and mock test series for Commerce Exam by signing up for free.
Applied Mathematics for Class 12
64 videos|110 docs|63 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup