All Exams >
Commerce >
Applied Mathematics for Class 12 >
All Questions
All questions of Pipes and Cisterns for Commerce Exam
.
- a)A
- b)B
- c)C
- d)D
Correct answer is option 'D'. Can you explain this answer?
a)
A
b)
B
c)
C
d)
D
|
Notes Wala answered |
(A + B)'s 1 hour's work =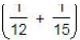 
= 9/60 = 3/20.
(A+C)'s hour's work =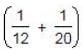
= 8/60 = 2/15.
Part filled in 2 hrs =
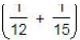= 9/60 = 3/20.(A+C)'s hour's work =
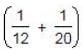= 8/60 = 2/15.Part filled in 2 hrs =
Part filled in 6 hrs =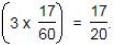 
Remaining part =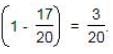
Now, it is the turn of A and B and 3/20 part is filled by A and B in 1 hour.
∴ Total time taken to fill the tank = (6+1) hrs = 7 hrs
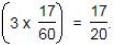
Remaining part =
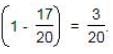
Now, it is the turn of A and B and 3/20 part is filled by A and B in 1 hour.
∴ Total time taken to fill the tank = (6+1) hrs = 7 hrs
A tap can fill a tank in 4 hours. After half the tank is filled, two more similar taps are opened. What is the total time taken to fill the tank completely?
- a)1 hr 20 min
- b)4 hr
- c)3 hr
- d)2 hr 40 min
Correct answer is option 'D'. Can you explain this answer?
A tap can fill a tank in 4 hours. After half the tank is filled, two more similar taps are opened. What is the total time taken to fill the tank completely?
a)
1 hr 20 min
b)
4 hr
c)
3 hr
d)
2 hr 40 min
|
Ishani Rane answered |
Explanation :
A tap can fill a tank in 4 hours
= The tap can fill half the tank in 2 hours
Remaining part = 1/2
After half the tank is filled, three more similar taps are opened.
Hence, total number of taps becomes 4.
Part filled by one tap in 1 hour = 1/4
Part filled by four taps in 1 hour =
4*1/4=1
i.e., 4 taps can fill remaining half in 40 minutes
total time taken = 2 hour + 40 minute = 2 hour 40 minutes
A tap can fill a tank in 4 hours. After half the tank is filled, three more similar taps are opened. What is the total time taken to fill the tank completely?
- a)3 hr
- b)1 hr 30 min
- c)2 hr 30 min
- d)2 hr
Correct answer is option 'C'. Can you explain this answer?
a)
3 hr
b)
1 hr 30 min
c)
2 hr 30 min
d)
2 hr
|
Aditya Kumar answered |
Time taken by one tap to fill half of the tank = 3 hrs.
Part filled by the four taps in 1 hour =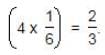
Remaining part =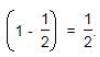
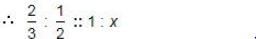
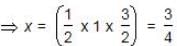hours i.e, 45 mins.
So, total time taken = 3 hrs. 45 mins.
Part filled by the four taps in 1 hour =
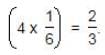
Remaining part =
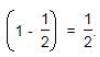
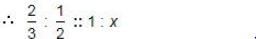
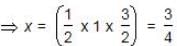hours i.e, 45 mins.So, total time taken = 3 hrs. 45 mins.
Bucket P has thrice the capacity as bucket Q. It takes 80 turns for bucket P to fill the empty drum. How many turns it will take for both the buckets P and Q, having each turn together to fill the empty drum?
a) 30
b) 45
c) 60
d) 80
Correct answer is option 'C'. Can you explain this answer?
|
Sameer Rane answered |
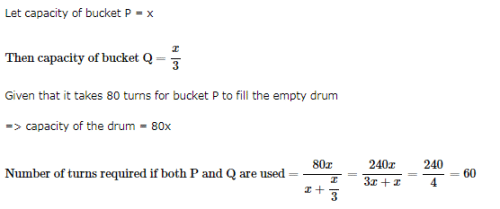
A large tanker can be filled by two pipes A and B in 60 minutes and 40 minutes respectively. How many minutes will it take to fill the tanker from empty state if B is used for half the time and A and B fill it together for the other half?
- a)15 min
- b)20 min
- c)27.5 min
- d)30 min
Correct answer is option 'D'. Can you explain this answer?
a)
15 min
b)
20 min
c)
27.5 min
d)
30 min
|
Pallabi Deshpande answered |
A = 60 2 120
B = 40 3 120
Suppose it will take x minute
3x/2 + 5x/2 = 120
8x=240
x = 30 min
A leak in the bottom of a tank can empty the full tank in 6 hours. An inlet pipe fills water at the rate of 4 liters a minute. When the tank is full, the inlet is opened and due to the leak, the tank is empty in 24 hours. How many liters does the cistern hold?
- a)4010 litre
- b)2220 litre
- c)1920 litre
- d)2020 litre
Correct answer is option 'C'. Can you explain this answer?
a)
4010 litre
b)
2220 litre
c)
1920 litre
d)
2020 litre
|
Dhruv Mehra answered |
Two taps A and B can fill a tank in 5 hours and 20 hours respectively. If both the taps are open then due to a leakage, it took 40 minutes more to fill the tank. If the tank is full, how long will it take for the leakage alone to empty the tank?
- a)28 hr
- b)16 hr
- c)22 hr
- d)32 hr
Correct answer is option 'A'. Can you explain this answer?
a)
28 hr
b)
16 hr
c)
22 hr
d)
32 hr
|
|
Pallabi Deshpande answered |
Three pipes A, B and C can fill a tank in 6 hours. After working at it together for 2 hours, C is closed and A and B can fill the remaining part in 7 hours. The number of hours taken by C alone to fill the tank is:
- a)10
- b)12
- c)14
- d)16
Correct answer is option 'C'. Can you explain this answer?
a)
10
b)
12
c)
14
d)
16
|
|
Pallabi Deshpande answered |
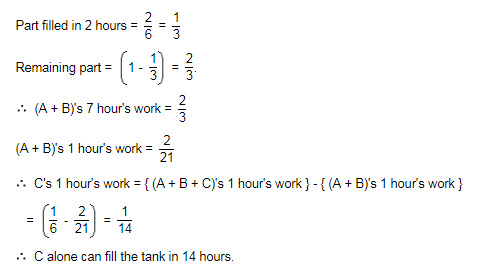
Two pipes A and B together can fill a cistern in 4 hours. Had they been opened separately, then B would have taken 6 hours more than A to fill the cistern. How much time will be taken by A to fill the cistern separately?- a)6 hours
- b)4 hours
- c)2 hours
- d)3 hours
Correct answer is option 'A'. Can you explain this answer?
Two pipes A and B together can fill a cistern in 4 hours. Had they been opened separately, then B would have taken 6 hours more than A to fill the cistern. How much time will be taken by A to fill the cistern separately?
a)
6 hours
b)
4 hours
c)
2 hours
d)
3 hours
|
Arnav Sen answered |
Given Information:
- Together, pipes A and B can fill the cistern in 4 hours.
- If opened separately, pipe B takes 6 hours more than pipe A to fill the cistern.
Let's Assume:
- Let the time taken by pipe A to fill the cistern separately be x hours.
- Therefore, the time taken by pipe B to fill the cistern separately would be (x + 6) hours.
Calculations:
- The combined rate of pipes A and B = 1/4 cistern per hour (since they can fill the cistern in 4 hours together)
- The individual rate of pipe A = 1/x cistern per hour
- The individual rate of pipe B = 1/(x + 6) cistern per hour
- According to the given information, the sum of individual rates of A and B is equal to their combined rate:
1/x + 1/(x + 6) = 1/4
- Solving the above equation, we get:
(x + 6 + x) / (x(x + 6)) = 1/4
(2x + 6) / (x^2 + 6x) = 1/4
8x + 24 = x^2 + 6x
x^2 - 2x - 24 = 0
(x - 6)(x + 4) = 0
x = 6 or x = -4
Conclusion:
- Since time cannot be negative, the time taken by pipe A to fill the cistern separately is 6 hours (option A).
Two pipes A and B can fill a tank in 15 minutes and 40 minutes respectively. Both the pipes are opened together but after 4 minutes, pipe A is turned off. What is the total time required to fill the tank?- a)10 min 10 sec
- b)25 min 20 sec
- c)29 min 20 sec
- d)20 min 10 sec
Correct answer is option 'C'. Can you explain this answer?
Two pipes A and B can fill a tank in 15 minutes and 40 minutes respectively. Both the pipes are opened together but after 4 minutes, pipe A is turned off. What is the total time required to fill the tank?
a)
10 min 10 sec
b)
25 min 20 sec
c)
29 min 20 sec
d)
20 min 10 sec
|
|
Aman Roy answered |
Three pipes A, B and C can fill a tank from empty to full in 30 minutes, 20 minutes, and 10 minutes respectively. When the tank is empty, all the three pipes are opened. A, B and C discharge chemical solutions P,Q and R respectively. What is the proportion of the solution R in the liquid in the tank after 3 minutes?- a)6/11
- b)5/11
- c)8/11
- d)7/11
Correct answer is option 'A'. Can you explain this answer?
Three pipes A, B and C can fill a tank from empty to full in 30 minutes, 20 minutes, and 10 minutes respectively. When the tank is empty, all the three pipes are opened. A, B and C discharge chemical solutions P,Q and R respectively. What is the proportion of the solution R in the liquid in the tank after 3 minutes?
a)
6/11
b)
5/11
c)
8/11
d)
7/11
|
|
Aarav Menon answered |
Part of the tank filled by pipe A in 1 minute =1/30
Part of the tank filled by pipe B in 1 minute =1/20
Part of the tank filled by pipe C in 1 minute =1/10
Here we have to find the proportion of the solution R.
Pipe C discharges chemical solution R.
Part of the tank filled by pipe B in 1 minute =1/20
Part of the tank filled by pipe C in 1 minute =1/10
Here we have to find the proportion of the solution R.
Pipe C discharges chemical solution R.
A tank is filled by three pipes with uniform flow. The first two pipes operating simultaneously fill the tank in the same time during which the tank is filled by the third pipe alone. The second pipe fills the tank 5 hours faster than the first pipe and 4 hours slower than the third pipe. Time required by the first pipe to fill the tank is- a)30 hours
- b)15 hours
- c)10 hours
- d)6 hours
Correct answer is option 'B'. Can you explain this answer?
A tank is filled by three pipes with uniform flow. The first two pipes operating simultaneously fill the tank in the same time during which the tank is filled by the third pipe alone. The second pipe fills the tank 5 hours faster than the first pipe and 4 hours slower than the third pipe. Time required by the first pipe to fill the tank is
a)
30 hours
b)
15 hours
c)
10 hours
d)
6 hours
|
|
Raghav Choudhary answered |
We can not take the value x=3 because, (x−9) becomes negative which is not possible, because the third pipe can fill the tank in (x−9) hours.
Hence, x=15
Hence, x=15
A cistern can be filled by a tap in 3 hours while it can be emptied by another tap in 8 hours. If both the taps are opened simultaneously, then after how much time will the cistern get filled?
- a)4.8 hr
- b)2.4 hr
- c)3.6 hr
- d)1.8 hr
Correct answer is option 'A'. Can you explain this answer?
a)
4.8 hr
b)
2.4 hr
c)
3.6 hr
d)
1.8 hr
|
|
Dhruv Mehra answered |
One pipe can fill a tank four times as fast as another pipe. If together the two pipes can fill the tank in 36 minutes, then the slower pipe alone will be able to fill the tank in:- a)144 min
- b)180 min
- c)126 min
- d)114 min
Correct answer is option 'B'. Can you explain this answer?
One pipe can fill a tank four times as fast as another pipe. If together the two pipes can fill the tank in 36 minutes, then the slower pipe alone will be able to fill the tank in:
a)
144 min
b)
180 min
c)
126 min
d)
114 min
|
|
Mainak Saha answered |
Suppose the slower pipe can fill the tank in x minutes.
Then the faster pipe can fill in x/4 minutes.
Part filled by the slower pipe in 1 min =1/x
Part filled by the faster pipe in 1 min =4/x
Part filled by the both the pipes in 1 min =1/x +4/x
Therefore, both the pipes can fill together in 36 minutes.
Part filled by both in 1 minute = 1/36.
1/x + 4/x = 1/36
5/x = 1/36
x = 5 * 36 = 180
Then the faster pipe can fill in x/4 minutes.
Part filled by the slower pipe in 1 min =1/x
Part filled by the faster pipe in 1 min =4/x
Part filled by the both the pipes in 1 min =1/x +4/x
Therefore, both the pipes can fill together in 36 minutes.
Part filled by both in 1 minute = 1/36.
1/x + 4/x = 1/36
5/x = 1/36
x = 5 * 36 = 180
Two pipes can fill a tank in 25 and 30 minutes respectively and a waste pipe can empty 3 gallons per minute. All the three pipes working together can fill the tank in 15 minutes. The capacity of the tank is:- a)250 gallons
- b)450 gallons
- c)120 gallons
- d)150 gallons
Correct answer is option 'B'. Can you explain this answer?
Two pipes can fill a tank in 25 and 30 minutes respectively and a waste pipe can empty 3 gallons per minute. All the three pipes working together can fill the tank in 15 minutes. The capacity of the tank is:
a)
250 gallons
b)
450 gallons
c)
120 gallons
d)
150 gallons
|
|
Deepak Basu answered |
Two pipes A and B can fill a tank in 12 and 24 minutes respectively. If both the pipes are used together, then how long will it take to fill the tank?- a)9 min
- b)8 min
- c)6 min
- d)4 min
Correct answer is option 'B'. Can you explain this answer?
Two pipes A and B can fill a tank in 12 and 24 minutes respectively. If both the pipes are used together, then how long will it take to fill the tank?
a)
9 min
b)
8 min
c)
6 min
d)
4 min
|
|
Deepak Basu answered |
Learn all concepts & tricks of Pipes and Cisterns by going through the doc
hours to fill the tank. The leak can drain all the water of the tank in
minutes and 45 minutes respectively. Both pipes are opened. The cistern will be filled in just half an hour, if pipe B is turned off after
Chapter doubts & questions for Pipes and Cisterns - Applied Mathematics for Class 12 2025 is part of Commerce exam preparation. The chapters have been prepared according to the Commerce exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Commerce 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Pipes and Cisterns - Applied Mathematics for Class 12 in English & Hindi are available as part of Commerce exam.
Download more important topics, notes, lectures and mock test series for Commerce Exam by signing up for free.
Applied Mathematics for Class 12
58 videos|110 docs|63 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup