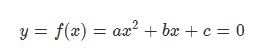All Exams >
Interview Preparation >
Quantitative Aptitude (Quant) >
All Questions
All questions of Functions for Interview Preparation Exam
If f(t) = 2t, then f(0), f(1), f(2) are in
- a)AP
- b)HP
- c)GP
- d)Cannot be said
Correct answer is option 'C'. Can you explain this answer?
If f(t) = 2t, then f(0), f(1), f(2) are in
a)
AP
b)
HP
c)
GP
d)
Cannot be said
|
Vikas Kushwaha answered |
F(0),f(1),f(2) are in APf(0)=0f(1)=2f(2)=4 so, 0,2,4,can not in GP
The minimum value of ax2 + bx + c is 7/8 at x = 5/4. Find the value of the expression at x = 5, ifthe value of the expression at x = 1 is 1.
- a)75
- b)29
- c)121
- d)129
Correct answer is option 'B'. Can you explain this answer?
The minimum value of ax2 + bx + c is 7/8 at x = 5/4. Find the value of the expression at x = 5, ifthe value of the expression at x = 1 is 1.
a)
75
b)
29
c)
121
d)
129
|
Maulik Rane answered |
The expression is 2x2 – 5x + 4, and its value at x = 5 would be equal to 100 – 25 + 4 = 79. Option
(b) is correct.
(b) is correct.
f(x*y) = f(x) + f(y)f(2401) = 103 and f(729) = 18then f(343√3) = ?- a)2
- b)3
- c)4
- d)5
Correct answer is option 'C'. Can you explain this answer?
f(x*y) = f(x) + f(y)
f(2401) = 103 and f(729) = 18
then f(343√3) = ?
a)
2
b)
3
c)
4
d)
5
|
Anaya Patel answered |
Given, f(2401) = 10/3
⇒ f(49*49) = 10/3
⇒ f(49) + f(49) = 10/3
⇒ 2 * f(49) = 10/3
⇒ 2 * f(7*7) = 10/3
⇒ 2 * [f(7) + f(7)] = 10/3
⇒ 4 * f(7) = 10/3
⇒ f(7) = 5/6
Also given that, f(729) = 18
⇒ f(36) = 18
⇒ f((√3)12) = 18
f(√3)12) can be re-written as: f [(√3)6 * (√3)6)] = f [(√3)6]+ f [(√3)6]
f [(√3)6)] can be re-written as: f [(√3)3 * (√3)3] = f [(√3)3)] + f [(√3)3]
f((√3)3) can be re-written as: f [(√3)2 * √3)] = f((√3)2) + f((√3))
f(√3)2 can be re-written as: f(√3 * √3) = f(√3) + f(√3)
So, f(√3)12) can also be expressed as:
f(√3) + f(√3) + f(√3) + f(√3) + ... upto 12 terms = 12 * f(√3)
So, 12 * f(√3) = 18
⇒ f(√3) = 3/2
So, f(343 * √3) = f(343) + f(√3)
= f(73) + f(√3)
= 3*f(7) + f(√3)
= 3 * 5/6 + 3/2
= 4
Let f(x) be a function satisfying f(x) f(y) = f (xy) for all real x, y. If f (2) = 4, then what is the value of f (1/2)?- a)0
- b)1/4
- c)1/2
- d)1
- e)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
Let f(x) be a function satisfying f(x) f(y) = f (xy) for all real x, y. If f (2) = 4, then what is the value of f (1/2)?
a)
0
b)
1/4
c)
1/2
d)
1
e)
Cannot be determined
|
Bank Exams India answered |
We need to find f(1/2).
According to the question, f(x) * f(y) = f(xy).
So, f(2) * f(1/2) = f(2*1/2) = f(1). ----------------(i)
But we do not know f(1).
Using the same formula, f(1)*f(2) = f(1*2) ;
According to the question, f(x) * f(y) = f(xy).
So, f(2) * f(1/2) = f(2*1/2) = f(1). ----------------(i)
But we do not know f(1).
Using the same formula, f(1)*f(2) = f(1*2) ;
i.e. f(1)*f(2) = f(2) f(1) = 1.
Substituting for f(1) in (i), we get f(2) * f(1/2) = 1.
f(2) = 4, so f(1/2) = 1/4.
f(2) = 4, so f(1/2) = 1/4.
The function f(x) = | x - 2| + | 2.5 - x| + |3.6 - x|, where x is a real number, attains a minimum at - a)x=2.3
- b)x=2.5
- c)x=2.4
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
The function f(x) = | x - 2| + | 2.5 - x| + |3.6 - x|, where x is a real number, attains a minimum at
a)
x=2.3
b)
x=2.5
c)
x=2.4
d)
None of the above
|
Rhea Reddy answered |
The best way of doing this question is to substitute the value of x in the option to the given expression in f(x).
We get the minimum value of 1.6 for f(x) when x=2.5.
Now, there is a question whether the minimum value of the expression can be lesser than this.
In order to resolve the ambiguity,plot f(x) vs x in the graph for x=1,2,3,4 and so on.
We find that the minimum value is acheived at x=2.5.
Hence option(2) is the answer.
Define the following functions:
(a) (a M b) = a – b (b) (a D b) = a + b
(c) (a H b) = (ab) (d) (a P b) = a/bQ.Which of the following functions will represent a2 – b2?- a)(a M b) H (a D b)
- b)(a H b) M (a P b)
- c)(a D b)/(a M b)
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Define the following functions:
(a) (a M b) = a – b (b) (a D b) = a + b
(c) (a H b) = (ab) (d) (a P b) = a/b
(a) (a M b) = a – b (b) (a D b) = a + b
(c) (a H b) = (ab) (d) (a P b) = a/b
Q.
Which of the following functions will represent a2 – b2?
a)
(a M b) H (a D b)
b)
(a H b) M (a P b)
c)
(a D b)/(a M b)
d)
None of these
|
|
Anaya Patel answered |
Option a = (a – b) (a + b) = a2 – b2
A function f(x) satisfies f(1) = 3600, and f(1) + f(2) +...+ f(n) = n² f(n), for all positive integers n > 1. What is the value of f(9) ?- a)80
- b)240
- c)200
- d)100
- e)120
Correct answer is option 'A'. Can you explain this answer?
A function f(x) satisfies f(1) = 3600, and f(1) + f(2) +...+ f(n) = n² f(n), for all positive integers n > 1. What is the value of f(9) ?
a)
80
b)
240
c)
200
d)
100
e)
120
|
Naroj Boda answered |
f(1) = 3600 , f(1) + f(2) = 4 * f(2).
f(2) = f(1)/3. We can write this as f(2) = f(1) * 1/3.
Now, f(1) + f(2) + f(3) = 9 * f(3).
f(3) = f(1) + f(2) / 8. We know f(2) = f(1) / 3.
So, f(3) = f(1) + (f(1)/3) / 8.
We can write this as f(3) = f(1) *1/3 * 2/4. Since we already have f(1) * 1/3, we write it in such a way that the equation has f(1) * 1/3 and then what comes rest, so that we can generalize
Calculating similarly for f(4), we get f(4) = f(1) * 1/3 * 2/4 * 3/5.
So, f(9) will be f(1) * 1/3 * 2/4 * 3/5 * 4/6 * 5/7 *6/8 * 7/9 * 8/10.
=> f(9) = (f(1) * 1 * 2) / (9 *10).
=> f(9) = 3600 * 2/ 9 * 10 = 80.
Calculating similarly for f(4), we get f(4) = f(1) * 1/3 * 2/4 * 3/5.
So, f(9) will be f(1) * 1/3 * 2/4 * 3/5 * 4/6 * 5/7 *6/8 * 7/9 * 8/10.
=> f(9) = (f(1) * 1 * 2) / (9 *10).
=> f(9) = 3600 * 2/ 9 * 10 = 80.
Let F(x) be a function such that F(x) F(x + 1) = – F(x – 1)F(x–2)F(x–3)F(x–4) for all x ≥ 0.Given the values of If F (83) = 81 and F(77) = 9, then the value of F(81) equals to- a)27
- b)54
- c)729
- d)Data Insufficient
Correct answer is option 'A'. Can you explain this answer?
Let F(x) be a function such that F(x) F(x + 1) = – F(x – 1)F(x–2)F(x–3)F(x–4) for all x ≥ 0.Given the values of If F (83) = 81 and F(77) = 9, then the value of F(81) equals to
a)
27
b)
54
c)
729
d)
Data Insufficient
|
Cstoppers Instructors answered |
When the value of x = 81 and 82 is substituted in the given expression, we get,
F (81) F (82) = – F (80) F (79) F(78) F(77)
F (82) F (83) = – F (81) F (80) F(79) F(78)
On dividing (i) by (a), we get
F (81) F (82) = – F (80) F (79) F(78) F(77)
F (82) F (83) = – F (81) F (80) F(79) F(78)
On dividing (i) by (a), we get
Option (a) is the correct answer.
Find the minimum value of the function fix) = log2 (x2 - 2x + 5).- a)-4
- b)2
- c)4
- d)-2
Correct answer is option 'B'. Can you explain this answer?
Find the minimum value of the function fix) = log2 (x2 - 2x + 5).
a)
-4
b)
2
c)
4
d)
-2
|
|
Alok Verma answered |
Method to Solve :
y= x2 – 2x + 5
Step 1 : Differentiate with respect to xStep 2 : Equate to 0
Step 3 : Find the value of x
dy/dx=2x-2 =0 implies x=1
Hence f(1)= 12 – 2 + 5= 4
Thus minimum value of the argument of the log is 4.
So minimum value of the function is log 4 (base 2) =2
If R(a/b) = Remainder when a is divided by b;
Q(a/b) = Quotient obtained when a is divided by b;
SQ(a) = Smallest integer just bigger than square root of a.Q.If a = 12, b = 5, then find the value of SQ[R {(a + b)/b}].- a)0
- b)1
- c)2
- d)3
Correct answer is option 'C'. Can you explain this answer?
If R(a/b) = Remainder when a is divided by b;
Q(a/b) = Quotient obtained when a is divided by b;
SQ(a) = Smallest integer just bigger than square root of a.
Q(a/b) = Quotient obtained when a is divided by b;
SQ(a) = Smallest integer just bigger than square root of a.
Q.
If a = 12, b = 5, then find the value of SQ[R {(a + b)/b}].
a)
0
b)
1
c)
2
d)
3
|
|
Aarav Sharma answered |
To find the value of SQ[R{(a - b)/b}], we need to follow the given steps:
Step 1: Calculate the value inside the square brackets.
(a - b)/b = (12 - 5)/5 = 7/5
Step 2: Calculate the remainder when 7 is divided by 5.
R(7/5) = Remainder when 7 is divided by 5 = 7 % 5 = 2
Step 3: Calculate the square root of 2.
SQ(2) = Smallest integer just bigger than the square root of 2 = 2
Therefore, the value of SQ[R{(a - b)/b}] = SQ[R(7/5)] = SQ(2) = 2.
Thus, the correct answer is option C) 2.
Step 1: Calculate the value inside the square brackets.
(a - b)/b = (12 - 5)/5 = 7/5
Step 2: Calculate the remainder when 7 is divided by 5.
R(7/5) = Remainder when 7 is divided by 5 = 7 % 5 = 2
Step 3: Calculate the square root of 2.
SQ(2) = Smallest integer just bigger than the square root of 2 = 2
Therefore, the value of SQ[R{(a - b)/b}] = SQ[R(7/5)] = SQ(2) = 2.
Thus, the correct answer is option C) 2.
Mr. David manufactures and sells a single product at a fixed price in a niche market. The selling price of each unit is Rs. 30. On the other hand, the cost, in rupees, of producing x units is 240 + bx + cx2, where b and c are some constants. Mr. David noticed that doubling the daily production from 20 to 40 units increases the daily production cost by 66.66%. However, an increase in daily production from 40 to 60 units results in an increase of only 50% in the daily production cost. Assume that demand is unlimited and that Mr. David can sell as much as he can produce. His objective is to maximize the profit.How many units should Mr. David produce daily ?- a)130
- b)100
- c)70
- d)150
- e)cannot be determined
Correct answer is option 'B'. Can you explain this answer?
Mr. David manufactures and sells a single product at a fixed price in a niche market. The selling price of each unit is Rs. 30. On the other hand, the cost, in rupees, of producing x units is 240 + bx + cx2, where b and c are some constants. Mr. David noticed that doubling the daily production from 20 to 40 units increases the daily production cost by 66.66%. However, an increase in daily production from 40 to 60 units results in an increase of only 50% in the daily production cost. Assume that demand is unlimited and that Mr. David can sell as much as he can produce. His objective is to maximize the profit.
How many units should Mr. David produce daily ?
a)
130
b)
100
c)
70
d)
150
e)
cannot be determined
|
Nikita Singh answered |
Cost price function f(x) = cx2 + bx + 240.
When x = 20, f(20) = 400c + 20b + 240.
=> f(40) = 1600c + 40b + 240
66.67% is 2/3.
=> f(40) – f(20) = 2/3 * f(20).
Substituting f(40) and f(20), we get, 1200c+ 20b =(2/3) * (400c + 20b + 240)
Solving, we get 20b + 2800c = 480.
When x = 20, f(20) = 400c + 20b + 240.
=> f(40) = 1600c + 40b + 240
66.67% is 2/3.
=> f(40) – f(20) = 2/3 * f(20).
Substituting f(40) and f(20), we get, 1200c+ 20b =(2/3) * (400c + 20b + 240)
Solving, we get 20b + 2800c = 480.
Now, f(60) = 3600c + 60b + 240.
f(60) – f(40) = ½ * f(40)
Substituting, and solving, we get, 360 + 60b + 2400c = 240 + 60b + 3600c
c = 1/10.
f(60) – f(40) = ½ * f(40)
Substituting, and solving, we get, 360 + 60b + 2400c = 240 + 60b + 3600c
c = 1/10.
Substituting we get, b = 10.
So, the cost function f(x) = 0.1x2 + 10x + 240.
Selling price = 30 * x. ( Each unit SP is 30)
So, profit = SP – CP = 30x – (0.1x2 + 10x + 240) = -x2/10 + 20x – 240.
Selling price = 30 * x. ( Each unit SP is 30)
So, profit = SP – CP = 30x – (0.1x2 + 10x + 240) = -x2/10 + 20x – 240.
For maximum profit, differentiating this should give 0.
dp/dt = 0, dp/dt = -x/5 + 20
20 – x/5 = 0. x= 100.
20 – x/5 = 0. x= 100.
Also double differentiating d2p / dt2, we get a negative number, so profit is maximum.
So, profit is maximum when 100 units are produced daily.
Read the instructions below and solve.
f(x) = f(x – 2) – f(x – 1), x is a natural number
f(1) = 0, f(2) = 1The value of f(8) is- a)0
- b)13
- c)–5
- d)–9
Correct answer is option 'B'. Can you explain this answer?
Read the instructions below and solve.
f(x) = f(x – 2) – f(x – 1), x is a natural number
f(1) = 0, f(2) = 1
f(x) = f(x – 2) – f(x – 1), x is a natural number
f(1) = 0, f(2) = 1
The value of f(8) is
a)
0
b)
13
c)
–5
d)
–9
|
|
Alok Verma answered |
f(1) = 0, f(2) = 1,
f(3) = f(1) – f(2) = –1
f(4) = f(2) – f(3) = 2
f(5) = f(3) – f(4) = –3
f(6) = f(4) – f(5) = 5
f(7) = f(5) – f(6) = –8
f(8) = f(6) – f(7) = 13
f(9) = f(7) – f(8) = –21
f(3) = f(1) – f(2) = –1
f(4) = f(2) – f(3) = 2
f(5) = f(3) – f(4) = –3
f(6) = f(4) – f(5) = 5
f(7) = f(5) – f(6) = –8
f(8) = f(6) – f(7) = 13
f(9) = f(7) – f(8) = –21
13
Let f (x) = max (2x + 1, 3 − 4x), where x is any real number. Then the minimum possible value of f(x) is :-- a)1/3
- b)1/2
- c)2/3
- d)4/3
- e)5/3
Correct answer is option 'E'. Can you explain this answer?
Let f (x) = max (2x + 1, 3 − 4x), where x is any real number. Then the minimum possible value of f(x) is :-
a)
1/3
b)
1/2
c)
2/3
d)
4/3
e)
5/3
|
|
Rajeev Kumar answered |
Ans.
Option (e)
To find out min of f(x) = max (2x + 1, 3 – 4x), we should be taking the point of intersection of (2x + 1) and (3 – 4x). [Since one of these equations is increasing and other one is decreasing]
2x + 1 = 3 – 4x, or, x = 1/3
2x + 1 = 3 – 4x = 5/3
Hence option (e) is the answer.
2x + 1 = 3 – 4x, or, x = 1/3
2x + 1 = 3 – 4x = 5/3
Hence option (e) is the answer.
Mr. David manufactures and sells a single product at a fixed price in a niche market. The selling price of each unit is Rs. 30. On the other hand, the cost, in rupees, of producing x units is 240 + bx + cx2, where b and c are some constants. Mr. David noticed that doubling the daily production from 20 to 40 units increases the daily production cost by 66.66%. However, an increase in daily production from 40 to 60 units results in an increase of only 50% in the daily production cost. Assume that demand is unlimited and that Mr. David can sell as much as he can produce. His objective is to maximize the profit. What is the maximum daily profit, in rupees, that Mr. David can realize from his business?- a)620
- b)920
- c)840
- d)760
- e)cannot be determined
Correct answer is option 'D'. Can you explain this answer?
Mr. David manufactures and sells a single product at a fixed price in a niche market. The selling price of each unit is Rs. 30. On the other hand, the cost, in rupees, of producing x units is 240 + bx + cx2, where b and c are some constants. Mr. David noticed that doubling the daily production from 20 to 40 units increases the daily production cost by 66.66%. However, an increase in daily production from 40 to 60 units results in an increase of only 50% in the daily production cost. Assume that demand is unlimited and that Mr. David can sell as much as he can produce. His objective is to maximize the profit.
What is the maximum daily profit, in rupees, that Mr. David can realize from his business?
a)
620
b)
920
c)
840
d)
760
e)
cannot be determined
|
KS Coaching Center answered |
Cost price function f(x) = cx2 + bx + 240.
When x = 20, f(20) = 400c + 20b + 240
f(40) = 1600c + 40b + 240
66.67% is 2/3.
f(40) – f(20) = 2/3 * f(20)
Substituting f(40) and f(20), we get, 1200c+ 20b =(2/3) * (400c + 20b + 240)
Solving, we get 20b + 2800c = 480
When x = 20, f(20) = 400c + 20b + 240
f(40) = 1600c + 40b + 240
66.67% is 2/3.
f(40) – f(20) = 2/3 * f(20)
Substituting f(40) and f(20), we get, 1200c+ 20b =(2/3) * (400c + 20b + 240)
Solving, we get 20b + 2800c = 480
Now, f(60) = 3600c + 60b + 240.
f(60) – f(40) = ½ * f(40).
Substituting, and solving, we get, 360 + 60b + 2400c = 240 + 60b + 3600c.
c = 1/10.
f(60) – f(40) = ½ * f(40).
Substituting, and solving, we get, 360 + 60b + 2400c = 240 + 60b + 3600c.
c = 1/10.
Substituting we get, b = 10.
So, the cost function f(x) = 0.1x2 + 10x + 240.
Selling price = 30*x. ( Each unit SP is 30)
So, profit = SP – CP = 30x – (0.1x2 + 10x + 240) = -x2/10 + 20x – 240.
Selling price = 30*x. ( Each unit SP is 30)
So, profit = SP – CP = 30x – (0.1x2 + 10x + 240) = -x2/10 + 20x – 240.
For maximum profit, differentiating this should give 0.
dp/dt = 0, dp/dt = -x/5 + 20
=> 20 – x/5 = 0.
=> 20 – x/5 = 0.
=>x= 100.
Also double differentiating d2p / dt2, we get a negative number, so profit is maximum. So, profit is maximum when 100 units are produced daily.
The maximum profit can be calculated with the equation -x2/10 + 20x – 240, with x = 100, and it is 760.
If 0 < a <1 and 0 < b < 1 and if a < b, which of the following expressions will have the highestvalue?- a)(a M b)
- b)(a D b)
- c)(a P b)
- d)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
If 0 < a <1 and 0 < b < 1 and if a < b, which of the following expressions will have the highestvalue?
a)
(a M b)
b)
(a D b)
c)
(a P b)
d)
Cannot be determined
|
Yash Patel answered |
Again (a + b) or a/b can both be greater than each other depending on the values we take for a and b.
E.g. for a = 0.9 and b = 0.91, a + b > a/b.
For a = 0.1 and b = 0.11, a + b < a/b
E.g. for a = 0.9 and b = 0.91, a + b > a/b.
For a = 0.1 and b = 0.11, a + b < a/b
f1 (x) = x 0 ≤ x ≤ 1
= 1 x ≥ 1
= 0 otherwisef2 (x) = f1(–x) for all xf3 (x) = –f2(x) for all xf4 (x) = f3(–x) for all xHow many of the following products are necessarily zero for every x:f1(x) f2 (x), f2 (x) f3 (x), f2(x) f4 (x)- a)0
- b)1
- c)2
- d)3
Correct answer is option 'C'. Can you explain this answer?
f1 (x) = x 0 ≤ x ≤ 1
= 1 x ≥ 1
= 0 otherwise
= 1 x ≥ 1
= 0 otherwise
f2 (x) = f1(–x) for all x
f3 (x) = –f2(x) for all x
f4 (x) = f3(–x) for all x
How many of the following products are necessarily zero for every x:
f1(x) f2 (x), f2 (x) f3 (x), f2(x) f4 (x)
a)
0
b)
1
c)
2
d)
3
|
|
Aditya Kumar answered |
We have to consider positive and negative numbers for all the cases.
f1(x) is positive for positive numbers, and 0 for negative numbers. (0 for x = 0)
f2(x) is 0 for positive numbers, and positive for negative numbers. (0 for x = 0)
f3(x) is 0 for positive numbers, and negative for negative numbers. (0 for x = 0)
f4(x) is negative for positive numbers, and 0 for negative numbers. (0 for x = 0)
So, we see that, out of the 3 products in the question, f1(x) * f2(x) and f2(x) * f4(x) are always zero, for any x.
f1(x) is positive for positive numbers, and 0 for negative numbers. (0 for x = 0)
f2(x) is 0 for positive numbers, and positive for negative numbers. (0 for x = 0)
f3(x) is 0 for positive numbers, and negative for negative numbers. (0 for x = 0)
f4(x) is negative for positive numbers, and 0 for negative numbers. (0 for x = 0)
So, we see that, out of the 3 products in the question, f1(x) * f2(x) and f2(x) * f4(x) are always zero, for any x.
Second sub question, f4(x) = f3(-x) = -f2(-x) = -f1(x).
Hence, 1st option is false.
–f3(-x) = f2(-x) = f1(x). Hence this is true.
Hence, 1st option is false.
–f3(-x) = f2(-x) = f1(x). Hence this is true.
0
Find the maximum value of the function 1/(x2 – 3x + 2).- a)11/4
- b)1/4
- c)0
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
Find the maximum value of the function 1/(x2 – 3x + 2).
a)
11/4
b)
1/4
c)
0
d)
None of these
|
|
Aryan Khanna answered |
The denominator x2 -3x + 2 has real roots. Hence the maximum value of the function f(x) will be infinity.
Read the instructions below and solve.
f(x) = f(x – 2) – f(x – 1), x is a natural number
f(1) = 0, f(2) = 1What will be the domain of the definition of the function f(x) = 8–xC 5–x for positive values of x?- a){1, 2, 3}
- b){1, 2, 3, 4}
- c){1, 2, 3, 4, 5}
- d){1, 2, 3, 4, 5, 6, 7, 8}
Correct answer is option 'C'. Can you explain this answer?
Read the instructions below and solve.
f(x) = f(x – 2) – f(x – 1), x is a natural number
f(1) = 0, f(2) = 1
f(x) = f(x – 2) – f(x – 1), x is a natural number
f(1) = 0, f(2) = 1
What will be the domain of the definition of the function f(x) = 8–xC 5–x for positive values of x?
a)
{1, 2, 3}
b)
{1, 2, 3, 4}
c)
{1, 2, 3, 4, 5}
d)
{1, 2, 3, 4, 5, 6, 7, 8}
|
|
Nikita Singh answered |
f(1) = 0, f(2) = 1,
f(3) = f(1) – f(2) = –1
f(4) = f(2) – f(3) = 2
f(5) = f(3) – f(4) = –3
f(6) = f(4) – f(5) = 5
f(7) = f(5) – f(6) = –8
f(8) = f(6) – f(7) = 13
f(9) = f(7) – f(8) = –21
f(3) = f(1) – f(2) = –1
f(4) = f(2) – f(3) = 2
f(5) = f(3) – f(4) = –3
f(6) = f(4) – f(5) = 5
f(7) = f(5) – f(6) = –8
f(8) = f(6) – f(7) = 13
f(9) = f(7) – f(8) = –21
For any nCr, n should be positive and r ≥ 0.
Thus, for positive x, 5 – x ≥ 0
fi x = 1, 2, 3, 4, 5.
Thus, for positive x, 5 – x ≥ 0
fi x = 1, 2, 3, 4, 5.
Ajesh saves Rs 50,000 every year and deposits the money in a bank at compound interest of 10%(compunded annually).What would be his total saving at the end of the 5th year?- a)Rs 3,05,255
- b)Rs 1,05,255
- c)Rs 8,05,255
- d)Rs 4,05,255
Correct answer is option 'A'. Can you explain this answer?
Ajesh saves Rs 50,000 every year and deposits the money in a bank at compound interest of 10%(compunded annually).What would be his total saving at the end of the 5th year?
a)
Rs 3,05,255
b)
Rs 1,05,255
c)
Rs 8,05,255
d)
Rs 4,05,255
|
|
Rajeev Kumar answered |
At the end of the 1st year, he will get Rs 50000, it will give him interest for 4 years compounded annually
Hence at the end of 5 years, this amount will become 50000(1.1)4
Similarly, the amount deposited in the 2nd year will give interest for 3 years. Hence it will become 50000(1.1)3
Similarly, we can calculate for the remaining years.
The total saving at the end of the 5th year would be a GP, given by
Net saving = 50000(1.1)4 + 50000(1.1)3 ..... 50000
Thus net saving =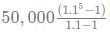
= Rs 3,05,255
Hence at the end of 5 years, this amount will become 50000(1.1)4
Similarly, the amount deposited in the 2nd year will give interest for 3 years. Hence it will become 50000(1.1)3
Similarly, we can calculate for the remaining years.
The total saving at the end of the 5th year would be a GP, given by
Net saving = 50000(1.1)4 + 50000(1.1)3 ..... 50000
Thus net saving =
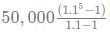= Rs 3,05,255Let f(x) = ax2 + bx + c, where a, b and c are certain constants and a ≠ 0. It is known that f (5) = −3f(2) and that 3 is a root of f(x) = 0.What is the other root of f(x) = 0?- a)-7
- b)-4
- c)2
- d)6
Correct answer is option 'B'. Can you explain this answer?
Let f(x) = ax2 + bx + c, where a, b and c are certain constants and a ≠ 0. It is known that f (5) = −3f(2) and that 3 is a root of f(x) = 0.
What is the other root of f(x) = 0?
a)
-7
b)
-4
c)
2
d)
6
|
Nisha Saha answered |
f(x) = ax2 + bx + c
f(5) = −3f(2) => 25a+5b+c = -3(4a+2b+c) => 37a+11b+4c = 0 ---(1)
3 is a root of f(x) = 0 => f(3) = 0 => 9a+3b+c = 0 ---(2)
On solving (1) and (2) we get, b = a, c = -12a ---(3)
Substituting (3) in f(x) = 0 => ax2 + ax – 12a = 0 => a(x2 + x – 12) = 0
Given that a ≠ 0 =>(x-3)(x+4) = 0 => x = 3 (or) -4
x=3 root is already given hence the other root is -4
f(5) = −3f(2) => 25a+5b+c = -3(4a+2b+c) => 37a+11b+4c = 0 ---(1)
3 is a root of f(x) = 0 => f(3) = 0 => 9a+3b+c = 0 ---(2)
On solving (1) and (2) we get, b = a, c = -12a ---(3)
Substituting (3) in f(x) = 0 => ax2 + ax – 12a = 0 => a(x2 + x – 12) = 0
Given that a ≠ 0 =>(x-3)(x+4) = 0 => x = 3 (or) -4
x=3 root is already given hence the other root is -4
Which of the following is an even function?- a)x–8
- b)x3
- c)x–33
- d)x73
Correct answer is option 'A'. Can you explain this answer?
Which of the following is an even function?
a)
x–8
b)
x3
c)
x–33
d)
x73
|
|
Anaya Patel answered |
x–8 is even since f(x) = f(–x) in this case.
Define the following functions:
(a) (a M b) = a – b (b) (a D b) = a + b
(c) (a H b) = (ab) (d) (a P b) = a/bQ.What is the value of (3M4H2D4P8M2)?- a)6.5
- b)6
- c)–6.5
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Define the following functions:
(a) (a M b) = a – b (b) (a D b) = a + b
(c) (a H b) = (ab) (d) (a P b) = a/b
(a) (a M b) = a – b (b) (a D b) = a + b
(c) (a H b) = (ab) (d) (a P b) = a/b
Q.
What is the value of (3M4H2D4P8M2)?
a)
6.5
b)
6
c)
–6.5
d)
None of these
|
|
Alok Verma answered |
3 – 4 × 2 + 4/8 – 2 = 3 – 8 + 0.5 – 2 = – 6.5
(using BODMAS rule)
(using BODMAS rule)
A quadratic function f(x) attains a maximum of 3 at x = 1. The value of the function at x = 0 is 1. What is the value of f(x) at x = 10 ?- a)-119
- b)-159
- c)-110
- d)-180
- e)-105
Correct answer is option 'B'. Can you explain this answer?
A quadratic function f(x) attains a maximum of 3 at x = 1. The value of the function at x = 0 is 1. What is the value of f(x) at x = 10 ?
a)
-119
b)
-159
c)
-110
d)
-180
e)
-105
|
Raghavendra Sharma answered |
We have f(x)=ax^2+bx+cf(x)=ax^2+bx+c.
f(0)=c=1f(0)=c=1 --> f(x)=ax^2+bx+1f(x)=ax^2+bx+1
We are told that fmax(1)=a+b+1=3
, --> a+b=2.
fmax is vertex of parabola and the x coordinate of vertex is
−b/2a=1−b2a=1
--> b=−2a
--> a+b=a
−2a=−a + b =a−2a=
−a=2 --> a=−2a=−2 and b=4b=4.
f(x)=−2x^2+4x+1 =f(x)=−2x^2+4x+1 --> f(10)=−200+40+1=−159
If f (x) = x3 – 4x + p, and f (0) and f(1) are of opposite signs, then which of the following is necessarily true?- a)–1 < p < 2
- b)0 < p < 3
- c)–2 < p < 1
- d)–3 < p < 0
Correct answer is option 'B'. Can you explain this answer?
If f (x) = x3 – 4x + p, and f (0) and f(1) are of opposite signs, then which of the following is necessarily true?
a)
–1 < p < 2
b)
0 < p < 3
c)
–2 < p < 1
d)
–3 < p < 0
|
|
Rajeev Kumar answered |
f(0) = p
f (1) = 1 – 4 + p = p + 3.
p and p+3 are of different signs.
Substitute for the options:
1st option, if p is a negative number, then p – 3 is also negative, and both are same sign.
For 3rd and 4th option, also it is the same.
For the 2nd option, value of p is between 0 and 3, and p – 3 is negative. Hence it agrees.
f (1) = 1 – 4 + p = p + 3.
p and p+3 are of different signs.
Substitute for the options:
1st option, if p is a negative number, then p – 3 is also negative, and both are same sign.
For 3rd and 4th option, also it is the same.
For the 2nd option, value of p is between 0 and 3, and p – 3 is negative. Hence it agrees.
Let f(x) = x2 + ax + b and g(x) = f(x + 1) − f(x - 1). If f(x) ≥ 0 for all real x and g(20) = 72, then the smallest possible value of b is- a)16
- b)4
- c)1
- d)0
Correct answer is option 'B'. Can you explain this answer?
Let f(x) = x2 + ax + b and g(x) = f(x + 1) − f(x - 1). If f(x) ≥ 0 for all real x and g(20) = 72, then the smallest possible value of b is
a)
16
b)
4
c)
1
d)
0
|
Jithin Majumdar answered |
Understanding the Functions
To solve the problem, we start with the function:
- f(x) = x² + ax + b
The condition f(x) ≥ 0 indicates that the quadratic must have no real roots, meaning its discriminant must be non-positive:
- Discriminant: D = a² - 4b ≤ 0
Defining g(x)
Next, we define g(x):
- g(x) = f(x + 1) - f(x - 1)
Calculating f(x + 1) and f(x - 1):
- f(x + 1) = (x + 1)² + a(x + 1) + b = x² + 2x + 1 + ax + a + b
- f(x - 1) = (x - 1)² + a(x - 1) + b = x² - 2x + 1 + ax - a + b
Now, we compute g(x):
- g(x) = [x² + 2x + 1 + ax + a + b] - [x² - 2x + 1 + ax - a + b]
- g(x) simplifies to: g(x) = 4x + 2a
Using the Given Condition
Given that g(20) = 72:
- 4(20) + 2a = 72
- This simplifies to: 80 + 2a = 72
- Therefore, 2a = -8, leading to a = -4.
Finding the Minimum Value of b
Substituting a = -4 into the discriminant condition:
- a² - 4b ≤ 0 becomes: 16 - 4b ≤ 0
- Hence, 4b ≥ 16, which means b ≥ 4.
Thus, the smallest possible value of b is:
- b = 4.
Conclusion
The answer is option 'B' (4), which satisfies both conditions of the problem.
To solve the problem, we start with the function:
- f(x) = x² + ax + b
The condition f(x) ≥ 0 indicates that the quadratic must have no real roots, meaning its discriminant must be non-positive:
- Discriminant: D = a² - 4b ≤ 0
Defining g(x)
Next, we define g(x):
- g(x) = f(x + 1) - f(x - 1)
Calculating f(x + 1) and f(x - 1):
- f(x + 1) = (x + 1)² + a(x + 1) + b = x² + 2x + 1 + ax + a + b
- f(x - 1) = (x - 1)² + a(x - 1) + b = x² - 2x + 1 + ax - a + b
Now, we compute g(x):
- g(x) = [x² + 2x + 1 + ax + a + b] - [x² - 2x + 1 + ax - a + b]
- g(x) simplifies to: g(x) = 4x + 2a
Using the Given Condition
Given that g(20) = 72:
- 4(20) + 2a = 72
- This simplifies to: 80 + 2a = 72
- Therefore, 2a = -8, leading to a = -4.
Finding the Minimum Value of b
Substituting a = -4 into the discriminant condition:
- a² - 4b ≤ 0 becomes: 16 - 4b ≤ 0
- Hence, 4b ≥ 16, which means b ≥ 4.
Thus, the smallest possible value of b is:
- b = 4.
Conclusion
The answer is option 'B' (4), which satisfies both conditions of the problem.
Read the instructions below and solve:
f(x) = f(x – 2) – f(x – 1), x is a natural number
f(1) = 0, f(2) = 1Q.The value of f[f(6)] is- a)5
- b)– 1
- c)– 3
- d)– 2
Correct answer is option 'C'. Can you explain this answer?
Read the instructions below and solve:
f(x) = f(x – 2) – f(x – 1), x is a natural number
f(1) = 0, f(2) = 1
f(x) = f(x – 2) – f(x – 1), x is a natural number
f(1) = 0, f(2) = 1
Q.
The value of f[f(6)] is
a)
5
b)
– 1
c)
– 3
d)
– 2
|
|
Ruchi Chavan answered |
f(1) = 0, f(2) = 1,
f(3) = f(1) – f(2) = –1
f(4) = f(2) – f(3) = 2
f(5) = f(3) – f(4) = –3
f(6) = f(4) – f(5) = 5
f(7) = f(5) – f(6) = –8
f(8) = f(6) – f(7) = 13
f(3) = f(1) – f(2) = –1
f(4) = f(2) – f(3) = 2
f(5) = f(3) – f(4) = –3
f(6) = f(4) – f(5) = 5
f(7) = f(5) – f(6) = –8
f(8) = f(6) – f(7) = 13
Ans:-
f(f(6) = f(5) = –3.
Define the functions:
A(x, y, z) = Max (max (x, y), min (y, z) min (x, z))
B(x, y, z) = Max (max (x, y), min (y, z) max (x, z))
C(x, y, z) = Max (min (x, y), min (y, z) min (x, z))
D(x, y, z) = Min (max (x, y), max (y, z) max (x, z))
Max (x, y, z) = Maximum of x, y and z.
Min (x, y, z) = Minimum of x, y and z.
Assume that x, y and z are distinct integers.Q.For what condition will A(x, y, z) not be equal to B (x, y, z)?- a)x > y > z
- b)y > z > x
- c)z > y > x
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Define the functions:
A(x, y, z) = Max (max (x, y), min (y, z) min (x, z))
B(x, y, z) = Max (max (x, y), min (y, z) max (x, z))
C(x, y, z) = Max (min (x, y), min (y, z) min (x, z))
D(x, y, z) = Min (max (x, y), max (y, z) max (x, z))
Max (x, y, z) = Maximum of x, y and z.
Min (x, y, z) = Minimum of x, y and z.
Assume that x, y and z are distinct integers.
A(x, y, z) = Max (max (x, y), min (y, z) min (x, z))
B(x, y, z) = Max (max (x, y), min (y, z) max (x, z))
C(x, y, z) = Max (min (x, y), min (y, z) min (x, z))
D(x, y, z) = Min (max (x, y), max (y, z) max (x, z))
Max (x, y, z) = Maximum of x, y and z.
Min (x, y, z) = Minimum of x, y and z.
Assume that x, y and z are distinct integers.
Q.
For what condition will A(x, y, z) not be equal to B (x, y, z)?
a)
x > y > z
b)
y > z > x
c)
z > y > x
d)
None of these
|
|
Ayush Rane answered |
A(x, y, z) = Max (max (x, y), min (y, z) min (x, z))
B(x, y, z) = Max (max (x, y), min (y, z) max (x, z))
C(x, y, z) = Max (min (x, y), min (y, z) min (x, z))
D(x, y, z) = Min (max (x, y), max (y, z) max (x, z))
Max (x, y, z) = Maximum of x, y and z.
Min (x, y, z) = Minimum of x, y and z.
Assume that x, y and z are distinct integers.
B(x, y, z) = Max (max (x, y), min (y, z) max (x, z))
C(x, y, z) = Max (min (x, y), min (y, z) min (x, z))
D(x, y, z) = Min (max (x, y), max (y, z) max (x, z))
Max (x, y, z) = Maximum of x, y and z.
Min (x, y, z) = Minimum of x, y and z.
Assume that x, y and z are distinct integers.
Ans:-
When z is maximum, A and B would give different values. Thus, option (c) is correct.
If R(a/b) = Remainder when a is divided by b;
Q(a/b) = Quotient obtained when a is divided by b;
SQ(a) = Smallest integer just bigger than square root of a.Q.If a =18, b = 2 and c = 7, then find the value of Q [{SQ(ab) + R(a/c)}/b].- a)3
- b)4
- c)5
- d)6
Correct answer is option 'C'. Can you explain this answer?
If R(a/b) = Remainder when a is divided by b;
Q(a/b) = Quotient obtained when a is divided by b;
SQ(a) = Smallest integer just bigger than square root of a.
Q(a/b) = Quotient obtained when a is divided by b;
SQ(a) = Smallest integer just bigger than square root of a.
Q.
If a =18, b = 2 and c = 7, then find the value of Q [{SQ(ab) + R(a/c)}/b].
a)
3
b)
4
c)
5
d)
6
|
|
Nandini Dasgupta answered |
Q [[SA (36) + R (18/7)]/2] = Q [(7 + 4)/2] = Q [11/2] = 5.
Define the functions:
A(x, y, z) = Max (max (x, y), min (y, z) min (x, z))
B(x, y, z) = Max (max (x, y), min (y, z) max (x, z))
C(x, y, z) = Max (min (x, y), min (y, z) min (x, z))
D(x, y, z) = Min (max (x, y), max (y, z) max (x, z))
Max (x, y, z) = Maximum of x, y and z.
Min (x, y, z) = Minimum of x, y and z.
Assume that x, y and z are distinct integers.Q.The highest value amongst the following will be- a)Max/Min
- b)A/B
- c)C/D
- d)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
Define the functions:
A(x, y, z) = Max (max (x, y), min (y, z) min (x, z))
B(x, y, z) = Max (max (x, y), min (y, z) max (x, z))
C(x, y, z) = Max (min (x, y), min (y, z) min (x, z))
D(x, y, z) = Min (max (x, y), max (y, z) max (x, z))
Max (x, y, z) = Maximum of x, y and z.
Min (x, y, z) = Minimum of x, y and z.
Assume that x, y and z are distinct integers.
A(x, y, z) = Max (max (x, y), min (y, z) min (x, z))
B(x, y, z) = Max (max (x, y), min (y, z) max (x, z))
C(x, y, z) = Max (min (x, y), min (y, z) min (x, z))
D(x, y, z) = Min (max (x, y), max (y, z) max (x, z))
Max (x, y, z) = Maximum of x, y and z.
Min (x, y, z) = Minimum of x, y and z.
Assume that x, y and z are distinct integers.
Q.
The highest value amongst the following will be
a)
Max/Min
b)
A/B
c)
C/D
d)
Cannot be determined
|
|
Arya Mehta answered |
A(x, y, z) = Max (max (x, y), min (y, z) min (x, z))
B(x, y, z) = Max (max (x, y), min (y, z) max (x, z))
C(x, y, z) = Max (min (x, y), min (y, z) min (x, z))
D(x, y, z) = Min (max (x, y), max (y, z) max (x, z))
Max (x, y, z) = Maximum of x, y and z.
Min (x, y, z) = Minimum of x, y and z.
Assume that x, y and z are distinct integers.
B(x, y, z) = Max (max (x, y), min (y, z) max (x, z))
C(x, y, z) = Max (min (x, y), min (y, z) min (x, z))
D(x, y, z) = Min (max (x, y), max (y, z) max (x, z))
Max (x, y, z) = Maximum of x, y and z.
Min (x, y, z) = Minimum of x, y and z.
Assume that x, y and z are distinct integers.
Ans:-
We cannot determine this because it would depend on whether the integers x, y, and z are positive
or negative.
or negative.
Define the following functions:
(a) (a M b) = a – b (b) (a D b) = a + b
(c) (a H b) = (ab) (d) (a P b) = a/bQ.Which of the four functions defined has the minimum value?- a)(a M b)
- b)(a D b)
- c)(a H b)
- d)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
Define the following functions:
(a) (a M b) = a – b (b) (a D b) = a + b
(c) (a H b) = (ab) (d) (a P b) = a/b
(a) (a M b) = a – b (b) (a D b) = a + b
(c) (a H b) = (ab) (d) (a P b) = a/b
Q.
Which of the four functions defined has the minimum value?
a)
(a M b)
b)
(a D b)
c)
(a H b)
d)
Cannot be determined
|
Preeti Khanna answered |
The minimum would depend on the values of a and b. Thus, cannot be determined.
If f(x) = |x – 2| , then which of the following is always true?- a)f(x) = (f(x))2
- b)f(x ) = f(–x)
- c)f(x) = x – 2
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
If f(x) = |x – 2| , then which of the following is always true?
a)
f(x) = (f(x))2
b)
f(x ) = f(–x)
c)
f(x) = x – 2
d)
None of these
|
|
Ayush Rane answered |
Take different values of n to check each option. Each of Options (a), (b) and (c) can be ruled out.
Hence, Option (d) is correct.
Hence, Option (d) is correct.
If f(x) = x2 and g(x) = logex, then f(x) + g(x) will be- a)Even function
- b)Odd function
- c)Both
- d)Neither (a) nor (b)
Correct answer is option 'D'. Can you explain this answer?
If f(x) = x2 and g(x) = logex, then f(x) + g(x) will be
a)
Even function
b)
Odd function
c)
Both
d)
Neither (a) nor (b)
|
|
Tushar Chauhan answered |
(x2 + loge x) would be neither odd nor even since it obeys neither of the rules for even function
(f(x) = f(–x)) nor for odd functions (f(x) = –f(–x)).
(f(x) = f(–x)) nor for odd functions (f(x) = –f(–x)).
If f(x) is a function satisfying f(x). f(1/x) = f(x) + f(1/x) and f(4) = 65, what will be the value off(6)?- a)37
- b)217
- c)64
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If f(x) is a function satisfying f(x). f(1/x) = f(x) + f(1/x) and f(4) = 65, what will be the value off(6)?
a)
37
b)
217
c)
64
d)
None of these
|
|
Arya Mehta answered |
We have f(x) ◊ f(1/x) = f(x) + f(1/x)
fi f(1/x) [f(x) – 1] = f(x)
For x = 4, we have f(1/4) [f(4) – 1] = f (4)
fi f(1/4) [64] = 65
fi f(1/4) = 65/64 = 1/64 + 1
This means f(x) = x3 + 1
For f(6) we have f(6) = 216 + 1 = 217.
fi f(1/x) [f(x) – 1] = f(x)
For x = 4, we have f(1/4) [f(4) – 1] = f (4)
fi f(1/4) [64] = 65
fi f(1/4) = 65/64 = 1/64 + 1
This means f(x) = x3 + 1
For f(6) we have f(6) = 216 + 1 = 217.
The function y = 1/x shifted 1 unit down and 1 unit right is given by- a)y – 1 = 1/ (x + 1)
- b)y – 1 = 1/(x – 1)
- c)y + 1 = 1/(x – 1)
- d)y + 1 = 1/(x + 1)
Correct answer is option 'C'. Can you explain this answer?
The function y = 1/x shifted 1 unit down and 1 unit right is given by
a)
y – 1 = 1/ (x + 1)
b)
y – 1 = 1/(x – 1)
c)
y + 1 = 1/(x – 1)
d)
y + 1 = 1/(x + 1)
|
|
Aarav Sharma answered |
Explanation:
To shift the graph of the function y = 1/x, we need to apply two transformations: one unit down and one unit right.
Shifting Down:
To shift the graph down by one unit, we subtract 1 from the original function. This can be represented as y - 1.
Shifting Right:
To shift the graph right by one unit, we replace x with (x - 1). This is because for every x value in the original function, we want to consider the value of x - 1 in the shifted function.
Therefore, the transformed function can be represented as:
y - 1 = 1 / (x - 1)
Answer:
The correct answer is option 'C' which represents the transformed function as:
y - 1 = 1 / (x - 1)
Read the following passage and try to answer questions based on
them.
[x] = Greatest integer less than or equal to x
{x} = Smallest integer greater than or equal to x.Q.If x is not an integer, then ({x} + [x]) is- a)An even number
- b)An odd integer
- c)> 3x
- d)< x
Correct answer is option 'B'. Can you explain this answer?
Read the following passage and try to answer questions based on
them.
[x] = Greatest integer less than or equal to x
{x} = Smallest integer greater than or equal to x.
them.
[x] = Greatest integer less than or equal to x
{x} = Smallest integer greater than or equal to x.
Q.
If x is not an integer, then ({x} + [x]) is
a)
An even number
b)
An odd integer
c)
> 3x
d)
< x
|
|
Tushar Chauhan answered |
[x] + {x} will always be odd as the values are consecutive integers.
The number of real-valued solutions of the equation 2x+ 2-x = 2 - (x - 2)2 is:- a)1
- b)2
- c)infinite
- d)0
Correct answer is option 'D'. Can you explain this answer?
The number of real-valued solutions of the equation 2x+ 2-x = 2 - (x - 2)2 is:
a)
1
b)
2
c)
infinite
d)
0
|
|
Anshul Ghoshal answered |
Understanding the Equation
To solve the equation 2x + 2 - x = 2 - (x - 2)², we first simplify both sides.
Left Side Simplification
- The left side is: 2x + 2 - x = x + 2.
Right Side Simplification
- The right side expands as follows:
- (x - 2)² = x² - 4x + 4
- Therefore, 2 - (x - 2)² = 2 - (x² - 4x + 4) = -x² + 4x - 2.
So, the equation simplifies to:
x + 2 = -x² + 4x - 2.
Rearranging the Equation
Now, we bring all terms to one side:
x² - 3x + 4 = 0.
Discriminant Calculation
Next, we check the discriminant (D) of this quadratic equation:
- D = b² - 4ac
- Here, a = 1, b = -3, c = 4.
- D = (-3)² - 4(1)(4) = 9 - 16 = -7.
Conclusion on Real Solutions
Since the discriminant is negative (D < 0),="" the="" quadratic="" equation="" has="" no="" real="" solutions.="" thus,="" the="" number="" of="" real-valued="" solutions="" for="" the="" given="" equation="" is:="" />Final Answer
- 0 (option D).
To solve the equation 2x + 2 - x = 2 - (x - 2)², we first simplify both sides.
Left Side Simplification
- The left side is: 2x + 2 - x = x + 2.
Right Side Simplification
- The right side expands as follows:
- (x - 2)² = x² - 4x + 4
- Therefore, 2 - (x - 2)² = 2 - (x² - 4x + 4) = -x² + 4x - 2.
So, the equation simplifies to:
x + 2 = -x² + 4x - 2.
Rearranging the Equation
Now, we bring all terms to one side:
x² - 3x + 4 = 0.
Discriminant Calculation
Next, we check the discriminant (D) of this quadratic equation:
- D = b² - 4ac
- Here, a = 1, b = -3, c = 4.
- D = (-3)² - 4(1)(4) = 9 - 16 = -7.
Conclusion on Real Solutions
Since the discriminant is negative (D < 0),="" the="" quadratic="" equation="" has="" no="" real="" solutions.="" thus,="" the="" number="" of="" real-valued="" solutions="" for="" the="" given="" equation="" is:="" />Final Answer
- 0 (option D).
If f(t) = t2 + 2 and g(t) = (1/t) + 2, then for t = 2, f [g(t)] – g[f(t)] = ?- a)1.2
- b)2.6
- c)4.34
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
If f(t) = t2 + 2 and g(t) = (1/t) + 2, then for t = 2, f [g(t)] – g[f(t)] = ?
a)
1.2
b)
2.6
c)
4.34
d)
None of these
|
|
Aarav Sharma answered |
To find f[g(t)] for t = 2, we first need to find g(t) and then substitute it into f(t).
Given g(t) = (1/t)^2, we substitute t = 2 into g(t):
g(2) = (1/2)^2
g(2) = 1/4
Now we substitute g(2) into f(t):
f[g(2)] = f(1/4)
f(1/4) = (1/4)^2
f(1/4) = 1/16
Therefore, f[g(t)] for t = 2 is 1/16.
Given g(t) = (1/t)^2, we substitute t = 2 into g(t):
g(2) = (1/2)^2
g(2) = 1/4
Now we substitute g(2) into f(t):
f[g(2)] = f(1/4)
f(1/4) = (1/4)^2
f(1/4) = 1/16
Therefore, f[g(t)] for t = 2 is 1/16.
Which of the following functions will have a minimum value at x = –3?- a)f(x) = 2x3 – 4x + 3
- b)f(x) = 4x4 – 3x + 5
- c)f(x) = x6 – 2x – 6
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
Which of the following functions will have a minimum value at x = –3?
a)
f(x) = 2x3 – 4x + 3
b)
f(x) = 4x4 – 3x + 5
c)
f(x) = x6 – 2x – 6
d)
None of these
|
|
Nandini Dasgupta answered |
If you differentiate each function with respect to x, and equate it to 0 you would see that for none
of the three options will get you a value of x = –3 as its solution. Thus, option (d) viz. None of
these is correct.
of the three options will get you a value of x = –3 as its solution. Thus, option (d) viz. None of
these is correct.
Find the domain of the definition of the functiony = [(x – 3)/(x + 3)]1/2 + [(1 – x)/(1 + x)]1/2.- a)x > 3
- b)x < –3
- c)-3 £ x £ 3
- d)Nowhere
Correct answer is option 'D'. Can you explain this answer?
Find the domain of the definition of the functiony = [(x – 3)/(x + 3)]1/2 + [(1 – x)/(1 + x)]1/2.
a)
x > 3
b)
x < –3
c)
-3 £ x £ 3
d)
Nowhere
|
|
Avik Choudhury answered |
Both the brackets should be non-negative and neither (x + 3) nor (1+ x) should be 0.
For (x – 3)/(x + 3) to be non negative we have x>3 or x< – 3.
Also for (1– x)/(1+ x) to be non-negative –1 < x < 1. Since there is no interference in the two
ranges, Option (d) would be correct.
For (x – 3)/(x + 3) to be non negative we have x>3 or x< – 3.
Also for (1– x)/(1+ x) to be non-negative –1 < x < 1. Since there is no interference in the two
ranges, Option (d) would be correct.
If f(x) = 2x+2 what is f(f(3))? - a)18
- b)20
- c)22
- d)24
Correct answer is option 'A'. Can you explain this answer?
If f(x) = 2x+2 what is f(f(3))?
a)
18
b)
20
c)
22
d)
24
|
|
Rhea Reddy answered |
This is very simple :
f(x) = 2x+2
f(3) = 2*3+2=8
f(f(3))= 2*f(3)+2
= 2*8+2
= 18
Hence (A) is the answer
Define the following functions:f(x, y, z) = xy + yz + zxg(x, y, z) = x2y + y2z + z2x andh(x, y, z) = 3 xyzQ.Find the value of the following expressions:37. h[f(2, 3, 1), g(3, 4, 2), h(1/3, 1/3, 3)]- a)0
- b)23760
- c)2640
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Define the following functions:
f(x, y, z) = xy + yz + zx
g(x, y, z) = x2y + y2z + z2x and
h(x, y, z) = 3 xyz
Q.
Find the value of the following expressions:37. h[f(2, 3, 1), g(3, 4, 2), h(1/3, 1/3, 3)]
a)
0
b)
23760
c)
2640
d)
None of these
|
Sagar Sharma answered |
Calculation:
Given functions:
- f(x, y, z) = xy yz zx
- g(x, y, z) = x^2y y^2z z^2x
- h(x, y, z) = 3xyz
Substitute values into functions:
- f(2, 3, 1) = 2*3 + 3*1 + 1*2 = 6 + 3 + 2 = 11
- g(3, 4, 2) = 3^2*4 + 4^2*2 + 2^2*3 = 36*4 + 16*2 + 4*3 = 144 + 32 + 12 = 188
- h(1/3, 1/3, 3) = 3*(1/3)*(1/3)*3 = 3*(1/9)*3 = 1
Plug the values into h function:
- h[f(2, 3, 1), g(3, 4, 2), h(1/3, 1/3, 3)] = h(11, 188, 1) = 3*11*188 = 3*2056 = 6168
Answer:
Therefore, the value of h[f(2, 3, 1), g(3, 4, 2), h(1/3, 1/3, 3)] is 6168. So, the correct option is (C) 2640.
The figure below shows the graph of a function f (x). How many solutions does the equation f ( f(x)) = 15 have?- a)5
- b)6
- c)7
- d)8
- e)Cannot be determined from the given graph
Correct answer is option 'E'. Can you explain this answer?
The figure below shows the graph of a function f (x). How many solutions does the equation f ( f(x)) = 15 have?
a)
5
b)
6
c)
7
d)
8
e)
Cannot be determined from the given graph
|
|
Ayush Rane answered |
f ( f (x) = 15 when f (x) = 4 or f (x) = 12 in the given function. The graph given in the figure
becomes equal to 4 at 4 points and it becomes equal to 12 at 2 points in the figure. This gives us 6
points in the given figure when f (f (x) =15. However, the given function is continuous beyond the
part of it which is shown between –10 and +13 in the figure. Hence, we do not know how many
more solutions to f (f (x) = 15 would be there. Hence, Option (e) is the correct answer.
becomes equal to 4 at 4 points and it becomes equal to 12 at 2 points in the figure. This gives us 6
points in the given figure when f (f (x) =15. However, the given function is continuous beyond the
part of it which is shown between –10 and +13 in the figure. Hence, we do not know how many
more solutions to f (f (x) = 15 would be there. Hence, Option (e) is the correct answer.
A function a(x) is defined for x as 3a(x) + 2a (2 – x) = (x + 3)2. What is the value of [G (–5)]where [x] represents the greatest integer less than or equal to x?- a)37
- b)–38
- c)–37
- d)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
A function a(x) is defined for x as 3a(x) + 2a (2 – x) = (x + 3)2. What is the value of [G (–5)]
where [x] represents the greatest integer less than or equal to x?
a)
37
b)
–38
c)
–37
d)
Cannot be determined
|
|
Ishaan Iyer answered |
The equation given in the question is: 3a(x) + 2a (2–x) = (x + 3)2
Replacing x by (2–x) in the above equation, we get
3a(2–x) + 2a(x) = (5–x)2
Solving the above pairs of equation, we get
a(x) = (x2 + 38 – 23)/5
Thus, G(–5) = –188/5 = –37.6. The value of [–37.6] = –37. Hence, Option (c) is the correct
answer.
Replacing x by (2–x) in the above equation, we get
3a(2–x) + 2a(x) = (5–x)2
Solving the above pairs of equation, we get
a(x) = (x2 + 38 – 23)/5
Thus, G(–5) = –188/5 = –37.6. The value of [–37.6] = –37. Hence, Option (c) is the correct
answer.
f(x) is any function and f–1(x) is known as inverse of f(x), then f–1(x) of f(x) = ex is- a)–ex
- b)e–x
- c)logex
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
f(x) is any function and f–1(x) is known as inverse of f(x), then f–1(x) of f(x) = ex is
a)
–ex
b)
e–x
c)
logex
d)
None of these
|
|
Aarav Sharma answered |
To understand why f1(x) of f(x) is equal to ex, we need to understand the concept of inverse functions and the relationship between exponents and logarithms.
Inverse Function:
The inverse of a function is a function that undoes the original function. In other words, if we apply the original function to a value x and then apply its inverse to the result, we should get back the original value x.
Relationship between exponents and logarithms:
The exponential function ex represents the value e raised to the power of x. On the other hand, the natural logarithm function ln(x) represents the inverse operation of exponentiation. In other words, ln(x) undoes the effect of the exponential function.
Explanation:
Given that f(x) is any function and f1(x) is its inverse, we need to find f1(x) of f(x). According to the answer, this expression is equal to ex.
We know that applying an inverse function undoes the effect of the original function. In this case, if we apply f(x) to a value x and then apply f1(x) to the result, we should get back the original value x.
If we consider f(x) = ex, then applying f(x) to a value x would result in ex. Now, if we apply f1(x) to the result ex, it should undo the effect of the exponential function.
The inverse function of the exponential function is the natural logarithm function. Therefore, applying f1(x) to ex would result in ln(ex). However, we also know that ln(ex) simplifies to just x.
Therefore, f1(x) of f(x) = ex simplifies to just ex, which matches the answer option C.
In conclusion, the inverse of the function f(x) = ex is f1(x) = ex.
Inverse Function:
The inverse of a function is a function that undoes the original function. In other words, if we apply the original function to a value x and then apply its inverse to the result, we should get back the original value x.
Relationship between exponents and logarithms:
The exponential function ex represents the value e raised to the power of x. On the other hand, the natural logarithm function ln(x) represents the inverse operation of exponentiation. In other words, ln(x) undoes the effect of the exponential function.
Explanation:
Given that f(x) is any function and f1(x) is its inverse, we need to find f1(x) of f(x). According to the answer, this expression is equal to ex.
We know that applying an inverse function undoes the effect of the original function. In this case, if we apply f(x) to a value x and then apply f1(x) to the result, we should get back the original value x.
If we consider f(x) = ex, then applying f(x) to a value x would result in ex. Now, if we apply f1(x) to the result ex, it should undo the effect of the exponential function.
The inverse function of the exponential function is the natural logarithm function. Therefore, applying f1(x) to ex would result in ln(ex). However, we also know that ln(ex) simplifies to just x.
Therefore, f1(x) of f(x) = ex simplifies to just ex, which matches the answer option C.
In conclusion, the inverse of the function f(x) = ex is f1(x) = ex.
Let f(x) = ax2 + bx + c, where a, b and c are certain constants and a ≠ 0. It is known that f (5) = −3f(2) and that 3 is a root of f(x) = 0.What is the value of a+b+c?- a)9
- b)14
- c)13
- d)17
- e)cannot be determined
Correct answer is option 'E'. Can you explain this answer?
Let f(x) = ax2 + bx + c, where a, b and c are certain constants and a ≠ 0. It is known that f (5) = −3f(2) and that 3 is a root of f(x) = 0.
What is the value of a+b+c?
a)
9
b)
14
c)
13
d)
17
e)
cannot be determined
|
|
Aarav Sharma answered |
The equation you provided seems to be incomplete. Could you please provide the full equation?
For the above question find the value of the expression: F(1) × F(2) × F(3) × F(4) ×….F(1000)- a)2001
- b)1999
- c)2004
- d)1997
Correct answer is 'A'. Can you explain this answer?
For the above question find the value of the expression: F(1) × F(2) × F(3) × F(4) ×….F(1000)
a)
2001
b)
1999
c)
2004
d)
1997
|
Shraddha Dasgupta answered |
The composition of f and g is given by f(g(x)) which is equal to 2(3x + 4) + 1.
A certain function always obeys the rule: If f (x.y) = f(x). f(y) where x and y are positive realnumbers. A certain Mr. Mogambo found that the value of f (128) = 4, then find the value of thevariable M = f (0.5). f (1). f (2). f (4). f (8). f (16). f (32). f (64). f (128). f (256)- a)128
- b)256
- c)512
- d)1024
Correct answer is option 'D'. Can you explain this answer?
A certain function always obeys the rule: If f (x.y) = f(x). f(y) where x and y are positive realnumbers. A certain Mr. Mogambo found that the value of f (128) = 4, then find the value of thevariable M = f (0.5). f (1). f (2). f (4). f (8). f (16). f (32). f (64). f (128). f (256)
a)
128
b)
256
c)
512
d)
1024
|
|
Nandini Dasgupta answered |
Since f (128) = 4, we can see that the product of f (256). f (0.5) = f (256 × 0.5) = f (128) = 4.
Similarly, the products f (1). f (128) = f (2). f (64)
= f (4). f (32) = f (8). f (16) = 4.
Thus, M = 4 × 4 × 4 × 4 × 4 = 1024.
Option (d) is the correct answer.
Similarly, the products f (1). f (128) = f (2). f (64)
= f (4). f (32) = f (8). f (16) = 4.
Thus, M = 4 × 4 × 4 × 4 × 4 = 1024.
Option (d) is the correct answer.
Chapter doubts & questions for Functions - Quantitative Aptitude (Quant) 2025 is part of Interview Preparation exam preparation. The chapters have been prepared according to the Interview Preparation exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Interview Preparation 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Functions - Quantitative Aptitude (Quant) in English & Hindi are available as part of Interview Preparation exam.
Download more important topics, notes, lectures and mock test series for Interview Preparation Exam by signing up for free.
Quantitative Aptitude (Quant)
164 videos|133 docs|118 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily