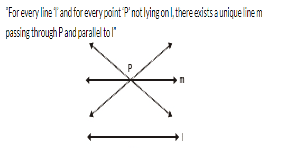All Exams >
Class 9 >
Mathematics (Maths) Class 9 >
All Questions
All questions of Introduction to Euclid's Geometry for Class 9 Exam
Euclid was a teacher of mathematics at ?
- a) Egypt
- b)Greece
- c)Babylonia
- d)Rome
Correct answer is option 'A'. Can you explain this answer?
Euclid was a teacher of mathematics at ?
a)
Egypt
b)
Greece
c)
Babylonia
d)
Rome
|
Arizona Academy answered |
Euclid belonged to Greece.
Ans- Option C.
Ans- Option C.
The number of line segments determined by three collinear points is:a)Twob)Threec)Fourd)Only oneCorrect answer is option 'D'. Can you explain this answer?
|
Arvind Singh answered |
if the points are collinear then only 1 line can pass through 3 points as colinear mean the points which are on same line.
Axiom or pastulates are- a)Conclusions
- b)Reasons
- c)Assumptions
- d)Questions
Correct answer is option 'C'. Can you explain this answer?
Axiom or pastulates are
a)
Conclusions
b)
Reasons
c)
Assumptions
d)
Questions
|
Arzoo Sharma answered |
Axioms and postulates are assumption that are taken bu euclid to prove several theorems , axioms and postulates can not be proved as they are universal truth .
If the point P lies in between M and N and C is midpoint of MP then:
- a)MP + CP = MN
- b)MP + CP + MN
- c)MC + CN = MN
- d)CP + CN = MN
Correct answer is option 'C'. Can you explain this answer?
If the point P lies in between M and N and C is midpoint of MP then:
a)
MP + CP = MN
b)
MP + CP + MN
c)
MC + CN = MN
d)
CP + CN = MN
|
Geetika Menon answered |
Explanation:
When a point P lies between two points M and N, we can say that M-P-N.
Given that C is the midpoint of MP.
So, we can say that MC = CP.
Also, as we know that C is the midpoint of MP, we can say that MP = 2*CP.
Now, we can write MN as:
MN = MP + PN
Substituting the value of MP in the above equation, we get:
MN = 2*CP + PN
Now, we can write PN as:
PN = CN - CP
Substituting the value of PN in the above equation, we get:
MN = 2*CP + CN - CP
Simplifying the above equation, we get:
MN = CP + CN
Therefore, we can say that MC * CN = MN.
Hence, option 'C' is the correct answer.
When a point P lies between two points M and N, we can say that M-P-N.
Given that C is the midpoint of MP.
So, we can say that MC = CP.
Also, as we know that C is the midpoint of MP, we can say that MP = 2*CP.
Now, we can write MN as:
MN = MP + PN
Substituting the value of MP in the above equation, we get:
MN = 2*CP + PN
Now, we can write PN as:
PN = CN - CP
Substituting the value of PN in the above equation, we get:
MN = 2*CP + CN - CP
Simplifying the above equation, we get:
MN = CP + CN
Therefore, we can say that MC * CN = MN.
Hence, option 'C' is the correct answer.
Can two intersecting lines be parallel to a common line?- a)sometimes
- b)Maybe
- c)Yes
- d)No
Correct answer is option 'D'. Can you explain this answer?
Can two intersecting lines be parallel to a common line?
a)
sometimes
b)
Maybe
c)
Yes
d)
No
|
Sabrina Singh answered |
Explanation:
Parallel lines are lines that never intersect, while intersecting lines are lines that cross each other at a point. Therefore, two intersecting lines cannot be parallel to a common line. This can be explained in the following ways:
Proof:
1. Definition of Parallel Lines: Two lines are said to be parallel if they lie in the same plane and do not intersect.
2. Definition of Intersecting Lines: Two lines are said to be intersecting if they meet or cross each other at a point.
3. If two lines are parallel, they can never intersect. This is because the definition of parallel lines states that they do not intersect.
4. If two lines intersect, they can never be parallel. This is because the definition of parallel lines states that they do not intersect.
5. Therefore, two intersecting lines cannot be parallel to a common line. This is because if the two lines intersect, they cannot be parallel, and if they are parallel, they cannot intersect.
Conclusion:
In conclusion, two intersecting lines cannot be parallel to a common line. This is because the definition of parallel lines states that they do not intersect, while the definition of intersecting lines states that they do intersect. Therefore, the correct answer to the question is option 'D', which is 'No'.
Parallel lines are lines that never intersect, while intersecting lines are lines that cross each other at a point. Therefore, two intersecting lines cannot be parallel to a common line. This can be explained in the following ways:
Proof:
1. Definition of Parallel Lines: Two lines are said to be parallel if they lie in the same plane and do not intersect.
2. Definition of Intersecting Lines: Two lines are said to be intersecting if they meet or cross each other at a point.
3. If two lines are parallel, they can never intersect. This is because the definition of parallel lines states that they do not intersect.
4. If two lines intersect, they can never be parallel. This is because the definition of parallel lines states that they do not intersect.
5. Therefore, two intersecting lines cannot be parallel to a common line. This is because if the two lines intersect, they cannot be parallel, and if they are parallel, they cannot intersect.
Conclusion:
In conclusion, two intersecting lines cannot be parallel to a common line. This is because the definition of parallel lines states that they do not intersect, while the definition of intersecting lines states that they do intersect. Therefore, the correct answer to the question is option 'D', which is 'No'.
Theorems are statements which are proved using definitions, _________, previously proved statements and deductive reasoning.- a)Definitions
- b)Axioms
- c)Theorems
- d)Statements
Correct answer is option 'B'. Can you explain this answer?
Theorems are statements which are proved using definitions, _________, previously proved statements and deductive reasoning.
a)
Definitions
b)
Axioms
c)
Theorems
d)
Statements
|
|
Venus Chaudhary answered |
Basically, anything declared to be true and accepted, but does not have any proof or has some practical way of proving it, is an axiom. It is also sometimes referred to as a postulate, or an assumption. A theorem, by definition, is a statement proven based on axioms, othertheorems, and some set of logical connectives.
If B lies on line AC and points A, B and C are distinct such that, AB + BC = AC, then- a)AB < AC
- b)AB > AC
- c)AB = AC
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If B lies on line AC and points A, B and C are distinct such that, AB + BC = AC, then
a)
AB < AC
b)
AB > AC
c)
AB = AC
d)
None of these
|
Jasneet Kaur answered |
Because AB is a part of AC and by Euclid fifth axiom which states that the whole is greater than the part ::AB < ac="">
How many points can be common in two distinct straight lines?- a)one
- b)two
- c)three
- d)None
Correct answer is option 'A'. Can you explain this answer?
How many points can be common in two distinct straight lines?
a)
one
b)
two
c)
three
d)
None
|
|
Arvind Singh answered |
Two distinct lines will always intersect in at most one point. This will be true no matter how many dimensions we're in, as long as we're in a standard Euclidean geometry. One way to see this is to consider what happens if we have two lines which intersect in more than one point.
Every line has- a)three mid-points
- b)two mid-points
- c)one and only mid-point
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Every line has
a)
three mid-points
b)
two mid-points
c)
one and only mid-point
d)
none of these
|
|
Meenakshi B Pillai answered |
Midpoint is the point which divides a line into two equal lines . when it become two equal we need to consider them as separate individual line in which each line has its own midpoint. so a line has only one midpoint which is unique.
If a > b and b > c, then,- a)a > c
- b)a < c
- c)a = c
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If a > b and b > c, then,
a)
a > c
b)
a < c
c)
a = c
d)
None of these
|
Nipun S answered |
As a>b and b>c it means that a >b>c obviasly a >c is corrrect answer.
A proof is required for:- a)Definition
- b)Postulate
- c)Axiom
- d)Theorem
Correct answer is option 'D'. Can you explain this answer?
A proof is required for:
a)
Definition
b)
Postulate
c)
Axiom
d)
Theorem
|
Prachi Rathore answered |
Theorem is a statement that requires a proof
The number of dimensions, a solid has- a)0
- b)1
- c)3
- d)2
Correct answer is option 'C'. Can you explain this answer?
The number of dimensions, a solid has
a)
0
b)
1
c)
3
d)
2
|
Winner Abcd answered |
A solid only has a length and breadth that is only two dimensions
Which of the following are boundaries of a surface?
- a)Points
- b) Curves
- c)Surfaces
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Which of the following are boundaries of a surface?
a)
Points
b)
Curves
c)
Surfaces
d)
None of these
|
|
Monika Riya answered |
Can anyone explain it me please?
The things which are double of same things are:- a)halves of same thing
- b)double of the same thing
- c)Equal
- d)Unequal
Correct answer is option 'C'. Can you explain this answer?
The things which are double of same things are:
a)
halves of same thing
b)
double of the same thing
c)
Equal
d)
Unequal
|
|
Arjun Sharma answered |
Things which are double of the same things are equal to one another.
Example :
1. If 2x = 2y then x = y.
2. If a = b, then 2a = 2b
Which of the following statement is true ?- a)Two lines are parallel, if they a common point
- b)Two lines are parallel, if they do not have common point
- c)Two lines can be never parallel
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Which of the following statement is true ?
a)
Two lines are parallel, if they a common point
b)
Two lines are parallel, if they do not have common point
c)
Two lines can be never parallel
d)
None of these
|
Niyati Shah answered |
Explanation:
Two lines are said to be parallel if they do not intersect each other at any point. In other words, they have no common point. Therefore, the correct statement is option 'b'.
Proof:
To understand why option 'b' is true, let's consider two lines, line AB and line CD.
Case 1: Suppose line AB and line CD intersect at point E.
In this case, line AB and line CD are not parallel because they have a common point of intersection, which is point E.
Case 2: Suppose line AB and line CD do not intersect.
In this case, line AB and line CD are parallel because they do not have any common point of intersection.
Conclusion:
From the above proof, we can conclude that two lines are parallel if they do not have any common point of intersection. Hence, option 'b' is the correct statement.
Additional Information:
- Two lines are said to be perpendicular if they intersect at a right angle (90 degrees). Perpendicular lines have negative reciprocal slopes.
- Two lines are said to be skew if they are not in the same plane and do not intersect. Skew lines have no common point and are not parallel.
- Two lines are said to be coincident if they completely overlap each other. Coincident lines have infinitely many common points and are not parallel.
Note:
It is important to note that the question states "Two lines are parallel, if they do not have a common point." This means that for two lines to be parallel, it is not necessary for them to have a common point. However, it is possible for parallel lines to have a common point at infinity, which is not considered in this context.
Two lines are said to be parallel if they do not intersect each other at any point. In other words, they have no common point. Therefore, the correct statement is option 'b'.
Proof:
To understand why option 'b' is true, let's consider two lines, line AB and line CD.
Case 1: Suppose line AB and line CD intersect at point E.
In this case, line AB and line CD are not parallel because they have a common point of intersection, which is point E.
Case 2: Suppose line AB and line CD do not intersect.
In this case, line AB and line CD are parallel because they do not have any common point of intersection.
Conclusion:
From the above proof, we can conclude that two lines are parallel if they do not have any common point of intersection. Hence, option 'b' is the correct statement.
Additional Information:
- Two lines are said to be perpendicular if they intersect at a right angle (90 degrees). Perpendicular lines have negative reciprocal slopes.
- Two lines are said to be skew if they are not in the same plane and do not intersect. Skew lines have no common point and are not parallel.
- Two lines are said to be coincident if they completely overlap each other. Coincident lines have infinitely many common points and are not parallel.
Note:
It is important to note that the question states "Two lines are parallel, if they do not have a common point." This means that for two lines to be parallel, it is not necessary for them to have a common point. However, it is possible for parallel lines to have a common point at infinity, which is not considered in this context.
The three steps from solids to points are- a)Solids – lines – points – surfaces
- b)Solids – points – lines – surfaces
- c)Solids – surfaces – lines – points
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The three steps from solids to points are
a)
Solids – lines – points – surfaces
b)
Solids – points – lines – surfaces
c)
Solids – surfaces – lines – points
d)
none of these
|
A Singh answered |
Firstly, a cube is a solid. It has 6 surfaces. After the breakdown a solid cube we get 6 surfaces. That is if we take 6 identical Squares of paper, and join them together in a particular order we get a cube.Now when we take one of its surfaces, we see that it is made up of 4 lines. That is for example if we take four matches and join their ends together to form a square, we get one surface of the cube. If we keep adding matchsticks, we get a cube.Now if we take one line which is one matchstick, we see that it is made of particles of wood joined together is a straight order to form a line. That is Many points come together to form a line.Thus breaking down a solid to its components, we can write that:-Solids are made of surfaces.Surfaces are made of lines.Lines are made of points.Therefore --- Solids-> Surfaces-> Lines-> Points.
The boundaries of surfaces are
- a)points
- b)surfaces
- c)lines
- d)curves
Correct answer is option 'D'. Can you explain this answer?
The boundaries of surfaces are
a)
points
b)
surfaces
c)
lines
d)
curves
|
|
Anita Menon answered |
Boundaries of surfaces are known as curves whereas boundaries of solids are known as surfaces. Therefore, the boundaries of surfaces are curves.
The total number of propositions in the Euclid’s Elements are- a)465
- b)460
- c)32
- d)13
Correct answer is option 'A'. Can you explain this answer?
The total number of propositions in the Euclid’s Elements are
a)
465
b)
460
c)
32
d)
13
|
|
Ananya Das answered |
In the thirteen books that comprise Euclid's Elements there is a total of 465 propositions.
The edges of a surface are- a)Plans
- b)Lines
- c)Points
- d)Rays
Correct answer is option 'B'. Can you explain this answer?
The edges of a surface are
a)
Plans
b)
Lines
c)
Points
d)
Rays
|
Prema Latha answered |
Because it is a plain surface
Two distinct points in a plane determine .................- a)Two lines
- b)Three lines
- c)A unique line
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Two distinct points in a plane determine .................
a)
Two lines
b)
Three lines
c)
A unique line
d)
None of these
|
Sankalp Kumar answered |
Because it is different line that means not part of the whole
It is known that if a + b = 4 then 1/2(a + b) = 2. The Euclid’s axiom that illustrates this statement is- a)VI axiom
- b)IV axiom
- c)V axiom
- d)VII axiom
Correct answer is option 'D'. Can you explain this answer?
It is known that if a + b = 4 then 1/2(a + b) = 2. The Euclid’s axiom that illustrates this statement is
a)
VI axiom
b)
IV axiom
c)
V axiom
d)
VII axiom
|
Sandeep Rane answered |
Understanding Euclid's Axioms
In Euclidean geometry, axioms serve as foundational truths that do not require proof. They help establish the principles of geometry and are essential for deriving other mathematical statements.
Context of the Statement
The statement provided, "if a + b = 4 then 1/2(a + b) = 2," illustrates a basic property of equality and operations in mathematics. This is a simple logical deduction demonstrating that if you divide both sides of an equation by a number, the equality remains valid.
Identification of the Correct Axiom
The correct choice for the axiom that illustrates this statement is:
- VII Axiom: This axiom states that "things which are equal to the same thing are also equal to one another."
Explanation of the VII Axiom
- Equality Principle: The VII Axiom emphasizes that if two quantities are equal to a third quantity, they are equal to each other.
- Application in the Given Statement: In the example, since a + b equals 4, dividing both sides by 2 provides the result that 1/2(a + b) equals 2, maintaining the equality.
Conclusion
The application of the VII Axiom in this context reinforces the understanding of equality in mathematical operations. Thus, the correct answer to the question is option D: VII Axiom. This axiom is crucial for understanding how equal values can be manipulated while retaining their equality.
In Euclidean geometry, axioms serve as foundational truths that do not require proof. They help establish the principles of geometry and are essential for deriving other mathematical statements.
Context of the Statement
The statement provided, "if a + b = 4 then 1/2(a + b) = 2," illustrates a basic property of equality and operations in mathematics. This is a simple logical deduction demonstrating that if you divide both sides of an equation by a number, the equality remains valid.
Identification of the Correct Axiom
The correct choice for the axiom that illustrates this statement is:
- VII Axiom: This axiom states that "things which are equal to the same thing are also equal to one another."
Explanation of the VII Axiom
- Equality Principle: The VII Axiom emphasizes that if two quantities are equal to a third quantity, they are equal to each other.
- Application in the Given Statement: In the example, since a + b equals 4, dividing both sides by 2 provides the result that 1/2(a + b) equals 2, maintaining the equality.
Conclusion
The application of the VII Axiom in this context reinforces the understanding of equality in mathematical operations. Thus, the correct answer to the question is option D: VII Axiom. This axiom is crucial for understanding how equal values can be manipulated while retaining their equality.
The boundaries of the solids are- a)curves
- b)lines
- c)surfaces
- d)points
Correct answer is option 'C'. Can you explain this answer?
The boundaries of the solids are
a)
curves
b)
lines
c)
surfaces
d)
points
|
Shiv Kumar answered |
Because solid has definite shape so that's why solid has a plane surface
The number of lines passing through two distinct points- a)4
- b)2
- c)3
- d)1
Correct answer is option 'D'. Can you explain this answer?
The number of lines passing through two distinct points
a)
4
b)
2
c)
3
d)
1
|
ARSHITA answered |
Correct answer is d) 1.
It is known that if a + b = 4 then a + b + c = 4 + c. The Euclid’s axiom that illustrates this statement is- a)III axiom
- b)IV axiom
- c)I axiom
- d)II axiom
Correct answer is option 'D'. Can you explain this answer?
It is known that if a + b = 4 then a + b + c = 4 + c. The Euclid’s axiom that illustrates this statement is
a)
III axiom
b)
IV axiom
c)
I axiom
d)
II axiom
|
|
Chirag Menon answered |
Ean algorithm is not applicable here as this is not a problem of finding the greatest common divisor of two numbers.
Instead, we can use algebraic manipulation to prove the statement.
Starting with a b = 4, we can rearrange it to get:
a = 4 / b
Substituting this into a b c = 4 c, we get:
(4 / b) b c = 4 c
Simplifying, we get:
4c = 4c
Which is true for any value of c.
Therefore, we have shown that if a b = 4, then a b c = 4 c.
Instead, we can use algebraic manipulation to prove the statement.
Starting with a b = 4, we can rearrange it to get:
a = 4 / b
Substituting this into a b c = 4 c, we get:
(4 / b) b c = 4 c
Simplifying, we get:
4c = 4c
Which is true for any value of c.
Therefore, we have shown that if a b = 4, then a b c = 4 c.
Two lines are intersecting, if they have :- a)A common point
- b)An uncommon point
- c)Two collinear point
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Two lines are intersecting, if they have :
a)
A common point
b)
An uncommon point
c)
Two collinear point
d)
None of these
|
Juhi Ahuja answered |
Two distinct lines will always intersect in at most one point. This will be true no matter how many dimensions we're in, as long as we're in a standard Euclidean geometry. ... Then, there must exist at least two distinct points in common to both lines (since they intersect at least twice).
Pythagoras was a student of- a)Thales
- b)Archimedes
- c)Euclid
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Pythagoras was a student of
a)
Thales
b)
Archimedes
c)
Euclid
d)
none of these
|
Imk Pathshala answered |
Pythagoras was notably a student of Thales, a prominent figure in ancient Greek philosophy and mathematics.
Key points about Thales:
- Thales is often regarded as the first philosopher in Western history.
- He laid the groundwork for mathematics and science by introducing logical reasoning.
- His contributions include early theories in geometry and astronomy.
- Thales is also known for predicting a solar eclipse and for his belief that water is the fundamental substance of the universe.
Pythagoras learned significant mathematical concepts from Thales, which influenced his own theories, including the famous Pythagorean theorem.
The number of dimension, a point has- a)1
- b)2
- c)3
- d)0
Correct answer is option 'D'. Can you explain this answer?
The number of dimension, a point has
a)
1
b)
2
c)
3
d)
0
|
Sayali Shah answered |
The correct answer is option 'D' - a point has 0 dimensions. Let's explore this concept in detail:
Understanding Dimensions:
In mathematics, dimensions refer to the number of coordinates required to specify the location of an object in space. It determines the minimum number of independent parameters needed to describe a point or an object.
Points and Dimensions:
A point is a fundamental object in geometry that does not have any size or shape. It is considered a 0-dimensional object because it does not require any coordinates to locate it. A point is simply a position in space without any extent.
Zero Dimensions:
Zero dimensions imply that an object does not have any extent or size. In the case of a point, it does not occupy any space and is infinitely small. A point is defined by its position, which can be described using coordinates, but it itself does not possess any dimensions.
Visualization:
To understand this concept visually, imagine a blank piece of paper. A point can be represented by a dot on this paper. The dot has no size or shape, and it does not cover any space on the paper. It is simply a position on the paper, representing a point in space.
Higher Dimensions:
In contrast to a point, higher-dimensional objects like lines, planes, and solids have dimensions. For example, a line in two-dimensional space requires two coordinates (x, y) to specify its position. Similarly, a plane in three-dimensional space requires three coordinates (x, y, z) to locate it.
Conclusion:
In summary, a point is a 0-dimensional object as it does not have any size, shape, or extent. It is simply a position in space without any dimensions. Therefore, the correct answer is option 'D' - a point has 0 dimensions.
Understanding Dimensions:
In mathematics, dimensions refer to the number of coordinates required to specify the location of an object in space. It determines the minimum number of independent parameters needed to describe a point or an object.
Points and Dimensions:
A point is a fundamental object in geometry that does not have any size or shape. It is considered a 0-dimensional object because it does not require any coordinates to locate it. A point is simply a position in space without any extent.
Zero Dimensions:
Zero dimensions imply that an object does not have any extent or size. In the case of a point, it does not occupy any space and is infinitely small. A point is defined by its position, which can be described using coordinates, but it itself does not possess any dimensions.
Visualization:
To understand this concept visually, imagine a blank piece of paper. A point can be represented by a dot on this paper. The dot has no size or shape, and it does not cover any space on the paper. It is simply a position on the paper, representing a point in space.
Higher Dimensions:
In contrast to a point, higher-dimensional objects like lines, planes, and solids have dimensions. For example, a line in two-dimensional space requires two coordinates (x, y) to specify its position. Similarly, a plane in three-dimensional space requires three coordinates (x, y, z) to locate it.
Conclusion:
In summary, a point is a 0-dimensional object as it does not have any size, shape, or extent. It is simply a position in space without any dimensions. Therefore, the correct answer is option 'D' - a point has 0 dimensions.
A pyramid is a solid figure, the base of which is.- a)Only a rectangle
- b)Only a square
- c)Only a triangle
- d)Any polygon
Correct answer is option 'D'. Can you explain this answer?
A pyramid is a solid figure, the base of which is.
a)
Only a rectangle
b)
Only a square
c)
Only a triangle
d)
Any polygon
|
Anchal Singh answered |
A pyramid is a polyhedron that has a base, which can be any polygon, and three or more triangular faces that meet at a point called the apex. A pyramid has one base and at least three triangular faces. It has edges where faces meet each other or the base, vertices where two faces meet the base, and a vertex at the top where all of the triangular faces meet. A pyramid is named by the shape of its base.
Euclid’s second postulate states that a terminated line can be:- a)Extended indefinitely
- b)Divided into two equal parts
- c)Drawn parallel to another line
- d)Measured accurately
Correct answer is option 'A'. Can you explain this answer?
Euclid’s second postulate states that a terminated line can be:
a)
Extended indefinitely
b)
Divided into two equal parts
c)
Drawn parallel to another line
d)
Measured accurately
|
EduRev Class 9 answered |
Euclid's second postulate states:
- A terminated line can be extended indefinitely.
This means that if you have a line segment, you can keep extending it in either direction without any limit.
In Indus Valley Civilisation the bricks used for construction work were having dimensions in the ratio- a)it is 1 : 3 : 4
- b)it is 4 : 2 : 1
- c)it is 4 : 3 : 2
- d)it is 4 : 4 : 1
Correct answer is option 'B'. Can you explain this answer?
In Indus Valley Civilisation the bricks used for construction work were having dimensions in the ratio
a)
it is 1 : 3 : 4
b)
it is 4 : 2 : 1
c)
it is 4 : 3 : 2
d)
it is 4 : 4 : 1
|
Shubham Iyer answered |
**Answer:**
The correct answer is option B: the dimensions of the bricks used in the Indus Valley Civilization were in the ratio of 4:2:1.
**Explanation:**
The Indus Valley Civilization, also known as the Harappan Civilization, was one of the most ancient civilizations in the world that existed around 3300 BCE to 1300 BCE in the region of the Indus River Valley, which is present-day Pakistan and northwestern India.
**1. Standardized Brick Size:**
One of the remarkable features of the Indus Valley Civilization was the standardized size of the bricks used in their construction activities. The bricks were uniformly sized, which suggests a planned and organized approach to construction.
**2. Ratio of Brick Dimensions:**
The dimensions of the bricks used in the construction of the Indus Valley Civilization were in the ratio of 4:2:1. This means that the length, width, and height of the bricks were in this proportion.
- The ratio of 4:2:1 suggests that the length of the brick was four times its height and twice its width.
**3. Advantages of Standardized Bricks:**
The use of standardized bricks provided several advantages to the builders of the Indus Valley Civilization. Some of these advantages include:
- Ease of construction: With standardized bricks, the builders could easily plan and construct buildings with uniform dimensions. This would have made the construction process more efficient and faster.
- Structural stability: The use of uniformly sized bricks allowed for stronger and more stable structures. The bricks could be easily stacked and interlocked, providing stability to the walls.
- Versatility: The standardized brick size allowed for flexibility in construction. The bricks could be used in various combinations to create different architectural elements such as walls, floors, roofs, and drainage systems.
**4. Evidence of Standardized Bricks:**
Archaeological excavations at Harappa and Mohenjo-Daro, two major cities of the Indus Valley Civilization, have provided evidence of the standardized brick size. The bricks found at these sites have consistent dimensions, with a length to width ratio of approximately 4:2:1.
**Conclusion:**
In conclusion, the bricks used in the construction of the Indus Valley Civilization were standardized, with dimensions in the ratio of 4:2:1. This standardized brick size provided several advantages in terms of ease of construction, structural stability, and versatility. The evidence from archaeological excavations supports this finding, further confirming the use of standardized bricks in the Indus Valley Civilization.
The correct answer is option B: the dimensions of the bricks used in the Indus Valley Civilization were in the ratio of 4:2:1.
**Explanation:**
The Indus Valley Civilization, also known as the Harappan Civilization, was one of the most ancient civilizations in the world that existed around 3300 BCE to 1300 BCE in the region of the Indus River Valley, which is present-day Pakistan and northwestern India.
**1. Standardized Brick Size:**
One of the remarkable features of the Indus Valley Civilization was the standardized size of the bricks used in their construction activities. The bricks were uniformly sized, which suggests a planned and organized approach to construction.
**2. Ratio of Brick Dimensions:**
The dimensions of the bricks used in the construction of the Indus Valley Civilization were in the ratio of 4:2:1. This means that the length, width, and height of the bricks were in this proportion.
- The ratio of 4:2:1 suggests that the length of the brick was four times its height and twice its width.
**3. Advantages of Standardized Bricks:**
The use of standardized bricks provided several advantages to the builders of the Indus Valley Civilization. Some of these advantages include:
- Ease of construction: With standardized bricks, the builders could easily plan and construct buildings with uniform dimensions. This would have made the construction process more efficient and faster.
- Structural stability: The use of uniformly sized bricks allowed for stronger and more stable structures. The bricks could be easily stacked and interlocked, providing stability to the walls.
- Versatility: The standardized brick size allowed for flexibility in construction. The bricks could be used in various combinations to create different architectural elements such as walls, floors, roofs, and drainage systems.
**4. Evidence of Standardized Bricks:**
Archaeological excavations at Harappa and Mohenjo-Daro, two major cities of the Indus Valley Civilization, have provided evidence of the standardized brick size. The bricks found at these sites have consistent dimensions, with a length to width ratio of approximately 4:2:1.
**Conclusion:**
In conclusion, the bricks used in the construction of the Indus Valley Civilization were standardized, with dimensions in the ratio of 4:2:1. This standardized brick size provided several advantages in terms of ease of construction, structural stability, and versatility. The evidence from archaeological excavations supports this finding, further confirming the use of standardized bricks in the Indus Valley Civilization.
The side faces of a pyramid are- a)rectangles
- b)squares
- c)triangles
- d)polygons
Correct answer is option 'C'. Can you explain this answer?
The side faces of a pyramid are
a)
rectangles
b)
squares
c)
triangles
d)
polygons
|
Sankar Dey answered |
Introduction:
A pyramid is a three-dimensional geometric shape that has a polygonal base and triangular faces that meet at a common vertex or apex. In this question, we are asked about the shape of the side faces of a pyramid.
Explanation:
The correct answer is option 'C', which states that the side faces of a pyramid are triangles. Let's understand why this is the case.
Definition of a Pyramid:
A pyramid is a polyhedron with a polygonal base and triangular faces that meet at a common vertex or apex. The base can be any polygon, such as a triangle, quadrilateral, pentagon, hexagon, etc. However, regardless of the shape of the base, the side faces of a pyramid are always triangles.
Properties of a Pyramid:
1. Triangular Faces: The side faces of a pyramid are always triangular. This means that each side face is a triangle formed by connecting the vertices of the base to the apex of the pyramid.
2. Base Shape: The base of a pyramid can be any polygon, such as a triangle, quadrilateral, pentagon, etc. However, the side faces are always triangular, regardless of the shape of the base.
3. Number of Side Faces: The number of side faces in a pyramid is equal to the number of sides of the base polygon. For example, a pyramid with a triangular base will have three side faces, a pyramid with a quadrilateral base will have four side faces, and so on.
4. Common Vertex: All the side faces of a pyramid meet at a common vertex or apex. This vertex is directly above the centroid or center of the base polygon.
Conclusion:
In conclusion, the side faces of a pyramid are always triangles, regardless of the shape of the base polygon. This is a fundamental property of a pyramid and helps to define its unique shape in three-dimensional space.
A pyramid is a three-dimensional geometric shape that has a polygonal base and triangular faces that meet at a common vertex or apex. In this question, we are asked about the shape of the side faces of a pyramid.
Explanation:
The correct answer is option 'C', which states that the side faces of a pyramid are triangles. Let's understand why this is the case.
Definition of a Pyramid:
A pyramid is a polyhedron with a polygonal base and triangular faces that meet at a common vertex or apex. The base can be any polygon, such as a triangle, quadrilateral, pentagon, hexagon, etc. However, regardless of the shape of the base, the side faces of a pyramid are always triangles.
Properties of a Pyramid:
1. Triangular Faces: The side faces of a pyramid are always triangular. This means that each side face is a triangle formed by connecting the vertices of the base to the apex of the pyramid.
2. Base Shape: The base of a pyramid can be any polygon, such as a triangle, quadrilateral, pentagon, etc. However, the side faces are always triangular, regardless of the shape of the base.
3. Number of Side Faces: The number of side faces in a pyramid is equal to the number of sides of the base polygon. For example, a pyramid with a triangular base will have three side faces, a pyramid with a quadrilateral base will have four side faces, and so on.
4. Common Vertex: All the side faces of a pyramid meet at a common vertex or apex. This vertex is directly above the centroid or center of the base polygon.
Conclusion:
In conclusion, the side faces of a pyramid are always triangles, regardless of the shape of the base polygon. This is a fundamental property of a pyramid and helps to define its unique shape in three-dimensional space.
The edge of a surface are- a)lines
- b)points
- c)curves
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The edge of a surface are
a)
lines
b)
points
c)
curves
d)
none of these
|
|
Sreyash Suyigya answered |
It can be explained by using 6 axiom of Euclid...
Can you explain the answer of this question below:Euclid's Postulate 1 is :
- A:
A straight line may be drawn from any point to any other point.
- B:
A terminated line can be produced indefinitely
- C:
All right angles are equal to one another
- D:
None of these
The answer is A.
Euclid's Postulate 1 is :
A straight line may be drawn from any point to any other point.
A terminated line can be produced indefinitely
All right angles are equal to one another
None of these
|
|
Prachi Rathore answered |
There are six euclid's postulates= Postulate .1. A straight line segment can be drawn joining any two points.2. Any straight line segment can be extended indefinitely in a straight line.3. Given any straight lines segment, a circle can be drawn having the segment as radius and one endpoint as center.4. All Right Angles are congruent.5. If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two Right Angles, then the two lines ......... and your question is what is the 1st postulate so your ans is a
‘Lines are parallel if they do not intersect’ – is stated in the form of:- a)A postulate
- b)An axiom
- c)A definition
- d)A proof
Correct answer is option 'C'. Can you explain this answer?
‘Lines are parallel if they do not intersect’ – is stated in the form of:
a)
A postulate
b)
An axiom
c)
A definition
d)
A proof
|
|
Arvind Singh answered |
‘Lines are parallel, if they do not intersect’ is the definition of parallel lines.
Euclid summarised these statements as definitions. He began his exposition by
listing 23 definitions in Book 1 of the ‘Elements’. A few of them are given below:
A point is that which has no part.
A line is breadth less length.
The ends of a line are points.
A straight line is a line which lies evenly with the points on itself.
A surface is that which has length and breadth only.
Lines are parallel, if they do not intersect.
The edges of a surface are lines.
A plane surface is a surface which lies evenly with the straight lines on
itself
It is known that if a + b = 4 then 2(a + b) = 8. The Euclid’s axiom that illustrates this statement is- a)VI axiom
- b)IV axiom
- c)III axiom
- d)I axiom
Correct answer is option 'A'. Can you explain this answer?
It is known that if a + b = 4 then 2(a + b) = 8. The Euclid’s axiom that illustrates this statement is
a)
VI axiom
b)
IV axiom
c)
III axiom
d)
I axiom
|
Asha Mukherjee answered |
Ean algorithm can be used to find the greatest common divisor of a and b, denoted as gcd(a,b).
The Euclidean algorithm involves repeatedly dividing the larger number by the smaller number and taking the remainder, until one of the numbers becomes zero. The last non-zero remainder is the gcd of the original two numbers.
For example, to find the gcd of 20 and 12:
- Divide 20 by 12 to get a quotient of 1 and a remainder of 8.
- Divide 12 by 8 to get a quotient of 1 and a remainder of 4.
- Divide 8 by 4 to get a quotient of 2 and no remainder.
Therefore, the gcd of 20 and 12 is 4.
The Euclidean algorithm involves repeatedly dividing the larger number by the smaller number and taking the remainder, until one of the numbers becomes zero. The last non-zero remainder is the gcd of the original two numbers.
For example, to find the gcd of 20 and 12:
- Divide 20 by 12 to get a quotient of 1 and a remainder of 8.
- Divide 12 by 8 to get a quotient of 1 and a remainder of 4.
- Divide 8 by 4 to get a quotient of 2 and no remainder.
Therefore, the gcd of 20 and 12 is 4.
If the point P lies in between M and N, C is the mid-point of MP then- a)CP + CN = MN
- b)MP + CP = MN
- c)MC + CN = MN
- d)MC + PN = MN
Correct answer is option 'C'. Can you explain this answer?
If the point P lies in between M and N, C is the mid-point of MP then
a)
CP + CN = MN
b)
MP + CP = MN
c)
MC + CN = MN
d)
MC + PN = MN
|
|
Ishan Choudhary answered |
Given information:
- Point P lies between points M and N.
- Point C is the midpoint of line segment MP.
To prove:
MC * CN = MN
Proof:
We can start by drawing a diagram to visualize the given information. Let's represent the given points on a line segment as shown below:
M ----- C ----- P ----- N
Step 1:
Since point C is the midpoint of line segment MP, we can say that MC = CP.
Step 2:
Using the given information that point P lies between points M and N, we can say that MP + PN = MN.
Step 3:
Substituting the value of MP from Step 1, we get CP + PN = MN.
Step 4:
Now, let's consider the line segment CN. Since C is the midpoint of MP, we can say that CN is also a midpoint of PN. Therefore, CN = NP.
Step 5:
Substituting the value of NP from Step 4, we get CP + CN = MN.
Step 6:
Rearranging the equation from Step 5, we have CN + CP = MN.
Step 7:
Using the commutative property of addition, we can write the equation as CP + CN = MN.
Step 8:
Comparing the equation from Step 8 with the equation from Step 3, we can see that they are the same. Therefore, we can conclude that:
MC * CN = MN
Hence, option 'c' is correct.
- Point P lies between points M and N.
- Point C is the midpoint of line segment MP.
To prove:
MC * CN = MN
Proof:
We can start by drawing a diagram to visualize the given information. Let's represent the given points on a line segment as shown below:
M ----- C ----- P ----- N
Step 1:
Since point C is the midpoint of line segment MP, we can say that MC = CP.
Step 2:
Using the given information that point P lies between points M and N, we can say that MP + PN = MN.
Step 3:
Substituting the value of MP from Step 1, we get CP + PN = MN.
Step 4:
Now, let's consider the line segment CN. Since C is the midpoint of MP, we can say that CN is also a midpoint of PN. Therefore, CN = NP.
Step 5:
Substituting the value of NP from Step 4, we get CP + CN = MN.
Step 6:
Rearranging the equation from Step 5, we have CN + CP = MN.
Step 7:
Using the commutative property of addition, we can write the equation as CP + CN = MN.
Step 8:
Comparing the equation from Step 8 with the equation from Step 3, we can see that they are the same. Therefore, we can conclude that:
MC * CN = MN
Hence, option 'c' is correct.
A surface is that which has- a)length only
- b)length and breadth only
- c)breadth only
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A surface is that which has
a)
length only
b)
length and breadth only
c)
breadth only
d)
none of these
|
|
Ishwarya💫 answered |
Because the surface is having both length and breadth it is called surface.
Maximum number of lines that can pass through a single point are
- a)three
- b)one
- c)infinite
- d)two
Correct answer is option 'C'. Can you explain this answer?
Maximum number of lines that can pass through a single point are
a)
three
b)
one
c)
infinite
d)
two
|
|
Gopal Majumdar answered |
Explanation:
In geometry, a line is defined as a straight path that extends indefinitely in both directions. It is made up of an infinite number of points.
Lines through a single point:
When considering lines passing through a single point, we need to understand that a point is defined by its coordinates (x, y). Any line passing through this point can be represented by an equation in the form y = mx + c, where m is the slope of the line and c is the y-intercept.
Infinite number of lines:
Given a single point, there are an infinite number of lines that can pass through it. This is because for any value of m, there is a line that can pass through the point. The slope determines the angle at which the line passes through the point, and there are infinite possible values for the slope.
Visualization:
Imagine a point on a piece of paper. You can draw a line passing through that point in any direction you choose. As long as the line passes through the point, it is valid. You can rotate the line, change its angle, or even make it vertical or horizontal. Each of these lines is unique, yet they all pass through the same point.
Conclusion:
Therefore, the maximum number of lines that can pass through a single point is infinite.
In geometry, a line is defined as a straight path that extends indefinitely in both directions. It is made up of an infinite number of points.
Lines through a single point:
When considering lines passing through a single point, we need to understand that a point is defined by its coordinates (x, y). Any line passing through this point can be represented by an equation in the form y = mx + c, where m is the slope of the line and c is the y-intercept.
Infinite number of lines:
Given a single point, there are an infinite number of lines that can pass through it. This is because for any value of m, there is a line that can pass through the point. The slope determines the angle at which the line passes through the point, and there are infinite possible values for the slope.
Visualization:
Imagine a point on a piece of paper. You can draw a line passing through that point in any direction you choose. As long as the line passes through the point, it is valid. You can rotate the line, change its angle, or even make it vertical or horizontal. Each of these lines is unique, yet they all pass through the same point.
Conclusion:
Therefore, the maximum number of lines that can pass through a single point is infinite.
Euclid divided his famous treatise “The Elements” into- a)13 chapters
- b)12 chapters
- c)11 chapters
- d)9 chapters
Correct answer is option 'A'. Can you explain this answer?
Euclid divided his famous treatise “The Elements” into
a)
13 chapters
b)
12 chapters
c)
11 chapters
d)
9 chapters
|
|
Ananya Sharma answered |
Euclid's "The Elements" is divided into 13 books. Each book is further divided into chapters, called "propositions." The number of propositions in each book varies, but there are a total of 13 books in "The Elements." Therefore, the correct answer is option (a) 13 chapters.
Euclid's Axiom 5 is :- a)The things which coincide with one another are equal to one another
- b)If equals are subtracted from equals, the remainder are equal
- c)The whole is greater than the part.
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Euclid's Axiom 5 is :
a)
The things which coincide with one another are equal to one another
b)
If equals are subtracted from equals, the remainder are equal
c)
The whole is greater than the part.
d)
None of these
|
Harini Paragshah answered |
The ans c is correct...
For example: if p=q+r ; then it is obvious that p > q & p > r.
Another example : we know that 5 = 2+3 so we can tell that 5 > 2 & 5 >3.
I hope this answer is helpful.
For example: if p=q+r ; then it is obvious that p > q & p > r.
Another example : we know that 5 = 2+3 so we can tell that 5 > 2 & 5 >3.
I hope this answer is helpful.
Which of the following needs a proof?- a)Axiom
- b)Postulate
- c)Theorem
- d)Definition
Correct answer is option 'C'. Can you explain this answer?
Which of the following needs a proof?
a)
Axiom
b)
Postulate
c)
Theorem
d)
Definition
|
|
Mohit Chavan answered |
Understanding Axioms, Postulates, Theorems, and Definitions
In the realm of mathematics and logic, different terms serve distinct purposes. Here's a breakdown of each:
Axioms
- Axioms are statements accepted as true without proof.
- They form the foundational building blocks of mathematical systems.
- Example: "Through any two points, there is exactly one straight line."
Postulates
- Postulates are similar to axioms; they are accepted statements used to derive further truths.
- They're often specific to a particular branch of mathematics.
- Example: "A straight line segment can be drawn joining any two points."
Theorems
- Theorems are propositions or statements that require proof.
- They are derived from axioms and postulates through logical reasoning.
- Example: "The sum of the angles in a triangle is 180 degrees" is a theorem needing proof.
Definitions
- Definitions explain the meaning of mathematical terms and concepts.
- They do not require proof; they establish the framework for understanding.
- Example: "A triangle is a polygon with three edges and three vertices."
Conclusion
In summary, the correct answer is option 'C' - Theorem, as it is the only one that necessitates a proof. Axioms and postulates are accepted truths, definitions clarify concepts, while theorems demand logical validation through proof. Understanding these classifications is crucial for grasping mathematical principles and reasoning.
In the realm of mathematics and logic, different terms serve distinct purposes. Here's a breakdown of each:
Axioms
- Axioms are statements accepted as true without proof.
- They form the foundational building blocks of mathematical systems.
- Example: "Through any two points, there is exactly one straight line."
Postulates
- Postulates are similar to axioms; they are accepted statements used to derive further truths.
- They're often specific to a particular branch of mathematics.
- Example: "A straight line segment can be drawn joining any two points."
Theorems
- Theorems are propositions or statements that require proof.
- They are derived from axioms and postulates through logical reasoning.
- Example: "The sum of the angles in a triangle is 180 degrees" is a theorem needing proof.
Definitions
- Definitions explain the meaning of mathematical terms and concepts.
- They do not require proof; they establish the framework for understanding.
- Example: "A triangle is a polygon with three edges and three vertices."
Conclusion
In summary, the correct answer is option 'C' - Theorem, as it is the only one that necessitates a proof. Axioms and postulates are accepted truths, definitions clarify concepts, while theorems demand logical validation through proof. Understanding these classifications is crucial for grasping mathematical principles and reasoning.
“Lines are parallel if they do not intersect” is stated in the form of- a)a postulate
- b)a proof
- c)an axiom
- d)a definition
Correct answer is option 'D'. Can you explain this answer?
“Lines are parallel if they do not intersect” is stated in the form of
a)
a postulate
b)
a proof
c)
an axiom
d)
a definition
|
|
Sagarika Tiwari answered |
It is the definition of parallel lines.
Chapter doubts & questions for Introduction to Euclid's Geometry - Mathematics (Maths) Class 9 2026 is part of Class 9 exam preparation. The chapters have been prepared according to the Class 9 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 9 2026 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Introduction to Euclid's Geometry - Mathematics (Maths) Class 9 in English & Hindi are available as part of Class 9 exam.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Mathematics (Maths) Class 9
40 videos|468 docs|55 tests
|
