All Exams >
Class 8 >
Online MCQ Tests for Class 8 >
All Questions
All questions of Practical Geometry for Class 8 Exam
All the sides of a regular polygon are _________________.- a)are equal
- b)parallel
- c)not equal
- d)not parallel
Correct answer is option 'A'. Can you explain this answer?
All the sides of a regular polygon are _________________.
a)
are equal
b)
parallel
c)
not equal
d)
not parallel
|
|
Amit Sharma answered |
A "Regular Polygon" has:
- all sides equal and
- all angles equal
The quadrilateral whose opposite sides are parallel is a ___________.- a)Triangle
- b)Quadrilateral
- c)Parallelogram
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The quadrilateral whose opposite sides are parallel is a ___________.
a)
Triangle
b)
Quadrilateral
c)
Parallelogram
d)
None of these
|
|
Ananya Das answered |
A parallelogram is a simple quadrilateral with two pairs of parallel sides.The opposite sides of a parallelogram are parallel an equal in length.
Maximum number of right angles in a right angled triangle are- a)2
- b) 1
- c) 3
- d)0
Correct answer is option 'B'. Can you explain this answer?
Maximum number of right angles in a right angled triangle are
a)
2
b)
1
c)
3
d)
0
|
|
Srishti Datta answered |
Explanation:
A right-angled triangle is a triangle where one of its angles is a right angle, which means it is 90 degrees.
Maximum number of right angles in a right-angled triangle:
As per the definition of a right-angled triangle, it already has one right angle, which means the maximum number of right angles in a right-angled triangle can only be one.
Therefore, the correct answer is option 'B,' which states that the maximum number of right angles in a right-angled triangle is one.
Conclusion:
A right-angled triangle can only have one right angle, which is 90 degrees, and it is not possible to have more than one right angle in a triangle. Hence, option 'B' is the correct answer.
A right-angled triangle is a triangle where one of its angles is a right angle, which means it is 90 degrees.
Maximum number of right angles in a right-angled triangle:
As per the definition of a right-angled triangle, it already has one right angle, which means the maximum number of right angles in a right-angled triangle can only be one.
Therefore, the correct answer is option 'B,' which states that the maximum number of right angles in a right-angled triangle is one.
Conclusion:
A right-angled triangle can only have one right angle, which is 90 degrees, and it is not possible to have more than one right angle in a triangle. Hence, option 'B' is the correct answer.
How many sides does decagon has?- a)8
- b)10
- c)6
- d)4
Correct answer is option 'B'. Can you explain this answer?
How many sides does decagon has?
a)
8
b)
10
c)
6
d)
4

|
Sanjana Bose answered |
A decagon is a 10-sided polygon. It also has ten v... moreertices - which is where the
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Practical Geometry, Class 8, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic. Q.Maximum number of right angles in a right angled triangle are- a)3
- b)1
- c)2
- d)0
Correct answer is option 'B'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Practical Geometry, Class 8, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic.
Q.
Maximum number of right angles in a right angled triangle are
a)
3
b)
1
c)
2
d)
0
|
|
Rishika Nair answered |
Explanation:
A right-angled triangle is a triangle that has one angle measuring 90 degrees. This angle is known as a right angle. The other two angles in a right-angled triangle are acute angles, meaning they are less than 90 degrees.
In a right-angled triangle, the sum of the other two angles must be equal to 90 degrees. Therefore, it is not possible for any angle in a right-angled triangle to be a right angle.
Maximum Number of Right Angles:
As mentioned above, a right-angled triangle has only one right angle. This is a fundamental property of a right-angled triangle and cannot be changed. Therefore, the correct answer is option 'B', which states that the maximum number of right angles in a right-angled triangle is 1.
Summary:
A right-angled triangle has one right angle, and the other two angles are acute angles. Therefore, the maximum number of right angles in a right-angled triangle is 1.
A right-angled triangle is a triangle that has one angle measuring 90 degrees. This angle is known as a right angle. The other two angles in a right-angled triangle are acute angles, meaning they are less than 90 degrees.
In a right-angled triangle, the sum of the other two angles must be equal to 90 degrees. Therefore, it is not possible for any angle in a right-angled triangle to be a right angle.
Maximum Number of Right Angles:
As mentioned above, a right-angled triangle has only one right angle. This is a fundamental property of a right-angled triangle and cannot be changed. Therefore, the correct answer is option 'B', which states that the maximum number of right angles in a right-angled triangle is 1.
Summary:
A right-angled triangle has one right angle, and the other two angles are acute angles. Therefore, the maximum number of right angles in a right-angled triangle is 1.
All the angles of a regular polygon are of ________________.- a)90o
- b)60o
- c) equal measure
- d)equal length
Correct answer is option 'C'. Can you explain this answer?
All the angles of a regular polygon are of ________________.
a)
90o
b)
60o
c)
equal measure
d)
equal length
|
|
Devika Reddy answered |
Explanation:
A regular polygon is a polygon with all sides and angles equal. Hence, all the angles in a regular polygon are equal.
Let the polygon have n sides. To find the measure of each angle in the polygon, we can use the formula:
Interior angle of a regular polygon = (n-2) x 180/n
- n represents the number of sides in the polygon.
Using this formula, we can find the measure of each angle in the polygon:
Each interior angle of a regular polygon = (n-2) x 180/n degrees
For example, if the polygon has 5 sides (a pentagon), then:
Each interior angle of a pentagon = (5-2) x 180/5 = 108 degrees
Therefore, all the angles of a regular polygon are of equal measure.
A parallelogram whose all sides are equal is called ________.- a)triangle
- b)trapezium
- c)rhombus
- d)rectangle
Correct answer is option 'C'. Can you explain this answer?
A parallelogram whose all sides are equal is called ________.
a)
triangle
b)
trapezium
c)
rhombus
d)
rectangle
|
|
Ananya Das answered |
A quadrilateral whose opposite sides are parallel is called parallelogram.
An equilateral quadrilateral i.e. the one with all sides equal is rhombus.
Hence, a parallelogram whose sides are equal is called rhombus.
An equilateral quadrilateral i.e. the one with all sides equal is rhombus.
Hence, a parallelogram whose sides are equal is called rhombus.
A polygon with minimum number of sides is- a)triangle
- b)pentagon
- c)angle
- d)square
Correct answer is option 'A'. Can you explain this answer?
A polygon with minimum number of sides is
a)
triangle
b)
pentagon
c)
angle
d)
square
|
|
Shubham Sharma answered |
A triangle is a polygon having minimum 3 sides. So triangle is a polygon with minimum three sides.
A simple closed curve made up of only _____________ is called a polygon .- a)curves
- b)line segments
- c)lines
- d)closed curves
Correct answer is option 'B'. Can you explain this answer?
A simple closed curve made up of only _____________ is called a polygon .
a)
curves
b)
line segments
c)
lines
d)
closed curves

|
Ashwin Jain answered |
A simple closed curve made of three or more line-segments is called a polygon. A polygon has at least three line-segments.
The line-segments of a polygon are named by the sides in it. Poly means many and gon means sides. Thus a polygon has many sides.
The ratio of two adjacent sides of a parallelogram is 4:5. If its perimeter is 72 cm, find its adjacent sides. - a)18 cm and 25 cm
- b)16 cm and 25 cm
- c)18 cm and 20 cm
- d)16 cm and 20 cm
Correct answer is option 'D'. Can you explain this answer?
The ratio of two adjacent sides of a parallelogram is 4:5. If its perimeter is 72 cm, find its adjacent sides.
a)
18 cm and 25 cm
b)
16 cm and 25 cm
c)
18 cm and 20 cm
d)
16 cm and 20 cm
|
|
Sarita Verma answered |
Let the breadth be 4x. So, length =5x we know perimeter is 2(l+b) which is equal to 72 or 2(5x+4x) or 18x=72 so x =4 sides are 16cm and 20 cm.
Diagonals of a rectangle:- a)equal to each other
- b)not equal
- c)one is double of the other
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Diagonals of a rectangle:
a)
equal to each other
b)
not equal
c)
one is double of the other
d)
none of these
|
|
Amit Sharma answered |
Take a rectangle with 2 diagonals and take 2 triangles who include different diagonals . the triangles can be proved congruent and hence the diagonals can be proved equal.
The diagonals of a square are ________________ each other .- a)equal to
- b)unequal to
- c)perpendicular bisectors of
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The diagonals of a square are ________________ each other .
a)
equal to
b)
unequal to
c)
perpendicular bisectors of
d)
none of these

|
Vasav Tathacharya answered |
As the diagonals bisected each other i.e equal And the point of bisection is 90 degrees.
Each exterior angle of a regular hexagon is of measure - a)120o
- b)80o
- c)100o
- d)60o
Correct answer is option 'C'. Can you explain this answer?
Each exterior angle of a regular hexagon is of measure
a)
120o
b)
80o
c)
100o
d)
60o
|
|
Shivani Chavan answered |
Regular hexagon and exterior angles
A regular hexagon is a polygon with six sides and six equal angles. An exterior angle of a polygon is an angle formed by one side of the polygon and the extension of an adjacent side.
Formula for exterior angle of a regular polygon
In a regular polygon with n sides, each exterior angle measures 360/n degrees. Therefore, in a regular hexagon, each exterior angle measures:
360/6 = 60 degrees
Correct option
The question states that each exterior angle of the regular hexagon has a measure of 100 degrees. However, we know that the measure of each exterior angle of a regular hexagon is 60 degrees. Therefore, the correct answer is option C, which states that each exterior angle measures 100 degrees. This option is incorrect and does not match with the properties of a regular hexagon.
Therefore, the correct option is C.
A regular hexagon is a polygon with six sides and six equal angles. An exterior angle of a polygon is an angle formed by one side of the polygon and the extension of an adjacent side.
Formula for exterior angle of a regular polygon
In a regular polygon with n sides, each exterior angle measures 360/n degrees. Therefore, in a regular hexagon, each exterior angle measures:
360/6 = 60 degrees
Correct option
The question states that each exterior angle of the regular hexagon has a measure of 100 degrees. However, we know that the measure of each exterior angle of a regular hexagon is 60 degrees. Therefore, the correct answer is option C, which states that each exterior angle measures 100 degrees. This option is incorrect and does not match with the properties of a regular hexagon.
Therefore, the correct option is C.
All the sides of a regular polygon are _________________.- a) Parallel
- b)equal in length
- c)not parallel
- d)not equal
Correct answer is option 'B'. Can you explain this answer?
All the sides of a regular polygon are _________________.
a)
Parallel
b)
equal in length
c)
not parallel
d)
not equal
|
|
Ameya Dasgupta answered |
All the sides of a regular polygon are equal in length.
A regular polygon is a polygon that has all sides of equal length and all angles of equal measure. In other words, it is a polygon that is both equilateral (all sides equal in length) and equiangular (all angles equal in measure).
A polygon is a closed figure formed by straight lines. Each line segment that forms the polygon is called a side. The sides of a polygon are connected at their endpoints, which are called vertices. The number of sides in a polygon determines its name. For example, a polygon with three sides is called a triangle, a polygon with four sides is called a quadrilateral, and so on.
A regular polygon has all sides and angles equal, while an irregular polygon has sides and/or angles of different lengths and measures.
Some examples of regular polygons include:
- Equilateral triangle: A triangle with all sides of equal length.
- Square: A quadrilateral with all sides of equal length and all angles of 90 degrees.
- Regular hexagon: A polygon with six sides of equal length and all angles of 120 degrees.
The fact that all sides of a regular polygon are equal in length can be proven using the properties of a regular polygon. Since a regular polygon is both equilateral and equiangular, we can show that all sides are equal by considering the angles and the length of the sides.
Let's consider a regular polygon with n sides. Each angle of the polygon measures (n-2) * 180 / n degrees. Since the polygon is equiangular, all these angles are equal.
Now, let's consider two consecutive sides of the polygon. The sum of the exterior angles of any polygon is always 360 degrees. In a regular polygon, each exterior angle measures 360 / n degrees. Since the polygon is equiangular, all exterior angles are equal.
From the properties of exterior angles, we know that the exterior angle and interior angle at a vertex are supplementary (add up to 180 degrees). Therefore, each interior angle of the regular polygon measures (n-2) * 180 / n degrees.
Using the fact that the interior angles are equal and sum up to 360 degrees, we can equate the two equations:
(n-2) * 180 / n = 360
Simplifying the equation, we get:
(n-2) * 180 = 360n
Expanding and rearranging, we get:
180n - 360 = 360n
180n - 360n = 360
-180n = 360
n = -2
Since the number of sides of a polygon cannot be negative, we have reached a contradiction. Therefore, the assumption that all sides of a regular polygon are not equal in length is false.
Therefore, it can be concluded that all sides of a regular polygon are equal in length. Thus, the correct answer is option B - equal in length.
Regular Polygon
A regular polygon is a polygon that has all sides of equal length and all angles of equal measure. In other words, it is a polygon that is both equilateral (all sides equal in length) and equiangular (all angles equal in measure).
Definition and Properties
A polygon is a closed figure formed by straight lines. Each line segment that forms the polygon is called a side. The sides of a polygon are connected at their endpoints, which are called vertices. The number of sides in a polygon determines its name. For example, a polygon with three sides is called a triangle, a polygon with four sides is called a quadrilateral, and so on.
Regular Polygon vs Irregular Polygon
A regular polygon has all sides and angles equal, while an irregular polygon has sides and/or angles of different lengths and measures.
Examples
Some examples of regular polygons include:
- Equilateral triangle: A triangle with all sides of equal length.
- Square: A quadrilateral with all sides of equal length and all angles of 90 degrees.
- Regular hexagon: A polygon with six sides of equal length and all angles of 120 degrees.
Proof
The fact that all sides of a regular polygon are equal in length can be proven using the properties of a regular polygon. Since a regular polygon is both equilateral and equiangular, we can show that all sides are equal by considering the angles and the length of the sides.
Let's consider a regular polygon with n sides. Each angle of the polygon measures (n-2) * 180 / n degrees. Since the polygon is equiangular, all these angles are equal.
Now, let's consider two consecutive sides of the polygon. The sum of the exterior angles of any polygon is always 360 degrees. In a regular polygon, each exterior angle measures 360 / n degrees. Since the polygon is equiangular, all exterior angles are equal.
From the properties of exterior angles, we know that the exterior angle and interior angle at a vertex are supplementary (add up to 180 degrees). Therefore, each interior angle of the regular polygon measures (n-2) * 180 / n degrees.
Using the fact that the interior angles are equal and sum up to 360 degrees, we can equate the two equations:
(n-2) * 180 / n = 360
Simplifying the equation, we get:
(n-2) * 180 = 360n
Expanding and rearranging, we get:
180n - 360 = 360n
180n - 360n = 360
-180n = 360
n = -2
Since the number of sides of a polygon cannot be negative, we have reached a contradiction. Therefore, the assumption that all sides of a regular polygon are not equal in length is false.
Therefore, it can be concluded that all sides of a regular polygon are equal in length. Thus, the correct answer is option B - equal in length.
A quadrilateral can be constructed uniquely if its _____ sides and two included angles are given.- a)1
- b)2
- c)3
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
A quadrilateral can be constructed uniquely if its _____ sides and two included angles are given.
a)
1
b)
2
c)
3
d)
none of these
|
|
Gurmannat Aujla answered |
3 sides and 2 angles there should be minimum 5 things in it to form a qaudrilateral. we cant form qaudrilateral by less then 5 main things. To form it we should know 5 things. For example - 2 sides and 3 included angles. or 3 sides and 2 included angles.
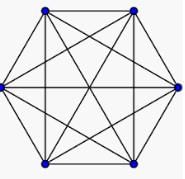
Which of the following polygons is convex polygon ?- a)
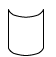
- b)

- c)

- d)
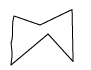
Correct answer is option 'C'. Can you explain this answer?
Which of the following polygons is convex polygon ?
a)

b)

c)

d)

|
|
Nila Jagesh answered |
Because if we take any two points in the pentagon as given in option c) and join it, the line segment will completely remain inside the polygon.
A parallelogram whose all sides are equal is called
- a)circle
- b)rectangle
- c)rhombus
- d)trapezium
Correct answer is option 'C'. Can you explain this answer?
A parallelogram whose all sides are equal is called
a)
circle
b)
rectangle
c)
rhombusd)
trapezium
|
|
Ananya Das answered |
Rhombus is a type of parallelogram whose all sides are equal
What is the sum of the measures of angles of a convex quadrilaterals?- a)180o
- b)90o
- c)360o
- d)45o
Correct answer is option 'C'. Can you explain this answer?
What is the sum of the measures of angles of a convex quadrilaterals?
a)
180o
b)
90o
c)
360o
d)
45o
|
|
Shraddha Ahuja answered |
Solution:
The sum of the measures of angles of a convex quadrilateral is 360°.
Explanation:
A convex quadrilateral is a four-sided polygon with all interior angles less than 180°. Since a polygon with n sides can be divided into n-2 triangles, the sum of the measures of angles of a polygon with n sides is (n-2) x 180°.
In the case of a convex quadrilateral, n=4. Therefore, the sum of the measures of angles of a convex quadrilateral is (4-2) x 180° = 2 x 180° = 360°.
Hence, the correct option is C.
The sum of the measures of angles of a convex quadrilateral is 360°.
Explanation:
A convex quadrilateral is a four-sided polygon with all interior angles less than 180°. Since a polygon with n sides can be divided into n-2 triangles, the sum of the measures of angles of a polygon with n sides is (n-2) x 180°.
In the case of a convex quadrilateral, n=4. Therefore, the sum of the measures of angles of a convex quadrilateral is (4-2) x 180° = 2 x 180° = 360°.
Hence, the correct option is C.
The diagonals of a square bisect each other at _________ angle.- a)acute
- b)right
- c)obtuse
- d)reflex
Correct answer is option 'B'. Can you explain this answer?
The diagonals of a square bisect each other at _________ angle.
a)
acute
b)
right
c)
obtuse
d)
reflex
|
|
Isha Dey answered |
The diagonals of a square bisect each other at a right angle.
Explanation:
- A square is a quadrilateral with all four sides equal in length and all four angles equal to 90 degrees.
- The diagonals of a square are the line segments that connect opposite corners of the square.
- When the diagonals of a square intersect, they divide each other into two equal halves.
- Since a square has four equal angles of 90 degrees, the diagonals of a square will also intersect at a right angle.
Proof:
- Let's consider a square ABCD with diagonals AC and BD.
- The diagonal AC divides the square into two right-angled triangles, namely triangle ABC and triangle CDA.
- Similarly, the diagonal BD divides the square into two right-angled triangles, namely triangle ABD and triangle BCD.
- In each of these triangles, the two legs are equal in length because the sides of the square are equal.
- By the property of a right-angled triangle, in a triangle where the two legs are equal, the angles opposite to the legs are also equal.
- Therefore, in triangle ABC and triangle CDA, angle BAC = angle CAD = 90 degrees/2 = 45 degrees.
- Similarly, in triangle ABD and triangle BCD, angle ABD = angle CBD = 90 degrees/2 = 45 degrees.
- Since angle BAC = angle CAD and angle ABD = angle CBD, the opposite angles of the intersecting diagonals AC and BD are equal.
- By the definition of a right angle, when two lines intersect and their opposite angles are equal, the lines are perpendicular to each other.
- Hence, the diagonals AC and BD of a square bisect each other at a right angle.
Therefore, the correct answer is option 'B' - right.
Explanation:
- A square is a quadrilateral with all four sides equal in length and all four angles equal to 90 degrees.
- The diagonals of a square are the line segments that connect opposite corners of the square.
- When the diagonals of a square intersect, they divide each other into two equal halves.
- Since a square has four equal angles of 90 degrees, the diagonals of a square will also intersect at a right angle.
Proof:
- Let's consider a square ABCD with diagonals AC and BD.
- The diagonal AC divides the square into two right-angled triangles, namely triangle ABC and triangle CDA.
- Similarly, the diagonal BD divides the square into two right-angled triangles, namely triangle ABD and triangle BCD.
- In each of these triangles, the two legs are equal in length because the sides of the square are equal.
- By the property of a right-angled triangle, in a triangle where the two legs are equal, the angles opposite to the legs are also equal.
- Therefore, in triangle ABC and triangle CDA, angle BAC = angle CAD = 90 degrees/2 = 45 degrees.
- Similarly, in triangle ABD and triangle BCD, angle ABD = angle CBD = 90 degrees/2 = 45 degrees.
- Since angle BAC = angle CAD and angle ABD = angle CBD, the opposite angles of the intersecting diagonals AC and BD are equal.
- By the definition of a right angle, when two lines intersect and their opposite angles are equal, the lines are perpendicular to each other.
- Hence, the diagonals AC and BD of a square bisect each other at a right angle.
Therefore, the correct answer is option 'B' - right.
The value of x in the following figure is: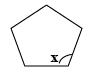
- a)100o
- b)90o
- c)108o
- d)120o
Correct answer is option 'C'. Can you explain this answer?
The value of x in the following figure is:

a)
100o
b)
90o
c)
108o
d)
120o
|
|
Kavya Saxena answered |
Each interior angle of a regular pentagon is 108o
A simple closed curve made up of only _____________ is called a polygon .- a)lines
- b)curves
- c)closed curves
- d)line segments
Correct answer is option 'D'. Can you explain this answer?
A simple closed curve made up of only _____________ is called a polygon .
a)
lines
b)
curves
c)
closed curves
d)
line segments
|
|
Sarita Verma answered |
In elementary geometry, a polygon is a plane figur... moree that is bounded by a finite
How many measurements can determine a quadrilateral uniquely?- a)4
- b)3
- c)5
- d)2
Correct answer is option 'C'. Can you explain this answer?
How many measurements can determine a quadrilateral uniquely?
a)
4
b)
3
c)
5
d)
2
|
|
Ananya Das answered |
We need 5 measurements such as 4 sides and 1 diagonal, or 3 sides and 2 diagonals or 2 sides and 3 angles
The perimeter of parallelogram PQRS is:
- a)12 cm
- b) 7 cm
- c) 38 cm
- d)19 cm
Correct answer is option 'C'. Can you explain this answer?
The perimeter of parallelogram PQRS is:

a)
12 cm
b)
7 cm
c)
38 cm
d)
19 cm
|
|
Shubham Sharma answered |
Perimeter of a parallelogram =sum of all sides. Since opposite sides of a parallelogram are equal, perimeter of parallelogram is 12+12+7+7=38cm
If in a parallelogram its diagonals bisect each other and are equal then it is a,- a)Square
- b)Rectangle
- c)Rhombus
- d)Parallelogram
Correct answer is option 'B'. Can you explain this answer?
If in a parallelogram its diagonals bisect each other and are equal then it is a,
a)
Square
b)
Rectangle
c)
Rhombus
d)
Parallelogram
|
|
Ananya Das answered |
A rhombus is a type of parallelogram, and what distinguishes its shape is that all four of its sides are congruent.
Polygons that have no portions of their diagonals in their exteriors are called - a)triangles
- b)convex
- c)concave
- d)squares
Correct answer is option 'B'. Can you explain this answer?
Polygons that have no portions of their diagonals in their exteriors are called
a)
triangles
b)
convex
c)
concave
d)
squares

|
Rishang Yadav answered |
Because they have all diagonals in interior.
The angle sum of all interior angles of a convex polygon of sides 7 is- a)180o
- b)540o
- c) 630o
- d)900o
Correct answer is option 'D'. Can you explain this answer?
The angle sum of all interior angles of a convex polygon of sides 7 is
a)
180o
b)
540o
c)
630o
d)
900o

|
Malavika Basu answered |
The interior angle sum of this polygon can now be ... morefound by multiplying the number of triangles by 180deg. Upon investigating, it is found that the number of triangles is always two less than the number of sides. This fact is stated as a
All the angles of a regular polygon are of ________________.- a)90°
- b)60°
- c)equal length
- d)equal measure
Correct answer is option 'D'. Can you explain this answer?
All the angles of a regular polygon are of ________________.
a)
90°
b)
60°
c)
equal length
d)
equal measure
|
|
Amit Sharma answered |
A "Regular Polygon" has:
- all sides equal and
- all angles equal
A parallelogram each of whose angles measures 90o is _____________.- a)rectangle
- b)rhombus
- c)kite
- d)trapezium
Correct answer is option 'A'. Can you explain this answer?
A parallelogram each of whose angles measures 90o is _____________.
a)
rectangle
b)
rhombus
c)
kite
d)
trapezium
|
|
Siddharth Nambiar answered |
**Explanation:**
A parallelogram is a quadrilateral with opposite sides that are parallel and equal in length. In a parallelogram, opposite angles are also equal.
To determine the type of parallelogram each of whose angles measures 90 degrees, we need to consider the properties of different quadrilaterals.
**1. Rectangle:** A rectangle is a parallelogram with all angles measuring 90 degrees. Therefore, a rectangle satisfies the condition stated in the question.
**2. Rhombus:** A rhombus is a parallelogram with all sides equal in length. While the opposite angles in a rhombus are equal, they are not necessarily 90 degrees. Therefore, a rhombus does not satisfy the condition stated in the question.
**3. Kite:** A kite is a quadrilateral with two pairs of adjacent sides that are equal in length. Kites do not have all angles measuring 90 degrees. Therefore, a kite does not satisfy the condition stated in the question.
**4. Trapezium:** A trapezium is a quadrilateral with one pair of parallel sides. Trapeziums do not have all angles measuring 90 degrees. Therefore, a trapezium does not satisfy the condition stated in the question.
Hence, the correct answer is **option A) rectangle**.
A parallelogram is a quadrilateral with opposite sides that are parallel and equal in length. In a parallelogram, opposite angles are also equal.
To determine the type of parallelogram each of whose angles measures 90 degrees, we need to consider the properties of different quadrilaterals.
**1. Rectangle:** A rectangle is a parallelogram with all angles measuring 90 degrees. Therefore, a rectangle satisfies the condition stated in the question.
**2. Rhombus:** A rhombus is a parallelogram with all sides equal in length. While the opposite angles in a rhombus are equal, they are not necessarily 90 degrees. Therefore, a rhombus does not satisfy the condition stated in the question.
**3. Kite:** A kite is a quadrilateral with two pairs of adjacent sides that are equal in length. Kites do not have all angles measuring 90 degrees. Therefore, a kite does not satisfy the condition stated in the question.
**4. Trapezium:** A trapezium is a quadrilateral with one pair of parallel sides. Trapeziums do not have all angles measuring 90 degrees. Therefore, a trapezium does not satisfy the condition stated in the question.
Hence, the correct answer is **option A) rectangle**.
A quadrilateral can be constructed uniquely if its two diagonals and _____ sides are known.- a)1
- b)2
- c)3
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
A quadrilateral can be constructed uniquely if its two diagonals and _____ sides are known.
a)
1
b)
2
c)
3
d)
none of these
|
|
Kajal Chavan answered |
Construction of a Quadrilateral
The construction of a quadrilateral involves creating a figure with four sides and four angles. To uniquely construct a quadrilateral, certain information is required.
Diagonals and Sides
In the given scenario, if the two diagonals and three sides of a quadrilateral are known, the quadrilateral can be constructed uniquely. This is because the diagonals of a quadrilateral play a crucial role in determining its shape and size. By having the lengths of the two diagonals and three sides, the remaining side can be accurately determined using geometric principles such as the triangle inequality theorem and properties of quadrilaterals.
Uniqueness of Construction
When the diagonals and three sides of a quadrilateral are known, the construction becomes unique because the diagonals intersect at a specific point within the quadrilateral, dividing it into distinct triangles. The lengths of the sides and diagonals provide enough information to accurately position the vertices of the quadrilateral, ensuring that only one configuration is possible.
Therefore, by knowing the diagonals and three sides of a quadrilateral, a unique construction can be achieved based on the geometric properties and relationships within the figure.
The construction of a quadrilateral involves creating a figure with four sides and four angles. To uniquely construct a quadrilateral, certain information is required.
Diagonals and Sides
In the given scenario, if the two diagonals and three sides of a quadrilateral are known, the quadrilateral can be constructed uniquely. This is because the diagonals of a quadrilateral play a crucial role in determining its shape and size. By having the lengths of the two diagonals and three sides, the remaining side can be accurately determined using geometric principles such as the triangle inequality theorem and properties of quadrilaterals.
Uniqueness of Construction
When the diagonals and three sides of a quadrilateral are known, the construction becomes unique because the diagonals intersect at a specific point within the quadrilateral, dividing it into distinct triangles. The lengths of the sides and diagonals provide enough information to accurately position the vertices of the quadrilateral, ensuring that only one configuration is possible.
Therefore, by knowing the diagonals and three sides of a quadrilateral, a unique construction can be achieved based on the geometric properties and relationships within the figure.
Which property is true for all trapezoids?- a)Only two opposite sides are parallel.
- b)All angles are equal.
- c)Consecutive angles are supplementary.
- d)The base angles are congruent.
Correct answer is option 'A'. Can you explain this answer?
Which property is true for all trapezoids?
a)
Only two opposite sides are parallel.
b)
All angles are equal.
c)
Consecutive angles are supplementary.
d)
The base angles are congruent.
|
|
Saranya Shah answered |
Explanation:
A trapezoid is a quadrilateral with at least one pair of parallel sides. Let us analyze the given options one by one:
a) Only two opposite sides are parallel:
This property is true for all trapezoids. In a trapezoid, only two opposite sides are parallel, and the other two sides are non-parallel.
b) All angles are equal:
This property is not true for all trapezoids. In general, trapezoids do not have equal angles.
c) Consecutive angles are supplementary:
This property is also not true for all trapezoids. In general, the consecutive angles of a trapezoid are not supplementary.
d) The base angles are congruent:
This property is true only for isosceles trapezoids, which have two pairs of congruent angles. However, not all trapezoids are isosceles.
Therefore, the correct answer is option 'A': Only two opposite sides are parallel, which is true for all trapezoids.
A trapezoid is a quadrilateral with at least one pair of parallel sides. Let us analyze the given options one by one:
a) Only two opposite sides are parallel:
This property is true for all trapezoids. In a trapezoid, only two opposite sides are parallel, and the other two sides are non-parallel.
b) All angles are equal:
This property is not true for all trapezoids. In general, trapezoids do not have equal angles.
c) Consecutive angles are supplementary:
This property is also not true for all trapezoids. In general, the consecutive angles of a trapezoid are not supplementary.
d) The base angles are congruent:
This property is true only for isosceles trapezoids, which have two pairs of congruent angles. However, not all trapezoids are isosceles.
Therefore, the correct answer is option 'A': Only two opposite sides are parallel, which is true for all trapezoids.
the diagonals of a rhombus bisect each other at _________ angles.- a)acute
- b)right
- c)obtuse
- d)reflex
Correct answer is option 'B'. Can you explain this answer?
the diagonals of a rhombus bisect each other at _________ angles.
a)
acute
b)
right
c)
obtuse
d)
reflex
|
|
Amit Sharma answered |
The diagonals of a rhombus are perpendicular bisectors of each other.
How many sides does a heptagon have ?- a)2
- b)4
- c) 7
- d)5
Correct answer is option 'C'. Can you explain this answer?
How many sides does a heptagon have ?
a)
2
b)
4
c)
7
d)
5

|
Pavithra Pravin answered |
Heptagon is a polygon of 7 sides
What do we require to construct a quadrilateral if lengths of four sides are given?- a)One of the angle
- b)Length of a diagonal
- c)Length of two diagonals
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
What do we require to construct a quadrilateral if lengths of four sides are given?
a)
One of the angle
b)
Length of a diagonal
c)
Length of two diagonals
d)
None of these
|
|
Geetika Shah answered |
Because you start by drawing a diagonal only, so length of one diagonal is needed.
What do we require to construct a quadrilateral if measures of two adjacent angles are given?- a)Lengths of three sides
- b)Length of one side
- c)Lengths of two sides
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
What do we require to construct a quadrilateral if measures of two adjacent angles are given?
a)
Lengths of three sides
b)
Length of one side
c)
Lengths of two sides
d)
None of these
|
|
Pooja Shah answered |
We first draw a line segment from A to B, then draw an angle at B and then extend it to the given second length making it C and then again draw an angle at C and extend it to the given third length and marking the end as D and joining A and D.
Polygons that have any portions of their diagonals in their exteriors are called - a)Squares
- b)triangles
- c)convex
- d)concave
Correct answer is option 'D'. Can you explain this answer?
Polygons that have any portions of their diagonals in their exteriors are called
a)
Squares
b)
triangles
c)
convex
d)
concave
|
|
Ameya Banerjee answered |
Explanation:
Convex and Concave Polygons:
Convex polygons are polygons in which all interior angles are less than 180 degrees, and all diagonals lie within the interior of the polygon. On the other hand, concave polygons have at least one interior angle greater than 180 degrees and have diagonals that extend outside the polygon.
Diagonals in Polygons:
Diagonals are line segments that connect two non-adjacent vertices in a polygon. In convex polygons, all diagonals remain within the interior of the polygon. However, in concave polygons, at least one diagonal extends outside the polygon's boundary.
Identification of Concave Polygons:
To determine if a polygon is concave, one must check if any of its interior angles are greater than 180 degrees. If such an angle exists, the polygon is concave. Concave polygons have portions of their diagonals outside their boundaries, making them different from convex polygons.
Answer:
The correct answer to the question is option 'D' - concave polygons. Concave polygons have portions of their diagonals extending outside their exterior boundaries, distinguishing them from convex polygons where all diagonals remain within the interior of the polygon.
Convex and Concave Polygons:
Convex polygons are polygons in which all interior angles are less than 180 degrees, and all diagonals lie within the interior of the polygon. On the other hand, concave polygons have at least one interior angle greater than 180 degrees and have diagonals that extend outside the polygon.
Diagonals in Polygons:
Diagonals are line segments that connect two non-adjacent vertices in a polygon. In convex polygons, all diagonals remain within the interior of the polygon. However, in concave polygons, at least one diagonal extends outside the polygon's boundary.
Identification of Concave Polygons:
To determine if a polygon is concave, one must check if any of its interior angles are greater than 180 degrees. If such an angle exists, the polygon is concave. Concave polygons have portions of their diagonals outside their boundaries, making them different from convex polygons.
Answer:
The correct answer to the question is option 'D' - concave polygons. Concave polygons have portions of their diagonals extending outside their exterior boundaries, distinguishing them from convex polygons where all diagonals remain within the interior of the polygon.
If the three angles of a quadrilateral are 120o, 130o, 10o then what is the fourth angle ?- a)30o
- b)100o
- c)40o
- d)90o
Correct answer is option 'B'. Can you explain this answer?
If the three angles of a quadrilateral are 120o, 130o, 10o then what is the fourth angle ?
a)
30o
b)
100o
c)
40o
d)
90o
|
|
Jithin Chatterjee answered |
Solution:
The sum of all angles of a quadrilateral is 360°. Therefore, the fourth angle can be found by subtracting the sum of the three given angles from 360°.
Given angles: 120°, 130°, 10°
Sum of given angles: 120° + 130° + 10° = 260°
Fourth angle = 360° - 260° = 100°
Therefore, the fourth angle of the quadrilateral is 100°.
Answer:
Option B
The sum of all angles of a quadrilateral is 360°. Therefore, the fourth angle can be found by subtracting the sum of the three given angles from 360°.
Given angles: 120°, 130°, 10°
Sum of given angles: 120° + 130° + 10° = 260°
Fourth angle = 360° - 260° = 100°
Therefore, the fourth angle of the quadrilateral is 100°.
Answer:
Option B
What do we require to construct a square?- a)Length of one side
- b)Lengths of three sides
- c)Lengths of two sides
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
What do we require to construct a square?
a)
Length of one side
b)
Lengths of three sides
c)
Lengths of two sides
d)
None of these
|
|
Ayush Pillai answered |
To construct a square, we only require the length of one side. The correct answer is option 'A'.
Explanation:
A square is a four-sided polygon with all sides of equal length and all angles equal to 90 degrees. The properties of a square make it unique and different from other polygons.
Constructing a square requires specific measurements and angles to ensure that all sides and angles are equal. However, only the length of one side is necessary to construct a square.
When we have the length of one side, we can use it to create the other sides of the square by measuring and marking the same length on each side. This will ensure that all sides are equal in length, which is a defining characteristic of a square.
Having the length of one side also allows us to determine the perimeter and area of the square. The perimeter is the sum of all four sides, which in the case of a square is four times the length of one side. The area is calculated by multiplying the length of one side by itself.
Therefore, knowing the length of one side is sufficient to construct a square and determine its properties such as side length, perimeter, and area.
Explanation:
A square is a four-sided polygon with all sides of equal length and all angles equal to 90 degrees. The properties of a square make it unique and different from other polygons.
Constructing a square requires specific measurements and angles to ensure that all sides and angles are equal. However, only the length of one side is necessary to construct a square.
When we have the length of one side, we can use it to create the other sides of the square by measuring and marking the same length on each side. This will ensure that all sides are equal in length, which is a defining characteristic of a square.
Having the length of one side also allows us to determine the perimeter and area of the square. The perimeter is the sum of all four sides, which in the case of a square is four times the length of one side. The area is calculated by multiplying the length of one side by itself.
Therefore, knowing the length of one side is sufficient to construct a square and determine its properties such as side length, perimeter, and area.
Minimum possible interior angle in a regular polygon is ___________.- a)70o
- b)60o
- c)90o
- d)120o
Correct answer is option 'B'. Can you explain this answer?
Minimum possible interior angle in a regular polygon is ___________.
a)
70o
b)
60o
c)
90o
d)
120o
|
|
Lakshmi Rane answered |
The minimum possible interior angle in a regular polygon can be determined by using the formula for the interior angles of a polygon.
Formula for the interior angles of a polygon:
The sum of the interior angles of a polygon can be calculated using the formula:
Sum of interior angles = (n - 2) * 180 degrees
Where n represents the number of sides of the polygon.
Explanation:
In a regular polygon, all sides and angles are equal. Therefore, to find the measure of each interior angle, you divide the sum of the interior angles by the number of sides.
Let's consider a regular polygon with n sides. The formula for each interior angle can be written as:
Each interior angle = (Sum of interior angles) / n
To find the minimum possible interior angle, we need to find the smallest value for n that still forms a regular polygon. The smallest regular polygon is a triangle (n = 3).
Using the formula for the sum of interior angles, we can calculate the sum of angles for a triangle:
Sum of interior angles = (n - 2) * 180 degrees
= (3 - 2) * 180 degrees
= 1 * 180 degrees
= 180 degrees
Now, we can calculate the measure of each interior angle:
Each interior angle = Sum of interior angles / n
= 180 degrees / 3
= 60 degrees
Therefore, the minimum possible interior angle in a regular polygon is 60 degrees.
Formula for the interior angles of a polygon:
The sum of the interior angles of a polygon can be calculated using the formula:
Sum of interior angles = (n - 2) * 180 degrees
Where n represents the number of sides of the polygon.
Explanation:
In a regular polygon, all sides and angles are equal. Therefore, to find the measure of each interior angle, you divide the sum of the interior angles by the number of sides.
Let's consider a regular polygon with n sides. The formula for each interior angle can be written as:
Each interior angle = (Sum of interior angles) / n
To find the minimum possible interior angle, we need to find the smallest value for n that still forms a regular polygon. The smallest regular polygon is a triangle (n = 3).
Using the formula for the sum of interior angles, we can calculate the sum of angles for a triangle:
Sum of interior angles = (n - 2) * 180 degrees
= (3 - 2) * 180 degrees
= 1 * 180 degrees
= 180 degrees
Now, we can calculate the measure of each interior angle:
Each interior angle = Sum of interior angles / n
= 180 degrees / 3
= 60 degrees
Therefore, the minimum possible interior angle in a regular polygon is 60 degrees.
A parallelogram must be a rectangle if its diagonals - a)bisect the angles to which they are drawn
- b)are perpendicular to each other
- c)bisect each other
- d)are congruent
Correct answer is option 'D'. Can you explain this answer?
A parallelogram must be a rectangle if its diagonals
a)
bisect the angles to which they are drawn
b)
are perpendicular to each other
c)
bisect each other
d)
are congruent
|
|
Ipsita Nair answered |
Explanation:
A parallelogram is a quadrilateral with opposite sides parallel to each other. It has several properties that distinguish it from other types of quadrilaterals. One of these properties is that its diagonals bisect each other.
In a parallelogram, the diagonals divide each other into two equal parts. This means that the two line segments that make up each diagonal are congruent. Therefore, the correct answer is option D, which states that the diagonals are congruent.
Why the Other Options are Incorrect:
Option A: If the diagonals bisect the angles to which they are drawn, it means that each diagonal divides one of the angles of the parallelogram into two equal parts. However, this property is not sufficient to prove that the parallelogram is a rectangle.
Option B: If the diagonals are perpendicular to each other, it means that the parallelogram is a rectangle, but this is not always the case. For example, a rhombus is a parallelogram with four equal sides, but its diagonals are perpendicular to each other without being a rectangle.
Option C: If the diagonals bisect each other, it means that they intersect at their midpoint. However, this property is not sufficient to prove that the parallelogram is a rectangle.
Conclusion:
In conclusion, a parallelogram must have diagonals that are congruent to be a rectangle. This property is one of the defining characteristics of a rectangle and is essential to its definition.
A parallelogram is a quadrilateral with opposite sides parallel to each other. It has several properties that distinguish it from other types of quadrilaterals. One of these properties is that its diagonals bisect each other.
In a parallelogram, the diagonals divide each other into two equal parts. This means that the two line segments that make up each diagonal are congruent. Therefore, the correct answer is option D, which states that the diagonals are congruent.
Why the Other Options are Incorrect:
Option A: If the diagonals bisect the angles to which they are drawn, it means that each diagonal divides one of the angles of the parallelogram into two equal parts. However, this property is not sufficient to prove that the parallelogram is a rectangle.
Option B: If the diagonals are perpendicular to each other, it means that the parallelogram is a rectangle, but this is not always the case. For example, a rhombus is a parallelogram with four equal sides, but its diagonals are perpendicular to each other without being a rectangle.
Option C: If the diagonals bisect each other, it means that they intersect at their midpoint. However, this property is not sufficient to prove that the parallelogram is a rectangle.
Conclusion:
In conclusion, a parallelogram must have diagonals that are congruent to be a rectangle. This property is one of the defining characteristics of a rectangle and is essential to its definition.
A quadrilateral can be constructed uniquely if the lengths of its ______ sides and a diagonal are given.- a)3
- b)1
- c)2
- d)4
Correct answer is option 'D'. Can you explain this answer?
A quadrilateral can be constructed uniquely if the lengths of its ______ sides and a diagonal are given.
a)
3
b)
1
c)
2
d)
4
|
|
nandhika krishnan answered |
Yeha sure your answer is 4 sides and one diagonal take an example imagine a quadrilateral we can draw a quadrilateral only if it's 4 sides and one diagonal are given
To construct a parallelogram we need to know:- a)Length of its parallel sides
- b)Measure of interior angles
- c)Two adjacent sides and one angle
- d)Two adjacent sides and two angles
Correct answer is option 'C'. Can you explain this answer?
To construct a parallelogram we need to know:
a)
Length of its parallel sides
b)
Measure of interior angles
c)
Two adjacent sides and one angle
d)
Two adjacent sides and two angles
|
|
Asha Datta answered |
Construction of a Parallelogram
To construct a parallelogram, we need to know two adjacent sides and one angle. Let's understand why this is the correct answer.
Parallelogram Properties:
1. Opposite sides of a parallelogram are parallel.
2. Opposite sides of a parallelogram are congruent (equal in length).
3. Opposite angles of a parallelogram are congruent.
4. Adjacent angles of a parallelogram are supplementary (add up to 180 degrees).
5. Diagonals of a parallelogram bisect each other.
Constructing a Parallelogram:
To construct a parallelogram, we start with two adjacent sides and one angle.
1. Draw the given two adjacent sides AB and AD using a ruler. Label the endpoints as A, B, C, and D.
2. From point A, construct an angle equal to the given angle. Label the vertex of this angle as E.
3. Using a compass, measure the length of one of the given sides and place the compass at point B. Draw an arc to intersect the angle bisector at F.
4. With the same compass setting, place the compass at point D and draw an arc to intersect the angle bisector at G.
5. Draw a line from point F to point D and extend it.
6. Draw a line from point G to point B and extend it.
7. The intersection of the extended lines from steps 5 and 6 will give us point C.
8. Connect points A, B, C, and D to complete the parallelogram ABCD.
Explanation:
By constructing a parallelogram using two adjacent sides and one angle, we ensure that the opposite sides are parallel and congruent. The given angle helps us determine the direction and shape of the parallelogram. The congruent opposite angles and supplementary adjacent angles are automatically satisfied due to the nature of parallelograms.
If we were given only the length of the parallel sides, we would not be able to determine the shape or the angles of the parallelogram. Similarly, if we were given only the measure of the angles, we would not have enough information to determine the length of the sides or the shape of the parallelogram.
Hence, the correct answer is option 'C' - Two adjacent sides and one angle.
To construct a parallelogram, we need to know two adjacent sides and one angle. Let's understand why this is the correct answer.
Parallelogram Properties:
1. Opposite sides of a parallelogram are parallel.
2. Opposite sides of a parallelogram are congruent (equal in length).
3. Opposite angles of a parallelogram are congruent.
4. Adjacent angles of a parallelogram are supplementary (add up to 180 degrees).
5. Diagonals of a parallelogram bisect each other.
Constructing a Parallelogram:
To construct a parallelogram, we start with two adjacent sides and one angle.
1. Draw the given two adjacent sides AB and AD using a ruler. Label the endpoints as A, B, C, and D.
2. From point A, construct an angle equal to the given angle. Label the vertex of this angle as E.
3. Using a compass, measure the length of one of the given sides and place the compass at point B. Draw an arc to intersect the angle bisector at F.
4. With the same compass setting, place the compass at point D and draw an arc to intersect the angle bisector at G.
5. Draw a line from point F to point D and extend it.
6. Draw a line from point G to point B and extend it.
7. The intersection of the extended lines from steps 5 and 6 will give us point C.
8. Connect points A, B, C, and D to complete the parallelogram ABCD.
Explanation:
By constructing a parallelogram using two adjacent sides and one angle, we ensure that the opposite sides are parallel and congruent. The given angle helps us determine the direction and shape of the parallelogram. The congruent opposite angles and supplementary adjacent angles are automatically satisfied due to the nature of parallelograms.
If we were given only the length of the parallel sides, we would not be able to determine the shape or the angles of the parallelogram. Similarly, if we were given only the measure of the angles, we would not have enough information to determine the length of the sides or the shape of the parallelogram.
Hence, the correct answer is option 'C' - Two adjacent sides and one angle.
Chapter doubts & questions for Practical Geometry - Online MCQ Tests for Class 8 2025 is part of Class 8 exam preparation. The chapters have been prepared according to the Class 8 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 8 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Practical Geometry - Online MCQ Tests for Class 8 in English & Hindi are available as part of Class 8 exam.
Download more important topics, notes, lectures and mock test series for Class 8 Exam by signing up for free.
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup