All Exams >
Class 10 >
Mathematics (Maths) Class 10 >
All Questions
All questions of Assertion & Reason Type Questions for Class 10 Exam
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): Corresponding sides of two similar triangles are in the ratio of 2 : 3. If the area of the smaller triangle is 48 cm2, then the area of the larger triangle is 108 cm2.Reason (R): If D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC, then CA2 = CB × CD.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'B'. Can you explain this answer?
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): Corresponding sides of two similar triangles are in the ratio of 2 : 3. If the area of the smaller triangle is 48 cm2, then the area of the larger triangle is 108 cm2.
Reason (R): If D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC, then CA2 = CB × CD.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
Krishna Iyer answered |
In case of assertion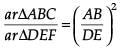
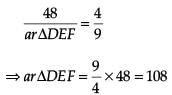
Let ΔABC and ΔDEF are two similar triangles.
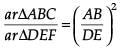
Given that ar ΔABC = 48 cm2. Then,
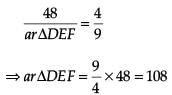
Thus, the area of larger triangle is 108 cm2.
∴ Assertion is correct.
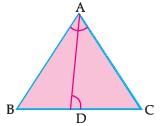
In case of reason:
In ΔBAC and ΔADC,
∠BAC= ∠ADC [Given]
∠BCA= ∠ACD [Common angle]
By AA similarity, ΔBAC ~ ΔADC
Thus,
CA/CD = BC/CA
∴ Reason is correct.
Hence, both assertion and reason are correct but reason is not the correct explanation for assertion.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : Pair of linear equations : 9x + 3y + 12 = 0, 8x + 6y + 24 = 0 have infinitely many solutions.Reason : Pair of linear equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 have infinitely many solutions, a1/a2 = b1/b2 = c1/c2- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'A'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : Pair of linear equations : 9x + 3y + 12 = 0, 8x + 6y + 24 = 0 have infinitely many solutions.
Reason : Pair of linear equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 have infinitely many solutions, a1/a2 = b1/b2 = c1/c2
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
Rohit Sharma answered |
From the given equations, we have
9/18 = 3/6 = 12/24
1/2 = 1/2 = 1/2 i.e, a1/a2 = b1/b2 = c1/c2
So, both A and R are correct and R explains A.
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion : If the circumference of two circles are in the ratio 2 : 3 then ratio of their areas is 4 : 9.Reason : The circumference of a circle of radius r is 2πr and its area is πr2.- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'A'. Can you explain this answer?
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Assertion : If the circumference of two circles are in the ratio 2 : 3 then ratio of their areas is 4 : 9.
Reason : The circumference of a circle of radius r is 2πr and its area is πr2.
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
Meera Rana answered |
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).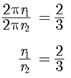
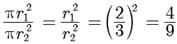
Given,
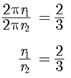
Now, ratio of their areas be
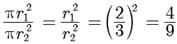
Also, circumference of circle = 2πr.
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : ABC is an isosceles, right triangle, right angled at C . Then AB2 = 3AC2Reason : In an isosceles triangle ABC if AC = BC and AB2 = 2AC2 , then ∠C = 90°- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'D'. Can you explain this answer?
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : ABC is an isosceles, right triangle, right angled at C . Then AB2 = 3AC2
Reason : In an isosceles triangle ABC if AC = BC and AB2 = 2AC2 , then ∠C = 90°
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
Ishan Choudhury answered |
If Assertion is incorrect, but Reason is correct.
In right angled ΔABC ,
AB2 = AC2 + BC2(By Pythagoras Theorem)
= AC2 + AC2 [BC = AC]
= 2AC2AB2 = 2AC2
Assertion is false.
Again since, AB2 = 2AC2
= AC2 + AC2 = AC2 + BC2 (AC = BC given)
∠ = 90°
(By converse of Pythagoras Theorem)Reason is true.
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion : The length of the minute hand of a clock is 7cm. Then the area swept by the minute hand in 5 minutes is 125/6cm2.Reason : The length of an arc of a sector of angle θ and radius r is given by l = θ/360 x 2πr- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'B'. Can you explain this answer?
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Assertion : The length of the minute hand of a clock is 7cm. Then the area swept by the minute hand in 5 minutes is 125/6cm2.
Reason : The length of an arc of a sector of angle θ and radius r is given by l = θ/360 x 2πr
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
|
Rohit Sharma answered |
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).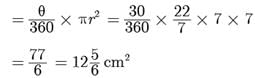
Area swept by minute hand in 5 minutes
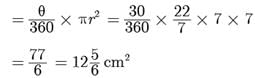
(Angle in 5 minutes by minute hand is 30o)
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:Assertion : an - an - 1 is not independent of n then the given sequence is an AP.Reason : Common difference d =an - an - 1 is constant or independent of n .- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'D'. Can you explain this answer?
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : an - an - 1 is not independent of n then the given sequence is an AP.
Reason : Common difference d =an - an - 1 is constant or independent of n .
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
Anita Menon answered |
We have, common difference of an AP
d =an - an - 1 is independent of n or constant.
So, A is correct but R is incorrect.
Assertion (A): A polynomial of degree n cannot have more than n terms.
Reason (R): The number of coefficients in a polynomial is always one more than its degree.- a)Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
- b)Both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
- c)The assertion is correct, but the Reason is incorrect.
- d)Assertion is incorrect, but Reason is correct.
Correct answer is option 'D'. Can you explain this answer?
Assertion (A): A polynomial of degree n cannot have more than n terms.
Reason (R): The number of coefficients in a polynomial is always one more than its degree.
Reason (R): The number of coefficients in a polynomial is always one more than its degree.
a)
Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
b)
Both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
c)
The assertion is correct, but the Reason is incorrect.
d)
Assertion is incorrect, but Reason is correct.
|
Khusboo shah answered |
Understanding the Assertion and Reason
The assertion (A) states that a polynomial of degree n cannot have more than n terms. The reason (R) states that the number of coefficients in a polynomial is always one more than its degree. Let's break down these statements.
Assertion (A): Analysis
- A polynomial of degree n is defined as a mathematical expression of the form:
- a_n * x^n + a_(n-1) * x^(n-1) + ... + a_1 * x + a_0
- The degree of a polynomial is determined by the highest power of the variable x.
- A polynomial can indeed have fewer than n terms (e.g., x^n + x^2 has 2 terms but is still degree n).
- Therefore, the assertion is incorrect as a polynomial can have more than n terms, as long as terms are combined appropriately.
Reason (R): Analysis
- The reason correctly states that the number of coefficients in a polynomial is always one more than its degree.
- This is because each term has a coefficient, including the constant term (a_0).
- For example, a polynomial of degree 3 (like x^3 + 2x^2 + 3x + 4) has 4 coefficients (a_3, a_2, a_1, and a_0).
Conclusion
- The assertion is incorrect, but the reason is correct.
- Thus, the correct option is D: Assertion is incorrect, but Reason is correct.
This analysis highlights the importance of understanding polynomials and their properties in mathematics.
The assertion (A) states that a polynomial of degree n cannot have more than n terms. The reason (R) states that the number of coefficients in a polynomial is always one more than its degree. Let's break down these statements.
Assertion (A): Analysis
- A polynomial of degree n is defined as a mathematical expression of the form:
- a_n * x^n + a_(n-1) * x^(n-1) + ... + a_1 * x + a_0
- The degree of a polynomial is determined by the highest power of the variable x.
- A polynomial can indeed have fewer than n terms (e.g., x^n + x^2 has 2 terms but is still degree n).
- Therefore, the assertion is incorrect as a polynomial can have more than n terms, as long as terms are combined appropriately.
Reason (R): Analysis
- The reason correctly states that the number of coefficients in a polynomial is always one more than its degree.
- This is because each term has a coefficient, including the constant term (a_0).
- For example, a polynomial of degree 3 (like x^3 + 2x^2 + 3x + 4) has 4 coefficients (a_3, a_2, a_1, and a_0).
Conclusion
- The assertion is incorrect, but the reason is correct.
- Thus, the correct option is D: Assertion is incorrect, but Reason is correct.
This analysis highlights the importance of understanding polynomials and their properties in mathematics.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): If the distance between the point (4, p) and (1, 0) is 5, then the value of p is 4.Reason (R): The point which divides the line segment joining the points (7, – 6) and (3, 4) in ratio 1 : 2 internally lies in the fourth quadrant.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'D'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If the distance between the point (4, p) and (1, 0) is 5, then the value of p is 4.
Reason (R): The point which divides the line segment joining the points (7, – 6) and (3, 4) in ratio 1 : 2 internally lies in the fourth quadrant.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Radha Iyer answered |
In case of assertion: Distance between two points (x1, y1) and (x2, y2) is given as,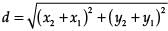
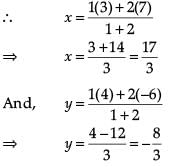
where, (x1, y1) = (4, p)
(x2, y2) = (1, 0)
And, d = 5
Put the values, we have
52 = (1 − 4)2 + (0 – p)2
25 = (–3)2 + (–p)2
25 – 9 = p2
16 = p2
+4, –4 = p
∴ Assertion is incorrect.
In case of reason:
Let (x, y) be the point
Here, x1 = 7, y1 = –6, x2 = 3, y2 = 4, m = 1 and n = 2
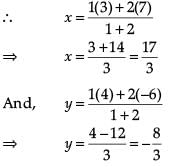
So, the required point 
lies in IVth quadrant.
lies in IVth quadrant.∴ Reason is correct.
Hence, assertion is incorrect but reason is correct.
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion : If the circumference of a circle is 176 cm, then its radius is 28 cm.Reason : Circumference = 2π x radius- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'A'. Can you explain this answer?
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Assertion : If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason : Circumference = 2π x radius
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
|
Avinash Patel answered |
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A). Both assertion and reason are correct. Also Reason is the correct explanation of the assertion.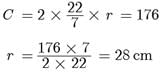
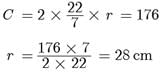
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : The value of k for which the system of linear equations 3x – 4y = 7 and 6x - 8y = k have infinite number of solution is 14.
Reason : The system of linear equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 has a unique solution if a1/a2 ≠ b1/b2
- a)A is true but R is false
- b)Both A and R are true but R is NOT the correct explanation of A
- c)Both A and R are true and R is the correct explanation of A
- d)A is false and R is True
Correct answer is option 'C'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : The value of k for which the system of linear equations 3x – 4y = 7 and 6x - 8y = k have infinite number of solution is 14.
Reason : The system of linear equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 has a unique solution if a1/a2 ≠ b1/b2
a)
A is true but R is false
b)
Both A and R are true but R is NOT the correct explanation of A
c)
Both A and R are true and R is the correct explanation of A
d)
A is false and R is True
|
Naina Sharma answered |
We know that the system of linear equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 has infinitely many solutions if a1/a2 = b1/b2 = c1/c2.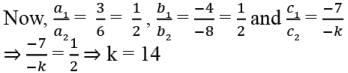
So, Reason is not correct For Assertion, we have, a1 = 3, b1 = -4, c1 = -7, a2 = 6, b2 = -8 and c2 = -k
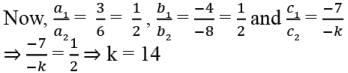
So, Assertion is correct.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : Zeroes of f(x) = x2 - 4x - 5 are 5, - 1
Reason : The polynomial whose zeroes are 2 + √3, 2 - √3 is x2 - 4x + 7.- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'C'. Can you explain this answer?
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : Zeroes of f(x) = x2 - 4x - 5 are 5, - 1
Reason : The polynomial whose zeroes are 2 + √3, 2 - √3 is x2 - 4x + 7.
Assertion : Zeroes of f(x) = x2 - 4x - 5 are 5, - 1
Reason : The polynomial whose zeroes are 2 + √3, 2 - √3 is x2 - 4x + 7.
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
|
Anita Menon answered |
Zeroes of f(x) = x2 − 4x − 5 are obtained by solving:
x2 − 4x − 5 = 0, which implies
x2 − 5x + x − 5 = 0 or, x(x − 5) + 1(x − 5) = 0
which means x = 5 or x = −1
Thus the assertion is correct.
However, the reason is incorrect.
The numbers given are not the zeroes of x2 − 4x + 7
x2 − 4x − 5 = 0, which implies
x2 − 5x + x − 5 = 0 or, x(x − 5) + 1(x − 5) = 0
which means x = 5 or x = −1
Thus the assertion is correct.
However, the reason is incorrect.
The numbers given are not the zeroes of x2 − 4x + 7
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The length of the side of a square whose diagonal is 16 cm, is 8√2 cmReason : In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'A'. Can you explain this answer?
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : The length of the side of a square whose diagonal is 16 cm, is 8√2 cm
Reason : In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Meera Rana answered |
We know that In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. This is Pythagoras theorem. So, Reason is correct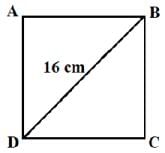
Let the side of square be x cm.
In ∆ABD, by Pythagoras theorem, we have BD2 = AB2 + AD2
⇒ 162 = x2 + x2
⇒ 2x2 = 256 ⇒ x2 = 128 ⇒ x = 8√2 cm
So, Assertion is also correct.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : Centroid of a triangle formed by the points (a, b) (b, c), and (c, a) is at origin, Then a + b + c = 0 .Reason : Centroid of a △ABC with vertices A (x1, y1), B(x2, y2) and C (x3, y3) is given by
- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'A'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : Centroid of a triangle formed by the points (a, b) (b, c), and (c, a) is at origin, Then a + b + c = 0 .
Reason : Centroid of a △ABC with vertices A (x1, y1), B(x2, y2) and C (x3, y3) is given by
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Avinash Patel answered |
Centroid of a triangle with vertices (a, b) (b, c), and (c, a) is
a + b + c = 0
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): The equation 8x2 + 3kx + 2 = 0 has equal roots than the value of k is ±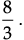 
Reason (R): The equation ax2 + bx + c = 0 has equal roots if D = b2 – 4ac = 0.- a)Both A and R are true and R is the correct explanation for A.
- b)Both A and R are true and R is not correct explanation for A.
- c)A is true but R is false.
- d)A is false but R is true.
Correct answer is option 'A'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The equation 8x2 + 3kx + 2 = 0 has equal roots than the value of k is ±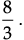
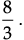
Reason (R): The equation ax2 + bx + c = 0 has equal roots if D = b2 – 4ac = 0.
a)
Both A and R are true and R is the correct explanation for A.
b)
Both A and R are true and R is not correct explanation for A.
c)
A is true but R is false.
d)
A is false but R is true.
|
Flembe Academy answered |
Reason perfectly explains the nature of roots when D = 0 for any quadratic equation.
Let us apply the reason on the equation,
8x2 + 3kx + 2 = 0
D = b2 – 4ac = 0
⇒ (3k)2 – 4(8) (2) = 0
⇒ 9k2 – 64 = 0
⇒ 
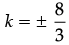
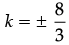
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:Assertion : Two identical solid cube of side 5 cm are joined end to end. Then total surface area of the resulting cuboid is 300 cm2 .Reason : Total surface area of a cuboid is 2(lb + bh + lh)- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'D'. Can you explain this answer?
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : Two identical solid cube of side 5 cm are joined end to end. Then total surface area of the resulting cuboid is 300 cm2 .
Reason : Total surface area of a cuboid is 2(lb + bh + lh)
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
|
Radha Iyer answered |
When cubes are joined end to end, it will form a cuboid.
l = 2 x 5 = 10 cm , b = 5 cm
and h = 5 cm
Total surface area = 2(lb + bh + lh)
= 2(10 x 5 + 5 + 5 x 10 x 5)
= 2 x 125 = 250 cm2
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, then triangles will be similar.Reason (R): If the ratio of the corresponding altitudes of two similar triangles is 3/5, then theratio of their areas is 6/5.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'C'. Can you explain this answer?
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, then triangles will be similar.
Reason (R): If the ratio of the corresponding altitudes of two similar triangles is 3/5, then the
ratio of their areas is 6/5.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Meera Rana answered |
In case of assertion: In the given two right triangles, both have equal right angles and one of the acute angles of one triangle is equal to an acute angle of the other triangle.
Thus, by AA similarity, the given two triangles are similar.
∴ Assertion is correct.
In case of reason:
We know that the ratio of the areas of two similar triangles is the square of the ratio of the corresponding altitudes of two similar triangles.
Thus, the ratio of the areas of two similar triangles is (3/5)2 = 9/25.
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:Assertion : Total surface area of the cylinder having radius of the base 14 cm and height 30 cm is 3872 cm2 .Reason : If r be the radius and h be the height of the cylinder, then total surface area = (2prh +2pr2).- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'A'. Can you explain this answer?
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : Total surface area of the cylinder having radius of the base 14 cm and height 30 cm is 3872 cm2 .
Reason : If r be the radius and h be the height of the cylinder, then total surface area = (2prh +2pr2).
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
|
Rohit Sharma answered |
Total surface area = 2prh +2pr2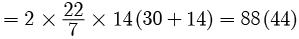
= 2p r (h + r)
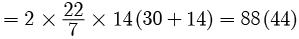
= 3872 cm2
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : A pair of linear equations has no solution (s) if it is represented by intersecting lines graphically.Reason: If the pair of lines are intersecting, then the pair has unique solution and is called consistent pair of equations.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'D'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : A pair of linear equations has no solution (s) if it is represented by intersecting lines graphically.
Reason: If the pair of lines are intersecting, then the pair has unique solution and is called consistent pair of equations.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Kiran Mehta answered |
We know that if the lines are parallel, then it has no solution.
So, Assertion is false. We know that if the lines are intersecting, then it has unique solution.
So, Reason is true.
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Assertion: A wire is looped in the form of a circle of radius 28 cm. It is bent into a square. Then the area of the square is 1936 cm2.
Reason : Angle described by a minute hand in 60 minutes = 360o.
- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Assertion (A) is false but reason (R) is true.
- c)Assertion (A) is true but reason (R) is false.
- d)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
Correct answer is option 'D'. Can you explain this answer?
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Assertion: A wire is looped in the form of a circle of radius 28 cm. It is bent into a square. Then the area of the square is 1936 cm2.
Reason : Angle described by a minute hand in 60 minutes = 360o.
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Assertion (A) is false but reason (R) is true.
c)
Assertion (A) is true but reason (R) is false.
d)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
|
|
Namrata singhania answered |
Assertion: A wire is looped in the form of a circle of radius 28 cm. It is bent into a square. Then the area of the square is 1936 cm^2.
Reason: Angle described by a minute hand in 60 minutes = 360°.
Explanation:
To understand why the correct answer is option 'D', let's break down the problem into two parts:
Part 1: Wire looped in the form of a circle and bent into a square
- When a wire is looped in the form of a circle, the wire forms the circumference of the circle.
- The formula for the circumference of a circle is C = 2πr, where r is the radius of the circle.
- Given that the radius of the circle is 28 cm, the circumference of the circle would be C = 2π(28) = 56π cm.
- Now, when the wire is bent into a square, the length of the wire becomes equal to the perimeter of the square.
- The formula for the perimeter of a square is P = 4s, where s is the length of one side of the square.
- Therefore, 56π cm = 4s, which gives us s = 14π cm.
Part 2: Determining the area of the square
- The area of a square is given by the formula A = s^2, where s is the length of one side of the square.
- Substituting the value of s from Part 1, we get A = (14π)^2 = 196π^2 cm^2.
- Now, if we approximate the value of π to be 3.14, the area of the square would be approximately 1936 cm^2 (196 * 3.14^2).
- Therefore, the area of the square is 1936 cm^2.
Conclusion:
The assertion that the area of the square formed by bending the wire into a square is 1936 cm^2 is true. However, the reason given about the angle described by a minute hand in 60 minutes being 360° is irrelevant and does not provide any explanation for the assertion. Hence, the reason is false. Therefore, the correct answer is option 'D' - Assertion (A) is false but reason (R) is true.
Reason: Angle described by a minute hand in 60 minutes = 360°.
Explanation:
To understand why the correct answer is option 'D', let's break down the problem into two parts:
Part 1: Wire looped in the form of a circle and bent into a square
- When a wire is looped in the form of a circle, the wire forms the circumference of the circle.
- The formula for the circumference of a circle is C = 2πr, where r is the radius of the circle.
- Given that the radius of the circle is 28 cm, the circumference of the circle would be C = 2π(28) = 56π cm.
- Now, when the wire is bent into a square, the length of the wire becomes equal to the perimeter of the square.
- The formula for the perimeter of a square is P = 4s, where s is the length of one side of the square.
- Therefore, 56π cm = 4s, which gives us s = 14π cm.
Part 2: Determining the area of the square
- The area of a square is given by the formula A = s^2, where s is the length of one side of the square.
- Substituting the value of s from Part 1, we get A = (14π)^2 = 196π^2 cm^2.
- Now, if we approximate the value of π to be 3.14, the area of the square would be approximately 1936 cm^2 (196 * 3.14^2).
- Therefore, the area of the square is 1936 cm^2.
Conclusion:
The assertion that the area of the square formed by bending the wire into a square is 1936 cm^2 is true. However, the reason given about the angle described by a minute hand in 60 minutes being 360° is irrelevant and does not provide any explanation for the assertion. Hence, the reason is false. Therefore, the correct answer is option 'D' - Assertion (A) is false but reason (R) is true.
Consider the following statement about the role of press and literature in the 19th century.
1. The press never criticised official Policies but urged the people to unite
2. There was the prolonged growth of Indian owned Vernacular newspapers because of numerous restrictions imposed on the press by the colonial rulers
Which of these statements is/are correct?
- a)1 Only
- b)Neither of them
- c)Both of them
- d)2 Only
Correct answer is option 'D'. Can you explain this answer?
Consider the following statement about the role of press and literature in the 19th century.
1. The press never criticised official Policies but urged the people to unite
2. There was the prolonged growth of Indian owned Vernacular newspapers because of numerous restrictions imposed on the press by the colonial rulers
Which of these statements is/are correct?
a)
1 Only
b)
Neither of them
c)
Both of them
d)
2 Only
|
Shruti Desai answered |
Explanation:
The given statement talks about the role of press and literature in the 19th century in India. Let's break down each statement and see if it is correct or not:
1. The press never criticised official Policies but urged the people to unite.
This statement is not entirely accurate. The press did criticize official policies, but they had to do it carefully because of the restrictions imposed by the colonial rulers. The press played a crucial role in shaping public opinion and creating awareness about the injustices of the colonial rule. They urged people to unite and fight for their rights. However, they had to do it without crossing the line and inviting censorship or prosecution.
2. There was the prolonged growth of Indian owned Vernacular newspapers because of numerous restrictions imposed on the press by the colonial rulers.
This statement is partially correct. Indian owned Vernacular newspapers did grow during the 19th century because they could cater to the local audience and address their concerns. However, the growth of these newspapers was not entirely due to the restrictions imposed by the colonial rulers. The vernacular press had to face numerous challenges, such as the lack of funds, illiteracy, and censorship. It was only after the Indian National Congress was formed in 1885 that the vernacular press gained momentum and started playing a more active role in the freedom struggle.
Therefore, neither of the given statements is entirely correct. The press did criticize official policies, but they had to do it cautiously. The growth of the vernacular press was not solely due to the restrictions imposed by the colonial rulers. It was a combination of various factors that contributed to its growth.
In conclusion, it is essential to understand the role of the press and literature in shaping public opinion and creating awareness about the injustices of the colonial rule. The press had to operate under challenging circumstances, but they managed to play a crucial role in the freedom struggle.
The given statement talks about the role of press and literature in the 19th century in India. Let's break down each statement and see if it is correct or not:
1. The press never criticised official Policies but urged the people to unite.
This statement is not entirely accurate. The press did criticize official policies, but they had to do it carefully because of the restrictions imposed by the colonial rulers. The press played a crucial role in shaping public opinion and creating awareness about the injustices of the colonial rule. They urged people to unite and fight for their rights. However, they had to do it without crossing the line and inviting censorship or prosecution.
2. There was the prolonged growth of Indian owned Vernacular newspapers because of numerous restrictions imposed on the press by the colonial rulers.
This statement is partially correct. Indian owned Vernacular newspapers did grow during the 19th century because they could cater to the local audience and address their concerns. However, the growth of these newspapers was not entirely due to the restrictions imposed by the colonial rulers. The vernacular press had to face numerous challenges, such as the lack of funds, illiteracy, and censorship. It was only after the Indian National Congress was formed in 1885 that the vernacular press gained momentum and started playing a more active role in the freedom struggle.
Therefore, neither of the given statements is entirely correct. The press did criticize official policies, but they had to do it cautiously. The growth of the vernacular press was not solely due to the restrictions imposed by the colonial rulers. It was a combination of various factors that contributed to its growth.
In conclusion, it is essential to understand the role of the press and literature in shaping public opinion and creating awareness about the injustices of the colonial rule. The press had to operate under challenging circumstances, but they managed to play a crucial role in the freedom struggle.
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion : An event is very unlikely to happen. Its probability is 0.0001Reason : If P(A) denotes the probability of an event A, then 0 ≤ P (A) ≤ 1.- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'B'. Can you explain this answer?
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Assertion : An event is very unlikely to happen. Its probability is 0.0001
Reason : If P(A) denotes the probability of an event A, then 0 ≤ P (A) ≤ 1.
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
|
Anita Menon answered |
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A). Assertion and Reason are correct but Reason is not the correct explanation for Assertion.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): The solution of the pair of linear equations x + y = 5 and 2x – 3y = 4 is x = 19/5 and y = 6/5.Reason (R): The solution of the pair of linear equations 3x + 4y = 10 and 2x – 2y = 2 is x = 2 and y = 1.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'B'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The solution of the pair of linear equations x + y = 5 and 2x – 3y = 4 is x = 19/5 and y = 6/5.
Reason (R): The solution of the pair of linear equations 3x + 4y = 10 and 2x – 2y = 2 is x = 2 and y = 1.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Ishan Choudhury answered |
In case of assertion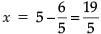
By elimination method,
x + y = 5 ...(i)
2x – 3y = 4 ...(ii)
Multiplying equation (i) by (ii), we obtain
2x + 2y = 10 ...(iii)
Subtracting equation (ii) from equation (iii), we obtain
5y = 6
y = 6/5 …(iv)
Substituting the value in equation (i), we obtain
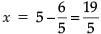
∴ x = 19/5 , y = 6/5
∴ Assertion is correct.
In case of reason:
By elimination method,
3x + 4y = 10 ...(i)
2x – 2y = 2 ...(ii)
Multiplying equation (ii) by 2, we obtain
4x – 4y = 4 ...(iii)
Adding equations (i) and (iii), we obtain
7x = 14
x = 2 ...(iv)
Substituting in equation (i), we obtain
6 + 4y = 10
4y = 4
y = 1
Hence, x = 2, y = 1
∴ Reason is correct.
Hence, both assertion and reason are correct but reason is not the correct explanation for assertion.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : Mid-point of a line segment divides line in the ratio 1 : 1.Reason : If area of triangle is zero that means points are collinear.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'B'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : Mid-point of a line segment divides line in the ratio 1 : 1.
Reason : If area of triangle is zero that means points are collinear.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Ishan Choudhury answered |
Let us assume that point B divides the line AC in the ratio k : 1
Let(x1, y1, z1) = (0, 0, 0)
(x, y ,z) = (2, −3, 3)
(x2, y2, z2) = (−2, 3, −3)
By section formula:
x = m1 + m2 m1 x 2 + m2 x 1
⇒ 2 = k + 1 k.(−2) + 1.(0)
⇒ k = 4 − 1 on neglecting the negative sign
we get, therefore ratio is 1:4.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): The degree of quadratic equation is always 2. Hence, x2 – 1 = 0 is pure quadratic equation.Reason (R): An equation of the form ax2 + c = 0 is known as pure quadratic equation.- a)Both A and R are true and R is the correct explanation for A.
- b)Both A and R are true and R is not correct explanation for A.
- c)A is true but R is false.
- d)A is false but R is true.
Correct answer is option 'B'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The degree of quadratic equation is always 2. Hence, x2 – 1 = 0 is pure quadratic equation.
Reason (R): An equation of the form ax2 + c = 0 is known as pure quadratic equation.
a)
Both A and R are true and R is the correct explanation for A.
b)
Both A and R are true and R is not correct explanation for A.
c)
A is true but R is false.
d)
A is false but R is true.
|
|
Tanvi choudhary answered |
Understanding the Assertion (A)
The assertion states that "The degree of a quadratic equation is always 2." This is true because, by definition, a quadratic equation is a polynomial equation of degree 2. The standard form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are constants and a is not zero.
Analyzing the Reason (R)
The reason given is that "An equation of the form ax² + c = 0 is known as a pure quadratic equation." This statement is also true. A pure quadratic equation lacks the linear term (bx) and can be expressed simply as ax² + c = 0, where a is non-zero.
Connection Between A and R
While both statements are true, the key is in their relationship. The assertion discusses the general nature of quadratic equations, while the reason specifically describes a subset of quadratic equations (pure quadratics). Thus, R does not directly explain why A is true.
Conclusion
Since both A and R are true but R does not serve as a correct explanation for A, the correct choice is:
- Option B: Both A and R are true, and R is not the correct explanation for A.
The assertion states that "The degree of a quadratic equation is always 2." This is true because, by definition, a quadratic equation is a polynomial equation of degree 2. The standard form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are constants and a is not zero.
Analyzing the Reason (R)
The reason given is that "An equation of the form ax² + c = 0 is known as a pure quadratic equation." This statement is also true. A pure quadratic equation lacks the linear term (bx) and can be expressed simply as ax² + c = 0, where a is non-zero.
Connection Between A and R
While both statements are true, the key is in their relationship. The assertion discusses the general nature of quadratic equations, while the reason specifically describes a subset of quadratic equations (pure quadratics). Thus, R does not directly explain why A is true.
Conclusion
Since both A and R are true but R does not serve as a correct explanation for A, the correct choice is:
- Option B: Both A and R are true, and R is not the correct explanation for A.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): In a ΔABC, ∠C = 3∠B = 2(∠A + ∠B), then ∠A = 20°.Reason (R): The angles of a triangle are x, y and 40°. The difference between the two angles x and y is 30°, then x = 85° and y = 55°.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'B'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): In a ΔABC, ∠C = 3∠B = 2(∠A + ∠B), then ∠A = 20°.
Reason (R): The angles of a triangle are x, y and 40°. The difference between the two angles x and y is 30°, then x = 85° and y = 55°.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Kiran Mehta answered |
In case of assertion
Given that, ∠C = 3∠B = 2(∠A + ∠B)
3∠B = 2(∠A + ∠B)
3∠B = 2∠A + 2∠B
∠B = 2∠A
2 ∠A − ∠B = 0 ...(i)
We know that the sum of the measures of all angles of a triangle is 180°.
Therefore, ∠A + ∠B + ∠C = 180°
∠A + ∠B + 3∠B = 180°
∠A + 4∠B = 180° ...(ii)
Multiplying equation (i) by 4, we obtain
8∠A − 4∠B = 0 ...(iii)
Adding equations (ii) and (iii), we obtain
9∠A = 180°
∠A = 20°
∴ Assertion is correct.
In case of reason: Given that, x, y and 40° are the angels of a triangle.
x + y + 40° = 180°
[Since the sum of all the angels of a triangle is 180°.]
⇒ x + y = 140° ...(i)
Also, x – y = 30° ...(ii)
On adding Eqs. (i) and (ii), we get
2x = 170°
⇒ x = 170/2
∴ x = 85°
On putting x = 85° in Eq. (i), we get
85° + y = 140°
y = 140° – 85° = 55°
∴ y = 55°
Hence, the required values of x and y are 85° and 55°, respectively.
∴ Reason is correct.
Hence, both assertion and reason are correct but reason is not the correct explanation for assertion.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): In covering a distance s meter, a circular wheel of radius r meter makes s/2πr revolution.Reason (R): The distance travelled by a circular wheel of diameter d cm in one revolution is 2πd cm.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'C'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): In covering a distance s meter, a circular wheel of radius r meter makes s/2πr revolution.
Reason (R): The distance travelled by a circular wheel of diameter d cm in one revolution is 2πd cm.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Ishan Choudhury answered |
In case of assertion
The distance covered in one revolution is 2πr, that is, its circumference.
∴ Assertion is correct
In case of reason:
Because the distance travelled by the wheel in one revolution is equal to its circumference Circumference of wheel = π × diameter
= π × d
= πd
Hence the given answer in the question is incorrect.
∴ Reason is incorrect.
Hence, assertion is correct and reason is incorrect.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The linear equations x - 2y - 3 = 0 and 3x + 4y - 20 = 0 = have exactly one solution.Reason : The linear equations 2x + 3y - 0 = and 4x + 6y - 18 = 0 = have a unique solution.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'C'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : The linear equations x - 2y - 3 = 0 and 3x + 4y - 20 = 0 = have exactly one solution.
Reason : The linear equations 2x + 3y - 0 = and 4x + 6y - 18 = 0 = have a unique solution.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Leena bajaj answered |
Assertion: The linear equations x - 2y - 3 = 0 and 3x + 4y - 20 = 0 have exactly one solution.
Reason: The linear equations 2x - 3y = 0 and 4x + 6y - 18 = 0 have a unique solution.
Explanation:
To determine if the given Assertion and Reason are true or false, let's analyze each statement separately.
Statement 1: The linear equations x - 2y - 3 = 0 and 3x + 4y - 20 = 0 have exactly one solution.
To find the solution of a system of linear equations, we need to check if the given equations intersect at a single point, which indicates a unique solution.
For the given system of equations:
x - 2y - 3 = 0 ...(1)
3x + 4y - 20 = 0 ...(2)
We can solve these equations simultaneously to find their solution.
Multiplying equation (1) by 3 and equation (2) by 1, we get:
3(x - 2y - 3) = 3(0)
3x - 6y - 9 = 0 ...(3)
3x + 4y - 20 = 0 ...(4)
Now, subtracting equation (3) from equation (4), we eliminate the 'x' term:
(3x + 4y - 20) - (3x - 6y - 9) = 0
3x - 3x + 4y + 6y - 20 + 9 = 0
10y - 11 = 0
10y = 11
y = 11/10
Substituting the value of 'y' into equation (1), we can find the value of 'x':
x - 2(11/10) - 3 = 0
x - 22/10 - 3 = 0
x - 22/10 - 30/10 = 0
x - 52/10 = 0
x - 26/5 = 0
x = 26/5
Therefore, the solution to the given system of equations is x = 26/5 and y = 11/10. This is a unique solution, which means the Assertion is true.
Statement 2: The linear equations 2x - 3y = 0 and 4x + 6y - 18 = 0 have a unique solution.
Similarly, we can solve the given system of equations to determine its solution.
For the system of equations:
2x - 3y = 0 ...(5)
4x + 6y - 18 = 0 ...(6)
Multiplying equation (5) by 2 and equation (6) by 1, we get:
2(2x - 3y) = 2(0)
4x - 6y = 0 ...(7)
4x + 6y - 18 = 0 ...(8)
Now, subtracting equation (7) from equation (8), we eliminate the 'x' term:
(4x
Reason: The linear equations 2x - 3y = 0 and 4x + 6y - 18 = 0 have a unique solution.
Explanation:
To determine if the given Assertion and Reason are true or false, let's analyze each statement separately.
Statement 1: The linear equations x - 2y - 3 = 0 and 3x + 4y - 20 = 0 have exactly one solution.
To find the solution of a system of linear equations, we need to check if the given equations intersect at a single point, which indicates a unique solution.
For the given system of equations:
x - 2y - 3 = 0 ...(1)
3x + 4y - 20 = 0 ...(2)
We can solve these equations simultaneously to find their solution.
Multiplying equation (1) by 3 and equation (2) by 1, we get:
3(x - 2y - 3) = 3(0)
3x - 6y - 9 = 0 ...(3)
3x + 4y - 20 = 0 ...(4)
Now, subtracting equation (3) from equation (4), we eliminate the 'x' term:
(3x + 4y - 20) - (3x - 6y - 9) = 0
3x - 3x + 4y + 6y - 20 + 9 = 0
10y - 11 = 0
10y = 11
y = 11/10
Substituting the value of 'y' into equation (1), we can find the value of 'x':
x - 2(11/10) - 3 = 0
x - 22/10 - 3 = 0
x - 22/10 - 30/10 = 0
x - 52/10 = 0
x - 26/5 = 0
x = 26/5
Therefore, the solution to the given system of equations is x = 26/5 and y = 11/10. This is a unique solution, which means the Assertion is true.
Statement 2: The linear equations 2x - 3y = 0 and 4x + 6y - 18 = 0 have a unique solution.
Similarly, we can solve the given system of equations to determine its solution.
For the system of equations:
2x - 3y = 0 ...(5)
4x + 6y - 18 = 0 ...(6)
Multiplying equation (5) by 2 and equation (6) by 1, we get:
2(2x - 3y) = 2(0)
4x - 6y = 0 ...(7)
4x + 6y - 18 = 0 ...(8)
Now, subtracting equation (7) from equation (8), we eliminate the 'x' term:
(4x
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): If 4 chairs and 3 tables cost ₹ 2100 and 5 chairs and 2 tables cost ₹ 1750, then the cost of 1 chair is ₹ 150.Reason (R): Sum of the ages of a father and the son is 40 years. If father's age is 3 times that of his son, then the son's age is 12 years.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'C'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If 4 chairs and 3 tables cost ₹ 2100 and 5 chairs and 2 tables cost ₹ 1750, then the cost of 1 chair is ₹ 150.
Reason (R): Sum of the ages of a father and the son is 40 years. If father's age is 3 times that of his son, then the son's age is 12 years.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Avinash Patel answered |
In case of assertion
Let cost of 1 chair be ₹ x and cost of 1 table be ₹ y
According to the question,
4x +3y = 2100 ...(i)
and 5x +2y = 1750 ...(ii)
Multiplying eqn. (i) by 2 and eqn. (ii) by 3, we get
8x +6y = 4200 ...(iii)
15x + 6y = 5250 ...(iv)
eqn. (iv) – eqn. (iii)
⇒ 7x = 1050
∴ x = 150
Substituting the value of x in (i) we get y = 500
Thus, the cost of one chair and one table are ₹ 150 and ₹ 500 respectively.
∴ Assertion is correct.
In case of reason:
Let age of father and son be x and y respectively.
Then, x + y = 40 ...(i)
and x = 3y ...(ii)
By solving eqns. (i) and (ii), we get
x = 30 and y = 10
Thus, the ages of father and son are 30 years and 10 years.
∴ Reason is incorrect.
Hence, Assertion is correct but reason is incorrect.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): The roots of the quadratic equation x2 + 2x + 2 = 0 are imaginary.Reason (B): If discriminant D = b2 – 4ac < 0="" then="" the="" roots="" of="" the="" quadratic="" equation="" />2 + bx + c = 0 are imaginary.- a)Both A and R are true and R is the correct explanation for A.
- b)Both A and R are true and R is not correct explanation for A.
- c)A is true but R is false.
- d)A is false but R is true.
Correct answer is option 'A'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The roots of the quadratic equation x2 + 2x + 2 = 0 are imaginary.
Reason (B): If discriminant D = b2 – 4ac < 0="" then="" the="" roots="" of="" the="" quadratic="" equation="" />2 + bx + c = 0 are imaginary.
a)
Both A and R are true and R is the correct explanation for A.
b)
Both A and R are true and R is not correct explanation for A.
c)
A is true but R is false.
d)
A is false but R is true.
|
|
Amit Sharma answered |
Let us apply the reason on the equation,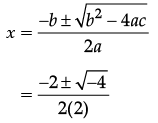
is unreal.
x2 + 2x + 2 = 0
D = b2 – 4ac = (2)2 – 4(1)(2) = 4 – 8 = – 4
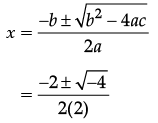
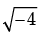is unreal.No real value is possible in this case.
Therefore, Both A and R are true and R is the correct explanation for A.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is 50 cm.Reason (R): If the perimeter and the area of a circle are numerically equal, then the radius of the circle is 2 units.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'B'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is 50 cm.
Reason (R): If the perimeter and the area of a circle are numerically equal, then the radius of the circle is 2 units.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
Dont Memorise answered |
In the case of assertion
Let r1 = 24 cm and r2 = 7 cm
Area of first circle = πr12 = π(24)2 = 576π cm2
Area of second circle = πr22 =π(7)2 = 49π cm2
According to question,
Area of circle = Area of first circle + Area of second circle
πR2 = 576π +49π
[where, R be radius of circle]
R2 = 625 =25 cm
Diameter of a circle = 2R = 2 × 25 = 50 cm.
∴ Assertion is correct.
In case of reason:
Let the radius of the circle be r.
Circumference of circle = 2πr
Area of circle = πr2
Given that, the circumference of the circle and the area of the circle are equal. This implies, 2πr = pπ2
r = 2
Therefore, the radius of the circle is 2 units.
∴ Reason is correct.
Hence, both assertion and reason are correct but reason is not the correct explanation for assertion.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): For all real values of c, the pair of equations x – 2y = 8 and 5x – 10y = c have a unique solution.Reason (R): Two lines are given to be parallel. The equation of one of the lines is 4x + 3y = 14, 12x + 9y = 5.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'D'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): For all real values of c, the pair of equations x – 2y = 8 and 5x – 10y = c have a unique solution.
Reason (R): Two lines are given to be parallel. The equation of one of the lines is 4x + 3y = 14, 12x + 9y = 5.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
Naina malhotra answered |
Assertion: For all real values of c, the pair of equations x – 2y = 8 and 5x – 10y = c have a unique solution.
Reason: Two lines are given to be parallel. The equation of one of the lines is 4x + 3y = 14, 12x + 9y = 5.
To determine the correctness of the assertion and the reason, let's analyze each statement individually.
Statement A: For all real values of c, the pair of equations x – 2y = 8 and 5x – 10y = c have a unique solution.
To solve the system of equations, we can use the method of substitution or elimination. Let's use the method of substitution to find the solution.
From the first equation, x - 2y = 8, we can rewrite it as x = 2y + 8.
Substituting this value of x into the second equation, we get 5(2y + 8) - 10y = c.
Simplifying further, we have 10y + 40 - 10y = c.
The y terms cancel out, and we're left with 40 = c.
Since the value of c is fixed at 40 for any real value, the second equation becomes 5x - 10y = 40.
Therefore, the system of equations x - 2y = 8 and 5x - 10y = c always has a unique solution, which is x = 2y + 8.
Statement R: Two lines are given to be parallel. The equation of one of the lines is 4x + 3y = 14, 12x + 9y = 5.
To determine if two lines are parallel, we need to compare their slopes. If the slopes are equal, the lines are parallel.
The slope-intercept form of a linear equation is y = mx + b, where m is the slope.
Let's rewrite the given equations in slope-intercept form:
4x + 3y = 14
3y = -4x + 14
y = (-4/3)x + 14/3
12x + 9y = 5
9y = -12x + 5
y = (-12/9)x + 5/9
y = (-4/3)x + 5/9
Comparing the slopes of both equations, we can see that they are equal (-4/3).
Therefore, the given lines 4x + 3y = 14 and 12x + 9y = 5 are parallel.
Conclusion:
From the analysis above, we can conclude that both Assertion (A) and Reason (R) are true. However, Reason (R) does not provide the correct explanation for Assertion (A). The parallel lines mentioned in Reason (R) are not directly related to the given system of equations in Assertion (A).
Reason: Two lines are given to be parallel. The equation of one of the lines is 4x + 3y = 14, 12x + 9y = 5.
To determine the correctness of the assertion and the reason, let's analyze each statement individually.
Statement A: For all real values of c, the pair of equations x – 2y = 8 and 5x – 10y = c have a unique solution.
To solve the system of equations, we can use the method of substitution or elimination. Let's use the method of substitution to find the solution.
From the first equation, x - 2y = 8, we can rewrite it as x = 2y + 8.
Substituting this value of x into the second equation, we get 5(2y + 8) - 10y = c.
Simplifying further, we have 10y + 40 - 10y = c.
The y terms cancel out, and we're left with 40 = c.
Since the value of c is fixed at 40 for any real value, the second equation becomes 5x - 10y = 40.
Therefore, the system of equations x - 2y = 8 and 5x - 10y = c always has a unique solution, which is x = 2y + 8.
Statement R: Two lines are given to be parallel. The equation of one of the lines is 4x + 3y = 14, 12x + 9y = 5.
To determine if two lines are parallel, we need to compare their slopes. If the slopes are equal, the lines are parallel.
The slope-intercept form of a linear equation is y = mx + b, where m is the slope.
Let's rewrite the given equations in slope-intercept form:
4x + 3y = 14
3y = -4x + 14
y = (-4/3)x + 14/3
12x + 9y = 5
9y = -12x + 5
y = (-12/9)x + 5/9
y = (-4/3)x + 5/9
Comparing the slopes of both equations, we can see that they are equal (-4/3).
Therefore, the given lines 4x + 3y = 14 and 12x + 9y = 5 are parallel.
Conclusion:
From the analysis above, we can conclude that both Assertion (A) and Reason (R) are true. However, Reason (R) does not provide the correct explanation for Assertion (A). The parallel lines mentioned in Reason (R) are not directly related to the given system of equations in Assertion (A).
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The value of k for which the system of linear equations kx – y = 2 and 6x – 2y = 3 has a unique solution is 3.Reason : The system of linear equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 has a unique solution if a1/a2 ≠ b1/b2- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'D'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : The value of k for which the system of linear equations kx – y = 2 and 6x – 2y = 3 has a unique solution is 3.
Reason : The system of linear equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 has a unique solution if a1/a2 ≠ b1/b2
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
Anoushka khanna answered |
Explanation:
The given system of linear equations is:
kx – y = 2 ...(i)
6x – 2y = 3 ...(ii)
To find the value of k for which the system has a unique solution, we need to solve the equations simultaneously.
Multiplying equation (i) by 2, we get:
2kx – 2y = 4 ...(iii)
Adding (ii) and (iii), we get:
8x = 7
x = 7/8
Substituting x = 7/8 in equation (i), we get:
k(7/8) – y = 2
y = k(7/8) – 2 ...(iv)
Substituting x = 7/8 and y = k(7/8) – 2 in equation (ii), we get:
6(7/8) – 2k(7/8) + 4 = 3
7 – 14k/8 = –1
14k = 16
k = 16/14 = 8/7
Therefore, the value of k for which the system of linear equations has a unique solution is 8/7 and not 3. Hence, Assertion is false.
The Reason given is true as well. If a1/a2 ≠ b1/b2, then the system of linear equations a1x + b1y = c1 and a2x + b2y = c2 has a unique solution. However, this reason does not explain why the given assertion is true. Therefore, Reason is also false.
Hence, the correct answer is option (D).
The given system of linear equations is:
kx – y = 2 ...(i)
6x – 2y = 3 ...(ii)
To find the value of k for which the system has a unique solution, we need to solve the equations simultaneously.
Multiplying equation (i) by 2, we get:
2kx – 2y = 4 ...(iii)
Adding (ii) and (iii), we get:
8x = 7
x = 7/8
Substituting x = 7/8 in equation (i), we get:
k(7/8) – y = 2
y = k(7/8) – 2 ...(iv)
Substituting x = 7/8 and y = k(7/8) – 2 in equation (ii), we get:
6(7/8) – 2k(7/8) + 4 = 3
7 – 14k/8 = –1
14k = 16
k = 16/14 = 8/7
Therefore, the value of k for which the system of linear equations has a unique solution is 8/7 and not 3. Hence, Assertion is false.
The Reason given is true as well. If a1/a2 ≠ b1/b2, then the system of linear equations a1x + b1y = c1 and a2x + b2y = c2 has a unique solution. However, this reason does not explain why the given assertion is true. Therefore, Reason is also false.
Hence, the correct answer is option (D).
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): The Volume and Surface Area of a sphere are related to each other by radius.Reason (R): Relation between Surface Area S and Volume V is S3 = 36πV2.- a)Both A and R are true and R is the correct explanation of A.
- b)Both A and R are true and R is not correct explanation of A.
- c)A is true but R is false.
- d)A is false but R is true.
Correct answer is option 'A'. Can you explain this answer?
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The Volume and Surface Area of a sphere are related to each other by radius.
Reason (R): Relation between Surface Area S and Volume V is S3 = 36πV2.
a)
Both A and R are true and R is the correct explanation of A.
b)
Both A and R are true and R is not correct explanation of A.
c)
A is true but R is false.
d)
A is false but R is true.
|
|
Anita Menon answered |
Volume of sphere =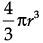 
⇒ 
⇒ 
⇒ 
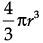
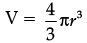
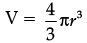
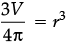
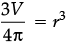
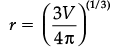
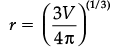
Also, S = 4πr2
⇒ 
⇒ 
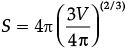
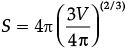
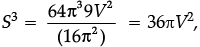which proves that assertion is correct.
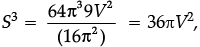which proves that assertion is correct.Therefore, Both A and R are true and R is the correct explanation for A.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): Values of x are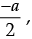 
a for a quadratic equation 2x2 + ax – a2 = 0.Reason (R): For quadratic equation ax2 + ax + c = 0,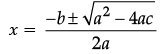 
- a)Both A and R are true and R is the correct explanation for A.
- b)Both A and R are true and R is not correct explanation for A.
- c)A is true but R is false.
- d)A is false but R is true.
Correct answer is option 'D'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): Values of x are 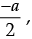a for a quadratic equation 2x2 + ax – a2 = 0.
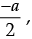a for a quadratic equation 2x2 + ax – a2 = 0.Reason (R): For quadratic equation ax2 + ax + c = 0,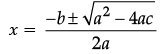
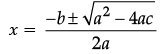
a)
Both A and R are true and R is the correct explanation for A.
b)
Both A and R are true and R is not correct explanation for A.
c)
A is true but R is false.
d)
A is false but R is true.
|
Subset Academy answered |
Reason is correct as the formula to find roots of an equation is x =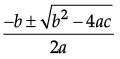 
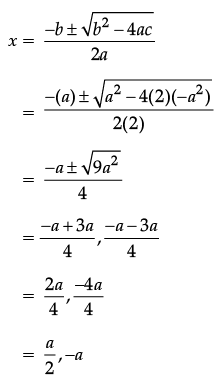
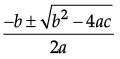
let us verify the reason on the equation
2x2 + ax – a2 = 0
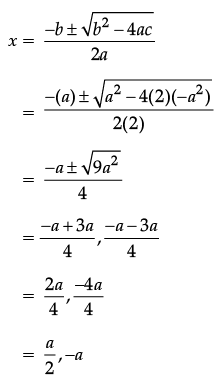
That means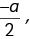 
a are not the zeroes.
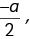a are not the zeroes.Therefore, A is false but R is true.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The lines 2x - 5y = 7 and 6x - 15y = 8 are parallel lines.Reason : The system of linear equations a1x + b1y+ c1 = 0 and a2x + b2y + c2 = 0 have infinitely many solutions if a1/a2 = b1/b2 = c1/c2- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'B'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : The lines 2x - 5y = 7 and 6x - 15y = 8 are parallel lines.
Reason : The system of linear equations a1x + b1y+ c1 = 0 and a2x + b2y + c2 = 0 have infinitely many solutions if a1/a2 = b1/b2 = c1/c2
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Ramya sengupta answered |
Assertion Explanation
The assertion states that the lines represented by the equations 2x - 5y = 7 and 6x - 15y = 8 are parallel. To determine if they are parallel, we can compare their slopes.
- The first equation can be rewritten in slope-intercept form (y = mx + b):
- 5y = 2x - 7
- y = (2/5)x - 7/5
- Slope (m1) = 2/5
- The second equation can also be transformed:
- 15y = 6x - 8
- y = (2/5)x - 8/15
- Slope (m2) = 2/5
Since both lines have the same slope (2/5), they are indeed parallel.
Reason Explanation
The reason discusses the condition for a system of linear equations to have infinitely many solutions. The condition is that the ratios of the coefficients must be equal for the lines to coincide, not merely to be parallel.
- The condition is:
- a1/a2 = b1/b2 = c1/c2
This means that if two lines are parallel, they do not share any points unless they are the same line. Therefore, the reason presented is not applicable to the assertion about parallel lines.
Conclusion
- Since both the assertion is true (the lines are parallel) but the reason does not correctly explain the assertion (it pertains to coinciding lines), the correct choice is:
Option B: Both A and R are true, but R is NOT the correct explanation of A.
The assertion states that the lines represented by the equations 2x - 5y = 7 and 6x - 15y = 8 are parallel. To determine if they are parallel, we can compare their slopes.
- The first equation can be rewritten in slope-intercept form (y = mx + b):
- 5y = 2x - 7
- y = (2/5)x - 7/5
- Slope (m1) = 2/5
- The second equation can also be transformed:
- 15y = 6x - 8
- y = (2/5)x - 8/15
- Slope (m2) = 2/5
Since both lines have the same slope (2/5), they are indeed parallel.
Reason Explanation
The reason discusses the condition for a system of linear equations to have infinitely many solutions. The condition is that the ratios of the coefficients must be equal for the lines to coincide, not merely to be parallel.
- The condition is:
- a1/a2 = b1/b2 = c1/c2
This means that if two lines are parallel, they do not share any points unless they are the same line. Therefore, the reason presented is not applicable to the assertion about parallel lines.
Conclusion
- Since both the assertion is true (the lines are parallel) but the reason does not correctly explain the assertion (it pertains to coinciding lines), the correct choice is:
Option B: Both A and R are true, but R is NOT the correct explanation of A.
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion: If A and B are two independent events and it is given that P (A) = 2/5, P(B) = 3/5, then P (A ∩ B) = 6/25.Reason : P (A ∩ B) = P (A) • P(B), where A and B are two independent events.- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'A'. Can you explain this answer?
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Assertion: If A and B are two independent events and it is given that P (A) = 2/5, P(B) = 3/5, then P (A ∩ B) = 6/25.
Reason : P (A ∩ B) = P (A) • P(B), where A and B are two independent events.
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
|
Shobha singhania answered |
Assertion and Reasoning Explanation:
Assertion:
- The assertion states that if A and B are two independent events with given probabilities, then the probability of their intersection (A ∩ B) is 6/25.
Reason:
- The reason provided is that for independent events A and B, the probability of their intersection (A ∩ B) is equal to the product of their individual probabilities, which is given by P(A) • P(B).
Explanation:
- The assertion is true because for independent events, the probability of their intersection is indeed calculated by multiplying the probabilities of the individual events.
- In this case, P(A) = 2/5 and P(B) = 3/5, so P(A ∩ B) = (2/5) • (3/5) = 6/25.
- Therefore, both the assertion and the reason are true, and the reason correctly explains why the probability of the intersection of two independent events is calculated as the product of their individual probabilities.
Therefore, the correct choice is:
Option A: Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
Assertion:
- The assertion states that if A and B are two independent events with given probabilities, then the probability of their intersection (A ∩ B) is 6/25.
Reason:
- The reason provided is that for independent events A and B, the probability of their intersection (A ∩ B) is equal to the product of their individual probabilities, which is given by P(A) • P(B).
Explanation:
- The assertion is true because for independent events, the probability of their intersection is indeed calculated by multiplying the probabilities of the individual events.
- In this case, P(A) = 2/5 and P(B) = 3/5, so P(A ∩ B) = (2/5) • (3/5) = 6/25.
- Therefore, both the assertion and the reason are true, and the reason correctly explains why the probability of the intersection of two independent events is calculated as the product of their individual probabilities.
Therefore, the correct choice is:
Option A: Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): Sum of first hundred even natural numbers divisible by 5 is 500.Reason (R): Sum of first n terms of an A.P is given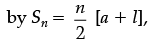 
l is last term- a)Both A and R are true and R is the correct explanation for A.
- b)Both A and R are true and R is not correct explanation for A.
- c)A is true but R is false.
- d)A is false but R is true.
Correct answer is option 'D'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): Sum of first hundred even natural numbers divisible by 5 is 500.
Reason (R): Sum of first n terms of an A.P is given 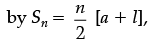l is last term
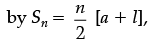l is last terma)
Both A and R are true and R is the correct explanation for A.
b)
Both A and R are true and R is not correct explanation for A.
c)
A is true but R is false.
d)
A is false but R is true.
|
|
Shaurya Goel answered |
Yes, R is true because the given formula is the apt way to find out the sum of n terms of a given AP.
Now, let's lee whether the Assertion is true or false.
Given:
n = 100
d = 10 [Since they are even multiples of 5]
a = 10 [The first even multiple of 5]
l = 200 [The last even multiple of 5]
Further working is attached below.
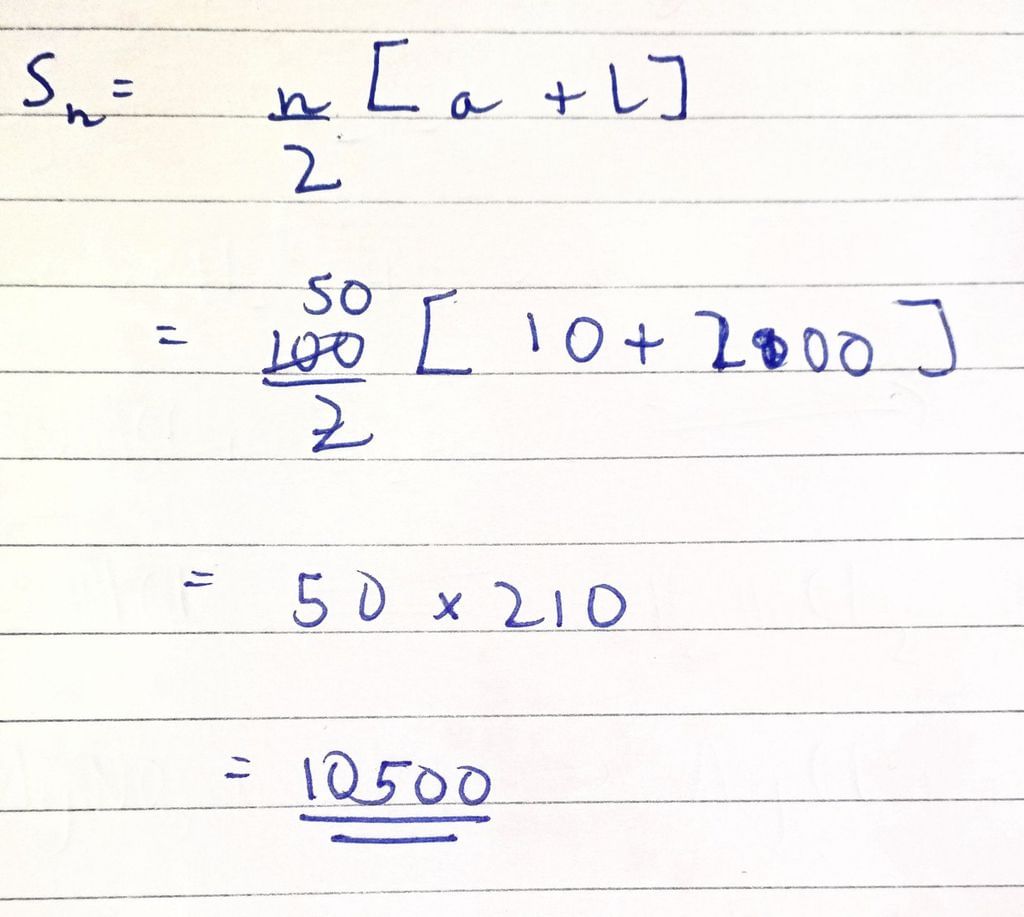
As you can see, the sum calculated and the sum given in the assertion are not similar at all.
Hence we can conclude that the given assertion is false.
∴ The correct option is:
(D) Assertion is false but Reason is true.
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:Assertion : If the radius of a cone is halved and volume is not changed, then height remains same.Reason : If the radius of a cone is halved and volume is not changed then height must become four times of the original height.- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'D'. Can you explain this answer?
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : If the radius of a cone is halved and volume is not changed, then height remains same.
Reason : If the radius of a cone is halved and volume is not changed then height must become four times of the original height.
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
|
Rohit Sharma answered |
As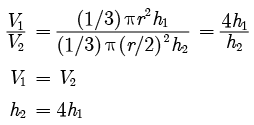
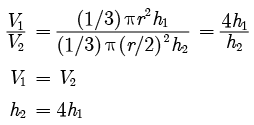
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion: The probability of getting a prime number. When a die is thrown once is 2/3.Reason : Prime numbers on a die are 2, 3, 5.- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'D'. Can you explain this answer?
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Assertion: The probability of getting a prime number. When a die is thrown once is 2/3.
Reason : Prime numbers on a die are 2, 3, 5.
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
|
Meera Rana answered |
Assertion (A) is false but reason (R) is true. When a die is thrown once, total possible outcomes = 6
and the prime numbers in it are {2,3,5}.
Total possible outcomes = 3
Probability of getting a prime = 3/6 = 1/2.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): If the equation 3x – y + 8 = 0 and 6x – ky = –16 represent coincident lines, then the value of k = 2.Reason (R): If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then the value of k is 15.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'C'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If the equation 3x – y + 8 = 0 and 6x – ky = –16 represent coincident lines, then the value of k = 2.
Reason (R): If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then the value of k is 15.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Arti khanna answered |
Explanation:
Assertion (A): If the equation 3x – y + 8 = 0 and 6x – ky = –16 represent coincident lines, then the value of k = 2.
Reason (R): If the lines given by 3x + 2ky = 2 and 2x + 5y – 1 = 0 are parallel, then the value of k is 15.
Explanation:
For two lines to be coincident, their equations must be identical. So, equating the two given equations and solving them simultaneously, we get:
3x – y + 8 = 0
6x – ky = –16
Multiplying the first equation by 2, we get:
6x – 2y + 16 = 0
Comparing this with the second equation, we get:
k = 2
Hence, Assertion (A) is true.
Now, let us consider the Reason (R). Two lines are parallel if their slopes are equal. The slope of the line 3x + 2ky = 2 is –3/2k and the slope of the line 2x + 5y – 1 = 0 is –2/5. If these lines are parallel, then their slopes are equal. Therefore, we have:
–3/2k = –2/5
Solving for k, we get:
k = 15
Hence, Reason (R) is true.
However, Reason (R) does not explain Assertion (A) because the two statements are independent of each other. Therefore, the correct answer is option (C) A is true but R is false.
Assertion (A): If the equation 3x – y + 8 = 0 and 6x – ky = –16 represent coincident lines, then the value of k = 2.
Reason (R): If the lines given by 3x + 2ky = 2 and 2x + 5y – 1 = 0 are parallel, then the value of k is 15.
Explanation:
For two lines to be coincident, their equations must be identical. So, equating the two given equations and solving them simultaneously, we get:
3x – y + 8 = 0
6x – ky = –16
Multiplying the first equation by 2, we get:
6x – 2y + 16 = 0
Comparing this with the second equation, we get:
k = 2
Hence, Assertion (A) is true.
Now, let us consider the Reason (R). Two lines are parallel if their slopes are equal. The slope of the line 3x + 2ky = 2 is –3/2k and the slope of the line 2x + 5y – 1 = 0 is –2/5. If these lines are parallel, then their slopes are equal. Therefore, we have:
–3/2k = –2/5
Solving for k, we get:
k = 15
Hence, Reason (R) is true.
However, Reason (R) does not explain Assertion (A) because the two statements are independent of each other. Therefore, the correct answer is option (C) A is true but R is false.
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion : In a circle of radius 6 cm, the angle of a sector 60o. Then the area of the sector is 186/7 cm2.Reason: Area of the circle with radius r is πr2.- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'B'. Can you explain this answer?
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Assertion : In a circle of radius 6 cm, the angle of a sector 60o. Then the area of the sector is 186/7 cm2.
Reason: Area of the circle with radius r is πr2.
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
|
Aditya Shah answered |
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
Area of the sector = θ/360 x πr2
= 60/360 x 22/7 x 6 x 6
= 132/7 = 186/7cm2.
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:Assertion : The equation x2 + 3x+1 = (x - 2)2 is a quadratic equation.Reason : Any equation of the form ax2 + bx + c = 0 where a ≠ 0 , is called a quadratic equation.- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'D'. Can you explain this answer?
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : The equation x2 + 3x+1 = (x - 2)2 is a quadratic equation.
Reason : Any equation of the form ax2 + bx + c = 0 where a ≠ 0 , is called a quadratic equation.
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
|
Anita Menon answered |
We have, x2 + 3x + 1 = (x - 2)2 = x2 - 4x + 4
⇒ x2 + 3x + 1 = x2 - 4x + 4
⇒ 7x - 3 = 0 ,
it is not of the form ax2 + 6x + c = 0
So, A is incorrect but R is correct.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:Assertion : (2 - √3) is one zero of the quadratic polynomial then other zero will be (2 + √3).Reason : Irrational zeros (roots) always occurs in pairs.- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'A'. Can you explain this answer?
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : (2 - √3) is one zero of the quadratic polynomial then other zero will be (2 + √3).
Reason : Irrational zeros (roots) always occurs in pairs.
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
|
Kiran Mehta answered |
As irrational roots/zeros always occurs in pairs therefore, when one zero is (2 - √3) then other will be (2 + √3). So, both A and R are correct and R explains A.
Assertion (A): A polynomial of degree 3 can have at most two real roots.Reason (R): According to the Fundamental Theorem of Algebra, a polynomial of degree n has exactly n roots, which can be real or complex.- a)Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
- b)Both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
- c)Assertion is correct, but Reason is incorrect.
- d)Assertion is incorrect, but Reason is correct.
Correct answer is option 'D'. Can you explain this answer?
Assertion (A): A polynomial of degree 3 can have at most two real roots.
Reason (R): According to the Fundamental Theorem of Algebra, a polynomial of degree n has exactly n roots, which can be real or complex.
a)
Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
b)
Both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
c)
Assertion is correct, but Reason is incorrect.
d)
Assertion is incorrect, but Reason is correct.
|
Kds Coaching answered |
Answer: d) Assertion is incorrect, but Reason is correct.
Explanation:
A polynomial of degree 3 can have at most three real roots. The assertion stating that it can have at most two real roots is incorrect.
A polynomial of degree 3 can have at most three real roots. The assertion stating that it can have at most two real roots is incorrect.
Assertion (A): The polynomial x2−5x + 6 can be factored as (x−2) (x−3)
Reason (R): The roots of the polynomial are 2 and 3, which can be used to express the polynomial in its factored form.- a)Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
- b)Both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
- c)Assertion is correct, but Reason is incorrect.
- d)Assertion is incorrect, but Reason is correct.
Correct answer is option 'A'. Can you explain this answer?
Assertion (A): The polynomial x2−5x + 6 can be factored as (x−2) (x−3)
Reason (R): The roots of the polynomial are 2 and 3, which can be used to express the polynomial in its factored form.
Reason (R): The roots of the polynomial are 2 and 3, which can be used to express the polynomial in its factored form.
a)
Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
b)
Both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
c)
Assertion is correct, but Reason is incorrect.
d)
Assertion is incorrect, but Reason is correct.
|
Krithika Iyer answered |
Understanding the Assertion and Reason
The given assertion and reason relate to the polynomial x^2 - 5x + 6 and its factored form.
Assertion (A):
- The polynomial x^2 - 5x + 6 can be factored as (x - 2)(x - 3).
Reason (R):
- The roots of the polynomial are 2 and 3, which can be used to express the polynomial in its factored form.
Explanation of Assertion (A):
- To factor the polynomial x^2 - 5x + 6, we look for two numbers that add up to -5 (the coefficient of x) and multiply to 6 (the constant term).
- The numbers -2 and -3 satisfy these conditions:
- (-2) + (-3) = -5
- (-2) * (-3) = 6
- Thus, the polynomial can indeed be expressed as (x - 2)(x - 3).
Explanation of Reason (R):
- The roots of the polynomial can be found by setting x^2 - 5x + 6 = 0.
- Solving, we find the roots are x = 2 and x = 3.
- These roots confirm that the polynomial can be factored as (x - 2)(x - 3).
Conclusion:
- Both the assertion and the reason are correct.
- The reason directly explains why the assertion holds true, as the roots of the polynomial provide the necessary factors.
Thus, the correct answer is option 'A': Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
The given assertion and reason relate to the polynomial x^2 - 5x + 6 and its factored form.
Assertion (A):
- The polynomial x^2 - 5x + 6 can be factored as (x - 2)(x - 3).
Reason (R):
- The roots of the polynomial are 2 and 3, which can be used to express the polynomial in its factored form.
Explanation of Assertion (A):
- To factor the polynomial x^2 - 5x + 6, we look for two numbers that add up to -5 (the coefficient of x) and multiply to 6 (the constant term).
- The numbers -2 and -3 satisfy these conditions:
- (-2) + (-3) = -5
- (-2) * (-3) = 6
- Thus, the polynomial can indeed be expressed as (x - 2)(x - 3).
Explanation of Reason (R):
- The roots of the polynomial can be found by setting x^2 - 5x + 6 = 0.
- Solving, we find the roots are x = 2 and x = 3.
- These roots confirm that the polynomial can be factored as (x - 2)(x - 3).
Conclusion:
- Both the assertion and the reason are correct.
- The reason directly explains why the assertion holds true, as the roots of the polynomial provide the necessary factors.
Thus, the correct answer is option 'A': Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): The product of two successive positive integral multiples of 5 is 300, then the two numbers are 15 and 20.Reason (R): The product of two consecutive integrals is a multiple of 2.- a)Both A and R are true and R is the correct explanation for A.
- b)Both A and R are true and R is not correct explanation for A.
- c)A is true but R is false.
- d)A is false but R is true.
Correct answer is option 'B'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The product of two successive positive integral multiples of 5 is 300, then the two numbers are 15 and 20.
Reason (R): The product of two consecutive integrals is a multiple of 2.
a)
Both A and R are true and R is the correct explanation for A.
b)
Both A and R are true and R is not correct explanation for A.
c)
A is true but R is false.
d)
A is false but R is true.
|
|
Meera Rana answered |
15 and 20 are the correct two successive positive integral multiples whose product is 300. So, this Assertion is true.
The reason is also true as n(n+1) is divisible by 2 always for all natural number n.
Therefore, Both A and R are true and R is not correct explanation for A.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): If five times the fifth term of an A.P. is equal to eight times its eighth term, then its 13th term is zero.Reason (R): Common difference of the A.P. a, a + d, a + 2d, …….., is given by d = 2nd term – 1st term.- a)Both A and R are true and R is the correct explanation for A.
- b)Both A and R are true and R is not correct explanation for A.
- c)A is true but R is false.
- d)A is false but R is true.
Correct answer is option 'B'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If five times the fifth term of an A.P. is equal to eight times its eighth term, then its 13th term is zero.
Reason (R): Common difference of the A.P. a, a + d, a + 2d, …….., is given by d = 2nd term – 1st term.
a)
Both A and R are true and R is the correct explanation for A.
b)
Both A and R are true and R is not correct explanation for A.
c)
A is true but R is false.
d)
A is false but R is true.
|
|
Arun Sharma answered |
Let the first term and common difference of the A.P. are a and d
5(a + 4d) = 8(a + 7d)
5a + 20d = 8a + 56d
3a + 36d = 0
a + 12d = 0
So, a13 = 0, which is true
Also, the expression d = 2nd term – 1st term
Therefore, Both A and R are true and R is not correct explanation for A.
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): A bag contains slips numbered from 1 to 100. If Fatima chooses a slip at random from the bag, it will either be an odd number or an even number. Since this situation has only two possible outcomes, the probability of each is 1/2.Reason (R): When we toss a coin, there are two possible outcomes: head or tail. Therefore, the probability of each outcome is 1/2.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'B'. Can you explain this answer?
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): A bag contains slips numbered from 1 to 100. If Fatima chooses a slip at random from the bag, it will either be an odd number or an even number. Since this situation has only two possible outcomes, the probability of each is 1/2.
Reason (R): When we toss a coin, there are two possible outcomes: head or tail. Therefore, the probability of each outcome is 1/2.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Anita Menon answered |
In case of assertion
From 1 to 100 numbers, there are 50 even and 50 odd numbers.
Total number of outcomes T(E) = 100
Number of outcomes favourable for event E (even numbers) = F(E) = 50
So, P(E) = 50/100 = 1/2
Similarly, the probability of getting odd numbers = 1/2.
Hence the probability of getting odd and even each = 1/2.
Hence, the given statement is true.
∴ Assertion is correct.
In case of reason: Since, there are two outcomes equal in all manners. So, the probability of both head and tail is equal to 1/2 each.
Hence, the given statement is true.
∴ Reason is correct:
Hence, both assertion and reason are correct but reason is not the correct explanation for assertion.
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): In an equilateral triangle of side 3√3 cm, then the length of the altitude is 4.5 cm.
Reason (R): If a ladder 10 cm long reaches a window 8 cm above the ground, then the distance of the foot of the ladder from the base of the wall is 6 cm.
- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'B'. Can you explain this answer?
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): In an equilateral triangle of side 3√3 cm, then the length of the altitude is 4.5 cm.
Reason (R): If a ladder 10 cm long reaches a window 8 cm above the ground, then the distance of the foot of the ladder from the base of the wall is 6 cm.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Nandini shah answered |
Assertion (A): In an equilateral triangle of side 3√3 cm, the length of the altitude is 4.5 cm.
Reason (R): If a ladder 10 cm long reaches a window 8 m above the ground, then the distance of the foot of the ladder from the base of the wall is 6 m.
To determine the correctness of the Assertion (A) and the Reason (R), let's analyze each statement separately.
Assertion (A): In an equilateral triangle of side 3√3 cm, the length of the altitude is 4.5 cm.
To find the length of the altitude in an equilateral triangle, we can use the formula:
Altitude = (sqrt(3)/2) * side length
Given that the side length of the equilateral triangle is 3√3 cm, we can substitute this value into the formula:
Altitude = (sqrt(3)/2) * 3√3
= (sqrt(3)/2) * 3 * √3
= (sqrt(3)/2) * 3 * √(3^2)
= (sqrt(3)/2) * 3 * 3
= (sqrt(3)/2) * 9
= 9√3/2
Simplifying further, we get:
Altitude = 4.5√3 cm
Therefore, Assertion (A) is true.
Reason (R): If a ladder 10 cm long reaches a window 8 m above the ground, then the distance of the foot of the ladder from the base of the wall is 6 m.
To understand this reason, we can consider a right-angled triangle formed by the ladder, the distance of the foot of the ladder from the base of the wall, and the height of the window.
Let the distance of the foot of the ladder from the base of the wall be x meters. According to the given information, the ladder is 10 m long and reaches a window 8 m above the ground. Using the Pythagorean theorem, we can establish the following relationship:
x^2 + 8^2 = 10^2
x^2 + 64 = 100
x^2 = 100 - 64
x^2 = 36
x = √36
x = 6
Therefore, the distance of the foot of the ladder from the base of the wall is 6 m.
After analyzing both the Assertion (A) and the Reason (R), we can conclude that both A and R are true, and R is the correct explanation of A. Hence, the correct answer is option B.
Reason (R): If a ladder 10 cm long reaches a window 8 m above the ground, then the distance of the foot of the ladder from the base of the wall is 6 m.
To determine the correctness of the Assertion (A) and the Reason (R), let's analyze each statement separately.
Assertion (A): In an equilateral triangle of side 3√3 cm, the length of the altitude is 4.5 cm.
To find the length of the altitude in an equilateral triangle, we can use the formula:
Altitude = (sqrt(3)/2) * side length
Given that the side length of the equilateral triangle is 3√3 cm, we can substitute this value into the formula:
Altitude = (sqrt(3)/2) * 3√3
= (sqrt(3)/2) * 3 * √3
= (sqrt(3)/2) * 3 * √(3^2)
= (sqrt(3)/2) * 3 * 3
= (sqrt(3)/2) * 9
= 9√3/2
Simplifying further, we get:
Altitude = 4.5√3 cm
Therefore, Assertion (A) is true.
Reason (R): If a ladder 10 cm long reaches a window 8 m above the ground, then the distance of the foot of the ladder from the base of the wall is 6 m.
To understand this reason, we can consider a right-angled triangle formed by the ladder, the distance of the foot of the ladder from the base of the wall, and the height of the window.
Let the distance of the foot of the ladder from the base of the wall be x meters. According to the given information, the ladder is 10 m long and reaches a window 8 m above the ground. Using the Pythagorean theorem, we can establish the following relationship:
x^2 + 8^2 = 10^2
x^2 + 64 = 100
x^2 = 100 - 64
x^2 = 36
x = √36
x = 6
Therefore, the distance of the foot of the ladder from the base of the wall is 6 m.
After analyzing both the Assertion (A) and the Reason (R), we can conclude that both A and R are true, and R is the correct explanation of A. Hence, the correct answer is option B.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : 3x - 4y = 7 and 6x - 8y = k have infinite number of solution if k = 14 .Reason : a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 have a unique solution if a1/a2 ≠ b1/b2.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'B'. Can you explain this answer?
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : 3x - 4y = 7 and 6x - 8y = k have infinite number of solution if k = 14 .
Reason : a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 have a unique solution if a1/a2 ≠ b1/b2.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
Girish mehra answered |
Explanation:
Assertion:
- The given system of linear equations 3x - 4y = 7 and 6x - 8y = 14 has an infinite number of solutions if k = 14.
Reason:
- When two linear equations in two variables have the same slope but different y-intercepts, they are parallel lines and have no common solution. However, if the two lines coincide, they have infinite solutions.
- In this case, the two equations are multiples of each other, which means they represent the same line. When k = 14, the second equation becomes 6x - 8y = 14, which is a multiple of the first equation. Hence, they represent the same line and have infinite solutions.
Therefore, both the assertion and reason are true, and the reason correctly explains why the assertion is true. Hence, option 'A' is the correct choice.
Assertion:
- The given system of linear equations 3x - 4y = 7 and 6x - 8y = 14 has an infinite number of solutions if k = 14.
Reason:
- When two linear equations in two variables have the same slope but different y-intercepts, they are parallel lines and have no common solution. However, if the two lines coincide, they have infinite solutions.
- In this case, the two equations are multiples of each other, which means they represent the same line. When k = 14, the second equation becomes 6x - 8y = 14, which is a multiple of the first equation. Hence, they represent the same line and have infinite solutions.
Therefore, both the assertion and reason are true, and the reason correctly explains why the assertion is true. Hence, option 'A' is the correct choice.
Chapter doubts & questions for Assertion & Reason Type Questions - Mathematics (Maths) Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Assertion & Reason Type Questions - Mathematics (Maths) Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Mathematics (Maths) Class 10
127 videos|584 docs|79 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup