All Exams >
Commerce >
Mathematics CUET Preparation >
All Questions
All questions of Chapter 1 - Relations and Functions for Commerce Exam
Let f and g be the function from the set of integers to itself, defined by f(x) = 2x + 1 and g(x) = 3x + 4. Then the composition of f and g is ____________- a)6x + 9
- b)6x + 7
- c)6x + 6
- d)6x + 8
Correct answer is option 'A'. Can you explain this answer?
Let f and g be the function from the set of integers to itself, defined by f(x) = 2x + 1 and g(x) = 3x + 4. Then the composition of f and g is ____________
a)
6x + 9
b)
6x + 7
c)
6x + 6
d)
6x + 8
|
|
Arjun Singhania answered |
The composition of f and g is given by f(g(x)) which is equal to 2(3x + 4) + 1.
The function, f(x) = 2x - 1 is
- a)It is not surjective
- b)It is surjective
- c)It is surjective in some intervals of the domain
- d)Insufficient information
Correct answer is option 'B'. Can you explain this answer?
The function, f(x) = 2x - 1 is
a)
It is not surjective
b)
It is surjective
c)
It is surjective in some intervals of the domain
d)
Insufficient information
|
|
Vivek Patel answered |
The function f(x) = 2x - 1 is surjective.
Explanation:
A function is surjective (also called onto) if for every element y in the codomain, there exists an element x in the domain such that f(x) = y.
In this case, the function f(x) = 2x - 1 is a linear function. For any given y value, we can find an x value such that f(x) = y:
y = 2x - 1
x = (y + 1) / 2
So, for any y value, there exists an x value that satisfies the equation. Therefore, the function is surjective.
Explanation:
A function is surjective (also called onto) if for every element y in the codomain, there exists an element x in the domain such that f(x) = y.
In this case, the function f(x) = 2x - 1 is a linear function. For any given y value, we can find an x value such that f(x) = y:
y = 2x - 1
x = (y + 1) / 2
So, for any y value, there exists an x value that satisfies the equation. Therefore, the function is surjective.
The void relation (a subset of A x A) on a non empty set A is :- a)Anti symmetric
- b)transitive
- c)Reflexive
- d)Transitive and symmetric
Correct answer is option 'D'. Can you explain this answer?
The void relation (a subset of A x A) on a non empty set A is :
a)
Anti symmetric
b)
transitive
c)
Reflexive
d)
Transitive and symmetric

|
Tejas Chawla answered |
The relation { }⊂ A x A on a is surely not reflexive.However ,neither symmetry nor transitivity is contradicted .So { } is a transitive and symmetry relation on A.
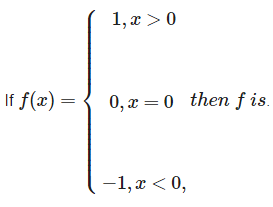
- a)the greatest integer function
- b)a constant function.
- c)the absolute value function
- d)The signum function
Correct answer is option 'D'. Can you explain this answer?
a)
the greatest integer function
b)
a constant function.
c)
the absolute value function
d)
The signum function
|
|
Om Desai answered |
By definition, The Signum function =
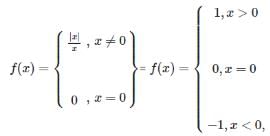
If A = {1, 2, 3, 4} and B = {1, 3, 5} and R is a relation from A to B defined by(a, b) ∈ element of R ⇔ a < b. Then, R = ?- a){(2, 3), (4, 5), (1, 3), (2, 5)}
- b){(1, 3), (1, 5), (2, 3), (2, 5), (3, 5), (4, 5)}
- c){(2, 3), (4, 5), (1, 3), (2, 5), (5, 3)}
- d){(5, 3), (3, 5), (5, 4), (4, 5)}
Correct answer is option 'B'. Can you explain this answer?
If A = {1, 2, 3, 4} and B = {1, 3, 5} and R is a relation from A to B defined by(a, b) ∈ element of R ⇔ a < b. Then, R = ?
a)
{(2, 3), (4, 5), (1, 3), (2, 5)}
b)
{(1, 3), (1, 5), (2, 3), (2, 5), (3, 5), (4, 5)}
c)
{(2, 3), (4, 5), (1, 3), (2, 5), (5, 3)}
d)
{(5, 3), (3, 5), (5, 4), (4, 5)}
|
|
Lavanya Menon answered |
A = {1, 2, 3, 4}
B = {1, 3, 5}
(a, b) ∈ element of R ⇔ a < b for all a ∈ A, b ∈ B
(a, b) pairs satisfying the condition of R are:
(1, 3), (1, 5), (2, 3), (2, 5), (3, 5), (4, 5)
So,
R = {(1, 3), (1, 5), (2, 3), (2, 5), (3, 5), (4, 5)}
B = {1, 3, 5}
(a, b) ∈ element of R ⇔ a < b for all a ∈ A, b ∈ B
(a, b) pairs satisfying the condition of R are:
(1, 3), (1, 5), (2, 3), (2, 5), (3, 5), (4, 5)
So,
R = {(1, 3), (1, 5), (2, 3), (2, 5), (3, 5), (4, 5)}
The binary relation S = Φ (empty set) on set A = {1, 2,3} is- a)transitive and relexive
- b)symmetric and relexive
- c)transitive and symmetric
- d)neither reflexive nor symmetric
Correct answer is option 'C'. Can you explain this answer?
The binary relation S = Φ (empty set) on set A = {1, 2,3} is
a)
transitive and relexive
b)
symmetric and relexive
c)
transitive and symmetric
d)
neither reflexive nor symmetric
|
|
Rohit Jain answered |
Reflexive : A relation is reflexive if every element of set is paired with itself. Here none of the element of A is paired with themselves, so S is not reflexive.
Symmetric : This property says that if there is a pair (a, b) in S, then there must be a pair (b, a) in S. Since there is no pair here in S, this is trivially true, so S is symmetric.
Transitive : This says that if there are pairs (a, b) and (b, c) in S, then there must be pair (a,c) in S. Again, this condition is trivially true, so S is transitive.
Symmetric : This property says that if there is a pair (a, b) in S, then there must be a pair (b, a) in S. Since there is no pair here in S, this is trivially true, so S is symmetric.
Transitive : This says that if there are pairs (a, b) and (b, c) in S, then there must be pair (a,c) in S. Again, this condition is trivially true, so S is transitive.
Let R = {(1, 3), (4, 2), (2, 4), (2, 3), (3, 1)} be a relations on the set A = {1, 2, 3, 4}. the relation R is- a)Reflexive
- b)transitive
- c)not symmetric
- d)a function
Correct answer is option 'C'. Can you explain this answer?
Let R = {(1, 3), (4, 2), (2, 4), (2, 3), (3, 1)} be a relations on the set A = {1, 2, 3, 4}. the relation R is
a)
Reflexive
b)
transitive
c)
not symmetric
d)
a function

|
Shubham Rajput answered |
Clearly it is not reflexive,not symmetric and not transitive
f: R → R is defined by 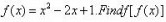
- a)x4 + 4x3 - 4x2
- b)x4 - 4x3 + 4x2
- c)x4 + 4x3 + 4x2
- d)x4 - 4x3 - 4x2
Correct answer is option 'B'. Can you explain this answer?
f: R → R is defined by 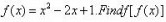
a)
x4 + 4x3 - 4x2
b)
x4 - 4x3 + 4x2
c)
x4 + 4x3 + 4x2
d)
x4 - 4x3 - 4x2
|
|
Sounak Pillai answered |
I'm sorry, could you please provide more context or a specific question related to the variable "f:R"?
Let a relation T on the set R of real numbers be T = {(a,b) : 1 + ab < 0, a,∈ R}. Then from among the ordered pairs (1,1) (1,2)(1,-2)(2,2), the only pair that belongs to T is________.- a)(2,2),
- b)(1,1),
- c)(1,-2)
- d)(1,2)
Correct answer is option 'C'. Can you explain this answer?
Let a relation T on the set R of real numbers be T = {(a,b) : 1 + ab < 0, a,∈ R}. Then from among the ordered pairs (1,1) (1,2)(1,-2)(2,2), the only pair that belongs to T is________.
a)
(2,2),
b)
(1,1),
c)
(1,-2)
d)
(1,2)
|
|
Keerthana Deshpande answered |
Relation T on R of real numbers
Definition of Relation T: T is a relation on the set R of real numbers and it is defined as T = {(a,b) : 1 ≤ ab ≤ 0, a ε R}
Explanation: This means that T is a set of ordered pairs (a,b) such that a is a real number and b is a real number, and the product of a and b is between 1 and 0, inclusive. In other words, either a and b are both negative or one of them is negative and the other is between 0 and 1.
Given ordered pairs: (1,1), (1,2), (1,-2), (2,2)
Checking which pairs belong to T:
- (1,1): 1 ≤ 1*1 ≤ 0 is false, so (1,1) does not belong to T
- (1,2): 1 ≤ 1*2 ≤ 0 is false, so (1,2) does not belong to T
- (1,-2): 1 ≤ 1*(-2) ≤ 0 is true, so (1,-2) belongs to T
- (2,2): 1 ≤ 2*2 ≤ 0 is false, so (2,2) does not belong to T
Conclusion: The only ordered pair that belongs to T is (1,-2). Therefore, the correct answer is option C, (1,-2).
Definition of Relation T: T is a relation on the set R of real numbers and it is defined as T = {(a,b) : 1 ≤ ab ≤ 0, a ε R}
Explanation: This means that T is a set of ordered pairs (a,b) such that a is a real number and b is a real number, and the product of a and b is between 1 and 0, inclusive. In other words, either a and b are both negative or one of them is negative and the other is between 0 and 1.
Given ordered pairs: (1,1), (1,2), (1,-2), (2,2)
Checking which pairs belong to T:
- (1,1): 1 ≤ 1*1 ≤ 0 is false, so (1,1) does not belong to T
- (1,2): 1 ≤ 1*2 ≤ 0 is false, so (1,2) does not belong to T
- (1,-2): 1 ≤ 1*(-2) ≤ 0 is true, so (1,-2) belongs to T
- (2,2): 1 ≤ 2*2 ≤ 0 is false, so (2,2) does not belong to T
Conclusion: The only ordered pair that belongs to T is (1,-2). Therefore, the correct answer is option C, (1,-2).
Given below is binary composition table a* b = LCM of a and b on S = { 1,2,3,4}. Then, from the table determine which one of these options is correct.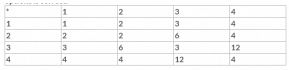
- a)a* b is a distributive binary operation
- b)a* b is an associative binary operation
- c)a* b is not a binary operation
- d)a* b is a commutative binary operation
Correct answer is option 'C'. Can you explain this answer?
Given below is binary composition table a* b = LCM of a and b on S = { 1,2,3,4}. Then, from the table determine which one of these options is correct.
a)
a* b is a distributive binary operation
b)
a* b is an associative binary operation
c)
a* b is not a binary operation
d)
a* b is a commutative binary operation
|
|
Lavanya Menon answered |
We have ∗ is defined on the set {1,2,3,4,5} by a∗b = LCM of a and b
Now, 3∗4 = LCM of 3 and 4=12
But, 12 does not belong to {1,2,3,4,5}.
Hence, ′∗′ is not a binary operation.
Now, 3∗4 = LCM of 3 and 4=12
But, 12 does not belong to {1,2,3,4,5}.
Hence, ′∗′ is not a binary operation.
Let R be the relation on the set {1, 2, 3, 4} given by R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3,3), (3,2)}. then R is- a)R is reflexive and symmetric but not transitive.
- b)R is symmetric and transitive but not reflexive.
- c)R is an equivalence relation.
- d)R is reflexive and transitive but not symmetric.
Correct answer is option 'D'. Can you explain this answer?
Let R be the relation on the set {1, 2, 3, 4} given by R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3,3), (3,2)}. then R is
a)
R is reflexive and symmetric but not transitive.
b)
R is symmetric and transitive but not reflexive.
c)
R is an equivalence relation.
d)
R is reflexive and transitive but not symmetric.

|
Pragati Dey answered |
R be the relation in the set {1,2,3,4] given by R ={(1,2),(2,2),(1,1),(4,4),(1,3),(3,3),(3,2)}
it is seen that (a,a)∈ R for every a∈{1,2,3,4}
so,R is feflexive.
it is seen that (a,b) = (b,a) ∈ R
because, (1,2)∈ R but (2,1) ∉R
so, R is not symmetric.
it is seen that (a, b), (b, c) ∈ R ⇒ (a, c) ∈ R for all a, b, c ∈ {1, 2, 3, 4}.
so, R is transitive.
Hence, R is reflexive and transitive but not symmetric.
Let R be a relation on set A of triangles in a plane.R = {(T1 , T2) : T1 , T2 element of A and T1 is congruent to T2} Then the relation R is______- a)Equivalence relation
- b)Transitive
- c)Symmetric
- d)Reflexive
Correct answer is option 'A'. Can you explain this answer?
Let R be a relation on set A of triangles in a plane.
R = {(T1 , T2) : T1 , T2 element of A and T1 is congruent to T2} Then the relation R is______
a)
Equivalence relation
b)
Transitive
c)
Symmetric
d)
Reflexive

|
Akash Singh answered |
It is equivalence relation...
as a triangle is congruent to itself that means (T1 , T1) exist in relation...which implies it is reflexive.
And also if T1 is congruent to T2 then T2 is also congruent to T1 as simple...that means (T1,T2) and (T2,T1) both belongs to relation ...which implies it is symmetric.
And is T1 is congruent to T2 and T2 is congruent to T3...then T1 is also congruent to T3.... congruency rule...that means (T1,T2),(T2,T3)and(T1,T3) belongs to relation...which implies it transitive....
this relation is reflexive, symmetric, and transitive...hence it is equivalence relation..
Let A = {1,2,3,4,5,6,7}. P = {1,2}, Q = {3, 7}. Write the elements of the set R so that P, Q and R form a partition that results in equivalence relation.- a){4,5,6}
- b){0}
- c){1,2,3,4,5,6,7}
- d){ }
Correct answer is option 'A'. Can you explain this answer?
Let A = {1,2,3,4,5,6,7}. P = {1,2}, Q = {3, 7}. Write the elements of the set R so that P, Q and R form a partition that results in equivalence relation.
a)
{4,5,6}
b)
{0}
c)
{1,2,3,4,5,6,7}
d)
{ }
|
|
Rajdeep Singh answered |
Solution:
Equivalence relation is a relation that is reflexive, symmetric and transitive. A partition of a set is a collection of non-empty subsets whose union is the original set and whose members are pairwise disjoint. Let's find the set R so that P, Q and R form a partition that results in equivalence relation.
Reflexive property: Every element is related to itself.
Symmetric property: If a is related to b, then b is related to a.
Transitive property: If a is related to b and b is related to c, then a is related to c.
Partition: P, Q and R are pairwise disjoint. Their union is A.
Elements of the set R: {4, 5, 6}
Explanation:
We can choose the set R as {4, 5, 6} because it is disjoint from both P and Q. This means that the sets P, Q and R are pairwise disjoint. Also, their union is A, which means that every element of A belongs to exactly one of the sets P, Q and R.
Now, let's check whether the partition formed by P, Q and R results in an equivalence relation.
Reflexive property: Every element is related to itself.
- For any element x in A, x belongs to exactly one of the sets P, Q and R.
- If x belongs to P or Q, then x is related to itself because P and Q are both reflexive.
- If x belongs to R, then x is related to itself because R is a set of elements.
Symmetric property: If a is related to b, then b is related to a.
- For any elements a and b in A, a belongs to exactly one of the sets P, Q and R, and b belongs to exactly one of the sets P, Q and R.
- If a and b belong to the same set (P, Q or R), then the relation between them is symmetric because P, Q and R are all symmetric.
- If a and b belong to different sets, then they are not related. Therefore, the relation between them is trivially symmetric.
Transitive property: If a is related to b and b is related to c, then a is related to c.
- For any elements a, b and c in A, a belongs to exactly one of the sets P, Q and R, b belongs to exactly one of the sets P, Q and R, and c belongs to exactly one of the sets P, Q and R.
- If a and b belong to the same set and b and c belong to the same set, then a and c belong to the same set by the transitive property of P, Q and R.
- If a and b belong to different sets or b and c belong to different sets, then a and c are not related. Therefore, the relation between them is trivially transitive.
Therefore, the partition formed by P, Q and R results in an equivalence relation.
Equivalence relation is a relation that is reflexive, symmetric and transitive. A partition of a set is a collection of non-empty subsets whose union is the original set and whose members are pairwise disjoint. Let's find the set R so that P, Q and R form a partition that results in equivalence relation.
Reflexive property: Every element is related to itself.
Symmetric property: If a is related to b, then b is related to a.
Transitive property: If a is related to b and b is related to c, then a is related to c.
Partition: P, Q and R are pairwise disjoint. Their union is A.
Elements of the set R: {4, 5, 6}
Explanation:
We can choose the set R as {4, 5, 6} because it is disjoint from both P and Q. This means that the sets P, Q and R are pairwise disjoint. Also, their union is A, which means that every element of A belongs to exactly one of the sets P, Q and R.
Now, let's check whether the partition formed by P, Q and R results in an equivalence relation.
Reflexive property: Every element is related to itself.
- For any element x in A, x belongs to exactly one of the sets P, Q and R.
- If x belongs to P or Q, then x is related to itself because P and Q are both reflexive.
- If x belongs to R, then x is related to itself because R is a set of elements.
Symmetric property: If a is related to b, then b is related to a.
- For any elements a and b in A, a belongs to exactly one of the sets P, Q and R, and b belongs to exactly one of the sets P, Q and R.
- If a and b belong to the same set (P, Q or R), then the relation between them is symmetric because P, Q and R are all symmetric.
- If a and b belong to different sets, then they are not related. Therefore, the relation between them is trivially symmetric.
Transitive property: If a is related to b and b is related to c, then a is related to c.
- For any elements a, b and c in A, a belongs to exactly one of the sets P, Q and R, b belongs to exactly one of the sets P, Q and R, and c belongs to exactly one of the sets P, Q and R.
- If a and b belong to the same set and b and c belong to the same set, then a and c belong to the same set by the transitive property of P, Q and R.
- If a and b belong to different sets or b and c belong to different sets, then a and c are not related. Therefore, the relation between them is trivially transitive.
Therefore, the partition formed by P, Q and R results in an equivalence relation.
Let A = {a, b, c} and R = {(a, a), (b, b), (c, c), (b, c)} be a relation on A. Here, R is- a)Transitive
- b)anti – symmetric
- c)symmetric
- d)reflexive
Correct answer is option 'D'. Can you explain this answer?
Let A = {a, b, c} and R = {(a, a), (b, b), (c, c), (b, c)} be a relation on A. Here, R is
a)
Transitive
b)
anti – symmetric
c)
symmetric
d)
reflexive

|
Anjali Deshpande answered |
Any relation R is reflexive if fx Rx for all x ∈ R. Here ,(a, a), (b, b), (c, c) ∈ R. Therefore , R is reflexive.
If f: R → R and g: R → R defined by f(x) = 2x + 3 and g(x) = x2 + 7, then the value of x for which f(g(x)) = 25 is- a)±3
- b)±1
- c)±4
- d)±2
Correct answer is option 'D'. Can you explain this answer?
If f: R → R and g: R → R defined by f(x) = 2x + 3 and g(x) = x2 + 7, then the value of x for which f(g(x)) = 25 is
a)
±3
b)
±1
c)
±4
d)
±2
|
|
Devika Choudhury answered |
To find the value of x for which f(g(x)) = 25, we need to substitute g(x) into the function f(x) and solve for x.
Given:
f(x) = 2x - 3
g(x) = x^2 - 7
Substituting g(x) into f(x), we have:
f(g(x)) = 2(g(x)) - 3
= 2(x^2 - 7) - 3
= 2x^2 - 14 - 3
= 2x^2 - 17
Now we can set this expression equal to 25 and solve for x:
2x^2 - 17 = 25
Adding 17 to both sides:
2x^2 = 42
Dividing both sides by 2:
x^2 = 21
Taking the square root of both sides:
x = ±√21
Since we are looking for a real value of x, we can discard the negative square root.
Therefore, the value of x for which f(g(x)) = 25 is x = √21, which is approximately 4.58.
So, the correct answer is option D) 2.
Given:
f(x) = 2x - 3
g(x) = x^2 - 7
Substituting g(x) into f(x), we have:
f(g(x)) = 2(g(x)) - 3
= 2(x^2 - 7) - 3
= 2x^2 - 14 - 3
= 2x^2 - 17
Now we can set this expression equal to 25 and solve for x:
2x^2 - 17 = 25
Adding 17 to both sides:
2x^2 = 42
Dividing both sides by 2:
x^2 = 21
Taking the square root of both sides:
x = ±√21
Since we are looking for a real value of x, we can discard the negative square root.
Therefore, the value of x for which f(g(x)) = 25 is x = √21, which is approximately 4.58.
So, the correct answer is option D) 2.
Let A = {1,2,3,4} and B = { x,y,z}. Then R = {(1,x) , ( 2,z), (1,y), (3,x)} is- a)relation from B to A
- b)Is not a relation
- c)relation from A to B
- d)relation from B to B
Correct answer is option 'C'. Can you explain this answer?
Let A = {1,2,3,4} and B = { x,y,z}. Then R = {(1,x) , ( 2,z), (1,y), (3,x)} is
a)
relation from B to A
b)
Is not a relation
c)
relation from A to B
d)
relation from B to B
|
|
Om Desai answered |
Let a set of A = (1, 2, 3, 4) and set B (x, y, z) so. set A of all elements in set B then the relation of A to B
If f : A→B and g : B →C be two functions. Then, composition of f and g, gof : A→C is defined a- a)(gof)(x) = f(g(x)), for all x ∈ A
- b)(gof)(x) = g(f(x)), for all x ∈ A
- c)(gof)(x) = g(x), for all x ∈ A
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
If f : A→B and g : B →C be two functions. Then, composition of f and g, gof : A→C is defined a
a)
(gof)(x) = f(g(x)), for all x ∈ A
b)
(gof)(x) = g(f(x)), for all x ∈ A
c)
(gof)(x) = g(x), for all x ∈ A
d)
None of the above
|
|
Rashi Nair answered |
Please provide additional details or context for me to assist you better.
Find the number of bijective functions from set A to itself when A contains 106 elements.- a)106
- b)1062
- c)106!
- d)2106
Correct answer is option 'D'. Can you explain this answer?
Find the number of bijective functions from set A to itself when A contains 106 elements.
a)
106
b)
1062
c)
106!
d)
2106
|
|
Varun Kapoor answered |
For a finite set S, there is a bijection between the set of possible total orderings of the elements and the set of bijections from S to S. That is to say, the number of permutations of elements of S is the same as the number of total orderings of that set, i.e. n!.
We have the set A that contains 106 elements, so the number of bijective functions from set A to itself is 106!.
We have the set A that contains 106 elements, so the number of bijective functions from set A to itself is 106!.
Let R be an equivalence relation on Z, the set of integers.R = {(a,b): a,b∈Z and a – b is a multiple of 3} The Equivalence class of [1] is- a){..-7,-4,2,5,8,.}
- b){.-4,-1,2,5,8,.}
- c){.-6,-1,3,5,9,.}
- d){…..-5,-2,1,4,7,.}
Correct answer is option 'D'. Can you explain this answer?
Let R be an equivalence relation on Z, the set of integers.
R = {(a,b): a,b∈Z and a – b is a multiple of 3} The Equivalence class of [1] is
a)
{..-7,-4,2,5,8,.}
b)
{.-4,-1,2,5,8,.}
c)
{.-6,-1,3,5,9,.}
d)
{…..-5,-2,1,4,7,.}
|
|
Gaurav Kumar answered |
Correct Answer :- d
Explanation : R = (a,b) : 3 divides (a-b)
⇒(a−b) is a multiple of 3.
To find equivalence class 1, put b=1
So, (a−0) is a multiple of 3
⇒ a is a multiple of 3
So, In set z of integers, all the multiple
of 3 will come in equivalence
class {1}
Hence, equivalence class {1} = {3x+1}
{-5,-2,1,4,7}
Chapter doubts & questions for Chapter 1 - Relations and Functions - Mathematics CUET Preparation 2025 is part of Commerce exam preparation. The chapters have been prepared according to the Commerce exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Commerce 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chapter 1 - Relations and Functions - Mathematics CUET Preparation in English & Hindi are available as part of Commerce exam.
Download more important topics, notes, lectures and mock test series for Commerce Exam by signing up for free.
Mathematics CUET Preparation
145 videos|67 docs|105 tests
|





















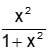 . Then f is
. Then f is













